Как найти наибольшее и наименьшее значение функции через производную: Наибольшее и наименьшее значение функций (профильный уровень, 12)

По графику производной найти наибольшее значение функции

Рассмотрим задания, в которых дан график производной функции и требуется найти, в какой точке данного отрезка эта функция принимает наибольшее значение.

№1

На рисунке изображён график производной функции f(x), определённой на интервале (-14;8). В какой точке отрезка [-11;-8] функция f(x) принимает наибольшее значение?

Решение:

Выделяем отрезок [-11;-8].

На этом отрезке производная f'(x) принимает положительные значения.

Следовательно, функция f(x) на этом отрезке возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:

x₁,x₂ ∈[-11;-8], x₂>x₁, ⇒ f(x₂)>f(x₁).

Поэтому наибольшее значение функция f(x) на отрезке принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=-8.

Ответ: -8.

№2

На рисунке изображён график производной функции f(x), определённой на интервале (-7;9).

В какой точке отрезка [4;8] функция f(x) принимает наибольшее значение?

Решение:

Выделяем отрезок [4;8].

Так как этом отрезке производная f'(x)<o, то функция f(x) на [4;8] убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:

x₁,x₂ ∈[4;8], x₂>x₁, ⇒ f(x₂)<f(x₁).

Поэтому наибольшее значение f(x) принимает в этом случае при наименьшем значении аргумента, то есть на левом конце отрезка, при x=4.

Ответ: 4.

№3

Функция y=f(x) определена на промежутке (-5;9). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наибольшее значение.

Решение:

В точке с абсциссой x=6 производная меняет знак с плюса на минус.

Следовательно, x=6 — точка максимума.

Производная f'(x) существует на всём интервале (-5;9), следовательно, функция f(x) непрерывна на (-5;9).

Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума x_o и это точка максимума, то на (a;b) функция принимает своё наибольшее значение в точке x_o.

Таким образом, функция f(x) на интервале (-5;9) принимает наибольшее значение в точке x=6.

Ответ: 6.

№4

Функция y=f(x) определена и непрерывна на отрезке [-1;9]. На рисунке изображён график её производной. Найти точку x_o, в которой функция принимает наибольшее значение, если f(-1)≥f(9).

Решение:

На промежутках (-1;3) и (8;9) производная f'(x)>0, поэтому на этих промежутках функция f(x) возрастает.

На промежутке (3;9) производная f'(x)<0, поэтому на (3;9) функция f(x) убывает.

Так как функция определена и непрерывна на отрезке [-1;9], то точки -1, 3, 8 и 9 можно включать в промежутки монотонности.

Следовательно, на отрезках [-1;3] и [8;9] функция f(x) возрастает, на отрезке [3;8] — убывает.

На промежутках возрастания наибольшее значение функция принимает на правом конце отрезка. На [-1;3]  наибольшее значение f(x) принимает в точке x=3 (точке максимума), на [8;9] — в точке x=9.

Так как на [-1;3] f(x) возрастает, то f(3)>f(-1). По условию, f(-1)≥f(9), значит f(3)>f(9).

Таким образом, наибольшее значение функции f(x) принимает в точке x=3.

Ответ: 3.

Найти наибольшее и наименьшее значение функции на отрезке.

Пример 1:

Найти наибольшее и наименьшее значения функции y=f(x) на отрезке [a, b].

Решение от преподавателя:

Пример 2:

Найти наибольшее и наименьшее значение функции на отрезке, если

Решение от преподавателя:

Находим первую производную функции:

Приравниваем ее к нулю:

Данная критическая точка принадлежит интервалу

Вычисляем значения функции на концах отрезка и в критической точке x=1.   

 

Пример 3:

Найти наименьшее и наибольшее значения функции y=f(x) на заданном отрезке [a;b]:

Решение от преподавателя:

Пример 4:

Найти наибольшее и наименьшее значение функции на отрезке.

Решение от преподавателя:

Наибольшим, наименьшим значением функции на отрезке могут быть точки минимума, максимума или значения функции на концах отрезка.

1. Находим стационарные точки:

Для нахождения стационарных точек найдем первую производную и приравняем ее к нулю

2) Выбираем из полученных стационарных точек те, которые принадлежат заданному отрезку.

Найденная точка х =-1 принадлежат отрезку [-3; 3].

Найденная точка х =3 принадлежат отрезку [-3; 3].

Найдем значение функции в стационарной точке и на концах отрезка.

3) Из полученных значений функции выбираем наибольшее и наименьшее значения.

Наибольшее значение: y(3) = 3.

Наименьшее значение: y(-1) = 1.

Ответ: y_наиб =3,   y_наим =1.

Пример 5:

Найдите наибольшее и наименьшее значения функции

 

на отрезке [-6; -1].

Решение от преподавателя:

Пример 6:

Найти наибольшее и наименьшее значение функции на отрезке.

Решение от преподавателя:

Наибольшим, наименьшим значением функции на отрезке могут быть точки минимума, максимума или значения функции на концах отрезка.

1. Находим стационарные точки:

Для нахождения стационарных точек найдем первую производную и приравняем ее к нулю

2) Выбираем из полученных стационарных точек те, которые принадлежат заданному отрезку.

Найденная точка х = e принадлежат отрезку 

Найдем значение функции в стационарной точке и на концах отрезка.

3) Из полученных значений функции выбираем наибольшее и наименьшее значения.

Наибольшее значение: y(e²) = 2e²

Наименьшее значение: y() =

Ответ: y_наиб = 2e²,   y_наим =

Пример 7:

Определить производную функции  в точке х₀ = — 1. Найти наибольшее и наименьшее значения функции на отрезке [-2; 3] и соответствующие  значения аргумента.

Решение от преподавателя:

Пример 8:

Найти наибольшее и наименьшее значение функции  на отрезке .

Решение от преподавателя:

Функция определена на всем отрезке.

Находим производную:

Вычисляем значение функции в этой точке, принадлежащих заданному интервалу:

Находим значение функции на границах:

Наименьшее значение функция достигает в точке x=1 и x=5

Наибольшее значение функция достигает в точке x=2.

Ответ:

Пример 9:

Решение от преподавателя:

 

Пример 10:

Найти наибольшее и наименьшее значение функции на отрезке:

Решение от преподавателя:

В этой задаче используется теорема о том, что непрерывная функция достигает своего наибольшего и наименьшего значений на отрезке: либо в критических точках, где производная обращается в нуль или не существует; либо на концах отрезка. Таким образом, для того, чтобы найти наибольшее и наименьшее значения функции на данном отрезке, необходимо найти её значения в критических точках и на концах отрезка, а затем сравнить эти значения.

Найдем производную данной функции

Приравняем производную к нулю и найдем критические точки

Точка x=2 заданному отрезку.

Вычислим значения функции в найденной точке и на концах отрезка:

Сравнивая полученные значения, можем заключить, что наибольшее значение равно f(4) = 54, а наименьшее значение равно f(2) = 46.

Ответ: Наибольшее значение функции на отрезке равно f(4) = 54.

           Наименьшее значение функции на отрезке равно f(2) = 46.

Как найти максимальную и минимальную точки с помощью дифференцирования

Следующие шаги были бы полезны для нахождения максимального и минимального значения функции с использованием первой и второй производной.

Шаг 1: 

Пусть f(x) f(x) — функция. Найдите первую производную от f(x), которая равна f'(x).

Шаг 2 : 

Приравняйте первую производную f'(x) к нулю и найдите x, которые называются критическими числами.

Шаг 3 : 

Найдите вторую производную от f(x), которая равна f»(x). 

Шаг 4: 

Подставьте критические числа, найденные на шаге 2, во вторую производную f»(x).

Шаг 5:

Если f»(x) < 0 для некоторого значения x, скажем, x = a , то функция f(x) максимальна при x = a.

Если f»(x) > 0 для некоторого значения x, скажем, x = b, то функция f(x) минимальна при x = b. 

Шаг 6: 

Чтобы получить максимальное и минимальное значения замена функции x = a и x = b в f(x). 

Максимальное значение = f(a)

Минимальное значение = f(b)

Шаг 7: 

Максимальная точка: (a, f(a))

Минимальная точка: (b, f(b))

Найдите максимум и минимум Точки следующих функций:

Пример 1:

2x ³ — 3x ² — 12x + 5

Решение:

. 12x + 5.

f'(x) = 2(3x ² ) — 3(2x) — 12(1) + 0

f'(x) = 6x ² — 6x — 12

Приравниваем f'(x) к нулю,

f'(x) = 0

 6x ² — 6x — 12 = 0

2 Разделим обе части на 0 4.

² — х — 2 = 0

(х — 2)((х + 1) = 0

х — 2 = 0 или х + 1 = 0

х = 2 или х = -1

Найти вторая производная:

f'(x) = 6x ²  — 6x — 12

f»(x) = 6(2x) — 6(1) — 0

f»(x) = 12 x — 6

Подставить x = 2 в f»(x).

f»(2)  =  12(2) — 6

=  24 — 6

f»(2)  =  18 > 0 Минимум

Чтобы найти минимальное значение, подставьте x = 2 в f( Икс).

f(x) = 2x ³  — 3 x ²  — 12 x + 5

f (2) = 2(2) ³  — 3(2) ^{2 (2) + 1 5}

= 2(8) — 3(4) — 24 + 5

= 16 — 12 — 24 + 5

= 21 — 36

= -15

2 = -15

2 = -15

2 f»(x).

f»(-1)  =  12(-1) -6

  =  -12 — 6

f»(-1) = -18 > 0 Максимум

Чтобы найти максимальное значение, подставьте x = -1 в f(x).

f(x) = 2x ³  — 3x ²  — 12 x + 5 1) + 5

= 2(-1) — 3(1) + 12 + 5

= -2 — 3 + 12 + 5

= -5 + 17

= 3

Таким образом,

максимальная точка = (-1, 12)

Минимальная точка = (2, 15)

Пример 2:

Найдите максимальное и минимальное значение функции

x ³ — 3x ² — 9x + 12

Решение:

(x) = x ³ — 3x ² — 9 x + 12.

f'(x) = 3x ² — 3(2x) — 9(1) + 0

f'(x ) = 3x ² — 6x — 9

f'(x) = 0

3x ² — 6x — 9 = 0

Разделите обе части на 3.

x ² — 2x — 3 = 0

(x + 1)(x — 3) = 0

x + 1 = 0 или x — 3 = 0

x = -1 или x = 3

Найдите вторую производную:

f'(x) = 3x ² — 6x — 9

f»(x) = 3(2x) — 6(1) — 0

f»(x) = 6x — 6

Подставить x = -1 в f»(x).

f»(-1) = 6(-1) — 6

= -6 — 6

f»(-1) ) = -12 < 0 ----> f(x) максимальное

Чтобы найти максимальное значение, подставьте x = -1 в f(x)

f(x) = x ³ — 3x ² — 9 x + 12 ) + 12

= -1 — 3(1) + 9 + 12

= -1 — 3 + 9 + 12

= -4 + 21

= 17

3 в Заменить «(x).

f»(3) = 6(3) — 6

  = 18 — 6

 f»(3) = 12 > 0 —-> f(x) минимум

Чтобы найти минимальное значение, подставьте x = 3 в f(x).0004

f(x) = x ³  — 3x ²  — 9 x + 12

f(3) = 3 ³ — 3(3) ² — 9(3) + 12 900 27 — 3(9) — 27 + 12

= 27 — 27 — 27 + 12

= -27 + 12

= -15

Следовательно,

максимум = 7 () балл

минимальный балл = (3, -15)

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены.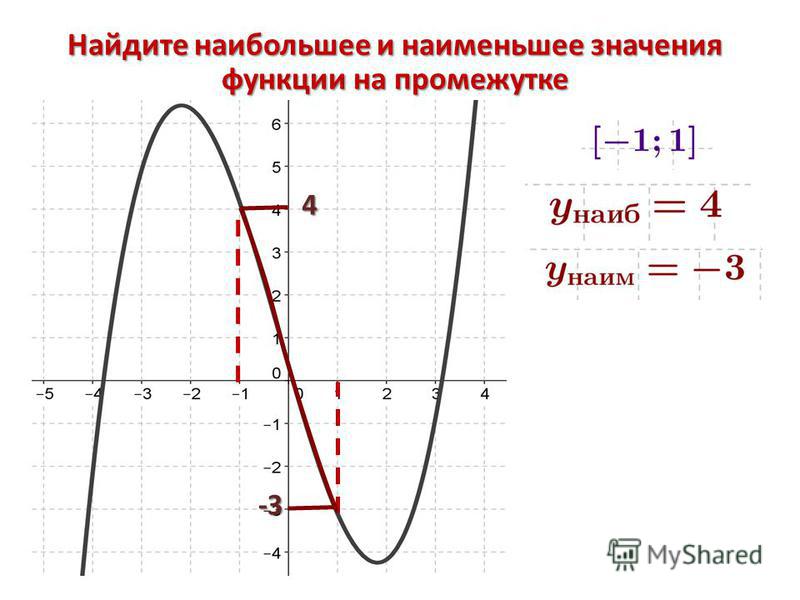

онлайнmath5all.com 92\ле 225$.

Найдя первые частные производные, я обнаружил, что $(1, 0)$ является критической точкой, и я обнаружил, что это локальный минимум из теста второй производной. Таким образом, минимальное значение $f(x, y)$ будет равно $-7$ в точке $(1, 0)$.

Однако я не понимаю, как найти максимальное значение и точку. Поскольку у этой функции нет точки локального максимума, я подумал, что ответ будет просто на границах неравенства. Однако кажется, что ни точка $(15, 0)$, ни $(0, 15)$ не дают правильного ответа.

Если кто-нибудь знает, как мне решить эту проблему, и может дать отзыв, я был бы очень благодарен!

• исчисление
• многомерное исчисление
• оптимизация
• частная производная

$\endgroup$

3

$\begingroup$

Согласно методу параметров Лагранжа градиент $f$ будет нормален к границе в экстремальном значении.

Нормаль к окружности в заданной точке $(x,y)$ — это просто вектор положения $(x,y)$, поэтому вам нужно искать точки, где $\nabla f$ является кратным этому вектору. 92=225$

Это верно тогда и только тогда, когда ($\lambda = 6$ или $y=0$).

Если $\lambda = 6$, то легко видеть, что тогда $x=-2$ и $y$ определяется побочным условием.

Если $y=0$, то $x$ определяется боковым условием (а $\lambda$ — уравнением для $x$ и $\lambda$).

Подстановка $x$ и $y$ в функцию покажет, есть ли у вас максимум или минимум.

$\endgroup$

1 92 = 225 -4 = 221$$ $$y = \sqrt{221}$$

Возвращение $x=-2$ и $y=\sqrt{221}$ в исходную функцию

$$f(x,y) = 674$$

$\endgroup$

10

$\begingroup$

Если вы не знаете или хотите использовать множители Лагранжа, как в ответе Томаса, и хотите найти локальные экстремумы на границе, чтобы ничего не пропустить, то вы можете либо обрабатывать конечные точки с помощью $x=\pm15$, которые Саухард Шарма не упомянул в своем ответе, или вы можете дать кругу более естественную параметризацию.