Обратная матрица онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор позволит вам легко найти обратную матрицу при помощи матрицы алгебраических дополнений, а так же получить подробное решение. Калькулятор вычисляет обратную матрицу для матриц размерности от 2 × 2 до 9 × 9.
 При помощи данного калькулятора
вы сможете быстро научиться находить обратную матрицу, благодаря подробно составленному алгоритму решения
При помощи данного калькулятора
вы сможете быстро научиться находить обратную матрицу, благодаря подробно составленному алгоритму решенияМатрица размерности m × n – это таблица чисел у которой m строк и n столбцов.
Элементы матрицы обозначаются как aij, где i – номер строки, j – номер столбца.
Матрица A-1 называется обратной к матрице A, если A ⋅ A-1 = A-1 ⋅ A = E, где E — единичная матрица.
Для нахождения обратной матрицы необходимо, чтобы матрица A была квадратной и не равнялась нулю.
Как найти обратную матрицу с помощью матрицы алгебраических дополнений
Обратная матрица A обозначается как A-1.
Обратная матрица A-1 существует только если матрица A квадратная и ее определитель не равен нулю.
При умножении сходной матрицы A на обратную матрицу A-1 получается единичная матрица E.
AA-1 = E
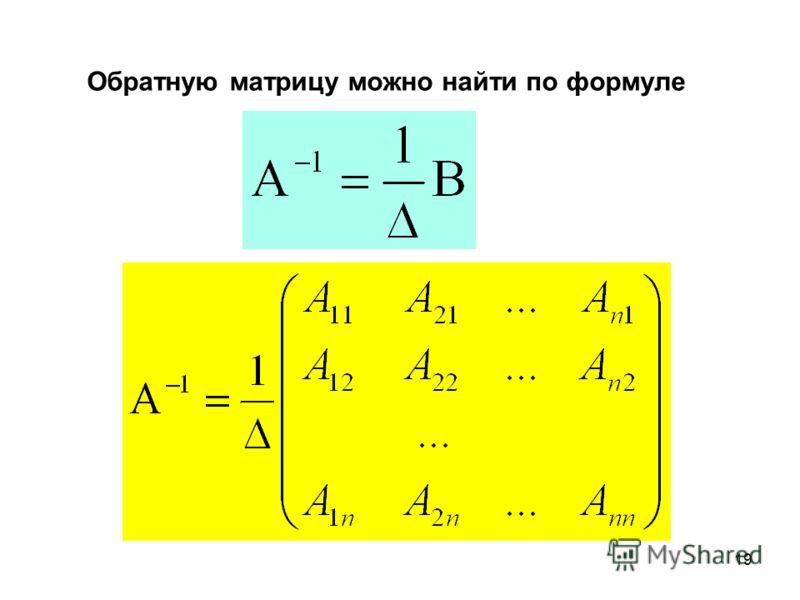
Обратная матрица A-1 определяется как:
где,
adj(A) — присоединенная матрица, составленная из алгебраических дополнений
det(A) — определитель матрицы A
Присоединённая матрица adj(A), составленная из алгебраических дополнений определяется как:
где,
Mij — дополнительный минор (определитель матрицы), полученный из исходной матрицы A путем вычеркивания i-й строки и j-го столбца
Чтобы найти обратную матрицу A-1 матрицы A необходимо:
1. Вычислить определитель матрицы A.
Вычислить определитель матрицы A.
2. Найти присоединённую матрицу adj(A).
3. Транспонировать присоединённую матрицу adj(A).
4. Разделить все элементы присоединённой матрицы adj(A) на определитель det(A) исходной матрицы A.
Приведем пример, найдем обратную матрицу A
Найдем обратную матрицу для матрицы A при помощи матрицы алгебраических дополнений.
adj(A) — присоединенная матрица составленная из алгебраических дополнений
det(A) — определитель матрицы A
1. Найдем определитель для матрицы A
det A = 5
(Если вы хотите получить детальное решение нахождения определителя, то воспользуйтесь калькулятором для нахождения определителя матрицы)
2. Найдем присоединенную матрицу adj(A) составленную из алгебраических дополнений. Для этого каждый элемент исходной матрицы aij заменим на его алгебраическое дополнение Aij
Mij — дополнительный минор, полученный из исходной матрицы A путем вычеркивания i-й строки и j-го столбца
Исходная матрицы A состоит из 4 элементов, следовательно нам необходимо найти 4 дополнительных миноров Mij
M11 =
=
= 1
M12 =
=
= -2
M21 =
=
= 0
M22 =
=
= 5
Теперь запишем значение всех элементов присоединенной матрицы adj(A)
A11 = (-1)1 + 1 ⋅ M11 = (-1)2 ⋅ 1 = 1
A12 = (-1)1 + 2 ⋅ M12 = (-1)3 ⋅ (-2) = 2
A21 = (-1)2 + 1 ⋅ M21 = (-1)3 ⋅ 0 = 0
A22 = (-1)2 + 2 ⋅ M22 = (-1)4 ⋅ 5 = 5
| adj(A) = |
| = |
3. Транспонируем присоединенную матрицу adj(A)
Транспонируем присоединенную матрицу adj(A)
| adj(A)T = |
4. Разделим все элементы матрицы adj(A)T на определитель исходной матрицы A
| A-1 = |
|
| A-1 = |
|
| A-1 = |
|
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Решение высшей математики онлайн
‹— Назад
Определение 14.8 Матрица называется обратной матрицей для квадратной матрицы , если .
Из определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица (иначе одно из произведений или было бы не определено).
Обратная матрица для матрицы обозначается . Таким образом, если существует, то .
Таким образом, если существует, то .
Из определения обратной матрицы следует, что матрица является обратной для матрицы , то есть . Про матрицы и можно говорить, что они обратны друг другу или взаимно обратны.
Предложение 14.20 Если матрица имеет обратную, то и .
Доказательство. Так как определитель произведения матриц равен произведению определителей ( предложение 14.7), то . По следствию 14.1 , поэтому , что невозможно при . Из предыдущего равенства следует также .
Последнее предложение можно сформулировать в следующем виде.
Если определитель матрицы равен нулю, то обратная к ней не существует.
Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Определение 14.9 Квадратную матрицу назовем вырожденной или особенной матрицей, если , и невырожденной или неособенной матрицей, если .
Предложение 14.21 Если обратная матрица существует, то она единственна.
Доказательство. Пусть две матрицы и являются обратными для матрицы . Тогда
и
Следовательно, .
Предложение 14.22 Если квадратная матрица является невырожденной, то обратная для нее существует и
| (14.14) |
где — алгебраические дополнения к элементам .
Доказательство. Так как для невырожденной матрицы правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, что и что . Докажем первое из этих равенств, второе доказывается аналогично.
Так как для невырожденной матрицы правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, что и что . Докажем первое из этих равенств, второе доказывается аналогично.
Пусть . Найдем элементы матрицы , учитывая, что :
Если , то по предложению 14.17 сумма справа равна нулю, то есть при .
Если , то
Сумма справа представляет собой разложение определителя матрицы по -ой строке (предложение 14.16). Таким образом,
Итак, в матрице диагональные элементы равны 1, а остальные равны нулю, то есть .
Результаты предложений 14.20, 14.21, 14.22 соберем в одну теорему.
Теорема 14.1 Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица — невырожденная, обратная матрица единственна, и справедлива формула (14. 14).
14).
Замечание 14.12 Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца, а второй — номер строки, в которые нужно записать вычисленное алгебраическое дополнение.
Пример 14.7 Найдите обратную матрицу для матрицы .
Решение. Находим определитель
Так как , то матрица — невырожденная, и обратная для нее существует.
Находим алгебраические дополнения:
Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй — строке:
| (14.15) |
Полученная матрица и служит ответом к задаче.
Замечание 14.13 В предыдущем примере было бы точнее ответ записать так:
| (14.16) |
Однако запись (14.15) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (14.15) предпочтительнее, если элементы матриц — целые числа. И наоборот, если элементы матрицы — десятичные дроби, то обратную матрицу лучше записать без множителя впереди.
Замечание 14.14 При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
Пример 14.8 Найдите обратную матрицу для матрицы .
Решение.
— существует.
Ответ: .
Нахождение обратной матрицы по формуле (14.14) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Функция МОБР
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще. ..Меньше
..Меньше
Функция МОБР возвращает обратную матрицу для матрицы, храняной в массиве.
Примечание: Если у вас установлена текущая версия Microsoft 365, можно просто ввести формулу в верхней левой ячейке диапазона вывода и нажать клавишу ВВОД, чтобы подтвердить использование формулы динамического массива. Иначе формулу необходимо вводить с использованием прежней версии массива, выбрав диапазон вывода, введя формулу в левой верхней ячейке диапазона и нажав клавиши CTRL+SHIFT+ВВОД для подтверждения. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Синтаксис
МОБР(массив)
Аргументы функции МОБР описаны ниже.
Замечания
- org/ListItem»>
-
Если какие-либо ячейки в массиве пустые или содержат текст, функции МОБР возвращают #VALUE! ошибку «#ВЫЧИС!».
-
МоБР также возвращает #VALUE! если массив не имеет равного числа строк и столбцов.
-
Обратные матрицы, такие как определители, обычно используются для решения систем математических уравнений с несколькими переменными. Произведением матрицы и обратной является матрица удостоверений — квадратный массив, в котором диагональные значения равны 1, а все остальные — 0.

-
В качестве примера вычисления обратной матрицы, рассмотрим массив из двух строк и двух столбцов A1:B2, который содержит буквы a, b, c и d, представляющие любые четыре числа. В таблице приведена обратная матрица для массива A1:B2.
Массив может быть задан как диапазон ячеек, например A1:C3 как массив констант, например {1;2;3: 4;5;6: 7;8;9} или как имя диапазона или массива.
|
Столбец A |
Столбец B |
|
|---|---|---|
|
Строка 1 |
d/(a*d-b*c) |
b/(b*c-a*d) |
|
Строка 2 |
c/(b*c-a*d) |
a/(a*d-b*c) |
- org/ListItem»>
-
Некоторые квадратные матрицы невозможно инвертировать и возвращают #NUM! в функции МОБР. Определител непревратимой матрицы 0.
Функция МОБР производит вычисления с точностью до 16 значащих цифр, что может привести к незначительным ошибкам округления.
Примеры
Чтобы указанные выше формулы вычислялись правильно, нужно вводить их в виде формул массивов. После ввода формулы нажмите ввод, если у вас есть текущая Microsoft 365 подписка. в противном случае нажмите CTRL+SHIFT+ВВОД. Если формула не будет введена как формула массива, возвращается единственный результат.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Вычислить обратную комплексную матрицу
|
|
||||||||||||||||||
Формула обратной матрицы второго порядка.
 {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы
Метод Гаусса-Жордана
Возьмём две матрицы: саму A и единичную E . Приведём матрицу A к единичной матрице методом Гаусса-Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам, но не в перемешку). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A −1 .
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i {\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
Λ
1
⋅
⋯
⋅
Λ
n
⋅
A
=
Λ
A
=
E
⇒
Λ
=
A
−
1
{\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}}
. {-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
где adj (A) {\displaystyle {\mbox{adj}}(A)} — присоединенная матрица ;
Сложность алгоритма зависит от сложности алгоритма расчета определителя O det и равна O(n²)·O det .
Использование LU/LUP-разложения
Матричное уравнение
A
X
=
I
n
{\displaystyle AX=I_{n}}
для обратной матрицы
X
{\displaystyle X}
можно рассматривать как совокупность
n
{\displaystyle n}
систем вида
A
x
=
b
{\displaystyle Ax=b}
. Обозначим
i
{\displaystyle i}
-ый столбец матрицы
X
{\displaystyle X}
через
X
i
{\displaystyle X_{i}}
; тогда
A
X
i
=
e
i
{\displaystyle AX_{i}=e_{i}}
,
i
=
1
,
…
,
n
{\displaystyle i=1,\ldots ,n}
,поскольку
i
{\displaystyle i}
-м столбцом матрицы
I
n
{\displaystyle I_{n}}
является единичный вектор
e
i
{\displaystyle e_{i}}
. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³) .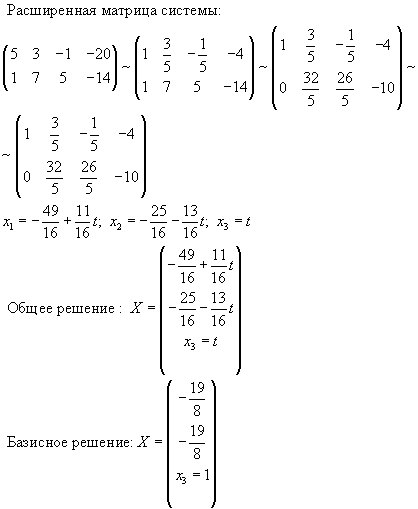 {-1} = \frac{1}{\det(\mathbf{A})} \begin& \!\!-b \\ -c & \,a \\ \end{bmatrix} = \frac{1}{ad — bc} \begin{bmatrix} \,\,\,d & \!\!-b\\ -c & \,a \\ \end{bmatrix}.}
{-1} = \frac{1}{\det(\mathbf{A})} \begin& \!\!-b \\ -c & \,a \\ \end{bmatrix} = \frac{1}{ad — bc} \begin{bmatrix} \,\,\,d & \!\!-b\\ -c & \,a \\ \end{bmatrix}.}
Обращение матрицы 2х2 возможно только при условии, что a d − b c = det A ≠ 0 {\displaystyle ad-bc=\det A\neq 0} .
Пусть имеется квадратная матрица n-го порядка
Матрица А -1 называется обратной матрицей по отношению к матрице А, если А*А -1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…А n) называется невырожденной , если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы
- Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
- Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
- Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
- Записать обратную матрицу А -1 , которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А -1
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А -1 .
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.
Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Пример 2
Решить уравнение АХ = В, если
Решение : Так как обратная матрица равняется (см. пример 1)
пример 1)
Матричный метод в экономическом анализе
Наряду с другими в находят применение также матричные методы . Эти методы базируются на линейной и векторно-матричной алгебре. Такие методы применяются для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений.
В процессе применения матричных методов анализа можно выделить несколько этапов.
На первом этапе осуществляется формирование системы экономических показателей и на ее основе составляется матрица исходных данных , которая представляет собой таблицу, в которой по ее отдельным строкам показываются номера систем (i = 1,2,….,n) , а по вертикальным графам — номера показателей (j = 1,2,….,m) .
На втором этапе по каждой вертикальной графе выявляется наибольшее из имеющихся значений показателей, которое и принимается за единицу.
После этого все суммы, отраженные в данной графе делят на наибольшее значение и формируется матрица стандартизированных коэффициентов .
На третьем этапе все составные части матрицы возводят в квадрат. Если они имеют различную значимость, то каждому показателю матрицы присваивается определенный весовой коэффициент k . Величина последнего определяется экспертным путем.
На последнем, четвертом этапе найденные величины рейтинговых оценок R j группируются в порядке их увеличения или уменьшения.
Изложенные матричные методы следует использовать, например, при сравнительном анализе различных инвестиционных проектов, а также при оценке других экономических показателей деятельности организаций.
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Определение 1
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Пример 1
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
. . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи : А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.
X = x 1 x 2 ⋮ x n — столбец неизвестных,
B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1:
A — 1 × A × X = A — 1 × B .
Так как А — 1 × А = Е, то Е × X = А — 1 × В или X = А — 1 × В.
Замечание
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю. Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А.
В том случае, если d e t A н е р а в е н н у л ю, у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Пример решения системы линейных уравнений с помощью метода обратной матрицы
Пример 2
Решаем СЛАУ методом обратной матрицы:
2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2
Как решить?
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X:
- Находим определитель матрицы А:
d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 — 3 × (- 2) × 3 — — 1 × (- 4) × 5 — 2 × 4 — (- 1) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25
d e t А не равняется 0, следовательно для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А:
А 11 = (- 1) (1 + 1) — 2 4 — 1 5 = — 10 + 4 = — 6 ,
А 12 = (- 1) 1 + 2 1 4 3 5 = — (5 — 12) = 7 ,
А 13 = (- 1) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,
А 21 = (- 1) 2 + 1 — 4 3 — 1 5 = — (- 20 + 3) = 17 ,
А 22 = (- 1) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,
А 23 = (- 1) 2 + 3 2 — 4 3 — 1 = — (- 2 + 12) = — 10 ,
А 31 = (- 1) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,
А 32 = (- 1) 3 + 2 2 3 1 4 = — (8 — 3) = — 5 ,
А 33 = (- 1) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 . (2+1) = -1.
(2+1) = -1.
В результате вы получите матрицу дополнений, теперь транспонируйте ее. Транспонирование — это операция, симметричная относительно главной диагонали матрицы, столбцы и строки меняются местами. Таким образом, вы нашли присоединенную матрицу A*.
Обратная матрица для данной это такая матрица, умножение исходной на которую дает единичную матрицу: Обязательным и достаточным условием наличия обратной матрицы является неравенство нулю детерминанта исходной (что в свою очередь подразумевает, что матрица должна быть квадратная). Если же определитель матрицы равняется нулю, то ее называют вырожденной и такая матрица не имеет обратной. В высшей математике обратные матрицы имеют важное значение и применяются для решения ряда задач. Например, на нахождении обратной матрицы построен матричный метод решения систем уравнений. Наш сервис сайт позволяет вычислять обратную матрицу онлайн двумя методами: методом Гаусса-Жордана и с помощью матрицы алгебраических дополнений.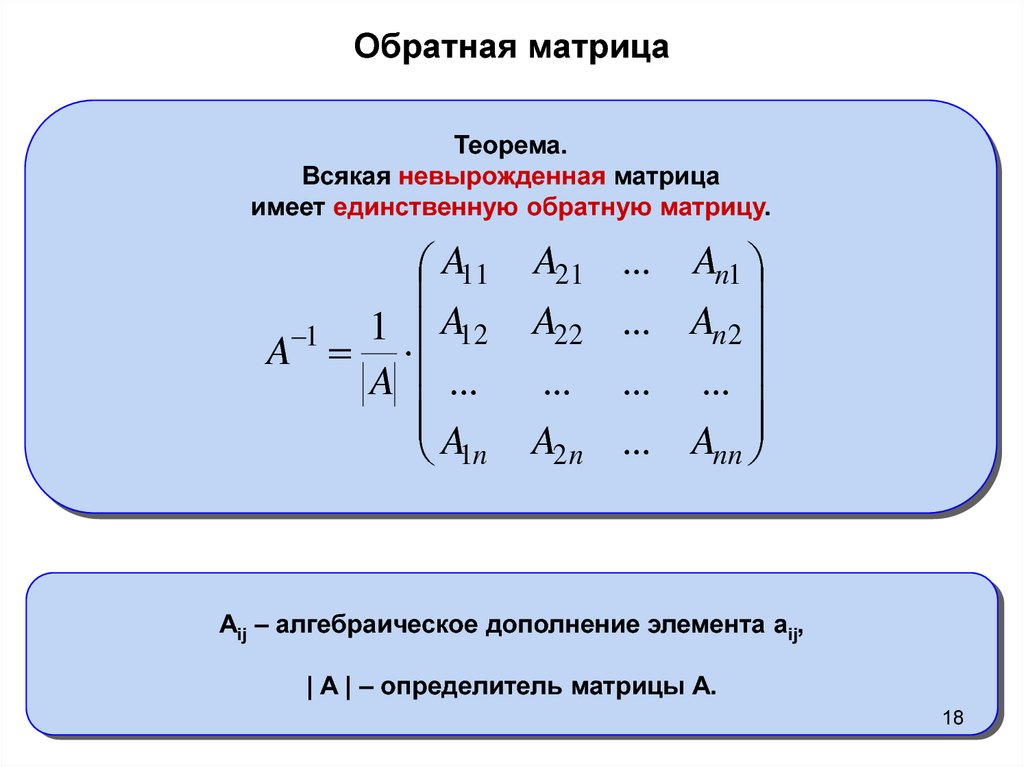 Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн
Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн
.
Найти обратную матрицу на сайт
сайт позволяет находить обратную матрицу онлайн быстро и бесплатно. На сайте произвордятся вычисления нашим сервисом и выдается результат с подробным решением по нахождению обратной матрицы . Сервер всегда выдает только точный и верный ответ. В задачах по определению обратной матрицы онлайн , необходимо, чтобы определитель матрицы был отличным от нуля, иначе сайт сообщит о невозможности найти обратную матрицу ввиду равенства нулю определителя исходной матрицы. Задача по нахождению обратной матрицы встречается во многих разделах математики, являясь одним из самых базовых понятий алгебры и математическим инструментом в прикладных задачах. Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Обратный калькулятор матрицы — MathPortal
- Калькуляторы
- ::
- Матрицы
- ::
- Калькулятор обратной матрицы
Этот калькулятор найдет обратную квадратную матрицу методом сопряжения. Калькулятор покажет пошаговое объяснение.
Матрица ввода
работающий…
Полиномиальные калькуляторы
Факторные полиномы
- Полиномиальные корни
- Синтетический отдел
- Полиномиальные операции
- Графические полиномы
- Расширить и упростить
- Генерировать из корней
Рациональные выражения
Упрощение
- Умножение/деление
- Сложение/вычитание
Подкоренные выражения
Рационализировать знаменатель
- Упрощение
Решение уравнений
Квадратные уравнения (с шагами)
- Полиномиальные уравнения
- Решение уравнений — с шагами
Квадратное уравнение
Решение (с шагами)
- Квадратичный плоттер
- Факторинг трехчленов
Геометрия
Равносторонний треугольник
- Прямоугольный треугольник
- Косой треугольник
- Калькулятор площади
- Калькулятор прямоугольника
- Калькулятор круга
Калькулятор шестиугольника
- Калькулятор ромба
Комплексные номера
Модуль, обратный, полярная форма
- Подразделение
- Упростить выражение
Системы уравнений
Система 2×2
- Система 3х3
- Система 4×4
Матрицы
Векторы (2D и 3D)
- Сложить, вычесть, умножить
- Калькулятор определителя
- Матрица обратная
- Характеристический полином
- собственные значения
- Собственные векторы
- Разложение матрицы
Расчетные калькуляторы
Калькулятор лимита
- Калькулятор производных
- Интегральный калькулятор
Последовательности и серии
Арифметические последовательности
- Геометрические последовательности
- Найти n th Срок
Аналитическая геометрия
Расстояние и середина
- Калькулятор треугольника
- Графические линии
- Пересечение линий
- Двухточечная форма
- Расстояние от линии до точки
- Параллельно/Перпендикулярно
- Уравнение окружности
- Круг из 3 точек
- Пересечение круговой линии
Тригонометрия
Градусов в Радиан
- Триггер Уравнения
Номера
Длинная дивизия
- Вычислить выражения
- Калькулятор дробей
- Наибольший общий делитель НОД
- Наименее распространенное кратное LCM
- Простые множители
- Научная нотация
- Калькулятор процентов
- Dec / Bin / Hex
- Калькулятор вероятности
- Распределения вероятностей
Описательная статистика
- Стандартное отклонение
- Z — Калькулятор очков
- Нормальное распределение
- Калькулятор Т-теста
- Корреляция и регрессия
Финансовые калькуляторы
Простые проценты
- Сложные проценты
- Калькулятор амортизации
- Калькулятор ренты
Прочие калькуляторы
Наборы
Проблемы с работой
примеры
пример 1:ex 1:
Что является обратной матрицей
$ A = \left[ \begin{массив}{cc}
-\frac{1}{2} & -\frac{3}{5} \\
\фракция{5}{2} и -4
\end{массив} \right]$.
пример 2:ex 2:
Найти обратную матрицу $ A = \left[ \begin{массив}{cc} 1 и 2 и -5 \\ -3&2&6\ 2 и -3 и 5 \end{массив} \right]$.
пример 3:ex 3:
Вычислить обратную матрицу $ A = \left[ \begin{массив}{cc} 5/2 и 1 и 0 и 1/2 \\ 4 и 3 и 1 и 1 \\ 3 и 14 и 9 и 3 \\ 2 и 3 и 2 и -3 \end{массив} \right]$.
Как ввести матрицу?
1: Матрица ввода, начиная с верхнего левого угла.
| Пример: Для ввода матрицы: | $ \left[ \begin{массив}{cc} -7 и 1/4\ -1,3 и -2/5 \end{массив} \right] $ | тип |
2: Нули вводить не нужно.
| Пример: Для ввода матрицы: | $ \left[ \begin{массив}{ccc} 0 и 1 и 0 \\ -1 & 0 & 0 \\ 0 и 0 и 2/3 \end{массив} \right] $ | тип |
3: Вы можете скопировать и вставить матрицу из Excel в 3 шага.
| Шаг 1: Скопируйте матрицу из Excel | Шаг 2: Выберите верхнюю правую ячейку | Шаг 3: Нажмите Ctrl+V |
4: Вам не нужно использовать полосы прокрутки, так как калькулятор автоматически удалит пустые строки и столбцы.

5: для удаления матрицы
| Выделить всю матрицу | и нажмите удалить |
Найдите в нашей базе данных более 200 калькуляторов
227 735 213 решенных задач
Калькулятор обратной матрицы
| 0 | ||||
| АС | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Этот калькулятор позволяет легко вычислить обратную матрицу с помощью матричных алгебраических сложений, а также получить подробное решение.
 Калькулятор вычисляет обратную матрицу для матриц размерностью от 2×2 до 9×9. С помощью этого калькулятора можно быстро научиться вычислять обратную матрицу, благодаря подробному алгоритму решения.
Калькулятор вычисляет обратную матрицу для матриц размерностью от 2×2 до 9×9. С помощью этого калькулятора можно быстро научиться вычислять обратную матрицу, благодаря подробному алгоритму решения. Матрица размера m × n представляет собой таблицу чисел с m строками и n столбцами.
Элементы матрицы обозначаются как ij , где i — номер строки, j — номер столбца.
Матрица A -1 называется обратной к матрице A, если A ⋅ A -1 = A -1 ⋅ A = E, где E — единичная матрица.
Для вычисления обратной матрицы матрица A должна быть квадратной и не равной нулю.
| Вам также могут пригодиться следующие калькуляторы |
| Linear Algebra and Analytical Geometers Calculators |
| Matrix Addition and Subtraction Calculator |
| Matrix Multiplication Calculator |
| Matrix Transpose Calculator |
| Matrix Determinant Calculator |
| Inverse Matrix Calculator |
Длина сегмента линии. Онлайн-калькулятор расстояния между точками. Онлайн-калькулятор расстояния между точками. |
| Калькулятор векторных координат по двум точкам |
| Калькулятор векторного модуля (длины) |
| Калькулятор векторного сложения и вычитания |
| Калькулятор векторного скалярного произведения. Используя длину векторов и косинус угла между векторами. |
| Калькулятор векторного скалярного произведения. Используя векторные координаты. |
| Калькулятор векторного произведения. Используя векторные координаты. |
| Векторный калькулятор тройного произведения |
| Vector Multiplication by Number Calculator |
| Angle Between Vectors Calculator |
| Vector Collinearity Check Calculator |
| Vector Coplanarity Calculator |
| Combinatorics Calculators |
| Permutations of N Elements Calculator |
| Комбинации N элементов с помощью М-калькулятора |
| Перестановки N элементов с помощью М-калькулятора |
| Калькуляторы численных систем |
| Римский цифровой калькулятор |
| Римские цифры от 1 до 3999 |
Numeral Systems Systems Systemal. Сложение, вычитание, умножение и деление двоичных чисел. Сложение, вычитание, умножение и деление двоичных чисел. |
| Калькулятор дробей |
| Калькулятор упрощения дробей |
| Не подходит для калькулятора смешанных дробей |
| Калькулятор неправильных дробей |
| Калькулятор дробей с пошаговым решением |
| Возведение дроби в степень. Онлайн калькулятор. |
| Десятичный до фракции калькулятор |
| Фракция с десятичным калькулятором |
| Сравнение кальцилятор |
| Common Denomanator Calculator |
| Общий денообразование Denomanator Calculator |
| Common Denomanator Calculator |
| Common Denomanator Denomanator |
| .0324 |
| Sine Calculator |
| Cosine Calculator |
| Tangent Calculator |
| Cotangent Calculator |
| Secant Calculator |
| Cosecant Calculator |
| Arcsine Calculator |
| Arccosine Калькулятор |
| Калькулятор арктангенса |
| Калькулятор арккотангенса |
| Arcsecant Calculator |
| Arccosecant Calculator |
| Calculators (Number theory) |
| Mathematical Expressions Calculator |
| Calculator Parentheses |
| Prime Factorization Calculator |
| Gcd and Lcm Calculator With Шаги |
| Калькулятор Gcd и Lcm с использованием алгоритма Евклида |
| Калькулятор Gcd и Lcm для любого количества чисел |
| Разбить число на его разрядное значение |
Разделить число на коэффициент. Online Calculator With Steps Online Calculator With Steps |
| Percentage Calculator With Steps |
| Scientific Notation to Decimal Conversion Calculator |
| Scientific Notation Converter |
| Factorial Calculator With Steps |
| Logarithm Calculator |
| Quadratic Equations Calculator С шагами |
| Remainder Calculator |
| Root Calculator |
| Decimal Period Calculator |
| Big Number Calculator |
| Rounding Numbers Calculator |
| Properties of Roots and Exponents Calculator |
| Complex Number Calculator |
| Калькулятор площади |
| Калькулятор площади квадрата |
| Area of a Rectangle Calculator |
| Math Trainers |
| Addition Math Trainer |
| Subtraction Math Trainer |
| Multiplication Math Trainer |
| Division Math Trainer |
| Multiplication Table Math Trainer |
| Онлайн-тренажер счета для дошкольников |
| Онлайн-тренажер внимательности для дошкольников |
Онлайн-тренажер по математике сложения, вычитания, умножения. Найдите правильный ответ. Найдите правильный ответ. |
| Online Numeric Expression Trainer |
| Converters |
| Length Converter |
| Speed Converter |
| Acceleration Converter |
| Physics Calculators |
Mechanics |
| Speed Time Калькулятор расстояния |
| Калькулятор расстояния скорости ускорения |
| Калькулятор времени перемещения |
| Time Calculator |
| Newton’s Second Law Calculator |
| Gravitational Force Calculator |
| Momentum Calculator |
| Impulse Calculator |
| Object Weight Calculator |
Optics |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Ohm’s Law Calculator |
| Coulomb’s Law Calculator |
| Electric Field Strength Calculator |
| Point Electric Charge Calculator Q |
| Force Acting on Charge Calculator |
| Distance From Charge Calculator |
| Калькулятор потенциальной энергии заряда |
| Калькулятор потенциала электрического поля |
| Калькулятор емкости проводника и сферы |
Конденсаторы |
| Калькулятор емкости плоскопараллельных, цилиндрических и сферических конденсаторов |
| Калькулятор напряженности электрического поля в плоскопараллельных, цилиндрических и сферических конденсаторах |
| Напряжение (разность потенциалов) плоскопараллельных, цилиндрических и сферических конденсаторов Калькулятор |
| Калькулятор расстояния между пластинами в параллельном пластинчатом конденсаторе |
| Калькулятор площади пластин в параллельном пластинчатом конденсаторе |
| Калькулятор запасенной энергии в заряженном конденсаторе |
9 Вычислить обратную матрицу 2 × 2 A
| А -1 = |
|
| А -1 = |
|
Решение
Вычислим обратную матрицу A, используя матрицу алгебраических дополнений.
adj(A) — сопряженная матрица, составленная из алгебраических дополнений
det(A) — определитель матрицы A
1. Вычислить определитель матрицы A
det A = 14
(Если вы хотите получить подробное решение для вычисления определителя, то
используйте калькулятор определителя матрицы)
2. Вычислите сопряженную матрицу adj (A), составленную из алгебраических дополнений. Для этого заменим каждый элемент исходной матрицы a ij на его алгебраическое дополнение A ij
M ij — дополнительный минор, вычисленный из исходной матрицы A удалением i-й строки и j-го столбца
Исходная матрица A состоит из 4 элементов, поэтому нужно вычислить 4 дополнительных минора M ij
M 11 =
=
= 7
M 12 =
=
= 4
M 21 =
=
= 0
M 22 =
=
= 2
Now we запишите значения всех элементов присоединенной матрицы adj(A)
A 11 = (-1) 1 + 1 ⋅ M 11 = (-1) 2 ⋅ 7 = 7
A 12 = (-1) 1 + 2 ⋅ М 12 = (-1) 3 ⋅ 4 = -4
А 21 = (-1) 2 + 1 ⋅ М 21 = (-1) 3 ⋅ 0 = 0
А 22 +
= (-7
) 20 2 ⋅ М 22 = (-1) 4 ⋅ 2 = 2
| adj(A) = |
| = |
3. Transpose the attached matrix adj(A)
Transpose the attached matrix adj(A)
| adj(A) T = |
|
4. Делим все элементы матрицы adj(A) T определителем исходной матрицы A
| A -1 = |
|
| A -1 = |
|
| A -1 = |
Перейти к калькулятору Calculate the inverse of a 3 × 3 matrix A
Решение Вычислим обратную матрицу A, используя матрицу алгебраических дополнений. adj(A) — сопряженная матрица, составленная из алгебраических дополнений 1. Вычислить определитель матрицы A 2. Вычислить сопряженную матрицу adj (A), состоящую из алгебраических дополнений. Для этого заменим каждый элемент исходной матрицы a ij на его алгебраическое дополнение A ij M ij — дополнительный минор, вычисленный из исходной матрицы A удалением i-й строки и j-го столбца M 11 =
=
= -1128 М 12 =
=
= -876 M 13 =
=
= -470 M 21 =
= = -752 M 22 =
= = -584 M 23 =
=
= 303 M 31 =
= = 12 М 32 =
=
= 88 M 33 =
= = 5 Теперь запишем значения всех элементов присоединенной матрицы adj(A) A 11 = (-1) 1 + 1 ⋅
M 11 = (-1) 2 ⋅ (-1128) = -1128
3.
4. Разделим все элементы матрицы adj(A) T на определитель исходной матрицы A
Перейти к калькулятору Эти числовые инструменты уже в пути Создание номеров Numberwang Создание списка номеров Numberwang. Переписать числа Учитывая числа и грамматику, рекурсивно переписать их. 9б форма. Преобразование научной записи в число Преобразование числа в научной записи в обычное число. Создать символьную нумерацию Создать список буквенных чисел (a, b, c, …, z, aa, ab, …). Создать римскую нумерацию Создать список римских цифр (i, ii, iii, iv, v…). Создать нумерацию Брайля Создать список цифр Брайля (⠂, ⠆, ⠒, ⠲, ⠢, …). Генерация случайных двоичных чисел Создать список случайных двоичных чисел. Создание случайных восьмеричных чисел Создание списка случайных восьмеричных чисел. Создание случайных десятичных чисел Создание списка случайных десятичных чисел. Создание случайных шестнадцатеричных чисел Создание списка случайных шестнадцатеричных чисел. Вычисление текущей суммы Вычисление кумулятивной суммы списка чисел. Вычисление текущего произведения Вычисление кумулятивного произведения списка чисел. Вычислить факториал Найти факториал числа. Создание числовых анаграмм Создание одной или нескольких числовых анаграмм. Создание числовых биграмм Создание списка цифровых биграмм из числа. Создание числовых триграмм Создание списка цифровых триграмм из числа. Генерировать N-граммы чисел Создать список цифровых nграмм из числа. Создание полиномиальной последовательности Создайте список чисел полиномиальной прогрессии. Создание префиксов SI Создание списка префиксов показателей. Анализ числа Сообщить, сколько цифр встречается сколько раз. Преобразование числа в порядковое Преобразование количественного числительного в порядковое. Преобразование порядкового числа в число Преобразование порядкового числа в количественное. Преобразование числа в римское число Преобразование арабских цифр в римские. Преобразование римских чисел в обычные числа Преобразование римских цифр в арабские. Создание чисел Негафибоначчи Вычисление ряда расширенных чисел Фибоначчи. Генерация простых чисел Фибоначчи Поиск чисел, которые являются одновременно числами Фибоначчи и простыми числами. Проверка числа Фибоначчи Проверка, является ли число числом Фибоначчи. Проверка простых чисел Фибоначчи Проверяет, является ли число одновременно числом Фибоначчи и простым числом. Построить слова Фибоначчи Создать последовательность слов Фибоначчи. Создать слова Трибоначчи Создать последовательность слов Трибоначчи. Генерация чисел Негалука Вычисление ряда расширенных чисел Лукаса. Генерация простых чисел Лукаса Вычисление ряда расширенных чисел Лукаса. Тест Лукаса Прайм Проверяет, является ли число одновременно числом Лукаса и простым числом. Вычисление следа матрицы Найдите сумму элементов главной диагонали матрицы. Вычислить собственные значения матрицы Найти собственные значения матрицы. Умножение матриц Вычисление произведения двух матриц. Добавить матрицы Вычислить сумму двух матриц. Вычитание матриц Вычисление разности двух матриц. Генерация чисел Мозера де Брюйна Вычисление последовательности чисел Мозера-Брейна. Генерация чисел Колакоски Вычисление последовательности чисел Ольденбургера-Колакоски. Сгенерировать числа Стэнли Вычислить последовательность чисел Стэнли. Генерация чисел Гийсвейта Вычисление последовательности чисел Гийсвейта с самоописанием. Сгенерировать числа Рудина-Шапиро Вычислить последовательность чисел Русина-Шапиро. Генерация чисел Баума-Свита Вычисление последовательности чисел Баума-Свита. Генерация последовательности Туэ-Морса Вычисление элементов ряда чисел Туэ-Морса. Создание идеальных чисел Создание списка совершенных чисел. Создание почти идеальных чисел Создание списка почти идеальных чисел. Создание последовательности избыточных чисел Вычисление последовательности избыточных чисел. Создать последовательность неполных чисел Вычислить последовательность неполных чисел. Расчет чисел кривой дракона Создайте список порядковых номеров для складывания бумаги. Создание составных чисел Создание списка чисел, которые не являются простыми. Нарисовать таблицу чисел Создать таблицу чисел. Проверить, является ли число совершенным Проверить, является ли заданное число совершенным числом. Проверить, является ли число обильным Проверить, является ли данное число обильным числом. Проверить, является ли число недостаточным Проверить, является ли данное число недостаточным. Вычислить модуль Найти модуль числа. Группировка цифр числа Группировка цифр числа. Разделить число на цифры Создать список цифр из числа. Printf Numbers Применить функцию sprintf или printf к числам. Создайте номера Zalgo Позвольте Zalgo уничтожить ваши номера. Повторить номер Повторить номер несколько раз. Зеркало номер Создать зеркальную копию номера. Дополнение числа нулями Добавление нулей к числу. Обратное число Обратное порядок цифр числа. Поворот числа Циклический поворот цифр числа влево или вправо. Увеличить число Добавить единицу к заданному числу. Увеличить все цифры в числе Добавить единицу к каждой цифре в числе. Уменьшить число Вычесть единицу из заданного числа. Уменьшить все цифры в числе Вычесть единицу из каждой цифры в числе. Находить закономерности в числах Находить закономерности в последовательностях чисел. Подсчет вхождений чисел Определите, как часто встречаются числовые значения. Вычисление процентов Найти x% числа. Создание больших чисел Создание списка больших чисел. Генерация малых чисел Создать список маленьких чисел. Создание натуральных чисел Создание списка натуральных чисел. Создание рациональных чисел Создание списка рациональных чисел. Создать последовательность констант Создать серию чисел, в которой все элементы одинаковы. Генерация действительных чисел Создание последовательности действительных чисел. Создание комплексных чисел Создание списка комплексных чисел. Создание двоичных чисел Создание последовательности двоичных чисел. Создание пар чисел Создание последовательности пар чисел. Создание троек чисел Создание последовательности троек чисел. Создание кортежей чисел Создание последовательности n-кортежей чисел. Переплетение чисел Переплетение двух или более чисел поразрядно. Найти десятичное представление числа Переписать число в десятичной форме. Преобразование дроби в десятичную Преобразование дроби в десятичное число. Преобразование десятичного числа в дробь Преобразование десятичного числа в дробь. Преобразование двоичного числа в восьмеричное Преобразование числа с основанием два в число с основанием восемь. Преобразование двоичного числа в десятичное число Преобразование числа с основанием два в число с основанием десять. Преобразование двоичного числа в шестнадцатеричное Преобразование числа с основанием два в число с основанием шестнадцать. Преобразование восьмеричного числа в двоичное Преобразование числа с основанием восемь в число с основанием два. Преобразование восьмеричного числа в десятичное Преобразование числа с основанием восемь в число с основанием десять. Преобразование восьмеричного числа в шестнадцатеричное Преобразование числа с основанием восемь в число с основанием шестнадцать. Преобразование десятичного числа в двоичное Преобразование числа с основанием десять в число с основанием два. Преобразование десятичного числа в восьмеричное число Преобразование десятичного числа в восьмеричное. Преобразование десятичного числа в шестнадцатеричное Преобразование числа с основанием десять в число с основанием шестнадцать. Преобразование шестнадцатеричного числа в двоичное число Преобразование числа с основанием шестнадцать в число с основанием два. Преобразование шестнадцатеричного числа в восьмеричное Преобразование числа с основанием шестнадцать в число с основанием восемь. Преобразование шестнадцатеричного числа в десятичное число Преобразование числа с основанием шестнадцать в число с основанием десять. Преобразование любого числа в любое основание Преобразование любого числа в любом основании в любое другое основание. Изменение мантиссы числа Изменение значения числа. Изменить показатель степени числа Изменить степень числа. Замена цифр буквами Замена цифр в числе буквами алфавита. Создание спирали чисел Создание спирали из цифр числа. Удалить десятичную точку Удалить десятичный разделитель из десятичного числа. Проверка числа Numberwang Проверка, является ли данный номер числом numberwang. Обратная матрица 3 на 3 — Решенные примерыРешение обратной матрицы 3 на 3 может показаться сложным для некоторых учащихся, и поэтому им может понадобиться обратная матрица 3 на 3 — Решенные примеры, которые помогут им понять концепции и хорошо решать вопросы. И по той же причине мы предоставили примеры примеров обратной матрицы 3 на 3 вместе с некоторыми отличными упражнениями, которые вы можете решить самостоятельно с помощью Vedantu, которые не только помогут вам хорошо понять концепции, но и подготовят вас к экзаменам. Обратные операции — это то, что обычно используется в алгебре для решения того, что в противном случае могло бы быть очень сложным вопросом. Советы по решению обратной матрицы 3 на 3
Обратная матрица 3 на 3 — немного сложная задача, но ее можно оценить, выполнив шаги, указанные ниже. Матрица 3 на 3 включает 3 строки и 3 столбца. Элементами матрицы являются числа, образующие матрицу. Одиночная матрица — это та, определитель которой не равен нулю. Для каждой квадратной матрицы x x x существует обратная каждой матрице. Обратная матрица x * x представлена X. Обратная матрица не может быть легко вычислена с помощью калькулятора и сокращенного метода. 9{-1} X = I_{2}\]
Как найти обратную матрицу 3 на 3?Здесь вы можете увидеть обратный шаг матрицы 3 на 3, чтобы найти обратную матрицу 3 на 3 онлайн. Вычислите определитель матрицы 2 x 2. Подготовьте матрицу сомножителей Наконец, разделите каждый член матрицы сопряжения на определитель 9{-1} = 1/ |А | Adj (A)\] Обратная матрица 3 X 3 ПримерДавайте решим матрицу 3 X 3 \[\begin{bmatrix} a & b &c \\ d & e & f\\ g & h & i\end{bmatrix}\] Проверить данную матрицу 3 X 3 A = \[\begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4\\ 5 & 6 & 0\end {bmatrix}\] Давайте узнаем, как найти обратную матрицу 3 X 3 онлайн Проверить, является ли данная матрица обратимой Это можно доказать, если его определитель отличен от нуля. det(A) = 1(0-24) – 2(0-20) + 3(0-5) det(A) = -24 + 40 – 15 det (A) = 1 Поскольку определитель значения равен 1, мы можем сказать, что данная матрица имеет обратную матрицу.
Нахождение транспонирования данной матрицыНахождение транспонирования заданной матрицы 3 X 3 9{-1}\] = \[\begin{bmatrix} 1 & 0 & 5 \\ 2 & 1 & 6\\ 3 & 4 & 0\end{bmatrix}\] Определение определителей 2 X 2 малые матрицы. Теперь мы определим определитель каждой второстепенной матрицы размера 2 X 2. Для элементов первой строки \[\begin{bmatrix} 1 & 6\\ 4 & 0\end{bmatrix}\] = -24 \[\begin{bmatrix} 12 & 6\\ 3 & 0 \end{bmatrix}\] = -18 \[\begin{bmatrix} 2 & 1\\ 3 & 4\end{bmatrix}\] = 5 Для элементов второй строки \[\begin{bmatrix} 0 & 5\\ 4 & 0\end{bmatrix}\] = -20 \[\begin{bmatrix} 1 & 5\\ 3 & 0\end{bmatrix}\] = -15 \[\begin{bmatrix} 1 & 0\\ 3 & 4\end{bmatrix}\] = 4 Для элемента третьей строки \[\begin {bmatrix} 10 и 65\\ 14 и 60\end{bmatrix}\] = -5 \[\begin{bmatrix} 1 и 5\\ 2 и 6\end{bmatrix}\] = -4 \[\begin{bmatrix} 1 & 0\\ 2 & 1\end{bmatrix}\] = 1 Теперь новая матрица \[\begin{bmatrix} -24 & -18 & 5 \\ -20 & -15 & 4\\ -5 & 14 & 1\end{bmatrix}\] Создание матрицы кофакторовЧтобы сформулировать сопряженную или сопряженную матрицу, измените знак чередующихся членов, как показано ниже: Мы получим новую матрицу как A = \[\begin{bmatrix} -24 & -18 & 5 \\ -20 & -15 & 4\\ -5 & 14 & 1\end{bmatrix}\] Adj (A) = новая матрица 9{-1}\] = (1/1) = \[\begin{bmatrix} -24 и 18 и 5 \\ 20 и -15 и -4\\ -5 и 4 и 1\end{bmatrix}\]
Решенные примеры 1. 1 \[\begin{bmatrix} 2 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & -1 & 2\end{ bmatrix}\] Решение: \[ -2\begin{bmatrix} 1 & 1\\ -1 & 2\end{bmatrix} -1\begin{bmatrix} 1 & 1\\ 1 & 2\end {bmatrix} +1\begin{bmatrix} 1 и 1\\ 1 и -1\end{bmatrix} \] 9{-1}\] существует Минор и сомножители строки 1 Минор 2 \[\begin{bmatrix} 1 & 1\\ -1 & 2\end{bmatrix}\] = (2 -(-1)) = (2 + 1) = (3) = 3 Сомножитель 2 = + (3) = 3 Минор 1 927{16 \[\begin bmatrix} 1 & 1\\ 1 & 2\end{bmatrix}\]= (2-1) = (2) = 2 Коэффициент 1 = (-1) = -1 Младший из 1 \[\begin{bmatrix} 1 & 1\\ 1 & -1\end{bmatrix}\] =(-1-1) = (-2) = -2 Кофактор 1 = + (-2) = -2 Минор и сомножители строки 2 Минор 1 \[\begin{bmatrix} 1 & 1\\ 1 & -2\end{bmatrix}\] = (-2-1) = -3 Сомножитель 1 = — (-3) = -3 Минор 1 \[\begin{bmatrix} 2 & 1\\ 1 & 2\конец{bmatrix}\] = (4 -1) = (3) = 3 Сомножитель 1 = — (-3) = -3 Минор от 1 \[\begin{bmatrix} 2 1\\ 1 & -1\end{bmatrix}\] (-2-1) = (-3) = -3 Коэффициент 1 = — (-3) = 3 Минор и сомножители строки 3 Минор 1 \[\begin{bmatrix} 1 & 1\\ 1 & 1\end{bmatrix}\] = (1-1) = 0 Кофактор 1 = + (0) = 0 Минор от -1 \[\begin{bmatrix} 2 & 1\\ 1 & 1\end{bmatrix}\] = (2-1) = 1 Кофактор -1 = — (1) = -1 Минор от 2 \[\begin{bmatrix} 2 & 1\\ 1 & 1\end{bmatrix}\] = (2-1) = 1 Кофактор 2 = + (1) = 1 Кофактор Матрица \[\begin{bmatrix} 3 & -1 & -2 \\ -3 & 3 & 3\\ 0 & — 1 и 1\конец{bmatrix}\] 9{-1}\] = \[\frac{1}{3}\] \[\begin{bmatrix} -3 & 3 & 0 \\ 1 & -3 & 1\\ 2 & -3 & -1\ end{bmatrix}\] 1. |


 {-1}=\frac{1}{det(a)}\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{n1}&a_{n2}&…&a_{nn}\end{pmatrix}\)
{-1}=\frac{1}{det(a)}\begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\\a_{21}&a_{22}&…&a_{2n}\\…&…&…&…\\a_{n1}&a_{n2}&…&a_{nn}\end{pmatrix}\) {1.433} & -8\end{pmatrix}\)
{1.433} & -8\end{pmatrix}\) Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн
 {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе. {-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}} {-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
{-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
 Матричный способ (метод
обратной матрицы) решения СЛАУ и условия
его применимости.
Матричный способ (метод
обратной матрицы) решения СЛАУ и условия
его применимости.
 Система,
состоящая из однородных уравнений,
называется однородной и имеет общий
вид:
Система,
состоящая из однородных уравнений,
называется однородной и имеет общий
вид: Другими
словами, функции y 1 (x ), y 2 (x ),
…, y n (x ) линейно
зависимы на
интервале (a , b ),
если существует равная нулю на (a , b ) их
нетривиальная линейная комбинация.
Функции y 1 (x ),y 2 (x ),
…, y n (x ) линейно
независимы на
интервале (a , b ),
если только тривиальная их линейная
комбинация тождественно равна нулю
на (a , b ).
Другими
словами, функции y 1 (x ), y 2 (x ),
…, y n (x ) линейно
зависимы на
интервале (a , b ),
если существует равная нулю на (a , b ) их
нетривиальная линейная комбинация.
Функции y 1 (x ),y 2 (x ),
…, y n (x ) линейно
независимы на
интервале (a , b ),
если только тривиальная их линейная
комбинация тождественно равна нулю
на (a , b ).
 теорему 3.4).
теорему 3.4).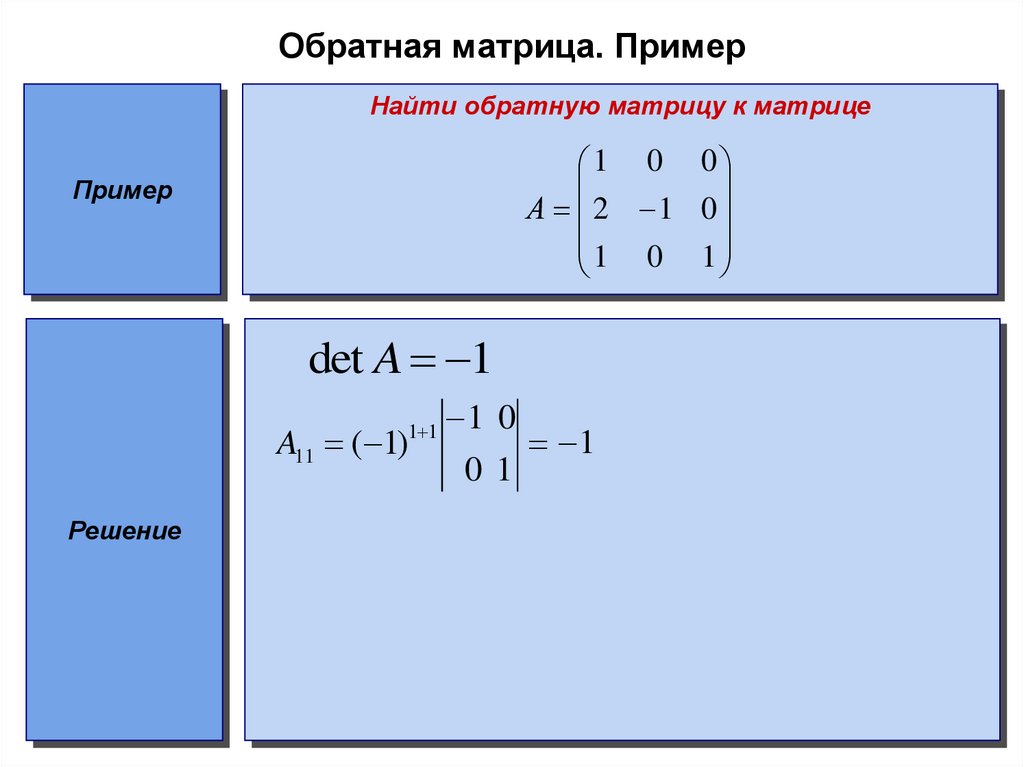 Ранг нулевой матрицы по определению
считают 0.
Ранг нулевой матрицы по определению
считают 0. 1.
Правило параллелограмма. Чтобы сложить
векторы и,
помещаем начала обоих в одну точку.
Достраиваем до параллелограмма
и из той же точки проводим
диагональ параллелограмма. Это и будет
сумма векторови.
1.
Правило параллелограмма. Чтобы сложить
векторы и,
помещаем начала обоих в одну точку.
Достраиваем до параллелограмма
и из той же точки проводим
диагональ параллелограмма. Это и будет
сумма векторови. Если
векторы перпендикулярны, их скалярное
произведение равно нулю.
А вот
так скалярное произведение выражается
через координаты векторов и .
Если
векторы перпендикулярны, их скалярное
произведение равно нулю.
А вот
так скалярное произведение выражается
через координаты векторов и .

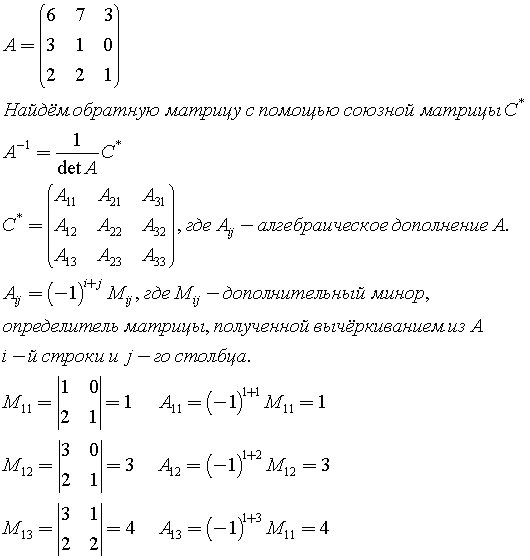 Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн
Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.
Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде. Более того, матрицы делить нельзя, поэтому нужно умножать на обратную матрицу. Вычислять матрицу, обратную матрице размером 3х3, довольно утомительно, но нужно уметь делать это вручную. Также обратную величину можно найти с помощью хорошего графического калькулятора.
Более того, матрицы делить нельзя, поэтому нужно умножать на обратную матрицу. Вычислять матрицу, обратную матрице размером 3х3, довольно утомительно, но нужно уметь делать это вручную. Также обратную величину можно найти с помощью хорошего графического калькулятора. Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2.
Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2. Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.
Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.

 На экране калькулятора отобразится матрица. Если ранее в калькулятор уже вводилась матрица, она появится на экране. Курсор выделит первый элемент матрицы. Введите значение первого элемента и нажмите Enter. Курсор автоматически переместится к следующему элементу матрицы.
На экране калькулятора отобразится матрица. Если ранее в калькулятор уже вводилась матрица, она появится на экране. Курсор выделит первый элемент матрицы. Введите значение первого элемента и нажмите Enter. Курсор автоматически переместится к следующему элементу матрицы.




 33,1)
x 1 =
2
x 2 =
-1
x 3 =
-0.33
x 4 =
1
33,1)
x 1 =
2
x 2 =
-1
x 3 =
-0.33
x 4 =
1 Если матрица А —
невырожденная (ее определитель отличен
от нуля, то она имеет обратную матрицу
А -1 .
Умножив обе части уравнения на А -1 ,
получим: А -1 *А*Х
= А -1 *B,
А -1 *А=Е.
Это
равенство называется матричной
записью решения системы линейных
уравнений .
Для нахождения решения системы уравнений
необходимо вычислить обратную матрицу
А -1 .
Система
будет иметь решение, если определитель
матрицы A отличен от нуля.
Найдем
главный
определитель.
∆=-1 (-2 (-1)-1 1)-3 (3 (-1)-1 0)+2 (3 1-(-2 0))=14
Итак,
определитель 14 ≠ 0, поэтому продолжаем
решение. Для этого найдем обратную
матрицу через алгебраические
дополнения.
Пусть имеем невырожденную
матрицу А:
Если матрица А —
невырожденная (ее определитель отличен
от нуля, то она имеет обратную матрицу
А -1 .
Умножив обе части уравнения на А -1 ,
получим: А -1 *А*Х
= А -1 *B,
А -1 *А=Е.
Это
равенство называется матричной
записью решения системы линейных
уравнений .
Для нахождения решения системы уравнений
необходимо вычислить обратную матрицу
А -1 .
Система
будет иметь решение, если определитель
матрицы A отличен от нуля.
Найдем
главный
определитель.
∆=-1 (-2 (-1)-1 1)-3 (3 (-1)-1 0)+2 (3 1-(-2 0))=14
Итак,
определитель 14 ≠ 0, поэтому продолжаем
решение. Для этого найдем обратную
матрицу через алгебраические
дополнения.
Пусть имеем невырожденную
матрицу А: -1 -1+3 1+0 2=4
3 -1+-2 1+1 2=-3
2 -1+1 1+-1 2=-3 doc :xml :xls Ответ: -1,1,2.
-1 -1+3 1+0 2=4
3 -1+-2 1+1 2=-3
2 -1+1 1+-1 2=-3 doc :xml :xls Ответ: -1,1,2. 152514872
152514872 Transpose the attached matrix adj(A)
Transpose the attached matrix adj(A) 0,152514872
0,152514872









 Если определитель данной матрицы равен нулю, то обратной данной матрицы не будет.
Если определитель данной матрицы равен нулю, то обратной данной матрицы не будет. Найдите обратную следующую матрицу
Найдите обратную следующую матрицу