Правило как находить площадь периметр. Как найти площадь и периметр прямоугольника? Периметр и площадь прямоугольника
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ.
 Сложить ширину и длину, и умножить на 2. P = (a + b) · 2.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Среди неиссякаемого многообразия геометрических фигур есть те, которые наиболее применимы в нашей жизни, например, параллелограмм, круг, овал и др. Геометрические фигуры повсюду, в связи с этим зачастую возникает необходимость определения их числовых характеристик: площадь, периметр, объем.
Прямоугольник обладает многими отличительными особенностями, исходя из которых выработаны правила вычисления его различных числовых характеристик.
- это плоская геометрическая фигура;
- это четырехугольник;
- это фигура, у которой противоположные стороны равны и параллельны, все углы прямые, т.е. по 90°.
Рассмотрим нахождение значений периметра и площади прямоугольника на конкретном примере:
- имеется прямоугольник ABCD;
- стороны AB и CD равны 5 см;
- стороны BC и AD равны 7 см.
Периметр или длина границы прямоугольника – это сумма длин всех сторон фигуры. Исходя из этого, периметр прямоугольника вычисляется суммированием числовых значений всех четырех его сторон. Периметр ABCD = 5+7+5+7= 2× 5 + 2× 7 = 24 см.
Для вычисления площади прямоугольника существует простая формула: площадь фигуры равна произведению значений любых двух смежных сторон, имеющих общий угол. Площадь ABCD = AB × AC = 5 × 7 = 35 см.
Для того, чтобы находить периметр и площадь прямоугольника, нужно знать формулы и главное — уметь применять их для решения задач — ведь они бывают разной сложности.
Очень часто при решении задач легкого уровня достаточно знать основные формулы и решить их просто подставляя нужные значения.
Если задачи посложнее и в их условии нет данных нужных для формулы, нужно их находить с помощью других алгебраических действий.
В этом случае можно навести следующий пример
нужно найти площадь прямоугольника, если его периметр равен 120 см, а стороны относятся как 2 к 3
сначала составляем уравнение , чтобы найти стороны используя при этом формулу периметра (
2*(2х+3Х)=120 решаем его, х=12 значит стороны равны 24 см и 36 см и теперь уже подставляем значения в формулу площади S=ab и находим ее S=24*36=864 см.кв.
Площадь прямоугольника равна произведению длины и ширины и вычисляется по формуле a*b, где а и b -стороны прямоугольника. Периметр прямоугольника равен сумме всех его сторон и вычисляется по формуле a+b+a+b.
Нахождение площади прямоугольника — умножим длину прямоугольника на его ширину.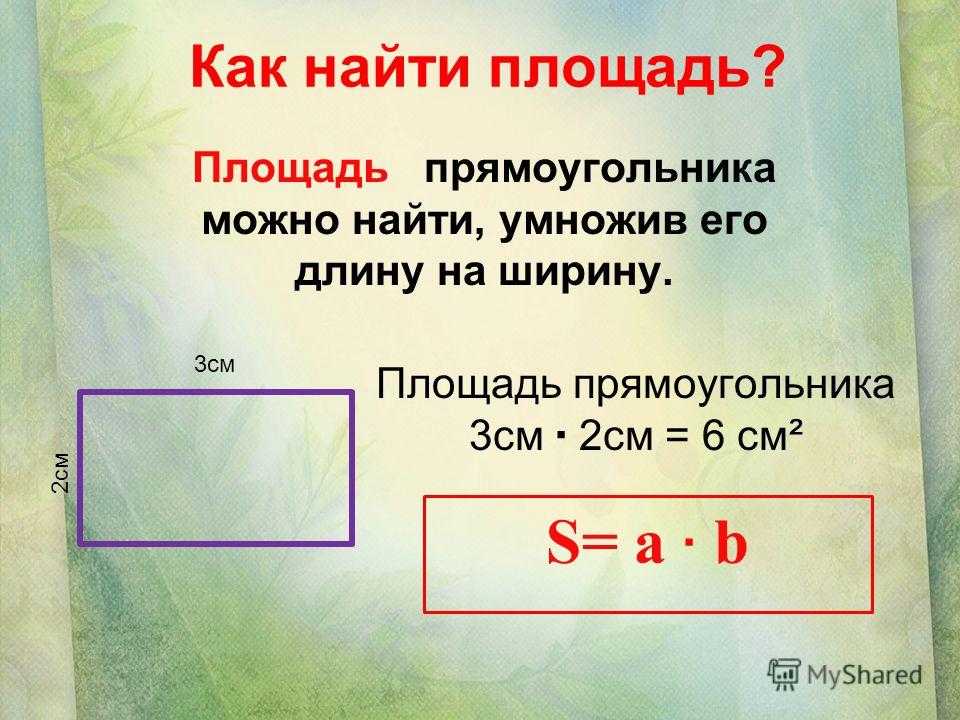
Нахождение периметра прямоугольника (сумма длин всех сторон) — простым сложением длин всех сторон, либо к длине продольной стороны прямоугольника, прибавляем длину поперечной и полученную сумму умножаем на два.
Если представить, что ваш огород прямоугольной формы и вам необходимо участок обложить забором, то наверное перед вами возникнет вопрос, а какой длины будет забор, чтобы правильно рассчитать расход стройматериалов. Вы сложите длины сторон забора и найдете ПЕРИМЕТР. Если зададитесь вопросом, какое количество земли нужно перекопать на этом участке, то придется искать ПЛОЩАДЬ, а для этого нужно будет перемножить длину на ширину участка, ведь как известно у прямоугольника противоположные стороны попарно равны. Не стоит забывать, что квадрат тоже прямоугольник, чтобы найти периметр квадрата, нужно длину умножить на 4, а площадь — длину стороны умножить на себя.
Вспомним школьный курс математики. Так периметр прямоугольника находится по формуле суммы двух его сторон умноженных на 2. То есть Р=2*(а+b), где а и b это стороны прямоугольника. Площадь, соответственно находится с помощью формулы S=a*b, где a и b также являются его сторонами.
То есть Р=2*(а+b), где а и b это стороны прямоугольника. Площадь, соответственно находится с помощью формулы S=a*b, где a и b также являются его сторонами.
Если не вдаваться в глубокие подробности, то найти площадь и периметр геометрической фигуры прямоугольник очень просто. Обозначим стороны такого прямоугольника латинскими буквами: a, b, c и d. Пусть a = c — это длина прямоугольника, а b и d — это ширина прямоугольника.
Площадь прямоугольника:
Периметр прямоугольника:
S = a + b + c + d
Периметр прямоугольника — это длины всех его сторон. Исходя из того, что у этой фигуры четыре стороны, или две пары, при этом противолежащие стороны равны друг другу, можно прийти к выводу, что уместно сложить значения двух разновеликих сторон и умножить полученное значение на два.
Площадь находится также просто: мы просто перемножаем разновеликие стороны.
Площадь вычисляется при умножении длинной стороны прямоугольника с короткой. А периметр-это (длин. сторона+ кор. сторона)*2
сторона+ кор. сторона)*2
Можно пойти самым простым путем нахождения площади прямоугольника. А именно, умножить длину прямоугольника (как правило, это a) на ширину прямоугольника (как правило, это B). А вот периметр ищем при помощи сложения всех сторон, или, проще говоря: 2a+2b
Прямоугольник это геометрическая фигура, а именно четырехугольник, у которого все углы прямые. Получается, что противоположные стороны равны друг другу.
Периметр прямоугольника это сумма длин всех сторон прямоугольника, либо сумма длины и ширины, умноженная на 2.
Периметр это длина всех сторон прямоугольника, то он измеряется в единицах длины: см, мм, м, дм, км.
P=AB+CD+AD+BC или P=2*(AB+AD).
Площадь измеряется квадратными единицами длины: м2, см2, дм2 и обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника рассчитывается путем умножения его длины на ширину полученное произведение и будет площадь.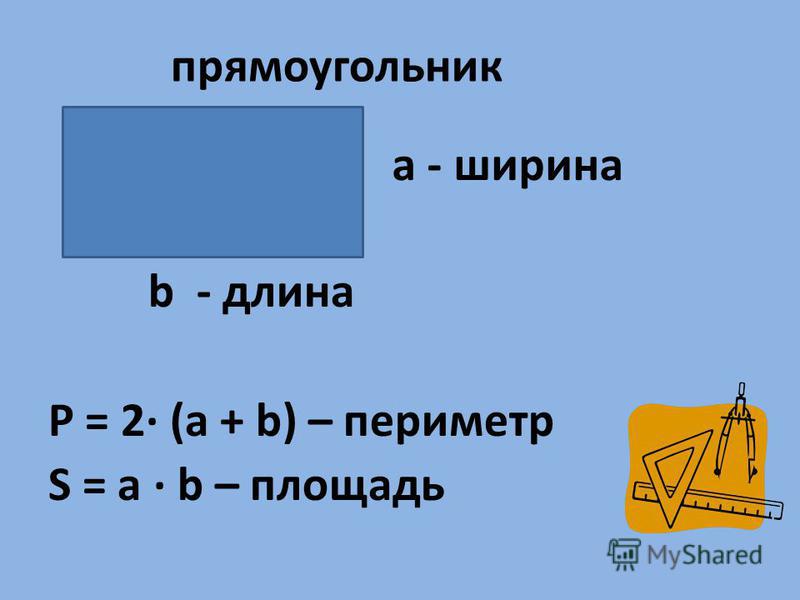
Периметр прямоугольника находится путем суммирования длины и ширины, полученную сумму нужно еще умножить на два, это и будет искомый периметр.
Если у прямоугольника заданы две противолежащие стороны, то все просто перемножаем их и получаем площадь, складываем и удваиваем и получаем периметр. Однако чаще в учебниках задают самый разнобой — сторону и периметр, сторону и площадь, сторону и диагональ. Как поступать в этих случаях.
Вот это идеальная задача.
Могут быть заданы сторона и диагональ. В этом случае находим вторую сторону по теореме Пифагора — как второй катет в треугольнике где гипотенуза диагональ прямоугольника.
В итоге мы имеем вот какие формулы для нахождения периметра прямоугольника:
А если по простому преобразовать эти же формулы, то получаются формулы для нахождения площади во всех вариантах задач:
Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.
Основные понятия
Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника, например, поверхность стола, тетрадь и прочее.
Рассмотрим пример: по границам земельного участка необходимо поставить забор. Для того чтобы узнать длину каждой из сторон необходимо их измерить.
Рис. 1. Земельный участок формой прямоугольника.
Земельный участок имеет стороны длиной 2 м., 4 м., 2 м., 4 м. потому чтобы общую узнать длину забора необходимо сложить длины всех сторон:
2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.
Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют букву P.
Для вычисления периметра прямоугольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.
Периметр прямоугольника измеряется в мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одинаковую систему измерения.
Периметр прямоугольника измеряется в различных единицах: мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одну систему измерения.
Формула периметра фигуры
Если принять к вниманию тот факт, что противоположные стороны прямоугольника равны, то можно вывести формула периметра прямоугольника:
$P = (a+b) * 2$, где а, b – стороны фигуры.
Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.
Существует и другой способ найти периметр. Если в задание дано лишь одну сторону и площадь фигуры, можно использовать выразить другую сторону через площадь. Тогда формула будет выглядеть следующим образом:
$P = {{2S + 2a2}\over{a}}$, где S – площадь прямоугольника.
Рис. 3. Прямоугольник с сторонами a, b .
Задание : Вычислить периметр прямоугольника, если его стороны равны 4 см.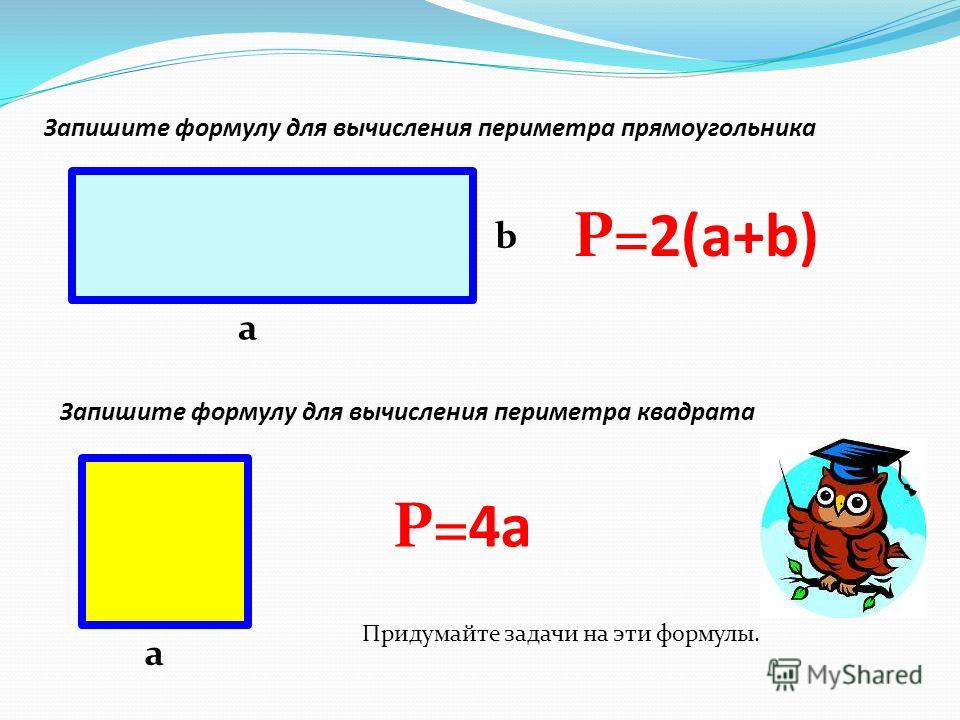 и 6 см.
и 6 см.
Решение:
Используем формулу $P = (a+b)*2$
$P = (4+6)*2=20 см$
Таким образом, периметр фигуры $P = 20 см$.
Так как периметр – это сумма все сторон фигуры, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.
Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.
Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….
I уровень
1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.
2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.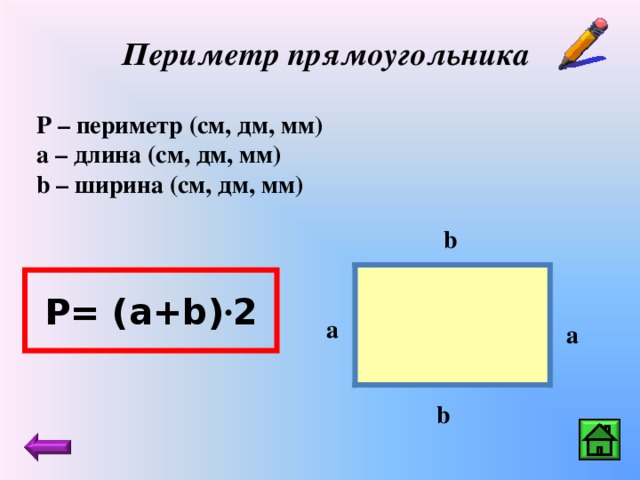
5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.
6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.
7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.
8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.
9.Длина стороны квадрата 6 см. Узнай площадь.
10.Вычисли периметр квадрата со стороной 4 см.
11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.
12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.
14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.
15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.
16.Сторона квадрата равна 3 см. Чему равен периметр?
17. Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?
Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?
18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?
19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.
21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?
II уровень
1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.
2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.
4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.
5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.
6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.
7.Периметр квадрата равен 32 см. Чему равна его сторона?
8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.
9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.
10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.
11.Периметр прямоугольника равен 54 м . Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.
12. Найдите площадь квадрата, периметр которого равен 360 мм.
13. Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?
14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.
15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
Чему равна длина стороны квадрата?
17. У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?
18. Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.
20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.
Составила К ислова Людмила Борисовна
Периметр и площадь. Что такое периметр? Как найти периметр? Периметр сложной фигуры
Наверняка каждый из нас учил в школе такую важную составляющую геометрии, как периметр. Нахождение периметра просто необходимо для решения множества задач. О том, как найти периметр, расскажет наша статья.
Стоит помнить, что периметр любой фигуры это почти всегда сумма ее сторон. Давайте рассмотрим несколько разных геометрических фигур.
- Прямоугольник — это такой четырехугольник, у которого параллельные стороны равны попарно между собой.
 Если одна сторона X, а другая Y, то мы получим такую формулу для нахождения периметра этой фигуры:
Если одна сторона X, а другая Y, то мы получим такую формулу для нахождения периметра этой фигуры:P = 2(X+Y) = X+Y+X+Y = 2X+2Y.
Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см + 2* 10см = 30 см.
- Трапеция — это четырехугольник, у которого две противоположные стороны параллельны, но не равны между собой. Периметр трапеции — это сумма всех четырех её сторон:
P = X+Y+Z+W, где X, Y, Z, W — стороны фигуры.
Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см, сторона Z = 8 см, сторона W = 20 см. Значит, подставив эти значения в нашу формулу, мы получим — P = 5 см + 10 см + 8 см + 20 см = 43 см.
- Периметр круга (длину окружности) можно вычислить по формуле:
P = 2rπ = dπ, где r — это радиус круга, d — диаметр круга.
Пример решения задачи:
Допустим, что радиус r нашего круга равен 5 см, тогда диаметр d будет равен 2*5 см = 10 см.
 Известно, что π = 3,14. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см*3,14 = 31,4 см.
Известно, что π = 3,14. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см*3,14 = 31,4 см. - Если Вам необходимо найти периметр треугольника, то Вы можете столкнуться с рядом проблем при этом, поскольку треугольники могут иметь очень разные формы. Например, есть острый, тупой, равнобедренный, прямоугольный или равносторонний треугольники. Хотя формула для всех видов треугольников такая:
P = X+Y+Z, где X, Y, Z — стороны фигуры.
Проблема в том, что при решении многих задач на нахождение периметра этой фигуры Вам не всегда будут известны длины всех сторон. Например, вместо информации о длине одной из сторон Вы можете иметь градус угла или длину высоты конкретного треугольника. Это существенно осложнит задачу, но не сделает ее решение нереальным. О том, как найти периметр треугольника, какой формы бы он не был можно прочитать » «.
- Периметр такой фигуры, как ромб находят также как и периметр квадрата, ведь ромб — это параллелограмм, который имеет равные стороны.
 Узнать, как найти периметр квадрата можно прочитав статью на нашем сайте » «.
Узнать, как найти периметр квадрата можно прочитав статью на нашем сайте » «.Теперь Вы знаете, как найти сторону периметра той геометрической фигуры, какой Вам нужно!
Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.
Общая для всех фигур теория
Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.
Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.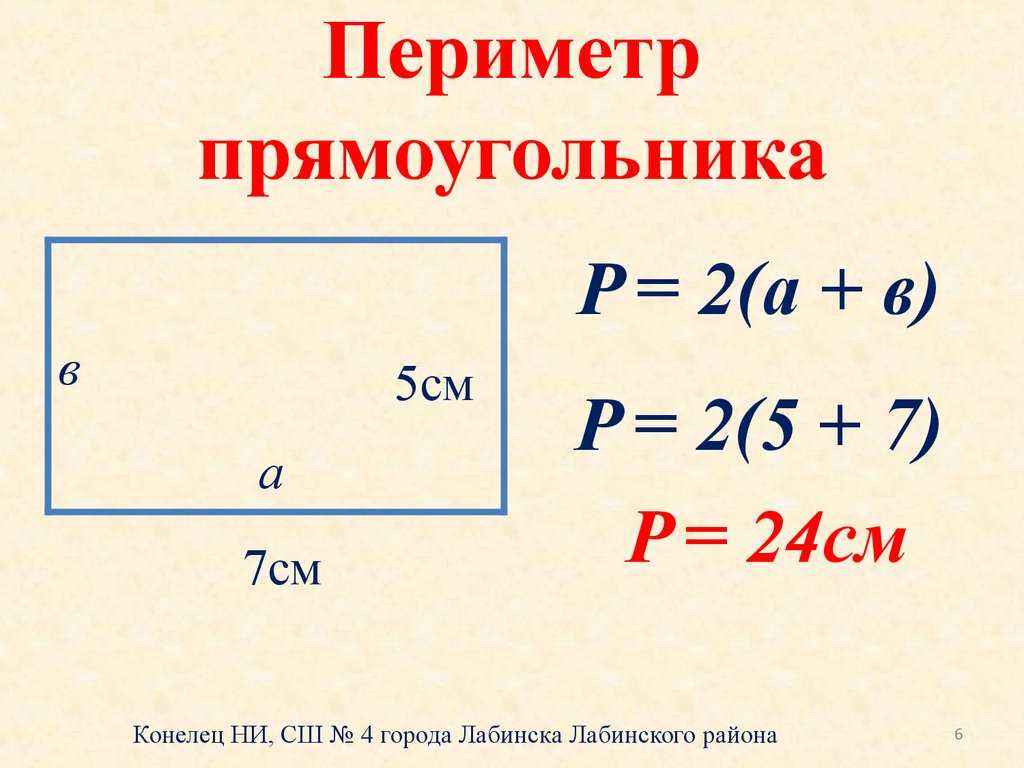
Формулы периметров разных фигур
Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.
Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).
Как быть, если неизвестна длина одной или нескольких сторон треугольника?
Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).
Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.
Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.
Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.
В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.
Примеры задач
Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.
Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.
Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.
, ломаная и т. д.:
Если внимательно посмотреть на все эти фигуры, то можно выделить две из них, которые образованы замкнутыми линиями (окружность и треугольник). Эти фигуры имеют своего рода границу, отделяющую то что находится внутри, от того что находится снаружи. То есть граница делит плоскость на две части: внутреннюю и внешнюю область относительно фигуры, к которой она относится:
Эти фигуры имеют своего рода границу, отделяющую то что находится внутри, от того что находится снаружи. То есть граница делит плоскость на две части: внутреннюю и внешнюю область относительно фигуры, к которой она относится:
Периметр
Периметр — это замкнутая граница плоской геометрической фигуры, отделяющая её внутреннюю область от внешней.
Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Обратите внимание, что периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
У всех многоугольников нахождение периметра сводится к сложению длин всех сторон, то есть периметр многоугольника всегда равен сумме длин его сторон. При вычислении периметр часто обозначают большой латинской буквой P:
Площадь
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой.
Любая плоская замкнутая геометрическая фигура имеет определённую площадь. На чертежах площадью геометрических фигур является внутренняя область, то есть та часть плоскости, которая находится внутри периметра.
На чертежах площадью геометрических фигур является внутренняя область, то есть та часть плоскости, которая находится внутри периметра.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Обычно за единицу измерения площади принимается квадрат, у которого сторона равна единице измерения длины: миллиметру, сантиметру, метру и т. д.
На рисунке изображён квадратный сантиметр. — квадрат, у которого каждая сторона имеет длину 1 см:
Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм 2 , см 2 , м 2 , км 2 и т. д.
Таблица перевода квадратных единиц
| мм 2 | см 2 | дм 2 | м 2 | ар (сотка) | гектар (га) | км 2 | |
|---|---|---|---|---|---|---|---|
| мм 2 | 1 мм 2 | 0,01 см 2 | 10 -4 дм 2 | 10 -6 м 2 | 10 -8 ар | 10 -10 га | 10 -12 км 2 |
| см 2 | 100 мм 2 | 1 см 2 | 0,01 дм 2 | 10 -4 м 2 | 10 -6 ар | 10 -8 га | 10 -10 км 2 |
| дм 2 | 10 4 мм 2 | 100 см 2 | 1 дм 2 | 0,01 м 2 | 10 -4 ар | 10 -6 га | 10 -8 км 2 |
| м 2 | 10 6 мм 2 | 10 4 см 2 | 100 дм 2 | 1 м 2 | 0,01 ар | 10 -4 га | 10 -6 км 2 |
| ар | 10 8 мм 2 | 10 6 см 2 | 10 4 дм 2 | 100 м 2 | 1 ар | 0,01 га | 10 -4 км 2 |
| га | 10 10 мм 2 | 10 8 см 2 | 10 6 дм 2 | 10 4 м 2 | 100 ар | 1 га | 0,01 км 2 |
| км 2 | 10 12 мм 2 | 10 10 см 2 | 10 8 дм 2 | 10 6 м 2 | 10 4 ар | 100 га | 1 км 2 |
| 10 4 = 10 000 | 10 -4 = 0,000 1 |
| 10 6 = 1 000 000 | 10 -6 = 0,000 001 |
| 10 8 = 100 000 000 | 10 -8 = 0,000 000 01 |
| 10 10 = 10 000 000 000 | 10 -10 = 0,000 000 000 1 |
| 10 12 = 1 000 000 000 000 | 10 -12 = 0,000 000 000 001 |
В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.
Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).
Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.
Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.
C) .
Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника
В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .
C) .
После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.
Итого, P=32x+2∙2x+2∙x=38x .
?) .
Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .
D) .
Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.
Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .
E) .
Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .
Итого, P=40x+8∙3x=64x .
B) .
Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .
D) .
Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.
Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .
B) .
Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:
P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .
К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .
Геометрия, если не ошибаюсь, в мое время изучалась с пятого класса и периметр был и есть одним из ключевых понятий. Итак, периметр — это сумма длин всех сторон (обозначается латинской литерой P) . Вообще, трактуют данный термин по разному, например,
- общая длина границы фигуры,
- длина всех ее сторон,
- сумма длин ее граней,
- длина ограничивающей фигуру линии,
- сумма всех длин сторон многоугольника
Для различных фигур существуют свои формулы определения периметра. Чтобы понять сам смысл, предлагаю самостоятельно вывести несколько несложных формул:
- для квадрата,
- для прямоугольника,
- для параллелограмма,
- для куба,
- для параллелепипеда
Периметр квадрата
Для примера возьмем самое простое — периметр квадрата.
Все стороны квадрата равны. Пусть одна сторона носит название «a» (также, как и остальные три), тогда
Пусть одна сторона носит название «a» (также, как и остальные три), тогда
P = a + a + a + a
или более компактная запись
Периметр прямоугольника
Усложним задачу и возьмем прямоугольник. В данном случае уже нельзя сказать, что все стороны равны, поэтому пусть длины сторон прямоугольника будут равны a и b.
Тогда формула будет иметь следующий вид:
P = a + b + a + b
Периметр параллелограмма
Аналогичная ситуация будет и с параллелограммом (см. периметр прямоугольника)
Периметр куба
Что же делать, если мы имеем дело с объемной фигурой? Например, возьмем куб. Куб имеет 12 сторон и все они равны. Соответственно, периметр куба можно вычислить следующим образом:
Периметр параллелепипеда
Ну, и для закрепления материала вычислим периметр параллелепипеда. Тут необходимо немного поразмышлять. Давайте делать это вместе. Как мы знаем, прямоугольный параллелепипед представляет собой фигуру, сторонами которой являются прямоугольники.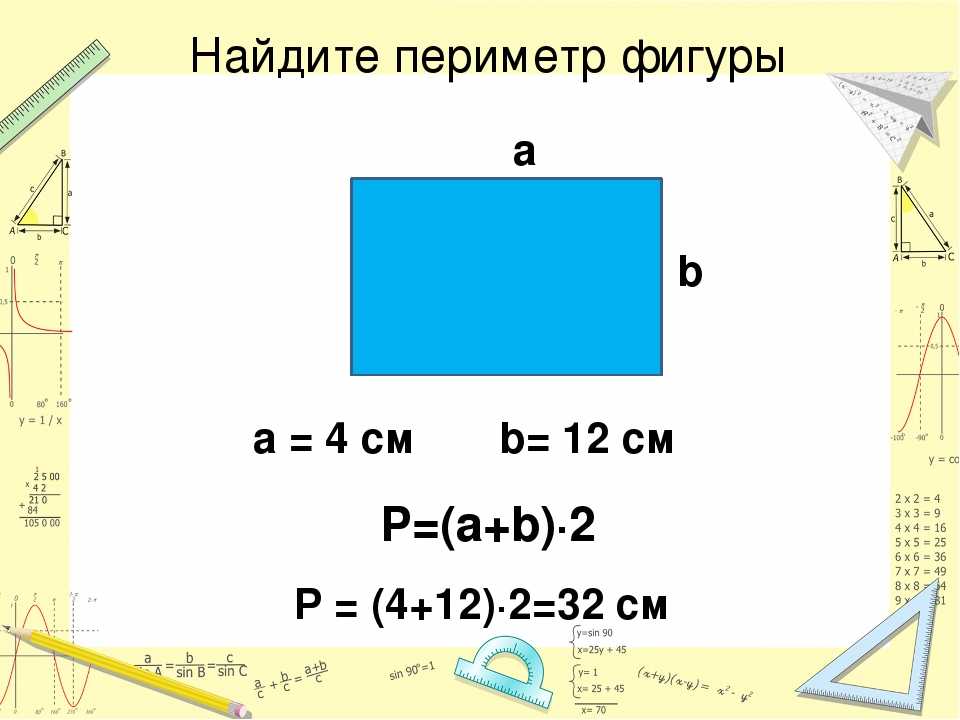 У каждого параллелепипеда есть два основания. Возьмем одно из оснований и посмотрим на его стороны — они имеют длину a и b. Соответственно, периметр основания есть P = 2a + 2b. Тогда периметр двух оснований есть
У каждого параллелепипеда есть два основания. Возьмем одно из оснований и посмотрим на его стороны — они имеют длину a и b. Соответственно, периметр основания есть P = 2a + 2b. Тогда периметр двух оснований есть
(2a + 2b) * 2 = 4a + 4b
Но ведь у нас есть еще и сторона «c». Значит формула для вычисления периметра параллелепипеда будет иметь следующий вид:
P = 4a + 4b + 4c
Как видно из примеров выше, всё, что необходимо сделать для определения периметра фигуры — найти длину каждой из сторон, а затем их сложить.
В заключение хочется отметить, что не всякая фигура имеет периметр. К примеру, у шара периметра нет.
Определение, формула и этапы расчета
Площадь, а также периметр составляют важную часть измерения 2d. Формулы площади и периметра применимы к любому типу формы и размера. Некоторыми из распространенных форм являются треугольник, квадрат, прямоугольник, круг, сфера и т. Д. Также в зависимости от формы формула различается.
Для всех двумерных фигур периметром является длина границы, покрывающей замкнутую фигуру. С другой стороны, площадь является мерой области внутри периметра данного объекта или структуры. В этой статье вы узнаете формулы площади и периметра для всех фигур, а также разницу между ними. Мы также репетируем некоторые решенные примеры.
Площадь и периметр
Рассмотрим ситуацию, когда вы хотите найти количество проволоки, необходимое для ограждения участка определенного размера, или вы хотите найти количество ковра, необходимое для покрытия всего участка. Есть много таких математических, а также реальных ситуаций, когда используются понятия периметра и площади.
Площадь
Площадь используется для расчета места, занимаемого плоскими фигурами. Другими словами, это область, определяемая формированием объекта в 2D-плоскости. Площадь различных типов фигур зависит от размеров; длина, ширина, радиус, сторона и т. д.
Периметр
Периметр используется для расчета границ закрытых образований. Другими словами, это общее расстояние, окружающее фигуру/объект.
Другими словами, это общее расстояние, окружающее фигуру/объект.
Шаги по вычислению площади и периметра
Теперь, когда вы понимаете определение периметра и площади в математике, давайте разберемся с шагами для их вычисления.
Шаги для вычисления площади
Шаг 1: Сначала проанализируйте данную фигуру. Для понимания расчета рассмотрим приведенный рисунок.
Здесь нам нужно найти площадь квадратной сетки, состоящей из 9 маленьких квадратных ячеек.
Шаг 2: В зависимости от формы объекта выберите нужную формулу.
Здесь у нас квадратная форма.
Шаг 3: Примените формулу для получения ответа.
Дано, что сторона маленького квадрата равна 2 см.
Таким образом, сторона большего квадрата равна 6 см (2+2+2).
Шаг 4: 9{2}\).
Узнайте о различных типах многоугольников здесь.
Шаги для расчета периметра
Чтобы понять расчет периметра, рассмотрите данный рисунок.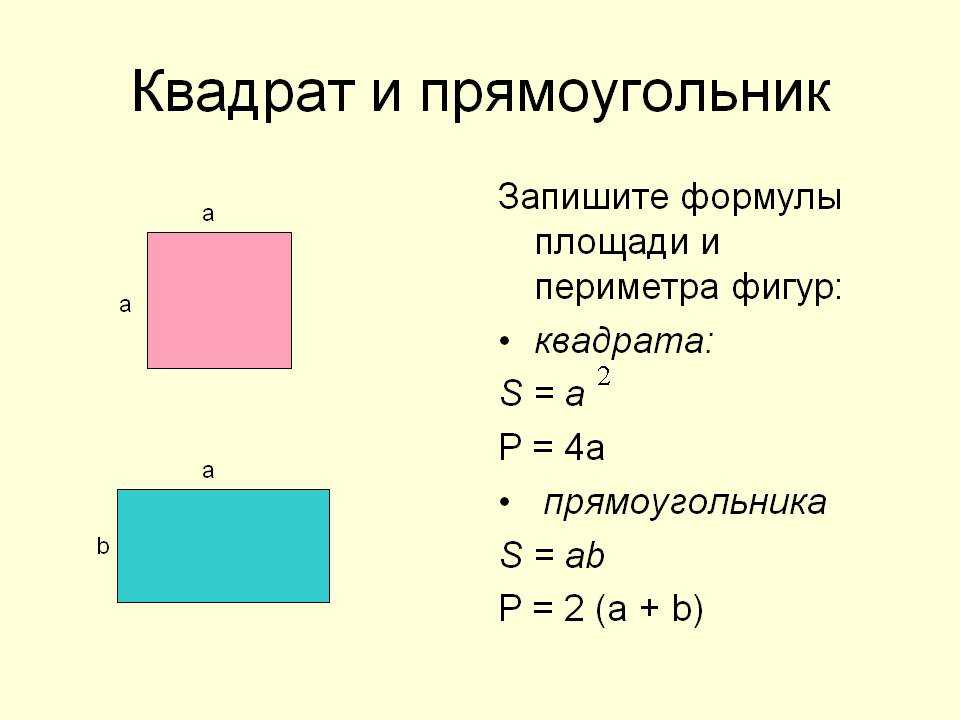 Здесь нам необходимо определить периметр объекта квадратной формы, учитывая, что размер сторон равен 3 см каждая.
Здесь нам необходимо определить периметр объекта квадратной формы, учитывая, что размер сторон равен 3 см каждая.
Шаг 1: Сначала изучите данный рисунок.
Шаг 2: В соответствии с формой объекта/фигуры выберите нужную формулу, здесь форма квадратная.
Шаг 3: Сложите все стороны, чтобы получить периметр. Здесь периметр квадратной формы=3+3+3+3=12 см.
Шаг 4: Ответ получается в сантиметрах – искомый периметр.
Для заданной формы периметр = 12 см
Узнайте больше о линиях.
Площадь и периметр всех фигур
Как мы обсуждали в предыдущих заголовках, существует несколько часто используемых фигур в математике и геометрии, для которых существует специальная формула для вычисления площади и периметра. Некоторые из общих форм; треугольник, квадрат, прямоугольник, воздушный змей, трапеция, круг и т. д. Чтобы узнать периметр и площадь всех этих фигур, мы применяем различные формулы. Некоторые из них обсуждаются ниже: 9{2}\) (где s — сторона квадрата)
Некоторые из них обсуждаются ниже: 9{2}\) (где s — сторона квадрата)
Прямоугольник
Прямоугольный объект — это объект, у которого противоположные стороны равны по размеру плюс все углы равны 90 градусов каждый. Полное пространство, ограниченное четырьмя сторонами прямоугольника, называется площадью прямоугольника.
Площадь прямоугольника = a × b (где b — длина, а а — ширина прямоугольника)
Периметр прямоугольника = 2(a+b)
Окружность
Окружность замкнута конфигурация, в которой все ее граничные точки находятся на равном расстоянии от фиксированной точки, называемой центром. 9{2}\)
Периметр или длина окружности – это измерение окружности.
Длина окружности = 2πr
В обеих формулах r — это радиус окружности.
Треугольник
Треугольник — объект замкнутой формы, имеющий 3 угла, 3 стороны и 3 вершины.
Площадь треугольника равна половине произведения основания на его высоту. т. е.
т. е.
Площадь =\(=\frac{1}{2}\times b\left(\text{base}\right)\times h\left(\text{height}\right)\)
Периметр — это длина вокруг треугольника, которая рассчитывается путем сложения всех трех сторон треугольника.
Периметр=Сторона 1+Сторона 2+Сторона 3
Узнайте больше о площади многоугольника здесь.
Формулы площади и периметра всех фигур
В предыдущем заголовке мы видели площадь и периметр прямоугольника, квадрата, треугольника и круга. В таблице ниже представлены диаграммы площади и периметра для всех часто используемых геометрических фигур. Это также поможет вам быстро просмотреть различные формулы.
| Shape | Area | Perimeter | Included Terms | ||
| Area and perimeter of triangle: | Area \(A=\frac{1}{2 }\times b\times h\) | Периметр( P) = a + b + c | Здесь a, b и c — разные стороны треугольника, а h — высота. 2\) 2\) | Периметр, P = 4a | Здесь a — стороны данного квадрата. |
| Площадь и периметр прямоугольника: | Площадь = lw | Периметр = 2(l + w) | Здесь l — длина, а w — ширина данного прямоугольника. | ||
| Площадь и периметр параллелограмма: | Площадь, A = bh | Периметр, P = 2(a + b) | Здесь a и b — смежные стороны параллелограмма, а h — высота. 92\) | Длина окружности = 2πr | Здесь r — радиус данной окружности. |
| Площадь и периметр ромба: | Площадь ромба =\(\frac{1}{2}\times d_1\times d_2\). | Периметр ромба =4×сторона (s=длина стороны) | Здесь \(d_1\text{ и }d_2\) — длины двух диагоналей ромба. |
Прочтите эту статью о площади четырехугольника.
Разница между площадью и периметром
Теперь, когда мы знаем формулу периметра и площади для различных фигур, а также этапы расчета. {2}\).
{2}\).
Площадь круглой земли равна произведению квадрата радиуса и величины круга.
Периметр круглой земли равен произведению удвоенного радиуса и величины круга.
Площадь Пентагона здесь.
Использование площади и периметра
Теперь, когда мы знаем определение, а также разницу между площадью и периметром, давайте разберемся, как их использовать.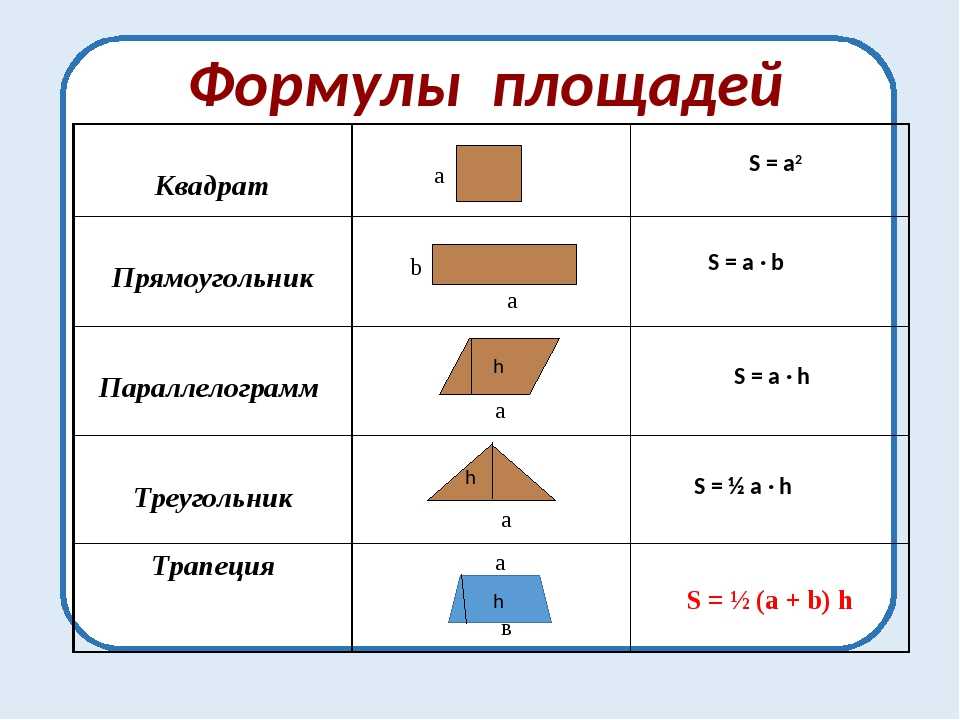
Периметр используется для;
- Знаем размер фотостенда и длину и ширину помещения, для которого мы требуем поставить забор или сделать разметку.
- В различных типах четырехугольников и треугольников периметр можно найти, сложив все стороны. Таким образом, меру сторон можно вычислить и с помощью периметра.
Область используется для;
- Рассчитайте стоимость цвета или краски, необходимой для покраски стен, и количество плиток, необходимых для покрытия пола.
- Геометрическое изображение фигур или фигур может быть дополнено разметкой периметра и областей для точного понимания.
- Эти концепции периметра и площади в дальнейшем используются для картографирования и съемки, а также в архитектуре.
Изучите различные типы геометрических фигур.
Решенные примеры по площади и периметру
Площадь, периметр, а также темы, связанные с объемом, лучше всего понять с помощью вопросов и примеров. Итак, давайте потренируемся на некоторых решенных примерах. 9{2}\).
Итак, давайте потренируемся на некоторых решенных примерах. 9{2}\).
Решенные примеры 2: Пастбище круглой формы с радиусом 21 см должно быть огорожено. Определить стоимость ограждения луга, если на ограждение одного см уходит 2 рупии.
Решение: Здесь нам нужно определить стоимость ограждения пастбища. Так как ограждение делается только по внешней границе. Внешняя граница равна периметру. Для расчета периметра пастбища круглой формы используется формула = 2πr см.
=2× 22/7× 21 9{2}\)
\(d_{1}\)= 3см
\(d_{2}\) =?
Площадь = \(\frac{1}{2}\left(d_1\times d_2\right)\)
9 = \(9=\frac{1}{2}\left(3\times d_2\) справа)\)
\(d_2=\frac{\left(9\times2\right)}{3}=6\text{см}\)
Таким образом, длина другой диагонали равна 6 см.
Примеры 5: Две стороны и периметр треугольника равны 2 см, 3 см и 13 см соответственно. Вычислите длину третьей стороны.
Решение:
Периметр треугольника =Сторона 1+Сторона 2+Сторона 3
13см=2см+3см+Сторона 3
Сторона 3=13-5=8 см
Таким образом, длина третьей стороны=8 см .
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
9{2}\).В.3 Как связаны площадь и периметр?
Ответ 3 Периметр описывает длину границы объекта. Однако площадь — это пространство, занимаемое объектом в пределах его периметра.
В.4 Как вычислить площадь и периметр прямоугольника?
Ответ 4 Периметр и площадь прямоугольника рассчитываются по приведенным ниже формулам;
Периметр, P = 2 (длина + ширина)
Площадь, A = длина × ширина
Q.5 Как найти площадь и периметр неправильной формы?
Ответ 5 Периметр любой неправильной формы получается простым сложением длин всех ее сторон. Чтобы вычислить площадь любой неправильной формы, сначала разбейте фигуру на известные фигуры обычных форм. Затем найдите площадь отдельной фигуры и добавьте их. Мы также можем поместить фигуру на миллиметровую бумагу и нарисовать ее контур. Количество единичных ячеек миллиметровки внутри границы можно использовать для аппроксимации площади неправильной формы.
Чтобы вычислить площадь любой неправильной формы, сначала разбейте фигуру на известные фигуры обычных форм. Затем найдите площадь отдельной фигуры и добавьте их. Мы также можем поместить фигуру на миллиметровую бумагу и нарисовать ее контур. Количество единичных ячеек миллиметровки внутри границы можно использовать для аппроксимации площади неправильной формы.
| Разница между ромбом и параллелограммом: изучите основные различия на примерах! |
| Уравнение прямой в форме двух точек, вывод с примерами |
| Многочлены: определение, типы, стандартная форма, свойства и решение с примерами решения |
| Острый угол: свойства, приложения и примеры решения |
| Белый свет: узнайте его источники, длину волны и свойства |
Площадь и периметр
Площадь и периметр Периметр и Площадь: Периметр : Периметр фигуры — это расстояние вокруг , которое форма. Это расстояние может состоять из прямых линий или кривых. Мы можем найти периметр путем сложения длин этих линий и кривых вместе. Рассмотрим первый пример, состоящий только из прямых линий.
Это расстояние может состоять из прямых линий или кривых. Мы можем найти периметр путем сложения длин этих линий и кривых вместе. Рассмотрим первый пример, состоящий только из прямых линий.
Пример 1) Найдите периметр следующей формы:
Хорошо найти периметр этой фигуры начните с угла и двигайтесь по часовой стрелке вокруг фигуры, добавляя кусочки пока мы снова не достигнем исходной точки. Обратите внимание, что в этой форме некоторые длины не даны и должны быть найдены.
| Р= 5 +3 + 6 + 7 + 8 + 2 + 3 + 12 = 46 |
Как упоминалось ранее, у нас могут быть порции кругов как часть нашей формы. Для того чтобы найти их длины, нужно использовать формулу расстояния по окружности или окружность круга.
Где «r» представляет длину радиуса круга и является константой (примерно 3,14). В этом курсе мы оставим все ответы в их точной форме (т. е. с точки зрения ).
В этом курсе мы оставим все ответы в их точной форме (т. е. с точки зрения ).
Пример 2) Найдите периметр следующей формы:
Эта фигура состоит из двух сегментов линии, четверть круга и полукруг. Кроме нахождения длины дуг, мы также должны найти длину недостающей части в нижний сегмент.
Р= 8 + 6+4 + 8 + 12
Р= 28 + 10
Район:
Площадь фигуры равна числу 1 единицы на 1 единицу квадратов (квадратных единиц), которые могут поместиться внутри фигуры. Если наш форма прямоугольника или квадрата это число легко найти. Все, что у нас есть сделать, это умножить длину и ширину формы. Но если наша форма имеет наклонные или изогнутые части, деление его на более мелкие квадраты не так легко выполняется. Чтобы найти площадь таких фигур, мы должны полагаться на формулы площади треугольников и кругов. В следующей таблице приведены вам формулы площади некоторых основных фигур.
Чтобы найти площадь таких фигур, мы должны полагаться на формулы площади треугольников и кругов. В следующей таблице приведены вам формулы площади некоторых основных фигур.
Теперь мы можем вернуться и найти площадь Форма в примере 2.
Пример 3) Найдите площадь следующая форма:
Чтобы найти площадь этой фигуры, мы разделим ее на три штуки; прямоугольник (I), полукруг (II) и четверть круга (III).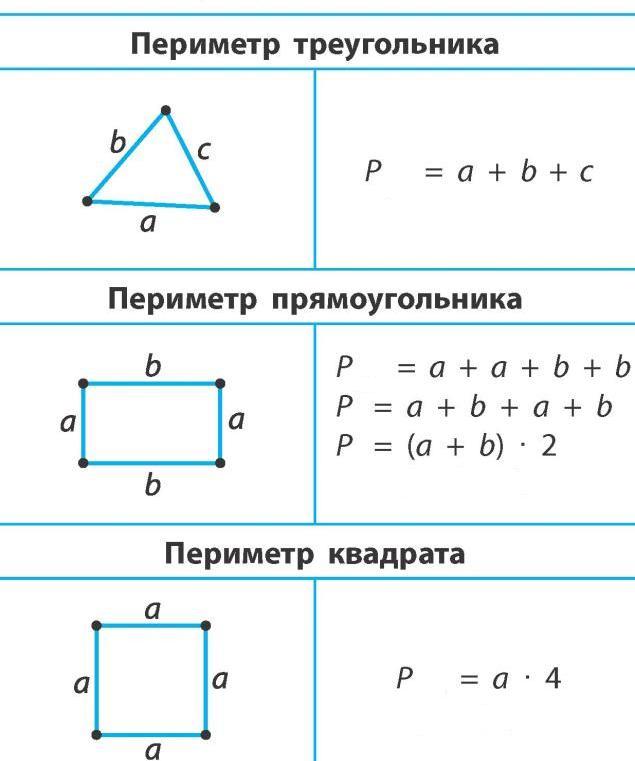 Найдем площадь каждого куска по отдельности, а затем найдем их сумму. Найдем площадь каждого куска по отдельности, а затем найдем их сумму. |
I : А = 12´ 8 = 96
II : А = ½ (6 2 ) = ½ (36) = 18 (Мы нашли ½ площади полного круга)
III: A= ¼ (8 2 ) = ¼ (64) = 16 (Мы нашли ¼ площади полного круга)
А= 96 + 18 + 16
А= 96 + 34
Практические задачи:
Найдите площадь и периметр для следующего:
1.
2.
3.
Решения пробных задач:
1.
Периметр = 18 + +12 + = 18+3+12+3= 30+6
Площадь= = 9+72+4,5= 72+13,5
2.
Периметр= 10 +12 + = 22 + 5
Площадь = 22 — = 22 12,5 (Обратите внимание, что в этом случае мы должны вычесть площади, но периметр еще добавляется.

 Сложить ширину и длину, и умножить на 2. P = (a + b) · 2.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. 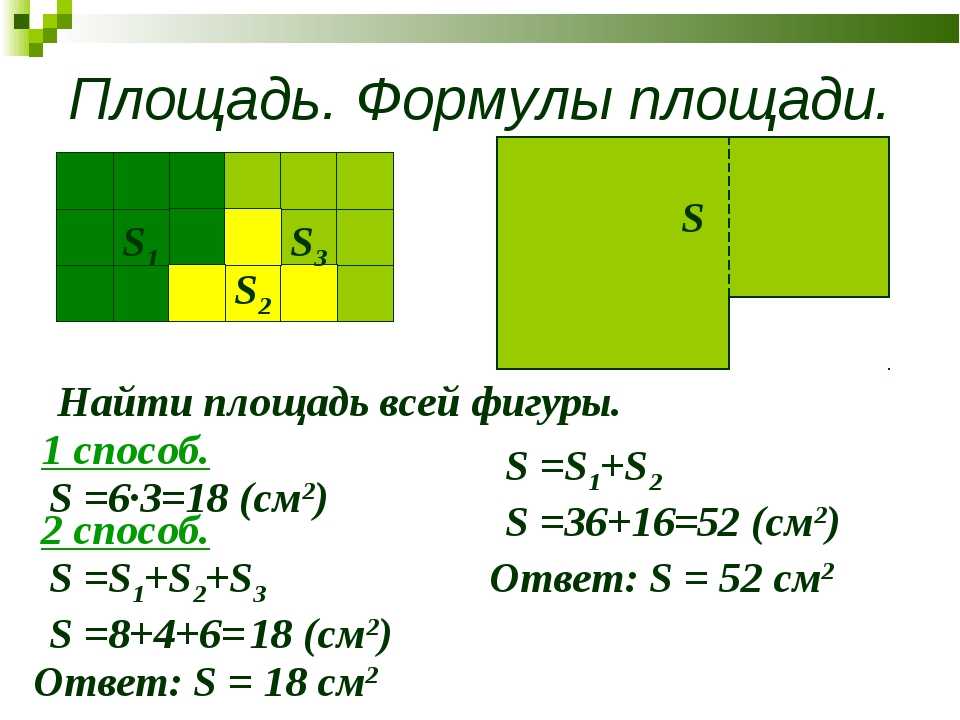 Если одна сторона X, а другая Y, то мы получим такую формулу для нахождения периметра этой фигуры:
Если одна сторона X, а другая Y, то мы получим такую формулу для нахождения периметра этой фигуры: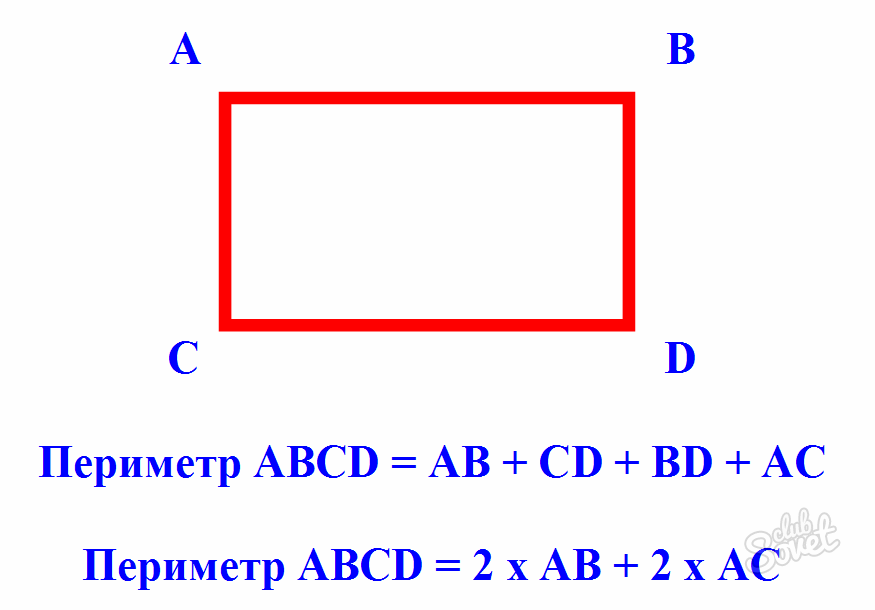 Известно, что π = 3,14. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см*3,14 = 31,4 см.
Известно, что π = 3,14. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см*3,14 = 31,4 см.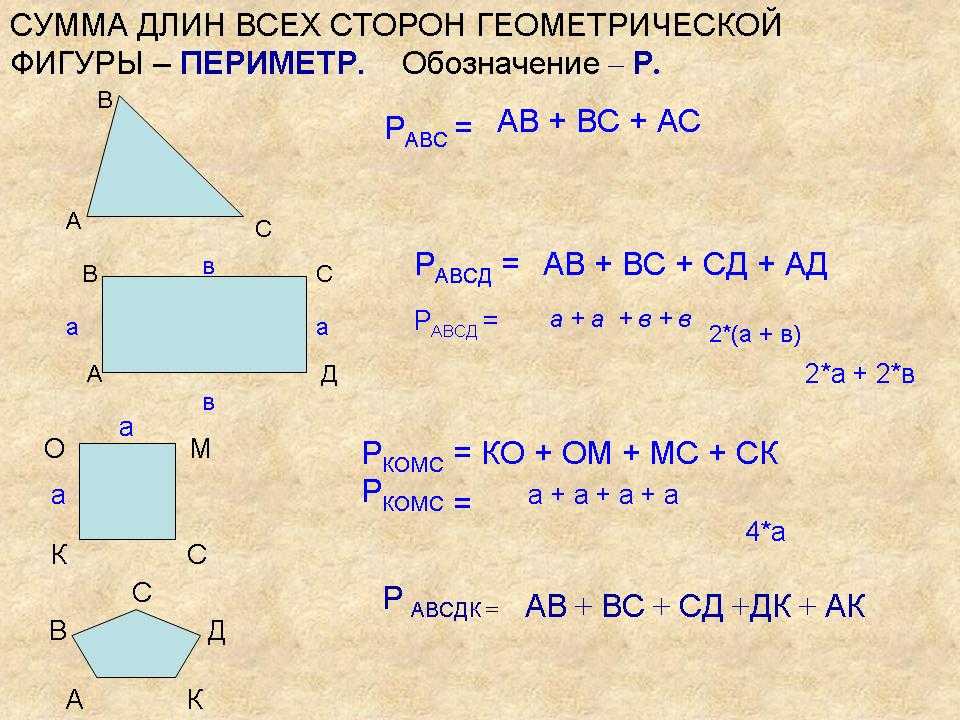 Узнать, как найти периметр квадрата можно прочитав статью на нашем сайте » «.
Узнать, как найти периметр квадрата можно прочитав статью на нашем сайте » «.