Как найти периметр зная площадь трапеции: Формулы трапеции, формулы для расчета площади и периметра трапеции

Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение периметра трапеции: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.

• Формула вычисления периметра
• Примеры задач

Формула вычисления периметра

Периметр (P) трапеции равняется сумме длин всех ее сторон.

P = a + b + c + d

• b и d – основания трапеции;
• a и с – ее боковые стороны.

Периметр равнобедренной трапеции

В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой.

Периметр считается так:

P =  2a + b + d или P = 2с + b + d

Периметр прямоугольной трапеции

Для расчета периметра используется такая же формула, что и для разносторонней трапеции.

P = a + b + c + d

Примеры задач

Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.

Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.

Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.

Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.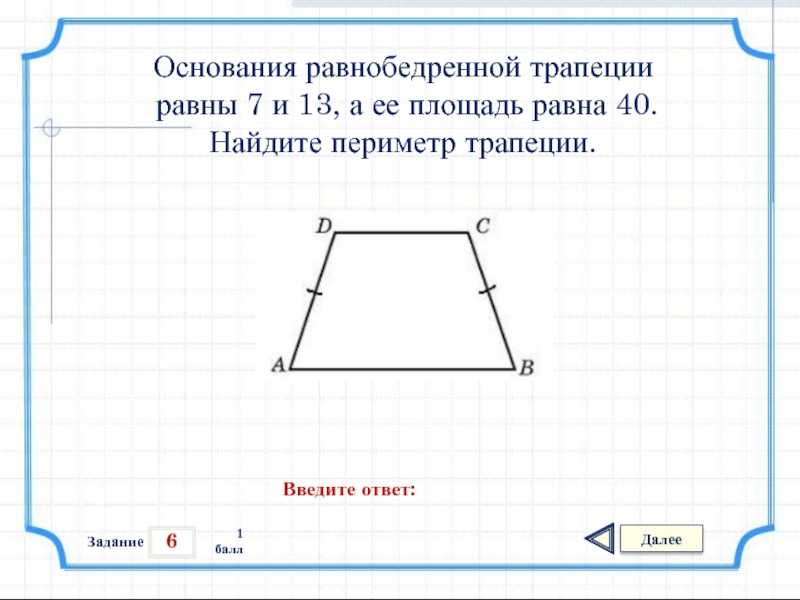

Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

6 способов найти площадь трапеции

27 марта 2020 Ликбез Образование

Выбирайте формулу в зависимости от известных величин.

1. Как найти площадь трапеции через основания и высоту

Посчитайте сумму оснований трапеции.

Умножьте результат на высоту и поделите на два.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• a и b – основания трапеции (её параллельные стороны).
• h – высота трапеции.

2. Как вычислить площадь трапеции через высоту и среднюю линию

Просто умножьте высоту трапеции на среднюю линию.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
• h – высота трапеции.

3. Как найти площадь трапеции через диагонали и угол между ними

Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.

Поделите результат на два.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• x и y – диагонали трапеции.
• α – любой угол между диагоналями.

4. Как найти площадь трапеции через четыре стороны

Отнимите от большего основания меньшее.

Найдите квадрат полученного числа.

Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.

Поделите полученное число на удвоенную разность оснований.

Найдите квадрат результата и отнимите его от квадрата боковой стороны.

Найдите корень из полученного числа.

Умножьте результат на половину от суммы оснований.

Иллюстрация: Лайфхакер

• S – искомая площадь трапеции.
• a, b – основания трапеции.
• c, d – боковые стороны.

5. Как вычислить площадь равнобедренной трапеции через четыре стороны

Отнимите от большего основания трапеции меньшее и поделите результат на два.

Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.

Найдите корень из результата.

Умножьте полученное число на сумму оснований и поделите на два.

Иллюстрация: Лайфхакер

• S — искомая площадь трапеции.
• a, b — основания трапеции.
• c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).

6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол

Найдите квадрат радиуса и умножьте его на четыре.

Поделите результат на синус известного угла.

Иллюстрация: Лайфхакер

• r — радиус вписанной окружности.
• α — любой угол трапеции.

Читайте также 📐✏️🎓

• 8 способов найти длину окружности
• 8 способов найти периметр треугольника
• 7 способов найти площадь прямоугольника
• Как перевести обычную дробь в десятичную
• Как освоить устный счёт школьникам и взрослым

Как найти периметр и площадь трапеции (видео и практика)

TranscriptFAQsPractice

Привет, и добро пожаловать в это видео о нахождении площади и периметра трапеции!

Что такое трапеция?

Трапеция — это четырехсторонний многоугольник , или «четырехугольник», который имеет по крайней мере один набор параллельных сторон.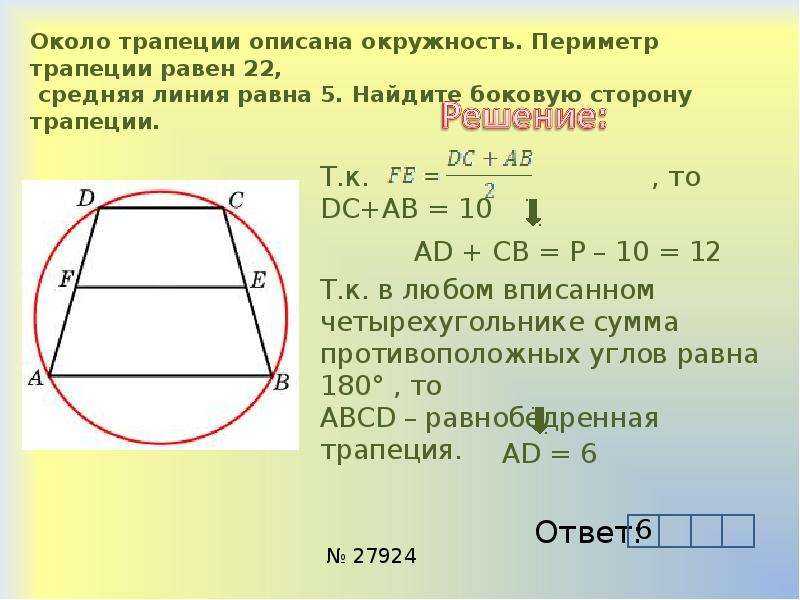 В трапеции есть два типа сторон: катеты и основания. У трапеции два катета и два основания.

Мы можем сказать, какие стороны являются основаниями, потому что они параллельны друг другу.

Здесь мы видим, что верх и низ параллельны из-за совпадающих стрелок на этих сторонах.

Как найти периметр трапеции

Зная длины катетов и длины оснований, мы можем найти периметр трапеции. Периметр — это расстояние вокруг объекта. Например, если мы хотим построить забор вокруг двора в форме трапеции, нам нужно знать периметр двора, чтобы знать, сколько забора нужно купить.

Формула периметра трапеции

Формула периметра трапеции: \(P=b_1+b_2+l_1+l_2\).

Нам не нужно запоминать эту формулу, потому что, как и в случае с любым другим типом многоугольника, это просто причудливый способ сказать, что складывает все стороны вместе !

Найдем периметр этой трапеции:

\(10+21+12+16=59 м\)

 

Вот и все! Переходим к область .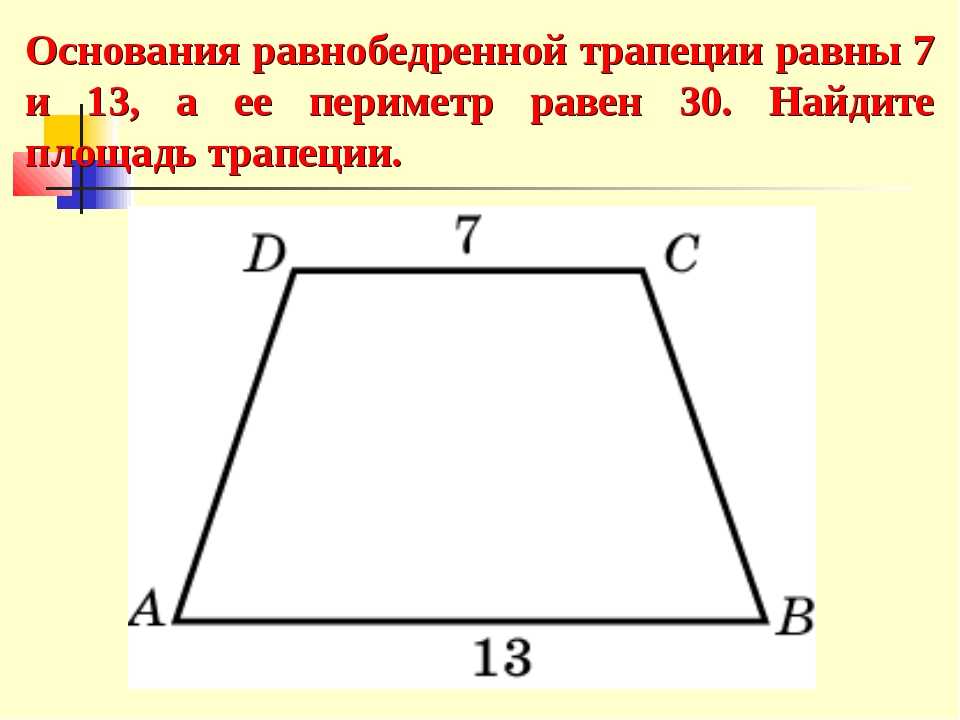

Как найти площадь трапеции

Вот трапеция на миллиметровой бумаге:

Помните, что площадь — это мера того, сколько квадратных единиц поместится внутри фигуры. Сколько квадратов внутри нашей трапеции?

Есть 24 полных квадрата плюс восемь полуквадратов, что означает, что площадь трапеции составляет 28 квадратных единиц. Но что, если у нас нет миллиметровой бумаги или трапеции подходящего размера? Вот почему нам нужна формула!

Формула площади трапеции

Формула для нахождения площади трапеции: \(A=h(\frac{b_1+b_2}{2})\).

Обратите внимание, что деление суммы оснований на два равно среднему значению этих длин. Поскольку наша примерная задача представлена ​​на графике, мы можем видеть, что верхнее основание, которое мы назовем основанием 1, имеет длину три единицы. Наша нижняя база, база 2, имеет длину 11 единиц. Высота трапеции, то есть расстояние между основаниями, равна четырем единицам:

92\)

 

Такой же ответ мы получили, когда считали!

Давайте попробуем еще один:

Хорошо, это выглядит немного иначе, чем трапеция, которую мы только что сделали.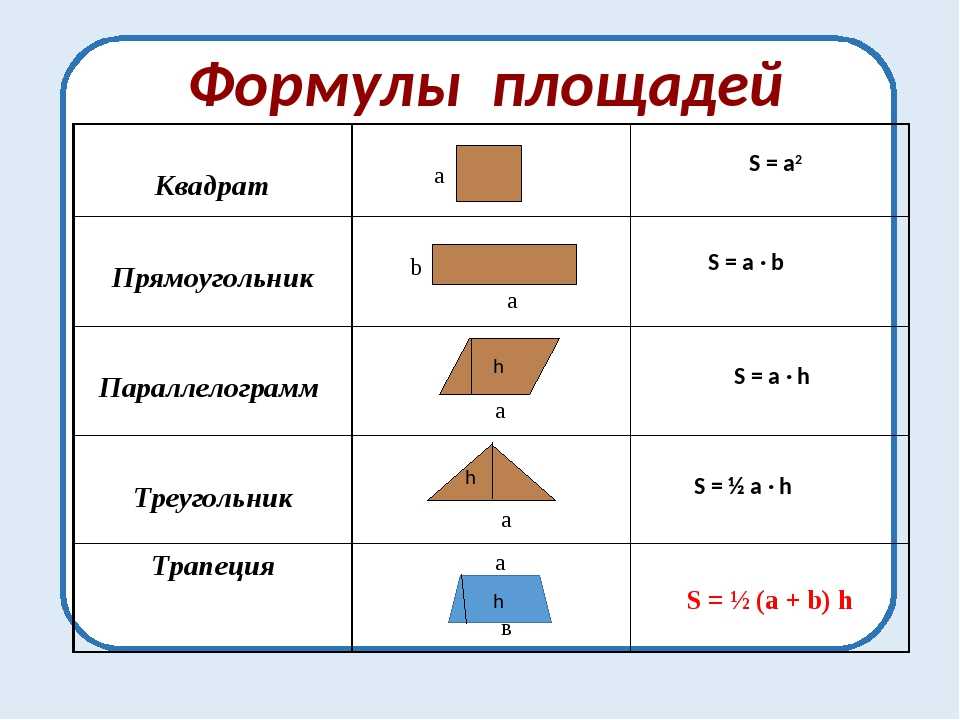 Но мы можем сказать, что это трапеция, потому что у нее один набор из параллельных сторон . Мы можем использовать формулу, так что теперь нам просто нужно выяснить, какие числа куда идут. Параллельные стороны — это основания, поэтому мы можем установить основание один равным 6 сантиметрам, а основание два равным 3 сантиметрам. Внутри трапеции нет пунктирной или цветной линии, соединяющей основания, которая явно была бы высотой, но нижняя сторона соединяет основания и перпендикулярна им, как мы можем сказать по символу прямого угла. Так 4 сантиметра это высота, хоть и сбоку! Подключим все: 92\)

 

Эта формула также работает для нахождения площади параллелограммов . Это потому, что все параллелограммы являются трапециями, поскольку у них есть хотя бы один набор параллельных сторон. На самом деле все параллелограммы имеют два множества.

Вот и все, что нужно для нахождения периметра и площади трапеций.

Спасибо за просмотр и удачной учебы!

Часто задаваемые вопросы

Q

Как найти площадь трапеции?

A

Каждая из двух параллельных сторон трапеции является основанием . Расстояние между основаниями (измеряемое перпендикулярно каждому) равно высоте . Чтобы найти площадь трапеции, мы умножаем среднюю длину двух оснований на высоту. В символах, если длины оснований равны \(a\) и \(b\), а высота равна \(h\) (см. диаграмму), то площадь \(A\) трапеции равна \ (A=\frac{(a+b)}{2}h\), что также можно записать как \(A=\frac{1}{2}(a+b)h\). 92\).

Q

Почему работает формула площади трапеции?

A

Формула площади трапеции работает, потому что она получена из формулы площади параллелограмма. Трапеция внизу (со сплошными сторонами) имеет основания длины \(a\) и \(b\) и высоты \(h\). Предположим, мы делаем ее копию, поворачиваем ее наполовину и помещаем рядом с исходной трапецией так, чтобы стороны (непараллельные стороны) одинаковой длины совпадали (заштрихованная трапеция со штрихованными сторонами). Вместе эти фигуры образуют параллелограмм с длиной основания \(a+b\) и высотой \(h\). По стандартной формуле площадь этого параллелограмма равна \(\text{площадь}=\text{основание}×\text{высота}=(a+b)h\). Площадь исходной трапеции равна половине этой, а именно \(\frac{1}{2}(a+b)h\) или, что то же самое, \(\frac{(a+b)}{2}h \). Эта же процедура работает для каждой трапеции. 92\) и т. д. Обычно мы используем квадрат единицы, используемой для измерения оснований и высоты трапеции. Например, если мы измеряем основания и высоту в сантиметрах, мы обычно даем площадь в квадратных сантиметрах.

Q

Как найти периметр трапеции?

A

Периметр фигуры — это расстояние вокруг нее. Найдем периметр трапеции, сложив длины ее четырех сторон.

Q

Как найти периметр трапеции по теореме Пифагора?

A

Если мы не знаем длины всех четырех сторон трапеции, иногда у нас достаточно другой информации, чтобы найти длины недостающих сторон по теореме Пифагора. Например, у трапеции на схеме основания равны 2 см и 9 см, высота 4 см, а более длинное основание выступает за более короткое основание на 3 см слева и 4 см справа. Это делает стороны \(c\) и \(d\) гипотенузами прямоугольных треугольников со сторонами, длина которых нам известна. 2=92=16+16=32\), поэтому \(d=\sqrt{32}=\sqrt{16\cdot2}=\sqrt{16}\cdot \sqrt{2}=4\sqrt{2} ≈5,7 \текст{см}\). Теперь мы можем найти периметр \(P\) трапеции, сложив четыре стороны: \(P=9+5+2+4sqrt{2}=16+4\sqrt{2}≈16+5,7 =21,7\текст{см}\). Это один из примеров нахождения периметра трапеции по теореме Пифагора.

Q

Как найти площадь трапеции без высоты?

A

Если мы не знаем высоту трапеции, иногда у нас достаточно другой информации, чтобы найти высоту по теореме Пифагора. Например, у трапеции на схеме основания равны 2 см и 92\). Это пример нахождения площади трапеции без высоты.

Практические вопросы

Вопрос №1:

 
Каков периметр этой трапеции?

74 в

86 в

142 в

300 в

Показать Ответ

Ответ:

Правильный ответ — 74 дюйма. .
\(P=23+12+27+12=74\текст{in}\)

Скрыть ответ

Вопрос №2:

 
Какова площадь этой трапеции?

96 см ²

81 см ²

57 CM ²

41 CM ²

Покажите. . Формула площади трапеции:
\(A=\frac{1}{2}(b_1+b_2)h\)
Длина основания 1 равна 12 см. Длина основания 2 равна 15 см. Длина по высоте 6 см. 92\)

Скрыть ответ

Вопрос №3:

 
Каков периметр этой трапеции?

34 в

48 в

36 в

42 в

Показать Ответ

Ответ:

Правильный ответ — 36 дюймов. Найдите периметр трапеции, добавив длины всех четырех сторон. вместе. 2\)

Скрыть ответ

Вопрос №5:

 
Каков периметр этой трапеции?

153 см

140 см

47 см

55 см

Показать ответ

Ответ:

см. Чтобы найти периметр трапеции, сложите длины всех четырех сторон.
\(P=15+8+20+12=55\text{ см}\)

Скрыть ответ

Вернуться к видео по геометрии

587523

Как найти периметр трапеции

Все ресурсы по промежуточной геометрии

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

Intermediate Geometry Help » Плоская геометрия » Четырехугольники » Трапеции » Как найти периметр трапеции

Найдите периметр следующей трапеции.

Возможные ответы:

Правильный ответ:

Объяснение:

Ответ: 50 футов. Чтобы найти периметр, нужно найти длину левой стороны. После некоторого вывода вы можете найти, что основание треугольника равно 6 футам.   Затем, используя теорему Пифагора, или 3-4-5 прямоугольных треугольников, вы можете найти, что высота треугольника и прямоугольника составляет 8 футов. 

Однажды вы обнаружите, что последняя сторона равна 8 футам, вы можете добавить

 

, чтобы получить ответ 50 футов для периметра.

Сообщить об ошибке

Высота трапеции  см, а длина  см.

Найдите периметр трапеции с точностью до сотых.

Возможные ответы:

Правильный ответ:

Пояснение:

Используйте треугольник, образованный высотой трапеции, чтобы найти длины двух сторон трапеции и длину:

 .

см.

Это находит основание треугольника, которое можно дважды прибавить к  , чтобы найти :  см.

Теперь используйте тот же треугольник, чтобы найти длины сторон.

 . см.

Наконец, сложите все длины вместе:  см.

Сообщить об ошибке

Найдите периметр трапеции ниже.

Возможные ответы:

Правильный ответ:

Объяснение:

Затем мы можем использовать теорему Пифагора, чтобы найти правую часть нижнего основания. Затем мы можем использовать это значение для определения левой части.

Снова используя теорему Пифагора, мы можем вычислить, что левая сторона равна 20. Это означает, что теперь мы знаем все четыре стороны. Периметр — это просто сумма.

Сообщить об ошибке

У равнобедренной трапеции два основания параллельны друг другу. Большее основание в раз больше меньшего. Меньшее основание имеет длину в дюймах, а длина непараллельных сторон трапеции имеет длину в дюймах.

Каков периметр трапеции?

Возможные ответы:

Правильный ответ:

 

Пояснение:

Чтобы найти периметр этой трапеции, сначала найдите длину большего основания. Затем найдите сумму всех сторон. Важно отметить, что поскольку это равнобедренная трапеция, обе непараллельные стороны будут иметь одинаковую длину.

Решение:

Меньшее основание равно  дюймам. Таким образом, большее основание равно:

, где  длина одной из непараллельных сторон равнобедренной трапеции.

Сообщить об ошибке

Собственность доктора Робинсона имеет форму равнобедренной трапеции. Доктор Робинсон дал подрядчику следующие размеры, чтобы подрядчик мог построить стену вокруг всего участка.