формула через диаметр, наружная поверхность, сечение, как посчитать и вычислить
Содержание:
Для чего нужны геометрические вычисления
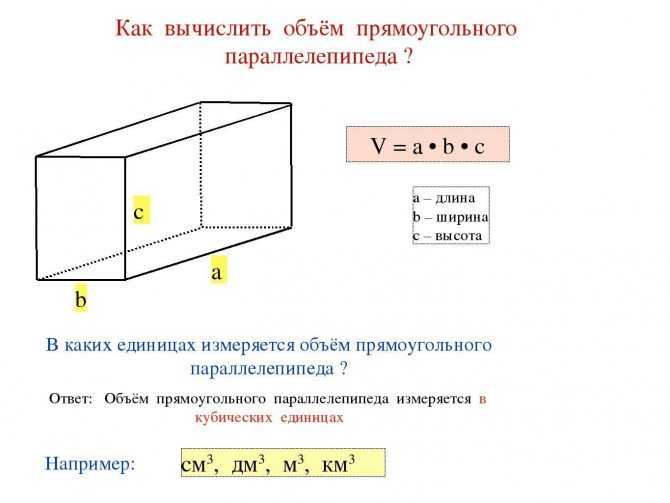
Формулы расчёта
Вычисление площади сечения
Вычисление площади наружной поверхности трубы
Вычисление площади внутренней поверхности трубы
Проектирование любого трубопровода – ответственное дело, от качественного проведения которого зависит скорость, дешевизна и даже сама возможность дальнейших работ. Краеугольный камень такого проектирования – расчёт геометрических параметров элементов системы: площади трубы (в сечении), площадей наружной поверхности трубы и внутренней. На этих параметрах строятся все дальнейшие расчёты, в том числе гидравлические, термодинамические и прочностные. Простейшим методам вычисления параметров труб посвящена эта статья.
Для чего нужны геометрические вычисления
Прежде чем начать замерять или узнавать исходные размеры, необходимо осознать, для каких целей послужат произведённые вычисления.
Таких целей несколько:
- Вычисление термодинамических параметров системы. Формула площади поверхности трубы необходима при расчёте теплоотдачи отдельной трубы, участка трубопровода или, к примеру, тёплого пола. Для того чтобы узнать эти параметры, необходимо высчитать общую площадь изделия или системы, с которой в окружающую среду происходит теплоотдача.
- Расчёт теплопотерь по направлению «источник тепла-отопительный прибор». В этом случае наибольшая потеря тепловой энергии происходит на самом длинном участке с наибольшей площадью контакта с окружающей средой, то есть опять-таки в трубах. Поэтому, как и в предыдущем случае, узнав площадь поверхности теплоотдачи, можно, основываясь на этом значении и количестве выделяемого тепла в исходной точке, спланировать число и размер отопительных приборов в будущей системе. Читайте также: «Как рассчитать площадь поверхности трубы – примеры расчета внешней и внутренней площади».

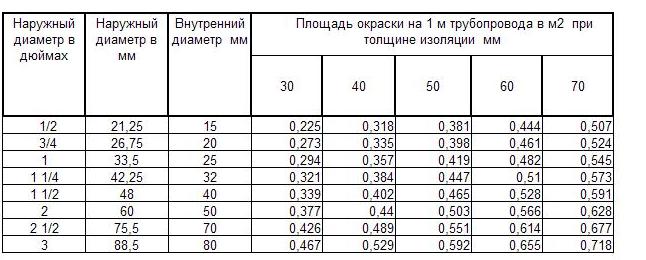
- Оценка необходимого количества теплоизоляционных материалов. При работе труб в условиях холодного климата или резких перепадов наружной температуры без использования утеплителя не обойтись, а чтобы рассчитать точное его количество, необходимо найти площадь труб (в данном случае наружную), которые нужно покрыть термоизоляционным слоем. Следует отметить, что в промышленных масштабах правильный расчёт количества утеплителя поможет значительно сэкономить средства предприятия, сократив затраты и на непредвиденный ремонт (если утеплителя закупили меньше и трубы промёрзли), и на ненужный материал. Впрочем, небольшой запас утеплителя при закупке всё же необходим.
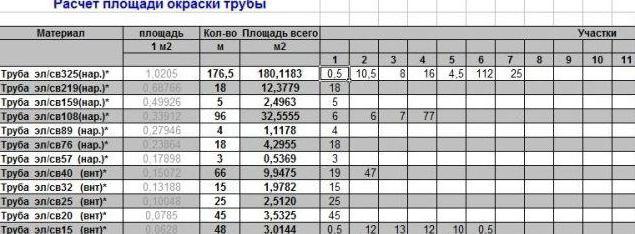
- Расчёт количества денежных средств, необходимых для приобретения нужного количества смазок, антикоррозийных покрытий, красящих веществ и т.п. К примеру, способ, как посчитать площадь трубы под покраску, достаточно прост: необходимое значение рассчитывается с помощью двух параметров – длины трубы и наружного диаметра (о формуле расчёта ниже).

- Вычисление максимальной пропускной способности трубы. Давайте разберемся, как рассчитать пропускную способность трубы правильно. В этом случае необходим расчёт площади сечения трубы. Опираясь на полученное максимальное значение производительности, рассчитывают (в процентном соотношении) и рабочее, которое в итоге и используется в технологической схеме. Следует отметить, что и расчёт проходимости трубы важен для проектирования трубопроводов.
 2,
2,
где l – толщина стенки трубы.
Совет: Используйте наши строительные калькуляторы онлайн, и вы выполните расчеты строительных материалов или конструкций быстро и точно.
Если в первой формуле принять R и D не внешними, а внутренними диаметрами, то учитывать толщину стенки не понадобится, и расчёт можно вести по первому уравнению.
Нужно понимать, что перед тем, как вычислить площадь трубы в сечении, все исходные параметры следует привести к одинаковым единицам измерения (детальнее: «Как рассчитать площадь сечения трубы – простые и проверенные способы»). В принципе, по желанию расчёты можно вести в любых единицах – миллиметрах, сантиметрах, метрах и т.д. главное при проведении дальнейших вычислительных операций привести значение площади к стандартному виду (квадратным метрам).
Следует ещё учитывать, что в напорных трубопроводах рабочая среда перемещается по всему объёму трубы, а в случае устройства самотёчной конструкции жидкость заполняет собой только часть объёма трубы – так называемое живое сечение (прочитайте также: «Как рассчитать объем трубы – советы из практики»).
 При гидравлических расчётах таких систем, соответственно, учитывается именно площадь живого сечения трубы, то есть площадь поперечного сечения перемещающегося в ней потока.
При гидравлических расчётах таких систем, соответственно, учитывается именно площадь живого сечения трубы, то есть площадь поперечного сечения перемещающегося в ней потока.
Вычисление площади наружной поверхности трубы
Как и в предыдущем случае, можно найти площадь трубы через диаметр. Формула расчёта также довольно проста, ведь развёртка площади цилиндра представляет собой прямоугольник, для которого длина одной стороны равна длине окружности наружного сечения, второй – длине отрезка трубы.
Соответственно, формула площади трубы имеет вид:
S=2πRL=πDL,
где R – наружный радиус изделия, D – наружный диаметр, L – продольная длина трубы.
Как и в предыдущем случае, расчёт необходимо вести в одинаковых единицах (например, если диаметр трубы равен 15 мм, а длина – 1,5 м, то при перерасчёте нужно использовать или значения 15 и 1500 мм, или 0,015 и 1,5 м).
Основываясь на величине площади внешней поверхности трубы, рассчитывают необходимое количество красящих материалов или теплоизоляционных веществ.

Вычисление площади внутренней поверхности трубы
Площадь вычисляют по той же формуле, заменяя значения R и D соответственно на внутренние радиус и диаметр.
Можно вычислить требуемое значение и с учётом наружных значений и толщины стенок изделия:
S=2π(R-l)∙L=2π(D/2-l)∙L
Вычисление внутренней площади изделия позволяет проводить гидродинамические расчёты, учитывающие внутреннюю шероховатость.
С этим параметром связано несколько закономерностей:
- при увеличении диаметра трубы влияние шероховатости на движение потока ослабляется;
- если внутренняя поверхность трубы имеет склонность к образованию отложений (например, в случае стальных труб), со временем площадь внутренней поверхности и внутреннего сечения изменяются, а пропускная способность изделия падает.
Как можно убедиться, формулы вычисления основных геометрических параметров труб достаточно просты и могут применяться в расчётах как профессионалами, так и новичками.
как вычислить площадь трубы зная диаметр и длину
Вы искали как вычислить площадь трубы зная диаметр и длину? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти площадь трубы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как вычислить площадь трубы зная диаметр и длину».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни.
 Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как вычислить площадь трубы зная диаметр и длину,как найти площадь трубы,как посчитать площадь поверхности трубы в м2,как посчитать площадь трубы,как посчитать площадь трубы в м2,как рассчитать площадь трубы,как рассчитать площадь трубы для покраски калькулятор,калькулятор площади трубы,калькулятор площади трубы для покраски,калькулятор площадь поперечного сечения трубы онлайн,калькулятор площадь трубы,калькулятор рассчитать площадь трубы,калькулятор расчета площади трубы,квадратный метр трубы,метр квадратный трубы,онлайн площадь трубы,площадь окраски трубы калькулятор,площадь поверхности труб,площадь поверхности трубы,площадь поверхности трубы калькулятор онлайн,площадь поверхности трубы формула,площадь покраски трубы калькулятор,площадь сечения трубы калькулятор онлайн,площадь трубопровода калькулятор,площадь трубы,площадь трубы как найти,площадь трубы калькулятор,площадь трубы калькулятор онлайн,площадь трубы онлайн,площадь трубы онлайн калькулятор,площадь трубы под окраску калькулятор,площадь трубы посчитать,площадь трубы прямоугольной,площадь трубы рассчитать,площадь трубы формула,площадь трубы формула через диаметр,посчитать площадь трубы,рассчитать площадь трубы,рассчитать площадь трубы под покраску,расчет площади для покраски трубы,расчет площади поверхности трубы,расчет площади поверхности трубы калькулятор,расчет площади трубы,расчет площади трубы для окраски,расчет площади трубы для покраски,расчет площади трубы онлайн калькулятор,формула площади трубы,формула площадь поверхности трубы,формула площадь трубы,формула расчета площади трубы.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как вычислить площадь трубы зная диаметр и длину,как найти площадь трубы,как посчитать площадь поверхности трубы в м2,как посчитать площадь трубы,как посчитать площадь трубы в м2,как рассчитать площадь трубы,как рассчитать площадь трубы для покраски калькулятор,калькулятор площади трубы,калькулятор площади трубы для покраски,калькулятор площадь поперечного сечения трубы онлайн,калькулятор площадь трубы,калькулятор рассчитать площадь трубы,калькулятор расчета площади трубы,квадратный метр трубы,метр квадратный трубы,онлайн площадь трубы,площадь окраски трубы калькулятор,площадь поверхности труб,площадь поверхности трубы,площадь поверхности трубы калькулятор онлайн,площадь поверхности трубы формула,площадь покраски трубы калькулятор,площадь сечения трубы калькулятор онлайн,площадь трубопровода калькулятор,площадь трубы,площадь трубы как найти,площадь трубы калькулятор,площадь трубы калькулятор онлайн,площадь трубы онлайн,площадь трубы онлайн калькулятор,площадь трубы под окраску калькулятор,площадь трубы посчитать,площадь трубы прямоугольной,площадь трубы рассчитать,площадь трубы формула,площадь трубы формула через диаметр,посчитать площадь трубы,рассчитать площадь трубы,рассчитать площадь трубы под покраску,расчет площади для покраски трубы,расчет площади поверхности трубы,расчет площади поверхности трубы калькулятор,расчет площади трубы,расчет площади трубы для окраски,расчет площади трубы для покраски,расчет площади трубы онлайн калькулятор,формула площади трубы,формула площадь поверхности трубы,формула площадь трубы,формула расчета площади трубы.
Где можно решить любую задачу по математике, а так же как вычислить площадь трубы зная диаметр и длину Онлайн?
Решить задачу как вычислить площадь трубы зная диаметр и длину вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор диаметра трубы и расхода, онлайн
Когда применим этот калькулятор?
Расчет диаметра трубы с помощью калькулятора диаметра трубы прост.
 Вы можете использовать калькулятор диаметра трубы и расхода для быстрого расчета диаметра трубы
в замкнутой, круглой, прямоугольной (только версия онлайн-калькулятора) и заполненной жидкостью или идеальным газом трубе.
Вы можете использовать калькулятор диаметра трубы и расхода для быстрого расчета диаметра трубы
в замкнутой, круглой, прямоугольной (только версия онлайн-калькулятора) и заполненной жидкостью или идеальным газом трубе.Если система, которую вы анализируете, имеет более одной трубы, вы можете использовать калькулятор анализа трубопроводной сети
Для расчета диаметра трубы с помощью этого калькулятора необходимо знать и ввести скорость потока. Если скорость потока неизвестна, вы должны использовать падение давления калькулятор для расчета диаметра трубы. Вы можете использовать калькулятор падения давления, когда разница давлений между началом и концом трубопровода (потеря напора) доступна как известное значение.
С помощью калькулятора диаметра трубы внутренний диаметр трубы рассчитывается с помощью простое соотношение между расходом, скоростью и площадью поперечного сечения (Q=v·A).

Чтобы рассчитать внутренний диаметр трубы, вы должны ввести только расход и скорость в соответствующие поля в калькуляторе и нажмите кнопку «Рассчитать», чтобы получить результаты.
Помимо внутреннего диаметра трубы, можно рассчитать и другие значения. Вы можете рассчитать скорость потока для заданного расхода жидкости и внутренний диаметр трубы. Поскольку скорость различна в разных местах трубы площадь поперечного сечения, средняя скорость потока вычисляется на основе уравнение непрерывности.
Расход, используемый в калькуляторе, может быть массовым или объемным расходом.
Преобразование между массовым и объемным расходом доступно для заданной плотности жидкости. Кроме того, для идеальных газов преобразование объемного расхода для различных условий потока (давления и температуры), поэтому вы можете быстро рассчитать объемный расход по удельному давлению или температуре в трубе, например, после редукционных клапанов.

Если протекающая жидкость представляет собой идеальный газ, вы можете рассчитать объемный расход этого газа при различные давления и температуры. Например, если вы знаете объемный расход какой-то идеальный газ при заданном давлении и температуре (как при обычном условиях p=101325 Па и T=273,15 K) можно рассчитать фактический объемный расход для давления и температуры, которые реально есть в трубе (например, реальное давление и температура в трубопроводе p=30 psi и t=70 F). Объемный расход идеального газа в этих двух условиях различен. Подробнее о нормальные условия для давления и температуры.
С помощью этого калькулятора вы можете перевести объемный расход из стандартного или какого-либо другого предопределенных условий в фактические условия и наоборот. Калькулятор использует закон сохранения массы для расчета объемного расхода для этих двух условий, что означает, что массовый расход постоянен, несмотря на то, что условия, такие как давление и температура, меняются.

Закон сохранения массы применим, только если поток в закрытой трубе, без добавленного или вычтенного потока, если поток не изменение во времени и некоторые другие условия. Подробнее о массе сохранение массы.
Так когда это не применимо?
Этот калькулятор имеет почти безграничное применение, но некоторые функции зависят от нескольких условия.
Как упоминалось выше, расчет диаметра трубы с помощью этого калькулятора невозможен, если вы не уверен в скорости потока и объемном/массовом расходе. Если что-то из этих двух отсутствует, то вам следует использовать Калькулятор падения давления.
Вы должны знать плотность жидкости, если доступен массовый расход вместо объемного расхода. Если плотность жидкости неизвестна, а известен только массовый расход, то требуемый объемный расход расчет диаметра трубы невозможен.

Для идеальных газов плотность жидкости не обязательна, если известны давление, температура и газовая постоянная для течет газ. Калькулятор использует уравнение идеального газа для расчета плотности. Однако, если текучая среда является газом, но не идеальным (идеальным) газом, т. е. если его давление, температура и плотность не связаны соотношением закон идеального газа, этот калькулятор неприменим, если вы пытаются рассчитать эту плотность газа для известных давления и температуры.
Что нужно знать для расчета диаметра трубы?
Чтобы рассчитать диаметр трубы, вы должны знать скорость потока и скорость потока. Если известен массовый расход, то должна быть известна плотность жидкости.
Если текучей средой является газ, то вместо плотности необходимо знать газовую постоянную, абсолютное давление и температуру. Плотность рассчитывается по формуле идеального газа.

Что нужно знать, чтобы рассчитать скорость потока?
Для расчета скорости потока необходимо знать скорость потока и внутренний диаметр трубы. Если известен массовый расход, то должна быть известна плотность жидкости.
Если текучей средой является газ, то вместо плотности необходимо знать газовую постоянную, абсолютное давление и температуру. Плотность рассчитывается по формуле идеального газа.
Как производится расчет?
Для расчета диаметра трубы и скорости потока используется уравнение неразрывности, которое дает связь между скоростью потока, скоростью потока и внутренним диаметром трубы.
Для потока газа уравнение идеального газа используется для расчета плотности по газовой постоянной, абсолютному давлению и температуре.
2.1: Формы вещей
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7127
- Майк Алворд
- College of the Canyons через учебники ZTC
- Длина = 30 футов, ширина = 10 футов 30 футов x 10 футов = 300 футов 2
- Высота = 15 футов, ширина = 7 футов 15 футов x 7 футов = 105 футов 2
- Ширина = 5 футов и 7 футов, высота = 6 футов
- (5 футов + 7 футов) / 2 x 6 футов = 36 футов 2
- Ширина = 8 футов и 12 футов, глубина = 10 футов
- (8 футов + 12 футов) / 2 x 10 футов = 100 футов 2
- D = 100 футов, высота = 20 футов
- 3,14 x 100 футов = 314 футов (что означает «L»)
- 314 футов x 20 футов = 6 280 футов 2
Какова площадь отверстия трубы диаметром 10 дюймов?
Прямоугольный канал пропускает через себя миллионы галлонов воды и сбрасывает ее в резервуар для хранения. Канал имеет длину 2 мили, ширину 3 фута и глубину 2 фута. Какова площадь раскрытия канала?
Канал имеет ширину 3 фута внизу и 5 футов наверху, а глубина воды составляет 4 фута, когда канал заполнен.
 Какова площадь канала?
Какова площадь канала?Приподнятый резервуар для хранения имеет форму сферы и нуждается в повторном покрытии. Если диаметр резервуара 65 футов, какова площадь поверхности?
Необходимо покрасить стояк. Какова площадь поверхности всего стояка? Он имеет диаметр 30 футов и высоту 80 футов.
Какова площадь поверхности сферической конструкции диаметром 42 фута?
Необходимо покрасить коробчатую конструкцию. Это 20 футов в ширину, 30 футов в длину и 10 футов в высоту. Какова общая площадь всех шести поверхностей (только внутри)?
Какова площадь внутренней поверхности трубы диаметром 32 дюйма и длиной 1000 футов, увенчанной полусферой на конце? (Предположим, что диаметр сферы не входит в длину)
Каков объем сферы диаметром 30 футов?
Каков объем 2000 футов трубы диаметром 18 дюймов?
Акведук длиной 5 миль имеет ширину 5 футов у дна и 8 футов у линии воды. Если глубина воды составляет 6 ½ футов, сколько акров футов воды находится в акведуке?
Отстойник имеет длину 100 футов, ширину 30 футов и глубину 20 футов. Сколько галлонов он может вместить?
Напорная труба имеет высоту 80 футов и диаметр 25 футов. Если предположить, что верхняя часть стояка имеет форму полусферы, сколько галлонов она вместит?
Для транспортировки воды от источника к очистке, к системе распределения и, в конечном итоге, к потребителю, ей необходимо протекать через геометрические фигуры.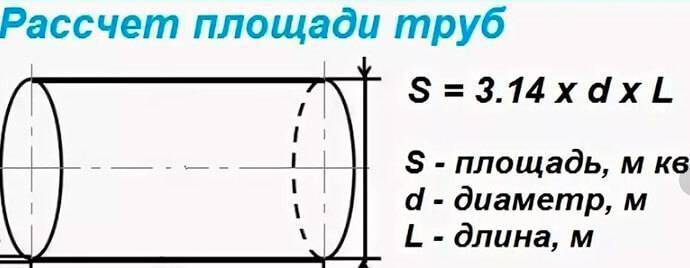 Акведук доставляет воду из Северной Калифорнии в Южную Калифорнию. Резервуары и резервуары хранят воду до того, как она попадет в процесс очистки. Трубы пропускают воду через очистные сооружения и через распределительную систему. Наземные резервуары для хранения и приподнятые резервуары для хранения содержат воду и обеспечивают давление в системе распределения. Это грубое описание пути, по которому идет вода, но оно иллюстрирует различные структуры и формы, через которые вода должна проходить.
Акведук доставляет воду из Северной Калифорнии в Южную Калифорнию. Резервуары и резервуары хранят воду до того, как она попадет в процесс очистки. Трубы пропускают воду через очистные сооружения и через распределительную систему. Наземные резервуары для хранения и приподнятые резервуары для хранения содержат воду и обеспечивают давление в системе распределения. Это грубое описание пути, по которому идет вода, но оно иллюстрирует различные структуры и формы, через которые вода должна проходить.
Площади
Вычисление площадей — это первый шаг в работе с геометрическими фигурами. Площади используются для определения того, сколько краски нужно купить, сколько воды может протекать по трубе и многого другого. Круг, прямоугольник и трапеция, вероятно, являются наиболее распространенными формами, с которыми вы столкнетесь в водном хозяйстве. Однако можно встретить и сферу, треугольник, полукруг с прямоугольником. Именно на этих структурах мы сосредоточимся в этой главе.
\[0,785 \mathrm{D}^{2} \quad \mathrm{LW}\left(\frac{b_{1}+b_{2}}{2}\right) H\] 92\]
0,785 заменяет \(\pi\), а диаметр заменяет радиус. Квадрат диаметра в четыре раза больше квадрата радиуса, а 0,785 составляет одну четвертую от \(\pi\).
Квадрат диаметра в четыре раза больше квадрата радиуса, а 0,785 составляет одну четвертую от \(\pi\).
Обратите особое внимание на единицы измерения диаметра. Много раз (особенно когда речь идет о трубах) диаметр будет указываться в какой-либо другой единице измерения, кроме футов (например, дюймов). Преобразование диаметра в футы в качестве первого шага позволит избежать получения квадратных единиц, отличных от квадратных футов. Иногда диаметр трубы может быть указан в метрических единицах. Это обычное дело при работе с Департаментом транспорта Калифорнии.
Примеры
Какова площадь каждого из перечисленных ниже диаметров?
Данный диаметр | Преобразование | Формула | Ответ |
|---|---|---|---|
24 в | 24 дюйма / 12 дюймов = 2 фута | 0,785 x (2 фута) 2 | 3,14 фута 2 |
130 в | 130 дюймов / 12 дюймов = 10,8 футов | 0,785 x (10,8 фута) 2 | 91,5 фута 2 |
813 мм | 813 мм / 304,5 мм = 2,67 фута | 0,785 x (2,67 фута) 2 | 5,6 фута 2 |
Прямоугольники
Для вычисления площади прямоугольника или квадрата достаточно просто умножить длину на ширину. Если вы рисуете стены, потолок или пол комнаты, перспектива немного меняется. Например, размеры стены могут выглядеть как ширина и высота, когда вы стоите и смотрите на нее. Пол может выглядеть как ширина и длина. Независимо от перспективы, формула площади одинакова.
Если вы рисуете стены, потолок или пол комнаты, перспектива немного меняется. Например, размеры стены могут выглядеть как ширина и высота, когда вы стоите и смотрите на нее. Пол может выглядеть как ширина и длина. Независимо от перспективы, формула площади одинакова.
Примеры
Какова площадь каждого из следующих прямоугольников, перечисленных ниже?
Трапеции
Трапеции чаще всего имеют форму акведука. Акведуки обычно представляют собой мили и мили бетонных каналов трапециевидной формы. У них плоское узкое дно, которое поднимается до более широких расстояний наверху. Чтобы вычислить различные расстояния поперек трапеции, добавьте расстояние (ширина, b2) через низ к расстоянию (ширина, b1) через верх и разделите на 2. Это дает среднюю ширину. Затем умножьте среднюю ширину на высоту или глубину трапеции, чтобы вычислить площадь.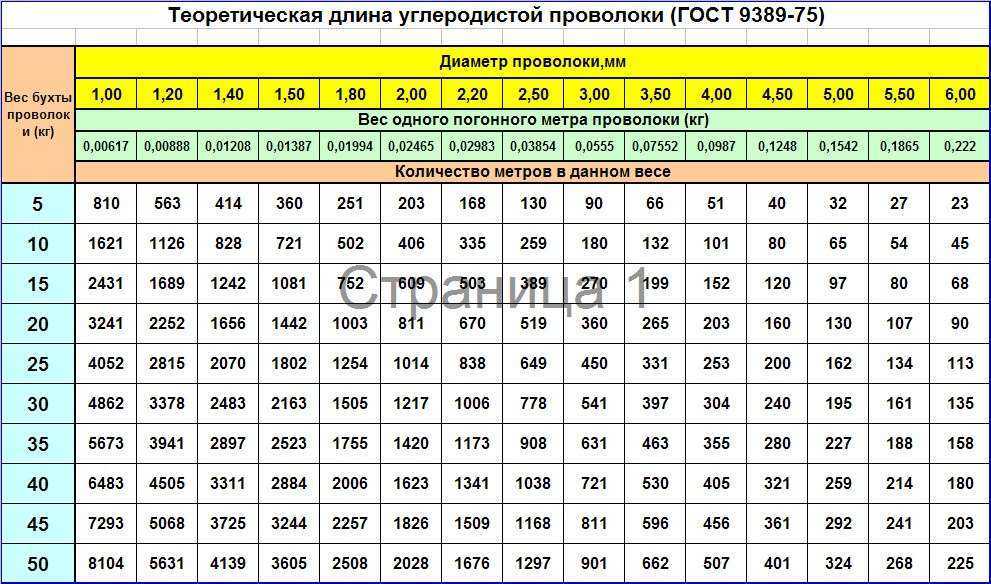
Примеры
Сферы и другие формы
Как указывалось ранее, круги, прямоугольники и трапеции являются наиболее распространенными формами в водном хозяйстве. Однако большие стояки в форме цилиндра со сферой наверху или приподнятый резервуар для хранения в форме сферы могут быть очень распространены на Среднем Западе. Полукруги и прямоугольники также могут быть резервуарами или отстойниками. Поэтому понимание того, как рассчитать площадь для этих типов конструкций, также важно.
Расстояние вокруг цилиндра рассчитывается как Пи (3.14), умноженное на диаметр. Пи — безразмерная константа. Его также можно рассматривать как «длину» вокруг цилиндра. Как только «длина» рассчитана, умножьте это число на высоту или глубину, чтобы получить площадь.
Примеры
Когда площадь вычисляется для сферы, это вся площадь поверхности «шара». Сферы могут быть обычным явлением на Среднем Западе в качестве приподнятых хранилищ. Формула площади сферы: 4 умножить на 0,785 диаметра в квадрате.
Примеры
D = 50 футов 4 x 0,785 x (50 футов) 2 = 7850 футов 2
D = 35 футов 4 x 0,785 x (35 футов) 3,4 3 2
Упражнения
Объемы
Чтобы рассчитать объем внутри конструкции, в формулу площади необходимо включить третье измерение.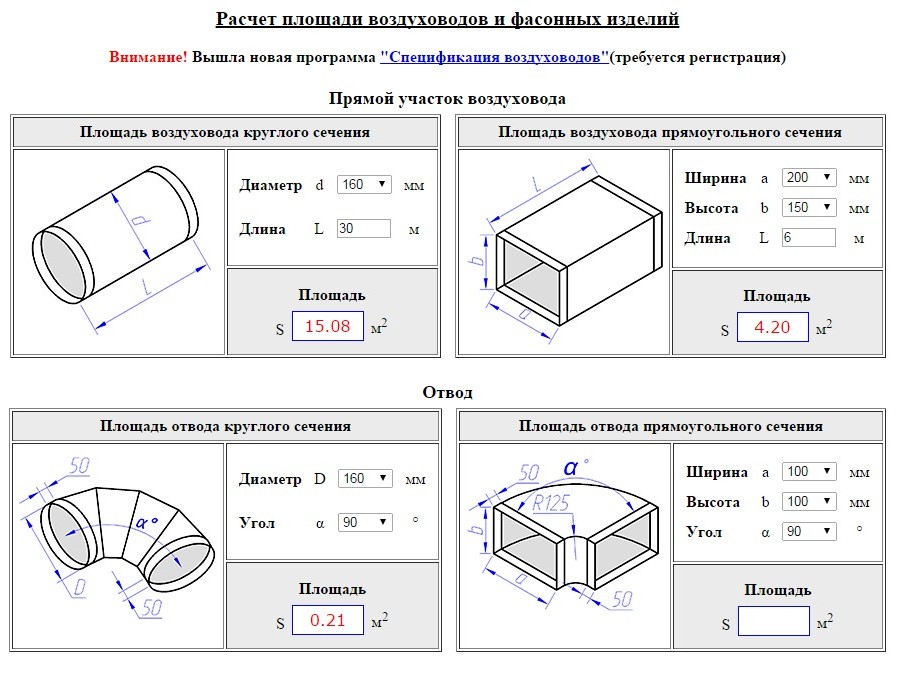 Например, если кругу задана длина или высота, он становится цилиндром, и можно вычислить объем. Если трапеция или прямоугольник имеют длину, они становятся трехмерной структурой с объемом, который можно вычислить.
Например, если кругу задана длина или высота, он становится цилиндром, и можно вычислить объем. Если трапеция или прямоугольник имеют длину, они становятся трехмерной структурой с объемом, который можно вычислить.
Упражнения
Эта страница под названием 2.



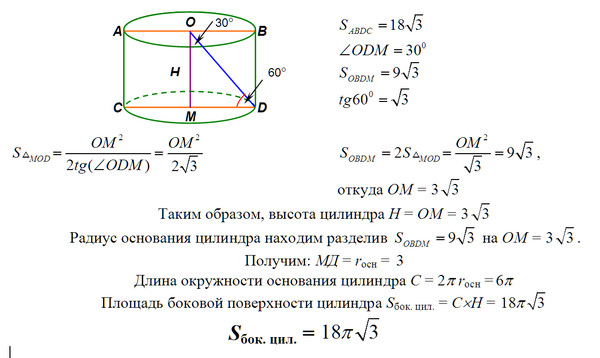 2,
2,
 При гидравлических расчётах таких систем, соответственно, учитывается именно площадь живого сечения трубы, то есть площадь поперечного сечения перемещающегося в ней потока.
При гидравлических расчётах таких систем, соответственно, учитывается именно площадь живого сечения трубы, то есть площадь поперечного сечения перемещающегося в ней потока.

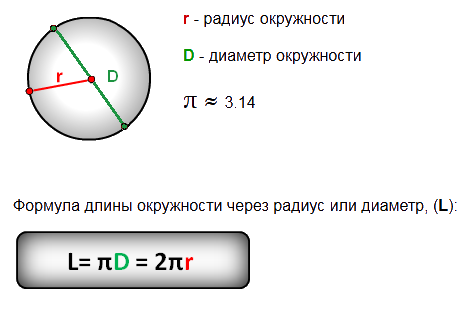 Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как вычислить площадь трубы зная диаметр и длину,как найти площадь трубы,как посчитать площадь поверхности трубы в м2,как посчитать площадь трубы,как посчитать площадь трубы в м2,как рассчитать площадь трубы,как рассчитать площадь трубы для покраски калькулятор,калькулятор площади трубы,калькулятор площади трубы для покраски,калькулятор площадь поперечного сечения трубы онлайн,калькулятор площадь трубы,калькулятор рассчитать площадь трубы,калькулятор расчета площади трубы,квадратный метр трубы,метр квадратный трубы,онлайн площадь трубы,площадь окраски трубы калькулятор,площадь поверхности труб,площадь поверхности трубы,площадь поверхности трубы калькулятор онлайн,площадь поверхности трубы формула,площадь покраски трубы калькулятор,площадь сечения трубы калькулятор онлайн,площадь трубопровода калькулятор,площадь трубы,площадь трубы как найти,площадь трубы калькулятор,площадь трубы калькулятор онлайн,площадь трубы онлайн,площадь трубы онлайн калькулятор,площадь трубы под окраску калькулятор,площадь трубы посчитать,площадь трубы прямоугольной,площадь трубы рассчитать,площадь трубы формула,площадь трубы формула через диаметр,посчитать площадь трубы,рассчитать площадь трубы,рассчитать площадь трубы под покраску,расчет площади для покраски трубы,расчет площади поверхности трубы,расчет площади поверхности трубы калькулятор,расчет площади трубы,расчет площади трубы для окраски,расчет площади трубы для покраски,расчет площади трубы онлайн калькулятор,формула площади трубы,формула площадь поверхности трубы,формула площадь трубы,формула расчета площади трубы.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как вычислить площадь трубы зная диаметр и длину,как найти площадь трубы,как посчитать площадь поверхности трубы в м2,как посчитать площадь трубы,как посчитать площадь трубы в м2,как рассчитать площадь трубы,как рассчитать площадь трубы для покраски калькулятор,калькулятор площади трубы,калькулятор площади трубы для покраски,калькулятор площадь поперечного сечения трубы онлайн,калькулятор площадь трубы,калькулятор рассчитать площадь трубы,калькулятор расчета площади трубы,квадратный метр трубы,метр квадратный трубы,онлайн площадь трубы,площадь окраски трубы калькулятор,площадь поверхности труб,площадь поверхности трубы,площадь поверхности трубы калькулятор онлайн,площадь поверхности трубы формула,площадь покраски трубы калькулятор,площадь сечения трубы калькулятор онлайн,площадь трубопровода калькулятор,площадь трубы,площадь трубы как найти,площадь трубы калькулятор,площадь трубы калькулятор онлайн,площадь трубы онлайн,площадь трубы онлайн калькулятор,площадь трубы под окраску калькулятор,площадь трубы посчитать,площадь трубы прямоугольной,площадь трубы рассчитать,площадь трубы формула,площадь трубы формула через диаметр,посчитать площадь трубы,рассчитать площадь трубы,рассчитать площадь трубы под покраску,расчет площади для покраски трубы,расчет площади поверхности трубы,расчет площади поверхности трубы калькулятор,расчет площади трубы,расчет площади трубы для окраски,расчет площади трубы для покраски,расчет площади трубы онлайн калькулятор,формула площади трубы,формула площадь поверхности трубы,формула площадь трубы,формула расчета площади трубы.
 Вы можете использовать калькулятор диаметра трубы и расхода для быстрого расчета диаметра трубы
в замкнутой, круглой, прямоугольной (только версия онлайн-калькулятора) и заполненной жидкостью или идеальным газом трубе.
Вы можете использовать калькулятор диаметра трубы и расхода для быстрого расчета диаметра трубы
в замкнутой, круглой, прямоугольной (только версия онлайн-калькулятора) и заполненной жидкостью или идеальным газом трубе.

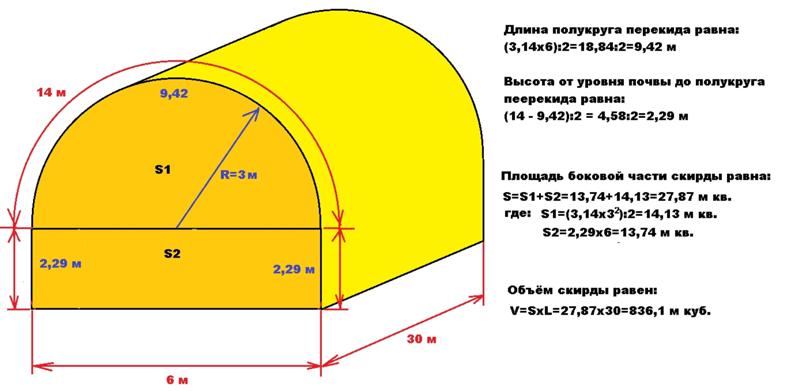
 Какова площадь канала?
Какова площадь канала?