Как найти сторону подобного треугольника: Стороны треугольника = 80, 160, 200. Найти стороны подобного ему треугольника периметр которого ревен 550см.

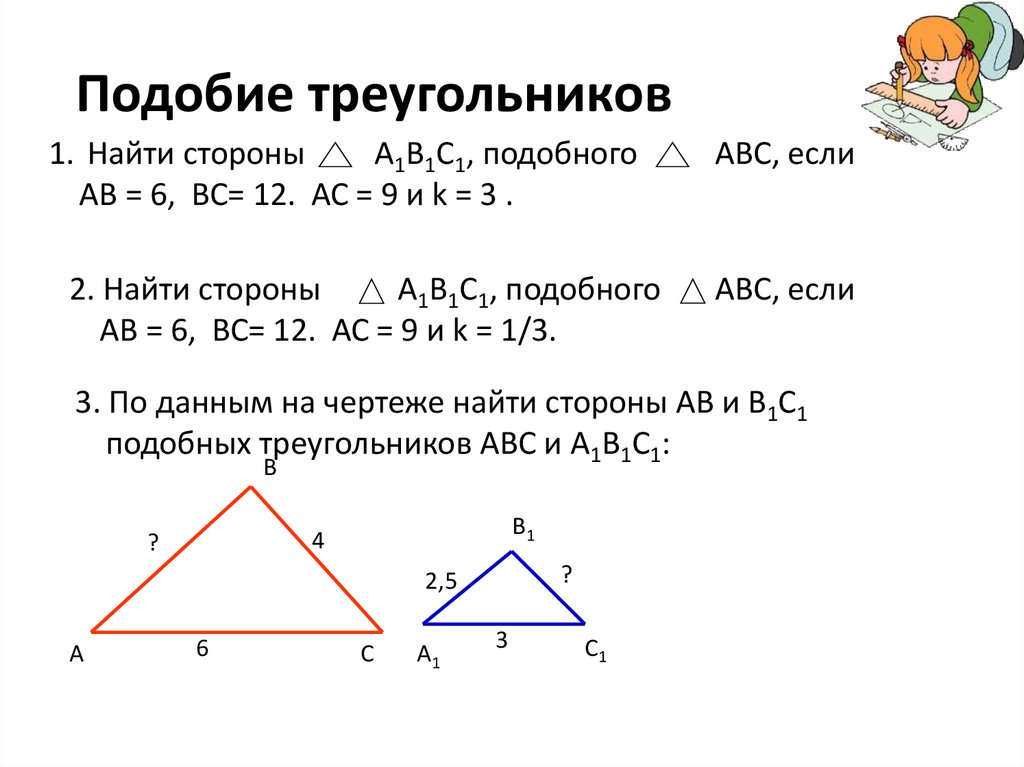
Подобные треугольники — презентация онлайн

1. Подобные треугольники.

Геометрия, 8 класс.
5klass.net

2. Урок 32. Пропорциональные отрезки.

Рассмотрим пропорцию: К
2 8
4 16
Х
Н
В
А
Отрезки называются
пропорциональными, если
равны отношения их длин.
КЕ АВ
НХ РТ
Е
Р
Решение задач:
№ 533 (устно)
№ 534.
Т

3. Свойство биссектрисы треугольника.

Биссектриса треугольника делит противоположную сторону на
отрезки, пропорциональные прилежащим сторонам треугольника.
В
АК СК
АВ СВ
А
К
С
Решение задач: № 536(а), 538.
Домашнее задание: п.56, № 536(б), 537.

4. Урок 33. Подобные треугольники.

В
А
М
С
Р
К
Два треугольника называются подобными,
если
их углы соответственно равны, и стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника.
АВ ВС АС
k
МР РК МК
где k – коэффициент подобия.
Говорят, что ∆АВС ~ ∆МРК

5. № 541.

А
106
E
5,2
106
4,4
С
34
15,6
В
7,6
13,2
40
F
22,8
Решение задач: № 542.
Домашнее задание: п.56-57, № 540.
D

6. Урок 34. Теорема об отношении площадей подобных треугольников.

В
ТЕОРЕМА.
Отношение площадей двух подобных
треугольников равно квадрату
коэффициента подобия.
А
М
С
Р
К
S ABC
k2
S MPK
где k – коэффициент подобия.
Отношение периметров двух
подобных
треугольников равно коэффициенту
РABC
подобия.
РMPK
k
Решение задач: № 545, 549.
Домашнее задание: п. 56-58, № 544, 548.

7. Урок 35. Первый признак подобия треугольников.

ТЕОРЕМА.
В
Если 2 угла одного треугольника равны
соответственно двум углам другого треугольника,
то такие треугольники подобны.
Доказательство: Так как углы А=А1 и С=С1, то угол
В=В1.
А
А1
С
В1
С1
Так как угол одного треугольника равен углу
другого треугольника, то площади этих
треугольников относятся как произведения
сторон, заключающих эти углы.
S ABC
S A1 B1C1
AB AC
;
A1 B1 A1C1
S ABC
S A1 B1C1
BC AC
;
B1C1 A1C1
AB
BC
;
A1 B1
B1C1
S ABC
AB BC
;
S A1 B1C 1
A1 B1 B1C1
AB
BC
AC
A1 B1
B1C1
A1C1
Следовательно, ∆АВС ~ ∆А1В1С1

8. № 550.

а
x
8
а
12
6
y
10
20
8
Домашнее задание: п. 59, № 553, 561.

9. Урок 36. Первый признак подобия треугольников.

№ 551(а)
B
C
7
4
10
A
?
E
8
D
?
F

10. № 552(а)

A
B
4
10
D
O
25
C

11. № 557(в).

D
B
12
A
C
E
Домашнее задание: стр.160, вопросы 15,

12. Урок 37. Второй признак подобия треугольников.

В1 Самостоятельная работа: стр.120, вариант А1,А2, №1.
С1
А
1
В
А
С
1
2
В2
ТЕОРЕМА. Если 2 стороны одного
треугольника пропорциональны двум
сторонам другого треугольника и углы,
заключенные между этими сторонами равны,
то такие треугольники подобны.
Доказательство:
Достаточно доказать, что углы С = С1.
Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1.
∆А1В1С1 ~∆АВ2С по 2 углам, следовательно
АС
АВ2
АС
АВ
; но
А1С1 А1 В1
А1С1 А1 В1
Значит АВ2 = АВ и ∆АВ2С = ∆АВС по 2 сторонам
и углу между ними => угол С=2, но угол 2=С1 =>
угол С1 = С => ∆А1В1С1 ~∆АВС по 2 углам

13. Задача 1.

O
6
9
B
A
12
15
5
D
?
C

14. Задача 2.

D
?
1 часть
5
Домашнее
задание:
C
O
п. 59, 60, № 559.
15
3 части
A
?
B

15. Задача.

В
Задача.
Р
К
А
М
С
Стороны треугольника АВС в 2,5 раза больше сторон
треугольника КРМ, углы В = Р, АС + КМ = 4,2. Найти
АС и КМ.

16. Урок 38. Третий признак подобия треугольников.

ТЕОРЕМА. Если 3 стороны одного
треугольника пропорциональны трем
сторонам другого треугольника, то такие
треугольники подобны.
Доказательство:
Достаточно доказать, что углы А = А1.
Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1.
∆А1В1С1 ~∆АВ2С по 2 углам, следовательно
В1
С1
А
1
В
А
С
1
2
АВ2 В2С
СА
А1 В1 В1С1 С1 А1
Но мы знаем, что
АВ
ВС
СА
А1 В1 В1С1 С1 А1
В2
Значит АВ2 = АВ, СВ2=СВ и ∆АВ2С = ∆АВС по 2
сторонам и углу между ними => угол А=1, но
угол
1=А1 => угол С1 = С => ∆А1В1С1 ~∆АВС по 2
признаку

17. Задачи.

1.
2.
Подобны ли ∆АВС и ∆КРМ, если АВ = 1м, АС = 2м, ВС = 1,5 м,
КР = 8 дм, КМ = 16 дм, РМ = 12 дм.
Стороны треугольника равны 0,8 м, 1,6 м, 2 м. Найти стороны
подобного ему треугольника, периметр которого равен 5,5 м.
Домашнее задание: п. 59-61, № 560.

18. Математический диктант.

1.
2.
3.
4.
5.
Третий признак подобия
треугольников.
Второй признак подобия
треугольников.
У двух треугольников по одному
равному углу. Какого условия
недостает, чтобы треугольники
были подобны по 1 признаку?
Стороны одного треугольника
равны 3 см, 6 см и 7 см, а 2
стороны подобного ему
треугольника равны 15 см и 35
см. Найти третью сторону.
Соответствующие катеты двух
подобных треугольников 6 дм и
18 дм. Найти гипотенузу
меньшего треугольника, если
гипотенуза большего 27 дм.
1.
2.
3.
4.
5.
Первый признак подобия
треугольников.
Третий признак подобия
треугольников.
У двух треугольников по одному
равному углу. Какого условия
недостает, чтобы треугольники
были подобны по 2 признаку?
Соответствующие катеты двух
подобных треугольников 5 дм и
10 дм. Найти гипотенузу
большего треугольника, если
гипотенуза меньшего 7 дм.
Стороны одного треугольника
равны 15 см, 35 см и 30 см, а 2
стороны подобного ему
треугольника равны 6 см и 7 см.
Найти третью сторону.

19. Ответы.

1.
2.
3.
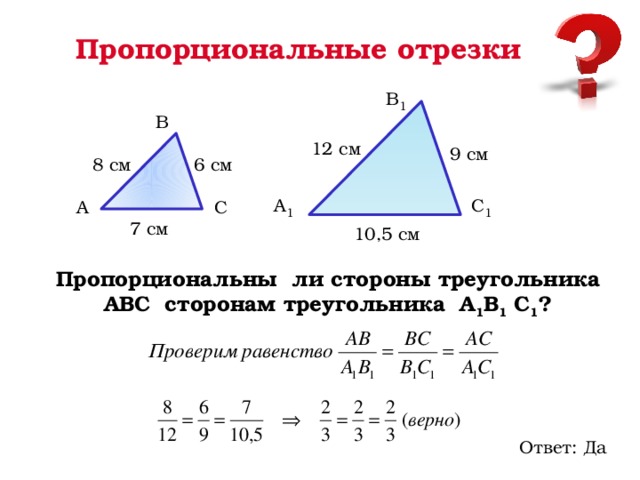
4.
5.
По 3 пропорциональным сторонам.
По 2 пропорциональным сторонам и углу
между ними.
Пара равных углов.
30 см.
9 дм.
1. По 2 равным углам.
2. По 3
пропорциональным
сторонам.
3. Пропорциональност
ь сторон угла.
4. 14 дм.
5. 3 м.

20. Подобие прямоугольных треугольников.

1.
2.
3.
Два прямоугольных треугольника подобны,
если:
У них есть по равному острому углу.
Катеты одного треугольника
пропорциональны катетам другого
треугольника.
Гипотенуза и катет одного треугольника
пропорциональны гипотенузе и катету
другого треугольника.

21. Задача.

B
C
15
18
12
O
10
D
A
Доказать, что ABCD – трапеция.

22. № 554.

M
Домашнее
задание:
п. 59-61,
Стр. 160,
вопросы 1-7,
задача
A
B
C
5
3,6
3,9
8
D
Задача. Продолжение боковых сторон АВ и CD трапеции
ABCD пересекаются в точке Е. 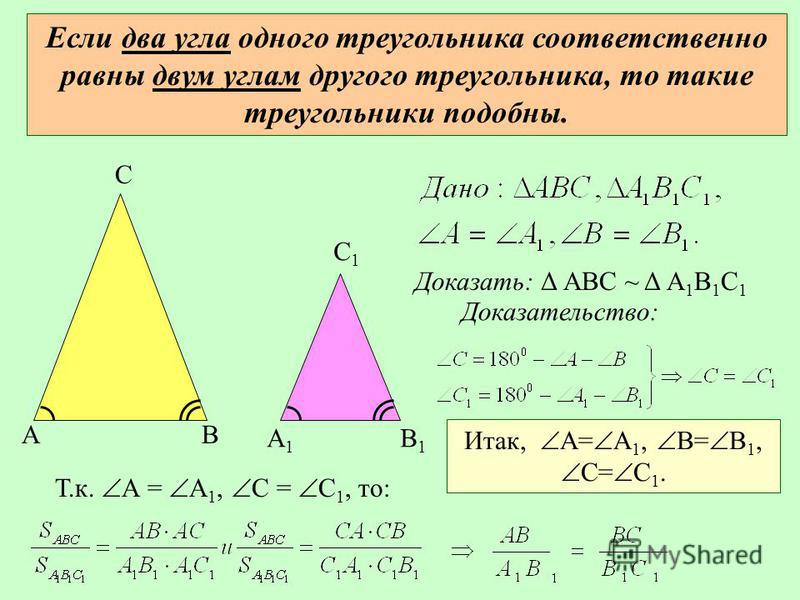Найти стороны ∆АЕD,
если АВ = 5 см, ВС = 10 см, АD = 15 см, СD = 8 см.

23. Урок 39. Средняя линия треугольника.

В
К
А
Р
С
ТЕОРЕМА.
Средняя линия треугольника
параллельна одной из его сторон и
равна половине этой стороны.
Доказательство:
∆АВС ~ ∆КВР, так как угол В-общий, а
стороны АВ и КВ, СВ и РВ
пропорциональны => угол А=ВКР, но это
соответственные углы => КР ll АС.
Средней линией
треугольника называется
КВ КВ 1 ВР 1
КР 1
1
;
КР АС
отрезок, соединяющий
АВ 2 КВ 2 ВС 2
АС 2
2
середины двух его
сторон.
ТЕОРЕМА. Медианы
треугольника
пересекаются в одной
точке, которая делит
каждую медиану в
отношении 2:1, считая от
вершины.

24. Решение задач.

№ 564.
№ 570.
В
8
M
5
7
С
18
O
А
Домашнее задание: п. 62, № 566.
D

25. Математический диктант.

1.
2.
3.
4.
Две стороны треугольника
соединили отрезком,
непараллельным третьей
стороне. Является ли этот отрезок
средней линией треугольника?
Сторона АВ ∆АВС равна 6 см.
Чему равна средняя линия
треугольника, параллельная этой
стороне?
Точки М, Р и О – середины сторон
∆АВС. Найти стороны ∆АВС,
если стороны ∆МРО равны 3 см,
4 см и 5 см.
Концы отрезка АВ лежат на двух
сторонах треугольника, а длина
этого отрезка равна половине
третьей стороны. Обязательно ли
этот отрезок является средней
линией треугольника?
1.
2.
3.
4.
Точки А и В являются
серединами двух сторон
треугольника. Как называется
отрезок АВ?
Средней линией ∆АВС,
параллельная стороне ВС, равна
4 см. Найти сторону ВС.
Точки А, В, С – середины сторон
∆МРО. Найти периметр ∆АВС,
если отрезки МР, РО и МО
равны 3 дм, 4 дм и 5 дм.
Концы отрезка КР лежат на двух
сторонах треугольника, он
параллелен третьей стороне
треугольника и равен ее
половине. Является ли КР
средней линией?

26.

Ответы.1.
2.
3.
4.
Нет
Средняя линия
24 см
Нет
1.
2.
3.
4.
Средняя линия
8 см
6 дм
Нет

27. Задачи.

1. Дано:
2. Дано:
РАВС= 12 см
AD=2BC, MB=MK,
Найти: РМРО
NC=NK, BC=6 см
В
Р
Найти PQ
B
C
6
P
Q
M
N
D
A
О
3. Дано:
А
С
М
АС=10см, BD=8см
Найти РMNPK
M
B
N
C
A
K
P
D

28. Урок 40. Пропорциональные отрезки в прямоугольном треугольнике.

С
b
h
a
с
А
bc
Н ac В
Высота прямоугольного
треугольника, проведенная
из вершины прямого угла,
делит треугольник на 2
подобных прямоугольных
треугольника, каждый из
которых подобен данному
треугольнику.
• Признак подобия прямоугольных
треугольников. Два прямоугольных
треугольника подобны, если у них есть
по равному острому углу.
• Отрезок XY называется средним
пропорциональным (средним
геометрическим) для отрезков АВ и CD,
если XY AB CН
• Свойство 1. 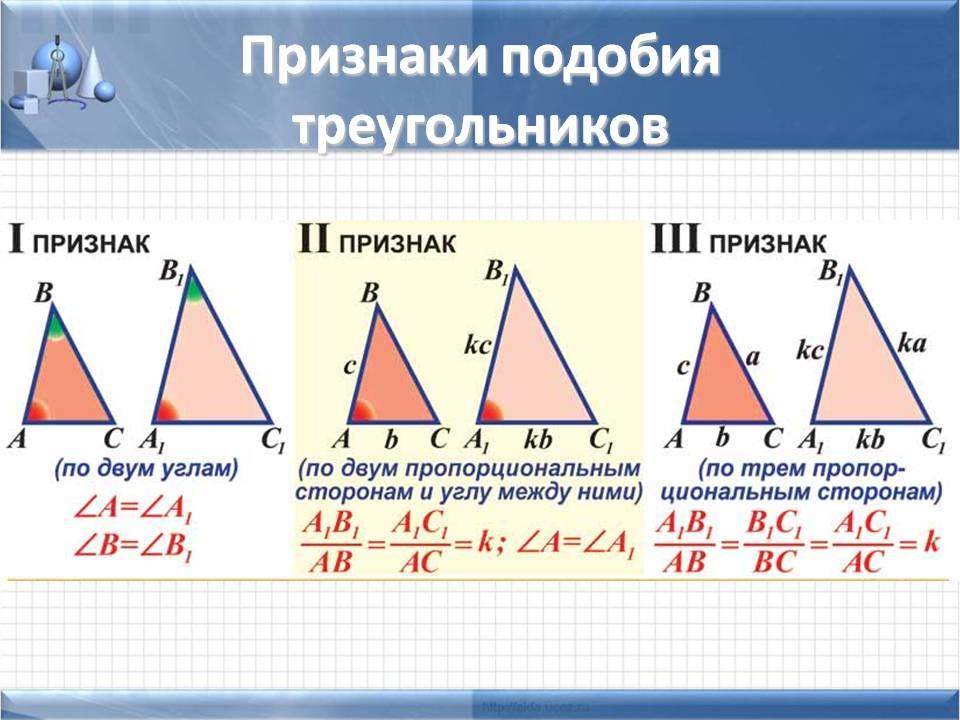Высота прямоугольного
треугольника, проведенная из вершины
прямого угла, есть среднее
пропорциональное между проекциями
катетов на гипотенузу.
СН АН ВН
Свойство 2. Катет прямоугольного
треугольника есть среднее
пропорциональное между гипотенузой и
проекцией этого катета на гипотенузу.
АС АВ АН ;
ВС АВ ВН
• Решение задач: № 572, 575, 577.
• Домашнее задание:
стр.160, вопросы 8-11, принести циркуль,
№ 576, 578-в общую тетрадь.
• Проверочная работа.
стр. 124, вариант А1, А2,
задачи 1, 2.

30. Урок 42. Синус, косинус и тангенс острого угла прямоугольного треугольника.

В
• Синусом острого угла прямоугольного
β
α
А
С
BC
sin
AB
cos
AC
AB
BC
tg
AC
треугольника называется отношение
противолежащего катета к гипотенузе.
• Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе.
• Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему.
• Тангенс угла равен отношению синуса к
косинусу этого угла.
BC
sin A
BC
AB
tgA
AC
cos A
AC
AB

31. Основное тригонометрическое тождество.

sin 2 cos 2 ?
BC 2 AC 2 BC 2 AC 2 AB 2
1
2
2
2
2
AB
AB
AB
AB
sin 2 cos 2 1
Решение задач: № 591(а,б), 592(а,в,д), 593(а,в).
Домашнее задание: п.66, № 593(б,г), 592(б,г,е), 591(в,г).

32. Урок 43. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.

BC
В
60°
30°
А
С
1
AB,
2
cos A cos 30
tg 30
sin 30
cos 30
cos B cos 60
sin 60
1 1
4
sin 60
tg 60
cos 60
1
AB
1
2
;
AB
2
3
3
1 1
;
4
4
2
1
2 1 ;
3
3
2
1 AB
BC
1
2
;
AB
AB
2
3
3
;
4
2
BC
sin A sin 30
AB
3
2
1
2
3;

33. Урок 43. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.

А
Пусть АС = ВС = а, тогда
45°
АВ а 2 а 2 2а 2 а 2 ;
а
С
а
В
BC
a
1
2
sin 45
;
AB a 2
2
2
AC
a
1
2
cos 45
;
AB a 2
2
2
sin 45
tg 45
1.
cos 45

34. Решение задач.

1.
2.
3.
4.
Найти площадь равнобедренного прямоугольного
треугольника с основанием 10 см и углом при основании
45°.
Найти катеты прямоугольного треугольника, гипотенуза
которого 2 см, один из острых углов 30°.
В треугольнике АВС угол А=45°, угол С=60°, ВС=2 см.
Найти АС.
№ 600.
Домашнее задание: п. 66, 67, № 602.

35. Контрольная работа № 4.

1.
2.
3.
Средняя линия равнобедренного треугольника,
параллельная боковой
стороне, равна 13 см, а
медиана, проведенная к
основанию — 24 см. Найти
среднюю линию, параллельную основанию
треугольника.
Найти sin α и tg α, если
cosα=8/17.
Найти синус, косинус
тангенс большего острого
угла прямоугольного
треугольника с катетами 7
см и 24 см.
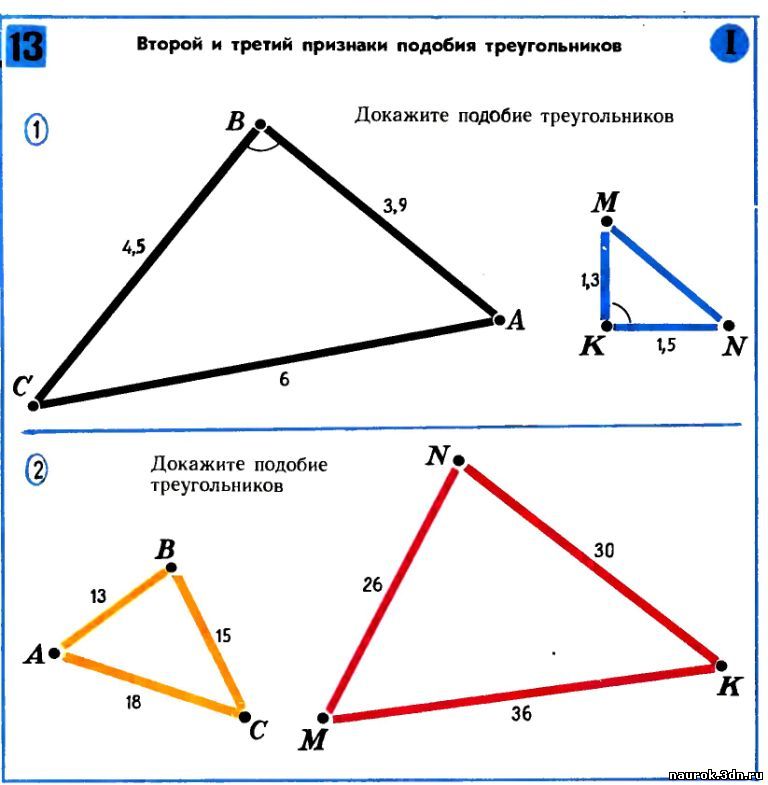
1.
2.
3.
Средняя линия равнобедренного треугольника,
параллельная основанию,
равна 16 см, а биссектриса, проведенная к
основанию — 30 см.
Найти среднюю линию,
парал-лельную боковой
стороне треугольника.
Найти cos α и tg α, если
sinα=5/12.
Найти синус, косинус
тангенс меньшего острого
угла прямоугольного
треугольника с катетом
40 см и гипотенузой 41
см.

Отношение площадей подобных треугольников – определение

3.9

Средняя оценка: 3.9

Всего получено оценок: 309.

3.9

Средняя оценка: 3.9

Всего получено оценок: 309.

Знание признаков подобия треугольников и умение эти признаки использовать открывает новые пути в решениях задач. Иногда ученики встают в ступор при необходимости определения отношения площадей подобных треугольников из-за новизны подхода к выводу формулы. Рассмотрим сам вывод для того, чтобы понять принцип и использовать его в дальнейшем для решения задач.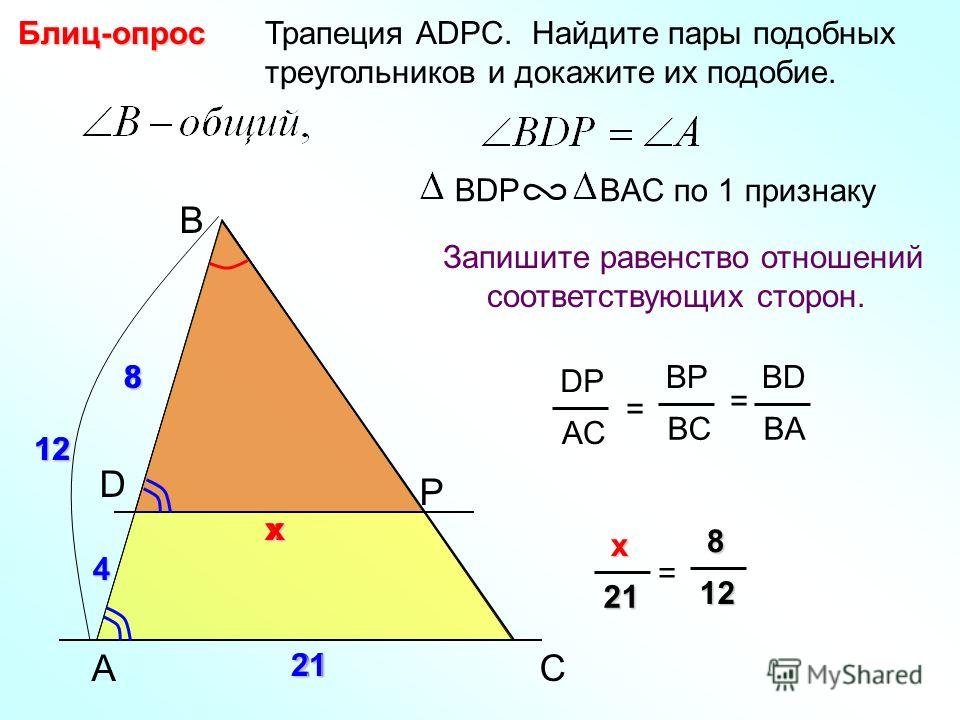

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Подобие

Подобными треугольниками называются треугольники, длины всех сторон которых пропорциональны друг другу, а углы равны. Отношение соответствующих сторон в подобных треугольниках всегда равно одному и тому же числу, которое называется коэффициентом подобия.

Рис. 1. Подобные треугольники

Коэффициент подобия часто используется для решения задач на подобные треугольники, ведь можно через одно отношение найти коэффициент, после выразить неизвестную сторону через известную. Коэффициент подобия обозначают буквой k.

Не нужно зацикливаться только на треугольниках. Хотя признаки подобия выведены только для них, любая фигура в геометрии имеет подобную. То же касается и равенства фигур: любая фигура в геометрии имеет равную себе, ведь равенство это частный случай подобия с коэффициентом k=1

Рис. 2. Подобные фигуры

Признаки подобия

На сегодняшний день для произвольного треугольника существует 3 признака подобия.

• По двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
• По сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.
• По трем сторонам. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Рис. 3. Признаки подобия треугольников

Для того, чтобы доказать пропорциональность сторон нужно посчитать отношение длин соответствующих сторон. У пропорциональных сторон результаты получатся одинаковыми.

У пропорциональны треугольников будут также пропорциональны и все характеризующие отрезки: высота, медиана, биссектриса. Коэффициент подобия одинаков для всех отрезков треугольника. Этот факт нужно запомнить, он важен для решения многих задач и выведения формулы отношения площадей подобных треугольников.

2$$ – то есть площади подобных треугольников относятся друг к другу с коэффициентом пропорциональности, равным коэффициенту подобия в квадрате

Что мы узнали?

Мы вспомнили, что такое подобные фигуры. Поговорили о подобных треугольниках. Выделили три признака подобия треугольников. Выяснили, что коэффициент подобия можно использовать не только для работы со сторонами треугольников, но и для любых характеризующих отрезков. Вывели формулу отношения площадей подобных треугольников.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Наталья Карасёва

  10/10

Оценка статьи

3.9

Средняя оценка: 3.9

Всего получено оценок: 309.

---

А какая ваша оценка?

Формула подобных треугольников — Изучите формулу для нахождения подобных треугольников

Прежде чем мы изучим формулу подобных треугольников, мы должны понять, когда две фигуры считаются подобными.

Если одна фигура может быть получена из другой с помощью последовательности преобразований, таких как изменение размера, отражение, скольжение или поворот. То есть подобные фигуры имеют одинаковую форму, но не обязательно одинаковый размер.

Два треугольника называются подобными, если их:

• соответствующие углы равны
• соответствующие стороны находятся в одинаковом соотношении

Однако, чтобы убедиться, что два треугольника подобны, нам не обязательно иметь информацию обо всех сторонах и всех углах. Давайте узнаем о формуле подобных треугольников.

Что такое формула подобных треугольников?

Существует три критерия, по которым можно определить, подобны ли два треугольника.

1. AA (Угол Угол): Если любые два угла треугольников равны, то говорят, что треугольники подобны.
2. SAS (Side Angle Side): если два треугольника имеют две пары сторон в одинаковом отношении, а прилежащие к ним углы также равны, то треугольники подобны.
3. SSS (Side Side Side): если два треугольника имеют три пары сторон в одинаковом соотношении, то такие треугольники подобны.

Символ, используемый для обозначения сходства между треугольниками, — «~».
Подобные треугольники \(ABC\) и \(DEF\) обозначаются символом \(\bigtriangleup ABC\sim \bigtriangleup DEF\).

Рассмотрим применение формулы подобных треугольников в следующем разделе.

Примеры с использованием формулы подобных треугольников

Пример 1:   Размеры треугольников ABC и DEF следующие:

AB = 4 единицы, BC2 = 5 единиц, AC = 6 единиц

=16 единиц, EF=20 единиц, DF=24 единиц

С помощью формулы подобных треугольников проверьте, подобны ли треугольники.

Решение:

Определите отношение соответствующих сторон треугольников, чтобы проверить, подобны ли они.

Возьмите отношение самых коротких сторон обоих треугольников и отношение самых длинных сторон обоих треугольников.

\(\begin{align}\dfrac{AB}{DE}&=\dfrac{4}{16}=\dfrac{1}{4}\\\dfrac{BC}{EF}&=\dfrac {5}{20}=\dfrac{1}{4}\\\dfrac{AC}{FG}&=\dfrac{6}{24}=\dfrac{1}{4} \end{align}\ )

Поскольку соответствующие стороны треугольников находятся в одинаковом отношении, значит, они подобны. 9{\circ}\), треугольники подобны.

Ответ: Да, каждая пара равносторонних треугольников подобна.

Пример 3: Столб высотой 2 ярда отбрасывает тень длиной 4 ярда. Дерево отбрасывает тень на 24 метра.

Найдите высоту дерева, если известно, что треугольники, образованные при соединении вершины дерева и тени дерева, подобны треугольнику, образованному при соединении вершины шеста с вершиной тень столба.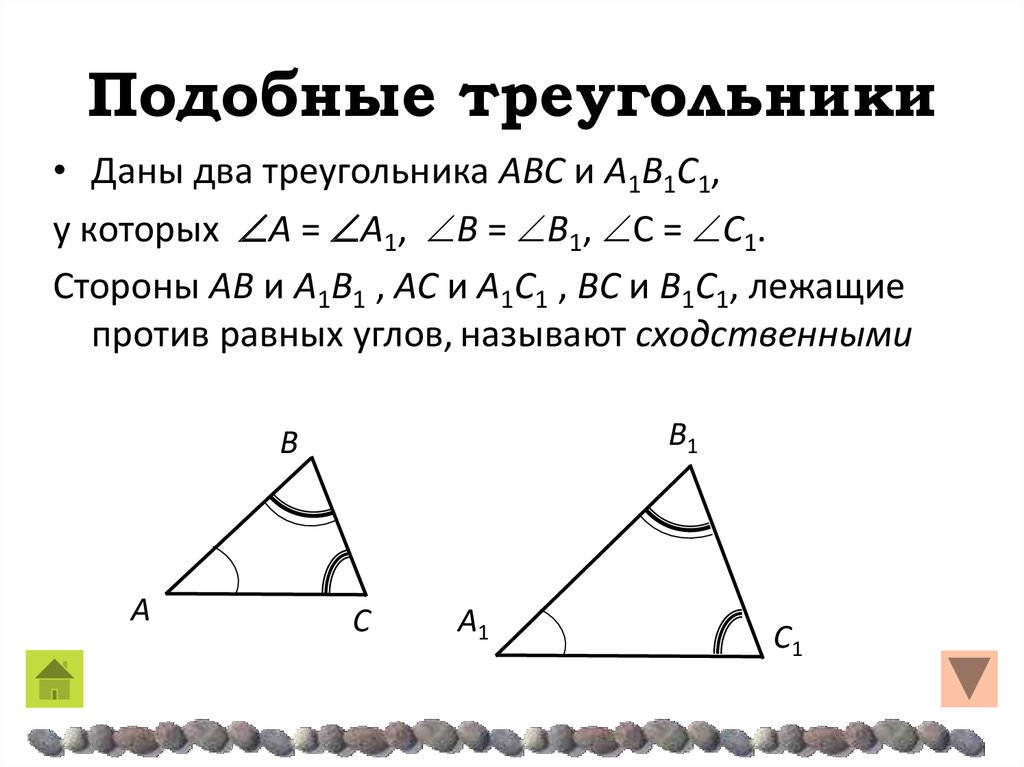

Решение:

Здесь мы видим, что △PQR подобен △ABC

Поскольку соответствующие стороны подобных треугольников находятся в одинаковом отношении,

получаем, PQ/AB = QR/BC = PR/AC

Подставляя значения, получаем

PQ/2 = 24/4

При решении получаем

PQ = 12

Ответ: Высота дерева 12 ярдов.

Часто задаваемые вопросы о формуле подобных треугольников

Как узнать, подобны ли два треугольника?

Два треугольника подобны, если их соответствующие углы равны и их соответствующие стороны находятся в одном и том же отношении. Подобные треугольники — это треугольники, которые выглядят одинаково, но их размеры могут быть разными.

Как найти недостающие стороны подобных треугольников?

Недостающие стороны подобного треугольника можно узнать, сравнив отношения последовательных соответствующих сторон треугольника. Сравниваем отношения и находим длину неизвестной стороны треугольника.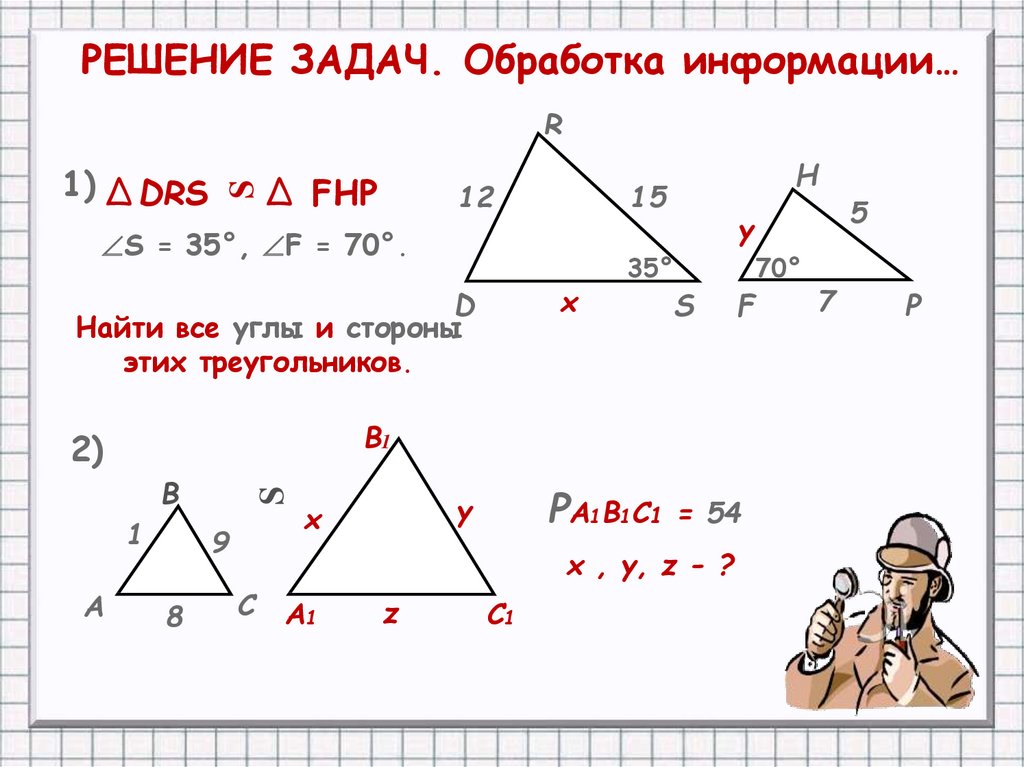

Могут ли два треугольника быть подобными и конгруэнтными?

Все конгруэнтные треугольники также являются подобными треугольниками, но не все подобные треугольники являются конгруэнтными треугольниками. Таким образом, два подобных треугольника могут быть равны, но не всегда. Чтобы два подобных треугольника были равны, они должны иметь одинаковый размер, одинаковую форму и одинаковую меру соответствующих углов.

Какой тип треугольников всегда похож?

Равносторонние треугольники всегда подобны. Любые два равносторонних треугольника всегда подобны независимо от длины сторон равностороннего треугольника. Два равнобедренных прямоугольных треугольника также всегда подобны.

Видео-вопрос: Определение длины стороны треугольника по соответствующей стороне подобного треугольника и отношению сходства между ними

На рисунке отрезок 𝐵𝐷 пересекается с отрезком 𝐴𝐸 в точке 𝐶, которая также является серединой отрезка 𝐵𝐷.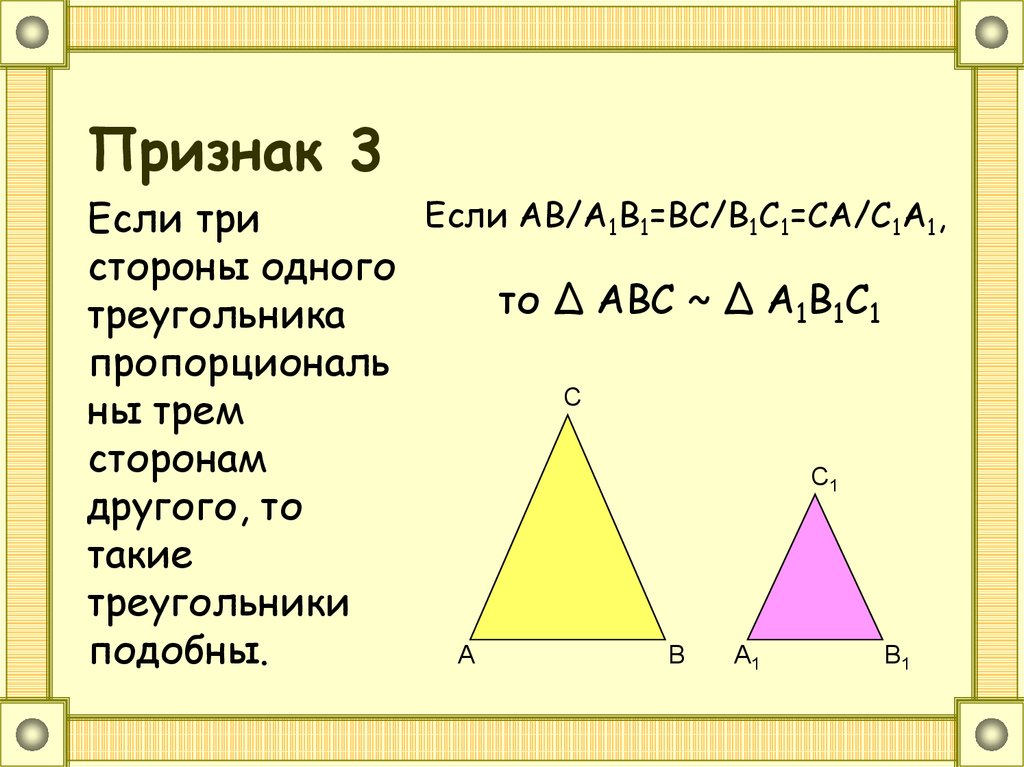

Найдите длину отрезка 𝐶𝐸.

Стенограмма видео

На рисунке отрезок 𝐵𝐷 пересекается с отрезком 𝐴𝐸 в точке 𝐶, которая также является серединой отрезка 𝐵𝐷. Найдите длину отрезка 𝐶𝐸.

Первое, что мы замечаем, это то, что 𝐶 — это середина отрезка 𝐵𝐷. Мы знаем, что длина отрезка 𝐵𝐶 равна 27. А это значит, что длина 𝐷𝐶 тоже будет равна 27. Поскольку середина 𝐶 делит отрезок 𝐵𝐷 пополам, каждая сторона равна 27. Нас интересует отрезок 𝐶𝐸 . Но на данный момент не похоже, что информации достаточно для решения вопроса. Нам нужно подумать, можем ли мы сказать что-нибудь еще об углах или длинах сторон.

Мы знаем, что угол 𝐵𝐶𝐴 и угол 𝐷𝐶𝐸 являются вертикальными углами. Это углы, противоположные друг другу при пересечении двух прямых. Следовательно, мера угла 𝐵𝐶𝐴 равна мере угла 𝐷𝐶𝐸. Мы также можем сказать, что два прямоугольных треугольника конгруэнтны, если катет и острый угол одного треугольника конгруэнтны соответствующим частям другого треугольника.

На этом изображении немного сложно увидеть, какие части соответствуют друг другу. Таким образом, мы можем переставить треугольники, чтобы лучше видеть соответствующие части. Вот треугольник 𝐸𝐷𝐶. Мы знаем, что длина стороны 𝐷𝐶 равна 27. И мы повернули треугольник 𝐴𝐵𝐶 так, чтобы их прямые углы оказались в одном положении. Мы знаем, что длина стороны 𝐵𝐶 равна 27. И здесь у нас есть две конгруэнтные стороны, две конгруэнтные соответствующие стороны. Мы также знаем, что мера угла 𝐷𝐶𝐸 равна мере 𝐵𝐶𝐴. А это значит, что у нас есть соответствующие конгруэнтные углы.

Исходя из этого, мы можем сказать, что треугольник 𝐸𝐷𝐶 равен треугольнику 𝐴𝐵𝐶. И если эти два треугольника конгруэнтны, то и все их соответствующие части будут конгруэнтны. Это означает, что длина 𝐸𝐷 будет равна длине 𝐴𝐵. А гипотенуза 𝐸𝐶 будет равна длине гипотенузы другого треугольника, прямой 𝐴𝐶. Для треугольника 𝐴𝐵𝐶 мы также знаем, что длина стороны 𝐴𝐵 равна 36. Мы можем найти длину 𝐴𝐶 по теореме Пифагора. И как только мы найдем длину 𝐴𝐶, она также будет длиной 𝐸𝐶.