Условная вероятность — формулы и события с примерами решения
Содержание:
- Примеры с решением
При совместном рассмотрении двух случайных событий часто возникает вопрос: насколько связаны эти события друг с другом, в какой мере наступление одного из них влияет на возможность наступления другого?
Простейшим примером связи между двумя событиями может служить причинная связь — когда наступление одного из событий ведет к обязательному осуществлению другого или же, наоборот, когда наступление одного события исключает шансы другого. Скажем, если событие заключается в том, что выбранное наугад изделие данного предприятия не содержит брака, а событие — в том, что изделие является первосортным, то ясно, что наступление влечет за собой в обязательном порядке наступление напротив, событие исключает событие
- Однако наряду с такими крайними случаями существует и много промежуточных, когда непосредственная причинная зависимость одного события от другого отсутствует, но некоторая зависимость все же имеется.

По этой ссылке вы найдёте полный курс лекций по теории вероятности:
| Предмет теория вероятности |
Бросается игральная кость. Событие — выпадение четного числа очков, событие — выпадение числа очков, большего чем 3. Очевидно, было бы неверно утверждать, что одно из этих событий влечет за собой другое или, наоборот, одно из них исключает другое. В то же время между событиями и имеется какая-то зависимость. В самом деле, из трех случаев, к которым сводится (выпадение 4, 5 или 6 очков), событию будут благоприятны два; поэтому, если считать наступившим событие то шансы события будут В то же время при отсутсвии предварительной информации об исходе бросания шансы события оцениваются отношением Так как то следует признать, что наступление события повышает шансы события
Для характеристики зависимости одних событий от других вводится понятие условной вероятности.
Определение. Пусть — два случайных события по отношению к некоторому опыту причем Число называется вероятностью события при условии, что наступило событие или просто условной вероятностью события
Вероятность при условии обозначается Таким образом, по определению имеем следующее равенство:
Смысл числа как вероятности события при условии, что наступило событие можно подтвердить таким рассуждением. Пусть опыт имеет равновероятных исходов (классическая схема), из которых исходов благоприятны событию — событию — событию Если известно, что в результате опыта наступило событие то число возможных исходов сокращается до из них ровно исходов будут такими, при которых наступает и событие Таким образом, вероятность при условии наступления будет, согласно классическому способу подсчета вероятности, равна отношению или
что делает оправданным определение (1.44).
Возможно вам будут полезны данные страницы:
Теория вероятности: формулы, примеры |
Найти вероятность: пример решения |
Независимые события в теории вероятности |
Формула полной вероятности |
Из равенства (1.
44), являющегося определением условной вероятности, следует:
Это означает, что вероятность произведения двух событий равна вероятности одного из этих событий при условии другого, умноженной на вероятность самого условия. Если то наряду с равенством (1.45) имеет место
Сравнивая эти равенства, мы видим, чтоПерепишем формулу (1.45) (с учетом (1.46)) в виде
Нетрудно видеть, что справедлива аналогичная формула для трех событий
Действительно,
Вообще, для событий справедлива формула
Примеры с решениемПример 1.19.
Все грани игральной кости заклеены непрозрачной бумагой: грани 1, 2, 3 — красной, грани — 4, 5, 6 — черной. При бросании кости выпала черная грань. Какова вероятность того, что на этой грани стоит четное число?
Решение:
Очевидно, мы должны найти условную вероятность где событие есть выпадение четного числа очков, а событие — выпадение числа очков, большего 3. Имеем:
Имеем:
Для, сравнения отметим, что безусловная вероятность события (просто равна
Пример 1.20.
Слово «фото», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекаются одна за другой все буквы. Какова вероятность того, что при этом снова появится слово «фото» (событие ?
Решение:
Введем обозначения для событий:
первой извлечена буква «ф»,
второй извлечена буква «о»,
третей извлечена буква «т»,
четвертой извлечена буква «о».
Очевидно,
По формуле (1.48) для имеем
Пример 1.21.
В команде из 12 спортсменов 5 мастеров спорта. По жеребьевке из команды выбирают 3 спортсменов. Какова вероятность того, что все выбранные спортсмены являются мастерами спорта?
Решение:
Укажем 2 способа решения, из которых первый способ состоит в непосредственном подсчете искомой вероятности по классической схеме, а второй — в применении формулы (1. 48).
48).
Первый способ. Представим себе урну, в которой 5 красных шаров и 7 белых. Красные шары соответствуют мастерам спорта, а белые — остальным спортсменам. Из этой урны наудачу извлекают 3 шара, и пусть событие состоит в появлении 3 красных шаров. Тогда искомая вероятность равна
Второй способ. Из урны последовательно без возвращения извлекаются 3 шара. Введем обозначения: первый шар красный, второй шар красный, третий шар красный. Тогда и по формуле (1.48) при имеем
Условная вероятность. Теорема Байеса
В рассмотренных ранее примерах вычислялись вероятности элементарных событий. Возникает вопрос: как определить вероятность события, если известна некая информация о событиях, происшедших до него? [1] Вероятность события А, при вычислении которой учитывается информация о событии В, называется условной и обозначается как Р(А|В).
Вероятность события А при условии, что наступило событие В, равна вероятности события А и В, деленной на вероятность события В:
Вероятность события В при условии, что наступило событие А, равна вероятности события А и В, деленной на вероятность события А:
где Р(А и В) – вероятность события А и В, Р(А) – вероятность события А, Р(В) – вероятность события В.
Скачать заметку в формате Word или pdf
Фактически формулы (1) и (2) это краткая запись условной вероятности на основе таблицы сопряженности признаков. Вернемся к примеру, рассмотренному в предыдущей заметке (рис. 1). Предположим, что нам стало известно, будто некая семья собирается купить широкоэкранный телевизор. Какова вероятность того, что эта семья действительно купит такой телевизор?
Рис. 1. Поведение покупателей широкоэкранных телевизоров
В данном случае нам необходимо вычислить условную вероятность Р (покупка совершена | покупка планировалась). Поскольку нам известно, что семья планирует покупку, выборочное пространство состоит не из всех 1000 семей, а только из тех, которые планируют покупку широкоэкранного телевизора. Из 250 таких семей 200 действительно купили этот телевизор. Следовательно, вероятность того, что семья действительно купит широкоэкранный телевизор, если она это запланировала, можно вычислить по следующей формуле:
Р (покупка совершена | покупка планировалась) = количество семей, планировавших и купивших широкоэкранный телевизор / количество семей, планировавших купить широкоэкранный телевизор = 200 / 250 = 0,8
Этот же результат дает формула (2):
где событие А заключается в том, что семья планирует покупку широкоформатного телевизора, а событие В — в том, что она его действительно купит. Подставляя в формулу реальные данные, получаем:
Подставляя в формулу реальные данные, получаем:
Дерево решений
На рис. 1 семьи разделены на четыре категории: планировавшие покупку широкоэкранного телевизора и не планировавшие, а также купившие такой телевизор и не купившие. Аналогичную классификацию можно выполнить с помощью дерева решений (рис. 2). Дерево, изображенное на рис. 2, имеет две ветви, соответствующие семьям, которые планировали приобрести широкоэкранный телевизор, и семьям, которые не делали этого. Каждая из этих ветвей разделяется на две дополнительные ветви, соответствующие семьям, купившим и не купившим широкоэкранный телевизор. Вероятности, записанные на концах двух основных ветвей, являются безусловными вероятностями событий 
Рис. 2. Дерево решений
Например, чтобы вычислить вероятность того, что семья купит широкоэкранный телевизор, если она запланировала сделать это, следует определить вероятность события покупка запланирована и совершена, а затем поделить его на вероятность события покупка запланирована. Перемещаясь по дереву решения, изображенному на рис. 2, получаем следующий (аналогичный предыдущему) ответ:
Статистическая независимость
В примере с покупкой широкоэкранного телевизора вероятность того, что случайно выбранная семья приобрела широкоэкранный телевизор при условии, что она планировала это сделать, равна 200/250 = 0,8. Напомним, что безусловная вероятность того, что случайно выбранная семья приобрела широкоэкранный телевизор, равна 300/1000 = 0,3. Отсюда следует очень важный вывод. Априорная информация о том, что семья планировала покупку, влияет на вероятность самой покупки. Иначе говоря, эти два события зависят друг от друга.
Обратите внимание на то, что события А и В являются статистически независимыми друг от друга тогда и только тогда, когда Р(А|В) = Р(А). Если в таблице сопряженности признаков, имеющей размер 2×2, это условие выполняется хотя бы для одной комбинации событий А и В, оно будет справедливым и для любой другой комбинации. В нашем примере события покупка запланирована и покупка совершена не являются статистически независимыми, поскольку информация об одном событии влияет на вероятность другого.
Рассмотрим пример, в котором показано, как проверить статистическую независимость двух событий. Спросим у 300 семей, купивших широкоформатный телевизор, довольны ли они своей покупкой (рис. 3). Определите, связаны ли между собой степень удовлетворенности покупкой и тип телевизора.
Спросим у 300 семей, купивших широкоформатный телевизор, довольны ли они своей покупкой (рис. 3). Определите, связаны ли между собой степень удовлетворенности покупкой и тип телевизора.
Рис. 3. Данные, характеризующие степень удовлетворенности покупателей широкоэкранных телевизоров
Судя по этим данным,
В то же время,
Р (покупатель удовлетворен) = 240 / 300 = 0,80
Следовательно, вероятность того, что покупатель удовлетворен покупкой, и того, что семья купила HDTV-телевизор, равны между собой, и эти события являются статистически независимыми, поскольку никак не связаны между собой.
Правило умножения вероятностей
Формула для вычисления условной вероятности позволяет определить вероятность совместного события
относительно совместной вероятности Р(А и В), получаем общее, правило умножения вероятностей. Вероятность события А и В равна вероятности события А при условии, что наступило событие В, умноженной на вероятность события В:
(3) Р(А и В) = Р(А|В) * Р(В)
Рассмотрим в качестве примера 80 семей, купивших широкоэкранный HDTV-телевизор (рис. 3). В таблице указано, что 64 семьи удовлетворены покупкой и 16 — нет. Предположим, что среди них случайным образом выбираются две семьи. Определите вероятность, что оба покупателя окажутся довольными. Используя формулу (3), получаем:
3). В таблице указано, что 64 семьи удовлетворены покупкой и 16 — нет. Предположим, что среди них случайным образом выбираются две семьи. Определите вероятность, что оба покупателя окажутся довольными. Используя формулу (3), получаем:
Р(А и В) = Р(А|В) * Р(В)
где событие А заключается в том, что вторая семья удовлетворена своей покупкой, а событие В — в том, что первая семья удовлетворена своей покупкой. Вероятность того, что первая семья удовлетворена своей покупкой, равна 64/80. Однако вероятность того, что вторая семья также удовлетворена своей покупкой, зависит от ответа первой семьи. Если первая семья после опроса не возвращается в выборку (выбор без возвращения), количество респондентов снижается до 79. Если первая семья оказалась удовлетворенной своей покупкой, вероятность того, что вторая семья также будет довольна, равна 63/79, поскольку в выборке осталось только 63 семьи, удовлетворенные своим приобретением. Таким образом, подставляя в формулу (3) конкретные данные, получим следующий ответ:
Р(А и В) = (63/79)(64/80) = 0,638.
Следовательно, вероятность того, что обе семьи довольны своими покупками, равна 63,8%.
Предположим, что после опроса первая семья возвращается в выборку. Определите вероятность того, что обе семьи окажутся довольными своей покупкой. В этом случае вероятности того, что обе семьи удовлетворены своей покупкой одинаковы, и равны 64/80. Следовательно, Р(А и В) = (64/80)(64/80) = 0,64. Таким образом, вероятность того, что обе семьи довольны своими покупками, равна 64,0%. Этот пример показывает, что выбор второй семьи не зависит от выбора первой. Таким образом, заменяя в формуле (3) условную вероятность Р(А|В) вероятностью Р(А), мы получаем формулу умножения вероятностей независимых событий.
Правило умножения вероятностей независимых событий. Если события А и В являются статистически независимыми, вероятность события А и В равна вероятности события А, умноженной на вероятность события В.
(4) Р(А и В) = Р(А)Р(В)
Если это правило выполняется для событий А и В, значит, они являются статистически независимыми. Таким образом, существуют два способа определить статистическую независимость двух событий:
Таким образом, существуют два способа определить статистическую независимость двух событий:
- События А и В являются статистически независимыми друг от друга тогда и только тогда, когда Р(А|В) = Р(А).
- События А и B являются статистически независимыми друг от друга тогда и только тогда, когда Р(А и В) = Р(А)Р(В).
Если в таблице сопряженности признаков, имеющей размер 2×2, одно из этих условий выполняется хотя бы для одной комбинации событий А и B, оно будет справедливым и для любой другой комбинации.
Безусловная вероятность элементарного события
(5) Р(А) = P(A|B1)Р(B1) + P(A|B2)Р(B2) + … + P(A|Bk)Р(Bk)
где события B1, B2, … Bk являются взаимоисключающими и исчерпывающими.
Проиллюстрируем применение этой формулы на примере рис.1. Используя формулу (5), получаем:
Р(А) = P(A|B1)Р(B1) + P(A|B2)Р(B2)
где Р(А) — вероятность того, что покупка планировалась, Р(В1) — вероятность того, что покупка совершена, Р(В2) — вероятность того, что покупка не совершена.
ТЕОРЕМА БАЙЕСА
Условная вероятность события учитывает информацию о том, что произошло некое другое событие. Этот подход можно использовать как для уточнения вероятности с учетом вновь поступившей информации, так и для вычисления вероятности, что наблюдаемый эффект является следствием некоей конкретной причины. Процедура уточнения этих вероятностей называется теоремой Байеса. Впервые она была разработана Томасом Байесом в 18 веке.
Предположим, что компания, упомянутая выше, исследует рынок сбыта новой модели телевизора. В прошлом 40% телевизоров, созданных компанией, пользовались успехом, а 60% моделей признания не получили. Прежде чем объявить о выпуске новой модели, специалисты по маркетингу тщательно исследуют рынок и фиксируют спрос. В прошлом успех 80% моделей, получивших признание, прогнозировался заранее, в то же время 30% благоприятных прогнозов оказались неверными. Для новой модели отдел маркетинга дал благоприятный прогноз. Какова вероятность того, что новая модель телевизора будет пользоваться спросом?
Теорему Байеса можно вывести из определений условной вероятности (1) и (2). Чтобы вычислить вероятность Р(В|А), возьмем формулу (2):
Чтобы вычислить вероятность Р(В|А), возьмем формулу (2):
и подставим вместо Р(А и В) значение из формулы (3):
Р(А и В) = Р(А|В) * Р(В)
Получим:
Подставляя вместо Р(А) формулу (5), получаем теорему Байеса:
где события B1, В2, … Вk являются взаимоисключающими и исчерпывающими.
Введем следующие обозначения: событие S — телевизор пользуется спросом, событие S’ — телевизор не пользуется спросом, событие F — благоприятный прогноз, событие F’ — неблагоприятный прогноз. Допустим, что P(S) = 0,4, P(S’) = 0,6, P(F|S) = 0,8, P(F|S’) = 0,3. Применяя теорему Байеса получаем:
Вероятность спроса на новую модель телевизора при условии благоприятного прогноза равна 0,64. Таким образом, вероятность отсутствия спроса при условии благоприятного прогноза равна 1–0,64=0,36. Процесс вычислений представлен на рис. 4.
Рис. 4. (а) Вычисления по формуле Байеса для оценки вероятности спроса телевизоров; (б) Дерево решения при исследовании спроса на новую модель телевизора
Рассмотрим пример применения теоремы Байеса для медицинской диагностики.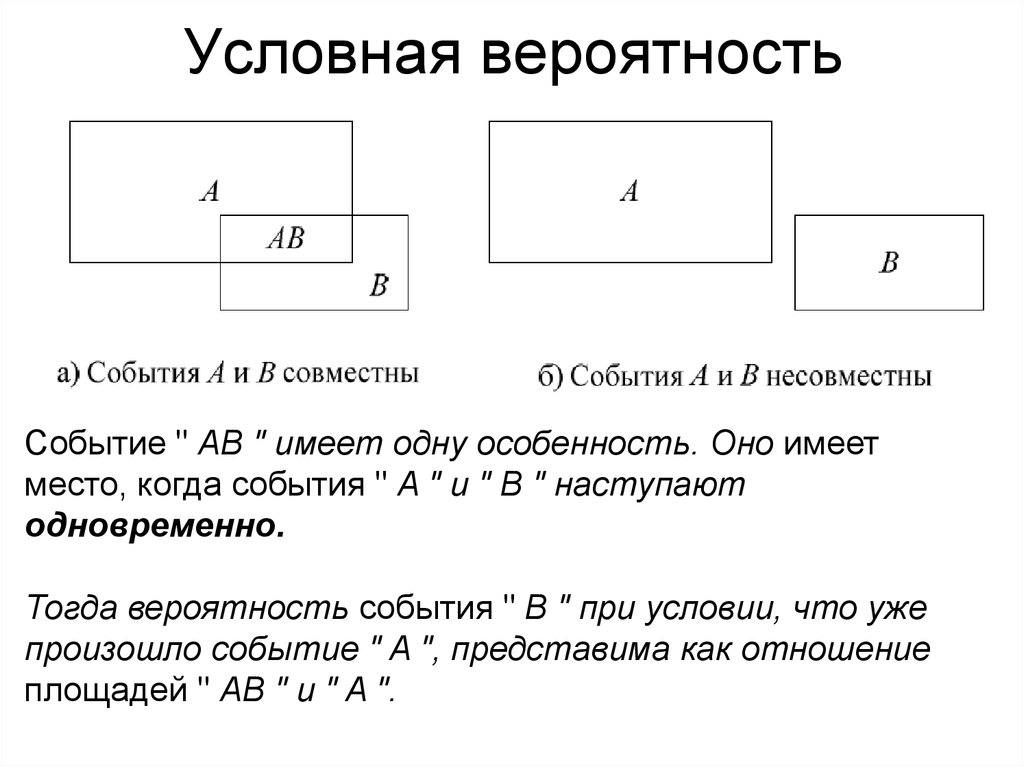 Вероятность того, что человек страдает от определенного заболевания, равна 0,03. Медицинский тест позволяет проверить, так ли это. Если человек действительно болен, вероятность точного диагноза (утверждающего, что человек болен, когда он действительно болен) равна 0,9. Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02. Допустим, что медицинский тест дал положительный результат. Какова вероятность того, что человек действительно болен? Какова вероятность точного диагноза?
Вероятность того, что человек страдает от определенного заболевания, равна 0,03. Медицинский тест позволяет проверить, так ли это. Если человек действительно болен, вероятность точного диагноза (утверждающего, что человек болен, когда он действительно болен) равна 0,9. Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02. Допустим, что медицинский тест дал положительный результат. Какова вероятность того, что человек действительно болен? Какова вероятность точного диагноза?
Введем следующие обозначения: событие D — человек болен, событие D’ — человек здоров, событие Т — диагноз положительный, событие Т’ — диагноз отрицательный. Из условия задачи следует, что Р(D) = 0,03, P(D’) = 0,97, Р(T|D) = 0,90, P(T|D’) = 0,02. Применяя формулу (6), получаем:
Вероятность того, что при положительном диагнозе человек действительно болен, равна 0,582 (см. также рис. 5). Обратите внимание на то, что знаменатель формулы Байеса равен вероятности положительного диагноза, т. е. 0,0464.
е. 0,0464.
Рис. 5. (а) Вычисления по формуле Байеса для оценки точности медицинского диагноза; (б) Дерево решения при оценке точности медицинского диагноза
Предыдущая заметка Основные понятия теории вероятностей
Следующая заметка Распределение дискретной случайной величины
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
Возможно, вас также заинтересует:
Дуглас Хаббард. Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе
Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью
Канеман, Словик, Тверски. Принятие решений в неопределенности: Правила и предубеждения
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 265–279
Условная вероятность: определение и примеры из жизни
Условная вероятность — это вероятность того, что одно событие произойдет в некоторой связи с одним или несколькими другими событиями.
Посмотрите видео с несколькими примерами формулы:
Примеры условной вероятности
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
События с условной вероятностью
Условная вероятность может описывать события следующим образом:
- Событие A состоит в том, что на улице идет дождь, и вероятность дождя сегодня составляет 0,3 (30%).
- Событие B заключается в том, что вам нужно будет выйти на улицу, и это имеет вероятность 0,5 (50%).
Условная вероятность будет рассматривать эти два события во взаимосвязи друг с другом, например вероятность того, что идет дождь и вам нужно будет выйти на улицу.
Формула условной вероятности:
P(B|A) = P(A и B) / P(A)
, который вы также можете переписать как:
P(B|A) = P(A∩B) / P(A)
Нужна помощь с домашним заданием? Посетите нашу обучающую страницу!
Формула условной вероятности Примеры
Пример 1
В группе из 100 покупателей спортивных автомобилей 40 купили системы сигнализации, 30 купили ковшеобразные сиденья и 20 приобрели систему сигнализации и ковшеобразные сиденья. Если случайно выбранный покупатель автомобиля купил сигнализацию, какова вероятность того, что он также купил ковшеобразные сиденья?
Если случайно выбранный покупатель автомобиля купил сигнализацию, какова вероятность того, что он также купил ковшеобразные сиденья?
Шаг 1: Рассчитайте P(A). В вопросе указано 40%, или 0,4.
Шаг 2: вычислить P(A∩B). Это пересечение А и Б: оба происходят вместе. В вопросе указано 20 из 100 покупателей, или 0,2.
Шаг 3: Подставьте свои ответы в формулу:
P(B|A) = P(A∩B) / P(A) = 0,2 / 0,4 = 0,5.
Вероятность того, что покупатель купил ковшеобразные сиденья, при условии, что он приобрел сигнализацию, составляет 50%.
Диаграмма Венна для 90 покупателей, показывающая, что 20 покупателей сигнализации также приобрели ковшеобразные сиденья.
Пример 2:
В этом вопросе используется следующая таблица сопряженности:
Какова вероятность того, что случайно выбранный человек будет мужчиной, если у него есть домашнее животное?
Шаг 1. Повторно заполните формулу новыми переменными, чтобы она имела смысл для вопроса (необязательно, но помогает уточнить, что вы ищете). Я собираюсь сказать, что M означает «самец», а PO означает «владелец домашнего животного», поэтому формула будет выглядеть так:
Я собираюсь сказать, что M означает «самец», а PO означает «владелец домашнего животного», поэтому формула будет выглядеть так:
P(M|PO) = P(M∩PO) / P(PO)
Шаг 2: вычислить P( M∩PO) из таблицы. Пересечение самец/домашние животные (пересечение в таблице этих двух факторов) составляет 0,41.
Шаг 3: Определите P(PO) из таблицы. Из общей колонки 86% (0,86) респондентов имели домашних животных.
Шаг 4: Подставьте свои значения в формулу:
P(M|PO) = P(M∩PO) / P(M) = 0,41 / 0,86 = 0,477, или 47,7%.
Зачем нам условная вероятность? События в жизни редко имеют простую вероятность. Подумайте о вероятности дождя.
Условная вероятность в реальной жизни
Условная вероятность используется во многих областях, таких как расчеты, страхование и политика. Например, переизбрание президента зависит от предпочтений избирателей при голосовании и, возможно, от успеха телевизионной рекламы — даже от вероятности оплошности оппонента во время дебатов!
Метеоролог может заявить, что вероятность дождя в вашем районе составляет 40 процентов. Однако этот факт является условным по многим вещам, таким как вероятность…
Однако этот факт является условным по многим вещам, таким как вероятность…
- …холодного фронта, приходящего на вашу территорию.
- …формируются дождевые облака.
- …еще один фронт, разгоняющий дождевые тучи.
Мы говорим, что условная вероятность выпадения дождя зависит от всех вышеперечисленных событий.
Дополнительные примеры условной вероятности из реальной жизни
- Представьте, что вы продавец мебели . Вероятность того, что новый покупатель в вашем магазине купит диван в конкретный день, составляет 30%. Однако, если они заходят в ваш магазин за месяц до Суперкубка, вероятность может составлять 70%. Мы можем представить условную вероятность продажи кушетки, если это месяц, предшествующий Суперкубку, как P (Продажа кушетки | Месяц Суперкубка), где | символ означает «при условии, что». Эта условная вероятность дает нам способ выразить вероятности, когда наши убеждения меняются относительно вероятности того, что произойдет одно событие (в данном примере продажа дивана) при условии, что произошло определенное событие (в данном случае наступление месяца, предшествующего Суперкубку).
 ).
). - Вероятность наличия у женщины в возрасте от 40 до 50 лет рака молочной железы составляет около 1%. Однако эта вероятность меняется, если у женщины положительный результат маммографии: вероятность рака у женщины при положительном результате маммограммы возрастает примерно до 8,3% [1].
- Четыре кандидата A, B, C и D баллотируются на политический пост . У каждого равные шансы на победу: 25%. Однако, если кандидат А выбывает из гонки по состоянию здоровья, вероятность изменится: P(Победа | Выбывает один кандидат) = 33,33%.
- Если вы беременны, вероятность рождения мальчика или девочки одинакова: 50%. Однако, если у вас уже есть один ребенок (скажем, мальчик), ваши шансы меняются. Учитывая, что ваш первый ребенок — мальчик, ваши шансы родить еще одного мальчика падают до одной трети (33,33%). Причина этого в том, что выборочное пространство для случая, когда у вас есть один мальчик из двух, равно S = {BB, BG, GB}.
 Если у вас есть один мальчик, единственным возможным событием в этом пространстве будет BB, что составляет одну треть выборочного пространства [2].
Если у вас есть один мальчик, единственным возможным событием в этом пространстве будет BB, что составляет одну треть выборочного пространства [2].
Откуда взялась формула условной вероятности?
Формула условной вероятности выводится из правила умножения вероятностей P(A и B) = P(A)*P(B|A).
Шаг за шагом, вот как получить уравнение условной вероятности из правила умножения:
Шаг 1 : Запишите правило умножения:
P(A и B) = P(A)*P(B|A )
Шаг 2: Разделите обе части уравнения на P(A):
P(A и B) / P(A) = P(A)*P(B|A) / / P(A)
Шаг 3 : Отменить P(A) в правой части уравнения:
P(A и B) / P(A) = P(B|A)
Шаг 4 : Переписать уравнение:
P(B|A) = P(A и B) / P(A)
Посетите наш канал на YouTube, чтобы получить дополнительную статистику, справку и советы!
Ссылки
[1] Формула Байеса. Статья размещена на сайте Корнельского университета.
[2] Митчелл, Дж. Примеры: условная вероятность. Получено 8 ноября 2021 г. с: http://www.ams.sunysb.edu/~jsbm/courses/311/conditioning.pdf
Бехара, Р. Справочник по краткому изучению вероятностей. гистограммы; Издание Lam Rfc Cr. 2010.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Условная вероятность: определение и примеры из реальной жизни» от StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/conditional-probability-definition-examples/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Условная вероятность: определение, формула и примеры
Что такое условная вероятность?
Условная вероятность — это вероятность того, что событие произойдет при условии, что другое событие уже произошло. Условные вероятности позволяют оценить, как априорная информация влияет на вероятности. Например, какова вероятность того, что произошло событие А при условии, что произошло событие В? Когда вы включаете существующие факты в расчеты, это может изменить вероятность результата.
Как правило, постановка задачи для вопросов с условной вероятностью предполагает, что начальное событие произошло, или указывает, что наблюдатель стал его свидетелем. Цель состоит в том, чтобы вычислить шансы второго события при условии, что произошло первое событие.
Эта концепция может показаться сложной, но есть смысл в том, что знание того, что событие произошло, может повлиять на шансы другого события.
Например, если кто-то спросит вас, какова вероятность того, что у вас есть зонт? Разве ваш первый вопрос не будет, идет ли дождь? Очевидно, что знание того, идет ли дождь, влияет на вероятность того, что вы носите с собой зонт.
Связанный пост : Основы вероятности
Примеры условной вероятности
P (A|B) обозначает условную вероятность события A при условии, что произошло событие B.
В качестве примера с условной вероятностью представьте, что мы оцениваем вероятность того, что у кого-то есть кошка, учитывая наличие пустой картонной коробки на полу. Мы будем использовать следующие обозначения:
P (Кот | Открытый ящик на полу) = 0,8
Это обозначение указывает на то, что вероятность того, что у кого-то есть кошка, при наличии открытой коробки на полу равна 0,8.
Я знаю, потому что у меня есть кошки, и у меня на полу часто стоит пустая коробка, чтобы они могли повеселиться!
В качестве более серьезного примера условной вероятности рассмотрим медицинские тесты, такие как тесты на COVID. В этом контексте оценка условных вероятностей имеет решающее значение. Необходимо знать вероятность получения положительного результата теста при наличии у человека COVID и шансы на отрицательный результат при отсутствии у человека COVID.
Для исследований, которые оценивают медицинские тесты, исследователи уже знают, есть ли у добровольца COVID (или другое заболевание, которое они тестируют). Затем они проводят тест на COVID и записывают результаты. Следовательно, мы оцениваем вероятность результата теста с учетом известного статуса участника.
Следующие обозначения условной вероятности представляют эти два случая:
- P (положительный результат теста на COVID | У человека COVID)
- P (Отрицательный тест на COVID | У человека нет COVID)
Тесты могут работать хорошо для одного, обоих или ни одного из этих условий. Им нужны высокие условные вероятности для обоих случаев, чтобы ограничить шансы на ложные отрицательные и положительные результаты соответственно.
Формула условной вероятности
Используйте следующую формулу условной вероятности, чтобы найти вероятность A при заданном B:
В формуле условной вероятности числитель отношения представляет собой общую вероятность того, что A и B встречаются вместе. Нам нужна совместная вероятность в числителе, потому что нас интересует подмножество случаев, когда происходят оба события.
Нам нужна совместная вероятность в числителе, потому что нас интересует подмножество случаев, когда происходят оба события.
Знаменатель формулы условной вероятности — это вероятность того, что B произойдет. Мы используем это значение в знаменателе, потому что шансы события B определяют общее пространство выборки. Помните, природа условной вероятности заключается в том, что данное событие происходит, и знаменатель учитывает это событие.
В формуле условной вероятности числитель является подмножеством знаменателя. Вместе формула дает нам отношение шансов обоих событий к вероятности того, что данное событие произойдет, что является условной вероятностью!
Следовательно, если отношение равно единице, событие A всегда происходит, когда произошло событие B. И наоборот, когда отношение равно нулю, событие А никогда не происходит после того, как произошло Б. Для большинства примеров условной вероятности отношение находится где-то между 0 и 1, что указывает на то, что А иногда встречается после Б. Следовательно, мы находим вероятность А при заданном В!
Следовательно, мы находим вероятность А при заданном В!
Пример условной вероятности с работой
Вернемся к примеру с условной вероятностью ношения зонта во время дождя. Предположим, что исследование в дождливом городе оценивает шансы, связанные с дождливыми днями и ношением зонтиков. Исследователи наблюдали за погодой и людьми.
Мы хотим посмотреть, как меняются шансы взять с собой зонт в зависимости от того, идет дождь или нет. Для этого необходимо рассчитать следующие две условные вероятности:
- P (Зонтик | Дождь): какова вероятность того, что кто-то носит зонт, учитывая, что идет дождь.
- P (Зонтик | Нет дождя): Какова вероятность того, что кто-то носит зонт, если дождя нет.
Чтобы найти наши ответы, мы будем использовать следующие две формулы условной вероятности:
Исследователи находят следующие вероятности:
- P(Зонтик ⋂ Дождь): 0,20
- P(Зонтик ⋂ Без дождя): 0,40
- P(Дождь): 0,25
- P (без дождя): 0,75
Вычисление условных вероятностей
Если вы посмотрите на совместные вероятности в первых двух пунктах, окажется, что шанс носить с собой зонт, когда не идет дождь (0,40), выше, чем когда идет дождь (0,20). Это кажется отсталым, и мы вернемся к этому. Для правильного ответа нам нужно рассчитать условную вероятность. Подставим эти числа в формулу условной вероятности!
Это кажется отсталым, и мы вернемся к этому. Для правильного ответа нам нужно рассчитать условную вероятность. Подставим эти числа в формулу условной вероятности!
Основываясь на условных вероятностях, мы видим, что люди чаще носят зонт, если идет дождь (0,80), чем когда дождя нет (0,53). Это имеет смысл!
Совместные вероятности вводили в заблуждение, поскольку они не учитывали тот факт, что дни без дождя в три раза более вероятны, чем дождливые дни (0,75 против 0,25)! В этом исследовании вы, скорее всего, увидите людей с зонтиками, когда нет дождя, потому что дней без дождя гораздо больше. Условные вероятности учитывают этот факт.
Этот пример условных вероятностей включает зависимые события. Мы знаем, что это так, потому что, когда вы меняете начальное событие, шансы второго события меняются. Следовательно, вероятность второго события зависит от первого события.
Теперь давайте посмотрим, что происходит, когда мы смотрим на независимые события.
Связанный пост : Диаграммы Венна могут эффективно отображать вероятности
Пример условных вероятностей с независимыми событиями
При оценке условных вероятностей независимых событий верно следующее:
P (A|B) = P (A)
Что это значит?
Вероятность A при условии, что B произошло, равна вероятности A. Другими словами, произойдет B или нет, не влияет на шансы A. Это имеет смысл, потому что события независимы ! Для этого также есть математическое доказательство, которое я не буду освещать.
Давайте рассмотрим пример условной вероятности, чтобы вы могли увидеть, как это работает!
Представьте, что мы играем в игру. За каждый ход вы бросаете два кубика, но бросаете их по одному. Вы хотите выбросить две шестерки. Броски костей являются независимыми событиями, поскольку результат первого броска не влияет на второй бросок.
Вычисления
Мы воспользуемся формулой условной вероятности, чтобы найти вероятность выпадения второй шестерки при условии, что первой выпала шестерка.

 44), являющегося определением условной вероятности, следует:
44), являющегося определением условной вероятности, следует: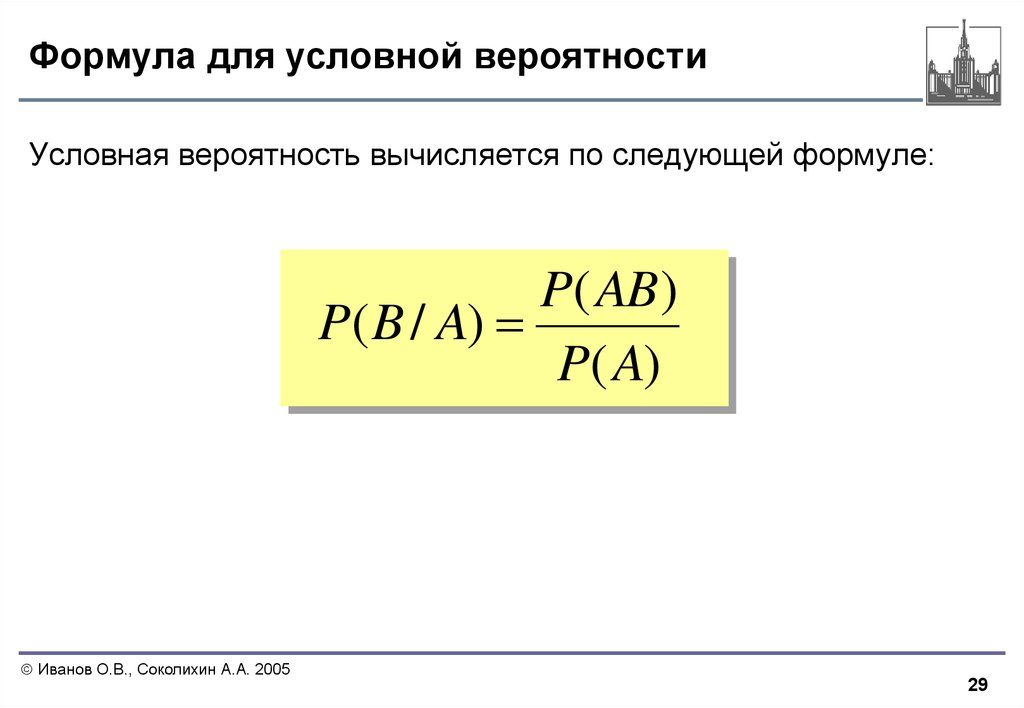 ).
). Если у вас есть один мальчик, единственным возможным событием в этом пространстве будет BB, что составляет одну треть выборочного пространства [2].
Если у вас есть один мальчик, единственным возможным событием в этом пространстве будет BB, что составляет одну треть выборочного пространства [2].