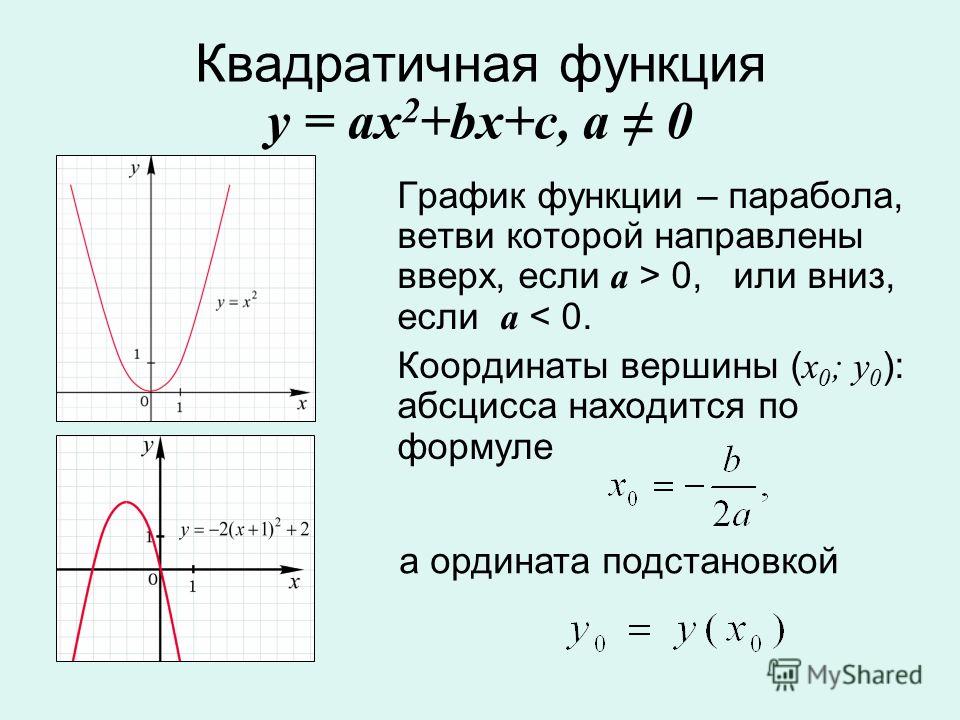
Как найти x0 y0: Вершина параболы — урок. Алгебра, 8 класс.

Содержание

Функция у = а (х -x0) +y0

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Функция
2
у = а (х -x ) +y
0
0

2. Функция у = а (х -x0) +y0

Указать координаты
вершины параболы
2
1)у=-2(х-7) +3
(7;3)
2)у=3(х-8)
2
2
(8;0)
3)у=-(х+2) -6
(-2;-6)
2
4)у=4х -1
(0;-1)

3. Указать координаты вершины параболы

y x
2
y x 3
2
y x 3
2
y x
2
y x 2
2
y x 2
2
y 2x
2
y 2 x 1
2
y 2 x 1 3
2
Решить № 617 (1)
2
у=(х+2)

7.

Решить № 617 (1)2
у=(х+2)

8. Решить № 617 (1)

Решить № 617 (2-6).
В каком пункте
получается
такой график?
2
2)у = (х-3)

9. Решить № 617 (2-6).

В каком пункте
получается
такой график?
2
4)у = — х +1

10. Решить № 617 (2-6).

В каком пункте
получается
такой график?
2
6)y= (х+2) + 1

11. Решить № 617 (2-6).

В каком пункте
получается такой
график?
2
3) y = х — 2

12. Решить № 617 (2-6).

В каком пункте
получается такой
график?
2
5)y= — (х — 1) — 3

13. Решить № 617 (2-6).

Решить № 619 (1)
2
2
уУ=
= |х
х — -22|
2
у=│Х — 2│

14. Решить № 619 (1)

Решить № 619 (2)
2
у=│1-х │
2
У=│1 – Х │
у=1-х
2

15. Решить № 619 (2)

Построить график функции
2
у=││-х +4│- 5│
2y=│-x 2+4│
y=││-x +4│-5│
2
y=│-x +4│-5
2
y=-x +4
Решите графически уравнение
2
2
(х-2) = -x +10
y = (x-2)
2
2
y = (x-2)
2
y=-x +10
-1
2
y=-x +10
3
Ответ:х=-1;х=3

17.

Решите графически уравнение (х-2) = -x +10Преобразование
графика функции
y= f(x)
y=f(x-m)
y=f(x+m)
вправо на m
влево на m
y=f(x)-n
y=f(x)+n
вниз на n
на n
вверх
y=f(x-m)+n
вправо на m вверх на n
у=│f(x)│
m>0
n>0

18. Преобразование графика функции y= f(x)

№1 Найдите пары: «Квадратичная функция-график этой
функции» и отметьте знаком «+»
у=-(х-1) 2-2
+
2
у=(х-2) +1
+
2
у=-(х+1) +2
+
2
у=(х+2) +1
+
у=х 2-2х+3
+
№2 Даны пары: «Квадратичная функция- координаты вершины
параболы».Укажите верные и неверные соответствия
№
Квадратичная функция
2
1
у=(х+4) — 5
2
у=(х+12) — 4
3
у=-(х- 5) +3
4
у=-(х+8) — 9
5
у=(х+12) +20
2
2
2
2
Координаты вершины параболы
(- 4;- 5)
(12;- 4)
(- 5;- 3)
(- 8;- 9)
(-12;20)
+
+
+
Домашнее задание
№608(1,2) ПОСТРОИТЬ ГРАФИКИ
№618,№619(3)
Решить графически уравнения:
2
2
1)х +2= — (х+2)
2
2
2)х +2= 5(х-3)

20.

2}=2a$$ $ 92}=1$$$

Похожие темы

Уравнение эллипса с фокусами на оси OY
Уравнение эллипса с центром (x0, y0) и фокальной осью, параллельной оси y
Исследование эллипса

Теория математики в твоем мобильном

Скачать бесплатно

java — Учитывая две точки внутри рамки окна (x0, y0 и x1, y1) — Какой метод вы бы использовали, чтобы продлить линию до краев окна?

спросил

6 лет, 3 месяца назад

Изменено 6 лет, 3 месяца назад

Просмотрено 367 раз

Для введения в компьютерную графику Я изо всех сил пытаюсь продлить линию, определяемую двумя точками, используя тот же градиент до края окна. Это довольно сложно объяснить, поэтому это изображение, вероятно, поможет.

Пунктирная линия — это часть, не определяемая линией (от x0,y0 до x1,y1).

Мы попробовали кое-что, используя неявное уравнение линии (ax+bx+c = 0) и найдя точку пересечения со всеми четырьмя краями оконной рамы.

Любая помощь очень ценится!

java
math
псевдокод

Ваша первая задача — проверить, что (x0, y0) и

(x1, y1) являются различными точками.

Неявное уравнение невертикальной линии на самом деле y = mx + c , где градиент м это (y1 - y0) / (x1 - x0) , а c это точка пересечения на оси y , которую можно найти, применив c = y1 - mx1 или с = у0 - тх0 .

Когда у вас есть значения m и c , вы можете применить уравнение линии, чтобы найти y точек, учитывая ваш набор x точек (или наоборот), чтобы построить линию до нужной длины.

Вертикальная линия характеризуется x0 равно x1 . В этом случае ваш график представляет собой просто линию, пересекающую ось x в точке x0 .

Также обратите внимание, что линия пересекается только с двумя ребрами (если только линия не коллинеарна одному из ребер).

Вы можете придумать нормальную форму уравнения прямой:

 n = (y1-y0, x0-x1)

(n — направление из одной точки в другую, повернутое на 90°)

Уравнение для точек p на линии:

 p * n = (x0, y0) * n

или

 (p - (x0, y0)) * n = 0

* обозначает скалярное произведение выше, но не ниже.

поэтому нужно решить уравнение

 (px - x0) * (y1 - y0) + (py - y0) * (x0 - x1) = 0

Все скоординированы, кроме px и py (координаты x и y точки) и один из px и py определяется стороной, которую вы хотите пересечь.