Тесты для педагогов по всем школьным предметам с ответами
0
- #6 класс
- #Математика
- #Проверочная работа
Десятичные дроби и проценты
Тест состоит из 10 вопросов.
26 декабря 2022Костицина Инна Геннадьевна
0
- #11 класс
- #Русский язык
- #Подготовка к ЕГЭ
Тест по русскому языку 11 класс
Задание 10 ЕГЭ русский язык
25 декабря 2022Цыбульникова Ольга Михайловна
0
- #10 класс
- #Правоведение
- #Проверочная работа
- #Проверочная работа за четверть
Тест по дисциплине «Правовое обеспечение профессиональной деятельности»
Тест по основам трудового и гражданского права
12 декабря 2022Татьяна Алексеевна
0
- #9 класс
- #Геометрия
- #Проверочная работа
Соотношение в прямоугольном треугольнике
Соотношение в прямоугольном треугольнике
11 декабря 2022Ахременко Марина Анатольевна
0
- #9 класс
- #История
- #Проверочная работа
США в эпоху «позолоченного века» и «прогрессивной эры».
В тест для 9-го класса по Истории Нового времени вошли такие темы, как «Реконструкция Юга», «Экономический рывок», «Монополии, рабочее и фермерское движение», «Двухпартийная система в конце XIX-начале ХХ в.», «Расовая проблема после Гражданской войны», «Идеи экспансии».
8 декабря 2022Уразалеев Руслан Фаритович
0
- #9 класс
- #Геометрия
- #Проверочная работа
Вписанные и описанные четырехугольника
Теоретический тест по геометрии в 9 классе «Вписанные и описанные четырехугольника»
5 декабря 2022Ахременко Марина Анатольевна
0
- #5 класс
- #География
- #Проверочная работа
- #Итоговое тестирование
Географическое изучение Земли
Тестовая работа составлена в двух вариантах. В задания включены вопросы: география древности, эпохи Средневековья и ВГО, география открытий 18-19 в.в. и исследования 20 века.
21 ноября 2022Яблочкина Марина Ивановна
0
- #9 класс
- #Литература
- #Проверочная работа
Жизнь и творчество Г.Р. Державина
Тест содержит вопросы, ответы на которые должны быть развернутыми.
11 ноября 2022Татьяна Сергеевна Корепанова
0
- #7 класс
- #Биология
- #Проверочная работа
- #Подготовка к ОГЭ
- #Подготовка к ЕГЭ
Промежуточный контроль знаний по теме: «Тип Кишечнополостные».
Тематические тестовые задания помогут учащимся при подготовке к ОГЭ и ЕГЭ. Разработка рассчитана на учеников 7 классов общеобразовательных школ, надеюсь, окажет помощь учителям биологии при проведении промежуточного контроля знаний по теме: «Тип Кишечнополостные»
10 ноября 2022Цителадзе Елена Петровна
0
- #7 класс
- #Биология
- #Проверочная работа
- #Подготовка к ОГЭ
- #Подготовка к ЕГЭ
Промежуточный контроль знаний по теме: «Членистоногие»
Тематические тестовые задания помогут учащимся при подготовке к ОГЭ и ЕГЭ. Разработка рассчитана на учеников 7 классов общеобразовательных школ, надеюсь, окажет помощь учителям биологии при проведении промежуточного контроля знаний по теме: «Членистоногие»
Разработка рассчитана на учеников 7 классов общеобразовательных школ, надеюсь, окажет помощь учителям биологии при проведении промежуточного контроля знаний по теме: «Членистоногие»
7 ноября 2022Цителадзе Елена Петровна
0
- #7 класс
- #Английский язык
- #Итоговое тестирование
Итоговый тест по английскому языку для 7 класса
Итоговый тест по английскому языку для 7 класса
5 ноября 2022Екатеринка
0
- #7 класс
- #Биология
- #Проверочная работа
- #Подготовка к ОГЭ
- #Подготовка к ЕГЭ
Промежуточный контроль знаний по теме: «Надкласс Рыбы»
Тематические тестовые задания в нескольких вариантах с ответами помогут учащимся при подготовке к ОГЭ и ЕГЭ. Разработка рассчитана на учеников 7 классов общеобразовательных школ, надеюсь, окажет помощь учителям биологии при проведении промежуточного контроля знаний по теме: «Надкласс Рыбы»
3 ноября 2022Цителадзе Елена Петровна
0
- #7 класс
- #Биология
- #Проверочная работа
- #Подготовка к ОГЭ
- #Подготовка к ЕГЭ
Промежуточный контроль знаний по теме: «Пресмыкающиеся »
Тематические тестовые задания в нескольких вариантах с ответами помогут учащимся при подготовке к ОГЭ и ЕГЭ. Разработка рассчитана на учеников 7 классов общеобразовательных школ, надеюсь, окажет помощь учителям биологии при проведении промежуточного контроля знаний по теме: «Пресмыкающиеся»
Разработка рассчитана на учеников 7 классов общеобразовательных школ, надеюсь, окажет помощь учителям биологии при проведении промежуточного контроля знаний по теме: «Пресмыкающиеся»
2 ноября 2022Цителадзе Елена Петровна
0
- #5 класс
- #Английский язык
- #Проверочная работа
Present Simple or Present Progressive?
Тест рассчитан на 5-10 минут.
1 ноября 2022Дагирова Хеда Ильясовна
0
- #7 класс
- #Биология
- #Проверочная работа
- #Подготовка к ОГЭ
- #Подготовка к ЕГЭ
Промежуточный контроль знаний по теме: «Земноводные».
Тематические тестовые задания помогут учащимся при подготовке к ОГЭ и ЕГЭ. Разработка рассчитана на учеников 7 классов общеобразовательных школ, надеюсь, окажет помощь учителям биологии при проведении промежуточного контроля знаний по теме: «Земноводные».
28 октября 2022Цителадзе Елена Петровна
0
- #10 класс
- #Химия
- #Проверочная работа
- #Подготовка к ЕГЭ
Классификация органических веществ
Классификация органических веществ
24 октября 2022Ряснова Людмила Григорьевна
0
- #4 класс
- #Русский язык
- #Итоговое тестирование
Состав слова.
Тест предназначен для групповых и индивидуальных логопедических занятий (в 3-4 классе начальной школы) на этапе коррекции нарушений лексико-грамматического строя речи и представляет заключительную часть работы на данном этапе. Его могут и применять учителя начальных классов в качестве контроля за правильно усвоенным материалом по словоупотреблению.
17 октября 2022Кичигина Татьяна Анатольевна
-1
- #4 класс
- #Русский язык
- #Итоговое тестирование
Приставочное словообразование.
Тест предназначен для групповых и индивидуальных логопедических занятий (в 3-4 классе начальной школы) на этапе коррекции нарушений лексико-грамматического строя речи и представляет заключительную часть работы на данном этапе. Его могут и применять учителя начальных классов в качестве контроля за правильно усвоенным материалом по словоупотреблению.
17 октября 2022Кичигина Татьяна Анатольевна
0
- #8 класс
- #Труд
- #Проверочная работа
Технология домашнего хозяйства, электротехника
Тесты для 8 класса по предмету технология
16 октября 2022Васильев Алексей Фёдорович
0
- #5 класс
- #Математика
- #Проверочная работа
Признаки делимости
Признаки делимости на 2, на 3, на 5, на 9, на 10
15 октября 2022Бузанова Вероника Андреевна
2.1 ¥ªâ®àë
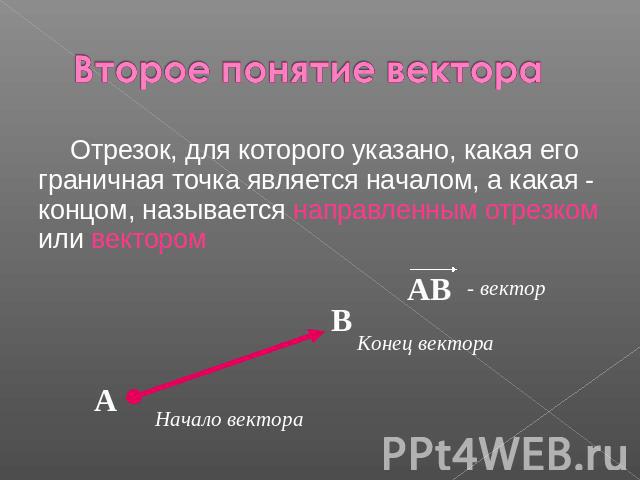
2.1 Векторы
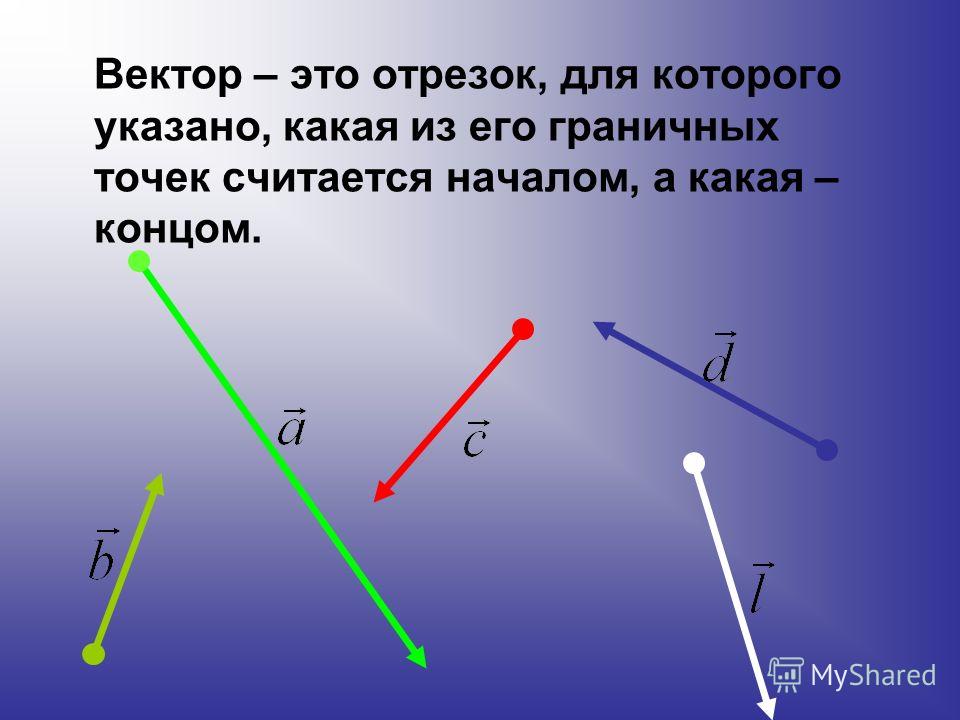
Вектором (геометрическим вектором) называется
направленный отрезок, то есть такой
отрезок, обе граничные точки которого
поименованы: одна граничная точка
отрезка названа началом (по-другому –
точкой приложения), а другая граничная
точка отрезка названа концом.
Операции над векторами
Сложение
Правило Треугольник
Правило Параллелограмма
Модуль (длину) вектора суммы можно вычислить, например, используя теорему косинусов где — угол между отрезками, изображающими данные векторы, когда начало одного вектора совпадает с концом другого.
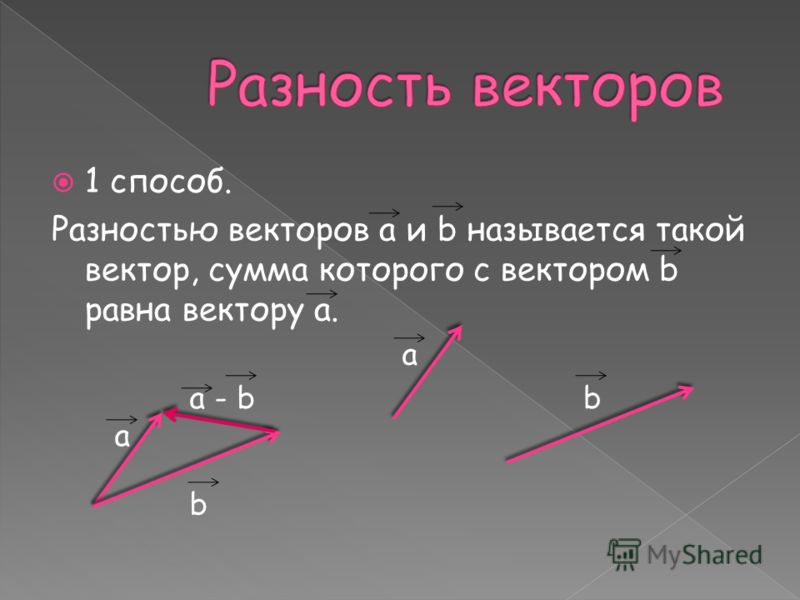
Вычитание
Операция вычитания из вектора вектора сводится к сложению первого вектора и вектора, противоположного второму:
Скалярное произведение
Скалярное произведение двух векторов
Скалярное произведение на множестве геометрических векторов вводится, как
Скалярное произведение любого вектора и какого-то единичного вектора есть проекция (ортогональная проекция) вектора на направление этого единичного вектора:
Легко видеть, что скалярное произведение может быть записано через операцию (ортогонального) проецирования:
(где —
проекция вектора на
направление , —
проекция вектора на
направление ).
В абстрактном подходе обычно сперва вводят скалярное произведение, а уже через него определяют понятие угла, ортогональность, ортогональную проекцию.
Векторное произведение
Векторное произведение двух векторов
Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:
Обозначение:
Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
Векторное произведение обладает распределительным свойством:
Векторное произведение обладает распределительным свойством:
]Смешанное произведение
Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и :
(равенство
здесь записано для разных обозначений
скалярного и векторного произведения,
часто встречающихся в литературе).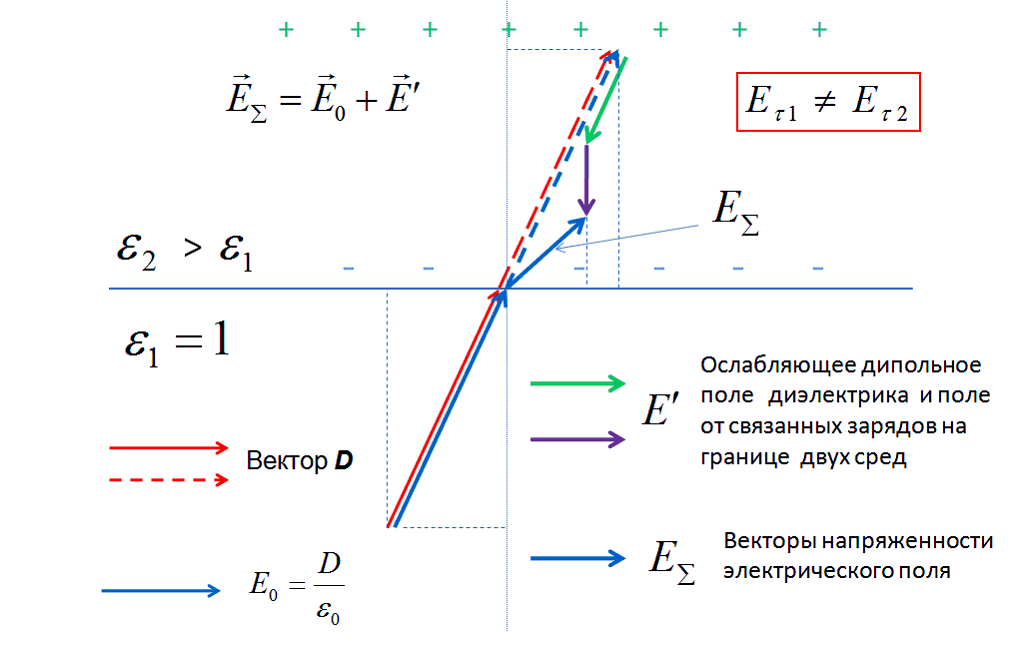
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение есть (ориентированный) объём параллелепипеда, построенного на векторах .
То есть абсолютная величина его есть просто объем этого параллелепипеда (в общем случае — косоугольного), а знак определяется тем, представляют ли векторы правую тройку (тогда плюс) или левую (тогда минус). Иногда при использовании левого базиса знак может быть определен противоположным образом.
Базис и разложение по базису
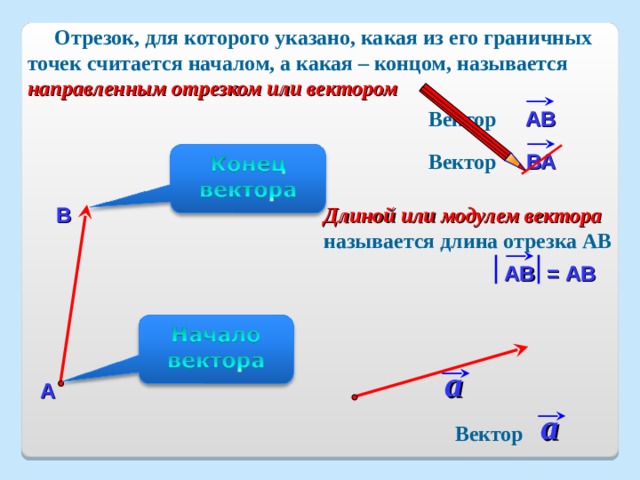
Разложение вектора по трём ортогональным векторам трёхмерного евклидова пространства
Векторы
(как направленные отрезки), лежащие на
прямых, параллельных одной
прямой, называются коллинеарными,
а векторы, лежащие в плоскостях,
параллельных одной плоскости — компланарными.
Для свободных векторов коллинеарность
и компланарность определяется как такие
понятия для изображающих их направленных
отрезков (то есть представителей
соответствующих свободным векторам
классов эквивалентности).
Условия коллинеарности векторов
Два вектора коллинеарные, если отношения их координат равны.
Два вектора коллинеарные, если их векторное произведение равно нулю.
Условия компланарности векторов
Три вектора компланарны если их смешанное произведение равно нулю.
Три вектора компланарны если они линейно зависимы.
Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
Даны два вектора a(xa;ya) и b(xb;yb). Эти векторы будут перпендикулярны, если выражение xaxb + yayb = 0.
cos α = | a·b |
|a|·|b| |
линейная алгебра — английские названия начала и конца вектора
Задай вопрос
спросил
Изменено 1 год, 1 месяц назад
Просмотрено 4к раз
$\begingroup$
Я провел небольшое исследование, но, поскольку английский не является моим родным языком, я изо всех сил пытаюсь найти ответ на этот вопрос:
Учитывая вектор, как вы называете его начальную и конечную точки?
Лучшее, что я пока нашел, это слово «база» для обозначения начальной точки вектора, но я понятия не имею, правильно ли это. Лучшее, что у меня есть для конечной точки, — это «конец» вектора, хотя применяется то же самое, что и раньше.
Лучшее, что у меня есть для конечной точки, — это «конец» вектора, хотя применяется то же самое, что и раньше.
- линейная алгебра
- векторы
- терминология
$\endgroup$
14
$\begingroup$
Хороший вопрос. Поскольку важным свойством вектора является его направление, трудно говорить о векторах, не имея слов, обозначающих их начало и конец.
По моему опыту, мы обычно называем источник или начало вектора его «хвостом», а пункт назначения или конец вектора — его «головой».
$\endgroup$
3
$\begingroup$
Их иногда называют начальной и конечной точками. Начальная точка — это точка, в которой начинается, а конечная точка — это точка, в которой она заканчивается.
$\endgroup$
$\begingroup$
В статье Википедии Евклидов вектор говорится, что когда вы строите вектор с именем $\overrightarrow{AB}$ из двух точек $A$ и $B$ в евклидовом пространстве, тогда $A$ называется начальная точка , а $B$ называется конечной точкой .
Конечно, все зависит от вашего определения вектора. Например, принято рассматривать вектор как класс эквивалентности всех тех ориентированных отрезков линии этого вида, которые имеют одинаковую длину (величину) и одно и то же направление. При таком определении «вектор» не имеет ни начальной, ни конечной точки, хотя вы можете выбрать любую начальную точку и рассмотреть представитель ориентированного отрезка линии, исходящего из этой точки.
В более общем случае гладкого многообразия у вас часто есть касательный вектор в конкретном касательном пространстве (или слое) $T_pM$, который соответствует точке $p$ на многообразии. В таком случае вам нужны как эта опорная точка (это общепринятое название?) $p$, так и представление вектора в касательном пространстве, «сидящего» в этой точке. В этой общей постановке нет канонической эквивалентности между вектором из $T_pM$ и вектором из другого слоя $T_qM$ (здесь $q\ne p$ — другая точка многообразия $M$).
В таком случае вам нужны как эта опорная точка (это общепринятое название?) $p$, так и представление вектора в касательном пространстве, «сидящего» в этой точке. В этой общей постановке нет канонической эквивалентности между вектором из $T_pM$ и вектором из другого слоя $T_qM$ (здесь $q\ne p$ — другая точка многообразия $M$).
Обычно, когда $v\in T_pM$, мы просто говорим, что $v$ является касательным вектором «at» $p$. Как я уже сказал, мне кажется, я слышал, что $p$ называют фут-точкой $v$.
$\endgroup$
$\begingroup$
Эээ, на самом деле вы не говорите о векторе. Вектор не определяется начальной и конечной точкой. У него есть направление и величина (и эквиваленты в других системах координат), но нет фиксированного начала.
Вектор может иметь местоположение , где берутся координаты. Это особенно актуально в криволинейных системах координат. Если вы рисуете там вектор, вы обычно рисуете соответствующую стрелку с основанием в месте расположения вектора, ее ось является прямой и касательной к направлениям координат в начале вектора, а размеры компонентов пропорциональны.
Если вы рисуете там вектор, вы обычно рисуете соответствующую стрелку с основанием в месте расположения вектора, ее ось является прямой и касательной к направлениям координат в начале вектора, а размеры компонентов пропорциональны.
Иногда стрелки изображают направленные отрезки. У них есть начальная и конечная точка. В этом случае древки этих стрел будут соответствует любой криволинейной системе координат. Визуализация направленного отрезка линии, заданного начальной точкой и вектором смещения, выполняется редко, когда с тех пор фактически изменяется более одной координаты. Путь , вдоль которого достигается смещение, не имеет очевидного кандидата: нет явно предпочтительного маршрута между начальным и конечным указать больше.
$\endgroup$
1
линейная алгебра — В чем разница между точкой и вектором?
Задай вопрос
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 69 тысяч раз
$\begingroup$
Я понимаю, что у вектора есть направление и величина, а у точки нет.
Однако в примечаниях к курсу, которые я использую, говорится, что точка — это то же самое, что и вектор.
Кроме того, можно ли выполнять перекрестное произведение и скалярное произведение, используя две точки вместо двух векторов? Я так не думаю, но мой сосед по комнате настаивает на том, что да, и теперь я немного сбит с толку.
- линейная алгебра
- векторы
- терминология
- определение
$\endgroup$
13
$\begingroup$
Вот ответ без использования символов.
Разница именно в том, что между расположение и смещение .
- Точки — это местоположений в пространстве .
- Векторы — это перемещений в пространстве .
Аналогия со временем работает хорошо.
- Времена (также называемые моментами или датами и временем) равны мест во времени .

- Продолжительность перемещений во времени .
Таким образом, во времени
- 16:00, полдень, полночь, 12:20, 23:11 и т. д. составляют раза
- +3 часа, -2,5 часа, +17 секунд и т. д., продолжительности
Обратите внимание, что продолжительность может быть положительной или отрицательной; это дает им «направление» в дополнение к их чистому скалярному значению. Теперь лучший способ мысленно различать время и продолжительность — это операции, которые они поддерживают.0003
- Учитывая время, вы можете добавить продолжительность, чтобы получить новое время (3:00 + 2 часа = 5:00)
- Вы можете вычесть два раза, чтобы получить продолжительность (7:00 — 1:00 = 6 часов)
- Вы можете добавить две длительности (3 часа 20 минут + 6 часов, 50 минут = 10 часов 10 минут)
Но нельзя сложить два раза (3:15 + полдень = ???)
Продолжим аналогию с пространством:
- $(3,5)$, $(-2,25) ,7)$, $(0,-1)$ и т.
 д. составляют точки
д. составляют точки - $\langle 4,-5 \rangle$ — это вектор , что означает 4 единицы на восток, затем 5 на юг, при условии, что север находится вверху (извините, жители южного полушария)
Теперь у нас точно такие же операции с пространством, как и со временем:
- Вы можете добавить точку и вектор: Начиная с $(4,5)$ и заканчивая $\langle -1,3 \rangle $ перенесет вас в точку $(3,8)$
- Вы можете вычесть две точки, чтобы получить смещение между ними: $(10,10) — (3,1) = \langle 7,9\rangle$, которое представляет собой смещение, которое вы должны предпринять из второго местоположения, чтобы добраться до первого
- Вы можете добавить два смещения, чтобы получить составное смещение: $\langle 1,3 \rangle + \langle -5,8 \rangle = \langle -4,11 \rangle$. То есть сделать 1 шаг на север и 3 на восток, ЗАТЕМ сделать 5 на юг и 8 на восток — это то же самое, что и просто сделать 4 на юг и 11 на восток.
Но две точки добавить нельзя.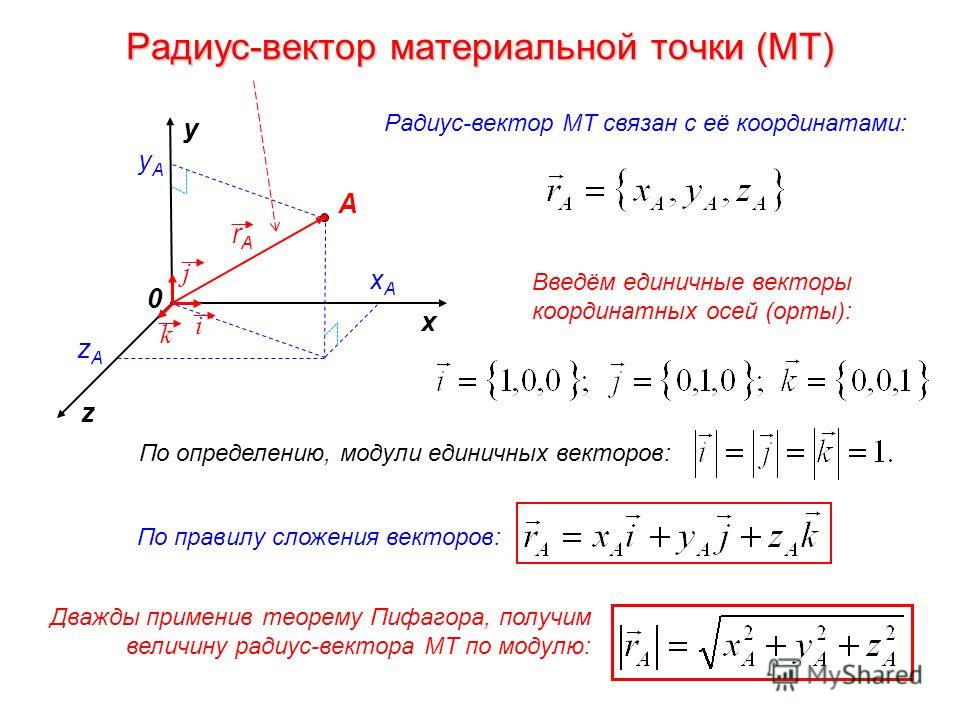
Если говорить более конкретно: Москва + $\langle\text{200 км на север, 7000 км на запад}\rangle$ — это другое место (точка) где-то на земле. Но Москва + Лос-Анджелес смысла нет.
Подводя итог, локация — это то, где (или когда) вы находитесь, а смещение — это как добраться из одной локации в другую . Смещения имеют как величину (как далеко идти), так и направление (которое во времени, в одномерном пространстве, просто положительное или отрицательное). В космосе местоположения — это точек , а смещения — векторов . Во времени местоположения — это (точки) времени, также известные как мгновений , а смещения — это длительностей .
РЕДАКТИРОВАТЬ 1 : В ответ на некоторые комментарии я должен указать, что 16:00. НЕ водоизмещение, но «+4 часа» и «-7 часов» являются. Конечно, вы можете добраться до 16:00. (мгновение), добавив смещение «+16 часов» к моменту полуночи. Вы также можете добраться до 16:00. добавив смещение «-3 часа» к 19:00. Источником путаницы между местоположениями и смещениями является то, что люди мысленно работают в системах координат относительно некоторого начала (будь то $(0,0)$, «полночь» или что-то подобное), и оба эти понятия представлены в виде координат. Думаю, в этом и был смысл вопроса.
Вы также можете добраться до 16:00. добавив смещение «-3 часа» к 19:00. Источником путаницы между местоположениями и смещениями является то, что люди мысленно работают в системах координат относительно некоторого начала (будь то $(0,0)$, «полночь» или что-то подобное), и оба эти понятия представлены в виде координат. Думаю, в этом и был смысл вопроса.
РЕДАКТИРОВАТЬ 2 : я добавил текст, чтобы прояснить, что продолжительность действительно имеет направление; Ранее я писал и -2,5 часа, и +3 часа, но некоторые могли пропустить, что отрицание инкапсулирует направление, и считало, что продолжительность — это «всего лишь скаляр», когда на самом деле добавление $+$ или $-$ действительно дает ему направление.
РЕДАКТИРОВАТЬ 3 : Сводка в виде таблицы:
+--------------------+------------- --------------------------+-----------------------+ | Концепция | ПРОСТРАНСТВО | ВРЕМЯ | +----------------------------------+-----------+--- --------------------+ | РАСПОЛОЖЕНИЕ | ТОЧКА | ВРЕМЯ | | ПЕРЕМЕЩЕНИЕ | ВЕКТОР | ПРОДОЛЖИТЕЛЬНОСТЬ | +----------------------------------+-----------+--- --------------------+ | Лок - Лок = Отображение | Pt - Pt = Vec | Время - Время = Длительность | | | (3,5)-(10,2) = <-7,3> | 7:30 - 1:15 = 6 часов 15 минут | +----------------------------------+-----------+--- --------------------+ | Лок + Дисп = Лок | Pt + Vec = Pt | Время + Длительность = Время | | | (10,2)+<-7,3> = (3,5) | 3:15 + 2 часа = 5:15 | +----------------------------------+-----------+--- --------------------+ | Отображение + Отображение = Отображение | Век + Век = Век | Длительность + Длительность = Длительность | | | <8,-5>+<-7,3> = <1,-2> | 3 часа + 5 часов = 8 часов | +----------------------------------+-----------+--- --------------------+ 9n$, в общем случае) находятся в очень хорошем соответствии с векторами, начинающимися в точке $(0,0,0)$.По сути, идея состоит в том, что мы можем представить вектор с его конечной точкой, и никакая информация не будет потеряна. Иногда это называют помещением вектора в «стандартное положение».
Для такого курса, как векторное исчисление, важно четко различать точки и векторы. Точки соответствуют векторам, начинающимся в начале координат, но нам могут понадобиться векторы, начинающиеся в других точках.
Например, имея три точки $A$, $B$ и $C$ в трехмерном пространстве, мы можем захотеть найти уравнение плоскости, которая их охватывает. Если бы мы знали вектор нормали $\vec n$ плоскости, мы могли бы записать уравнение непосредственно как $\vec n \cdot (x,y,z) = \vec n \cdot A$. Итак, нам нужно найти этот нормальный $\vec n$. Для этого вычислим векторное произведение векторов $\vec{AB}$ и $\vec{AC}$. Если бы вместо этого мы вычислили векторное произведение $A$ и $C$ (притворяясь, что они являются векторами в стандартном положении), мы не смогли бы получить правильный вектор нормали.
Например, если $A = (1,0,0)$, $B = (0,1,0)$ и $C = (0,0,1)$, вектор нормали к соответствующей плоскости не будет параллельна ни одной оси координат. Но если мы возьмем любые два из $A$, $B$ и $C$ и вычислим векторное произведение, мы получим вектор, параллельный одной из координатных осей.
$\endgroup$
9
$\begingroup$
По духу это разные вещи. Но принято считать, что вектор на плоскости или в трехмерном пространстве начинается в начале координат. В этом случае вектор идентифицируется точно по его конечной точке, что дает вам идентификацию между точками и векторами.
Один из способов увидеть, что это разные вещи (даже если они идентифицируются во многих обстоятельствах), заключается в том, что вы можете складывать векторы, в то время как сумма точек не имеет смысла. То же самое с точечным и перекрестным произведениями.
n$, равен всего 92}. $$ Итак, если вы настаиваете на том, чтобы говорить о величине точки, то вы «свободны» делать это (т.е. свободны определять это). Но имейте в виду, что вы также вызовете путаницу, делая это. А с выполнением математики мы хотим ясно общаться и так...
Таким же образом можно определить сложение или перекрестное произведение точек.
Может быть, было бы лучше сказать так: Является ли векторное пространство таким же, как множество? Да, векторное пространство — это множество. Но это также больше, чем набор. Мы не можем добавлять элементы множества, но мы можем добавлять элементы векторного пространства, потому что с векторным пространством вы получаете определение сложения. Так что в этом смысле точка и вектор очень разные.
Добавлено : Если вы хотите найти уравнение плоскости, которое содержит три точки $a$, $b$ и $c$, то вы не будете вычитать точки. Так как же вы так это. Ну, а если координаты точки $a$ равны $(a_1, a_2, a_3)$, т.
е. если $a = (a_1, a_2, a_3)$, (и аналогично для $b$ и $c$), то сначала определить векторы $$ \vec{ab} = (b_1 - a_1, b_2- a_2, b_3 - a_3) $$ и $$ \vec{ac} = (c_1 - a_1, c_2 - a_2, c_3 - a_3). $$ Тогда нормальный вектор к/к плоскости есть векторное произведение векторов: $\vec{ab}\times \vec{ac}$.
$\endgroup$
9
$\begingroup$
Точка обычно относится к топологической структуре. Например, точечно-множественная топология; последовательность сходящихся точек; окрестность точки; и т.д.
Вектор обычно относится к векторному пространству/нормированному пространству/структуре пространства внутреннего произведения - например, добавление двух векторов; масштабирование вектора; взятие нормы вектора; и т.д.
В наборе с обеими структурами — векторном пространстве с заданной топологией — контекст аргумента имеет тенденцию определять, какое слово используется.
$\endgroup$
$\begingroup$
Этот вопрос вызывает много путаницы, и хорошо, что вы пытаетесь прояснить его как можно раньше. Это явно вопрос о геометрическом значении векторов, поэтому ИМХО бесполезно, когда люди начинают вовлекать в обсуждение векторные пространства.
Позвольте мне сделать предположение, что вы знаете, что такое точка, и что путаница начинается, когда вводятся векторы. Я не знаю, как включать диаграммы в сообщение, поэтому я должен попросить вас нарисовать свои собственные. Вы можете визуализировать вектор как стрелку на плоскости (или в $3$-мерном пространстве, но давайте пока остановимся на плоскости). Обычное понимание состоит в том, что вектор определяется его длиной и направлением, и , а не по месту расположения в плоскости. Например, нарисуйте стрелку от $(1,-2)$ до $(3,1)$ и другую от $(0,2)$ до $(2,5)$. Две стрелки имеют одинаковую длину и направление, поэтому они считаются одним и тем же вектором , и его можно записать как вектор $(2,5)$ или $2{\bf i}+5{\bf j }$, если это обозначение, которое используют ваши преподаватели.
Мы часто используем язык несколько расплывчато и называем точку вектором. (Было бы точнее сказать, что точка представляет по вектору, но вопреки распространенному мнению математики не всегда на 100% точны в том, как они говорят!) В данном случае мы имеем в виду вектор от начала координат до указанной точки. Таким образом, первый вектор, нарисованный выше, не представляет точку $(3,1)$, поскольку он не начинается с начала координат. С другой стороны, если вы нарисуете стрелку от $(0,0)$ до $(2,5)$, то увидите, что это тот же вектор (то есть имеет ту же длину и направление), что и другой вектор. два. Поскольку он начинается с начала координат, этот вектор представляет точку $(2,5)$, как и два других, поскольку они являются одним и тем же вектором. Как видите, вектор из начала координат и точка, которую он представляет, совпадают численно , но они разные концептуально и стоит потратить некоторое время на то, чтобы понять это.
Еще один пример. Если вы еще этого не видели, надеюсь, скоро увидите. Уравнение линии можно записать в «параметрической векторной форме», как, например, $${\bf x}=(1,2)+\lambda(3,4)\quad\hbox{для $\lambda\in{\Bbb R}$}.$$ Здесь мы думаем о векторе $(1,2)$ как о задании точки на линии, а о $(3,4)$ как о задании направления линии. Так что — это , важно, чтобы мы рисовали $(1,2)$, начиная с начала координат (пожалуйста, нарисуйте это), но , а не важно, где мы рисуем $(3,4)$, и самый простой способ — это нарисуйте его, начиная с $(1,2)$ и заканчивая $(4,6)$. Затем вы можете провести линию через $(1,2)$ в направлении $(3,4)$, и это линия, заданная приведенным выше уравнением. Обозначение ${\bf x}$ будет представлять собой переменную точку на прямой или, другими словами, переменный вектор от начала координат до прямой.
Надеюсь, это поможет - удачи!
$\endgroup$
4
$\begingroup$
Векторы и точки — это две разные вещи, и их не следует путать.
Они оба имеют определенное сходство, что делает преобразование одного в другое очень простым, но они используются по-разному, а также описывают разные математические объекты.
Точка — это положение в системе координат, т. е. положение, определенное относительно начала координат. Если бы вы переместили начало координат, не перемещая точку, то координаты точки изменятся .
Вектор является более общим объектом. Независимо от того, где вы рисуете вектор $\vec{v}$ на плоскости, он остается тем же самым. Если бы вы переместили начало координат, компоненты вектора не изменились бы . Вы также можете думать о векторе как о преобразовании. Его можно применять где угодно и иметь тот же эффект: смещение точки на определенное расстояние в точном направлении.
Путаница между вектором и точкой возникает из-за того, что точку $P$ можно также представить как вектор $\vec{OP}$, то есть вектор, начинающийся из начала координат $O$ и идущий в точку $П$. Только тогда вектор и точка несколько эквивалентны.
Вектор, определенный как $\vec{AB}$ с точками $A$ и $B$, не следует путать с некоторой точкой $X$, такой что $\vec{AB} = \vec{OX}$ .
Вы понимаете, что хотя иногда полезно представлять точку как вектор, обычно не следует представлять вектор как точку.
$\endgroup$
1
$\begingroup$
Несмотря на то, что это math.stackexchange, я постараюсь дать вам интуитивно понятный ответ, основанный на физике. Надеюсь, это поможет вам самостоятельно разобраться с формальной математической стороной.
Я предполагаю, что вы думаете о точке как о некотором положении или месте в пространстве, с чего можно начать. Теперь представьте себе стрелу, идущую от начала пространства к этой точке. Это определяет вектор. Каждая точка в пространстве будет иметь уникальный такой вектор, так что не будет никакой двусмысленности, если я скажу что-то вроде «вектор для точки P».
Но это работает и в другую сторону: если я возьму любую стрелку, начинающуюся в начале координат, она будет связана с уникальной точкой в пространстве (кончиком стрелки). Так что нет никакой двусмысленности, если я скажу «точка для вектора V». Поскольку между векторами и точками в пространстве есть словарь взаимно-однозначный, мы можем пойти дальше и просто определить точку с точки зрения ее вектора, что, как я подозреваю, и делается в используемой вами ссылке.
Это интуитивно понятно, но, как вы можете видеть из других комментариев и ответов здесь, я опускаю технические детали и отсылаю вас к ним за тонкостями.
$\endgroup$
6
$\begingroup$
Вектор, основанный на начале координат (единственный вид, который имеет только "направление и величину", как вы пишете) может быть представлен точкой в начале. Так что естественное соответствие между точками и векторами в этом контексте, что легче всего увидеть, если вы добавите декартовы координаты, чтобы и то, и другое можно было выразить как кортеж действительных чисел.
Однако то, что одно может представлять другое, не означает, что это одно и то же. Вы можете говорить о расстоянии между точками, но сумма и скалярное произведение имеют смысл только для векторов. Если вы применяете их к «точке», вы действительно просто рассматриваете ее как замену соответствующего вектора. И наоборот, точки появляются во многих местах, где вы не можете сформировать векторное пространство. Подумайте о $\mathbb Z \times \mathbb Z$: это (дискретное) пространство, но не векторное пространство. 94$ может представлять (обычный) вектор или матрицу $2 \times 2$. Что отличает их, так это операции, которые мы определяем над ними.
$\endgroup$
$\begingroup$
Это, без каламбура, абсолютно одно и то же.
$\endgroup$
$\begingroup$
Ну, есть огромная техническая разница.
Хотя концептуальная разница на самом деле зависит от того, как человек пытается визуализировать вещи, и от того, для чего нам нужно их визуализировать.
В некоторых предметах, таких как исчисление, я обычно воображаю точки и вектора вволю (точки и стрелки, плавающие вокруг графиков функций). Это связано с тем, что обычно (в исчислении для начинающих) существует неявное соглашение об использовании стандартных координат единичного вектора. Однако в геометрии серьезное техническое различие почти требует концептуального различия. Я попытаюсь проиллюстрировать техническую разницу следующим образом: точки являются элементами некоторого множества, назовем его $G$, характеристики которого нам не обязательно известны, но если мы всегда можем найти уникальное 9*$, что соответствует двум точкам $p,q$ (в таком порядке), то у нас есть новая структура на $G$ (множество точек), называемая аффинной геометрией (в основном "нормальной" геометрией, за исключением расстояний). Конечно, поскольку теперь у нас есть это соответствие, мы можем представить любую точку $q$ как уникальный вектор, который соответствует двум точкам $o,p$ для некоторой точки $o$ (начало координат), но принципиально точки и вектора - это две разные вещи.
Кроме того, в других геометриях взаимодействие точек и векторов может быть другим.
*Помимо всего этого, вектор имеет собственное определение, связанное с такими операциями, как сложение и умножение на скаляры, и никакая ссылка не делается на точки.
$\endgroup$
$\begingroup$
Точки описывают местоположения, а векторы описывают направления.
Представьте мяч. Ряд координат можно использовать для описания точек на этом шаре. Точно так же в любой заданной точке можно использовать ряд компонентов для описания направлений (векторов) в окрестности точки.
Оба для описания используют набор чисел, поэтому может быть не очевидно, чем они отличаются, но векторы можно складывать или вычитать, умножать на скаляры и т. д. Структура векторного пространства важна для алгебры направлений: например, вы можете сложить любые два направления, чтобы получить третье.
Имеет ли смысл добавлять баллы? Вы можете добавить координаты точек, и вы можете получить или не получить другую точку.
Не очевидно, что два разных способа присвоения координат точкам позволили бы «добавлять» точки таким образом, чтобы получить один и тот же результат для обеих систем — на самом деле я не верю, что это так. Рассмотрим, например, что произойдет, если у вас есть точка $(\theta, \phi) = (\pi/2, \pi)$ на сфере и добавлена точка $(\pi/2, -\pi)$ . Вы получите $(\pi, 0)$, что описывает южный полюс. Но в равной степени допустимо описать верхнюю полусферу в терминах $(x,y)$, и вы получите $(0, 1) + (0, -1) = (0, 0)$, что больше не лежит на сфере.
Итак, после всего того, что было сказано для описания разницы между точками и векторами, почему мы иногда связываем векторы с точками? Что ж, иногда вы можете делать это осмысленно — когда пространство, так сказать, «плоское». Это распространено, например, во вводной физике. Очень немногое из простой механики или электромагнетизма ставит вас в ситуацию, когда вы не можете описать точки с помощью векторов. На мой взгляд, все еще полезно различать так называемые «векторы положения» (описывающие направления относительно начала координат) и векторы, описывающие направления относительно какой-либо другой фиксированной точки.
93$, в пространстве всех трехмерных векторов есть вектор $(a, b, c)$.
$\endgroup$
$\begingroup$
Поскольку существует тривиальный перевод между векторами и точками, в которых они заканчиваются, когда они основаны на исходной точке, это различие без разницы в большинстве контекстов.
Итак, если вы хотите быть точным, вы можете преобразовать свои точки в соответствующие векторы, выполнить над ними векторные операции и снова преобразовать их в точки.
$\endgroup$
1
$\begingroup$
Кажется, что происхождение путаницы происходит от представления точки и вектора в виде списка координат, который обычно действительно одинаково для обоих и при просмотре координаты, скажем,
a=(3,2,7)в 3D, нет возможности сказать это точка или вектор.Разницу легко понять, если еще Координата добавлена, чтобы отметить это: это
0для векторов, и1для действительной точки: теперь будет две действительных случаи:a=(3,2,7,0)означает вектор, иa=(3,2,7,1)означает правильную точку.Тогда ясно, что любая сумма (+/-) векторов даст допустимый вектор; разница двух точек есть вектор, вектор, добавленный к другой точке, приводит к другой действительной точке. Особый случай, когда взвешенная сумма баллов приводит к другому действительному баллу. происходит только в том случае, если дополнительная координата также равна
1(сумма весов=1).$\endgroup$
$\begingroup$
На декартовой плоскости вектор представляет движение: влево (на -x) или вправо (на x), а затем вниз (на -y) или вверх (на y). По отношению к вектору точка — это место на сетке, где это движение начинается или заканчивается.
Несмотря на концептуальное разделение, вектор, начинающийся в начале координат (0,0) и ведущий к заданной точке, численно идентичен этой точке.
$\endgroup$
$\begingroup$
A Вектор (или его координатное представление) инвариантен относительно переноса начала координат; a Точка (или ее координатное представление) не является. Если это не является четким различием, доказывающим, что они разные, я съем свою шляпу (шляпы) в следующем декабре.
$\endgroup$
0
$\begingroup$
Я думаю, вы думаете о геометрии и алгебре, но в более широком математическом смысле вы можете обойтись, просто поговорив о векторах, и все. Вектор — это определенный элемент в векторном пространстве.
В гильбертовом пространстве, например, вектор может быть функцией Sinc для действительных чисел, и это не точка в пространстве, не стрелка, указывающая направление или смещение или что-то еще.


 д. составляют точки
д. составляют точки  По сути, идея состоит в том, что мы можем представить вектор с его конечной точкой, и никакая информация не будет потеряна. Иногда это называют помещением вектора в «стандартное положение».
По сути, идея состоит в том, что мы можем представить вектор с его конечной точкой, и никакая информация не будет потеряна. Иногда это называют помещением вектора в «стандартное положение».
 n$, равен всего 92}.
$$
Итак, если вы настаиваете на том, чтобы говорить о величине точки, то вы «свободны» делать это (т.е. свободны определять это). Но имейте в виду, что вы также вызовете путаницу, делая это. А с выполнением математики мы хотим ясно общаться и так...
n$, равен всего 92}.
$$
Итак, если вы настаиваете на том, чтобы говорить о величине точки, то вы «свободны» делать это (т.е. свободны определять это). Но имейте в виду, что вы также вызовете путаницу, делая это. А с выполнением математики мы хотим ясно общаться и так...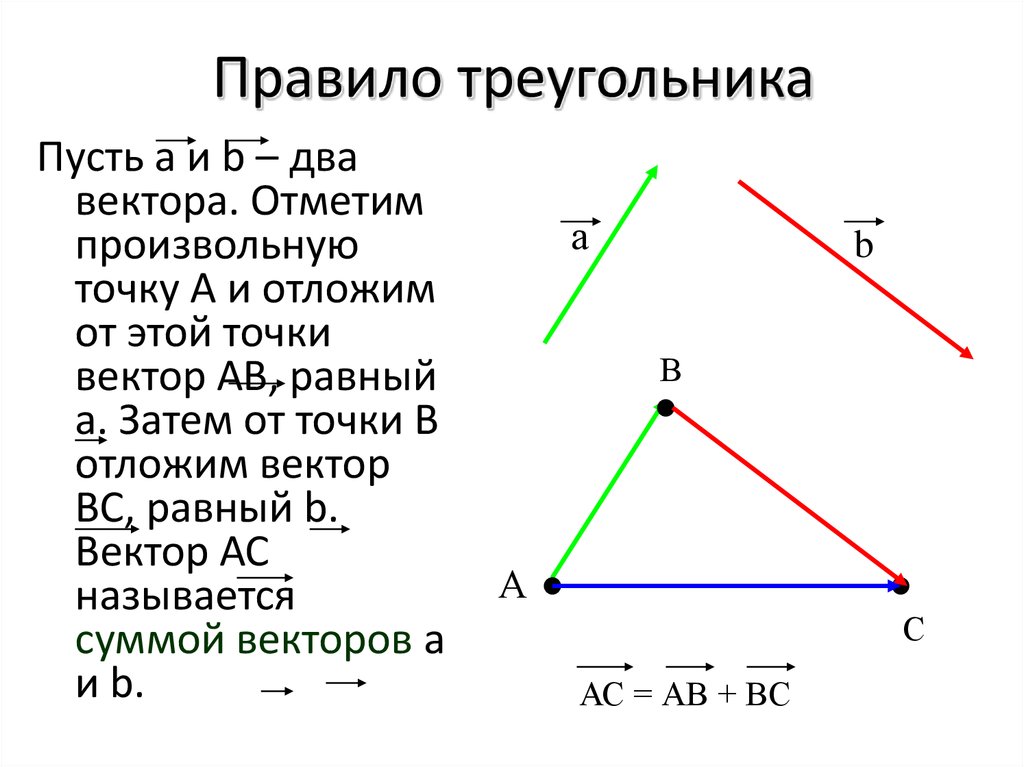 е. если $a = (a_1, a_2, a_3)$, (и аналогично для $b$ и $c$), то сначала определить векторы
$$
\vec{ab} = (b_1 - a_1, b_2- a_2, b_3 - a_3)
$$
и
$$
\vec{ac} = (c_1 - a_1, c_2 - a_2, c_3 - a_3).
$$
Тогда нормальный вектор к/к плоскости есть векторное произведение векторов: $\vec{ab}\times \vec{ac}$.
е. если $a = (a_1, a_2, a_3)$, (и аналогично для $b$ и $c$), то сначала определить векторы
$$
\vec{ab} = (b_1 - a_1, b_2- a_2, b_3 - a_3)
$$
и
$$
\vec{ac} = (c_1 - a_1, c_2 - a_2, c_3 - a_3).
$$
Тогда нормальный вектор к/к плоскости есть векторное произведение векторов: $\vec{ab}\times \vec{ac}$.

 Они оба имеют определенное сходство, что делает преобразование одного в другое очень простым, но они используются по-разному, а также описывают разные математические объекты.
Они оба имеют определенное сходство, что делает преобразование одного в другое очень простым, но они используются по-разному, а также описывают разные математические объекты. Вектор, определенный как $\vec{AB}$ с точками $A$ и $B$, не следует путать с некоторой точкой $X$, такой что $\vec{AB} = \vec{OX}$ .
Вектор, определенный как $\vec{AB}$ с точками $A$ и $B$, не следует путать с некоторой точкой $X$, такой что $\vec{AB} = \vec{OX}$ . Но это работает и в другую сторону: если я возьму любую стрелку, начинающуюся в начале координат, она будет связана с уникальной точкой в пространстве (кончиком стрелки). Так что нет никакой двусмысленности, если я скажу «точка для вектора V». Поскольку между векторами и точками в пространстве есть словарь взаимно-однозначный, мы можем пойти дальше и просто определить точку с точки зрения ее вектора, что, как я подозреваю, и делается в используемой вами ссылке.
Но это работает и в другую сторону: если я возьму любую стрелку, начинающуюся в начале координат, она будет связана с уникальной точкой в пространстве (кончиком стрелки). Так что нет никакой двусмысленности, если я скажу «точка для вектора V». Поскольку между векторами и точками в пространстве есть словарь взаимно-однозначный, мы можем пойти дальше и просто определить точку с точки зрения ее вектора, что, как я подозреваю, и делается в используемой вами ссылке.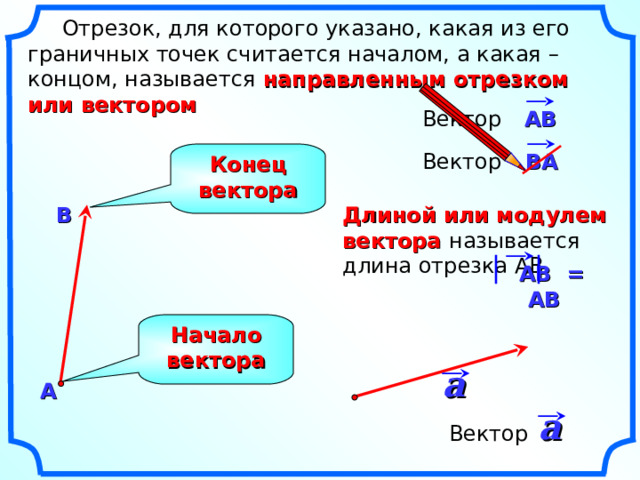
 Хотя концептуальная разница на самом деле зависит от того, как человек пытается визуализировать вещи, и от того, для чего нам нужно их визуализировать.
Хотя концептуальная разница на самом деле зависит от того, как человек пытается визуализировать вещи, и от того, для чего нам нужно их визуализировать. Кроме того, в других геометриях взаимодействие точек и векторов может быть другим.
Кроме того, в других геометриях взаимодействие точек и векторов может быть другим. Не очевидно, что два разных способа присвоения координат точкам позволили бы «добавлять» точки таким образом, чтобы получить один и тот же результат для обеих систем — на самом деле я не верю, что это так. Рассмотрим, например, что произойдет, если у вас есть точка $(\theta, \phi) = (\pi/2, \pi)$ на сфере и добавлена точка $(\pi/2, -\pi)$ . Вы получите $(\pi, 0)$, что описывает южный полюс. Но в равной степени допустимо описать верхнюю полусферу в терминах $(x,y)$, и вы получите $(0, 1) + (0, -1) = (0, 0)$, что больше не лежит на сфере.
Не очевидно, что два разных способа присвоения координат точкам позволили бы «добавлять» точки таким образом, чтобы получить один и тот же результат для обеих систем — на самом деле я не верю, что это так. Рассмотрим, например, что произойдет, если у вас есть точка $(\theta, \phi) = (\pi/2, \pi)$ на сфере и добавлена точка $(\pi/2, -\pi)$ . Вы получите $(\pi, 0)$, что описывает южный полюс. Но в равной степени допустимо описать верхнюю полусферу в терминах $(x,y)$, и вы получите $(0, 1) + (0, -1) = (0, 0)$, что больше не лежит на сфере. 93$, в пространстве всех трехмерных векторов есть вектор $(a, b, c)$.
93$, в пространстве всех трехмерных векторов есть вектор $(a, b, c)$.
 Несмотря на концептуальное разделение, вектор, начинающийся в начале координат (0,0) и ведущий к заданной точке, численно идентичен этой точке.
Несмотря на концептуальное разделение, вектор, начинающийся в начале координат (0,0) и ведущий к заданной точке, численно идентичен этой точке.