Решение иррациональных уравнений
Решение иррациональных уравнений.
В этой статье мы поговорим о способах решения простейших иррациональных уравнений.
Иррациональным уравнением называется уравнение, которое содержит неизвестное под знаком корня.
Давайте рассмотрим два вида иррациональных уравнений, которые очень похожи на первый взгляд, но по сути сильно друг от друга отличаются.
(1)
и
(2)
В первом уравнении мы видим, что неизвестное стоит под знаком корня третьей степени. Мы можем извлекать корень нечетной степени из отрицательного числа, поэтому в этом уравнении нет никаких ограничений ни на выражение, стоящее под знаком корня, ни на выражение, стоящее в правой части уравнения. Мы можем возвести обе части уравнения в третью степень, чтобы избавиться от корня. Получим равносильное уравнение:
При возведении правой и левой части уравнения в нечетную степень мы можем не опасаться получить посторонние корни.
Пример 1. Решим уравнение
Возведем обе части уравнения в третью степень. Получим равносильное уравнение:
Перенесем все слагаемые в одну сторону и вынесем за скобки х:
Приравняем каждый множитель к нулю, получим:
, ,
Ответ: {0;1;2}
Посмотрим внимательно на второе уравнение: . В левой части уравнения стоит квадратный корень, который принимает только неотрицательные значения. Поэтому, чтобы уравнение имело решения, правая часть тоже должна быть неотрицательной. Поэтому на правую часть уравнения накладывается условие:
— это условие существования корней.
Чтобы решить уравнение такого вида, нужно обе части уравнения возвести в квадрат:
(3)
Возведение в квадрат может привести к появлению посторонних корней, поэтому нам надо учесть ОДЗ уравнения:
(4)
Однако, неравенство (4) следует из условия (3): если в правой части равенства стоит квадрат какого-то выражения, а квадрат любого выражения может принимать только неотрицательные значения, следовательно левая часть тоже должна быть неотрицательна. Поэтому условие (4) автоматически следует из условия (3) и наше уравнение равносильно системе:
Поэтому условие (4) автоматически следует из условия (3) и наше уравнение равносильно системе:
Пример 2. Решим уравнение:
.
Перейдем к равносильной системе:
Решим первое уравнение системы и проверим, какие корни удовлетворяют неравеству.
,
Неравеству удовлетворяет только корень
Ответ: x=1
Внимание! Если мы в процессе решения возводим обе части уравнения в квадрат, то нужно помнить, что могут появиться посторонние корни. Поэтому либо нужно переходить к равносильной системе, либо в конце решения СДЕЛАТЬ ПРОВЕРКУ: найти корни и подставить их в исходное уравнение.
Пример 3. Решим уравнение:
Чтобы решить это уравнение, нам также нужно возвести обе части в квадрат. Давайте в этом уравнении не будем заморачиваться с ОДЗ и условием существования корней, а просто в конце решения сделаем проверку.
Воозведем обе части уравнения в квадрат:
Перенесем слагаемое, содержащее корень влево, а все остальные слагаемые вправо:
Еще раз возведем обе части уравнения в квадрат:
По тереме Виета:
,
Сделаем проверку. Для этого подставим найденные корни в исходное уравнение. Очевидно, что при правая часть исходного уравнения отрицательна, а левая положительна.
Для этого подставим найденные корни в исходное уравнение. Очевидно, что при правая часть исходного уравнения отрицательна, а левая положительна.
При получаем верное равенство.
Ответ:
И.В. Фельдман, репетитор по математике.
Наибольший корень уравнения онлайн. Решение уравнений с двумя переменными
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Степенные или показательные уравнения называют уравнения, в которых переменные находятся в степенях, а основанием является число. Например:
Решение показательного уравнения сводится к 2 довольно простым действиям:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания неодинаковые, ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение. {nm}:\]
{nm}:\]
Прибавляем к исходному уравнению:
Вынесем за скобки \
Выразим \
Поскольку степени одинаковые, отбрасываем их:
Ответ: \
Где можно решить показательное уравнение онлайн решателем?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или . База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
Предлагаемый вашему вниманию бесплатный калькулятор располагает богатым арсеналом возможностей для математических вычислений. Он позволяет использовать онлайн калькулятор в различных сферах деятельности: образовательной , профессиональной и коммерческой
. Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников , он значительно облегчает им выполнение самых разных расчётов.
Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников , он значительно облегчает им выполнение самых разных расчётов.Вместе с тем калькулятор может стать полезным инструментом в некоторых направлениях бизнеса и для людей разных профессий. Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.
Данный онлайн калькулятор может
- Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемсчитаем огромные числа в онлайн калькулятореМы даже не знаем, как такое число назвать правильно (
- Кроме тангенса , косинуса , синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса , арккотангенса и прочих.

- Доступны в арсенале логарифмы , факториалы и другие интересные функции
- Данный онлайн калькулятор умеет строить графики !!!
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot). Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .
Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.
Построить можно абсолютно любую функцию, с любым количеством переменных, например такую: plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать. Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.
Как работать с Математическим калькулятором
1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.
Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.
2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге. В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.
3. Панель инструментов — это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.
Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.
Обратите внимание, при нажатии кнопок вызова дополнительных функций, конвертера величин, решения матриц и уравнений, построения графиков вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.
4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена.
| Клавиша | Символ | |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| () | () | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin(?) | Синус угла |
| cos | cos(?) | Косинус |
| tan | tan(y) | Тангенс |
| sinh | sinh() | Гиперболический синус |
| cosh | cosh() | Гиперболический косинус |
| tanh | tanh() | Гиперболический тангенс |
| sin -1 | asin() | Обратный синус |
| cos -1 | acos() | Обратный косинус |
| tan -1 | atan() | Обратный тангенс |
| sinh -1 | asinh() | Обратный гиперболический синус |
| cosh -1 | acosh() | Обратный гиперболический косинус |
| tanh -1 | atanh() | Обратный гиперболический тангенс |
| x 2 | ^2 | Возведение в квадрат |
| х 3 | ^3 | Возведение в куб |
| x y | ^ | Возведение в степень |
| 10 x | 10^() | Возведение в степень по основанию 10 |
| e x | exp() | Возведение в степень числа Эйлера |
| vx | sqrt(x) | Квадратный корень |
| 3 vx | sqrt3(x) | Корень 3-ей степени |
| y vx | sqrt(x,y) | Извлечение корня |
| log 2 x | log2(x) | Двоичный логарифм |
| log | log(x) | Десятичный логарифм |
| ln | ln(x) | Натуральный логарифм |
| log y x | log(x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re() | Выделение целой действительной части |
| Im | Im() | Исключение действительной части |
| |x| | abs() | Модуль числа |
| Arg | arg() | Аргумент функции |
| nCr | ncr() | Биноминальный коэффициент |
| gcd | gcd() | НОД |
| lcm | lcm() | НОК |
| sum | sum() | Суммарное значение всех решений |
| fac | factorize() | Разложение на простые множители |
| diff | diff() | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
Как решать уравнения?
В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.
Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.
Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.
4. Все остальные.)
Всех остальных, разумеется, больше всего, да…) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем.
Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.
Мы научимся их разматывать.
И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные — третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.) Просто для них существуют свои специальные приёмы и методы.
Но для любых (повторяю — для любых! ) уравнений есть надёжная и безотказная основа для решения. Работает везде и всегда. Эта основа — Звучит страшно, но штука очень простая. И очень (очень!) важная.
Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: «Как решать уравнения? » лежит, как раз, в этих преобразованиях. Намёк понятен?)
Тождественные преобразования уравнений.
В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример. Причем так, чтобы при смене внешнего вида суть уравнения не менялась. Такие преобразования называются тождественными или равносильными.
Такие преобразования называются тождественными или равносильными.
Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема.
Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений.
Базовые потому, что их можно применять к любым уравнениям – линейным, квадратным, дробным, тригонометрическим, показательным, логарифмическим и т.д. и т.п.
Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется.
Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа:
Дело знакомое, переносим двойку вправо, и получаем:
На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый:
Результат получается тот же самый:
х+2 — 2 = 3 — 2
Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….
Второе тождественное преобразование : обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа
Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.
Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.
Вот и всё.
Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?)
Примеры тождественных преобразований уравнений. Основные проблемы.
Начнём с первого тождественного преобразования. Перенос влево-вправо.
Пример для младшеньких.)
Допустим, надо решить вот такое уравнение:
3-2х=5-3х
Вспоминаем заклинание: «с иксами — влево, без иксов — вправо!» Это заклинание — инструкция по применению первого тождественного преобразования.) Какое выражение с иксом у нас справа? 3х ? Ответ неверный! Справа у нас — 3х ! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:
3-2х+3х=5
Так, иксы собрали в кучку. Займёмся числами. Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:
Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:
-2х+3х=5-3
Остались сущие пустяки. Слева — привести подобные, справа — посчитать. Сразу получается ответ:
В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.)
Пример для старшеньких.)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно на примерах решение систем.
Пример №1:
Решим методом подстановки
Решение системы уравнений методом подстановки
2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)
1. Выражаем
Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y
2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1
3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2
Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1
Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)
Решим методом почленного сложения (вычитания).
Решение системы уравнений методом сложения
3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)
1. Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2
5y=32 | :5
y=6,4
3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6
Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно . Без шуток.
9.1 Решение квадратных уравнений с использованием свойства квадратного корня — средний уровень алгебры 2e
Цели обучения
К концу этого раздела вы сможете:
- Решение квадратных уравнений вида ax2=kax2=k с использованием свойства квадратного корня
- Решение квадратных уравнений вида a(x–h)2=ka(x–h)2=k с использованием свойства квадратного корня
Приготовься 9.
 1
1Прежде чем начать, пройдите этот тест на готовность.
Упрощение: 128.128.
Если вы пропустили эту проблему, просмотрите пример 8.13.
Приготовься 9.2
Упрощение: 325325.
Если вы пропустили эту проблему, просмотрите пример 8.50.
Приготовься 9.3
Коэффициент: 9×2−12x+49×2−12x+4.
Если вы пропустили эту проблему, просмотрите пример 6.23.
Квадратное уравнение представляет собой уравнение вида x 2 + bx + c = 0, где a≠0a≠0. Квадратные уравнения отличаются от линейных уравнений наличием квадратного члена с переменной, возведенной во вторую степень вида 9.0015 топор 2 . Мы используем разные методы для решения квадратных уравнений, чем линейные уравнения, потому что простое сложение, вычитание, умножение и деление членов не изолирует переменную.
Мы видели, что некоторые квадратные уравнения можно решить с помощью факторизации. В этой главе мы изучим три других метода, которые можно использовать в случае, если квадратное уравнение нельзя разложить на множители.
Решение квадратных уравнений вида ax2=kax2=k с использованием свойства квадратного корня
Мы уже решили некоторые квадратные уравнения методом факторизации. Давайте рассмотрим, как мы использовали факторинг для решения квадратного уравнения 9.0015 х 2 = 9.
| х2=9х2=9 | |
| Приведите уравнение к стандартной форме. | х2-9=0х2-9=0 |
| Фактор разницы квадратов. | (х-3)(х+3)=0(х-3)(х+3)=0 |
| Использовать свойство нулевого продукта. | х-3=0х-3=0х-3=0х-3=0 |
Решите каждое уравнение. | х=3х=-3х=3х=-3 |
Мы можем легко использовать факторинг, чтобы найти решения подобных уравнений, таких как x 2 = 16 и x 2 = 25, потому что 16 и 25 являются полными квадратами. В каждом случае мы получили бы два решения: x=4,x=-4x=4,x=-4 и x=5,x=-5.x=5,x=-5.
Но что произойдет, если мы получим уравнение типа x 2 = 7? Поскольку 7 не является полным квадратом, мы не можем решить уравнение с помощью факторизации.
Ранее мы узнали, что с 169является квадратом 13, мы также можем сказать, что 13 является квадратным корнем из 169. Кроме того, (−13) 2 = 169, поэтому −13 также является квадратным корнем из 169. Следовательно, и 13, и − 13 — это квадратные корни из 169. Таким образом, каждое положительное число имеет два квадратных корня — положительный и отрицательный. Ранее мы определили квадратный корень числа следующим образом:
Ранее мы определили квадратный корень числа следующим образом:
Если n2=m, то это квадратный корень из m. Если n2=m, то это квадратный корень из m.
Поскольку все эти уравнения имеют форму x 2 = k , определение квадратного корня говорит нам, что решения представляют собой два квадратных корня из k . Это приводит к свойству квадратного корня.
Свойство квадратного корня
Если x 2 = k , то
x=korx=−korx=±k.x=korx=−korx=±k.
Обратите внимание, что свойство квадратного корня дает два решения уравнения вида x 2 = k , главного квадратного корня из kk и его противоположности. Мы могли бы также записать решение как x=±k.x=±k. Мы читаем это как x равно положительному или отрицательному квадратному корню из k .
Теперь мы снова решим уравнение x 2 = 9, на этот раз используя свойство квадратного корня.
| х2=9х2=9 | |
| Использование свойства квадратного корня. | х=±9х=±9 |
| х=±3х=±3 | |
| Sox=3orx=−3.Sox=3orx=−3. |
Что происходит, когда константа не является точным квадратом? Давайте воспользуемся свойством квадратного корня, чтобы решить уравнение x 2 = 7,
.| х2=7х2=7 | |
| Использование свойства квадратного корня. | х=7,х=-7х=7,х=-7 |
Мы не можем упростить 77, поэтому оставляем ответ радикальным.
Пример 9.
 1
1Как решить квадратное уравнение формы
ax 2 = k Используя свойство квадратного корняРешите: x2−50=0.x2−50=0.
Решение
Попробуй 9.1
Решите: x2−48=0.x2−48=0.
Попробуй 9.2
Решите: y2−27=0.y2−27=0.
Здесь перечислены шаги, необходимые для использования свойства Square Root для решения квадратного уравнения.
Как
Решите квадратное уравнение, используя свойство квадратного корня.
- Шаг 1. Выделите квадратичный член и сделайте его коэффициент единицей.
- Шаг 2. Используйте свойство квадратного корня.
- Шаг 3. Упростите радикал.
- Шаг 4. Проверьте решения.
Чтобы использовать свойство Square Root, коэффициент переменного члена должен быть равен единице. В следующем примере мы должны разделить обе части уравнения на коэффициент 3, прежде чем использовать свойство квадратного корня.
В следующем примере мы должны разделить обе части уравнения на коэффициент 3, прежде чем использовать свойство квадратного корня.
Пример 9.2
Решите: 3z2=108.3z2=108.
Решение
| 3z2=1083z2=108 | |
| Квадратичный член изолирован. Разделите на 3, чтобы получить коэффициент 1. | 3z23=10833z23=1083 |
| Упрощение. | z2=36z2=36 |
| Использование свойства квадратного корня. | г=±36г=±36 |
| Упростите радикальное. | г=±6г=±6 |
Перепишите, чтобы показать два решения. | z=6,z=-6z=6,z=-6 |
| Проверьте решения: |
Попробуй 9.3
Решите: 2×2=98,2×2=98.
Попробуй 9.4
Решите: 5м2=80,5м2=80.
Свойство квадратного корня гласит: «Если x2=kx2=k», что произойдет, если k<0?k<0? Это будет иметь место в следующем примере.
Пример 9.3
Решите: x2+72=0x2+72=0.
Решение
| х2+72=0х2+72=0 | |
| Выделить квадратичный член. | х2=-72х2=-72 |
| Использование свойства квадратного корня. | х=±-72х=±-72 |
Упростите, используя комплексные числа. | х=±72ix=±72i |
| Упростите радикальное. | х=±62ix=±62i |
| Перепишите, чтобы показать два решения. | х=62i,x=-62ix=62i,x=-62i |
| Проверьте решения: |
Попробуй 9,5
Решить: c2+12=0.c2+12=0.
Попробуй 9,6
Решите: q2+24=0.q2+24=0.
Наш метод работает и тогда, когда в уравнении встречаются дроби, решаем как любое уравнение с дробями. В следующем примере мы сначала выделяем квадратичный член, а затем делаем коэффициент равным единице.
Пример 9.4
Решите: 23u2+5=17,23u2+5=17.
Решение
| 23u2+5=1723u2+5=17 | |
Выделить квадратичный член. | |
| Умножьте на 3232, чтобы получить коэффициент 1. | |
| Упрощение. | |
| Использование свойства квадратного корня. | |
| Упростите радикальное. | |
| Упрощение. | |
| Перепишите, чтобы показать два решения. | |
| Чек: |
Попробуй 9,7
Решите: 12×2+4=24,12×2+4=24.
Попробуй 9,8
Решите: 34y2−3=18,34y2−3=18.
В решениях некоторых уравнений в радикалах могут быть дроби. Когда это происходит, мы должны рационализировать знаменатель.
Пример 9,5
Решите: 2×2−8=41,2×2−8=41.
Решение
| Выделить квадратичный член. | |
| Разделите на 22, чтобы получить коэффициент 1. | |
| Упрощение. | |
| Использование свойства квадратного корня. | |
Перепишите радикал как часть квадратных корней. | |
| Рационализируйте знаменатель. | |
| Упрощение. | |
| Перепишите, чтобы показать два решения. | |
| Чек: Мы оставляем вам чек. |
Попробуй 9,9
Решите: 5r2−2=34,5r2−2=34.
Попробуй 9.10
Решите: 3t2+6=70,3t2+6=70.
Решение квадратных уравнений формы
a ( x − h ) 2 = k Использование свойства квадратного корня Мы также можем использовать свойство квадратного корня, чтобы решить уравнение формы a ( x − h ) 2 = k . Обратите внимание, что квадратичный член x в исходной форме x 2 = k заменен на ( x − ч ).
Обратите внимание, что квадратичный член x в исходной форме x 2 = k заменен на ( x − ч ).
Первый шаг, как и прежде, состоит в том, чтобы изолировать терм, у которого переменная возведена в квадрат. В данном случае бином возводится в квадрат. После того, как бином изолирован, путем деления каждой стороны на коэффициент a , то свойство квадратного корня можно использовать для ( x − h ) 2 .
Пример 9,6
Решите: 4(y−7)2=48,4(y−7)2=48.
Решение
| 4(у-7)2=484(у-7)2=48 | |
Разделите обе части на коэффициент 4.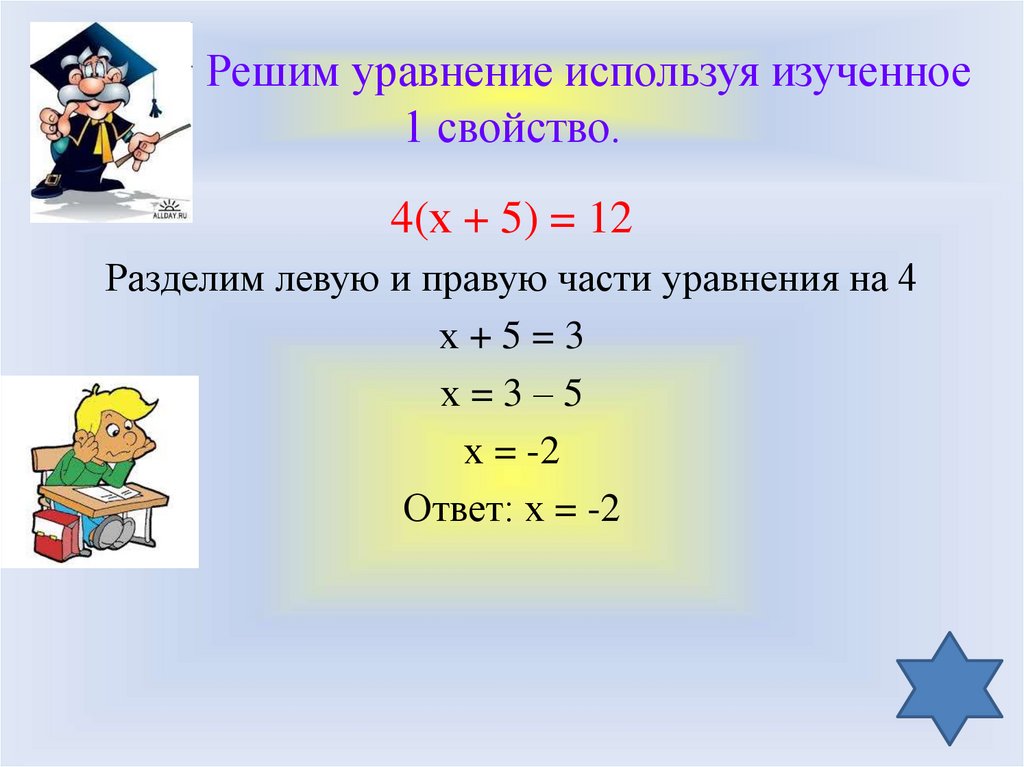 | (у-7)2=12(у-7)2=12 |
| Использование свойства квадратного корня в биноме | г-7=±12г-7=±12 |
| Упростите радикальное. | г-7=±23г-7=±23 |
| Решите для гг. | у=7±23у=7±23 |
| Перепишите, чтобы показать два решения. | у=7+23,у=7+23,у=7-23у=7-23 |
| Чек: |
Попробуй 9.11
Решите: 3(a−3)2=54,3(a−3)2=54.
Попробуй 9.12
Решите: 2(b+2)2=80,2(b+2)2=80.
Помните, что когда мы извлекаем квадратный корень из дроби, мы можем извлечь квадратный корень из числителя и знаменателя отдельно.
Пример 9,7
Решите: (x−13)2=59.(x−13)2=59.
Решение
| (х-13)2=59(х-13)2=59 | |
| Использование свойства квадратного корня. | х-13=±59х-13=±59 |
| Перепишите радикал как часть квадратных корней. | х-13=±59х-13=±59 |
| Упростите радикальное. | х-13=±53х-13=±53 |
| Решите для xx. | х=13±53х=13±53 |
| Перепишите, чтобы показать два решения. | х=13+53,х=13-53х=13+53,х=13-53 |
| Чек: Мы оставляем вам чек. |
Попробуй 9.13
Решите: (x−12)2=54.(x−12)2=54.
Попробуй 9.14
Решите: (y+34)2=716.(y+34)2=716.
Мы начнем решение следующего примера с выделения биномиального члена.
Пример 9,8
Решите: 2(x−2)2+3=57,2(x−2)2+3=57.
Решение
| 2(х-2)2+3=572(х-2)2+3=57 | |
| Вычтите 3 из обеих частей, чтобы выделить биномиальный член. | 2(х-2)2=542(х-2)2=54 |
| Разделите обе части на 2. | (х-2)2=27(х-2)2=27 |
| Использование свойства квадратного корня. | х-2=±27х-2=±27 |
| Упрости радикал. | х-2=±33х-2=±33 |
| Решите для xx. | х=2±33х=2±33 |
| Перепишите, чтобы показать два решения. | х=2+33,х=2-33х=2+33,х=2-33 |
| Чек: Мы оставляем вам чек. |
Попробуй 9.
 15
15Решите: 5(a−5)2+4=104,5(a−5)2+4=104.
Попробуй 9.16
Решите: 3(b+3)2−8=88,3(b+3)2−8=88.
Иногда решения представляют собой комплексные числа.
Пример 9,9
Решите: (2x−3)2=−12.(2x−3)2=−12.
Решение
| (2x−3)2=−12(2x−3)2=−12 | |
| Использование свойства квадратного корня. | 2x−3=±−122x−3=±−12 |
| Упростите радикальное. | 2x−3=±23i2x−3=±23i |
| Добавьте 3 с обеих сторон. | 2x=3±23i2x=3±23i |
| Разделите обе части на 2. | х=3±23i2x=3±23i2 |
| Переписать в стандартной форме. | х=32±23i2x=32±23i2 |
| Упрощение. | х=32±3ix=32±3i |
| Перепишите, чтобы показать два решения. | х=32+3i,x=32−3ix=32+3i,x=32−3i |
| Чек: Мы оставляем вам чек.  |
Попробуй 9.17
Решите: (3r+4)2=−8.(3r+4)2=−8.
Попробуй 9.18
Решите: (2t−8)2=−10.(2t−8)2=−10.
Левые части уравнений в следующих двух примерах, кажется, не имеют формы a ( x − h ) 2 . Но они представляют собой совершенные квадратные трехчлены, поэтому мы приведем их к нужному нам виду.
Пример 9.10
Решите: 4n2+4n+1=16,4n2+4n+1=16.
Решение
Мы замечаем, что левая часть уравнения представляет собой совершенный квадратный трехчлен. Мы учтем это в первую очередь.
| 4n2+4n+1=164n2+4n+1=16 | |
Разложите на множители совершенный квадратный трехчлен. | (2n+1)2=16(2n+1)2=16 |
| Использование свойства квадратного корня. | 2n+1=±162n+1=±16 |
| Упростите радикальное. | 2n+1=±42n+1=±4 |
| Решите для nn. | 2n=-1±42n=-1±4 |
| Разделите каждую сторону на 2. | 2n2=-1±422n2=-1±42 n=-1±42n=-1±42 |
| Перепишите, чтобы показать два решения. | n=-1+42n=-1+42, n=-1-42n=-1-42 |
| Упростите каждое уравнение. | n=32n=32, n=-52n=-52 |
| Чек: |
Попробуй 9.
 19
19Решите: 9м2−12м+4=25,9м2−12м+4=25.
Попробуй 9.20
Решите: 16n2+40n+25=4,16n2+40n+25=4.
Раздел 9.1 Упражнения
Практика делает совершенным
Решение квадратных уравнений вида x 2 = k Использование свойства квадратного корня
В следующих упражнениях решите каждое уравнение.
1.
а2=49а2=49
2.
b2=144b2=144
3.
r2-24=0r2-24=0
4.
t2-75=0t2-75=0
5.
и2-300=0и2-300=0
6.
v2-80=0v2-80=0
7.
4м2=364м2=36
8.
3n2=483n2=48
9.
43×2=4843×2=48
10.
53y2=6053y2=60
11.
х2+25=0х2+25=0
12.
у2+64=0у2+64=0
13.
х2+63=0х2+63=0
14.
у2+45=0у2+45=0
15.
43×2+2=11043×2+2=110
16.
23y2−8=−223y2−8=−2
17.
25a2+3=1125a2+3=11
18.
32b2−7=4132b2−7=41
19.
7п2+10=267п2+10=26
20.
2q2+5=302q2+5=30
21.
5y2−7=255y2−7=25
22.
3×2−8=463×2−8=46
Решение квадратных уравнений вида a ( x − h ) 2 = k Использование свойства квадратного корня
В следующих упражнениях решите каждое уравнение.
23.
(и-6)2=64(и-6)2=64
24.
(v+10)2=121(v+10)2=121
25.
(м-6)2=20(м-6)2=20
26.
(n+5)2=32(n+5)2=32
27.
(r−12)2=34(r−12)2=34
28.
(х+15)2=725(х+15)2=725
29.
(у+23)2=881(у+23)2=881
30.
(т-56)2=1125(т-56)2=1125
31.
(а-7)2+5=55(а-7)2+5=55
32.
(б-1)2-9=39(б-1)2-9=39
33.
4(х+3)2-5=274(х+3)2-5=27
34.
5(х+3)2-7=685(х+3)2-7=68
35.
(5с+1)2=-27(5с+1)2=-27
36.
(8d−6)2=−24(8d−6)2=−24
37.
(4x−3)2+11=−17(4x−3)2+11=−17
38.
(2у+1)2-5=-23(2у+1)2-5=-23
39.
м2−4м+4=8м2−4м+4=8
40.
п2+8п+16=27п2+8п+16=27
41.
х2-6х+9=12х2-6х+9=12
42.
у2+12у+36=32у2+12у+36=32
43.
25×2−30x+9=3625×2−30x+9=36
44.
9y2+12y+4=99y2+12y+4=9
45.
36×2−24x+4=8136×2−24x+4=81
46.
64×2+144x+81=2564×2+144x+81=25
Смешанная практика
В следующих упражнениях решите, используя свойство Square Root.
47.
2r2=322r2=32
48.
4t2=164t2=16
49.
(а-4)2=28(а-4)2=28
50.
(б+7)2=8(б+7)2=8
51.
9w2−24w+16=19w2−24w+16=1
52.
4z2+4z+1=494z2+4z+1=49
53.
а2-18=0а2-18=0
54.
b2-108=0b2-108=0
55.
(р-13)2=79(р-13)2=79
56.
(q−35)2=34(q−35)2=34
57.
м2+12=0м2+12=0
58.
n2+48=0.n2+48=0.
59.
u2−14u+49=72u2−14u+49=72
60.
v2+18v+81=50v2+18v+81=50
61.
(м−4)2+3=15(м−4)2+3=15
62.
(n−7)2−8=64(n−7)2−8=64
63.
(х+5)2=4(х+5)2=4
64.
(у-4)2=64(у-4)2=64
65.
6с2+4=296с2+4=29
66.
2d2−4=772d2−4=77
67.
(х-6)2+7=3(х-6)2+7=3
68.
(у-4)2+10=9(у-4)2+10=9
Письменные упражнения
69.
Своими словами объясните свойство квадратного корня.
70.
Своими словами объясните, как использовать свойство квадратного корня для решения квадратного уравнения (x+2)2=16(x+2)2=16.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
Выберите, как бы вы отреагировали на утверждение «Я могу решить квадратное уравнение вида a, умноженное на квадрат x минус h, равно k, используя свойство квадратного корня». «Уверенно», «с некоторой помощью» или «Нет, я не понимаю».
ⓑ Если большинство ваших чеков было:
…уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретной.
…с некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого вы можете попросить о помощи? Ваши одноклассники и преподаватель являются хорошими источниками информации. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого вы можете попросить о помощи? Ваши одноклассники и преподаватель являются хорошими источниками информации. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет — не понимаю! Это предупреждающий знак, и вы не должны его игнорировать. Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
Квадратное уравнение Python — javatpoint
следующий → ← предыдущая Квадратное уравнение: Квадратное уравнение образовано от латинского термина «quadrates», что означает квадрат. топор 2 +bx+c=0 Здесь «x» неизвестен, который нужно найти, а «a», «b», «c» задает такие числа, что «a» не равно 0. Если a = 0, то уравнение становится линейным, а не квадратичным больше. В уравнении a, b и c называются коэффициентами. Возьмем пример решения квадратного уравнения 8x 2 + 16x + 8 = 0 См. этот пример: # импортировать сложный математический модуль импортировать cmath a = float(input(‘Введите a:’)) b = float(input(‘Введите b:’)) c = float(input(‘Введите c:’)) # вычисляем дискриминант д = (б**2) — (4*а*в) # найти два решения sol1 = (-b-cmath.sqrt(d))/(2*a) sol2 = (-b+cmath.sqrt(d))/(2*a) print(‘Решение: {0} и {1}’.format(sol1,sol2)) Вывод: Введите: 8 Введите б: 5 Введите с: 9 Решение: (-0,3125-1,0135796712641785j) и (-0,3125+1,0135796712641785j) Пояснение — В первой строке мы импортировали модуль cmath и определили три переменные с именами a, b и c, которые принимают ввод от пользователя. Второй методМы можем получить решение квадратного уравнения, используя прямую формулу. Давайте разберем следующий пример. Вышеприведенная формула состоит из следующих случаев.
Пример — # Программа Python для поиска корней квадратного уравнения
импортировать математику # функция поиска корней
def findRoots(a, b, c): dis_form = б * б — 4 * а * с
sqrt_val = math. Вывод: Введите a:7 Введите б:5 Введите c:2 Сложные корни -0,35714285714285715 + i 5,5677643628300215 -0,35714285714285715 - я 5,5677643628300215 Пояснение — В приведенном выше коде мы импортировали математический модуль и определили формулу для вычисления дискриминанта. |


 Это особый тип уравнения, имеющий форму:
Это особый тип уравнения, имеющий форму: Затем вычисляем дискриминант по формуле. Используя метод cmath.sqrt() , мы вычислили два решения и распечатали результат.
Затем вычисляем дискриминант по формуле. Используя метод cmath.sqrt() , мы вычислили два решения и распечатали результат. sqrt (abs (dis_form)) если dis_form > 0:
print(«настоящие и разные корни»)
print((-b + sqrt_val) / (2 * a))
print((-b — sqrt_val) / (2 * a)) Элиф dis_form == 0:
print(» действительные и одинаковые корни»)
напечатать (-b / (2 * а)) еще:
print(«Сложные корни»)
print(- b / (2 * a), » + i», sqrt_val)
print(- b / (2 * a), «- i», sqrt_val) a = int(input(‘Введите a:’))
b = int(input(‘Введите b:’))
c = int(input(‘Введите c:’)) # Если a равно 0, то неверное уравнение
если а == 0:
print(«Введите правильное квадратное уравнение») еще:
найтиКорни (а, б, в)
sqrt (abs (dis_form)) если dis_form > 0:
print(«настоящие и разные корни»)
print((-b + sqrt_val) / (2 * a))
print((-b — sqrt_val) / (2 * a)) Элиф dis_form == 0:
print(» действительные и одинаковые корни»)
напечатать (-b / (2 * а)) еще:
print(«Сложные корни»)
print(- b / (2 * a), » + i», sqrt_val)
print(- b / (2 * a), «- i», sqrt_val) a = int(input(‘Введите a:’))
b = int(input(‘Введите b:’))
c = int(input(‘Введите c:’)) # Если a равно 0, то неверное уравнение
если а == 0:
print(«Введите правильное квадратное уравнение») еще:
найтиКорни (а, б, в)