Как определить длину вектора по координатам: Найдите длину вектора а (-10,24)

Как найти длину вектора

Понятие длины вектора

Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. 2 }=\sqrt{68}=2\sqrt{17}$

Складывая, получим

Ответ: $7\sqrt{2}+\sqrt{82}+2\sqrt{17}$

Вычисление длины (модуля) вектора в EXCEL. Примеры и описание

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.

1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a _x и a _y , то длину вектора можно найти по формуле

В случае вектора в пространстве добавляется третья координата

В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).

Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .

В файле примера также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .

2. Нахождение длины вектора через координаты точек

Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.

Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.

По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.

3. Нахождение длины вектора по теореме косинусов

Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).

Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).

Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL

4. Нахождение длины вектора через координаты точек треугольника

Пусть заданы 3 точки треугольника, образованного векторами.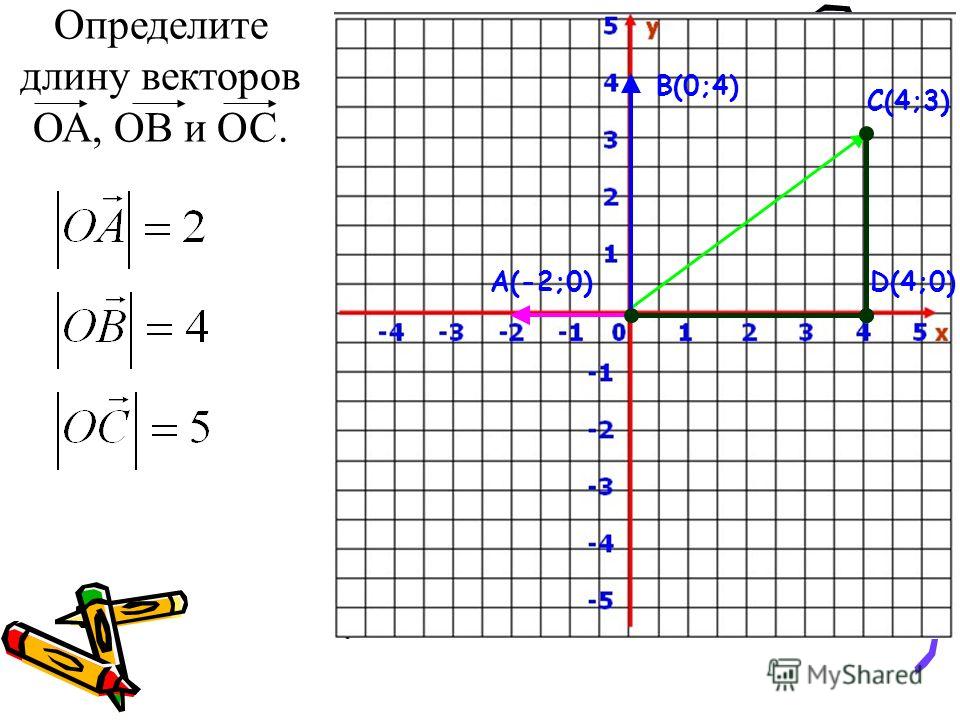

Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .

Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).

5. Нахождение координат вектора через координаты точек

Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.

векторов — Нахождение длины между двумя точками в 3-х измерениях с помощью теоремы Пифагора

спросил 4 года, 7 месяцев назад

Изменено 4 года, 7 месяцев назад

Просмотрено 738 раз

$\begingroup$

Я учусь в 11 классе, и мне нужно учить векторы для экзамена IB. 2}. \конец{выравнивание*} Мне трудно визуализировать и понять, почему здесь вычитаются координаты точек. Я очень ценю обратную связь. Извините за низкое качество ссылки, но я думаю, что у меня еще недостаточно репутации, чтобы напрямую вставлять изображения. Кроме того, в формуле все индексы должны быть перевернуты. Таким образом, x1 становится x2 и наоборот. 92}$

$\endgroup$

$\begingroup$

Вычитание представляет собой расстояние между двумя точками (вдоль оси). Например, по оси $x$ расстояние от $3$ до $7$ равно $4$: $$|3-7| = |7-3| = 4.$$

Для теоремы Пифагора вам нужны длины сторон треугольников; это $|x_1-x_2|$ и $|y_1-y_2|$ (а также $|z_1-z_2|$, если вы обобщаете теорему на три измерения). Обратите внимание, что порядок вычитания не имеет значения, и когда мы возводим эти величины в квадрат, знаки абсолютного значения становятся излишними.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

javascript — Вычислить вектор с заданным углом и длиной

спросил 7 лет, 11 месяцев назад

Изменено 9 месяцев назад

Просмотрено 9к раз

Есть ли способ, которым в javascript я могу вызвать функцию с координатами x и y и направлением (угол в градусах), и она вернет набор новых координат, которые были «перемещены» на 10 пикселей в направлении, заданном исходными координатами? Я осмотрелся, но все, что я могу найти, это способы получить угол двух заданных координат.

• javascript
• координаты
• угол

1

Эта функция возвращает массив [xCoord, yCoord ] новых координат:

 function myFunction(xCoord, yCoord, angle, length) {
    длина = тип длины !== 'undefined' ? длина: 10;
    угол = угол * Math. PI / 180; // если вы используете градусы вместо радианов
    return [длина * Math.cos(угол) + xCoord, длина * Math.sin(угол) + yCoord]
}
 

2

Я просто хотел указать, что ответы неверны ИМХО. Я создал JSFiddle, показывающий, что правильная реализация должна быть примерно такой:

 function getRelativeVector(angle, length, xOffset, yOffset) {
    угол = угол * Math.PI / 180;
    возвращаться {
        X:длина * Math.sin(угол) + xOffset,
        Y:длина * Math.cos(угол) + yOffset
    };
}
 

Другие решения, показанные здесь от @Audrius и @Markus, просто перекручены в коснется и коснется . Они работают только для углов от 0 до 45 градусов.

Формула будет следующей:

• X = длина * sin(угол) + xLocation
• Y = длина * cos(угол) + yLocation

Сдвиг по координате x равен L*cos(a) , а сдвиг по координате y равен L*sin(a) , где a — это угол («заданное направление»), а L равен 10 px в вашем случае.