Определение функций | Основы JavaScript
Для перемещения по курсу нужно зарегистрироваться
1. Введение ↳ теория
2. Hello, World! ↳ теория / тесты / упражнение
3. Инструкции ↳ теория / тесты / упражнение
4. Арифметические операции ↳ теория / тесты / упражнение
5. Ошибки оформления (синтаксиса и линтера) ↳ теория / тесты / упражнение
6. Строки ↳ теория / тесты / упражнение
7. Переменные ↳ теория / тесты / упражнение
8. Выражения в определениях ↳ теория / тесты / упражнение
9. Именование ↳ теория / тесты / упражнение
10. Интерполяция ↳ теория / тесты / упражнение
11. Извлечение символов из строки ↳ теория / тесты / упражнение
12. Типы данных ↳ теория / тесты / упражнение
13. Неизменяемость и примитивные типы ↳ теория / тесты / упражнение
14. Функции и их вызов ↳ теория / тесты / упражнение
15. Сигнатура функции ↳ теория / тесты / упражнение
16. Вызов функции — выражение ↳ теория / тесты / упражнение
17.
18. Детерминированность ↳ теория / тесты / упражнение
19. Стандартная библиотека ↳ теория / тесты / упражнение
20. Свойства и методы ↳ теория / тесты / упражнение
21. Цепочка вызовов ↳ теория / тесты / упражнение
22. Определение функций ↳ теория / тесты / упражнение
23. Возврат значений ↳ теория / тесты / упражнение
24. Параметры функций ↳ теория / тесты / упражнение
25. Необязательные параметры функций ↳ теория / тесты / упражнение
26. Упрощенный синтаксис функций ↳ теория / тесты / упражнение
27. Логика ↳ теория / тесты / упражнение
28. Логические операторы ↳ теория / тесты / упражнение
29. Результат логических операций ↳ теория / тесты / упражнение
30. Условные конструкции ↳ теория / тесты / упражнение
31. Тернарный оператор ↳ теория / тесты / упражнение
32. Конструкция Switch ↳ теория / тесты / упражнение
33. Цикл while ↳ теория / тесты / упражнение
34.
Агрегация данных
↳
теория
/
тесты
/
упражнение
35. Обход строк в цикле ↳ теория / тесты / упражнение
36. Условия внутри тела цикла ↳ теория / тесты / упражнение
37. Инкремент и декремент ↳ теория / тесты / упражнение
38. Цикл for ↳ теория / тесты / упражнение
39. Модули ↳ теория / тесты / упражнение
Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как
Не понятна формулировка, нашли опечатку?
Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку
Что-то не получается в уроке?
Загляните в раздел «Обсуждение»:
- Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
- Если вопросы остались, задайте свой. Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
- Мы отвечаем на сообщения в течение 2-3 дней.
К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!Подробнее о том, как задавать вопросы по уроку
Функции и Графики — сайт по математике и не только!!! ОПРЕДЕЛЕНИЕ ФУНКЦИИ Всё о Математических функциях и их графиках…
Функции и Графики — сайт по математике и не только!!! ОПРЕДЕЛЕНИЕ ФУНКЦИИ Всё о Математических функциях и их графиках…
|
Используются технологии uCoz |
функция | Определение, типы, примеры и факты
кубическое уравнение
Просмотреть все СМИ
- Ключевые люди:
- Поль Пенлеве Карл Вейерштрасс Эмиль Борель Эдвард Чарльз Титчмарш Питер Густав Лежен Дирихле
- Похожие темы:
- специальная функция корень преемственность Дзета-функция Римана рекурсивная функция
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
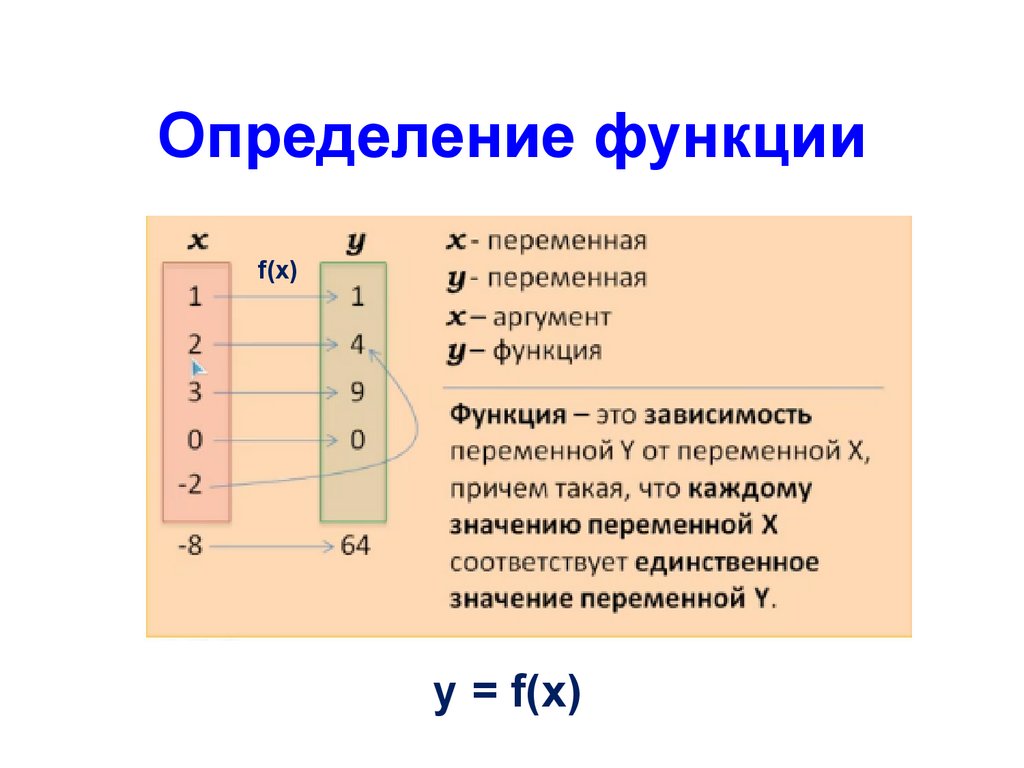
функция , в математике выражение, правило или закон, определяющие связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной).
Функции повсеместно используются в математике и необходимы для формулирования физических отношений в естественных науках. Современное определение функции впервые было дано в 1837 году немецким математиком Петером Дирихле:
Если переменная y так связана с переменной x , что всякий раз, когда числовое значение присваивается x , существует правило, согласно которому определяется уникальное значение y , тогда y Говорят, что является функцией независимой переменной x .
Это соотношение обычно обозначается как y = f ( x ) — что называется « f из x » — и y и x связаны таким образом, что для каждых x существует уникальное значение y . То есть f ( x ) не может иметь более одного значения для одного и того же x . Говоря языком теории множеств, функция связывает элемент x с элементом f
Набор значений х называется областью определения функции, а набор значений f ( х ), сгенерированный значениями в домене, называется диапазоном функции. В дополнение к f ( x ) другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда характер функции неизвестен или не определен.Общие функции
Многие широко используемые математические формулы являются выражениями известных функций. Например, формула площади круга A = π r 2 дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных (называемые многомерными или многомерными функциями), также распространены в математике, как это видно из формулы площади треугольника A = b h /2, которая определяет A в зависимости от b (базовый) и h (высота).
В этих примерах физические ограничения заставляют независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.
Викторина по Британике
Дайте определение: математические термины
Вот ваша миссия, если вы решите ее принять: Дайте определение следующим математическим терминам до того, как истечет время.
Формула площади круга является примером полиномиальной функции. Общий вид для таких функций P ( x ) =
. . . 31313131. . . . . . . . может быть любым действительным числом и всеми степенями x — это счетные числа (1, 2, 3,…). (Когда степени x могут быть любыми действительными числами, результат известен как алгебраическая функция.) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любое отношение, включающее действительные числа, может быть точно аппроксимировано с помощью полиномиальная функция. Полиномиальные функции характеризуются наибольшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартическая и квинтическая для высших степеней, равных 1, 2, 3, 4 и 5 соответственно. Полиномиальные функции могут иметь геометрическое представление с помощью аналитической геометрии. Независимая переменная x откладывается по оси x (горизонтальная линия), а зависимая переменная y откладывается по оси y (вертикальная линия).
Когда график отношения между х и y строится в плоскости х — y , отношение является функцией, если вертикальная линия всегда проходит только через одну точку на графике кривой; то есть была бы только одна точка f ( x ) соответствует каждому x , что является определением функции. Затем график функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 − 3 x + 2.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Другим распространенным типом функций, которые изучались с древних времен, являются тригонометрические функции, такие как sin x и cos x , где x — мера угла ( см. рисунок ). Из-за своего периодического характера тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».
Экспоненциальная функция представляет собой отношение вида y = a x с независимой переменной x в диапазоне по всей строке действительных чисел как показатель степени положительного числа a . Вероятно, наиболее важной из экспоненциальных функций является y = e x , иногда пишется как y = exp ( x ), в которой e (2,7182818) является основанием натурального числа. система логарифмов (ln). По определению x — это логарифм, и, таким образом, существует логарифмическая функция, обратная экспоненциальной функции. В частности, если y = e x , тогда x = ln y . Неалгебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.
Сложные функции
Практические приложения функций, переменными которых являются комплексные числа, не так просто проиллюстрировать, но тем не менее они очень обширны.
Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена в виде z = x + i y , где i — мнимая единица (квадратный корень из −1), а x и y — действительные переменные ( см. цифру 9). возможно разделить сложную функцию на реальные и мнимые детали: F ( Z ) = P ( x , Y ) + I Q ( X , Y ). .
Функция Определение и значение | Словарь.com
- Основные определения
- Викторина
- Связанный контент
- Примеры
- Британский
- Научный
- Культурный
Показывает уровень сложности на основе слова.
[ fuhngk-shuhn ]
/ ˈfʌŋk ʃən /
Сохранить это слово!
См. синонимы для: функция / функционировал / функционировал / функции на Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
сущ.
вид действия или деятельности, присущий лицу, предмету или учреждению; цель, для которой что-то разработано или существует; роль.
любое торжественное общественное или общественное собрание или событие.
фактор, связанный с другими факторами или зависящий от них: Цена является функцией спроса и предложения.
Математика.
- Также называется соответствием, картой, отображением, преобразованием. отношение между двумя множествами, в котором каждому элементу первого множества ставится в соответствие один элемент второго множества, как выражение у = х2; оператор.
- Также называется многозначной функцией. отношение между двумя множествами, в котором два или более элемента второго множества присваиваются каждому элементу первого множества, как y2 = x2, которое присваивает каждому x два значения y = +x и y = -x.
- набор упорядоченных пар, в котором ни один из первых элементов пар не встречается дважды.
Геометрия.
- формула, выражающая отношение между углами треугольника и его сторонами в виде синуса или косинуса.
- гиперболическая функция.
Грамматика.
- грамматическая роль языковой формы или место, которое она занимает в определенной конструкции.
- грамматические роли или позиции языковой формы или класса формы в совокупности.
Социология. вклад, вносимый социокультурным явлением в существующую социальную систему.
глагол (используется без объекта)
для выполнения определенного действия или деятельности; Работа; эксплуатация: компьютер сейчас не работает. Он редко работает до полудня.
иметь или выполнять какую-либо функцию; serve: в более раннем английском языке настоящее время часто функционировало как будущее.
Этот оранжевый ящик может служить стулом.
ВИКТОРИНА
Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма обычно используется с другими глаголами для выражения намерения?
Происхождение функции
1525–35; <лат. functiōn- (основа functiō) исполнение, исполнение, эквивалентное funct(us) (причастие прошедшего времени от fungī) выполненное, выполненное + -iōn--ion
ДРУГИЕ СЛОВА ОТ функция
интерфункция, прилагательноемногофункциональность, прилагательноенефункционирование, прилагательноенадфункционирование, прилагательное
предфункция , существительное-функция, глагол (используется без объекта)подфункция, существительное-су-за-функция, существительное-функция-инг, прилагательноехорошо-функция-инг, прилагательное
Слова рядом с функцией
Funabashi, Funafuti, funambulist, развлечения и игры, Funchal, функция, функциональный, функциональный, функциональный анализ, функциональное исчисление, функциональное заболевание
Dictionary.
com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
Слова, относящиеся к функции
действие, деятельность, дело, поведение, бизнес, долг, упражнение, цель, операция, часть, сила, цель, ответственность, роль , услуга, ситуация, задача, работа, сбор, встреча
Как использовать функцию в предложении
Не на каждом веб-сайте она есть, и даже на тех, которые имеют очень поверхностные функции.
Как внедрять цифровые инновации, необходимые во время пандемии|Ник Часинов|16 сентября 2020 г.|Search Engine Watch
Отчасти это было связано с оставшейся неопределенностью в отношении того, как вирус распространяется наиболее эффективно.
Анализ сбивающих с толку комментариев Трампа о ношении масок|Филип Бамп|16 сентября 2020 г.|Washington Post
Вспомогательные вещества являются важными материалами и выполняют широкий спектр функций.
«Неактивные» ингредиенты в ваших таблетках могут навредить вам|Елена Ионова/The Conversation|15 сентября 2020 г.
|Popular-ScienceНапример, доставка и прослушивание социальных сетей кажутся разрозненными функциями, но на самом деле они тесно связаны.
Глубокое погружение: как лето 2020 года заставило бренд-маркетинг измениться к лучшему|jim cooper|14 сентября 2020|Digiday
|Popular-ScienceЭто потому, что ежедневные упражнения не только помогают детям оставаться физически и эмоционально здоровыми, но и повышает когнитивную функцию.
15-недельный план упражнений для детей и семей|Криста Ланглуа|12 сентября 2020 г.|Outside Online
Но медь выполняет еще одну важную функцию: работает как катализатор в процессе дистилляции.
Когда дело доходит до отличного виски, размер вашего по-прежнему имеет значение||9 декабря 2014|DAILY BEAST
iPad стал еще большим хитом, тем более что он имел новую функцию, которая позволяла ему играть в рисунок назад.
Множество жизней художника Дэвида Хокни|Уильям О’Коннор|23 ноября 2014 г.
|DAILY BEASTОткрытость также может быть функцией сексуальности и пола.
Извращенный выход к своему доктору в черном и синем|Хизер Бернер|25 октября 2014 г.|DAILY BEAST
Под названием «Пожалуйста, идите домой» пародия на Даниэля Францезе, известного как «слишком гей, чтобы функционировать». Дамиан из «Дрянных девчонок».
Голограммы аниме-поп-звезд, возвращение «свежего принца» Карлтона и другие вирусные видео|Алекс Чанси|12 октября 2014 г.|DAILY BEAST
Секс — это основная функция человека; физиологический драйв, который мы не можем игнорировать.
Христианские правые любят порно: новые исследования показывают, что библейский пояс имеет извращенную сторону|Аврора Сноу|11 октября 2014|DAILY BEAST
Функция Внимания.
Ассимиляционная память|Маркус Дуайт Ларроу (также известный как профессор А. Луазетт)
Маленькие девочки, возможно, представляют привлекательную функцию украшения: им нравится, когда их считают красивыми.
Children’s Ways|Джеймс Салли
Вряд ли это функция — вечеринки даже в больших политических загородных домах более или менее неформальны.
Предки|Gertrude Atherton
Однако до сих пор не было представлено никаких определенных доказательств этой позиции, и функция соединения полностью неизвестна.
Элементы агрохимии|Томас Андерсон
После того, как было выпущено официальное объявление, мероприятие завершилось банкетом для 200 известных повстанцев.
The Philippine Islands|John Foreman
|DAILY BEAST
Британский словарь определений для функции
функция
/ (ˈfʌŋkʃən) /
существительноеестественная цель человека или предназначенная функция
молоток для забивания гвоздей в дерево
официальное или официальное общественное собрание или церемония
фактор, зависящий от другого или других факторовпродолжительность полета зависит от погоды
Также называется: карта, сопоставление, математическая логика, отношение между двумя множествами, которое связывает уникальный элемент (значение) второго (диапазона) с каждым элементом (аргументом) первого (домена): множество-один связь.
Символ: f(x) Значение f(x) для x = 2 равно f(2)
глагол (intr)
действовать или выполнять, как указано; правильно работать
(следовать как) выполнять действие или роль (чего-то или кого-то) монета может работать как отвертка
Производные формы функции
functionless, прилагательноеПроисхождение слова для функции
C16: от латинского functiō, от fungī выполнять, разряжать
Collins English Dictionary — Complete & Unabridged 2012 Digital Edition © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins
Научные определения функции
function
единственный член второго набора. Функции часто выражаются в виде уравнения, такого как y = x + 5, что означает, что y является функцией x, так что для любого значения x значение y будет на 5 больше, чем x.
Величина, значение которой зависит от значения, присвоенного одной или нескольким связанным величинам. Например, площадь квадрата зависит от длины его сторон.