Как определить порядок матрицы: определение, методы нахождения и примеры решения задач

Определение ранга матрицы. Вычисление ранга матрицы по определению.

Высшая математика » Матрицы и определители » Ранг матрицы » Определение ранга матрицы. Вычисление ранга матрицы по определению.

Для работы с понятием ранга матрицы нам понадобятся сведения из темы «Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений». В первую очередь это касается термина «минор матрицы», так как ранг матрицы станем определять именно через миноры.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Эквивалентные матрицы – матрицы, ранги которых равны между собой.

Поясним подробнее. Допустим, среди миноров второго порядка есть хотя бы один, отличный от нуля. А все миноры, порядок которых выше двух, равны нулю. Вывод: ранг матрицы равен 2. Или, к примеру, среди миноров десятого порядка есть хоть один, не равный нулю. А все миноры, порядок которых выше 10, равны нулю.

Вывод: ранг матрицы равен 10.

Обозначается ранг матрицы $A$ так: $\rang A$ или $r(A)$. Ранг нулевой матрицы $O$ полагают равным нулю, $\rang O=0$. Напомню, что для образования минора матрицы требуется вычёркивать строки и столбцы, – однако вычеркнуть строк и столбцов более, чем содержит сама матрица, невозможно. Например, если матрица $F$ имеет размер $5\times 4$ (т.е. содержит 5 строк и 4 столбца), то максимальный порядок её миноров равен четырём. Миноры пятого порядка образовать уже не удастся, так как для них потребуется 5 столбцов (а у нас всего 4). Это означает, что ранг матрицы $F$ не может быть больше четырёх, т.е. $\rang F≤4$.

В более общей форме вышеизложенное означает, что если матрица содержит $m$ строк и $n$ столбцов, то её ранг не может превышать наименьшего из чисел $m$ и $n$, т.е. $\rang A≤\min(m,n)$.

В принципе, из самого определения ранга следует метод его нахождения. Процесс нахождения ранга матрицы по определению можно схематически представить так:

Поясню эту схему более подробно. Начнём рассуждать с самого начала, т.е. с миноров первого порядка некоторой матрицы $A$.

1. Если все миноры первого порядка (т.е. элементы матрицы $A$) равны нулю, то $\rang A=0$. Если среди миноров первого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 1$. Переходим к проверке миноров второго порядка.
2. Если все миноры второго порядка равны нулю, то $\rang A=1$. Если среди миноров второго порядка есть хотя бы один, не равный нулю, то $\rang A≥ 2$. Переходим к проверке миноров третьего порядка.
3. Если все миноры третьего порядка равны нулю, то $\rang A=2$. Если среди миноров третьего порядка есть хотя бы один, не равный нулю, то $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.
4. Если все миноры четвёртого порядка равны нулю, то $\rang A=3$. Если среди миноров четвёртого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 4$. Переходим к проверке миноров пятого порядка и так далее.

Что ждёт нас в конце этой процедуры? Возможно, что среди миноров k-го порядка найдётся хоть один, отличный от нуля, а все миноры (k+1)-го порядка будут равны нулю. Это значит, что k – максимальный порядок миноров, среди которых есть хотя бы один, не равный нулю, т.е. ранг будет равен k. Может быть иная ситуация: среди миноров k-го порядка будет хоть один не равный нулю, а миноры (k+1)-го порядка образовать уже не удастся. В этом случае ранг матрицы также равен k. Короче говоря, порядок последнего составленного ненулевого минора и будет равен рангу матрицы.

Перейдём к примерам, в которых процесс нахождения ранга матрицы по определению будет проиллюстрирован наглядно. Ещё раз подчеркну, что в примерах данной темы мы станем находить ранг матриц, используя лишь определение ранга. Иные методы (вычисление ранга матрицы методом окаймляющих миноров, вычисление ранга матрицы методом элементарных преобразований) рассмотрены в следующих темах.

Кстати, вовсе не обязательно начинать процедуру нахождения ранга с миноров самого малого порядка, как это сделано в примерах №1 и №2. Можно сразу перейти к минорам более высоких порядков (см. пример №3).

Пример №1

Найти ранг матрицы $A=\left(\begin{array}{ccccc} 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end{array} \right)$.

Решение

Данная матрица имеет размер $3\times 5$, т.е. содержит три строки и пять столбцов. Из чисел 3 и 5 минимальным является 3, посему ранг матрицы $A$ не больше 3, т.е. $\rang A≤ 3$. И это неравенство очевидно, так как миноры четвёртого порядка образовать мы уже не сможем, – для них нужно 4 строки, а у нас всего 3. Перейдём непосредственно к процессу нахождения ранга заданной матрицы.

Среди миноров первого порядка (т.е среди элементов матрицы $A$) есть ненулевые. Например, 5, -3, 2, 7. Вообще, нас не интересует общее количество ненулевых элементов. Есть хотя бы один не равный нулю элемент – и этого достаточно. Так как среди миноров первого порядка есть хотя бы один, отличный от нуля, то делаем вывод, что $\rang A≥ 1$ и переходим к проверке миноров второго порядка.

Начнём исследовать миноры второго порядка. Например, на пересечении строк №1, №2 и столбцов №1, №4 расположены элементы такого минора: $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|$. У этого определителя все элементы второго столбца равны нулю, поэтому и сам определитель равен нулю, т.е. $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=0$ (см. свойство №3 в теме свойства определителей). Или же можно банально вычислить сей определитель, используя формулу №1 из раздела по вычислению определителей второго и третьего порядков:

$$ \left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=5\cdot 0-0\cdot 7=0. $$

Первый проверенный нами минор второго порядка оказался равен нулю. О чём это говорит? О том, что нужно дальше проверять миноры второго порядка. Либо они все окажутся нулевыми (и тогда ранг будет равен 1), либо среди них найдётся хотя бы один минор, отличный от нуля. Попробуем осуществить более удачный выбор, записав минор второго порядка, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №5: $\left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|$. Найдём значение этого минора второго порядка:

$$ \left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|=5\cdot 3-2\cdot 7=1. $$

Данный минор не равен нулю. Вывод: среди миноров второго порядка есть хотя бы один, отличный от нуля. Следовательно $\rang A≥ 2$. Нужно переходить к исследованию миноров третьего порядка.

Если для формирования миноров третьего порядка мы станем выбирать столбец №2 или столбец №4, то такие миноры будут равными нулю (ибо они будут содержать нулевой столбец). Остаётся проверить лишь один минор третьего порядка, элементы которого расположены на пересечении столбцов №1, №3, №5 и строк №1, №2, №3. Запишем этот минор и найдём его значение:

$$ \left|\begin{array}{ccc} 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end{array} \right|=-20-18-14+16+21+15=0.

$$

Итак, все миноры третьего порядка равны нулю. Последний составленный нами ненулевой минор был второго порядка. Вывод: максимальный порядок миноров, среди которых есть хотя бы один, отличный от нуля, равен 2. Следовательно, $\rang A=2$.

Ответ: $\rang A=2$.

Пример №2

Найти ранг матрицы $A=\left( \begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right)$.

Решение

Имеем квадратную матрицу четвёртого порядка. Сразу отметим, что ранг данной матрицы не превышает 4, т.е. $\rang A≤ 4$. Приступим к нахождению ранга матрицы.

Среди миноров первого порядка (т.е среди элементов матрицы $A$) есть хотя бы один, не равный нулю, поэтому $\rang A≥ 1$. Переходим к проверке миноров второго порядка. Например, на пересечении строк №2, №3 и столбцов №1 и №2 получим такой минор второго порядка: $\left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|$.

Вычислим его:

$$ \left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|=0-10=-10. $$

Среди миноров второго порядка есть хотя бы один, не равный нулю, поэтому $\rang A≥ 2$.

Перейдём к минорам третьего порядка. Найдём, к примеру, минор, элементы которого расположены на пересечении строк №1, №3, №4 и столбцов №1, №2, №4:

$$ \left | \begin{array} {cccc} -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end{array} \right|=105-105=0. $$

Так как данный минор третьего порядка оказался равным нулю, то нужно исследовать иной минор третьего порядка. Либо все они окажутся равными нулю (тогда ранг будет равен 2), либо среди них найдётся хоть один, не равный нулю (тогда станем исследовать миноры четвёртого порядка). Рассмотрим минор третьего порядка, элементы которого расположены на пересечении строк №2, №3, №4 и столбцов №2, №3, №4:

$$ \left| \begin{array} {ccc} -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end{array} \right|=-28. $$

Среди миноров третьего порядка есть хотя бы один, отличный от нуля, поэтому $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.

Любой минор четвёртого порядка располагается на пересечении четырёх строк и четырёх столбцов матрицы $A$. Иными словами, минор четвёртого порядка – это определитель матрицы $A$, так как данная матрица как раз и содержит 4 строки и 4 столбца. Определитель этой матрицы был вычислен в примере №2 темы «Понижение порядка определителя. Разложение определителя по строке (столбцу)», поэтому просто возьмём готовый результат:

$$ \left| \begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right|=86. $$

Итак, минор четвертого порядка не равен нулю. Миноров пятого порядка образовать мы уже не можем. Вывод: наивысший порядок миноров, среди которых есть хотя бы один отличный от нуля, равен 4. Итог: $\rang A=4$.

Ответ: $\rang A=4$.

Пример №3

Найти ранг матрицы $A=\left( \begin{array} {cccc} -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end{array} \right)$.

Решение

Сразу отметим, что данная матрица содержит 3 строки и 4 столбца, поэтому $\rang A≤ 3$. В предыдущих примерах мы начинали процесс нахождения ранга с рассмотрения миноров наименьшего (первого) порядка. Здесь же попробуем сразу проверить миноры максимально возможного порядка. Для матрицы $A$ такими являются миноры третьего порядка. Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №4:

$$ \left| \begin{array} {ccc} 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end{array} \right|=-8-60-20=-88. $$

Итак, наивысший порядок миноров, среди которых есть хоть один, не равный нулю, равен 3. Поэтому ранг матрицы равен 3, т.е. $\rang A=3$.

Ответ: $\rang A=3$.

Вообще, нахождение ранга матрицы по определению – в общем случае задача довольно-таки трудоёмкая. Например у матрицы сравнительно небольшого размера $5\times 4$ имеется 60 миноров второго порядка. И если даже 59 из них будут равны нулю, то 60й минор может оказаться ненулевым. Тогда придётся исследовать миноры третьего порядка, которых у данной матрицы 40 штук. Обычно стараются использовать менее громоздкие способы, такие как метод окаймляющих миноров или метод эквивалентных преобразований.

Вернуться к списку тем

Задать вопрос на форуме

Записаться на занятия

Онлайн-занятия по высшей математике

Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы

Пятый урок посвящен нахождению обратной матрицы, ее свойствам, а также определению ранга матрицы

• Обратная матрица
• Ранг матрицы

Обратная матрица

Обратной матрицей A^-1 матрицы A называют матрицу, удовлетворяющую следующему равенству:

где – E это единичная матрица.

Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы. Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.

Исходная матрица:

Союзная ей матрица A*:

Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A*^T:

Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A^-1, обратную матрице A:

➣ Численный пример

Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:

Для начала найдем определитель матрицы A:

Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная.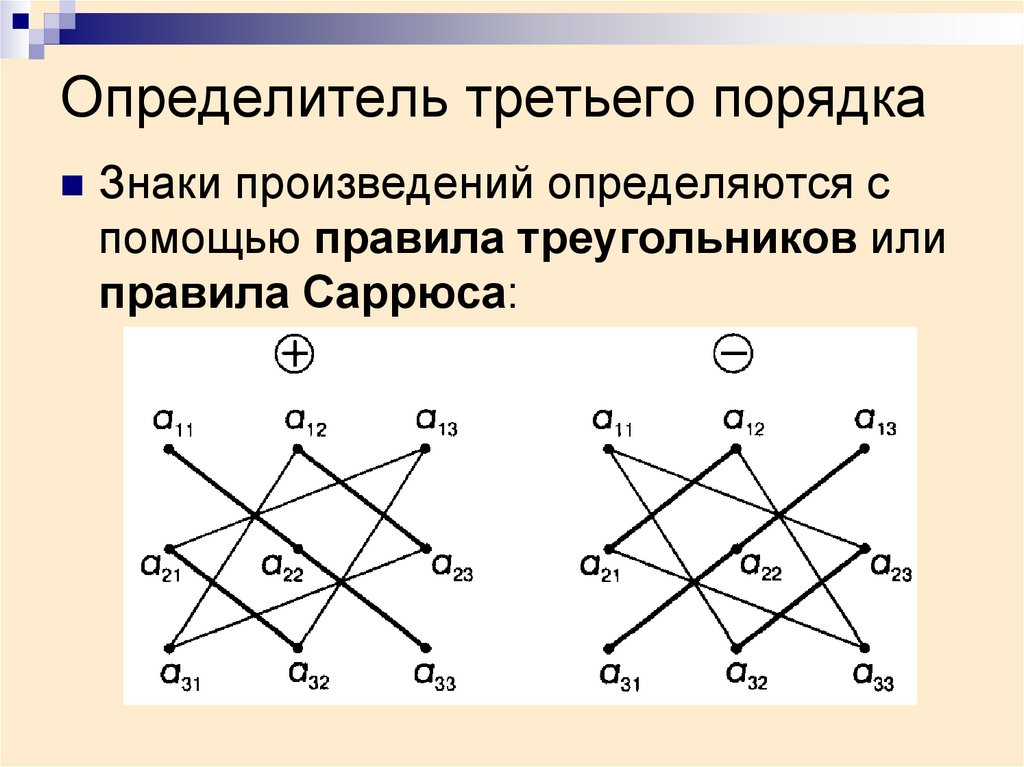 Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:

Союзная матрица будет иметь следующий вид:

Присоединенная матрица получается из союзной путем транспонирования:

Находим обратную матрицу:

➤ Пример на Python

Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():

>>> A = np.matrix('1 -3; 2 5')
>>> A_inv = np.linalg.inv(A)
>>> print(A_inv)
[[ 0.45454545 0.27272727]
 [-0.18181818 0.09090909]]

Рассмотрим свойства обратной матрицы.

Свойство 1. Обратная матрица обратной матрицы есть исходная матрица:

➤Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> A_inv = np.linalg.inv(A)
>>> A_inv_inv = np. linalg.inv(A_inv)
>>> print(A)
[[1. -3.]
 [2. 5.]]
>>> print(A_inv_inv)
[[1. -3.]
 [2. 5.]]

Свойство 2. Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:

➤ Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
 [ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
 [ 0.27272727 0.09090909]]

Свойство 3. Обратная матрица произведения матриц равна произведению обратных матриц:

➤ Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> B = np.matrix('7. 6.; 1. 8.')
>>> L = np.linalg.inv(A.dot(B))
>>> R = np.linalg.inv(B).dot(np.linalg.inv(A))
>>> print(L)
[[ 0. 09454545 0.03272727]
 [-0.03454545 0.00727273]]
>>> print(R)
[[ 0.09454545 0.03272727]
 [-0.03454545 0.00727273]]

Ранг матрицы

Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.

Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:

>>> m_eye = np.eye(4)
>>> print(m_eye)
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]

Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():

>>> rank = np. linalg.matrix_rank(m_eye)
>>> print(rank)
4

Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:

>>> m_eye[3][3] = 0
>>> print(m_eye)
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 0.]]
>>> rank = np.linalg.matrix_rank(m_eye)
>>> print(rank)
3

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.  Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Порядок матрицы — формула, определение, типы, примеры

Порядок матрицы представляет количество строк и столбцов в матрице. Матрица — это массив элементов, расположенных в строках и столбцах, и порядок матрицы помогает получить количество строк и столбцов в матрице. Кроме того, порядок матрицы помогает узнать тип матрицы и общее количество элементов в матрице.

Порядок матрицы является важным аспектом, который помогает решить, может ли конкретная арифметическая операция выполняться над двумя матрицами. Здесь, основываясь на порядке матрицы, мы можем узнать о различных типах матриц и различных арифметических операциях, которые можно выполнять над матрицами.

1.	Что такое порядок матрицы?
2.	Тип матриц на основе порядка матрицы
3.	Порядок матрицы для различных операций с матрицей
4.	Примеры по порядку матрицы
5.	Практические вопросы
6.	Часто задаваемые вопросы по заказу Matrix

Что такое порядок матрицы?

Порядок матрицы дает размерность матрицы и количество строк и столбцов, присутствующих в матрице. Порядок матрицы обычно представляется как A _{m × n} , где m — количество строк, а n — количество столбцов в данной матрице. Кроме того, ответ на умножение порядка матрицы (m × n) дает количество элементов в матрице.

В приведенной выше матрице мы видим m строк и n столбцов. Первое число в порядке матрицы всегда представляет количество строк, а второе число в порядке матрицы всегда представляет количество столбцов в матрице.

Тип матриц на основе порядка матрицы

Порядок матрицы дает размеры матрицы и определяет различные типы матриц. Давайте проверим порядок некоторых из различных типов матриц.

• Порядок матрицы строк: Матрица строк состоит из одной строки и множества столбцов. Следовательно, порядок матрицы-строки имеет вид 1 × n. \[A_{1 × n} = \begin{bmatrix}a_1&a_2&a_3&\cdots&a_n\end{bmatrix}\]
• Порядок матрицы столбцов: Матрица столбцов состоит из одного столбца и множества строк. Следовательно, порядок матрицы-столбца равен n × 1. \[A_{n × 1} = \begin{bmatrix}a_1\\a_2\\a_3\\ \vdots\\a_n\end{bmatrix}\]
• Порядок квадратной матрицы: Квадратная матрица, как следует из названия, имеет одинаковое количество строк и столбцов. Следовательно, порядок квадратной матрицы имеет вид n × n. Здесь у нас есть равное количество 3 строк и 3 столбцов в приведенной ниже матрице. \[A_{3×3} = \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\]
• Порядок прямоугольной матрицы: Прямоугольная матрица имеет неравное количество строк и столбцов, поэтому порядок прямоугольной матрицы имеет вид m × n. Здесь, в приведенной ниже матрице, у нас есть 2 строки и 3 столбца. \[A_{2×3} = \begin{bmatrix}a&b&c\\ \\ d&e&f\end{bmatrix}\] 9T_{3×2} = \begin{bmatrix}a&d\\b&e\\c&f\end{bmatrix}\]

Порядок матрицы для различных операций над матрицей

Порядок матрицы относится к типу матрицы. Кроме того, многие арифметические операции с матрицами основаны на порядке упомянутой матрицы. Давайте проверим, как выполняются следующие операции над матрицами в зависимости от порядка .matrix.

Сложение и вычитание матриц: Для сложения или вычитания двух матриц порядок обеих матриц должен быть одинаковым. Количество строк в обеих матрицах должно быть одинаковым, и количество столбцов в обеих матрицах также должно быть равным. Давайте разберемся в этом на простом примере.

\( \left[\begin{массив}{ccc}
2&{-1}&3\\
0 & 5 & 2 \end{массив}\right]_{\!2 \!× \!3} + \left[\begin{массив}{ccc}
\!0 &\! 2&\!7\\\
\!1 & \!-2 & \!9
\end{массив}\right]_{\!2 \!× \!3}\)

\(= \left[\begin{массив}{ccc}
2+0 & {-1} \!+\!2 & 3 \!+\!7\\ \\
0\!+\!1 и 5\!+\!(-2) и 2\!+\!9
\!\end{массив}\right] \)

\(= \left[\begin{массив}{ccc}
\!2 & \!1 & \!10 \\ \\
\!1 & \!3 & \!11
\end{array}\right]_{\!2 \!× \!3} \)

Здесь соответствующие элементы обеих матриц складываются, чтобы получить элементы результирующей матрицы, а значит, количество элементов и порядок обеих матриц должен быть одинаковым. Порядок обеих матриц в приведенном выше сложении матриц равен 2 × 3.

Умножение матриц: Умножение матриц включает особое условие порядка матрицы. Количество столбцов в первой матрице для умножения должно быть равно количеству строк во второй матрице. Далее порядок полученной матрицы равен количеству строк первой матрицы и количеству столбцов второй матрицы.

\(AB=\left[ \begin{matrix} \!1 & \!2 & \!3 \\ \\ \!3 & \!1 & \!0 \\\end{matrix} \right] _{\!2 \!× \!3} \times \left[ \begin{matrix} \!1 & \!4 \\ \!3 & \!-1 \\ 2 & -3 \\\end{ матрица} \right]_{\!3 \!× \!2}\)

\(=\begin{bmatrix}\!1\!×\!1 \!+ \!2\!×\!3 \!+ \!3\!×\!2 &\!1 \!×\!4 \!+\!2\!×\!(-1) \!+\!3\!×\!(- 3)\\\!3\!×\!1 \!+ \!1\!×\!3 \!+ \!0\!×\!2 &\!3 \!×\!4 \!+ \!1\!×\!(-1) \!+\!0\!×\!(-3)\end{bmatrix}\)

\(=\left[ \begin{matrix} \!13 & \!-7\\ \\ \!6 & \!11 \\ \end{matrix} \right]_{\!2 × \!2}\)

В приведенном выше примере количество столбцов в первой матрице и количество строк во второй матрице равно 3. А порядок результирующей матрицы 2 × 2, так как она имеет 2 строки (что равно количество строк в первой матрице) и 2 столбца (что равно количеству столбцов во второй матрице).

☛ Связанные темы:

Следующие связанные темы помогут лучше понять концепцию порядка матрицы.

• Матричный калькулятор
• Транспонирование матрицы
• Сопряженная матрица
• Обратная матрица

Важные примечания по порядку матрицы:

Следующие пункты обобщают некоторые ключевые моменты, полученные в отношении порядка матрицы.

• В порядке матрицы m × n первое число m всегда представляет количество строк, а второе число n всегда представляет количество столбцов.
• Для сложения и вычитания двух матриц порядок матриц должен быть одинаковым.
• Для умножения двух матриц количество столбцов в первой матрице должно быть равно количеству строк в первой матрице.
• При умножении двух матриц порядок результирующей матрицы таков, что количество строк равно первой матрице, а количество столбцов равно второй матрице.

Часто задаваемые вопросы о заказе матрицы

Как найти порядок матрицы?

Порядок матрицы можно легко вычислить, проверив расположение элементов матрицы. Матрица — это набор элементов, расположенных в виде строк и столбцов. Порядок матрицы записывается как m × n, где m — количество строк в матрице, а n — количество столбцов в матрице.

Как узнать количество элементов по порядку матрицы?

Порядок матрицы записывается как m × n, и это произведение дает количество элементов в матрице. В качестве примера рассмотрим матрицу порядка 2 × 3, и это произведение 2 × 3 = 6 есть количество элементов в матрице.

Каково условие порядка матрицы для сложения и вычитания?

Чтобы сложить/вычесть две или более матриц, они должны быть одного порядка. Например, матрица порядка 2 x 3 не может быть добавлена ​​к матрице порядка 3 x 2.

Каково условие порядка матрицы для умножения матриц?

Важным условием умножения на основе порядка матрицы является то, что количество столбцов в первой матрице равно количеству строк во второй матрице. Также результирующая матрица умножения матриц имеет количество строк, равное количеству строк в первой матрице, и количество столбцов, равное количеству столбцов во второй матрице.

Как найти типы матриц на основе порядка матриц?

Порядок матрицы представлен как m × n, где m представляет количество строк, а n представляет количество столбцов в данной матрице. В зависимости от значений m и n изменяется размер матрицы. Различные матрицы, которые можно идентифицировать на основе порядка матрицы, следующие.

• Матрица строк. Здесь значение m = 1, и оно имеет одну строку и более одного столбца. Порядок матрицы-строки равен 1 × n.
• Матрица столбцов: Здесь значение n = 1, а матрица имеет один столбец и более одной строки. Порядок матрицы столбца m × 1
• Квадратная матрица: Здесь матрица имеет одинаковое количество строк и столбцов. м = п. Порядок квадратной матрицы равен n × n.
• Прямоугольная матрица: в этой матрице количество строк отличается от количества столбцов. м ≠ п. Порядок

Определить порядок матрицы

Прежде чем мы узнаем, что означает порядок матрицы, давайте сначала поймем, что такое матрицы. Матрицы могут быть определены как прямоугольные массивы чисел или функций. Поскольку матрица представляет собой прямоугольный массив, она двумерна. Двумерная матрица состоит из количества строк, обозначаемого (m), и количества столбцов, обозначаемого (n). Давайте лучше поймем концепцию на нескольких примерах.

Что такое матрица?

• Матрица представляет собой прямоугольный массив чисел или символов, которые обычно расположены в строках и столбцах.

• Порядок матрицы определяется количеством строк и столбцов.

• Элементы — это числа в матрице, и каждое число известно как элемент.

• Матрицы во множественном числе.

• Размер матрицы называется матрицей «n на m» и записывается как m × n, где n — количество строк, а m — количество столбцов.

• Например, у нас есть матрица 3 × 2, потому что количество строк здесь равно 3, а количество столбцов равно 2.

Как определить порядок матрицы?

Порядок матрицы можно легко определить, подсчитав количество строк и столбцов, из которых состоит матрица. Если у нас есть матрица, в которой m строк и n столбцов, то давайте узнаем, как найти порядок матрицы.

Вот несколько примеров того, как найти порядок матрицы,

[159−5]

[15]

Порядок матрицы выше (1×3), так как количество строк (m) = 1 и количество столбцов (n) = 3.

[7−6]

[7]

Порядок приведенной выше матрицы (1 × 2), поскольку количество строк (m) = 1, а количество столбцов (n) = 2.

[abcd]

[ac]

Порядок матрицы выше (2×2), так как количество строк (m) = 2 и количество столбцов (n) = 2.

[8a5−315b]

[8−3]

Порядок матрицы выше (2×3), так как количество строк (m) = 2 и количество столбцов (n) = 3.

Порядок матрицы ниже 3 x 4, что означает, что он имеет 3 строки и 4 столбца.

[173242466913]

Хорошо видно, что матрица порядка m × n имеет mn элементов. Следовательно, мы можем сказать, что если число элементов в матрице простое, то она должна иметь одну строку или один столбец. Для определения порядка матрицы квадратных матриц, таких как 1 x 1, 2 x 2, 3 x 3, ……., n x n, порядок будет представлен количеством строк или количеством столбцов, равным n.

Обычно мы обозначаем матрицу заглавной буквой, например A, B, C, D, M, N, X, Y, Z и т. д.

Небольшое примечание!

• Удивительно, что существует связь между количеством элементов, присутствующих в матрице, и порядком матрицы.

• Порядок матрицы обозначается m × n, а количество элементов, присутствующих в матрице, всегда будет равно произведению m и n.

Пример: [8a5−315b]

Каков порядок матрицы в приведенном выше примере? Математический порядок матрицы равен 2 × 3. Следовательно, количество элементов, присутствующих в приведенной выше матрице, также будет 2 умножить на 3, что равно 6.

Это дает нам важное понимание того, что если мы знаем порядок матрицы , нам было бы легко определить общее количество элементов, присутствующих в матрице. В заключение, если порядок матрицы m × n, она будет иметь mn (произведение m и n) элементов.

Теперь вы можете задаться вопросом, верно ли обратное утверждение предыдущего утверждения?

Обратное к предыдущему утверждению говорит, что: Если количество элементов равно mn, то порядок будет m × n. Но это определенно неправда. Это связано с тем, что произведение mn можно получить более чем одним способом; некоторые из способов перечислены ниже:

• mn × 1

• 1 × mn

• m × n

• n × m

Какие существуют типы матриц?

Существуют различные типы матриц. Вот они —

Пример: [137]1×3[1]

1×3

Пример: [1234]4×1

4×1

Пример: [5]1×1[5]

1× 1

Пример. В приведенном ниже примере показана матрица 3×4.

[173242466913]

Пример. В приведенном ниже примере показана квадратная матрица 3×3.[832646579]

Пример: [800040009]

• Скалярная матрица: Скалярная матрица — это тип матрицы, в которой диагональное значение одинаково, а все остальные значения равны нулю. Итак, это своего рода диагональная матрица, в которой все диагональные элементы одинаковы.

Пример: [400040004]

Пример: [100010001]

Пример: [832046009]

Пример: [800640579]

9006 6

Симметричная матрица: Симметричная матрица — это тип матрицы, значения которой равны ее транспонировать A= AT, т. е. amn = anm. Квадратная матрица является типом симметричной матрицы.

Пример: [123245356]

Пример: [0−2−32053−50]

Решенные примеры

Вопрос 1) Если матрица A имеет шесть элементов, то определите порядок матрицы.

Решение) Мы знаем, что количество элементов равно 6. Теперь вы можете подумать, каков порядок матрицы? Запишем все возможные делители числа 6.

• 6 = 1 × 6

• 6 = 6 × 1

• 6 = 2 × 3

  9007 0

• 6 = 3 × 2

Мы можем получить число 6 следующими 4 способами.