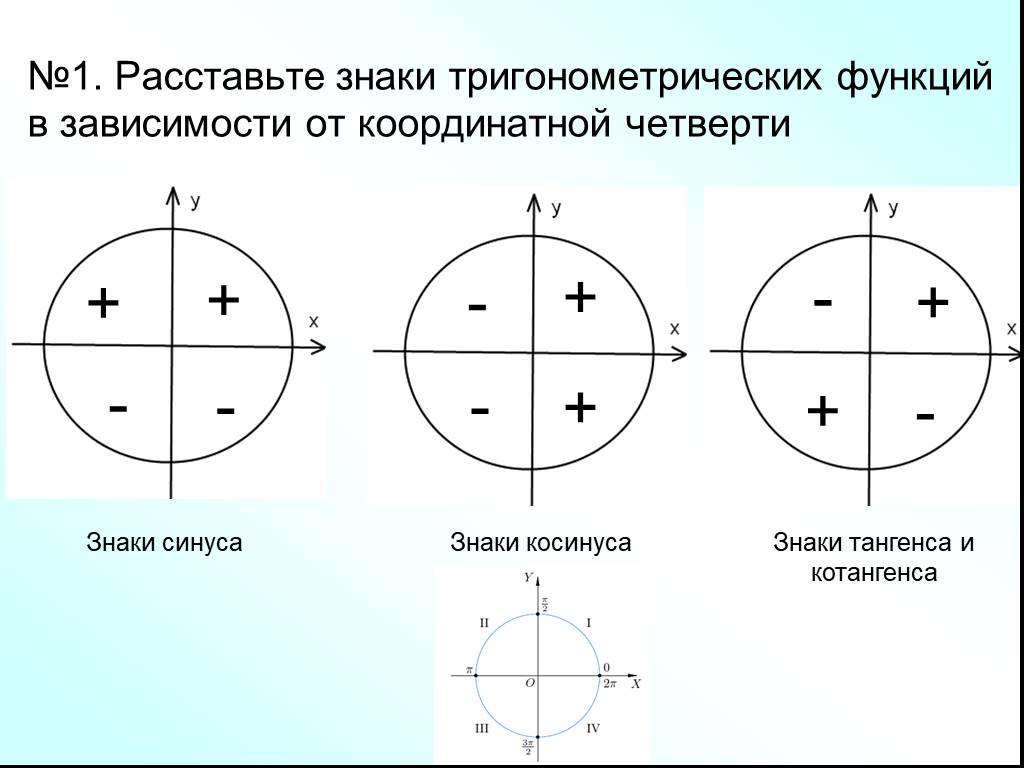
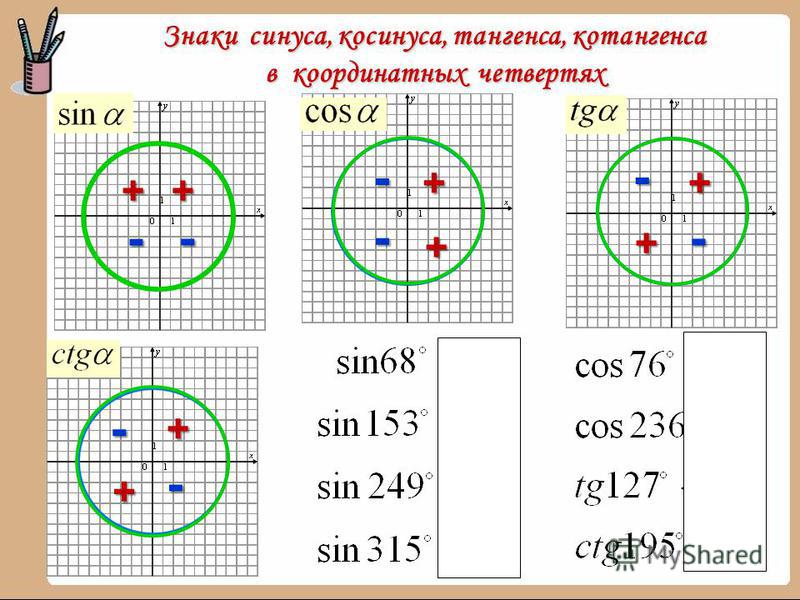
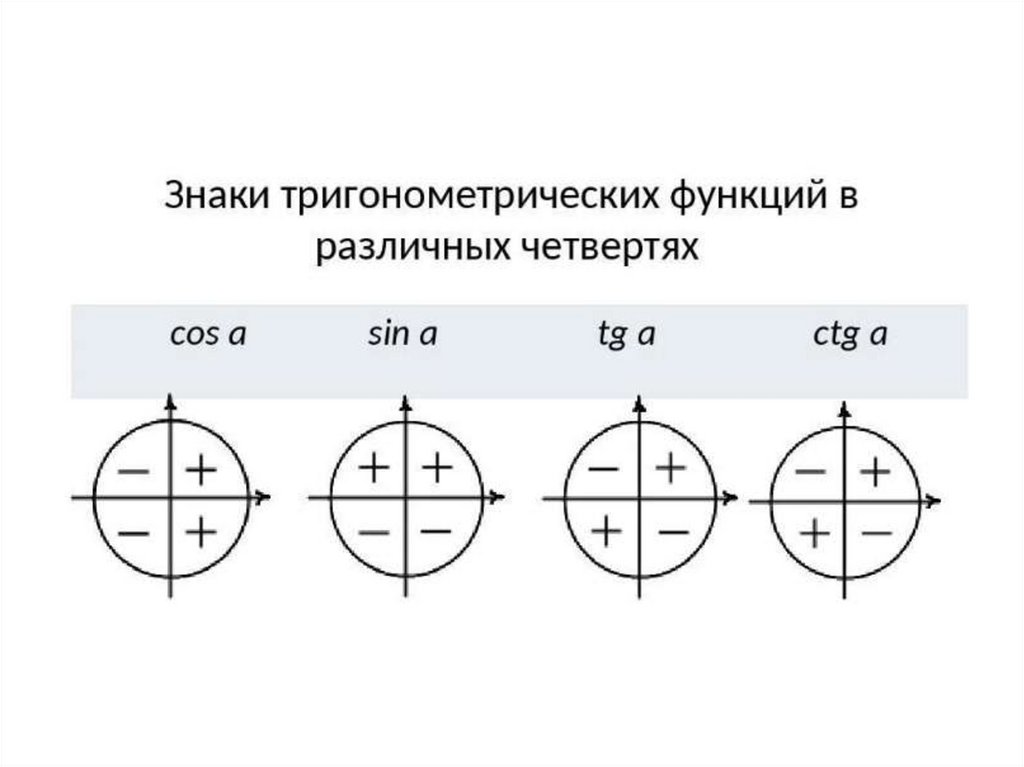
Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности. | |||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге. Поделиться:
| ||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||
Определение и знаки тригонометрических функций
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Определение и знаки тригонометрических функций
2. Угол поворота
уОР0 — неподвижный луч
1
II
Р
I
1Р0
О
-1
ОР — подвижный луч
III
IV
-1
х
Угол поворота соответствует
длине пути, пройденного
точкой Р от начального
положения Р0
Угол поворота можно измерить
двумя мерами : градусной и
радианной
3.
 Окружность с центром в начале системы координат Oxy и радиусом, равным единице, называется единичной, а ограниченный ей круг –тригонометрическим.
Окружность с центром в начале системы координат Oxy и радиусом, равным единице, называется единичной, а ограниченный ей круг –тригонометрическим.• Приняв точку пересечения
окружности с
положительной частью оси
Ох за начало отсчета;
• Выбрав положительное
направление – против
часовой стрелки,
отрицательное – по
часовой стрелке;
• Отложив от начала
отсчета дугу в 1 рад, мы
получим, что
тригонометрическая
окружность в некотором
смысле «эквивалентна»
понятию «числовая
прямая».
y
1
1
«+»
0
0
1
« »
x
4. Тригонометрические функции
Определение. Тригонометрические функции — этонеалгебраические функции, устанавливающие
зависимость между сторонами и углами треугольника.
Тригонометрические функции угла α определяются при
помощи числовой окружности, а также из
прямоугольного треугольника (для острых углов).
5. Определение синуса
• Синусом угла х называется ордината точки,полученной поворотом точки (1; 0) вокруг начала
координат на угол х (обозначается sin x).

sin x
x
(1;0)
6. Определение косинуса
• Косинусом угла х называется абсцисса точки,полученной поворотом точки (1; 0) вокруг начала
координат на угол х (обозначается cos x).
x
cos x
(1;0)
7. Определение тангенса
• Тангенсом угла х называется отношение синусаугла х к косинусу угла х.
sin
tg
cos
x
(1;0)
tg x
8. Определение котангенса
• Котангенсом угла х называется отношение косинусаугла х к синусу угла х.
cos
сtg
sin
9. Тригонометрическая окружность
ЗНАКИ тригонометрических функцийsin a
+
+
–
–
tg a
cos a
–
+
–
+
ctg a
–
+
–
+
+
–
+
–
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
ЗНАЧЕНИЙ СИНУСА, КОСИНУСА,
ТАНГЕНСА И КОТАНГЕНСА
sin α
cos α
Область
опреде- (- ∞;+ ∞) (- ∞;+ ∞)
ления
Область
значений
1;1 1;1
tg α
2
+
ctg α
n n
n-целое число
(- ∞;+ ∞)
n-целое число
(- ∞;+ ∞)
ТАБЛИЦА ЗНАЧЕНИЙ
ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
α
0° 30° 45° 60° 90° 180° 270° 360°
0
6
4
3
π
3
2
sin α 0
1
2
2
2
2
3
2
1
0
-1
0
cos α 1
3
2
2
2
1
2
0
-1
0
1
3
3
1
3
—
0
—
0
0
—
0
—
tg α 0
ctg α —
3
1
3
3
2π
14.
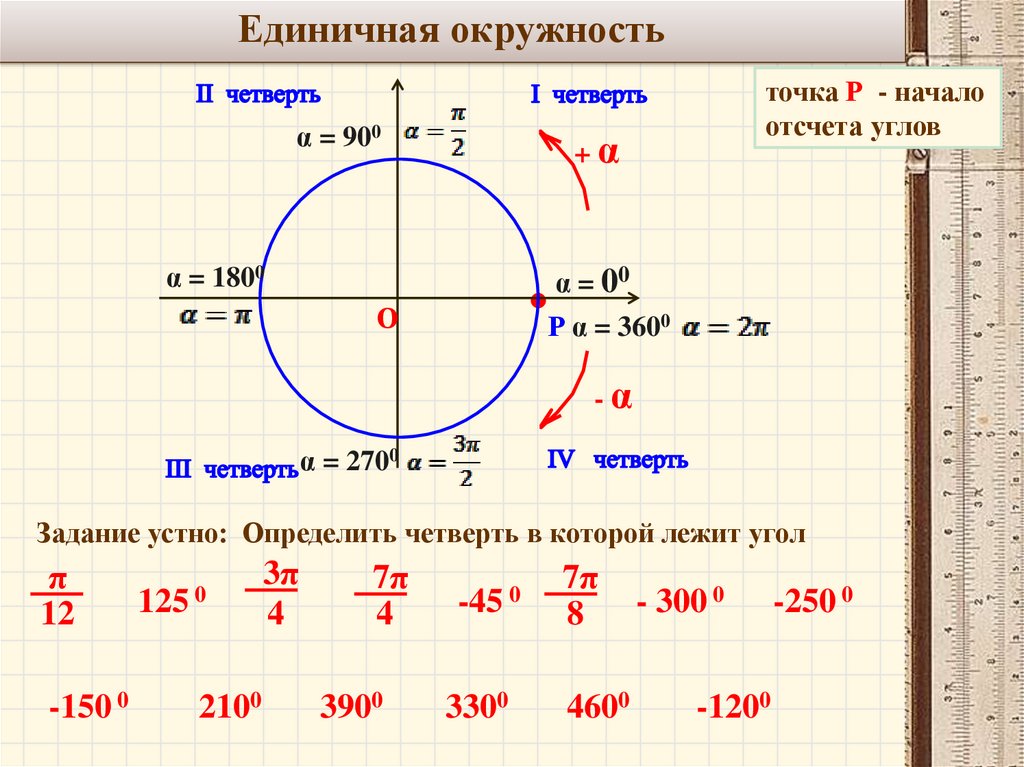 Пример: Вычислить3
Пример: Вычислить33 2 3
1
3
3
3sin +2cos -tg =3∙ +2∙ — 3 =
— 3= + 3- 3=
2
2
2
2
2
2
6
6
3
Задание:Вычислить
15. Учебник «Алгебра и начала анализа» (10 кл.)
Стр.178 № 563(2,3,4)Стр.179 № 567
Стр.179 № 566
English Русский Правила
Знаки тригонометрических функций
Знаки тригонометрических функций в каждом квадранте
Мы знаем, что cos α = x
Рассмотрим синусоидальную функцию \(\sin \alpha = \frac{y}{r}.\) Ее знак определяется знаком \(y.\). Следовательно, синус положителен в \( 1\text{st}\) и \(2\text{nd}\) квадранты, а отрицательное — в \(3\text{rd}\) и \(4\text{th}\) квадрантах.
Рис. 2. Ясно, что обратные функции \(\sec \alpha = \frac{1}{{\cos \alpha }}\) и \(\csc \alpha = \frac{1}{{\sin \alpha }}\) имеют те же знаки, что и \(\cos \alpha\) и \(\sin \alpha,\) соответственно.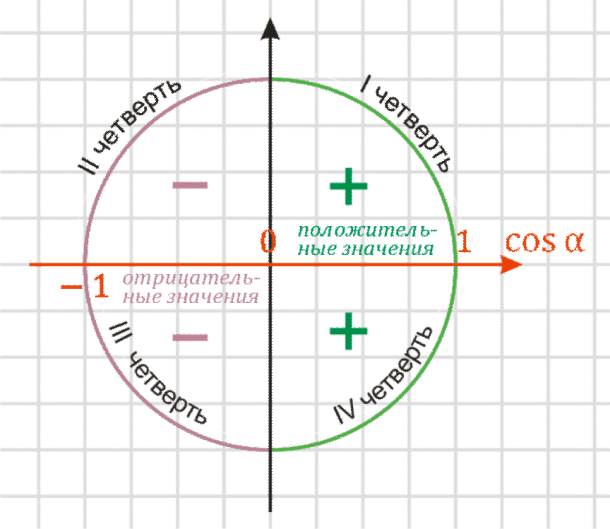
Знаки тангенса и котангенса зависят от знаков синуса и косинуса. Тангенс и котангенс положительны, когда \(x\) и \(y\) оба положительны или оба отрицательны. Это происходит в квадрантах \(1\text{st}\) и \(3\text{rd}\). В квадрантах \(2\text{nd}\) и \(4\text{th}\) эти функции отрицательны.
Рисунок 3.Мы можем обобщить эту информацию в следующей таблице:
Рисунок 4.Оценка тригонометрических функций
Для нахождения тригонометрической функции любого угла удобно использовать понятие исходного угла. Это включает в себя следующие шаги:
- Определите опорный угол для заданного угла в стандартном положении. Угол отсчета всегда острый.
- Вычислите значение тригонометрической функции для опорного угла. 92}\альфа = 1.\]
Зная одну из тригонометрических функций угла и квадрант, в котором лежит угол, мы можем определить все остальные тригонометрические функции этого угла. Это можно сделать с помощью перечисленных выше тождеств и определений тригонометрических функций.
 Обратите внимание, что если тригонометрическое выражение содержит частное, оно справедливо только для тех углов, при которых знаменатель не равен нулю.
Обратите внимание, что если тригонометрическое выражение содержит частное, оно справедливо только для тех углов, при которых знаменатель не равен нулю.См. решенные проблемы на стр. 2.
Как определить знаки тригонометрических функций
Тригонометрия является неотъемлемой частью математики. Изучение тригонометрии не ограничивается только нахождением функций или использованием тригонометрического калькулятора, но также предполагает знание знаков тригонометрических функций как целостного понятия. Знаки тригонометрических функций будут зависеть от углов крайних сторон. Зная, в какой четверти лежит конечная сторона угла, можно определить его знак.
Есть восемь областей, которые могут иметь конечную сторону угла — в четырех квадрантах или вдоль осей в квадрантных углах (положительное или отрицательное направление). В каждой ситуации знаки тригонометрических функций имеют разное значение.
Что такое тригонометрические функции?
Давайте на минутку освежим в памяти тригонометрические функции.
 Тригонометрические функции, также называемые круговыми функциями, представляют собой различные углы треугольника. Эти тригонометрические функции устанавливают отношения между углами и сторонами треугольника. Основными тригонометрическими функциями являются синус, секанс, тангенс, косинус, косеканс и котангенс.
Тригонометрические функции, также называемые круговыми функциями, представляют собой различные углы треугольника. Эти тригонометрические функции устанавливают отношения между углами и сторонами треугольника. Основными тригонометрическими функциями являются синус, секанс, тангенс, косинус, косеканс и котангенс.Углы синус, косинус и тангенс являются основными функциями, а остальные являются производными от этих основных функций.
Шесть функций тригонометрии обычно определяются с помощью прямоугольного треугольника.
Основные тригонометрические формулы следующие:
Функция синуса: Функция синуса представляет собой отношение длины, противоположной углу А, к длине гипотенузы.
– Sin A= Противоположный/гипотенуза
Функция cos: Функция cos представляет собой отношение длины стороны, примыкающей к углу A, к длине гипотенузы.
– Cos A= Смежная/Гипотенуза
Функция тангенса: Функция тангенса – это отношение длины противоположной стороны к длине примыкающей стороны к углу A.

– Tan A= Противоположная/Смежная
Синус и cos также можно использовать для определения Tan.
– Tan A= Sin A/Cos A
Остальные три функции, секанс, косеканс и котангенс, получаются из обратной величины косинуса, синуса и тангенса.
– Sec A= 1/ Cos A= гипотенуза/ смежный
– Cosec A= 1/ Sin A= Гипотенуза/ Противоположная
– Cot A = 1/ Tan A = Примыкающая/ Противоположная
Тригонометрический калькулятор может определять значения различных функций. Вы можете ввести два значения и легко ответить на третье. Однако необходимо запоминать формулы тригонометрии.
Знаки тригонометрических функций
Тригонометрические функции синуса, косинуса, тангенса и котангенса основаны на знаках координат x и y в соответствующих четырех квадрантах.
Расстояние от начала до точки всегда положительное. Однако знаки координат x и y могут быть положительными или отрицательными.
- В первом квадранте все функции положительны, поскольку все координаты x и y положительны.

- Во втором квадранте синус вместе с косекансом положителен. Все остальные четыре отрицательные.
- В третьем квадранте тангенс и котангенс положительны, а остальные отрицательны.
- В четвертом квадранте косинус и секанс положительны, а остальные четыре функции отрицательны.
Обратное число имеет тот же знак, что и исходное число.
Вот небольшая хитрость, чтобы запомнить функции по квадрантам. Помните правило ASTC, которое можно запомнить как «Добавить сахар в кофе». Первая буква первого слова — «А», что означает, что все тригонометрические функции положительны в первом квадранте. Первая буква второго слова, «S», указывает на то, что синус и его обратный косой угол во втором квадранте положительны. Первая буква третьего слова, «Т», указывает на то, что тангенс и обратный Котан положительны в третьем квадранте. Наконец, первая буква последнего слова «C» указывает на то, что косинус и его обратный секанс положительны в четвертом квадранте.

Тригонометрическая функция Квадрант I Квадрант II Квадрант III III Квадрант IV
SIN α положительный положительный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный
COS α положительный отрицательный отрицательный положительный положительный
TAN α положительный положительный положительный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный отрицательный
Cosec α -положительный положительный отрицательный отрицательный Отрицательный Положительный
кроватка α Положительный Отрицательный Положительный Отрицательный
Таблица, показывающая квадранты
В этой таблице суммируются знаки различных тригонометрических функций в разных квадрантах.
Значения квадрантных углов
Тригонометрическая функция 0 π/2 π 3π/2
SIN α 0 1 0 -1
COS α 1 0 -1 0
TAN α 0 Неопределенные 0 Не определено
COSEC α Не определено 0 Не определено 0
с α 1 Не определено -1 Не определено
COT α Не определено 1 не определенный -1
.
Когда значение не определено, коэффициент для этой конкретной функции делится на ноль. Эти точки технически не входят в область действия этой функции.
Из таблицы видно, что областью определения синуса и косиса являются все числа.
Другие виды тригонометрии
Раздел тригонометрии, изучающий отношение сторон прямоугольного треугольника, называется основной тригонометрией. Благодаря прогрессу ученых сегодня используются еще три вида тригонометрии: плоская, сферическая и аналитическая.
Плоская тригонометрия вычисляет углы простых треугольников. Этот угол имеет в основном три вершины на поверхности, и все стороны представляют собой прямые линии. Сумма плоскости равна 180 вместо обычных 90.
Сферическая тригонометрия используется для вычисления углов треугольников, нарисованных на сфере. Мера всех углов в этой ветви тригонометрии значительнее 180 градусов. Переменные широты и долготы используются вместе с тригонометрическими функциями. Как правило, для определения расстояний картографы и энтузиасты навигации регулярно используют сферическую тригонометрию.

- В первом квадранте все функции положительны, поскольку все координаты x и y положительны.


 Введите свой запрос:
Введите свой запрос: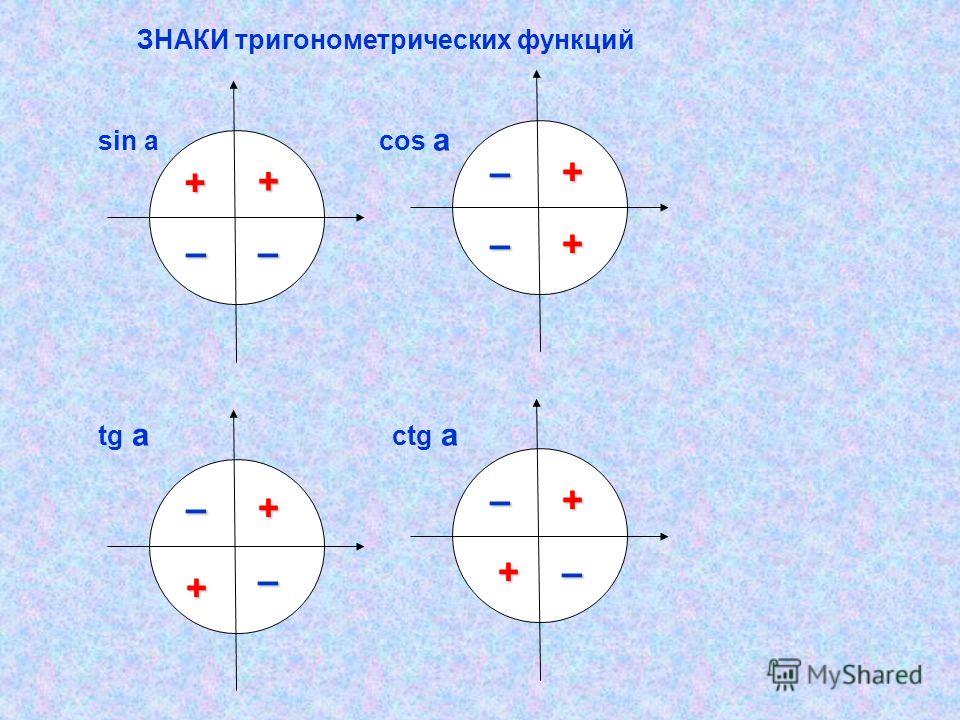 Обратите внимание, что если тригонометрическое выражение содержит частное, оно справедливо только для тех углов, при которых знаменатель не равен нулю.
Обратите внимание, что если тригонометрическое выражение содержит частное, оно справедливо только для тех углов, при которых знаменатель не равен нулю. Тригонометрические функции, также называемые круговыми функциями, представляют собой различные углы треугольника. Эти тригонометрические функции устанавливают отношения между углами и сторонами треугольника. Основными тригонометрическими функциями являются синус, секанс, тангенс, косинус, косеканс и котангенс.
Тригонометрические функции, также называемые круговыми функциями, представляют собой различные углы треугольника. Эти тригонометрические функции устанавливают отношения между углами и сторонами треугольника. Основными тригонометрическими функциями являются синус, секанс, тангенс, косинус, косеканс и котангенс.