Резистор. Параметры резисторов.
Резистор служит для ограничения тока в электрической цепи, создания падений напряжения на отдельных её участках и пр. Применений очень много, всех и не перечесть.
Другое название резистора – сопротивление. По сути, это просто игра слов, так как в переводе с английского resistance – это сопротивление (электрическому току).
Когда речь заходит об электронике, то порой можно встретить фразы типа: «Замени сопротивление», «Два сопротивления сгорели». В зависимости от контекста под сопротивлением может подразумеваться именно электронная деталь.
На схемах резистор обозначается прямоугольником с двумя выводами. На зарубежных схемах его изображают чуть-чуть иначе. «Тело» резистора обозначают ломаной линией – своеобразная стилизация под первые образцы резисторов, конструкция которых представляла собой катушку, намотанную высокоомным проводом на изоляционном каркасе.
Рядом с условным обозначением указывается тип элемента (R) и его порядковый номер в схеме (R1). Здесь же указано его номинальное сопротивление. Если указана только цифра или число, то это сопротивление в Омах. Иногда, рядом с числом пишут Ω – так, греческой заглавной буквой «Омега» обозначают омы. Ну, а, если так, – 10к, то этот резистор имеет сопротивление 10 килоОм (10 кОм – 10 000 Ом). Про множители и приставки «кило», «мега» можете почитать здесь.
Здесь же указано его номинальное сопротивление. Если указана только цифра или число, то это сопротивление в Омах. Иногда, рядом с числом пишут Ω – так, греческой заглавной буквой «Омега» обозначают омы. Ну, а, если так, – 10к, то этот резистор имеет сопротивление 10 килоОм (10 кОм – 10 000 Ом). Про множители и приставки «кило», «мега» можете почитать здесь.
Не стоит забывать о переменных и подстроечных резисторах, которые всё реже, но ещё встречаются в современной электронике. Об их устройстве и параметрах я уже рассказывал на страницах сайта.
Основные параметры резисторов.
Номинальное сопротивление.
Это заводское значение сопротивления конкретного прибора, измеряется это значение в Омах (производные килоОм – 1000 Ом, мегаОм – 1000000 Ом). Диапазон сопротивлений простирается от долей Ома (0,01 – 0,1 Ом) до сотен и тысяч килоОм (100 кОм – 1МОм). Для каждой электронной цепи необходимы свои наборы номиналов сопротивлений.
 Поэтому разброс значений номинальных сопротивлений столь велик.
Поэтому разброс значений номинальных сопротивлений столь велик.Рассеиваемая мощность.
Более подробно о мощности резистора я уже писал здесь.
При прохождении электрического тока через резистор происходит его нагрев. Если пропускать через него ток, превышающий заданное значение, то токопроводящее покрытие разогреется настолько, что резистор сгорает. Поэтому существует разделение резисторов по рассеиваемой мощности.
На графическом обозначении резистора внутри прямоугольника мощность обозначается наклонной, вертикальной или горизонтальной чертой. На рисунке обозначено соответствие графического обозначения и мощности указанного на схеме резистора.
К примеру, если через резистор потечёт ток 0,1А (100 mA), а его номинальное сопротивление 100 Ом, то необходим резистор мощностью не менее 1 Вт. Если вместо этого применить резистор на 0,5 Вт, то он вскоре выйдет из строя. Мощные резисторы применяются в сильноточных цепях, например, в блоках питания или сварочных инверторах.

Если необходим резистор мощностью более 2 Вт (5 Вт и более), то внутри прямоугольника на условном графическом обозначении пишется римская цифра. Например, V – 5 Вт, Х – 10 Вт, XII – 12 Вт.
Допуск.
При изготовлении резисторов не удаётся добиться абсолютной точности номинального сопротивления. Если на резисторе указано 10 Ом, то его реальное сопротивление будет в районе 10 Ом, но никак не ровно 10. Оно может быть и 9,88 и 10,5 Ом. Чтобы как-то обозначить пределы погрешности в номинальном сопротивлении резисторов, их делят на группы и присваивают им допуск. Допуск задаётся в процентах.
Если вы купили резистор на 100 Ом c допуском ±10%, то его реальное сопротивление может быть от 90 Ом до 110 Ом. Узнать точное сопротивление этого резистора можно лишь с помощью омметра или мультиметра, проведя соответствующее измерение. Но одно известно точно. Сопротивление этого резистора не будет меньше 90 или больше 110 Ом.
Строгая точность номиналов сопротивлений в обычной аппаратуре важна не всегда.
 Так, например, в бытовой электронике допускается замена резисторов с допуском ±20% от того номинала, что требуется в схеме. Это выручает в тех случаях, когда необходимо заменить неисправный резистор (например, на 10 Ом). Если нет подходящего элемента с нужным номиналом, то можно поставить резистор с номинальным сопротивлением от 8 Ом (10-2 Ом) до 12 Ом (10+2 Ом). Считается так (10 Ом/100%) * 20% = 2 Ом. Допуск составляет -2 Ом в сторону уменьшения, +2 Ом в сторону увеличения.
Так, например, в бытовой электронике допускается замена резисторов с допуском ±20% от того номинала, что требуется в схеме. Это выручает в тех случаях, когда необходимо заменить неисправный резистор (например, на 10 Ом). Если нет подходящего элемента с нужным номиналом, то можно поставить резистор с номинальным сопротивлением от 8 Ом (10-2 Ом) до 12 Ом (10+2 Ом). Считается так (10 Ом/100%) * 20% = 2 Ом. Допуск составляет -2 Ом в сторону уменьшения, +2 Ом в сторону увеличения.Для тех, кто ещё не знает, существует ещё одна возможность подобрать необходимое сопротивление – его можно составить, соединив вместе несколько резисторов разных номиналов. Об этом читайте в статье про соединение резисторов.
Существует аппаратура, где такой трюк не пройдёт – это прецизионная аппаратура. К ней относится медицинское оборудование, измерительные приборы, электронные узлы высокоточных систем, например, военных. В ответственной электронике используются высокоточные резисторы, допуск их составляет десятые и сотые доли процента (0,1-0,01%).
 Иногда такие резисторы можно встретить и в бытовой электронике.
Иногда такие резисторы можно встретить и в бытовой электронике.Стоит отметить, что в настоящее время в продаже можно встретить резисторы с допуском не более 10% (обычно 1%, 5% и реже 10%). Высокоточные резисторы имеют допуск в 0,25…0,05%.
Температурный коэффициент сопротивления (ТКС).
Под влиянием внешней температуры или собственного нагрева из-за протекающего тока, сопротивление резистора меняется. Иногда в тех пределах, которые нежелательны для работы схемы. Чтобы оценить изменение сопротивления из-за воздействия температуры, то есть термостабильность резистора, используется такой параметр, как ТКС (Температурный Коэффициент Сопротивления). За рубежом принято сокращение T.C.R.
В маркировке резистора величина ТКС, как правило, не указывается. Для нас же необходимо знать, что чем меньше ТКС, тем лучше резистор, так как он обладает лучшей термостабильностью. Более подробно о таком параметре, как ТКС, я рассказывал тут.
Перечислим их ещё раз:
Номинальное сопротивление (маркируется как 100 Ом, 10кОм, 1МОм.
 ..)
..)Рассеиваемая мощность (измеряется в Ваттах: 1 Вт, 0,5 Вт, 5 Вт…)
Допуск (выражается в процентах: 5%, 10%, 0,1%, 20%).
Так же стоит отметить конструктивное исполнение резисторов. Сейчас можно встретить как микроминиатюрные резисторы для поверхностного монтажа (SMD-резисторы), которые не имеют выводов, так и мощные, в керамических корпусах. Существуют и невозгораемые, разрывные и прочее. Перечислять можно очень долго, но основные параметры у них одинаковые: номинальное сопротивление, рассеиваемая мощность и допуск.
В настоящее время номинальное сопротивление резисторов и их допуск маркируют цветными полосами на корпусе самого элемента. Как правило, такая маркировка применяется для маломощных резисторов, которые имеют небольшие габариты и мощность менее 2…3 ватт. Каждая фирма-изготовитель устанавливает свою систему маркировки, что вносит некоторую путаницу. Но в основном присутствует одна устоявшаяся система маркировки.
Новичкам в электронике хотелось бы рассказать и о том, что кроме резисторов, цветовыми полосами маркируют и миниатюрные конденсаторы в цилиндрических корпусах. Иногда это вызывает путаницу, так как такие конденсаторы ложно принимают за резисторы.
Таблица цветового кодирования.
Рассчитывается сопротивление по цветным полосам так. Например, три первых полосы – красные, последняя четвёртая золотистого цвета. Тогда сопротивление резистора 2,2 кОм = 2200 Ом.
Первые две цифры согласно красному цвету – 22, третья красная полоса, это множитель. Стало быть, по таблице множитель для красной полосы – 100. На множитель необходимо умножить число 22. Тогда, 22
На практике широкое распространение имеют резисторы с допуском 5 и 10%. Поэтому за допуск отвечают полосы золотого и серебристого цвета. Понятно, что в таком случае, первая полоса находится с противоположной стороны элемента. С неё и нужно начинать считывание номинала.
Поэтому за допуск отвечают полосы золотого и серебристого цвета. Понятно, что в таком случае, первая полоса находится с противоположной стороны элемента. С неё и нужно начинать считывание номинала.
Но, как быть, если резистор имеет небольшой допуск, например 1 или 2% ? С какой стороны считывать номинал, если с обеих сторон присутствуют полосы красного и коричневого цветов?
Этот случай предусмотрели и первую полосу размещают ближе к одному из краёв резистора. Это можно заметить на рисунке таблицы. Полоски, обозначающие допуск расположены дальше от края элемента.
Конечно, бывают случаи, когда нет возможности считать цветовую маркировку резистора (забыли таблицу, стёрта/повреждена сама маркировка, некорректное нанесение полос и пр.).
В таком случае, узнать точное сопротивление резистора можно только, если измерить его сопротивление мультиметром или омметром. В таком случае вы будете 100% знать его реальную величину. Также при сборке электронных устройств рекомендуется проверять резисторы мультиметром для того, чтобы отсеить возможный брак.
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Научись паять! Как подготовить паяльник к работе?
Что такое динистор?
Собираем «мультирозетку» для рабочего места.
code golf — считать от 1 до 100… римскими цифрами
Perl 69 байт
s;.;y/XVI60-9/CLXVIX/dfor$a[$_].="32e$&"%72726 ;gefor 1..100;print"@a"
Работает по магической формуле. Выражение "32e$&"%72726 преобразует каждую цифру следующим образом:
0⇒32, 1⇒320, 2⇒3200, 3⇒32000, 4⇒29096, 5⇒56, 6⇒560, 7 ⇒5600, 8⇒56000, 9⇒50918
После применения перевода y/016/IXV/ вместо этого имеем:
0,32, 1,32 I , 2,32 II , 3 порядков 3,32 III , 4,29 I 9 V , 5 минут 5,5 В , 6 минут 5 В. , 7⇒5 VII , 8⇒5 VIII , 9⇒5 I 9 X 8
, 7⇒5 VII , 8⇒5 VIII , 9⇒5 I 9 X 8
Остальные цифры ( ) удаляются. Обратите внимание, что это можно улучшить на один байт, используя формулу, которая переводит После того, как одна цифра была преобразована таким образом, процесс повторяется для следующей цифры, добавляя результат и переводя предыдущие Обновление Этот использует замену Эта версия заметно отличается, поэтому, пожалуй, следует сказать о ней несколько слов. Формула, которую он использует, на самом деле на один байт длиннее! Не имея возможности сократить формулу больше, чем она есть, я решил поиграть в гольф на том, что у меня было. Вскоре я вспомнил о своем старом друге Гораздо лучше, но Также 67 байт из-за необходимого пробела между Редактировать : Это можно улучшить на один байт, переместив Поскольку подстановка должна полностью оцениваться до Но, если бы была формула, которая нигде не использует Оказывается, такая формула существует, но она на один байт длиннее исходной, в результате чего окончательный результат равен 65 байт : Был задан вопрос, как можно найти такую формулу. В общем, найти волшебную формулу для обобщения любого набора данных — вопрос вероятности. То есть вы хотите выбрать форму, которая с наибольшей вероятностью даст что-то похожее на желаемый результат. Проверка первых нескольких римских цифр: есть некоторая закономерность. В частности, от 0-3 и затем снова от 5-8 каждый последующий термин увеличивается в длину на одну цифру. Если бы мы хотели создать отображение цифр в числа, мы бы хотели иметь выражение, в котором и увеличиваются в длине на одну цифру для каждого последующего термина. Логичный выбор k • 10 d , где d — соответствующая цифра, а k — любая целая константа. Это работает для 0-3 , но 4 нужно сломать шаблон. Как видите, если мы заменим Я также экспериментировал с несколькими заменами Римские цифры от 1 до 100: Римские цифры или римские цифры — это просто счет или цифры, которые мы изучаем в детстве, написанные с использованием разных алфавитов и переведенные на латынь сценарий. Римские цифры от 1 до 100 — это список чисел от 1 до 100, переведенных в римские цифры. Римляне ввели римскую систему счисления около 500 г. до н.э., которая до сих пор широко используется в различных регионах мира. Для ценообразования различных товаров и услуг были приняты римские числа от 1 до 100. Римские числа от 1 до 100 помогут учащимся научиться преобразовывать числа в римские цифры. В этой статье упрощены все правила написания римских цифр от 1 до 100. Некоторые примеры использования римских чисел в древние времена перечислены ниже: С помощью этой статьи учащиеся смогут выучить римские цифры/цифры в очень упрощенной форме. В статье есть римские цифры от 1 до 100, которые являются основными строительными блоками в изучении римских чисел. В этой статье римские цифры перечислены вместе с их индийско-арабскими аналогами для лучшего понимания учащимися. The following is a table that shows the Roman Numbers from 1 to 100: 2-507-9 012 вместо 016 , упрощая /XVI60-9/ до /XVI0-9./ . Я не смог найти его, но, возможно, вам повезет больше. XVI s в CLX , в то же время происходит преобразование для новой цифры.
Полный поиск не дал ничего короче. Однако я нашел альтернативное 69-байтовое решение: s;.;y/XVI0-9/CLXIXV/dfor$a[$_].="57e$&"%474976;gefor 1..100;print"@a"
0-2 для IXV , но имеет модуль, который на одну цифру длиннее.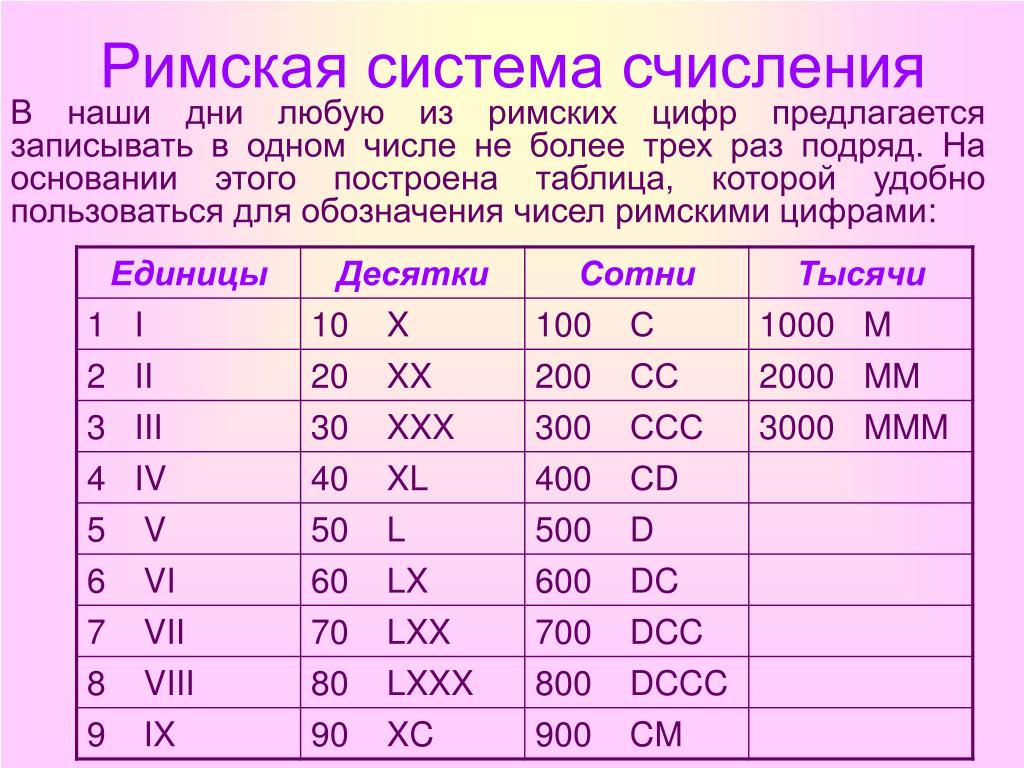
Обновление:
66 65 байт $\ . Когда выдается отчет print , $\ автоматически добавляется в конец вывода. Я смог избавиться от неудобной конструкции $a[$_] для двухбайтового улучшения: s;.;y/XVI60-9/CLXVIX/dfor$\.="32e$&"%72726 ;ge,$\=!print$" за 1..100
$\=!print$" по-прежнему выглядел немного многословно. Затем я вспомнил найденную мной альтернативную формулу равной длины, которая не содержала число 3 в любом из его цифровых преобразований. Таким образом, вместо этого можно использовать $\=2+print и заменить полученное 3 пробелом: s;.
 ;y/XVI0-9/CLXIIX V/dfor$\.=" 8e$&"%61535;ge,$\=2+печать за 1..100
;y/XVI0-9/CLXIIX V/dfor$\.=" 8e$&"%61535;ge,$\=2+печать за 1..100
для печати и для . печать вперед: $\=2+print!s;.;y/XVI0-9/CLXIIX V/dfor$\.="8e$&"%61535;gefor 1..100
печати , присвоение $\ все равно будет последним. Удаление пробела между ge и для вызовет предупреждение об устаревании, но в остальном допустимо. 1 , $\=2+print становится $\=print для экономии еще двух байтов. Даже если бы он был на один байт длиннее, это все равно было бы улучшением. $\=print!s;.
 ;y/XVI60-9 /CLXXI V/dfor$\.="37e$&"%97366;gefor 1..100
;y/XVI60-9 /CLXXI V/dfor$\.="37e$&"%97366;gefor 1..100
Методология
0:
1: я
2: II
3: III
4: IV
5: В
6: VI
7: VII
8: VIII
9: IX
 Здесь мы можем добавить по модулю:
Здесь мы можем добавить по модулю:
k • 10 d % m , где m находится где-то между k • 10 3 и k • 10 1 4 9.9. Это оставит диапазон 0-3 нетронутым и изменит 4 так, чтобы он не содержал четырех I s. Если мы дополнительно ограничим наш алгоритм поиска таким образом, чтобы модульный остаток 5 , назовем его j , был меньше, чем m / 1000 , это гарантирует, что у нас также будет регулярность от 5-8 . Результат примерно такой: 0:k
1: к0
2: к00
3: тыс. 000
4: ????
5: дж
6: j0
7: j00
8: j000
9: ????
0 на I , 0-3 и 5-8 гарантированно правильно отображаются! Однако значения для 4 и 9 должны быть грубыми. В частности, 4 должен содержать один 0 и один j (в указанном порядке), а 9 должен содержать один 0 , за которым следует еще одна цифра, которая больше нигде не встречается. Конечно, есть ряд других формул, которые по какому-то счастливому стечению обстоятельств могут дать желаемый результат. Некоторые из них могут быть даже короче. Но я не думаю, что есть такие, которые имеют такие же шансы на успех, как этот.
Конечно, есть ряд других формул, которые по какому-то счастливому стечению обстоятельств могут дать желаемый результат. Некоторые из них могут быть даже короче. Но я не думаю, что есть такие, которые имеют такие же шансы на успех, как этот. I и/или V с некоторым успехом. Но увы, ничего короче того, что у меня уже было. Вот список самых коротких решений, которые я нашел (количество решений на 1-2 байта тяжелее, слишком много, чтобы перечислять): y/XVI60-9/CLXVIX/dfor$\.="32e$&"%72726
y/XVI0-9/CLXIXV/dfor$\.="57e$&"%474976
y/XVI0-9/CLXIVXI/dfor$\.="49e$&"%87971
y/XVI0-9/CLXIIXIV/dfor$\.="7e$&"%10606 #
y/XVI0-9/CLXIIXIV/dfor$\.="7e$&"%15909 # Это все по сути одно и то же
y/XVI0-9/CLXIIXIV/dfor$\.="7e$&"%31818 #
y/XVI0-9/CLXIIX V/dfor$\.="8e$&"%61535 # Нигде не содержит 3
y/XVI60-9/CLXXI V/dfor$\.="37e$&"%97366 # Нигде не содержит 1
Римские цифры от 1 до 100, Таблица, Советы по обучению
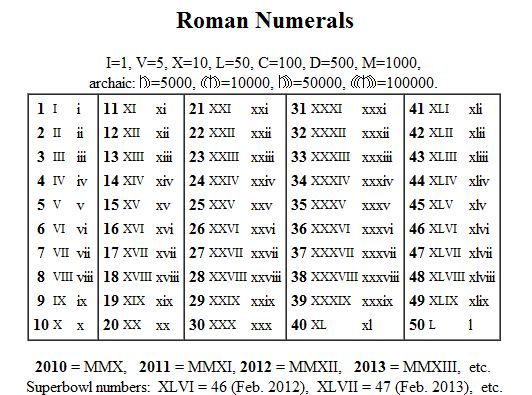 Римские цифры были введены римлянами в 5500 г. до н.э. для оценки различных товаров и услуг. Мысль о важности римских чисел может часто приходить в голову детям, когда они их изучают. Римские числа имеют различное применение и большое значение в современную эпоху.
Римские цифры были введены римлянами в 5500 г. до н.э. для оценки различных товаров и услуг. Мысль о важности римских чисел может часто приходить в голову детям, когда они их изучают. Римские числа имеют различное применение и большое значение в современную эпоху. Римские цифры

Roman Numbers 1 to 100
Number Roman Numbers Number in Words 1 I One 2 II Two 3 III Three 4 IV Four 5 V Five 6 VI Six 7 VII Seven 8 VIII Eight 9 IX Nine 10 X Ten 11 XI Eleven 12 XII Twelve 13 XIII Thirteen 14 XIV Fourteen 15 XV Fifteen 16 XVI Sixteen 17 XVII Seventeen 18 XVIII Eighteen 19 XIX Nineteen 20 XX Twenty 21 XXI Twenty-one 22 XXII Twenty-two 23 XXIII Twenty-three 24 XXIV Twenty-four 25 XXV Twenty-five 26 XXVI Twenty-six 27 XXVII Twenty-seven 28 XXVIII Twenty-eight 29 XXIX Twenty-nine 30 XXX Thirty 31 XXXI Thirty-one 32 XXXII Thirty-two 33 XXXIII Thirty-three 34 XXXIV Thirty-four 35 XXXV Thirty-five 36 XXXVI Thirty-six 37 XXXVII Thirty-seven 38 XXXVIII Thirty-eight 39 XXXIX Thirty-nine 40 XL Fourty 41 XLI Fourty-one 42 XLII Fourty-two 43 XLIII Fourty-three 44 XLIV Fourty- four 45 XLV Fourty-five 46 XLVI Fourty-six 47 XLVII Fourty-seven 48 XLVIII Fourty-eight 49 XLIX Fourty-nine 50 L Fifty 51 LI Fifty-one 52 LII Fifty-two 53 LIII Fifty-three 54 LIV Fifty-four 55 LV Fifty-five 56 LVI Fifty-six 57 LVII Fifty-seven 58 LVIII Fifty- eight 59 LIX Fifty-nine 60 LX Sixty 61 LXI Sixty-one 62 LXII Sixty-two 63 LXIII Sixty-three 64 LXIV Sixty-four 65 LXV Sixty-five 66 LXVI Sixty-six 67 LXVII Sixty-seven 68 LXVIII Sixty-eight 69 LXIX Sixty-nine 70 LXX Seventy 71 LXXI Seventy-one 72 LXXII Seventy-two 73 LXXIII Seventy-three 74 LXXIV Seventy-four 75 LXXV Seventy-five 76 LXXVI Seventy-six 77 LXXVII Seventy-seven 78 LXXVIII Seventy-eight 79 LXXIX Seventy- nine 80 LXXX Eighty 81 LXXXI Eighty-one 82 LXXXII Eighty-two 83 LXXXIII Eighty-three 84 LXXXIV Eighty-four 85 LXXXV Eighty-five 86 LXXXVI Eighty -six 87 LXXXVII Eighty-seven 88 LXXXVIII Eighty-eight 89 LXXXIX Eighty-nine 90 XC Ninety 91 XCI Ninety-one 92 XCII Ninety-two 93 XCIII Ninety-three 94 XCIV Ninety-four 95 XCV Ninety-five 96 XCVI Ninety-six 97 XCVII Ninety-seven 98 XCVIII Ninety-eight 99 XCIX Ninety-nine 100 C Сто Римские цифры от 1 до 100 Таблица
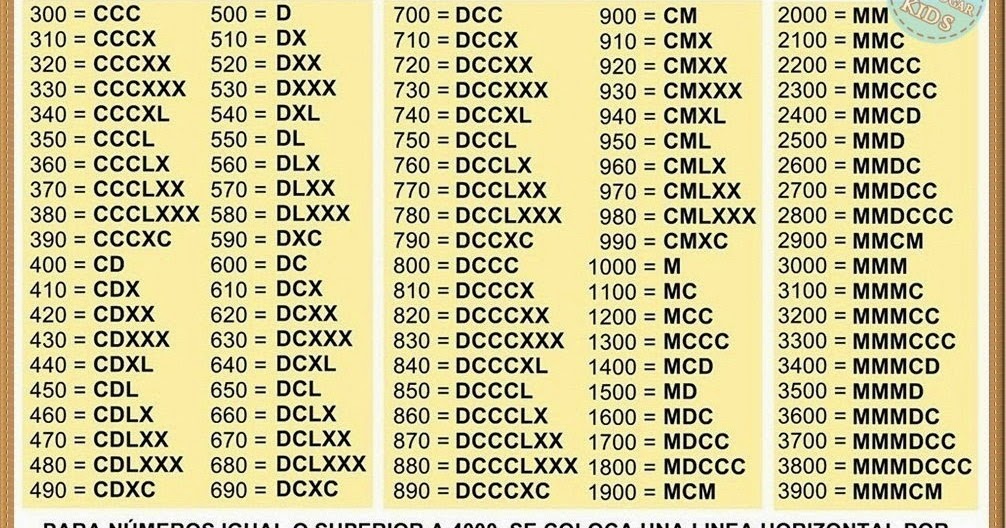
Римские цифры – Советы для изучения используя любой из двух приведенных ниже способов.
 Предположим, нам нужно записать 86 чисел в римские числа, изучите методы здесь.
Предположим, нам нужно записать 86 чисел в римские числа, изучите методы здесь.
Метод 1: В этом методе мы разбиваем 86 на наименее расширяемую форму, пишем соответствующую им латинскую букву и добавляем/вычитаем их, то есть 86 = 50 + 30 + 6 = L + XXX + VI = LXXXXVI
Метод 2: В этом методе мы рассматриваем группы чисел для сложения, такие как: 86 = 80 + 6 = LXXX + VI = LXXXVI
Учащиеся могут использовать любой из двух вышеуказанных методов для написания римских цифр от 1 до 100.
Римские цифры от 1 до 100: правила, которые следует помнить
При написании римских чисел от 1 до 100 необходимо соблюдать некоторые правила. Эти рекомендации подробно описаны в этой статье:
1. Когда буква большего размера предшествует букве меньшего размера, буквы добавляются.
Например: CX, C > X, поэтому CX = C + X = 100 + 10 = 110.
2. Когда меньшая буква предшествует большей, буквы вычитаются.
Например: IV, I < V, поэтому IV = V - I = 5 - 1 = 4.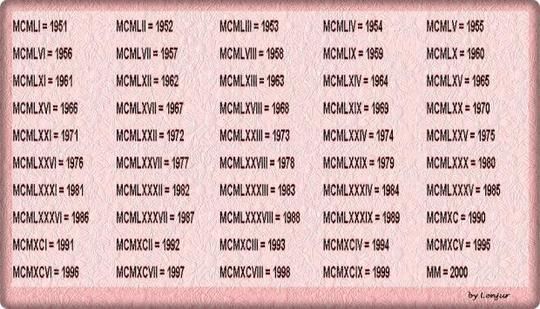
3. Когда буква повторяется несколько раз, они добавляются.
Например: МММ = М + М + М = 1000 + 1000 + 1000 = 3000
4. Одна и та же буква не может использоваться более трех раз подряд.
Например: V, L и D не могут повторяться, они появляются только один раз.
Преобразование римских чисел в индуистские арабские цифры
Вот как некоторые важные элементы представлены в индуистско-арабской системе счисления.
| Индо-арабские цифры | Римские цифры |
| 1 | I |
| 5 | V |
| 10 | X |
| 50 | L |
| 100 | C |
| 500 | D |
| 1000 | М |
Как это делается?
Ниже приведены шаги для преобразования индийско-арабских чисел в римские:
Возьмем число 19. 90.
90.
Шаг 1: Брейк Номер 1995 года на 1000, 900 и 90.
Шаг 2: Теперь Преобразование :
1000 + 900 + 90 + = 1990
● 1000 = МАТИ
● 900 = см
● 90 = XC
SO, 1990 год становится MCMXC
. Хотя вышеупомянутый метод упрощает переговорные числа арабских чисел с арабскими числами, с арабскими числами, с арабскими числами, с арабскими числами, с римщиками. немного различаются по своему использованию. Эту разницу можно наблюдать в расчетах, потому что в случае некоторых продвинутых чисел можно столкнуться с различными сложностями просто потому, что в римских числах нет места для нуля. Хотя можно научиться вычитанию и сложению римских цифр, деление и умножение — трудные задачи.
На что обратить внимание при работе с римскими цифрами
1. Максимальное количество повторений символа – три раза.

 Поэтому разброс значений номинальных сопротивлений столь велик.
Поэтому разброс значений номинальных сопротивлений столь велик.
 Так, например, в бытовой электронике допускается замена резисторов с допуском ±20% от того номинала, что требуется в схеме. Это выручает в тех случаях, когда необходимо заменить неисправный резистор (например, на 10 Ом). Если нет подходящего элемента с нужным номиналом, то можно поставить резистор с номинальным сопротивлением от 8 Ом (10-2 Ом) до 12 Ом (10+2 Ом). Считается так (10 Ом/100%) * 20% = 2 Ом. Допуск составляет -2 Ом в сторону уменьшения, +2 Ом в сторону увеличения.
Так, например, в бытовой электронике допускается замена резисторов с допуском ±20% от того номинала, что требуется в схеме. Это выручает в тех случаях, когда необходимо заменить неисправный резистор (например, на 10 Ом). Если нет подходящего элемента с нужным номиналом, то можно поставить резистор с номинальным сопротивлением от 8 Ом (10-2 Ом) до 12 Ом (10+2 Ом). Считается так (10 Ом/100%) * 20% = 2 Ом. Допуск составляет -2 Ом в сторону уменьшения, +2 Ом в сторону увеличения.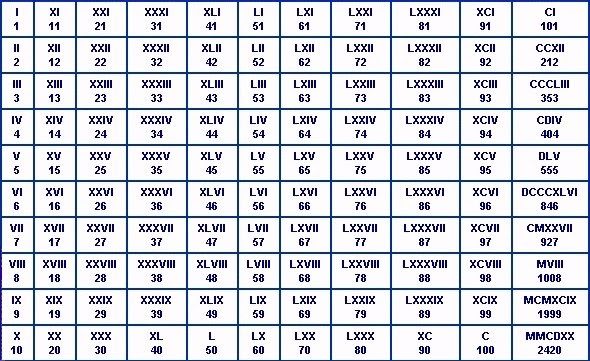 Иногда такие резисторы можно встретить и в бытовой электронике.
Иногда такие резисторы можно встретить и в бытовой электронике. ..)
..)