Длина окружности — Математика — Уроки
Математика 6 класс
Тема: «Длина окружности»
Цель: вывести формулы для нахождения длины окружности по длине ее диаметра и длине радиуса; отрабатывать умение применять эти формулы при решении задач.
Ход урока
Оргмомент
Для того чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать. (Р.Декарт)
Устный счет
Найдите отношение:
Вычислите:
Округлите 3,14159265 до сотых, единиц.
Актуализация знаний
Вроде круг, но дело в том,
Что иначе мы зовем
Нарисованный кружок.
В чем секрет? Скажи, дружок!
Эта странная наружность
Называется…. (окружность).
Сегодня на уроке мы научимся вычислять длину окружности. Запишите число, тему урока: « Длина окружности». Сначала повторим, что мы о ней знаем.
Сначала повторим, что мы о ней знаем.
На доске начерчена окружность (закрыта).
Начертите окружность.
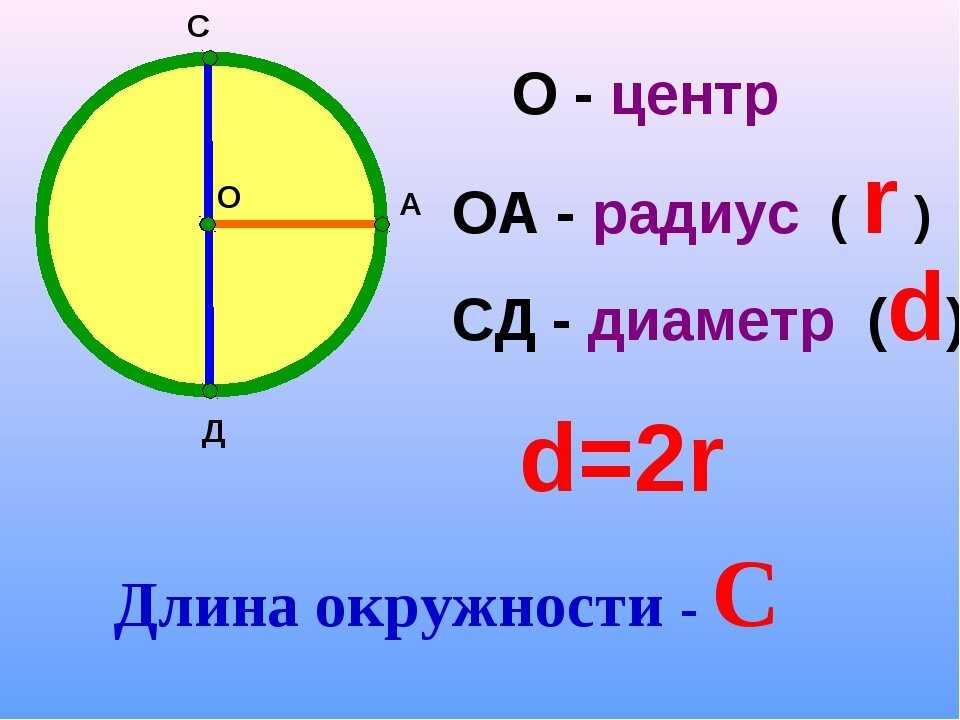
Проведите радиус (обозначения – на доску).
Проведите диаметр.
r=4 м найдите d. (d=2r)
d=10 см найдите r.
Изучение нового материала
Круглые клумбы смотрятся очень эффектно. Как измерить, какой длины декоративный забор нужно купить, чтобы огородить клумбу диаметром 2 м?
Чтобы определить длину забора для круглой клумбы нужно измерить длину окружности.
Длина окружности обозначается буквой С. А как измерить длину окружности, нарисованной на доске или длину экватора, или этой, изображенной на картоне? (Картонную можно прокатить вдоль линейки). Какие элементы окружности можно измерить с помощью линейки? (радиус, диаметр). Радиус, диаметр, длина это элементы одной и той же окружности. Логично предположить, что между ними есть какая-то зависимость.

Я предлагаю вам выполнить практическую работу, чтобы определить как связаны между собой С и d.
Группа 1 Задания:
Измерить длину окружности С с помощью нитки. Записать в тетрадь: С=
Измерить диаметр d этой окружности. Записать: d=
Найти отношение длины окружности C к d, результат округлить до единиц. Записать: С:d=
Группа 2 Задания:
Точку А картонного круга совместить с отметкой 0 линейки. Прокатить картонный круг вдоль линейки от точки А до точки А.
Измерить длину полученного отрезка. Записать в тетрадь: С=
Измерить диаметр d окружности. Записать: d=
Найти отношение длины окружности C к d, результат округлить до единиц. Записать: С:d=
Результаты заносятся в таблицу на доске.
C | d | С:d |
Обратите внимание на последний столбец.
 Мы сделали открытие: хотя вы измеряли различные окружности, у каждой из них отношение длины окружности C к диаметру d приблизительно равно 3.
Мы сделали открытие: хотя вы измеряли различные окружности, у каждой из них отношение длины окружности C к диаметру d приблизительно равно 3.
Еще древние люди , заметили, что для того, чтобы получить корзину нужного диаметра, необходимо брать прутья в 3 раза длиннее его. Впервые доказать, что отношение длины окружности к ее диаметру – одно и то же число удалось древнегреческому математику Архимеду.
Это число обозначают греческой буквой π (в переводе «периферия», «окружность»).
С:d=π
Впервые такое обозначение использовал в 1706 году британский математик Уильям Джонс, но общепринятым оно стало после того, как его стал систематически употреблять Леонард Эйлер, начиная с 1736 года. Числу Пи придают такое важное значение, что ему есть памятник- он установлен в Сиэтле перед зданием музея искусств.
Число π выражается бесконечной десятичной дробью. Сейчас известны миллионы цифр после запятой. π ≈ 3,14159265.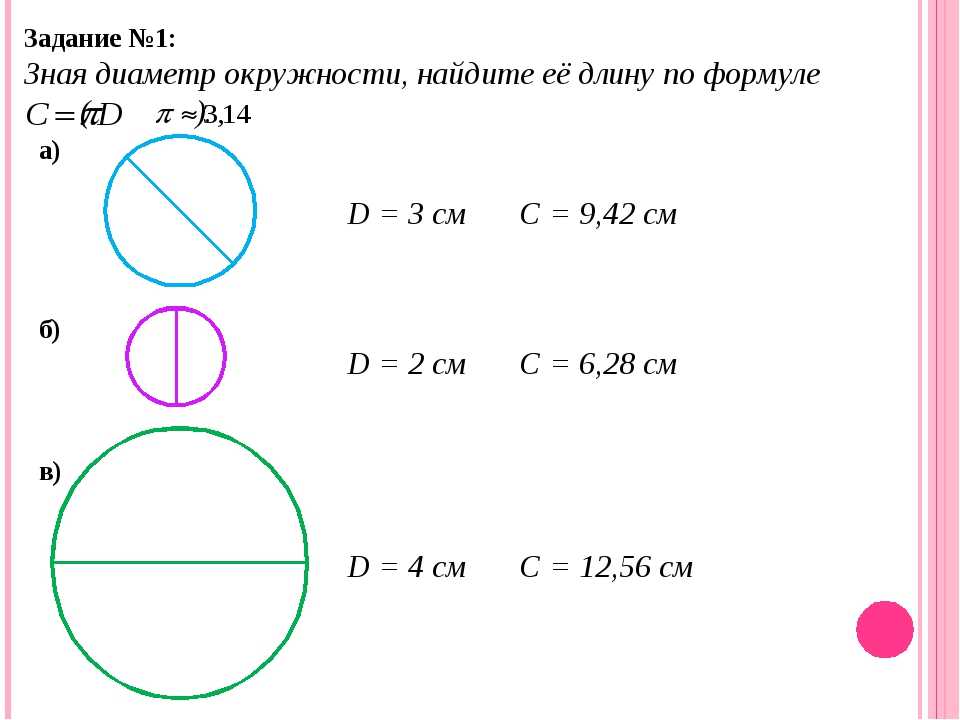
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».
Вам для дальнейших вычислений необходимо запомнить: π ≈ 3,14 или .
Итак,
С:d=π
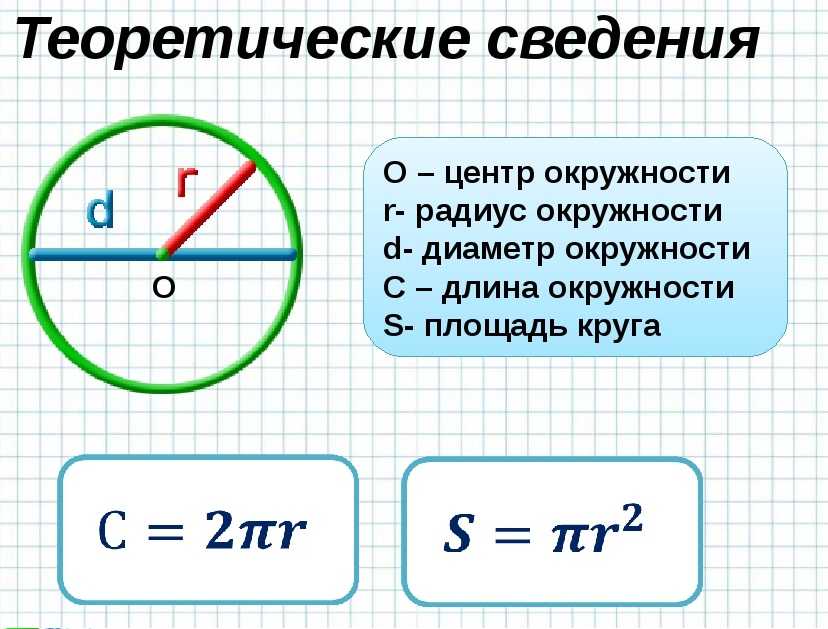
С= πd
С=2πr
Работа с учебником стр. 139
Задания на усвоение (с записью в тетради): вернемся к задаче о клумбе
d=2м, C — ?
d=100 дм, C — ?
r=7м, C — ?
C=314см, d — ?
Физкультминутка
Тест
В-1
Длина окружности вычисляется по формуле:
А) c=πd/2; B) s=2πd; C) c=2πr; Д) c=πr2.
Число π≈
А) 1,34; В) 3,14; С) 31,4; Д) 4,13.
r=5.
 Найти С?
Найти С?
А) 31,4; В) 3,14; С) 314; Д) 1,34
Чему равен d, если С= 31,4?
10
В-2
Длина окружности вычисляется по формуле:
А) c=πd/2; B) c=πd; C) s=2πd; Д) c=πr2.
Число π≈
А) 1,34; В) 31,4; С) 3,14; Д) 4,13.
r=10. Найти С?
А) 62,8; В) 6,28; С) 314; Д) 1,34
Чему равен d, если С= 3140?
1000
Взаимопроверка.
Закрепление
Предполагая, что Земля – идеальный шар радиуса 6400 км, натянем вдоль экватора проволоку. Затем по каким-то причинам проволока удлинилась ровно на один метр и равномерно отошла от земли.
 Сможет ли под этой проволокой пролезть мышь? Определить размер щели.
Сможет ли под этой проволокой пролезть мышь? Определить размер щели.
Вообразите, что земной шар обтянут по экватору обручем и что подобным же образом обтянут апельсин. Далее вообразите, что окружность каждого обруча удлинилась на 1 м. Тогда обручи отстанут от поверхности тел и образуют с ними некоторый зазор. В каком случае зазор будет больше – у земного шара или у апельсина? (Rз=6370 км, rа=3,5 см, обручи расположены, как показано на рисунке – имеют общий центр).
Решают по группам с оформлением на доске и в тетради.
Диаметр колеса велосипеда равен 70 см. за 2 мин колесо сделало 200 оборотов. С какой скоростью едет велосипед?
Домашнее задание: № 868, № 867, ребус, Мышь на экваторе
Как рассчитать внешнюю длину круга
Обновлено 26 марта 2020 г.
Кевин Бек
Если вам случится оказаться у окна и посмотреть на улицу, вы заметите большое присутствие кругов? Под это описание подходят автомобильные, грузовые и велосипедные шины, заглушки люков на улицах и некоторые другие объекты, созданные человеком. Многие другие вещи, такие как автомобильные фары и различные элементы архитектуры, «круглые», если не совсем круглые.
Многие другие вещи, такие как автомобильные фары и различные элементы архитектуры, «круглые», если не совсем круглые.
В естественном и математическом мирах двумерные круги и их аналоги в трехмерном пространстве, сферы, приобретают первостепенное значение. Ведь сама Земля, как и большинство других небесных тел, имеет примерно сферическую форму и на поперечном сечении образует круг или диск.
Расстояние вокруг любого круга можно определить, зная его ширину, и это, казалось бы, загадочное наблюдение находит применение в удивительном количестве физических и инженерных задач, во многом благодаря знаменитой математической константе π («пи» ).
Основные определения круга
Чтобы сформировать круг, начните с любой точки A на плоскости или плоской поверхности и двигайтесь в заданном направлении по прямой линии, пока не почувствуете, что хотите остановиться (точка r). Затем поверните налево или направо и идите до тех пор, пока не вернетесь к первой точке остановки (r), сохраняя расстояние между вами и исходной точкой (A) на протяжении всего пути одинаково.
Вы только что начертили окружность C вновь сформированного круга. Расстояние, которое вы прошли от центра круга A до края круга r равно радиус r , а самое дальнее расстояние по окружности диаметр D , равный 2r. Все круги одинаковой формы, но, конечно, не обязательно одинакового размера.
Если кто-то использует термин «длина круга», попытайтесь получить разъяснение; это может означать длину через ширину круга (диаметр) или какую-то другую часть круга (хорду), или это может означать длину всего вокруг круга (окружности).
Площадь и длина окружности
Теперь вы познакомитесь с константой π, греческой буквой пи. Это иррациональное число или десятичное число, которое никогда не заканчивается и не может быть точно выражено в виде дроби. Однако для большинства целей дробь 22/7, или около 3,14286, достаточно близка для использования в расчетах нетехнического уровня.
Длина окружности и диаметр круга связаны соотношением C = 2πr и, в более широком смысле, соотношением C = πD. Таким образом, знание радиуса круга позволяет вычислить его длину окружности и наоборот.
Площадь круга также связана с радиусом (или диаметром, если хотите) с помощью константы π, где площадь A = πr 2 . Это означает, что если вы хотите выразить площадь через окружность, вы должны решить уравнение C = 2πr и подставить:
r = C/2π
A = π(C/2π) 2
A = C 2 /4π
Площадь и объем сферы
Раз уж вы здесь, то можете заглянуть по лестнице правильных геометрических фигур в трехмерное пространство. Если у вас есть длина окружности сферы (то есть расстояние вокруг ее самой широкой точки, например, экватора, огибающего земной шар), вы можете вычислить ее радиус, а затем использовать r, чтобы вычислить площадь поверхности и объем сфера:
A сфера = 4πr 2
V сфера = (4/3)πr 3
Калькулятор диаметра окружности
поэкспериментировать с различными входными данными окружности (радиус, диаметр, длина окружности, площадь), чтобы увидеть, что произойдет с выходными данными. В частности, обратите внимание на то, как изменяются площадь и окружность при одном и том же ступенчатом изменении радиуса.
В частности, обратите внимание на то, как изменяются площадь и окружность при одном и том же ступенчатом изменении радиуса.
Что быстрее увеличивается в зависимости от r, площадь А или длина окружности С? Почему, математически, вы выбрали свой ответ?
Как найти длину дуги вокруг окружности (длина дуги окружности) — Криста Кинг Математика
Формулы для длины дуги
В этом уроке мы рассмотрим, как найти длину дуги, зная радиус и величину соответствующего центрального угла в градусах.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Формула длины дуги
Дугу можно измерять в градусах, но ее также можно измерять в единицах длины.
Длина окружности – это общая длина окружности («расстояние по окружности»). Дуга является частью окружности. На самом деле отношение меры ???m??? дуги окружности (в градусах) к мере всего круга (в градусах), то есть отношение (числового значения) ???m??? к ???360???, равно отношению длины дуги ???L??? к окружности (общая длина) ???C??? круга:
???\frac{m}{360}=\frac{L}{C}???
Формула длины окружности: ???C=2\pi r???, где ???r??? это радиус окружности.
???L=\frac{m}{360}\cdot 2\pi rL=\frac{m}{360}\cdot 2\pi r???
???L=\frac{86}{360}\cdot 2\pi (12)???
???L=\frac{43}{180}\cdot 24\pi???
???L=\frac{86}{15}\pi???
???л\ок 18.01???
Иногда вам дадут длину дуги и попросят найти градусную меру дуги или меру соответствующего центрального угла.
Длина окружности – это общая длина окружности («расстояние по окружности»).
Пример
Найдите величину центрального угла (в градусах), которая соответствует ???\overset\frown{ML}???.
Помните, что градусная мера ???m??? дуги равна мере центрального угла, соответствующего дуге. Мы будем использовать формулу длины дуги
???L=\frac{m}{360}\cdot 2\pi r???
Мы знаем, что ???L=15\pi??? и ???r=20???, поэтому найдем ???m???.

 Мы сделали открытие: хотя вы измеряли различные окружности, у каждой из них отношение длины окружности C к диаметру d приблизительно равно 3.
Мы сделали открытие: хотя вы измеряли различные окружности, у каждой из них отношение длины окружности C к диаметру d приблизительно равно 3.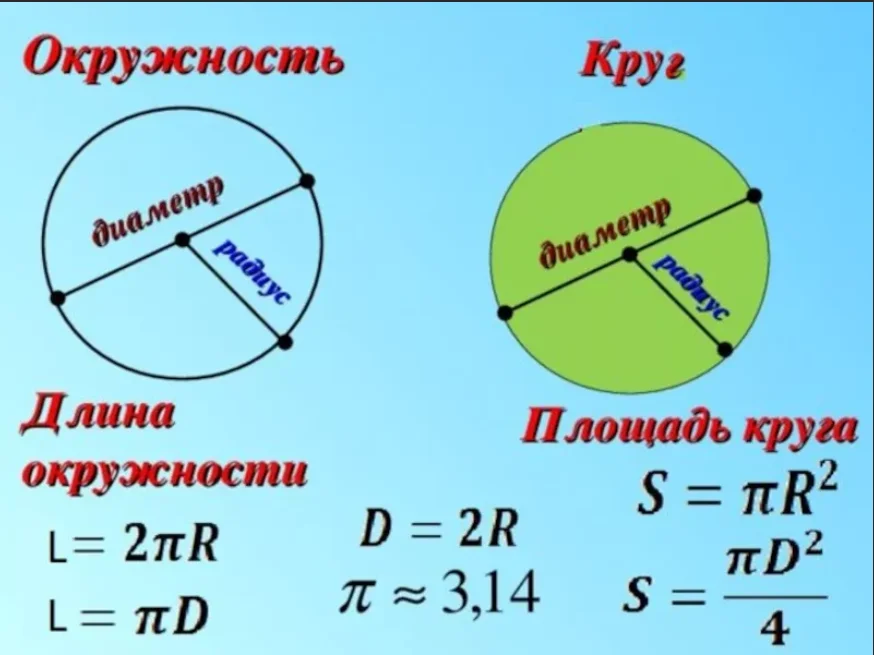 Найти С?
Найти С?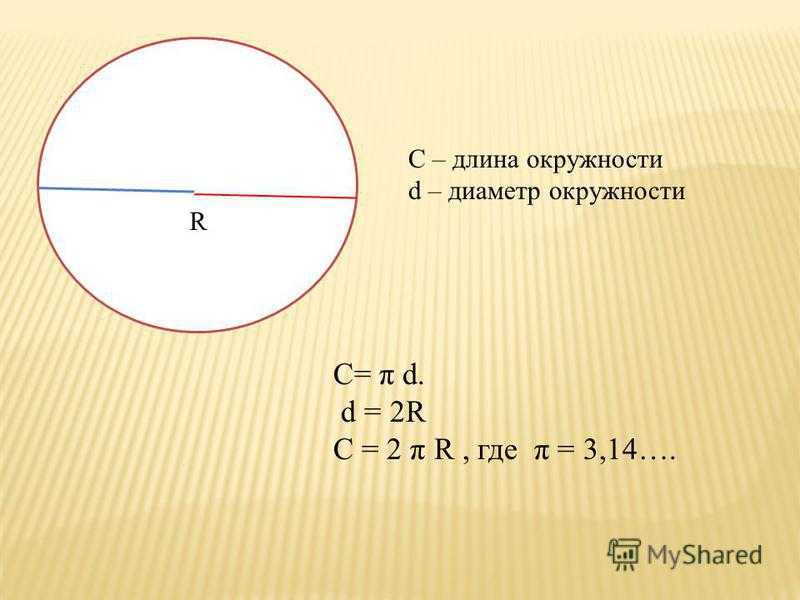 Сможет ли под этой проволокой пролезть мышь? Определить размер щели.
Сможет ли под этой проволокой пролезть мышь? Определить размер щели.