Презентация «Функция.Построение графиков функций» (8-9 класс)
| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека▪Публикации▪Статьи
Материал опубликовала
#8 класс #9 класс #Алгебра #ФГОС #Методические разработки #Учитель-предметник #Школьное образование #Фрагмент урока #УМК А. Г. Мордковича #УМК С. М. Никольского
Г. Мордковича #УМК С. М. Никольского
Функция. Построение графиков некоторых функций
Постройте график функции y= и определите, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Постройте график функции y=x|x|+|x|−3x. Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Постройте график функции y=x|x|+|x|−3x. Определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Функция y=f(x) х- независимая переменная или аргумент у-зависимая переменная или значение функции Пара х и у образуют точку (х,у)
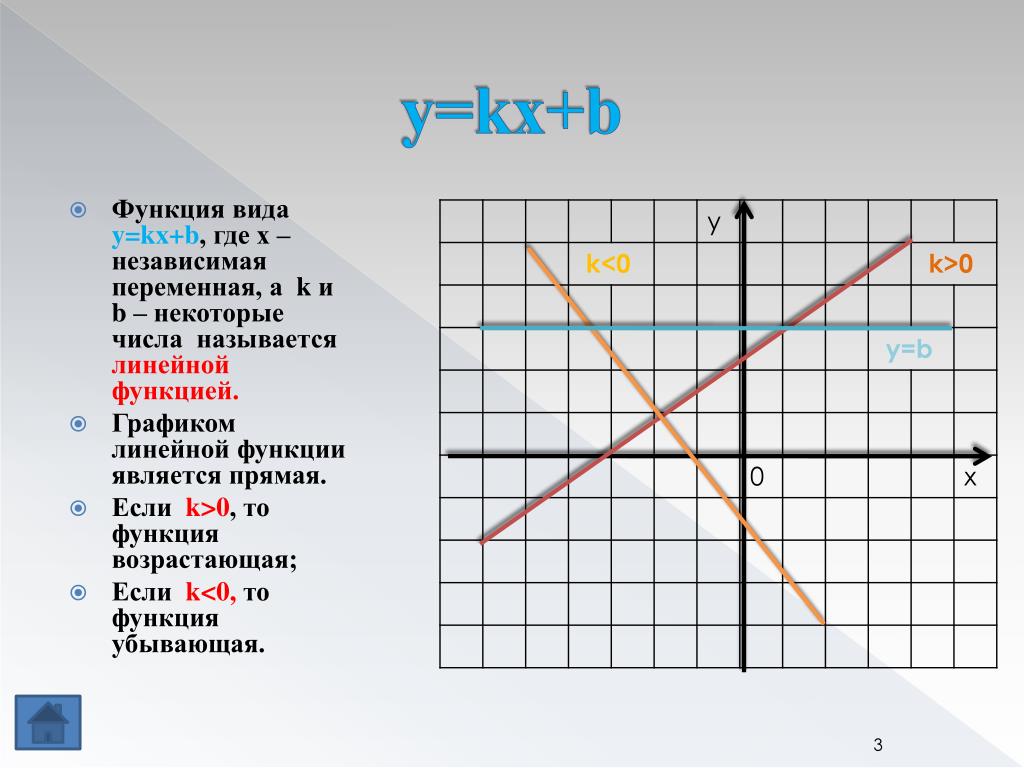
Линейная функция — функция, которая задана формулой y=kx+b, где k и b-действительные числа. у= -4х+5 у= х-2 у= -2 график линейной функции — прямая
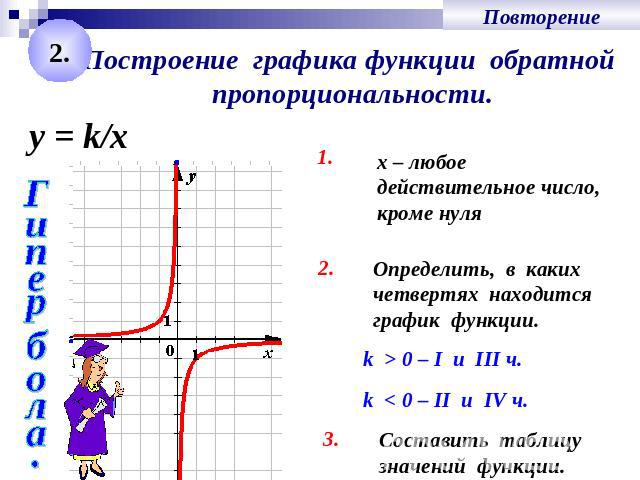
Обратная пропорциональность — функция, заданная формулой y=, где k≠0 Число k называют коэффициентом обратной пропорциональности.
Графиком обратной пропорциональности является гипербола.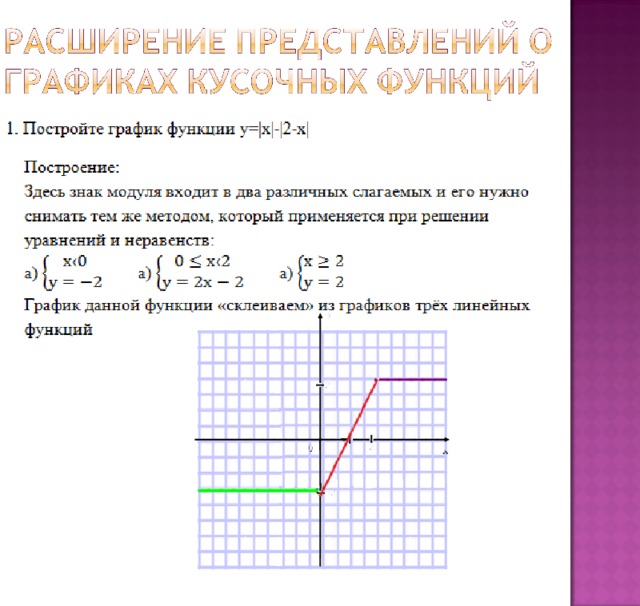
Квадратичная функция — функция, заданная формулой y=a+bx+c, ,где a, b, c − действительные числа (при этом a≠0). Примеры: y= -+4x+5 y=3 y=-2x График квадратичной функции — парабола. Направление ветвей параболы зависит от знака коэффициента a. При a>0 ветви параболы направлены вверх, при a<0 − вниз.
, x∈[0,∞).
y = |x|
Укажите формулу, задающую эту функцию ОСНОВНЫЕ ВИДЫ ФУНКЦИЙ И ИХ ГРАФИКИ
Укажите формулу, задающую эту функцию: ОСНОВНЫЕ ВИДЫ ФУНКЦИЙ И ИХ ГРАФИКИ
МОЛОДЦЫ! Назовите уравнение функции, график которой изображён ниже: ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
Уравнение касательной к графику функции. 10 класс
Похожие презентации:
Уравнение касательной к графику функции
Уравнение касательной к графику функции
Уравнение касательной к графику функции
Касательная к графику функции. (10 класс)
Касательная к графику функции
Касательная.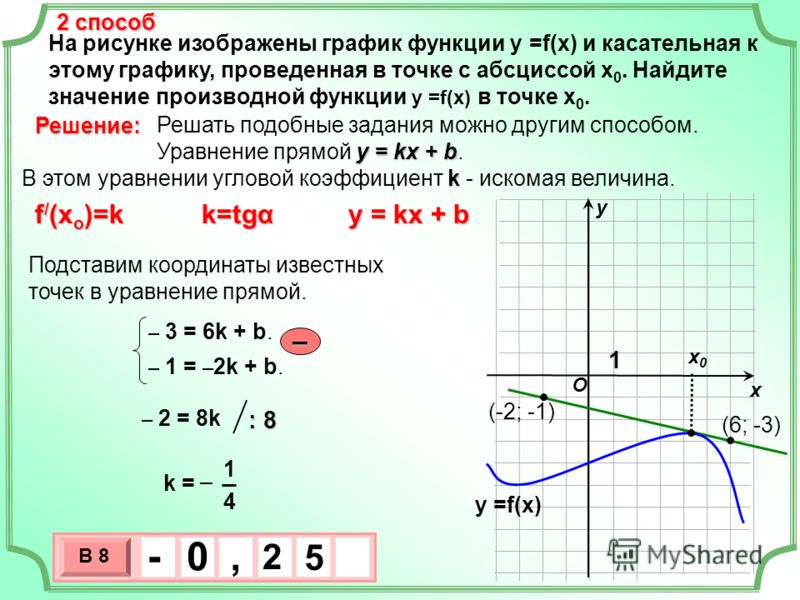 Уравнение касательной. 10 класс
Уравнение касательной. 10 класс
Уравнение касательной к графику функции
Касательная к графику функции
Устные упражнения. Определение производной. (10 класс)
Уравнение касательной. Условие касания
1. Уравнение касательной к графику функции
10 класс2. Верно ли определение?
Касательная – это прямая,имеющая с данной кривой
одну общую точку.
3. Пусть дана и две прямые и , имеющая с данной параболой одну общую точку М (1;1).
Пуст ь дана y x 2 и две прямые x 1 и y 2 x 1 ,имеющая с данной параболой одну общую т очку М
(1;1).
x 1
4. На данном уроке:
1. выясним, что же такое касательная кграфику функции в точке, как составить
уравнение касательной;
2. рассмотрим основные задачи на
составление уравнения касательной.
Для этого:
вспомним общий вид уравнения прямой
условия параллельности прямых
определение производной
правила дифференцирования
Формулы дифференцирования
5.
 Определение производнойПусть функция y f (x) определена в
Определение производнойПусть функция y f (x) определена внекотором интервале, содержащем внутри
себя точку x0 . Дадим аргументу x
приращение такое, чтобы не выйти из этого
интервала. Найдем соответствующее
приращение y функции и составим
y
отношение x .Если существует предел
отношения при x 0 , то указанный предел
называют производной функции
y f (x)
‘
в точке x0 и обозначают f ( x0 ) .
y
lim
f ‘ ( x0 )
x 0 x
6. Правила дифференцирования
1. Производная суммы равна сумме производных.f x g x ‘ f ‘ x g ‘ x
2. Постоянный множитель можно вынести за знак
производной.
‘
‘
kf x kf x
3. Производная произведения двух функций равна сумме
двух слагаемых; первое слагаемое есть произведение
производной первой функции на вторую функцию, а второе
слагаемое есть произведение первой функции на
производную второй функции.
f x g x f ‘ x g x f x g ‘ x
‘
4. Производная частного
f x
f ‘ x g x f x g ‘ x
2
x
g
x
g
‘
7.
 Основные формулы дифференцированияf (x)
Основные формулы дифференцированияf (x)С
1
x
x
x
‘
f ( x)
‘
f (x)
f ( x)
0
sin x
cos x
1
2
x
cos x
sin x
1
2 x
x
1
tgx
ctgx
1
cos 2 x
1
2
sin x
8. Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны
Параллельны ли прямые:a ) y 2 x 1;
б) y 2 x 2;
в) y 3 x 1.
9. Пусть дан график функции y=f(x). На нем выбрана точка M(a;f(a)), в этой точке к графику функции проведена касательная (мы
предполагаем, что она существует). Найти угловойкоэффициент касательной.
y f x , M a; f a
k сек
y
x
k кас lim kcек
x 0
k кас
y
lim
x 0 x
10. Геометрический смысл производной
Если к графику функции y = f (x) в точкеx a можно провести касательную,
непараллельную оси у, то f ‘ (a)
выражает угловой коэффициент
касательной
kкас
y
f (a x) f (a)
‘
lim
lim
f a
x 0 x
x a
(a x) a
11.
 Геометрический смысл производнойПроизводная в точке
Геометрический смысл производнойПроизводная в точкеx x0 равна
угловому коэффициенту
касательной к
графику функции
y = f(x) в этой точке.
.
Т.е.
f ( x0 ) tg
‘
Причем, если :
1. f ‘ ( x0 ) tg 0, то острый
2. f ‘ ( x0 ) tg 0, то развернутый
3. f ‘ ( x0 ) tg 0, то тупой
12. Вывод уравнения касательной
y kx m, M a; f aПусть прямая задана уравнением:
k f ‘ (a)
f a ka m
m f a ka
y kx f a ka
y f a f
‘
a x a
уравнение касательной к
графику функции
y f (x)
13. Составить уравнение касательной:
к графику функцииM 1;1
f (1) 12 1
f ‘ ( x) 2 x
f ‘ (1) 2 1 2
y f (a ) f ‘ (a )( x a )
y 1 2 ( x 1)
y 1 2x 2
y 2x 1
f ( x) x
2
в точке
14. Составить уравнение касательной:
к графику функцииf (0) tg 0 0
1
f ( x)
cos 2 x
1
‘
f ( 0)
1
2
cos 0
y f (a ) f ‘ (a )( x a )
‘
y 0 1 ( x 0)
y x
y tgx
в точке M 0;0
15.
 Алгоритм нахождения уравнения касательной к графику функции y=f(x).1. Обозначим абсциссу точки касания буквой
Алгоритм нахождения уравнения касательной к графику функции y=f(x).1. Обозначим абсциссу точки касания буквойx=a.
2. Вычислим f (a ) .
3. Найдем f ‘ ( x) и f ‘ (a) .
4. Подставим найденные числа a , в формулу
y f a f a x a .
‘
16. Составить уравнение касательной к графику функции в точке .
Составить уравнение касательной к1
графику функции y в точке x 1 .
x
1
f ( x)
x
1) a 1
2) f (a) f (1) 1
1
‘
3) f ( x) 2
x
1
f (a ) f (1) 2 1
1
‘
‘
4) y 1 ( x 1)
y 2 x
Ответ
y 2 x
:
17. К графику функции провести касательную так, чтобы она была параллельна прямой .
x3К графику функции y 3
провести касательную так,
чтобы она была параллельна прямой y 4 x 5 .
kкас 4, k кас f ‘ ( x) f ‘ ( x) 4
x
f ( x)
3
‘
1
3 x 2 x 2
3
f ‘ (a) a 2 a 2 4,
3
‘
.
1) a1 2, a2 2
3
(
2
)
8
2
8 , f (a )
2) f (a1 )
2
3
3
3 3
3
3) f ‘ (a1 ) f ‘ (a2 ) 4
16
16
4) y 4 x
, y 4x
3
3
,
18.
 Ответьте на вопросы:1. Что называется касательной к графику
Ответьте на вопросы:1. Что называется касательной к графикуфункции в точке?
2. В чем заключается геометрический
смысл производной?
3. Сформулируйте алгоритм нахождения
уравнения касательной?
19. Домашняя работа
Выучить алгоритмсоставления
уравнения
касательной
20. Литература
1.2.
3.
4.
Алгебра и начала математического анализа: Учеб. Для 10-11
кл. для учащихся общеобразовательных учреждений
(базовый уровень) / Под редакцией А.Г. Мордковича. – М.:
Мнемозина, 2009.
Алгебра и начала математического анализа: Задачник, Для
10-11 кл. для учащихся общеобразовательных учреждений
(базовый уровень) / Под редакцией А.Г. Мордковича. – М.:
Мнемозина, 2009.
Алгебра и начала анализа. Самостоятельные и контрольные
работы для 10-11 классов. / Ершова А.П., Голобородько В.В. –
М.: ИЛЕКСА, 2010
ЕГЭ 2010. Математика. Задача В8. Рабочая тетрадь / Под
редакцией А.Л.Семенова и И.В.Ященко – M.
 : Издательство
: ИздательствоМЦНМО, 2010
English Русский Правила
R Функция plot() (с примерами)
Функция plot() — это общая функция, которая используется для построения точек на графике.
Построить одну точку в R
Обычно упорядоченная пара (x,y) представляет собой точку на графике.
В R мы передаем определенные точки для осей x и y соответственно в качестве параметра функции plot() для создания графика. Например,
# создайте одну точку в (2,4) участок(2, 4)
Вывод
Построить одну точку В приведенном выше примере мы использовали функцию
plot(2, 4)
Здесь,
- 2 — указывает точку на оси x
- 4 — указывает точку на оси Y
Отображение нескольких точек в R
Мы также можем отобразить несколько точек на графике в R. Для этого мы используем R-вектора. Например,
Для этого мы используем R-вектора. Например,
# создаем вектор x х <- с (2, 4, 6, 8) # создаем вектор у у <- с(1, 3, 5, 7) # построить несколько точек график (х, у)
Выходные данные
Построить несколько точек В приведенном выше примере мы можем построить несколько точек на графике, используя функцию plot() и вектор R.
plot(x, y)
Здесь мы передали два вектора: x и y внутри plot() для построения нескольких точек.
Первый элемент x и y т.е. 2 и 1 соответственно отображает 1-ю точку на графике и второй элемент x и y отображают вторую точку на графике и так далее.
Примечание : Убедитесь, что количество точек на обоих векторах одинаково.
Построение последовательности точек в R
В R мы используем функцию plot() и оператор : для рисования последовательности точек. Например,
Например,
# нарисовать последовательность точек plot(1:5)
Вывод
Последовательность построения В приведенном выше примере мы использовали plot() и оператор : для рисования последовательности точек.
Графики нарисованы в порядке (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) .
Нарисуйте линию в R
Мы передаем параметр plot() для изменения типа графика. Например,
# нарисовать линию plot(1:5, type="l")
Вывод
Нарисовать линию В приведенном выше примере мы использовали параметр типа внутри plot() для изменения типа графика.
plot(1:5, type = "l")
Здесь type = "l" рисует линию, соединяющую все точки.
Различные типы графиков в R
В R мы можем изменить тип графика, используя параметр type внутри функции plot() .
Вот некоторые из наиболее часто используемых типов графиков, которые мы можем использовать внутри plot() :
| Значение | Описание |
|---|---|
| "р" | График 90 159 точек (по умолчанию) 90 160|
| "л" | Линейный график |
| "б" | И линия, и точки |
| "с" | Ступенчатый участок |
| "н" | Без печати |
| "ч" | График в виде гистограммы |
Добавить заголовок и метку к графику в R
Мы можем добавить заголовки, предоставить метки для осей графика в R. Например,
plot(1:5, main="Построить последовательность точек", xlab="ось x", ylab="ось Y")
Вывод
Добавить заголовок и метку к графикуНа приведенном выше рисунке мы видим, что мы добавили заголовок, метку к оси x и оси y.
Здесь,
-
основной- добавляет заголовок"Последовательность точек графика" -
xlab- добавляет метку"ось х"для оси х -
ylab- добавить метку"ось Y"для оси Y
Построить тригонометрическую функцию в R
В R мы также можем построить тригонометрические функции.
Создадим график синусоиды,
# вектор последовательности значений от -pi до pi с интервалом 0,1 х = последовательность (-пи, пи, 0,1) # соответствующее значение синуса x у = грех (х) # график y против x plot(x,y)
Выход
Создать синусоидуВ приведенном выше примере мы создали график синусоиды.
Мы использовали функцию seq() для создания вектора последовательности x значений от -pi до pi с интервалом 0,1 . И присвоены соответствующие значения синуса от x до y .
Наконец, мы построили y против x , используя plot() .
Примечание : Точно так же мы можем генерировать волновые графики других тригонометрических функций.
Учебник · Plots
Это руководство поможет вам начать работу с Plots.jl. Его основная цель — познакомить вас с терминологией, используемой в пакете, с тем, как использовать Plots.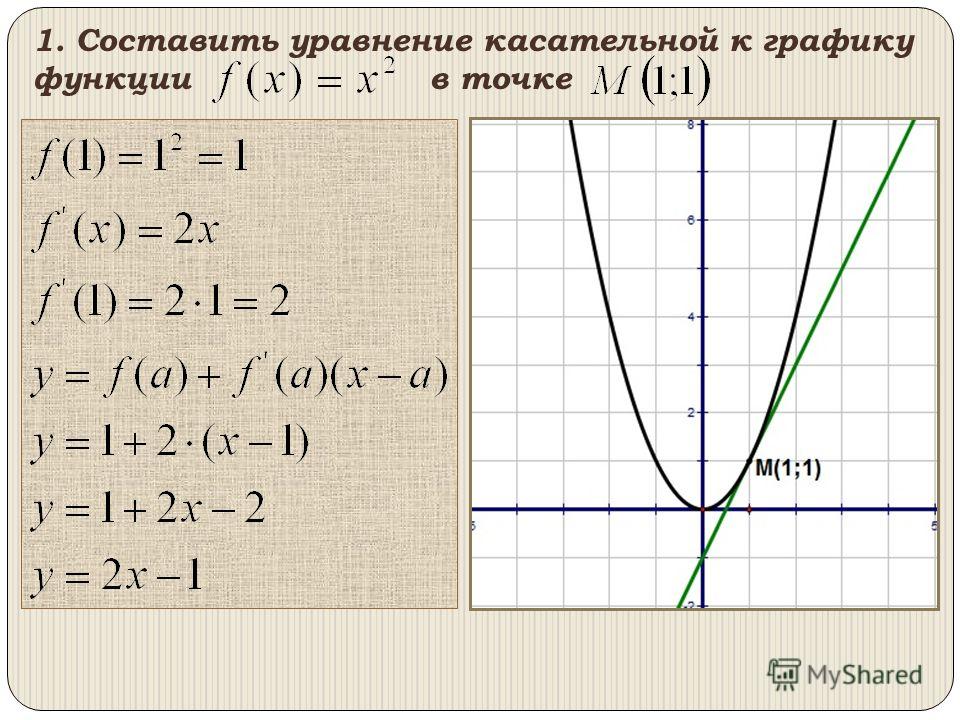
После установки Plots.jl с помощью Pkg.add("Plots") первым шагом является инициализация пакета. В зависимости от вашего компьютера это займет несколько секунд:
с использованием графиков
Для начала построим график некоторых тригонометрических функций. Для координат x мы можем создать диапазон от 0 до 10, скажем, 100 элементов. Для координат y мы можем создать вектор, оценив sin(x) поэлементно. Для этого в Julia мы ставим точку сразу после вызова функции. Наконец, мы используем plot()
х = диапазон (0, 10, длина = 100) у = грех. (х) график (х, у)
График отображается на панели графиков, в отдельном окне или в браузере, в зависимости от среды и бэкенда (см. ниже).
Если это ваш первый сюжет в сеансе, и для его отображения требуется некоторое время, это нормально; эта задержка называется проблемой «времени до первого графика» (или TTFP ), и последующие графики будут быстрыми.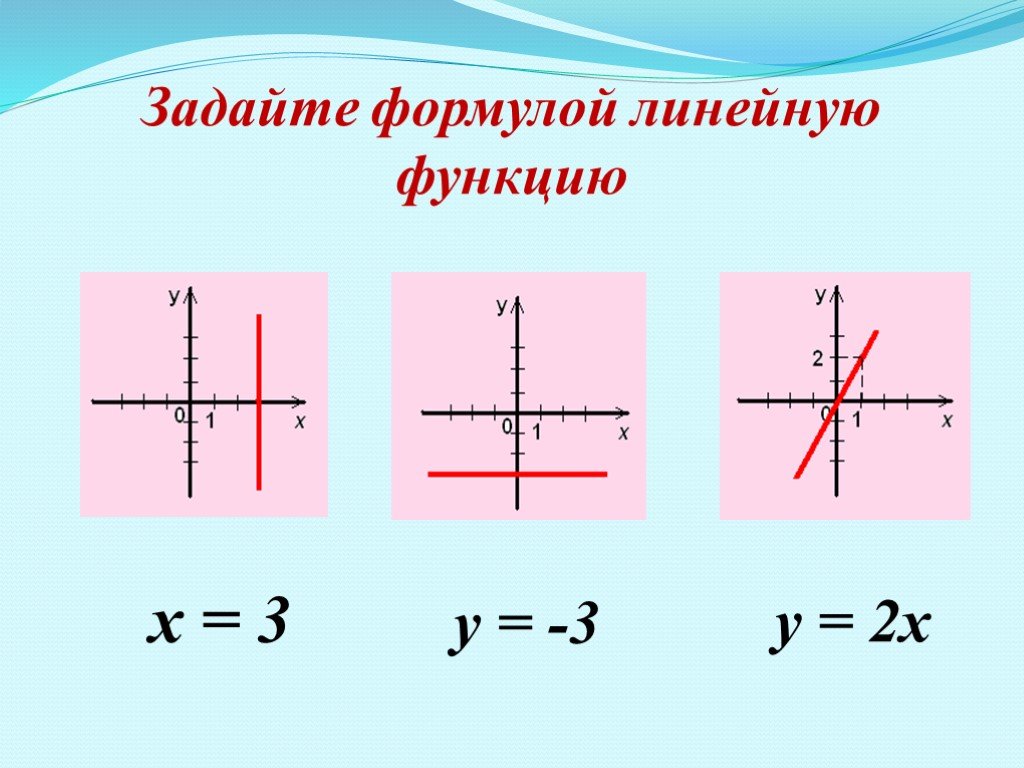 Из-за того, как Джулия работает под капотом, эту проблему трудно решить, но за последние несколько лет был достигнут значительный прогресс в сокращении времени компиляции.
Из-за того, как Джулия работает под капотом, эту проблему трудно решить, но за последние несколько лет был достигнут значительный прогресс в сокращении времени компиляции.
В Plots.jl каждый столбец представляет собой серию , набор связанных точек, которые образуют линии, поверхности или другие графические примитивы. Мы можем построить несколько строк, построив матрицу значений, где каждый столбец интерпретируется как отдельная строка. Ниже [y1 y2] образует матрицу 100x2 (100 элементов, 2 столбца).
х = диапазон (0, 10, длина = 100) у1 = грех.(х) y2 = cos.(x) plot(x, [y1 y2])
Кроме того, мы можем добавить больше строк, изменив объект графика. Это делается сюжет! Команда , где ! означает, что команда изменяет текущий график. Вы заметите, что мы также используем @. макрос. Это удобный макрос, который вставляет точки для каждого вызова функции справа от макроса, гарантируя, что все выражение будет оцениваться поэлементно.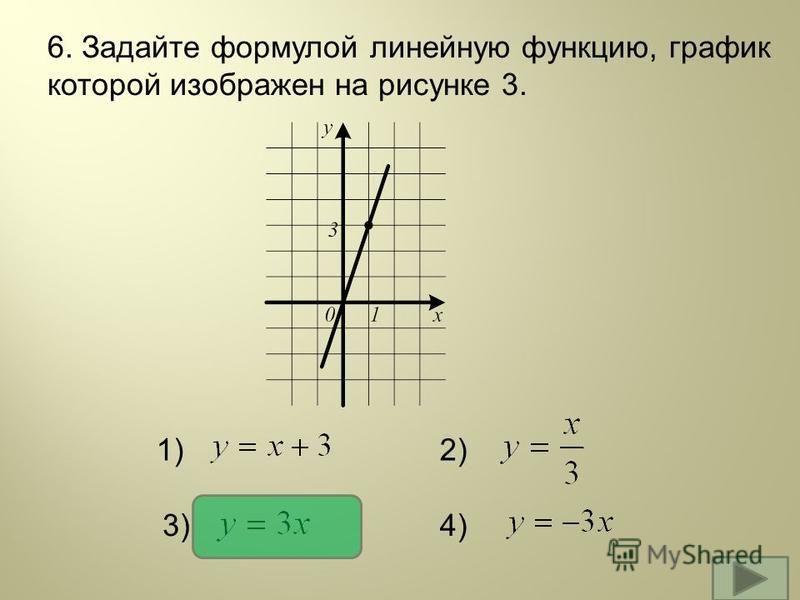 Если бы мы вводили точки вручную, нам понадобилось бы три из них для синуса, экспоненты и вычитания, и результирующий код был бы менее читаемым.
Если бы мы вводили точки вручную, нам понадобилось бы три из них для синуса, экспоненты и вычитания, и результирующий код был бы менее читаемым.
В случаях, когда переменная plot опущена, Plots.jl автоматически использует глобальный Plots.CURRENT_PLOT .
Сохранение рисунков
Сохранение графиков выполняется командой savefig . Например:
savefig("myplot.png") # сохраняет CURRENT_PLOT как .png
savefig(p, "myplot.pdf") # сохраняет график из p как векторную графику .pdf Также существуют вспомогательные функции png , Plots.pdf и другие неэкспортированные хелперы. При этом расширение не указывается в имени файла. Следующий код эквивалентен приведенному выше коду:
png("myplot")
Plots.pdf(p, "myplot") Дополнительную информацию о выводе цифр можно найти в разделе «Вывод» Руководства.
В предыдущем разделе мы делали графики… мы закончили, верно? Нет! Нам нужно стилизовать наши графики. В Plots.jl модификаторы графиков называются атрибутами , которые задокументированы на странице атрибутов. Plots.jl следует двум простым правилам с данными и атрибутами:
В Plots.jl модификаторы графиков называются атрибутами , которые задокументированы на странице атрибутов. Plots.jl следует двум простым правилам с данными и атрибутами:
- Позиционные аргументы соответствуют входным данным
- Аргументы ключевых слов соответствуют атрибутам
Таким образом, что-то вроде plot(x, y, z) представляет собой трехмерные данные для трехмерных графиков без атрибутов, а plot(x, y, attribute=value) — это двумерные данные с одним атрибутом, присвоенным некоторому значению.
Например, мы можем изменить толщину линии с помощью ширина линии (или ее псевдоним lw ), изменить метки легенды с помощью метка и добавьте заголовок с title . Обратите внимание, что ["sin(x)" "cos(x)"] имеет то же количество столбцов, что и данные. Кроме того, поскольку ширина линии приписывается [y1 y2] , присвоенное значение повлияет на обе строки.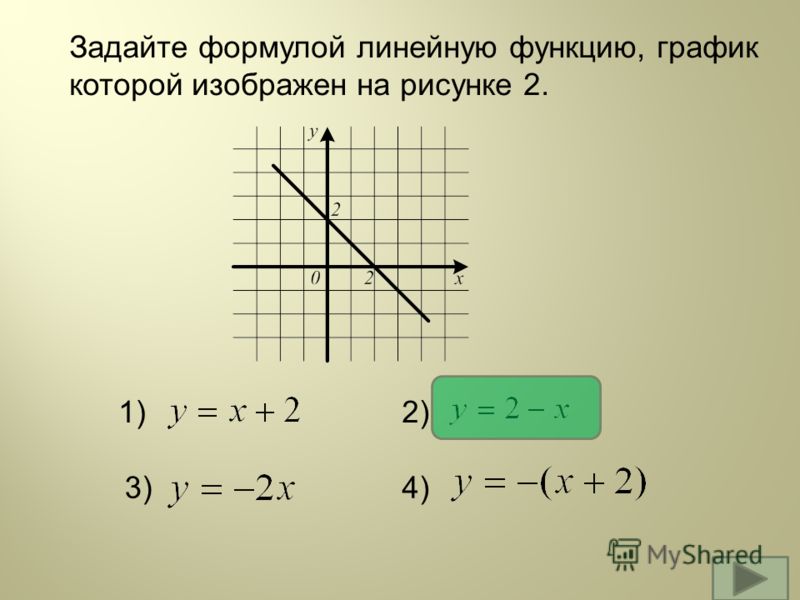 Давайте применим все это к нашему предыдущему графику:
Давайте применим все это к нашему предыдущему графику:
x = диапазон (0, 10, длина = 100) у1 = грех.(х) y2 = cos.(x) plot(x, [y1 y2], title="Тригонометрические функции", label=["sin(x)" "cos(x)"], linewidth=3)
Каждый атрибут также можно применить, изменив график с помощью функция модификатора. Некоторые атрибуты имеют свои собственные специальные функции-модификаторы, в то время как доступ к другим можно получить через сюжет!(атрибут=значение) . Например, атрибут xlabel добавляет метку для оси x. Мы можем указать его в команде построения с помощью xlabel=... или использовать функцию модификатора ниже, чтобы добавить его после того, как график уже был сгенерирован. Вам решать, что лучше для удобочитаемости кода.
xlabel!("x") Каждая функция модификатора представляет собой имя атрибута, за которым следует ! . Это будет неявно использовать глобальный Графики.CURRENT_PLOT . Мы можем применить его к другим объектам графика через атрибут !(p, значение) , где p — это имя объекта графика, который нужно изменить.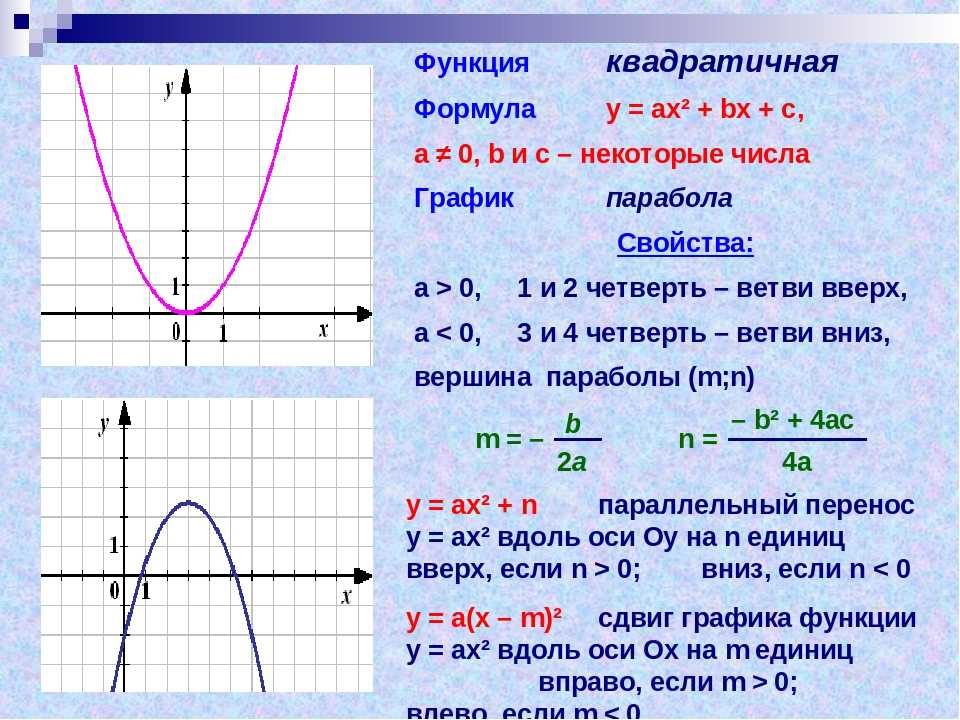
Давайте будем использовать ключевые слова и функции-модификаторы взаимозаменяемо, чтобы выполнить некоторые общие модификации нашего примера, перечисленные ниже. Вы заметите, что для атрибутов ls и легенда значения включают двоеточие : . Двоеточие обозначает символ в Юлии. Они обычно используются для значений атрибутов в Plots.jl, наряду со строками и числами.
- Метки для отдельных линий, видимые в легенде
- Толщина линий (мы будем использовать псевдоним
lwвместоlinewidth) - Стили линий (мы будем использовать псевдоним
lslinestyle )вместо
- Положение легенды (вне графика, так как по умолчанию он будет загромождать график)
- Столбцы легенды (3, чтобы лучше использовать горизонтальное пространство)
- X-пределы для перехода от
0до2pi 92 — 1/2″, lw=3, ls=:точка)
сюжет!(легенда=:внешнее дно, легендастолбцы=3)
xlims!(0, 2pi)
title!(«Тригонометрические функции»)
xметка!(«х»)
ylabel!(«y») -
lcforlinecolor -
lwforlinewidth -
mcformarkercolor -
msformarkersize -
maformarkeralpha
Обратите внимание, что y3 отображается пунктирной линией. Это отличается от графика рассеяния данных.
Это отличается от графика рассеяния данных.
Графики в логарифмическом масштабе
Иногда необходимо отображать данные по порядкам величин. В этом случае атрибуты xscale и yscale могут быть установлены на :log10 . Их также можно установить на 9диапазон (0, 4, длина = 100)
у = @. 1/(1+х)
график (х, у, метка = «1/(1 + х)»)
график!(xscale=:log10, yscale=:log10, minorgrid=true)
xlims!(1e+0, 1e+4)
ylims!(1e-5, 1e+0)
title!(«График логарифмический»)
xметка!(«х»)
ylabel!(«y»)
Дополнительную информацию об атрибутах можно найти в разделе «Атрибуты» Руководства.
Строки уравнений LaTeX
Plots.jl работает с LaTeXStrings.jl, пакетом, который позволяет пользователю вводить уравнения LaTeX в строковых литералах. Чтобы установить это, введите К этому моменту вы знаете о линейных графиках, но не хотите ли вы отображать свои данные другими способами? В Plots. Давайте снова начнем с функции синуса, но на этот раз мы определим вектор с именем Для каждого встроенного типа серии существует сокращенная функция для прямого вызова того типа серии, который соответствует его имени. Он обрабатывает атрибуты точно так же, как Доступные типы серий зависят от серверной части и задокументированы на странице Поддерживаемые атрибуты. Графики рассеяния будут иметь некоторые общие атрибуты, связанные с маркерами. Вот пример того же сюжета, но с уточнением некоторых атрибутов, чтобы сделать сюжет более презентабельным. Многие псевдонимы используются для краткости, и приведенный ниже список ни в коем случае не является исчерпывающим. Plots. Когда мы начали строить график выше, наш график использовал GR по умолчанию. Однако предположим, что нам нужен другой бэкэнд для построения графиков, который будет отображаться в красивом графическом интерфейсе или на панели графиков VS Code. Для этого нам понадобится серверная часть, совместимая с этими функциями. Некоторыми распространенными бэкэндами для этого являются PythonPlot и Plotly. Например, чтобы установить PythonPlot, просто введите команду Мы можем специально выбрать серверную часть, в которую мы строим график, используя имя серверной части в нижнем регистре в качестве функции. Давайте построим пример выше, используя Plotly, а затем GR: Каждый механизм построения графиков отличается от других. Дополнительную информацию о бэкендах см. на странице бэкендов. Примеры графиков из различных бэкендов см. в разделе «Примеры». В начале руководства мы рекомендовали следовать примерам кода в интерактивном сеансе по следующей причине: попробуйте добавить те же самые команды построения графика в сценарий. Теперь вызываю сценарий... а сюжет не появляется? Это связано с тем, что Джулия при интерактивном использовании через REPL вызывает Pkg.add("LaTeXStrings") 9диапазон (0, 4, длина = 100)
у = @. 1/(1+х)
график (х, у, метка = L "\ гидроразрыва {1} {1 + х}")
график!(xscale=:log10, yscale=:log10, minorgrid=true)
xlims!(1e+0, 1e+4)
ylims!(1e-5, 1e+0)
title!(L"Графический логарифм $\frac{1}{1+x}$")
xметка!(L"x")
ylabel!(L"y") . В каждом вышеприведенном случае интерактивное использование автоматически вызывало  jl эти другие способы построения серии называются типом серии . Линия является одним типом серии. Тем не менее, точечная диаграмма - это еще один тип ряда, который обычно используется.
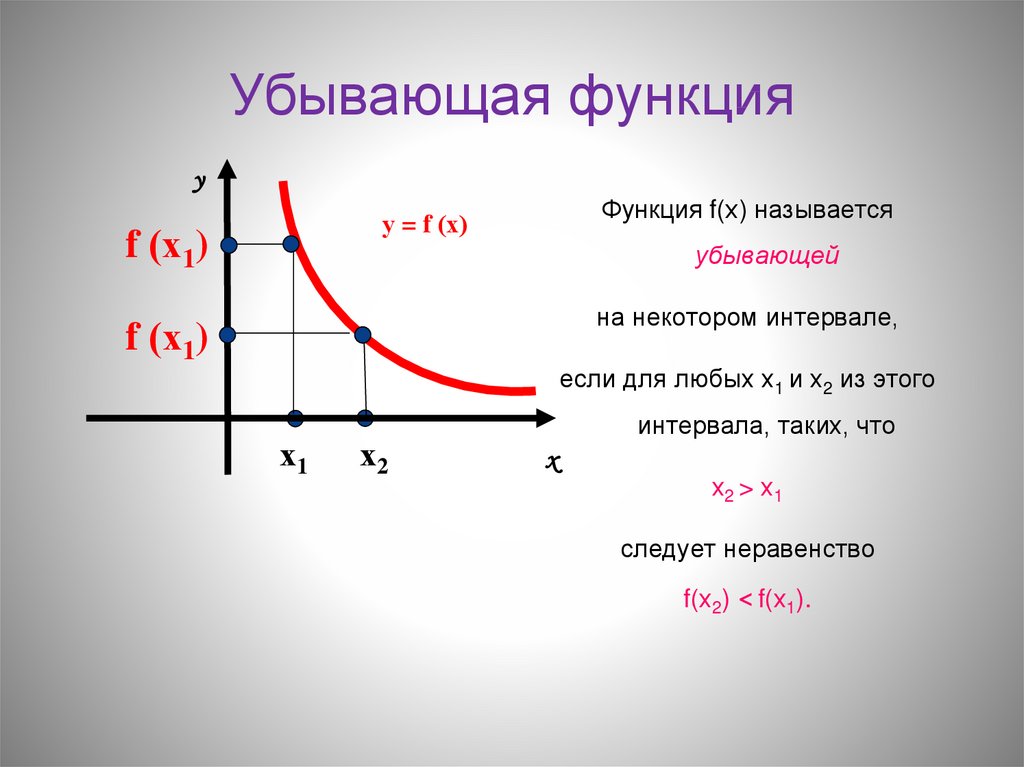
jl эти другие способы построения серии называются типом серии . Линия является одним типом серии. Тем не менее, точечная диаграмма - это еще один тип ряда, который обычно используется. y_noisy , который добавляет некоторую случайность. Мы можем изменить тип серии, используя атрибут seriestype . х = диапазон (0, 10, длина = 100)
у = грех. (х)
у_шумный = @. грех(х) + 0,1*ранд()
график (х, у, метка = "грех (х)")
plot!(x, y_noisy, seriestype=:scatter, label="data")
команда plot , и она имеет изменяющуюся форму, которая заканчивается на ! . Например, мы можем написать последнюю строку как: scatter!(x, y_noisy, label="data")
 Как мы опишем позже, другие библиотеки могут добавлять новые типы серий, используя рецептов .
Как мы опишем позже, другие библиотеки могут добавлять новые типы серий, используя рецептов . x = диапазон (0, 10, длина = 100)
у = грех. (х)
у_шумный = @. грех(х) + 0,1*ранд()
график (х, у, метка = "грех (х)", lc =: черный, lw = 2)
разброс!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
сюжет!(легенда=:внизу слева)
title!("Синус с шумом")
xметка!("х")
ylabel!("y") 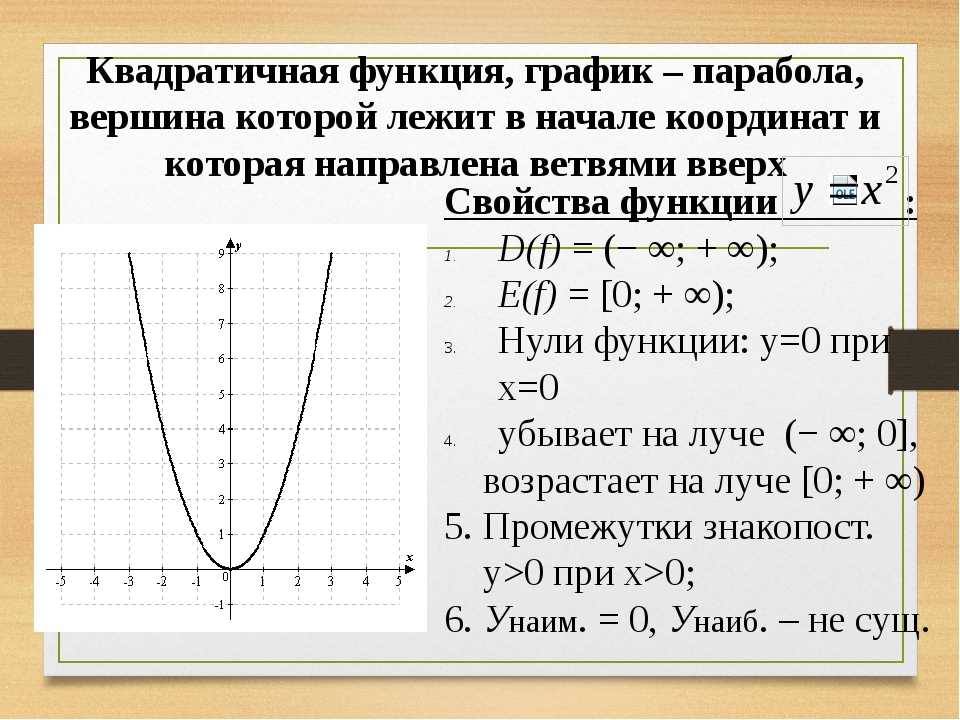 jl — это метапакет для построения графиков: это интерфейс для множества различных библиотек для построения графиков. На самом деле Plots.jl интерпретирует ваши команды, а затем генерирует графики с использованием другой библиотеки построения графиков, называемой бэкендом . Самое приятное в этом то, что вы можете использовать множество различных библиотек для построения графиков с синтаксисом Plots.jl, и вскоре мы увидим, что Plots.jl добавляет новые функции в каждую из этих библиотек!
jl — это метапакет для построения графиков: это интерфейс для множества различных библиотек для построения графиков. На самом деле Plots.jl интерпретирует ваши команды, а затем генерирует графики с использованием другой библиотеки построения графиков, называемой бэкендом . Самое приятное в этом то, что вы можете использовать множество различных библиотек для построения графиков с синтаксисом Plots.jl, и вскоре мы увидим, что Plots.jl добавляет новые функции в каждую из этих библиотек! Pkg.add("PythonPlot") в REPL; чтобы установить Plotly, введите Pkg. .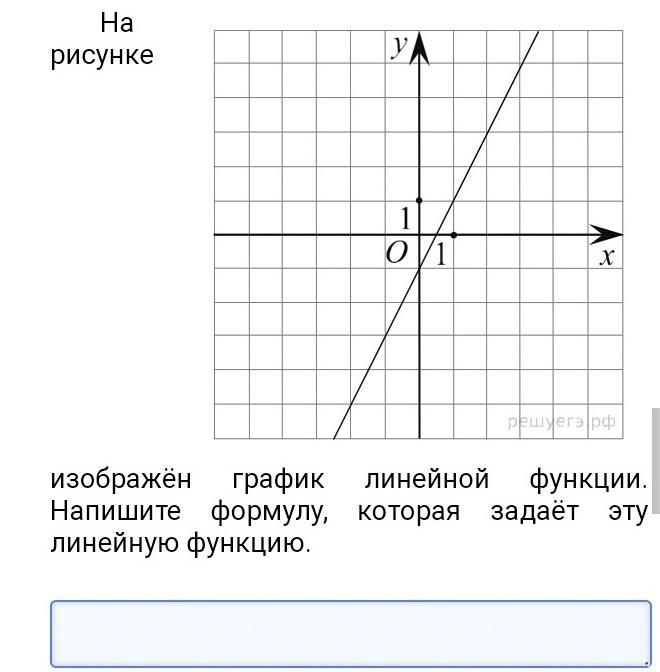 add("PlotlyJS")
add("PlotlyJS") plotlyjs() # установим бэкэнд на Plotly
х = диапазон (0, 10, длина = 100)
у = грех. (х)
у_шумный = @. грех(х) + 0,1*ранд()
# это отображается в отдельном окне через Plotly
график (х, у, метка = "грех (х)", lc =: черный, lw = 2)
разброс!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
сюжет!(легенда=:внизу слева)
title!("Синусоида с шумом, построенная с помощью Plotly")
xметка!("х")
ylabel!("y") "plotlyjs_tutorial.png"
gr() # установить бэкэнд на GR
# этот график использует GR
график (х, у, метка = "грех (х)", lc =: черный, lw = 2)
разброс!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
сюжет!(легенда=:внизу слева)
title!("Синус с шумом, построенный с помощью GR")
xметка!("х")
ylabel!("y")  Некоторые из них интерактивны, некоторые работают быстрее и могут работать с огромным количеством точек данных, а некоторые могут создавать трехмерные графики. Некоторые бэкенды, такие как GR, могут сохранять в векторную графику и PDF-файлы, в то время как другие, такие как Plotly, могут сохранять только в PNG.
Некоторые из них интерактивны, некоторые работают быстрее и могут работать с огромным количеством точек данных, а некоторые могут создавать трехмерные графики. Некоторые бэкенды, такие как GR, могут сохранять в векторную графику и PDF-файлы, в то время как другие, такие как Plotly, могут сохранять только в PNG., отображает для каждой переменной, возвращаемой командой без точки с запятой 9.0003 ; display для возвращаемых объектов графика.
В скрипте Джулия не делает автоматических показов, поэтому ; не нужно. Однако, если мы хотим отобразить наши графики в сценарии, это означает, что нам просто нужно добавить вызов display . Например:
display(plot(x, y))
В качестве альтернативы мы могли бы вызвать gui() в конце, чтобы сделать то же самое. Наконец, если у нас есть сюжетный объект p , мы можем ввести display(p) для отображения графика.
Мы можем объединить несколько графиков вместе в качестве подграфиков, используя макеты . Для этого существует множество способов, и мы покажем два простых способа создания простых макетов. Более сложные макеты показаны на странице «Макеты».
Первый метод заключается в определении макета, который будет разделять серию. Команда layout принимает двухкортежный макет = (N, M) , который строит сетку графиков NxM и автоматически разделяет серию на каждый график. Например, если мы введем
Например, если мы введем layout=(3, 1) на графике с тремя сериями, то мы получим три ряда графиков, в каждом из которых по одной серии.
Давайте определим некоторые функции и нанесем их на отдельные графики. Поскольку на каждом графике есть только одна серия, мы также удалим легенду на каждом графике, используя legend=false .
х = диапазон (0, 10, длина = 100) у1 = @. exp(-0.1x) * cos(4x) у2 = @. exp(-0.3x) * cos(4x) у3 = @. exp(-0.5x) * cos(4x) сюжет (x, [y1 y2 y3], макет = (3, 1), легенда = ложь)
Мы также можем использовать макеты на участках сюжетных объектов. Например, мы можем сгенерировать четыре отдельных графика и сделать один график, объединяющий их в сетку 2×2.
х = диапазон (0, 10, длина = 100) у1 = @. exp(-0.1x) * cos(4x) у2 = @. exp(-0.3x) * cos(4x) у3 = @. exp(-0.1x) у4 = @. exp(-0.3x) у = [у1 у2 у3 у4] p1 = график (х, у) p2 = график (x, y, title="Заголовок 2", lw=3) p3 = разброс (x, y, ms=2, ma=0,5, xlabel="xlabel 3") p4 = разброс (x, y, title="Заголовок 4", ms=2, ma=0,2) сюжет (p1, p2, p3, p4, макет = (2,2), легенда = ложь)
Обратите внимание, что атрибуты отдельных графиков применяются к этим отдельным графикам, тогда как атрибут legend=false в последнем вызове plot применяется ко всем подграфикам.
Теперь вы знаете всю основную терминологию Plots.jl и можете свободно просматривать документацию, чтобы стать мастером черчения. Однако осталось одно: рецептов . Рецепты построения графиков являются расширениями среды Plots.jl. Они добавляют:
- Новый
построитькоманды через пользовательских рецептов . - Интерпретация типов Julia по умолчанию как графических данных с помощью рецептов типов .
- Новые функции для создания участков с помощью рецептов участков .
- Новые типы серий с помощью рецептов серии .
Создание собственных рецептов — это дополнительная тема, описанная на странице рецептов. Вместо этого мы познакомим вас со способами использования рецепта.
Рецепты включены во многие библиотеки рецептов. Две основные библиотеки рецептов — это PlotRecipes.jl и StatsPlots.jl. Давайте посмотрим на StatsPlots.jl. StatsPlots.jl добавляет кучу рецептов, но мы сосредоточимся на них:
StatsPlots.jl добавляет кучу рецептов, но мы сосредоточимся на них:
- Добавляет рецепт типа для
Distributions. - Добавляет рецепт графика для маргинальных гистограмм.
- Добавляет несколько новых статистических рядов.
Помимо рецептов, StatsPlots.jl также предоставляет специализированный макрос @df для построения графиков непосредственно из таблиц данных.
Использование пользовательских рецептов
Пользовательский рецепт говорит, как интерпретировать команды построения графика для нового типа данных. В этом случае в StatsPlots.jl есть макрос @df , который позволяет отображать DataFrame напрямую, используя имена столбцов. Давайте создадим DataFrame со столбцами a , b и c и скажем Plots.jl использовать a в качестве оси x и построить ряд, определенный столбцами c и . :
:
# Pkg.add("StatsPlots")
# требуется для рецепта пользователя dataframe
используя StatsPlots
# теперь давайте создадим фрейм данных
используя кадры данных
df = DataFrame(a=1:10, b=10*rand(10), c=10*rand(10))
# построить фрейм данных, объявив точки именами столбцов
# x = :a, y = [:b :c] (обратите внимание, что y состоит из двух столбцов!)
@df df plot(:a, [:b :c]) Здесь не так много действий: все предыдущие команды (атрибуты, типы рядов и т. д.) по-прежнему будут работать с этими данными:
# x = :a, y = :b @df df scatter(:a, :b, title="My DataFrame Scatter Plot!")
Использование рецепта типа
Кроме того, StatsPlots.jl расширяет Distributions.jl, добавляя рецепт типа для его типов распределения, поэтому их можно напрямую интерпретировать как графические данные:
с использованием распределений график (нормальный (3, 5), lw = 3)
Рецепты шрифтов — это очень удобный способ начертания специализированного шрифта, который не требует больше вмешательства!
Использование рецептов построения
StatsPlots. jl добавляет мультиплот
jl добавляет мультиплот marginhist с помощью рецепта построения. Для наших данных мы возьмем знаменитый набор данных iris из RDatasets:
# Pkg.add("RDatasets")
используя RDatasets, StatsPlots
радужная оболочка = набор данных ("наборы данных", "радужная оболочка")
@df iris marginalhist(:PetalLength, :PetalWidth) Здесь iris — это DataFrame; используя @df макрос на DataFrame s, описанный выше, мы даем marginalhist(x, y) данные из столбцов PetalLength и PetalWidth .
Обратите внимание, что это больше, чем ряд, поскольку он генерирует несколько рядов (т. е. имеется несколько графиков из-за гистограммы вверху и справа). Таким образом, рецепт сюжета — это не просто серия, а нечто вроде новой команды plot .
Использование рецептов серии
StatsPlots.jl также представляет новые рецепты серии. Суть в том, что вам не нужно ничего делать по-другому.