Как по хорде найти радиус окружности: Найти длину радиуса окружности (круга), все основные формулы.

27. Окружность. Круг. Вписанные и описанные многоугольники

Касательная имеет с окружностью только одну общую точку. Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.

1. Сколько общих точек имеют прямая а и окружность с центром в точке О и радиусом, равным отрезку ОА?

Решение:

а) Возможны два случая: хорды лежат по одну сторону от центра окружности и по разные. Рассмотрим оба.

О1О₂— расстояние между хордами. 

1) Рассмотрим треугольник ВОС — равнобедренный (ОВ=ОС=R), следовательно ОО₂ является высотой и медианой и СО₂=ВО₂=ВС:2=3 см. По теореме Пифагора найдем ОО₂: ОО₂²=ОС²-СО₂²=25-9=16, ОО₂=4 см.

2) 

Рассмотрим треугольник АОD — равнобедренный (ОD=ОA=R), следовательно ОО₁ является высотой и медианой и AО₁=DО₁=AD:2=4 см. По теореме Пифагора найдем ОО₁: ОО₁²=ОA²-AО₁²=25-16=9, ОО₁=3 см.

3) В случае, когда хорды лежат по одну сторону от центра О₁О₂=4-3=1 см.

В случае, когда хорды лежат по разные стороны от центра, то О₁О₂=4+3=7 см.

Ответ: 1 см или 7 см.

---

5. а) В равнобедренном треугольнике угол при вершине равен 120°, боковая сторона равна 6 см. Найдите радиус описанной окружности.

∠ А=∠ С=(180-120):2=30°. 2) Найдем радиус описанной окружности:
R=AB: sin∠ А=6: sin 30°

=6:0,5=12 см.

---

6. Радиус окружности равен 6 см. 
а) Найдите длину дуги, которая содержит 120°.
б) Найдите площадь сектора, если его центральный угол равен 150°.

Решение:

а) l=πR*α : 180=π*6*120 : 180= 4π см.

Ответ: 4π см

---

7. а) Одна из сторон вписанного треугольника лежит на диаметре. Радиус описанной окружности равен 10 см. Одна из сторон треугольника равна 16 см. Найдите площадь треугольника.
    б) Одна из сторон вписанного треугольника лежит на диаметре. Радиус описанной окружности равен 25 см. Одна из сторон треугольника равна 14 см. Найдите площадь треугольника.

Решение:

а) Дано: Δ АВС; 

w(O,R) — описана около Δ АВС; 

R=10 см; ВС=16 см.

Найти S треугольника АВС.

1) Если сторона вписанного треугольника лежит на диаметре, то этот треугольник прямоугольный. АС=2R=20 см.

2) По теореме Пифагора найдем АВ: АВ²=АС²-ВС²=400-256=144, АВ=12 см.

3) Найдем площадь треугольника: S=AB*BC : 2=12*16:2=96 см².

Ответ: 96 см².

---

8. Найдите угол х:

Решение:

а) 1) Найдем длину дуги АВ:

∠АСВ — вписанный в окружность и он равен половине дуги АВ, следовательно  дуга АВ равна 50°*2=100°.

2) Угол между хордой СВ и касательной, проходящей через точку С  равен половине дуги, которая находится внутри угла, тогда дуга ВС равна 75

°*2=150°.

3) Найдем дугу СА:

дуга СА=360°-дуга АВ — дуга ВС=360°-100°-150°=110°.

4) ∠АВС — вписанный в окружность и равен половине дуги СА, т.е. ∠АВС =110°:2=55°.

Ответ: 55°.

---

9. а) Радиус описанной около треугольника окружности равен 10 см. Две стороны треугольника равны 12 см и 20 см. Найдите площадь треугольника.

    б) Радиус описанной около треугольника окружности равен 18,5 см. Две стороны треугольника равны 37 см и 12 см. Найдите площадь треугольника.

Решение:

а)

1) Так как одна из сторон треугольника ( 20 см) в два раза больше радиуса (10 см) описанной окружности, то она лежит на диаметре и треугольник является прямоугольным.

2) АС = 20 см; АВ=12 см. Найдем по теореме Пифагора ВС: ВС²=АС²-АВ²=400-144=256, ВС=16 см.

3) Найдем площадь треугольника: S=AB*BC : 2=12*16:2=96 см².

Ответ: 96 см².

---

10. а) Окружность радиуса 5 см вписана в равнобедренную трапецию с боковой стороной 16 см. Найдите площадь трапеции.
     б) Окружность вписана в равнобедренную трапецию с боковой стороной 8 см и площадью 48 см

2. Найдите радиус окружности.

Решение:

а) 

Дано: АВСD — равнобедренная трапеция;

АВ=СD=16 см; w(O,R) — описана около трапеции; R=5 см.

Найти S трапеции ABCD.

1) Т.к. в трапецию вписана окружность, то AD+DC=AB+CD=6+6=12 см — сумма оснований трапеции.

2) Высота равна двум радиусам вписанной окружности: КМ=2R=10 см.

3) Найдем площадь трапеции:

S=(AD+DC)*KM:2=12*10:2=60 см²

Ответ: 60 см²

---

11. а) Найдите площадь прямоугольной трапеции, если точка касания окружности, вписанной в прямоугольную трапецию делит большую боковую сторону на отрезки  4 см и 9 см. 

     б) Окружность, вписанная в прямоугольную трапецию, точкой касания делит большую боковую сторону на отрезки  4 см и 16 см. Найдите площадь трапеции.

Решение:

а)

Дано: ABCD -прямоугольная трапеция; 

CF= 4 см; FD=9 см.

Найти: S трапеции ABCD — ?

1) Рассмотрим треугольники ОКС и OFC, они равны по третьему признаку равенства треугольников:

OK=OF как радиусы;

СF=CK как отрезки касательных, проведенных из одной точки;

ОС — общая сторона.

Тогда ∠КСО=∠FCO и СО — биссектриса ∠KCF.

2) Рассмотрим треугольники ОMD и OFD, они равны по третьему признаку равенства треугольников:

OM=OF как радиусы;

DM=DF как отрезки касательных, проведенных из одной точки;

ОD — общая сторона.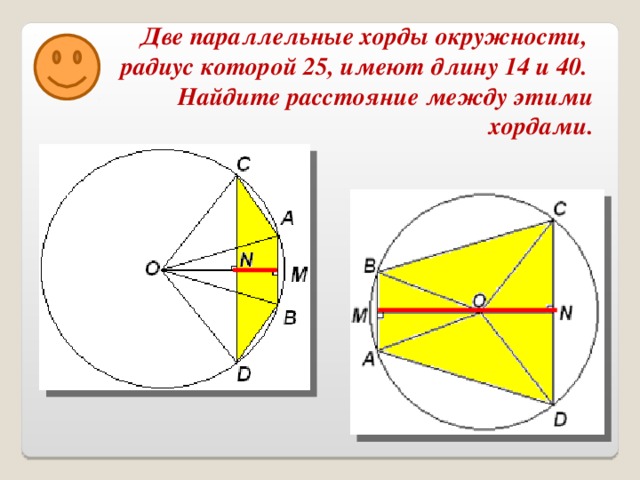

Тогда ∠MDО=∠FDO и DО — биссектриса ∠MDF.

3) Сумма углов трапеции равна 360°, т.к. ∠А=∠В=90°, то ∠С +∠D=360°-180°=180°.

∠OCF + ∠ODF= (∠A + ∠D):2=180°:2=90°. Тогда в треугольнике OCD ∠COD=180°-90°=90°. 

4) Треугольник OCD — прямоугольный. OF²=CF*FD=4*9=36. OF=6 см — радиус вписанной окружности.

АВ=2r=12 см.

5) Т.к. трапеция описана около окружности, то AD+DC=AB+CD=12+(4+9)=25 см — сумма оснований трапеции.

6) Найдем площадь трапеции:

S=(AD+DC)*KM:2=25*12:2=150 см².

Ответ: 150 см².

---

12. Найдите угол х:

Решение:

а) 

1) Найдем сумму углов А и С:

∠А + ∠С=180° —∠С=180°-70°=110°.

2) Центр вписанной окружности — точка пересечения биссектрис треугольника, тогда ∠ОАС=∠ВАС:2 и ∠ОСА=∠ВСА:2.

Сумма углов ОАС и ОСА равна половине суммы углов А и С и равна 55°.

3) Найдем угол х:

Сумма углов треугольника АОС равна 180°, тогда ∠х=180°-(∠ОАС+∠ОСА)=180°-55°=125°.

Ответ: 125°.

---

13. а) Доказать, что если в равнобедренную трапецию можно вписать окружность, то квадрат высоты трапеции равен произведению ее оснований.

     б) Доказать, что если в прямоугольную трапецию можно вписать окружность, то площадь трапеции равна произведению оснований.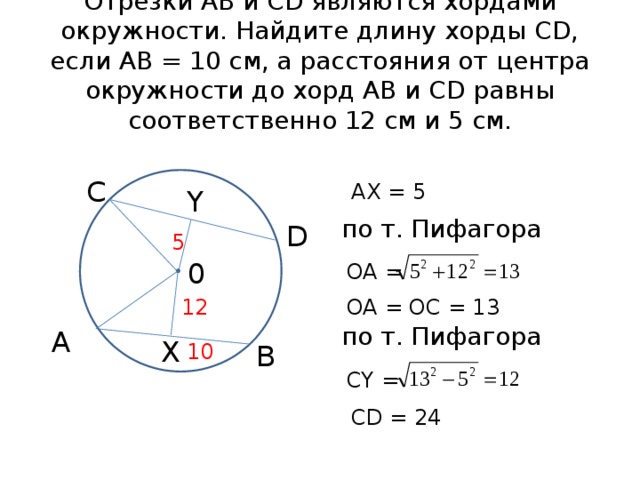

Решение:

а) 

Дано: AВCD — равнобедренная трапеция;

окружность вписана в трапецию.

Доказать: ВК²=ВС*АD.

Доказательство:

1) Обозначим основание ВС — а, основание AD — b. ВС=КМ и АК=(AD-DC):2=(b-a):2.

2) Т.к. в трапецию вписана окружность, то АВ+CD=DC+AD=a+b, а т.к. трапеция равнобедренная, то АВ=(a+b):2.

3) Найдем высоту ВК трапеции:

треугольника АВК — прямоугольный и по теореме Пифагора BK²=AB²-AK²

Следовательно, BK²=BC*AD. Что и требовалось доказать.

---

14. а) Стороны треугольника равны 9 см и 6 см, угол между ними равен 60°. Найдите площадь круга, ограниченного окружностью, описанной около треугольника.

      б) Сторона треугольника равна 9 см, угол, прилежащий к ней  равен 60°. Площадь круга, ограниченного окружностью, описанной около треугольника равна 39π см².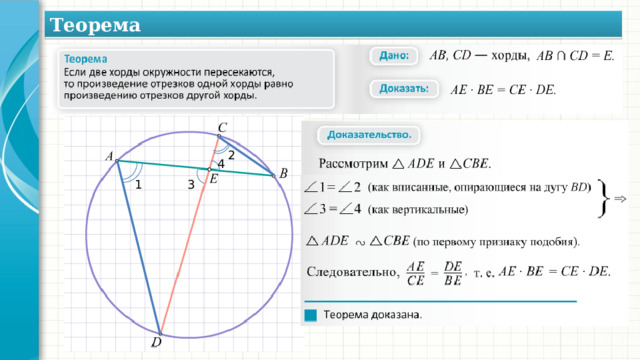 Найдите вторую сторону, которая прилежит к заданному углу.(№ 5.5.47 [7])

Решение:

а) 

Дано: АВС — треугольник;

АВ=6 см; АС=9 см; ∠ВАС=60.

Найти: S круга, ограниченного описанной окружностью.

1) Найдем сторону ВС:

по теореме косинусов ВС²=АВ²+АС²+2АВ*АС*cos∠A=36+81-2*6*9*0,5=63. 

2) Найдем площадь треугольника АВС:

S=(AB*AC*sin ∠A) :2=(6*9*sin 60) :2,

3) Найдем радиус описанной окружности:

Формула радиуса вписанной окружности около треугольника. Как найти радиус окружности

Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. {\circ}}

Используя радианную меру: CD = \alpha R

Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.

В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.

AN\cdot NB = CN \cdot ND

Касательная к окружности

Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.

Если же у прямой есть две общие точки, ее называют секущей .

Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.

Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.

AC = CB

Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.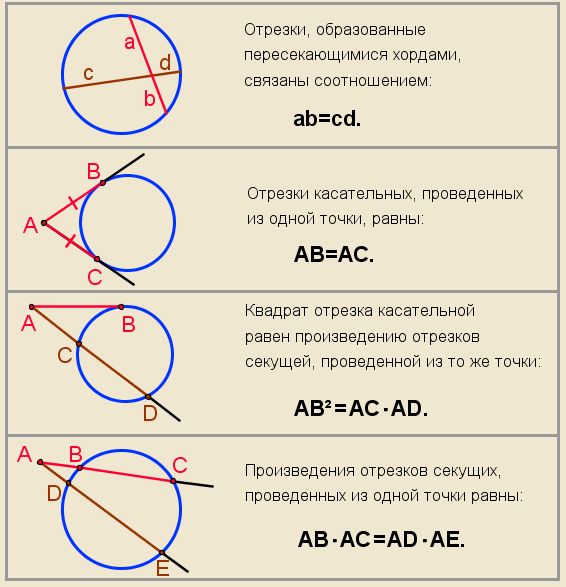 {\circ}

\angle ADB = \angle AEB = \angle AFB

На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.

Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.

\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)

Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.

\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)

Вписанная окружность

Вписанная окружность — это окружность, касающаяся сторон многоугольника.

В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.

Окружность может быть вписанной не в каждый многоугольник.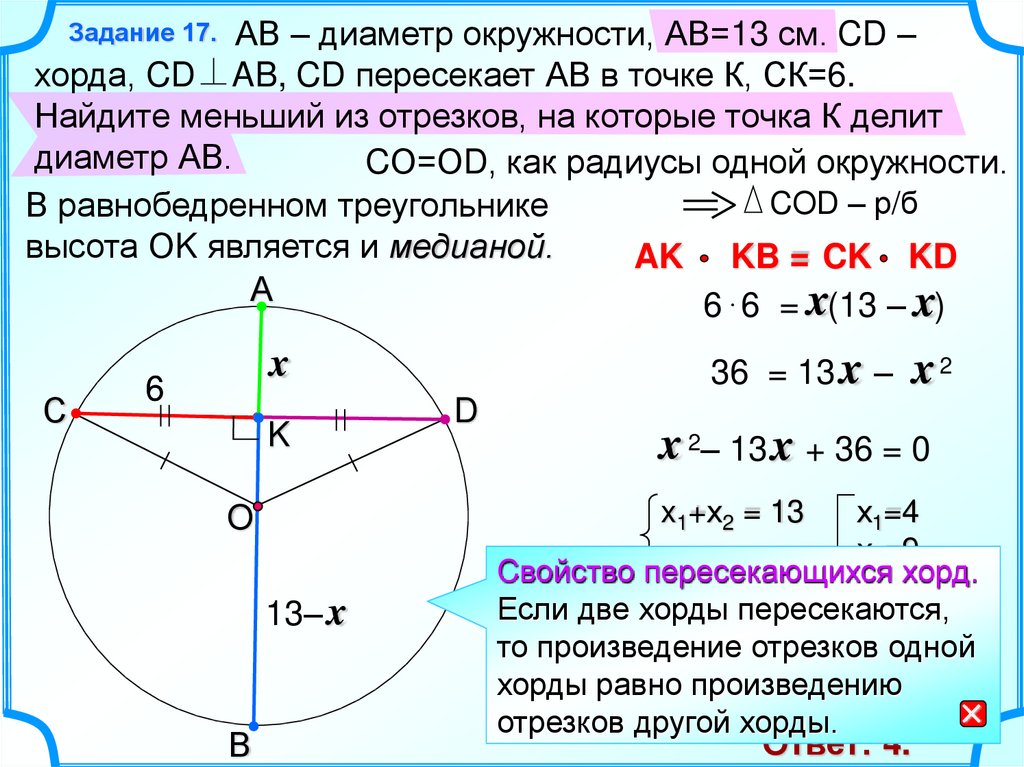

Площадь многоугольника с вписанной окружностью находится по формуле:

S = pr ,

p — полупериметр многоугольника,

r — радиус вписанной окружности.

Отсюда следует, что радиус вписанной окружности равен:

r = \frac{S}{p}

Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.

AB + DC = AD + BC

В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.

Радиус вписанной окружности вычисляется по формуле:

r = \frac{S}{p} ,

где p = \frac{a + b + c}{2}

Описанная окружность

Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника .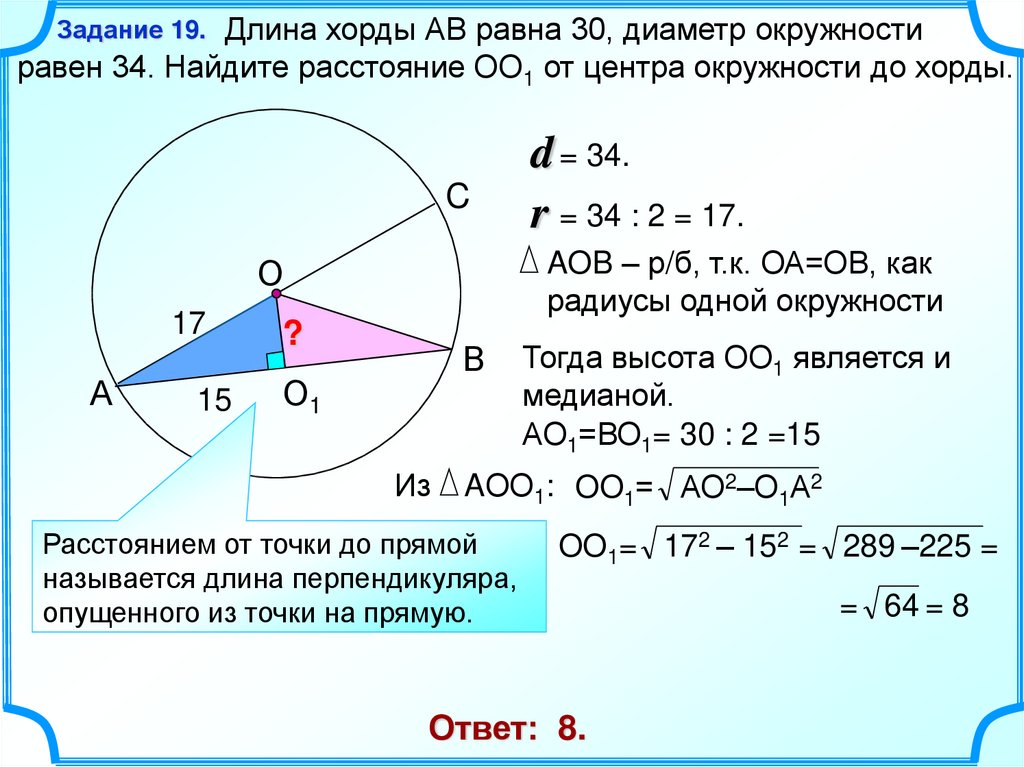 {\circ}

Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.

Радиус описанной окружности можно вычислить по формулам:

R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}

R = \frac{abc}{4 S}

a , b , c — длины сторон треугольника,

S — площадь треугольника.

Теорема Птолемея

Под конец, рассмотрим теорему Птолемея.

Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.

AC \cdot BD = AB \cdot CD + BC \cdot AD

МКОУ «Волчихинская СШ №2»

Учитель Бакута Е.П.

9 класс

Урок по теме «Формулы радиусов вписанных и описанных окружностей правильных многоугольников»

Цели урока:

Образовательные: изучение формул радиусов вписанных и описанных окружностей правильных многоугольников;

Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.

Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.

Оборудование: Мультимедийный компьютер, мультимедиапроектор, экспозиционный экран

Ход урок:

1. Организационный момент

Чтобы спорилось нужное дело,

А девизом нашего урока буду такие слова:

Думать — коллективно!

Решать — оперативно!

Отвечать — доказательно!

Бороться — старательно!

2. Мотивация урока.

3. Актуализация опорных знаний. Проверка д/з.

Фронтальный опрос:

Какая фигура называется многоугольником?

Какой многоугольник называется правильным?

Какое другое название правильного треугольника?

Какое другое название правильного четырехугольника?

Формула суммы углов выпуклого многоугольника.

Формула угла правильного многоугольника.

4. Изучение нового материала. (слайды)

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на окружности.

Окружность можно вписать или описать около любого треугольника, причём центр вписанной в треугольник окружности лежит на пересечении биссектрис треугольника, а центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров.

Около любого правильного многоугольника можно описать окружность, и в любой правильный многоугольник можно вписать окружность, причём центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Формулы для радиусов вписанных и описанных окружностей правильного треугольника, правильного четырехугольника, правильного шестиугольника.

Радиус вписанной окружности в правильный многоугольник (r):

a — сторона многоугольника, N — количество сторон многоугольника

Радиус описанной окружности правильного многоугольника(R):

a — сторона многоугольника, N — количество сторон многоугольника.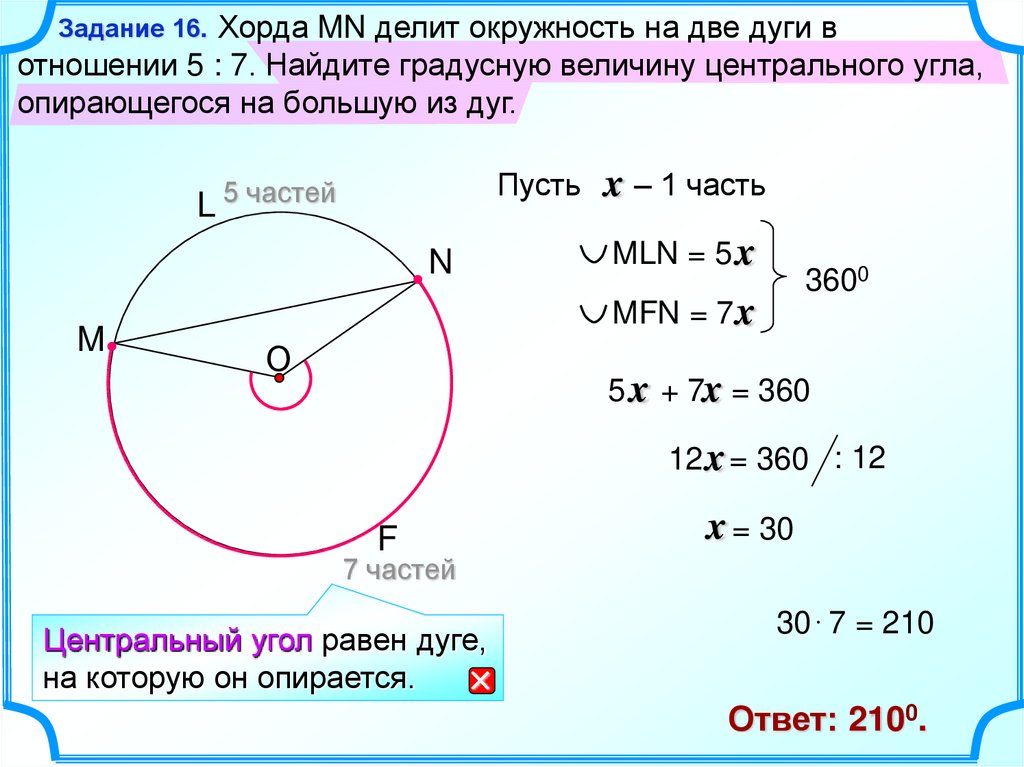

Заполним таблицу для правильного треугольника, правильного четырехугольника, правильного шестиугольника.

5. Закрепление нового материала.

Решить № 1088, 1090, 1092, 1099.

6. Физминутка . Раз – потянуться Два – нагнуться

Три – оглянуться Четыре – присест

Пять – руки вверх Шесть – вперед

Семь – опустили Восемь – сели

Девять – встали Десять – снова сели

7. Самостоятельная работа учащихся (работа в группах)

Решить № 1093.

8.Итоги урока. Рефлексия. Д/з.

Какое впечатление у Вас сложилось? (Понравилось – не понравилось)

– Какое настроение после урока? (Радостное – грустное)

– Какое самочувствие? (Устал – не устал)

– Какое отношение к пройденному материалу? (Понял – не понял)

– Какова твоя самооценка после урока? (Доволен – не доволен)

– Оцени свою активность на уроке. (Старался – не старался).

п.105-108 повторить;

выучить формулы;

№ 1090, 1091, 1087(3)

Есть у математики молва,

Что она в порядок ум приводит,

Потому хорошие слова

Часто говорят о ней в народе.

Ты нам, геометрия, даёшь

Для победы важную закалку.

Учится с тобою молодёжь

Развивать и волю, и смекалку.

Примечание Презентация содержит разделы:

Повторение теоретического материала

Проверка домашнего задания

Вывод основных формул, т.е. новый материал

Закрепление: решение задач в группах и самостоятельно

Просмотр содержимого презентации

«9_klass_pravilnye_mnogougolniki_urok_2»

• Чтобы спорилось нужное дело,
• Чтобы в жизни не знать неудач,
• В математики мир отправимся смело,
• В мир примеров и разных задач.

ДЕВИЗ УРОКА

Думать — коллективно!

Решать — оперативно!

Отвечать — доказательно!

Бороться — старательно!

И открытия нас ждут обязательно!

Повторение.

• Какая геометрическая фигура

изображена на рисунке?

D

Е

2. Какой многоугольник называется

правильным?

О

3.Какая окружность называется

вписанной в многоугольник?

F

С

4.Какая окружность называется

описанной около многоугольника?

5.Назовите радиус вписанной окружности.

А

В

Н

6.Назовите радиус описанной окружности.

7.Как найти центр вписанной в правильный

многоугольник окружности?

8.Как найти центр окружности описанной около

правильного многоугольника?

Проверка выполнения

домашнего задания ..

№ 1084.

β – угол, соответствующий

дуге, которую стягивает

сторона многоугольника .

О

А п

А 2

β

Ответы:

а) 6;

б) 12;

А

А 1

в) 4;

г) 8;

г) 10

д) 20;

е) 7.

е) 5.

ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК

Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

Сумма углов правильного n -угольника

Угол правильного n — угольника

Окружность называется вписанной в многоугольник,

если все стороны многоугольника касаются этой окружности.

Окружность называется описанной около многоугольника, если все его вершины лежат на этой

окружности.

Вписанная и описанная окружность

Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Выведем формулу радиуса вписанной и радиуса описанной окружности правильного многоугольника.

Пусть r – радиус вписанной окружности,

R – радиус описанной окружности,

п – количество сторон и углов многоугольника.

Рассмотрим правильный п-угольник.

Пусть а – сторона п-угольника,

α – угол.

Построим точку О – центр вписанной и описанной окружности.

ОС – высота ∆АОВ.

∟ С = 90 º — (по построению),

Рассмотрим ∆АОС:

∟ ОАС = α /2 — (ОА – биссектриса угла п- угольника),

АС = а/2 – (ОС – медиана к основанию равнобедренного треугольника),

∟ АОВ = 360 º: п,

пусть ∟АОС = β .

тогда β = 0,5 ∙ ∟АОВ

0,5 ∙ (360 º: п)

2 sin (180 º: п)

2 tg (180 º: п)

Площадь правильного многоугольника

Сторона правильного многоугольника

Радиус вписанной окружности

Группа 1 Дано: R , n =3 Найти: а

Группа 2 Дано: R , n =4 Найти: а

Группа 3 Дано: R , n =6 Найти: а

Группа 4 Дано: r , n =3 Найти: а

Группа 5 Дано: r , n = 4 Найти: а

Группа 6 Дано: r , n = 6 Найти: а

Группа 1 Дано: R , n =3 Найти: а

Группа 2 Дано: R , n =4 Найти: а

Группа 3 Дано: R , n =6 Найти: а

Группа 4 Дано: r , n =3 Найти: а

Группа 5 Дано: r , n = 4 Найти: а

Группа 6 Дано: r , n = 6 Найти: а

п = 3

п = 4

п = 6

2 tg (180 º: п)

2 sin (180 º: п)

тогда 180 º: п

У правильного треугольника п = 3,

откуда 2 sin 60 º =

тогда 180 º: п

У правильного четырехугольника п = 4,

откуда 2 sin 45 º =

У правильного шестиугольника п = 6,

тогда 180 º: п

откуда 2 sin 30 º =

Используя формулы радиусов вписанных и описанных окружностей некоторых правильных многоугольников, вывести формулы для нахождения зависимости сторон правильных многоугольников от радиусов вписанных и описанных окружностей и заполнить таблицу:

2 R ∙ sin (180 º: п)

2 r ∙ tg (180 º: п)

треугольник

шестиугольник

Пп. 105 – 108;

№ 1087;

№ 1088 – подготовить таблицу.

n = 4

R

r

a 4

P

2

6

4

S

28

16

3

3√2

24

32

2√2

4

16

16

16√2

32

4√2

2√2

7

3,5√2

3,5

49

4

2√2

16

2

№ 1087(5)

Дано: S=16 , n =4

Найти: a, r, R, P

Мы знаем формулы:

№ 1088( 5 )

Дано: P=6 , n = 3

Найти: R, a, r, S

Мы знаем формулы:

№ 108 9

Дано:

Найти:

Подведем итог

Мы знаем формулы:

• п. 105-108 повторить;
• выучить формулы;
• № 1090, 1091, 1087(3)

Окружность считается вписанной в границы правильного многоугольника, в случае, если лежит внутри него, касаясь при этом прямых, которые проходят через все стороны. Рассмотрим, как найти центр и радиус окружности. Центром окружности будет являться точка, в которой пересекаются биссектрисы углов многоугольника. Радиус рассчитывается: R=S/P; S – площадь многоугольника, Р – полупериметр окружности.

В треугольнике

В правильный треугольник вписывают лишь одну окружность, центр которой называется инцентром; он от всех сторон удалён на одинаковое расстояние и является местом пересечения биссектрис.

В четырёхугольнике

Часто приходится решать, как найти радиус вписанной окружности в эту геометрическую фигуру. Она должна быть выпуклой (если нет самопересечений). Окружность вписать в неё можно только в случае равенства сумм противоположных сторон: AB+CD=BC+AD.

При этом центр вписанной окружности, середины диагоналей, расположены на одной прямой (согласно теореме Ньютона). Отрезок, концы которого находятся там, где пересекаются противоположные стороны правильного четырёхугольника, лежит на этой же прямой, называемой прямой Гаусса. Центром окружности будет точка, в которой пересекаются высоты треугольника с вершинами, диагоналями (по теореме Брокара).

В ромбе

Им считается параллелограмм с одинаковой длиной сторон. Радиус окружности, вписываемой в него, можно рассчитать несколькими способами.

1. Чтобы сделать это правильно, найдите радиус вписанной окружности ромба, если известна площадь ромба, длина его стороны. Применяется формула r=S/(2Хa). К примеру, если площадь ромба составляет 200 мм кв., длина стороны 20 мм, то R=200/(2Х20), то есть, 5 мм.
2. Известен острый угол одной из вершин. Тогда необходимо использовать формулоу r=v(S*sin(α)/4). Например, при площади в 150 мм и известном угле в 25 градусов, R= v(150*sin(25°)/4) ≈ v(150*0,423/4) ≈ v15,8625 ≈ 3,983 мм.
3. Все углы в ромбе равны. В этой ситуации радиус окружности, вписанной в ромб, будет равен половине длины одной стороны данной фигуры. Если рассуждать по Евклиду, утверждающего, что сумма углов всякого четырёхугольника равна 360 градусов, то один угол будет равен 90 градусам; т.е. получится квадрат.

Рассмотрим окружность, вписанную в треугольник (рис. 302). Напомним, что ее центр О помещается на пересечении биссектрис внутренних углрв треугольника. Отрезки ОА, ОВ, ОС, соединяющие О с вершинами треугольника ABC, разобьют треугольник на три треугольника:

АОВ, ВОС, СОА. Высота каждого из этих треугольников равна радиусу , и потому их площади выразятся как

Площадь всего треугольника S равна сумме этих трех площадей:

где — полупериметр треугольника. Отсюда

Радиус вписанной окружности равен отношению площади треугольника к его полупериметру.

Для получения формулы для радиуса описанной окружности треугольника докажем следующее предложение.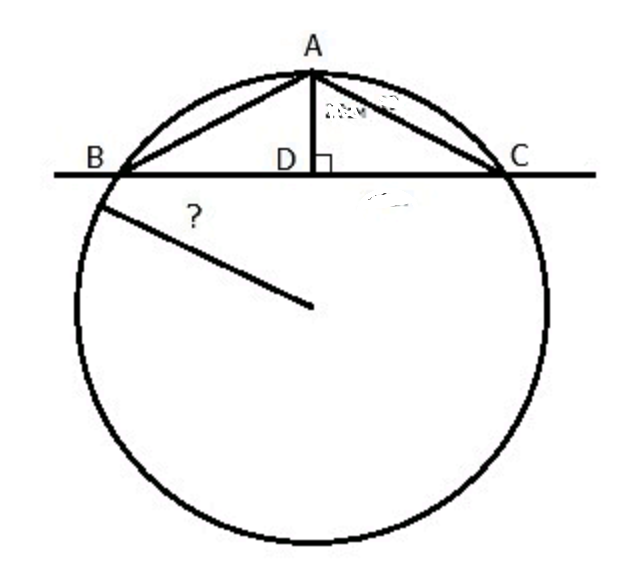

Теорем а: В любом треугольнике сторона равна диаметру описанной окружности, умноженному на синус противолежащего угла.

Доказательство. Рассмотрим произвольный треугольник ABC и описанную вокруг него окружность, радиус которой обозначим через R (рис. 303). Пусть А — острый угол треугольника. Проведем радиусы ОВ, ОС окружности и опустим из ее центра О перпендикуляр ОК на сторону ВС треугольника. Заметим, что угол а треугольника измеряется половиной дуги ВС, для которой угол ВОС является центральным углом. Отсюда видно, что . Поэтому из прямоугольного треугольника СОК находим , или , что и требовалось доказать.

Приведенный рис. 303 и рассуждение относятся к случаю острого угла треугольника; нетрудно было бы провести доказательство и для случаев прямого и тупого угла (читатель это проделает самостоятельно), но можно использовать теорему синусов (218.3). Так как должно быть откуда

Теорему синусов записывают также в. виде

и сравнение с формой записи (218. 3) дает для

Радиус описанной окружности равен отношению произведения трех сторон треугольника к его учетверенной площади.

Задача. Найти стороны равнобедренного треугольника, если его вписанная и описанная окружности имеют соответственно радиусы

Решение. Напишем формулы, выражающие радиусы вписанной и описанной окружностей треугольника:

Для равнобедренного треугольника с боковой стороной и основанием площадь выражается формулой

или, сократив дробь на отличный от нуля множитель , будем иметь

что приводит к квадратному уравнению относительно

Оно имеет два решения:

Подставив вместо его выражения в любое из уравнений для или R, найдем окончательно два ответа к нашей задаче:

Упражнения

1. Высота прямоугольного треугольника, проведенная из вершины прямого угла, делнт гипотенузу в отношении Найти отношение каждого из катетов к гипотенузе.

2. Основания равнобедренной трапеции, описанной около окружности, равны а и b. Найти радиус окружности.

3. Две окружности касаются внешним образом. Их общие касательные наклонены к линии центров под углом 30°. Длина отрезка касательной между точками касания равна 108 см. Найти радиусы окружностей.

4. Катеты прямоугольного треугольника равны а и b. Найти площадь треугольника, сторонами которого служат высота и медиана данного треугольника, проведенные из вершины прямого угла, и отрезок гипотенузы между точками их пересечения с гипотенузой.

5. Стороны треугольника равны 13, 14, 15. Найти проекцию каждой из них на две остальные.

6. В треугольнике известны сторона и высоты Найти стороны b и с.

7. Известны две стороны треугольника и медиана Найти третью сторону треугольника.

8. Даны две стороны треугольника и угол а между ними: Найти радиусы вписанной и описанной окружностей.

9. Известны стороны треугольника а, b, с. Чему равны отрезки, на которые они разбиваются точками касания вписанной окружности со сторонами треугольника?

Окружность вписана в треугольник.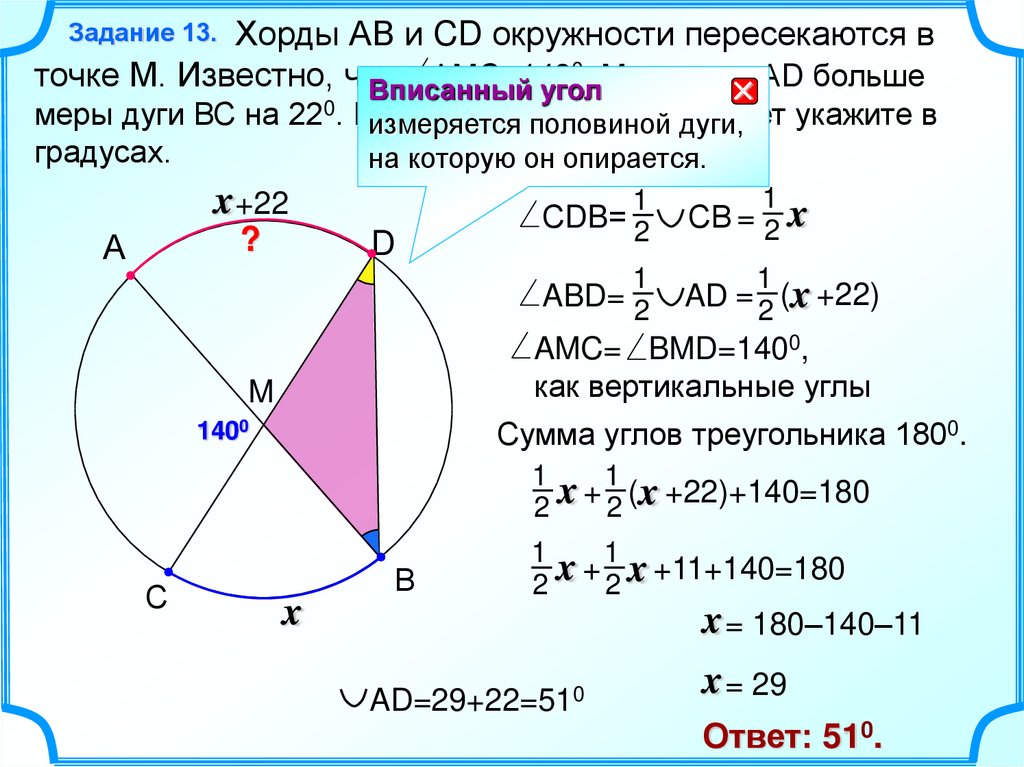 В данной статье собрал для вас задачи, в которых даётся треугольник с вписанной в него или описанной около него окружностью. В условии ставится вопрос о нахождении радиуса окружности или стороны треугольника.

Данные задания удобно решать используя представленные формулы. Рекомендую их выучить, бывают очень полезны не только при решении этого типа заданий. Одна формула выражает связь радиуса вписанной в треугольник окружности с его сторонами и площадью, другая радиус описанной около треугольника окружности также с его сторонами и площадью:

S – площадь треугольника

Рассмотрим задачи:

27900. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120 0 . Найдите диаметр описанной окружности этого треугольника.

Здесь окружность описана около треугольника.

Первый способ:

Диаметр мы сможем найти, если будет известен радиус. Используем формулу радиуса описанной около треугольника окружности:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны нам известны (боковые стороны равнобедренного треугольника), третью мы можем вычислить используя теорему косинусов:

Теперь вычислим площадь треугольника:

*Использовали формулу (2) из .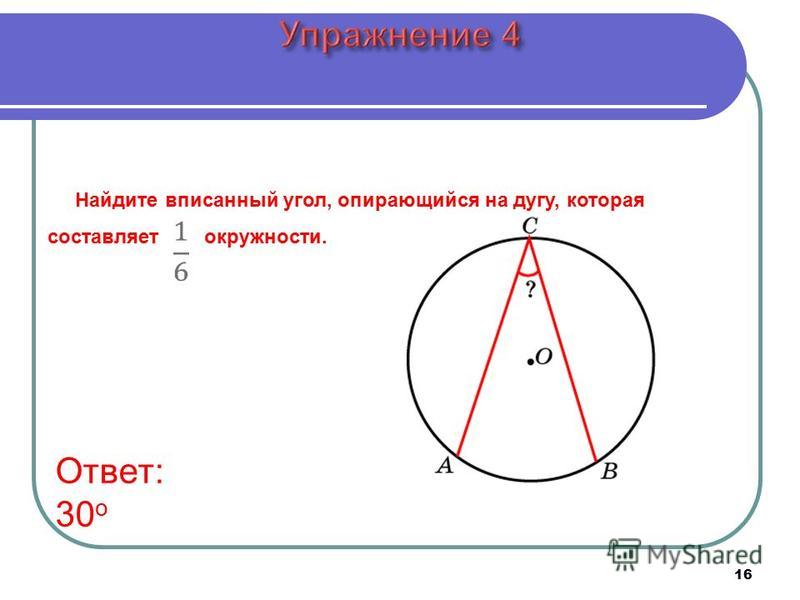

Вычисляем радиус:

Таким образом диаметр будет равен 2.

Второй способ:

Это устные вычисления. Для тех кто имеет навык решения заданий с вписанным в окружность шестиугольником, тот сразу определит, что стороны треугольника АС и ВС «совпадают» со сторонами вписанного в окружность шестиугольника (угол шестиугольника как раз равен 120 0 , как и в условии задачи). А далее на основании того, что сторона вписанного в окружность шестиугольника равна радиусу этой окружности не сложно сделать вывод о том, что диаметр будет равен 2АС, то есть двум.

Подробнее о шестиугольнике посмотрите информацию в (п.5).

Ответ: 2

27931. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите .

где a, b, c – стороны треугольника

S – площадь треугольника

Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:

А площадь треугольника будет равна 0,5х 2 .

Значит

Таким образом, гипотенуза будет равна:

В ответе требуется записать:

Ответ: 4

27933. В треугольнике ABC АС = 4, ВС = 3, угол C равен 90 0 . Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.

По теореме Пифагора:

Найдём площадь:

Таким образом:

Ответ: 1

27934. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:

Тогда

Таким образом:

Ответ: 1,5

27624. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. Посмотреть решение

27932. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Небольшой итог.

Если в условии дан треугольник и вписанная или описанная окружность, и речь идёт о сторонах, площади, радиусе, то сразу вспомните об указанных формулах и пробуйте использовать их при решении. Если не получается, то тогда уже ищите другие способы решения.

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Как найти длину хорды

Все математические ресурсы верхнего уровня ISEE

6 Диагностические тесты 244 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Справка по математике верхнего уровня ISEE » Геометрия » Плоская геометрия » Круги » Аккорды » Как найти длину хорды

Какое уравнение является формулой для длины хорды?

Примечание: это радиус окружности, а   это угол, разделенный хордой.

Возможные ответы:

Правильный ответ:

Объяснение:

Длина хорды окружности рассчитывается следующим образом:

 Длина хорды = 

Сообщить об ошибке

Радиус окружности равен , а расстояние по перпендикуляру от хорды до центра окружности равно . Укажите длину хорды.

Возможные ответы:

Правильный ответ:

Объяснение:

Длина хорды = , где   — радиус окружности, а   — расстояние по перпендикуляру от хорды до центра окружности.

Длина хорды =

Длина хорды =

Сообщить об ошибке

В круге ниже радиус равен , а длина хорды . Укажите перпендикулярное расстояние от хорды до центра окружности (d).

 

 

Возможные ответы:

Правильный ответ:

 

5 Объяснение:

Длина хорды = , где   — радиус окружности, а   — расстояние по перпендикуляру от хорды до центра окружности.

 

Длина хорды =  

Сообщить об ошибке

Укажите длину хорды центрального угла окружности радиусом 18,9.0005

Возможные ответы:

Правильный ответ:

Объяснение:

На рисунке ниже показано , что соответствует этому описанию, вместе с его хордой :

С помощью теоремы о равнобедренном треугольнике можно доказать, что треугольник 45-45-90 с катетами длины 18, поэтому его гипотенуза — желаемая длина хорды  — в раз больше или .

Сообщить об ошибке

Центральный угол окружности пересекает дугу длины; у него тоже есть аккорд. Какова длина этой хорды?

Возможные ответы:

Правильный ответ:

Объяснение:

Дуга, пересекаемая центральным углом, является дугой окружности, поэтому длина окружности равна . Радиус – это длина окружности, разделенная на  или .

На рисунке ниже показан центральный угол вместе с его хордой:

По теореме о равнобедренном треугольнике может быть доказано, что угол равносторонний, поэтому .

Сообщить об ошибке

Центральный угол окружности пересекает дугу длины; у него тоже есть аккорд. Какова длина этой хорды?

Возможные ответы:

Правильный ответ:

Объяснение:

Дуга, пересекаемая центральным углом, является дугой окружности, поэтому длина окружности равна . Радиус – это длина окружности, разделенная на  или .

На рисунке ниже показан центральный угол вместе с его хордой и биссектрисой треугольника.

Мы сосредоточимся на треугольнике 30-60-90. По теореме 30-60-90

и

 являются серединой , поэтому

Сообщить об ошибке

Укажите длину хорды окружности с центральным углом 2.

Возможные ответы:

Правильный ответ отсутствует среди других вариантов.

Правильный ответ:

Правильный ответ отсутствует среди других вариантов.

Объяснение:

На рисунке ниже показано , что соответствует этому описанию, вместе с его хордой :

С помощью теоремы о равнобедренном треугольнике можно доказать, что оно равностороннее, поэтому .

Этот ответ отсутствует среди предложенных вариантов.

Сообщить об ошибке

Укажите длину хорды центрального угла окружности радиусом .

Возможные ответы:

Правильный ответ:

Объяснение:

На рисунке ниже показано , соответствующее этому описанию, вместе с его хордой и биссектрисой треугольника .

Мы сосредоточимся на треугольнике 30-60-90. По теореме 30-60-90

и

 являются серединой , поэтому

Сообщить об ошибке

Рисунок НЕ выполнен в масштабе

На рисунке выше оцените .

Возможные ответы:

Правильный ответ:

Пояснение:

Если две хорды окружности пересекаются внутри окружности, произведение длин частей каждой хорды одинаково. Другими словами,

Решение для — распределить:

Вычесть из обеих сторон:

Разделите обе части на 20:

Сообщить об ошибке

На приведенном выше рисунке – это касательная к окружности.

Оценить .

Возможные ответы:

Правильный ответ:

Объяснение:

Если секущий отрезок и касательный отрезок строятся к окружности из точки вне ее, квадрат расстояния до окружности по касательной равен произведению расстояний до двух точек на окружности вдоль секущая; другими словами,

Решение для:

Упрощение радикала с использованием принципа продукта радикалов и отмечая, что 36 является наибольшим идеальным квадратным фактором 360:

Сообщение о ошибке

← Предыдущий 1 2 Далее →

Уведомление об авторских правах

Все математические ресурсы верхнего уровня ISEE

6 Диагностические тесты 244 практических теста Вопрос дня Карточки Учитесь по концепции

Видео-вопрос: Нахождение расстояния между хордой и центром окружности

Стенограмма видео

Предположим, что окружность диаметром 15 сантиметров содержит хорду длиной 11,8 сантиметра. Каково кратчайшее расстояние между хордой и центром окружности? Дайте ответ в сантиметрах с точностью до сотых.

Мы часто обнаруживаем, что такие вопросы намного легче решать, если мы начнем с наброска информации. Мы знаем, что окружность имеет диаметр 15 сантиметров, и начертим хорду 11,8 сантиметра. Хорда определяется как отрезок, соединяющий две различные точки на окружности. Нас просят найти кратчайшее расстояние между хордой и центром окружности.

Мы могли бы вычислить расстояние от любой точки этой хорды до центра окружности, но есть только одно место, которое было бы кратчайшим расстоянием. И это точка, где есть перпендикулярная линия от центра к хорде. Это расстояние, которое нам нужно рассчитать, поэтому давайте определим его как 𝑥 сантиметров. У нас все еще недостаточно информации, чтобы определить значение 𝑥. Итак, мы должны применить одно из известных нам свойств хорды и линии, проходящей через центр окружности.

Это свойство говорит нам, что если у нас есть окружность с центром 𝐴, содержащая хорду отрезка 𝐵𝐶, то прямая, проходящая через 𝐴 и перпендикулярная отрезку 𝐵𝐶, также делит пополам отрезок 𝐵𝐶. Здесь это означает, что эта линия, идущая из центра и перпендикулярная хорде, также делит хорду пополам. Итак, хорда разбита на два отрезка, которые конгруэнтны. Итак, если мы хотим определить длину одного из этих отрезков, она будет равна половине длины хорды. 11,8 разделить на два будет 5,9сантиметры. Итак, мы знаем, что длина этой половины хорды равна 5,9 сантиметра.

Последняя часть этой задачи заключается в том, чтобы признать, что мы можем создать прямоугольный треугольник. Этот отрезок, который образует гипотенузу прямоугольного треугольника, на самом деле является радиусом круга, потому что это отрезок от центра до точки на окружности. Итак, здесь мы можем применить информацию о том, что диаметр равен 15 сантиметрам. Радиус можно найти, вычислив половину диаметра. Итак, 15 разделить на два даст нам 7,5, а единицами измерения, разумеется, все равно будут сантиметры.

Теперь у нас есть прямоугольный треугольник с двумя известными длинами и одной неизвестной. А это значит, что мы можем применить теорему Пифагора.