Как построить на координатной плоскости рисунок: Рисуем по координатам. Рисунки и фигуры

Рисунки по координатам на координатной плоскости 6-7 класс математика | Методическая разработка по математике (6 класс):

Слоник 1

(-1; 4), (-2; 1), (-3; 2), (-4; 2), (-4; 3), (-6; 4), (-6; 6), (-8; 9), (-7; 10), (-6; 10), (-6; 11), (-5; 10), (-4; 10), (-3; 9), (-1; 9,5), (1; 9), (3; 10), (4; 11), (4; 16), (3; 18), (5; 17), (6; 17), (5; 16), (6; 12), (6; 9), (4; 7), (1; 6),

(2; 5), (5; 4), (5; 3), (4; 4), (1; 2), (1; 0), (3; -4), (4; -5), (1;-7), (1; -6), (0; -4), (-2; -7), (-1,5; -8), (-5; -7), (-4; -6), (-5; -4), (-7;-5), (-7; -7), (-6,5; -8), (-10,5; -8), (-10; -7), (-10; -6), (-11; -7),

(-11; -8), (-14; -6), (-13; -5), (-12; -3), (-13; -2), (-14; -3), (-12; 1), (-10; 3), (-8; 3), (-6; 4), глаз (-1; 7).

Верблюд

(-10; -2), (-11; -3), (-10,5; -5), (-11; -7), (-12; -10), (-11; -13), (-13; -13), (-13,5; -7,5), (-13; -7), (-12,5; -5), (-13; -3), (-14; -1), (-14; 4), (-15; -6), (-15; -3), (-14; 2), (-11; 4), (-10; 8), (-8; 9),

(-6; 8), (-5; 5), (-3;8),(-1;9), (0;8), (0,5;6), (0,5;4), (3;2,5), (4;3), (5;4), (6;6), (8;7), (9,5;7), (10;6), (11,5;5,5), (12;5), (12;4,5), (11;5), (12;4), (11;4), (10;3,5), (10,5;1,5), (10;0), (6;-3),

(2;-5), (1,5;-7), (1,5;-11), (2,5;-13), (1;-13), (0;-5), (-0,5;-11), (0;-13), (-1,5;-13), (-1,5;-7),

(-2;-5), (-3;-4), (-5;-4,5), (-7;4,5), (-9;-5), (-10;-6), (-9;-12), (-8,5;-13), (-10,5;-13), (-10;-9,5), (-11;-7), глаз (8,5;5,5)

Медведь 1

(4;-4), (4;-6), (8,5;-7,5), (9;-7), (9;-6), (9,5;-5), (9,5;-3,5), (10;-3), (9,5;-2,5), (4;5), (3;6), (2;6), (0;5),(-3;5), (-7;3), (-9;-1), (-8;-5), (-8;-7), (-4,5;-8), (-4,5;-7), (-5;-6,5), (-5;-6), (-4,5;-5), (-4;-5), (-4;-7), (-1;-7),(-1;-6), (-2;-6), (-1;-4), (1;-8), (3;-8), (3;-7), (2;-7), (2;-6), (3;-5), (3;-6), (5;-7),

(7;-7), ухо (6;-4), (6;-3), (7;-2,5), (7,5;-3), глаз (8;-6)

Лось

(-2;2), (-2;-4), (-3;-7), (-1;-7), (1;4), (2;3), (5;3), (7;5), (8;3), (8;-3), (6;-7), (8;-7), (10;-2), (10;1), (11;2,5),(11;0), (12;-2), (9;-7), (11;-7), (14;-2), (13;0), (13;5), (14;6), (11;11), (6;12), (3;12), (1;13), (-3;13), (-4;15),(-5;13), (-7;15), (-8;13), (-10;14), (-9;11), (-12;10), (-13;9), (-12;8),

(-11;9), (-12;8), (-11;8), (-10;7), (-9;8),(-8;7), (-7;8), (-7;7), (-6;7), (-4;5), (-4;-4), (-6;-7), (-4;-7), (-2;-4), глаз (-7;11)

Зайчонок

(5;1), (6;2), (6;3), (5;6), (4;7), (5;8), (6;8), (8;9), (9;9), (7;8), (9;8), (6;7), (7;6), (9;6), (11;5), (12;3), (12;2), (13;3), (12;1), (7;1), (8;2), (9;2), (8;3), (6;1), (5;1) и (5;7).

Лиса 1

(0,5;0), (1;2), (1;3), (2;4), (3;3,5), (3,5;4), (2,5;5), (2,5;6), (2;6,5), (2;8,5), (1;7), (0,5;6,5),

(-0,5;7), (-0,5;6), (-1;5,5), (-3;3), (-4;1), (-4,5;-1,5), (-4;-2,5), (-4,5;-3,5), (-3,5;-5), (-1;-6), (1;-7), (2;-8), (3,5;-10), (4,5;-9),(4,5;-7), (4;-6), (3;-5), (0;-4,5), (1;-1,5), (0,5;0).

Собака 1.

(1;-3), (2;-3), (3;-2), (3;3), (4;3), (5;4), (5;6), (4;7), (3;7), (2;6), (3;5), (3;5,5), (4;5), (3;4), (2;5), (-3;5),

(-4;6), (-4;9), (-5;10), (-5;11), (-6;10), (-7;10), (-7;10), (-7;8), (-9;8), (-9;7), (-8;6), (-6;6), (-7;3), (-6;2), (-6;-1), ў(-7;-2), (-7;-3), (-6;-3), (-4;-2), (-4;2), (1;2), (2;-1), (1;-2), (1;-3)

Лиса 2

(7,5;5), (-4;7), (-3;7), (-3;9), (1;1), (3;0), (5;-0,5), (7;-4), (7;-8), (10;-5), (13;-3), (17;-2), (19;-2), (17;-3), (14;-7), (7;-9), (6;-10), (2;-10), (2;-9), (5;-9), (3;-8), (1,5;-6), (0,5;-3),(0,5;-10),(-2,5;10), (-2,5;-9), (-1;-9), (-1;-3), (-3;-10), (-6;-10), (-6;-9), (-4,5;-9), (-3;-4), (-3;0,5), (-4;3), (-5;3),

(-7,5;4), (-7,5;5)

Собака 2.

а) (14;-3), (12;-3), (8,5;-2), (4;3), (2;4), (1;5), (1;8), (-2;5), (-3;5), (-6;3), (-7;1), (-11;-1), (-10;-3), (-6;-4), (-2;-4), (-1;-3), (1;-5), (1;-8), (-2;-10), (-11;-10), (-13;-11), (-13;-13), (4;-13), (5;-12),

(9;-12)

б) (14;-10), (10;-10), (9;-11), (9;-13), (14;-13)

Медведь 2

(-18;4), (-18;3), (-17;3), (-18;2), (-17;2), (-11;1), (-9;0), (-8;-1), (-11;-6), (-12;-8), (-14;-10),

(-10;-10), (-8;-6), (-5;-4), (-4;-7), (-4;-8), (-6;-10), (-1;-10), (-1;-2), (1;-4), (5;-4), (5;-8), (3;-10), (8;-10), (10;-4), (12;-6), (10;-8), (15;-8), (14;-2), (15;2), (14;6), (12;8), (8,9), (4;9), (0;8), (-6;9), (-11;7), (-15;6), (-18;4)

Воробей

(-6;1), (-5;-2), (-9;-7), (-9;-8), (-5;-8), (-1;-5), (3;-4), (5;-1), (8;1), (9;3), (2;2), (4;6), (3;11), (2;11), (-2;6), (-2;2), (-4;4), (-5;4), (-6;3), (-6;2), (-7;2), (-6;1)

Ёжик

(2;-1), (3,5;0,5), (4;-1), (5;0), (4;2), (2;1), (2;3), (4;5), (4;6), (2;5), (1;7), (1;8), (0;7), (0;9), (-1;7), (-2;8),(-2;7), (-3;7), (-2;6), (-4;6), (-3;5), (-4;5), (-3;4), (-5;4), (-4;3), (-5;3), (-4;2), (-6;2), (-5;1), (-6;1), (-5;0),(-6;0), (-5;-1), (-6;-2), (-4;-2), (-5;-3), (-3;-4), (-4;-5), (-2;-5), (-1;-6), (3;-6), (3;-5), (1;-5), (1;-4), (2;-3), (2;-1)

Заяц

(-14;2), (-12;4), (-10;5), (-8;10), (-7;11), (-8;5), (-7;4), (-5;1), (-3;1,5), (3;0), (8;1), (10;0), (11;2), (12;1), (12;0), (11,5;-1), (13;-5), (14;-4,5), (15;-9), (15;-11), (13,5;-6,5), (11;-8), (8;-5), (-1;-7),

(-5;-6), (-7;-7), (-9;-7), (-11;-6,5), (-13;-7), (-15;-6), (-12;-5,5), (-9;-6), (-11;-1), (-13;0), (-14;2).

Голубь

(-4;8), (-5;7), (-5;6), (-6;5), (-5;5), (-5;4), (-7;0), (-5;-5), (-1;-7), (3;-7), (9;-2), (13;-2), (14;-1), (6;1),(8;4), (15;7), (3;8), (2;7), (0;3), (-1;3), (-2;4), (-1;6), (-2;8), (-4;8)

Снегирь

(5;-2), (0;3), (-1;3), (-1,5;2,5), (-1;2), (-1;0), (0;-1), (2;-1,5), (3,5;-1,5), (5;-2)

Ландыш

(6,5;12), (6,75;11,5), (7;10,5), (6,5;10), (6,25;11), (6;10,5), (6,25;11,5), (6,5;12), (6,5;12,5), (5;10,5), (6;9,5)(6,5;8), (5,75;8,5), (5,5;7,5), (5,25;8,5), (4,5;8), (5;9,5), (5,5;10), (5;10,5), (3;8), (3,5;8),(4,5;7), (4,5;6,5),(5;5,5), (4,25;6), (4;5), (3,75;6), (3;5,5), (3,5;6,5), (3,5;7), (4;7,5), (3,5;8), (3;8), (1,5;6), (3;4,5), (3,5;3), (2,75;3,5), (2,5;2,5), (2,25;3,5), (1,5;3), (2;4,5), (2,5;5), (1,5;6), (0,5;0), (0,5;1,5), (1,5;7,5), (0,5;10,5), (-1,5;13), (-3;10,5), (-4;6), (-3,5;4), (0,5;0), (0;-3).

Машина

(-3,5;0,5), (-2,5;0,5), (-1,5;3,5), (0,5;3,5), (0,5;-0,5), (1;-0,5), (1;0), (1,5;0), (5,5;4), (5,75;4), (6,75;5), (5,5;5), (5,5;8), (8,5;5), (7,25;5), (6,25;4), (6,5;4), (4,5;2), (6;0) (6,5;0), (6,5;-1. 5),

(6;-1,5), (6;-2), (5,5;-2,5), (4,5;-2,5),(4;-2), (4;-1,5), (0;-1,5), (0;-2), (-0,5;-2,5),

(-1.5;-2,5),

(-2;-2), (-2;-1.5), (-3,5;-1.5), (-3,5;0,5).

Кошечка

(-2;-7), (-4;-7), (-3;-5), (-6;-2), (-7;-3), (-7;6), (-6;5), (-4;5), (-3;6), (-3;3), (-4;2), (-3;1), (-1;3), (1;3), (4;1), (4;2), (3;6), (4;7), (5;7), (6;6), (5;1), (5;-5), (6;-6), (5;-7), (3;-7), (4;-5), (2;-3), (2;-2), (1;-1), (-1;-1),(-2;-2),(-1;-6), (-2;-7)

усы 1) (-9;5), (-5;3), (-2;2).

2) (-2;3), (-8;3),      3) (-9;2), (-5;3), (-1;5)   глаза (-6;4) и (-4;4).

Рыбка

(-4;2), (-3;4), (2;4), (3;3), (5;2), (7;0), (5;-2), (3;-2), (2;-4), (0;-4), (-1;-2), (-5;0), (-7;-2), (-8;-1), (-7;1), (-8;3), (-7;4), (-5;2), (-2;2), (0;3), (3;3) и глаз (5;0).

Мышонок

(-6;-5), (-4,5;-4,5), (-3;-3,5), (-1,5;-2), (-2;1), (-2;0), (-1,5;1), (-1;1,5), (0,2), (0,5;2), (0,5;1,5), (0,5;2,5), (1;2,5), (1;2), (1,5;2), (2,5;1,5), (2,5;1), (1,5;1), (1,5;0,5), (2;0,5), (1,5;0), (1;0),

(0,5;-1), (0;-1,5), (1;-1,5), (0;-2), (-1,5;-2), глаз (1,5;1,5).

Лебедь

(2;12), (2;13), (3;13,5), (4;13,5), (5;13), (3;4), (8;4), (6;1), (3;1), (2;2), (2;4), (4;11), (4;12,5), (3,5;12,5), (2;11), (2;12), (3;12), и (3;3), (4;2), (6;2), и (2,5;12,5).

Петух

( 1,5;5.5), ( 2,5;3,5), (2; 3), (2,5; 3), (3; 3,5), (3;4,5), (2,5;5,5), (3,5;6), (2,5;6,5), (3;7), (2,5;7), (2,5;7), (2;7)(2;8), (1,5;7), (1,5;8,5), (1;7), (1;6,5), (0,5;6), (0,5;5), (-0,5;4), (-2,5;3), (-4,5;4),

(-5;5), (-4,5;6), (-5,5;8), (-6,5;8,5), (-7,5;8), (-8,5;7), (-9;6), (-9;4), (-8,5;2,5), (-8,5;1), (-8;0),

(-8;1), (-7,5;0,5), (-7,5;2), (-7;0,5), (-6,5;1,5), (-5,5;0,5), (-4,5;0), (-3,5;-2,5), (-3;-3), (-3;-5,5),

(-4;-5,5), (-3;-6), (-2;-6), (-2,5;-5,5), (-2,5;-4), (0;-1), (0;-0,5), (1;0), (2,5;1,5), (2,5;2,5), (2;3) и (-0,5;3), (-0,5;2,5), (-1,5;1), (-2,5;1), (-5;2,5), (-4,5;3), (-5;3,5), (-4,5;3,5)и (1,5;6,5).

Птенчик

(-1;-7), (-2;-8), (-5;-8), (-6;-7), (-5;-5), (-6;-5), (-7;-4), (-7,5;-4), (-8;-5), (-10;-6), (-9;-5), (-8;-3), (-9;-4), (-11;-5), (-9;-3), (-11;-4), (-9;-2), (-9;0), (-7;2), (-5;3), (-1,5;3), (-1,5;6), (-1;7), (1;8), (2;8), (4;10), (3;8), (3;7), (5;9), (4;7), (4,5;6), (4,5;4), (3;2), (2,5;1), (2,5;-2), (2;-3), (1;-4),

(-1;-5), (-2;-5), (-2;-5,5), (-1;-6), (1;-6), (0;-7), (-3;-7), (-3;-5), (-4;-5), (-4,5;-6), (-3;-7) и глаз (1,5;7).

Дельфин(-7;-2), (-3;4), (-1;4), (2;7), (2;4), (5;4), (9;-5), (10;-9), (8;-8), (5;-10)

, (7;-5), (3;-2), (-7;-2).ю ласт (0;0), (0;2),(2;1), (3;0), (0;0) и глаз (-4;0), (-4;1), (-3;1), (-3;0), (-4;0).

Петушок-золотой гребешок

(1;-5), (2;-4), (2;-1), (1;-1), (-4;4), (-4;8), (-5;9), (-7;9), (-4;11), (-5;12), (-5;13), (-4;12), (-3;13), (-2;12), (-1;13), (-1;12), (-2;11), (-1;10), (-2;6), (-1;5), (4;5), (1;10), (4;13), (8;13), (9;10), (7;11), (9;8), (7;8), (9;6), (8;6), (3;-1), (3;-4), (4;-5), (1;-5) соединить (-4;11) и (-2;11), глаз (-4;10), крыло (0;1), (0;3), (1;4), (2;4), (4;1), (2;1), (0;1).

Слоник 2

(-6;-1), (-5;-4), (-2;-6), (-1;-4), (0;-5), (1;-5), (3;-7), (2;-8), (0;-8), (0;-9), (3;-9), (4;-8), (4;-4),

(5;-6), (8;-4), (8;0), (6;2), (4;1), (0;1), (-2;2), (-6;-1), (-10;-2), (-13;-4), (-14;-7), (-16;-9),

(-13;-7), (-12;-10), (-13;-14),(-10;-14), (-10;-13), (-9;-13), (-10;-9), (-5;-9), (-5;-15), (-2;-15),

(-2;-13). (-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11), (2;-9) и глазки (0;-2) и (4;-2)

Слоник 3

(0;7), (4;8), (6;7), (8;6), (7;7), (6;9), (5;11), (5;12), (6;11), (7;12), (7;10), (10;7), (10;5), (8;3), (6;3), (7;2), (9;2), (9;1), (8;1), (7;0), (6;0), (7;-2), (8;-3), (8;-4), (10;-7,5), (9;-8), (7,5;-8), (7;-6), (5;-5), (6;-7), (4,5;-8), (4;-9), (2;-7), (3;-6), (2;-5) (1;-5,5), (0;-7), (0;-9), (-2;-10), (-3;-9,5), (-3,5;-8), (-5;-10), (-6,5;-9), (-7;-7), (-6;-7), (-5;-5), (-6;-3), (-8;-4), (-6;0), (-4;1), (-3;3), (-3;5), (-4,5;6), (-5; 7,5), (-3; 7,5), (-2;7), (-2;8), (0;7) и глаз (5;5)

Звезда

(-9;2), (-3;3), (0;8), (3;3), (9;2), (5;-3), (6;-9), (0;-7), (-6;-9), (-5;-3), (-9;2).

Рисунок по точкам с координатами

Рисунки по координатам с координатами

Рисунки на координатной плоскости

Система координат на плоскости рисунки

Декартова система координат на плоскости рисунки

Фигуры по точкам в системе координат

Построение фигур по точкам

Рисунки на координатной плоск

Декартова система координат на плоскости рисунки

Координатная плоскость с координатами

Декартова система координат на плоскости рисунки животных

Координатная плоскость рисунки животных с координатами

Рисунок на координатной плоскости с координатами

Фигурки на координатной плоскости

Рисунки на координатной плоскости

Рисунки по координатам с координатами

Декартова система координат на плоскости рисунки

Фигуры на координатной плоскости

Рестнуи по координатам

Математические рисунки с координатами

Рисование по координатам

Изображение на координатной плоскости

Рисунки по координатам кенгуру

Лось по координатам -2 2 -2 4

Фигуры на координатной прямой

Рисование по координатам сложные

Кумир чертежник слон 1068

Животные по координатным точкам

Координатная плоскость (-7, 5;4, 5) , (-8;5)

Прямоугольная система координат рисунок

Слоник на координатной плоскости 2 -3

Фигуры по координатным точкам

Слоник по координатным точкам

Рисунки на координатной плоскости 6 класс

Рисуем по координатам сложно

Лошадь по координатам

Рисунки на координатной плоскости

Кленовый лист по координатам

Координатные рисунки простые

Бабочка на координатной плоскости

Кумир чертежник собачка

Рисунки на координатной плоскости

Рисование по координатной

Попугай на координатной плоскости

Рисунки для чертежника

Построить фигуру по точкам

Ласточка по координатам

Координаты для рисования на плоскости

Рисунки на координатной плоскости

Рисунки на координатной плоскости

Рыба по координатам

Сердце по координатам

Бабочка на координатной плоскости

Симметричные рисунки

Рисунок в системе координат по точкам

Гриб по координатам

Симметричные рисунки карандашом

Построение координатной плоскости

Кумир чертежник слон

Рисунок на координатной плоскости с координатами

Рисунки по координатам Пикачу

Координатная плоскость рисунок зайца

Соединить по точкам

Рисунок по координатам космонавт

Чертежник задания

Медведь на координатной плоскости

Соединить по точкам и раскрасить

Пикачу обводить по точкам

Рисунки на координатной плоскости

Рисование по цифрам сложные

Соединить по точкам

Рисование по точкам с цифрами

Рисование по точкамсложне

Собачка по координатам

Рисование по точкам сложные

Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

8.1 Рисование фигур на декартовой плоскости | Аналитическая геометрия

Домашняя практика

Для учащихся и родителейДля учителей и школ

Учебники

Полный каталог

Списки лидеров

Таблица лидеров учащихсяСборка лидеров классов/классовСписок лидеров школ

ЦеныПоддержка

Справочный центрСвяжитесь с нами

Авторизоваться

Предыдущий Упражнения в конце главы

Следующий 8.2 Расстояние между двумя точками

• В этой главе рассматривается представление геометрических фигур в декартовой системе координат. Также охвачены формула расстояния, градиент линии и середина линии.
• Формулы расстояния, градиент линии и середина линии должны быть сначала получены, а затем применены к решать проблемы.
• Объединить знания евклидовой геометрии с аналитической геометрией. Может быть полезно предложить учащимся записать свойства специальных четырехугольников и держите это под рукой при работе с аналитической геометрией.
• Подчеркните ценность и важность создания эскизов.
• Подчеркните важность последовательного написания координат для формулы расстояния и градиента.
• Эта глава также опирается на уравнение прямой линии. Убедитесь, что учащимся комфортно работать с уравнением прямой.

mathopenref.com имеет много интерактивные элементы, которые можно использовать при обучении аналитической геометрии.

Аналитическая геометрия — это изучение геометрических свойств, отношений и измерения точек, линий и углов. в декартовой плоскости. Геометрические формы определяются с использованием системы координат и алгебраических принципов. Некоторый считать введение аналитической геометрии, также называемой координатной или декартовой геометрией, началом современной математики.

Движение снаряда можно изобразить на декартовой плоскости. Аниматоры используют эту информацию, чтобы помочь им создавать анимации.

8.1 Рисование фигур на декартовой плоскости (ЕМА68)

Если нам даны координаты вершин фигуры, мы можем нарисовать фигуру на декартовой плоскости. Для например, четырехугольник \(ABCD\) с координатами \(A\left(1;1\right)\), \(B\left(3;1\right)\), \(C\влево(3;3\вправо)\) и \(D\влево(1;3\вправо)\).

Мы используем точку с запятой (;) для разделения значений \(x\) и \(y\), но международно признанный метод состоит в том, чтобы используйте запятую (,). Если используется запятая, то становится неясным, разделяет ли запятая \(x\) и \(y\) значений или одно из значений является десятичным.

Например, точка \((\text{5,5},5)\) неоднозначна. Это Значение \(x\) \(\text{5,5}\) или значение \(y\) \(\text{5,5}\)?

Вы также можете увидеть координаты, записанные как \(A(1,1)\).

Порядок букв в названии фигуры важен. Он указывает порядок, в котором точки должны быть соединены: \(A\) в \(B\), \(B\) в \(C\), \(C\) в \(D\) и \(D\) обратно в \(A\). Таким образом, приведенный выше четырехугольник можно назвать в виде четырехугольника \(ABCD\) или \(CBAD\) или \(BADC\). Однако принято писать буквы в в алфавитном порядке, поэтому мы обозначаем четырехугольник только как \(ABCD\).

Вы можете использовать онлайн-инструмент, который поможет вам при построении точек на декартовой плоскости. Нажмите здесь, чтобы попробовать это на mathsisfun.com.

Учебник Упражнение 8.1

Вам дана следующая диаграмма, на которой показаны различные точки:

Найдите координаты точки \(D\).

В этом вопросе нас интересует только точка \(D\). Из графика мы можем прочитать \(x\) и \(у\) значений.

Точка \(D\) имеет следующие координаты: \((3;3)\).

Вам дана следующая диаграмма, на которой показаны различные точки:

Найдите координаты всех отмеченных точек.

Из графика мы можем прочитать значения \(x\) и \(y\) для каждой точки.

\(А(3;-4)\), \(В(3;-3)\), \(С(-3;-4)\), \(D(5;-3)\) и \(Е(5;-4)\).

Вам дана следующая диаграмма, на которой показаны различные точки:

Какая точка лежит в координатах \((5;-4)\)?

Для этого вопроса нужно найти точку \((5;-4)\).

На графике мы можем проследить значения \(x\) и \(y\), чтобы найти, какая точка лежит в координатах \((5;-4)\).

При этом находим, что точка \(E\) лежит в координатах \((5;-4)\).

Вам дана следующая диаграмма, на которой показаны различные точки:

Какая точка лежит в координатах \((-4;-3)\)?

Для этого вопроса нужно найти точку \((-4;-3)\).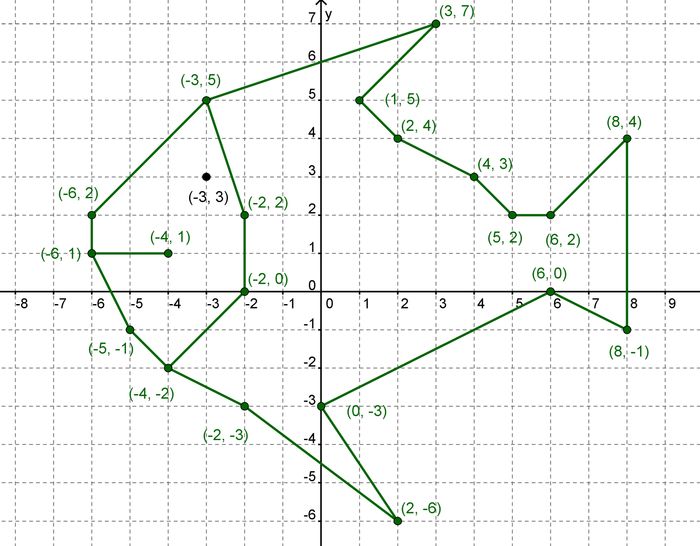

На графике мы можем проследить значения \(x\) и \(y\), чтобы найти, какая точка лежит в координатах \((-4;-3)\).

При этом находим, что точка \(B\) лежит в координатах \((-4;-3)\).

Вам дана следующая диаграмма, на которой нарисованы 4 фигуры.

Все фигуры идентичны, но каждая фигура использует свое соглашение об именах:

Какая фигура использует правильное соглашение об именах?

Мы помним, что правильное соглашение об именах для формы

в алфавитном порядке , либо по часовой стрелке, либо против часовой стрелки вокруг формы.

Из диаграммы видно, что только форма Z придерживается этого соглашения об именах.

Вам дана следующая диаграмма, на которой нарисованы 4 фигуры.

Все фигуры идентичны, но каждая фигура использует свое соглашение об именах:

Какая фигура использует правильное соглашение об именах?

Мы помним, что правильное соглашение об именах для формы в алфавитном порядке , либо по часовой стрелке, либо против часовой стрелки вокруг формы.

Из диаграммы видно, что только форма Z придерживается этого соглашения об именах.

Предыдущий Упражнения в конце главы

Оглавление

Следующий 8.2 Расстояние между двумя точками

Система координат и формы \ Tutorials

Это руководство предназначено для режима Python в Processing версия 2+. Если вы видите какие-либо ошибки или у вас есть комментарии, пожалуйста, дайте нам знать. Этот урок взят из книги Learning Обработка Дэниела Шиффмана, опубликованная Морганом Кауфманном. Издатели, Copyright © 2008 Elsevier Inc. Все права сдержанный.

 

Координатное пространство

Прежде чем мы начнем программирование с помощью обработки, мы должны сначала направить в себя восьмого класса, вытащить лист миллиметровой бумаги, и нарисуйте линию. Кратчайшее расстояние между двумя точками равно старая добрая линия, и здесь мы начнем с двух точек на этой миллиметровке.

На приведенном выше рисунке показана линия между точкой A (1,0) и точкой B. (4,5). Если вы хотите, чтобы ваш друг нарисовал это той же линии, вы бы кричали им и говорили: «Проведите линию от от точки один-ноль до точки четыре-пять, пожалуйста». момент, представьте, что ваш друг был компьютером, и вы хотели поручите этому цифровому приятелю отображать ту же самую строку на своем экран. Применяется та же команда (только на этот раз вы можете пропустить любезности, и вы должны будете использовать точный форматирование). Здесь инструкция будет выглядеть так:

строка(1,0,4,5)
 

Даже не изучив синтаксис написания кода, вышеизложенное утверждение должно иметь достаточный смысл. Мы предоставляем команда (которую мы будем называть «функцией») для машина, чтобы следовать под названием «линия». Кроме того, мы уточняем некоторые аргументы в пользу того, как должна быть проведена эта линия из точки А (1,0) в точку B (4,5). Если вы думаете об этой строке кода как о предложение, функция — это глагол, а аргументы — это объекты предложения. Кодовое предложение также заканчивается точка с запятой вместо точки.

Ключ здесь в том, чтобы понять, что экран компьютера ничто больше, чем причудливый кусок миллиметровой бумаги. Каждый пиксель экран представляет собой координату — два числа, «x» (по горизонтали) и «y» (вертикальный) — который определяет положение точки в космос. И наша работа — указать, какие формы и цвета должны появляются в этих координатах пикселей.

Тем не менее, здесь есть одна загвоздка. Графическая бумага с восьмого уклон («декартова система координат»), размещенный (0,0) в центре с осью у, направленной вверх, и осью х, указывающей вправо (в положительном направлении, отрицательном вниз и влево). система координат для пикселей в окне компьютера, однако, перевернуты по оси у.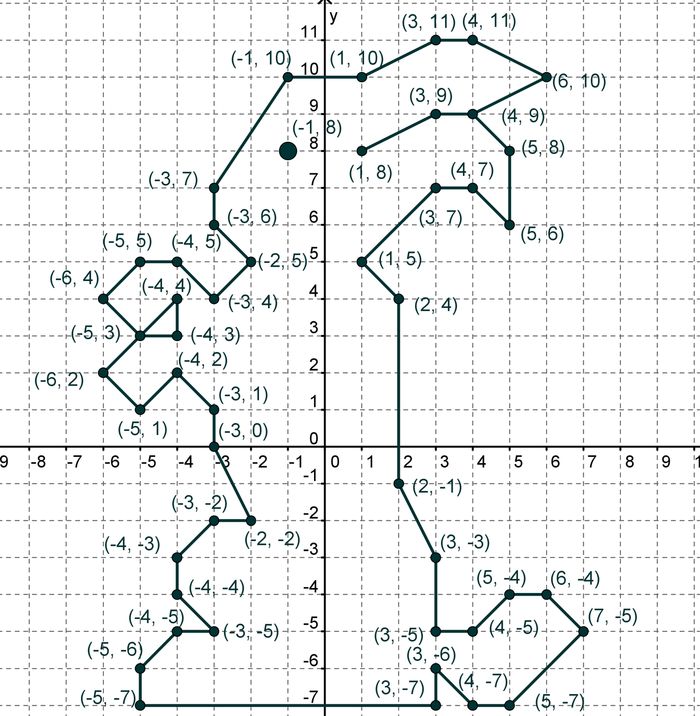 (0,0) можно найти в левом верхнем углу с положительным направлением вправо по горизонтали и вниз вертикально.

Простые формы

Подавляющее большинство примеров программирования, с которыми вы познакомитесь Обработки носят визуальный характер. Эти примеры, по своей сути, включают в себя рисование фигур и настройку пикселей. Начнем с поиска в четырех примитивных формах.

Для каждой формы мы спросим себя, какая информация необходимо указать расположение и размер (а позже и цвет) которые формируются, и узнайте, как Processing ожидает получить это информация. На каждой из приведенных ниже диаграмм мы предполагаем, что окно шириной 10 пикселей и высотой 10 пикселей. это не особенно реалистично, поскольку, когда вы действительно начинаете программировать, вы скорее всего, будет работать с окнами гораздо большего размера (10×10 пикселей всего несколько миллиметров экранного пространства.) Тем не менее для демонстрационные цели, приятно работать с меньшими числами чтобы представить пиксели так, как они могут отображаться на графике бумаги (пока), чтобы лучше проиллюстрировать внутреннюю работу каждого строка кода.

А точка() это самая простая из форм и хорошее место для начала. Чтобы нарисовать точки, нам нужны только координаты x и y.

А строка() тоже не очень сложно и просто требует двух пунктов: (x1,y1) и (x2,y2):

Как только мы получим rect() , все становится немного сложнее. В обработке прямоугольник задается координатой верхнего левого угла прямоугольника, а также его ширину и высоту.

Второй способ рисования прямоугольника заключается в указании центральная точка, а также ширина и высота. Если мы предпочитаем это мы сначала указываем, что хотим использовать режим «ЦЕНТР» перед инструкцией для самого прямоугольника. Обратите внимание, что Обработка чувствительна к регистру.

Наконец, мы также можем нарисовать прямоугольник с двумя точками (верхняя левый угол и правый нижний угол). Режим здесь «УГОЛКИ».

Как только мы освоились с концепцией рисования прямоугольник, эллипс() это несложно. Фактически он идентичен rect() с той разницей, что эллипс рисуется там, где ограничивающая рамка прямоугольника будет. Режим по умолчанию для ellipse() — это «ЦЕНТР», а не «УГОЛ».

Важно признать, что эти эллипсы не выглядят особенно круглая. Процессинг имеет встроенную методологию для выбор пикселей, которые следует использовать для создания круглой формы. При таком увеличении мы получаем кучу квадратов в виде круга. шаблон, но при уменьшении масштаба на экране компьютера мы получаем красивый круглый эллипс. Процессинг также дает нам возможность разрабатывать собственные алгоритмы раскрашивания отдельных пикселей (на самом деле мы можем уже представьте, как мы могли бы сделать это, используя «точку» снова и снова еще раз), но пока мы довольствуемся разрешением «эллипса» заявление, чтобы сделать тяжелую работу. (Чтобы узнать больше о пикселях, начните с: справочная страница пикселей, хотя имейте в виду, что это очень много более продвинутый, чем этот учебник.