Как построить разность векторов: Вычитание векторов — урок. Геометрия, 9 класс.

Разность векторов

Разностью x-y векторов x и y называется вектор z такой, что z+y=x.

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Построим разность векторов и .

Для построения разницы векторов z=x-y, нужно сложить вектор x с противоположным к y вектором y’. Противоположный вектор y’ строится просто:

Вектор y’ является противоположным к вектору y, так как y+y’=0, где 0 — нулевой вектор соответствующего размера. Далее выполняется сложение векторов x и y’:

Из выражения (1) видно что для построения разницы векторов достаточно вычислить разницы соответствующих координатов векторов x и y.

Рис. 1

На рисунке Рис. 1 в двухмерном пространстве представлен разность векторов x=(10,3) и

y=(2,4).

Вычислим z=x-y=(10-3,3-4)=(7,-1). Сравним полученный результат с геометрической интерпретацией. Действительно, после построения вектора y’ и параллельного перемещения начальной точки вектора y’ на конечную точку вектора x, получим вектор y», а после сложения векторов x и y», получим вектор z.

Вариант 2. Начальные точки векторов произвольные.

В этом случае процесс вычисления разницы векторов не так очевиден. Для построения разницы векторов z=x-y, нужно сложить вектор x с противоположным к y вектором y’. Здесь в качестве противоположного к вектору y можно взять тот же вектор y и поменять направление вектора, изменив начальный и коненый точки местами. Можно также взять вектор y’, который симметричен с y относительно начала координат. Если начальный и конечный точки вектора y и , то начальный и конечный точки противоположного вектора

y’ будут и соответственно.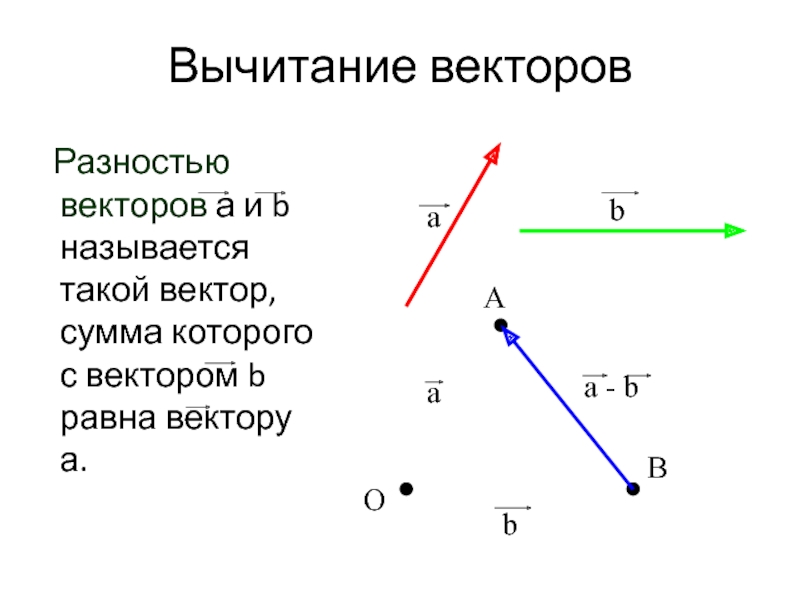 Таким образом для вычисления разницы векторов x и y, вычисляем сумму векторов x и y’ (подробно см. в разделе сложение векторов).

Рис. 2

На рисунке Рис. 2 в двухмерном пространстве представлен разность векторов x=AB и y=CD, где A(1,0), B(11,3), C(1,2), D(3,6). Для вычисления вектора z=x-y, построен противоположный к вектору y вектор y’:

Далее нужно сложить векторы x и y’. Вектор y’ перемещается параллельно так, чтобы точка C’ совпала с точкой B. Для этого вычисляются разницы координатов точек B и С:

Получаем:

Для перемещения точки D’ на точку E, сделаем следующее преобразование координат точки D’: В результате получим вектор z=AE, A(1,0), E(9, -1), который является разницей векторов x=AB и y=CD.

Разность векторов: определение, формула для нахождения, аналитический метод и графическое построение

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.

Оглавление:

• Определения векторной математики
• Аналитический метод
• Вычисление разности графически
• Решение задач

Максимально наглядно применение векторных величин объясняется в физике. Самыми простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, поскольку помимо численных значений они также обладают направлением действия. Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.

Содержание

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

1. Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
2. Длина (модуль) — это длина направленного отрезка.
3. Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
4. Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
5. Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
6. Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
7. Разностью векторов a и b называют сумму a и (— b), где (— b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a {a₁, a₂} и b {b₁, b₂} расчёты будут иметь следующий вид: c {c₁, c₂} = {a₁ b₁, a₂ b₂}.

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a {a₁, a₂, a₃} и b {b₁, b₂, b₃} координаты разности будут также получены попарным вычитанием: c {c₁, c₂, c₃} = {a₁ b₁, a₂ b₂, a₃ b₃}.

Вычисление разности графически

Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

1. По заданным координатам построить векторы, для которых нужно найти разность.
2. Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
3. Соединить начала обоих направленных отрезков и указать направление, результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.

Результат операции вычитания показан на рисунке ниже.

Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

1. Построить исходные направленные отрезки.
2. Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок, затем совместить его начало с уменьшаемым.
3. Построить сумму: соединить начало первого отрезка с концом второго.

Результат такого решения изображён на рисунке:

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1, —3), B (0, 4), C (5, 8), D (—3, 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1, —3), а концом B (0, 4). Рассчитаем координаты направленного отрезка:

AB {0 — 1, 4 — (— 3)} = {— 1, 7}

Аналогичный расчёт выполняется для CD:

CD {— 3 — 5, 2 — 8} = {— 8, — 6}

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид {c₁, c₂} = {a₁ b₁, a₂ b₂}. Для конкретного случая можно записать:

q = {— 1 — 8, 7 — ( — 6)} = { — 9, — 1}

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n, m — n, m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

• m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m,
• (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p,
• (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.

Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.

три разностных вектора и графики — ответы MATLAB

2 представления (последние 30 дней)

18 марта 2021 г.

Я хочу построить три разностных вектора на одном рисунке.

это пример данных. Я держу ошибку «векторы должны быть одинаковой длины».

как его изменить?

x = [1, 2, 3, 4, 5]

x1 = [1,1, 2,2, 3,4, 4, 4,5]

x2 = [0,9, 1,9, 3, 3,9, 4,3]

y= [ 1, 2, 3, 4, 5];

у1=[2, 3, 4, 5, 6];

y2 = [1, 3, 6, 7, 8]

удержание

график (x, y)

график (x1, y1)

график (x2, y2)

удержание

Ответы (1)

Ввод:

Я скопировал ваш код ниже, точно так же, как вы указали в своем вопросе. Он запускается и выдает график без ошибок. Я предлагаю вам тщательно перепроверить свой код. Если вы по-прежнему получаете сообщение об ошибке, скопируйте свой код из MATLAB прямо в комментарий сюда вместе с точным текстом любого сообщения об ошибке, чтобы мы могли посмотреть.

х = [1, 2, 3, 4, 5]

х = 1×5

1 2 3 4 5

x1 = [1,1, 2,2, 3,4, 4, 4,5]

x1 = 1×5

1,1000 2,2000 3,4000 4,0000 4,5000

x2 = [0,9, 1,9, 3, 3,9, 4,3]

x2 = 1×5

0,9000 1,9000 3,0000 3,9000 4,3000

у= [1, 2, 3, 4, 5];

у1=[2, 3, 4, 5, 6];

y2 = [1, 3, 6, 7, 8]

y2 = 1×5

1 3 6 7 8

удержание

график (x, y)

график (x1, y1)

график (x2, y2)

удержание

Произошла ошибка

Невозможно выполнить действие из-за внесенных изменений на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.

Переведено

Выбор сайта в Интернете

Выбор сайта в Интернете, чтобы визуализировать содержание транзакций, доступных для просмотра и просмотра событий и местных предложений. В базе alla tua area geografica, ti consigliamo di selezionare: .

Вы можете выбрать один из следующих веб-сайтов по телефону:

Америка

• Латиноамериканская Америка (Испания)
• Канада (английский)
• США (английский)

Европа

• Бельгия (английский)
• Дания (английский)
• Германия (нем.)
• Испания (Испания)
• Финляндия (английский)
• Франция (французский)
• Ирландия (английский)
• Италия (итальяно)
• Люксембург (английский)

• Нидерланды (английский)
• Норвегия (английский)
• Австрия (немецкий)
• Португалия (английский)
• Швеция (английский)
• Швейцария
  • немецкий
  • Английский
  • французский
• Великобритания (Английский)

Азиатско-Тихоокеанский регион

• Австралия (английский)
• Индия (английский)
• Новая Зеландия (английский)
• 中国
  • 简体中文Китайский
  • Английский
• 日本Японский (日本語)
• 한국Корейский (한국어)

Contatta l’ufficio locale

Графические методы – Колледж физики, главы 1-17

3 Двумерная кинематика

Резюме

• Понимание правил сложения, вычитания и умножения векторов.
• Применять графические методы сложения и вычитания векторов для определения смещения движущихся объектов.

Рисунок 1. Смещение можно определить графически с помощью масштабной карты, такой как карта Гавайских островов. Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (кредит: Геологическая служба США).

А вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный шрифт, такой как [latex]\textbf{D}[/latex], обозначает вектор. Его величина представлена ​​символом, выделенным курсивом, [латекс]\жирныйсимвол{D},[/латекс], а его направление — [латекс]\жирныйсимвол{\тета}.[/латекс]

ВЕКТОРА В ЭТОМ ТЕКСТЕ

В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором[latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена ​​переменной, выделенной курсивом, например [латекс]\жирныйсимвол{F},[/латекс], а направление переменной будет задано углом[латекс]\жирныйсимвол{\тета} .[/латекс]

Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Водоизмещение 10,3 блока под углом 29.1 ^o к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую общий вектор смещения D . С помощью транспортира начертите линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере магнитуда

D вектора составляет 10,3 единицы, а направление θ составляет 29,1 ^o к северу от востока.

Метод «голова к хвосту» — это графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а наконечник (или кончик) вектора является конечным заостренным концом стрелки.

Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, к началу вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 ⁰ .

Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .

Рис. 5.

Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .

Рисунок 6.

Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .

Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма других векторов.

Рисунок 7.

Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины. )

Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)

Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.

Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9о}[/latex]северо-восток. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.

Стратегия

Представьте каждый вектор смещения графически со стрелкой, обозначив первый[latex]\textbf{A},[/latex]второй[latex]\textbf{B},[/latex]и третий [latex]\textbf{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого[latex]\textbf{R}.[/latex]

Решение

(1) Нарисуйте три вектора смещения.

Рисунок 8.

(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.

Рисунок 9.

(3) Нарисуйте результирующий вектор,[latex]\textbf{R}.[/latex]

Рисунок 10.

(4) Используйте линейку для измерения величины[latex]\ textbf{R},[/latex]и транспортир для измерения направления[latex]\textbf{R}.[/latex]Хотя направление вектора можно задать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9о}[/latex]юго-восток.

Обсуждение

Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.

Рисунок 12.

Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.

[латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]

(Это верно для сложения обычных чисел как хорошо — вы получите тот же результат, если вы добавите, например, [латекс]\жирныйсимвол{2+3}[/латекс]или [латекс]\жирныйсимвол{3+2},[/латекс]).

Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс]из [латекс]\текстбф{А},[/латекс]написанного[латекс]\жирныйсимвол{\текстбф{А}-\текстбф {B}}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.0194 отрицательный вектора[latex]\textbf{B}[/latex] определяется как[latex]\boldsymbol{-\textbf{B}};[/latex]то есть графически отрицательный результат любого вектора имеет ту же величину, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.

Рисунок 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Так B является отрицательным значением -B ; он имеет ту же длину, но противоположное направление. o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.

Рисунок 14.

Стратегия

Мы можем представить первый этап пути с помощью вектора[latex]\textbf{A},[/latex], а второй этап пути с помощью вектора[latex] \textbf{B}.[/latex]Док расположен в месте[latex]\boldsymbol{\textbf{A}\:+\:\textbf{B}}.[/latex]Если женщина по ошибке путешествует в напротив 9о}[/latex]юго-восток. Мы представляем это как[latex]\boldsymbol{-\textbf{B}},[/latex], как показано ниже. Вектор[latex]\boldsymbol{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [латекс]\boldsymbol{\textbf{A}+(-\textbf{B})},[/latex]или[латекс]\boldsymbol{\textbf{A}-\textbf {B}}.[/latex]

Рисунок 15.

Выполним сложение векторов для сравнения расположения дока,[latex]\boldsymbol{\textbf{A}+\textbf{B}},[/ латекс]с местом, куда по ошибке прибыла женщина,[латекс]\boldsymbol{\textbf{A}+(-\textbf{B})}. [/latex]

Решение

(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы [latex]\textbf{A}[/latex]и [latex]\boldsymbol{-\textbf{B}} .[/latex]

(2) Разместите векторы от начала до конца.

(3) Нарисуйте результирующий вектор[latex]\textbf{R}.[/latex]

(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]

Рисунок 16.  

о}[/latex]юго-восток. 9о}[/latex]северо-восток.

Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.

Обсуждение

Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.

Если бы мы решили пройти в три раза больше первого этапа пути, рассмотренного в предыдущем примере, то мы бы прошли[latex]\boldsymbol{3 \times 27,5\textbf{ м}},[/latex]или 82,5 м, в направлении[латекс]\boldsymbol{66. o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0079 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.

Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору направление , противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: Когда вектор[латекс]\текстбф{А}[/латекс] умножается на скаляр[латекс]\жирныйсимвол{с},[/латекс]

• модуль вектора становится абсолютным значением[latex]\boldsymbol{cA},[/latex]
• , если [latex]\boldsymbol{c}[/latex] положительный, направление вектора не меняется,
• , если [латекс]\boldsymbol{c}[/латекс]отрицательно, направление меняется на противоположное.

В нашем случае [латекс]\boldsymbol{c=3}[/latex]и [латекс]\boldsymbol{\textbf{A}=27,5\textbf{ m}}.[/latex]Вектора умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.

В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает в себя определение перпендикулярных компонентов одного вектора, например x – и y -компоненты, или компонентов север-юг и восток-запад. 9o}[/latex]к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. Есть много приложений в физике, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0079 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.

PHET EXPLORATIONS: MAZE GAME

Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.

Рисунок 18. Игра «Лабиринт»

• Графический метод сложения векторов [latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex]предполагает рисование векторов на графике и их сложение с использованием прямого хвостовой метод. Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
• графический метод вычитания вектора [latex]\textbf{B}[/latex]из [latex]\textbf{A}[/latex] включает добавление противоположного вектора[latex]\textbf{B},[/latex ] который определяется как [латекс]\boldsymbol{-\textbf{B}}.[/latex]В этом случае [латекс]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{A} +(-\textbf{B})=\textbf{R}}.[/latex]Затем обычным методом сложения головы к хвосту получается результирующий вектор[latex]\textbf{R }.[/латекс]
• Сложение векторов коммутативно , так что [латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
• Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора.

  No related posts.