Мода и медиана. Примеры
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой дискретной случайной величины называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины , которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
В зависимости от вида функции случайная величина может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой случайной величины называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
Графически мода и медиана изображенные на рисунке
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью.
Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин то медиана равна средней величине
в случае четного количества полусумме средних величин
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины — количество дорожек, которые требуют уборки. Найти моду .
Решение. Случайной величина может принимать значения
Вероятности появления значений определяем по образующей функцией
Для заданной задачи входные величины принимают значения
Искомые вероятности входят множителями при степенях аргумента
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду , как значение при максимальной вероятности.
Получили одномодальное распределение
Пример 2. По заданной плотностью вероятностей
найти параметр , плотность вероятностей , моду .
Решение. Применяя условие нормирования выполняем интегрирование
после того определяем параметр
Плотность вероятностей, учитывая найденное значение будет иметь вид
а ее график изображен на рисунке ниже
Из графика плотности вероятностей видим, что мода принимает значение . Определим медиану с помощью функции распределения вероятностей. Ее значение на промежутке находим интегрированием
Функция распределения иметь следующий вид
а ее график будет иметь вид
Для определения медианы случайной величины применяем формулу
Медиану можно найти с помощью плотности вероятностей
для дискретной случайной величины из промежутка
Таким образом медиану — возможное значение случайной величины , при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости , делит площадь фигуры, ограниченной функцией плотности вероятностей на две равные части.
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.
Статистика для консультантов — 1. Мода, Медиана, Среднее
В статистике есть несколько понятий, знать которые необходимо, чтобы понимать научные статьи по своей тематике. Я решила сделать небольшой цикл статей об основах статистики, которые будут полезны консультантам и участницам групп поддержки ГВ, а также всем, кто хочет быть в курсе современных исследований, а особенно — сдавать экзамен на IBCLC (консультант по лактации, сертифицированный международным экзаменационным комитетом).
Самые базовые понятия статистики — это среднее, медиана и мода.
Если у нас есть набор некоторых чисел (например, количество молока, сцеженное разными женщинами, прибавка веса у разных детей, частота заболеваний у разных детей), для этого набора чисел можно посчитать среднее, моду и медиану. Про среднее многие из нас догадываются, что это такое, а вот «мода» и «медиана» для большинства — новые понятия, поэтому с них и начнем.
Чтобы было легче запомнить, немного подробнее расскажем о смысле этих чисел.
Мода (mode) — очень «женское» слово ))) И правда, в статистике моду часто используют для не-числовых величин. Например, людей спрашивают, какого цвета они хотели бы купить автомобиль. Люди выбирают из ответов — черный, синий, зеленый, красный, серебристый, белый. Какой цвет чаще встречается, тот и «мода» — «модный» ))
Задание 1 — ответы опрошенных о любимом цвете автомобиля были следующими:
черный зеленый зеленый синий синий синий серебристый серебристый красный белый
Какая мода?
Медиана (median).
Наверное, многие из нас помнят, что медиана в треугольнике делит его пополам.
Так и тут, медиана делит ровно пополам числа, среди которых мы ищем медиану, если их выписать в ряд в возрастающем порядке. Если количество чисел нечетное, посередине будет число, и ответ вычислить легко (просто берем число, которое посередине). Если число ответов четное, то медиана упадет ровно посередине между двух чисел, значит, чтобы ее найти, надо будет посчитать среднее между этими двумя «соседями».
Среднее (mean, average). Среднее полезно практически всегда. Например, мы хотим ехать в другой город через месяц, как раз в марте. Мы залезаем в интернет и узнаем среднее количество осадков в этом городе в марте, среднюю дневную температуру в марте, и так далее. И вот, мы уже кое-что себе представляем и можем подобрать одежду.
Однако не всегда среднее дает понимание о том, что на самом деле происходит. Например, если нам дадут не среднюю дневную температуру в марте, а среднесуточную температуру, у нас будет уже меньше представления о том, какова погода в этом городе.
Может быть, там ночью очень холодно, а днем жарко (-10 и +20) ? А может, днем и ночью примерно одинаково (+6 и +4)? Среднее будет одинаковым. Какое, кстати?
Ответ: (-10+20)/2=10/2=5. (6+4)/2=10/2=5. Средняя температура в обоих случаях будет +5.
(сперва посчитайте самостоятельно, а потом прочтите ответ, выделив текст в строке выше).
А если нам вместо этого дадут среднегодовую температуру в этом городе, мы вообще не узнаем, что же там происходит в марте днем )))
Поэтому часто шутят, — «да ну, это средняя температура по палате». То есть если в палате больные с высокой и низкой температурой, в среднем у них нормальная температура и их можно выписывать.
Задание 2. Температура больных в палате составляла
34 34 34 34.4 35 38 39 40 40.
Посчитайте, пожалуйста, среднее, медиану и моду.
Ответ. Среднее равно сумме температур больных, деленной на число больных.
Здесь указано 9 значений температуры. Значит, в палате лежит 9 человек. (34+34+34+34.4+35+38+39+40+40)/9=328.4/9=36.5 примерно (нормальная температура)
Медиана — посередине, если значения температуры расположены в возрастающем порядке. Значит, это 35
Мода — наиболее частое значение температуры, 34.
Пример задачи, похожей на задачи экзамена на IBCLC.
Задание 3.
Вы сделали доклад на встрече консультантов по ГВ, вас слушало 10 коллег. После доклада вы раздали анкету, где задали вопрос, насколько им понравился ваш доклад и насколько полезной оказалась информация. При ответе на вопрос слушателям нужно было выбрать число от 1 до 5 (1, 2, 3, 4, 5). Эти числа были выбраны следующее число раз: 0 2 1 3 4. Чему равны мода ответов, медиана и средний балл?
Ответ.
Таким образом, ваши коллеги поставили следующие баллы — ни одной единицы, две двойки, одна тройка, три четверки и четыре пятерки.
Перечислим эти цифры.
2 2 3 4 4 4 5 5 5 5
Теперь вычислим то, что спрашивается в вопросе.
Мода — это наиболее часто встречающееся число. Это, конечно, число 5.
Медиана — это число, которое находится посередине, если выписать все ответы подряд. В данном случае это 4. Если бы ответы коллег были такими — 4 4 4 4 4 5 5 5 5 5, медиана бы получилась между четверкой и пятеркой, т.е. 4.5
Среднее. Это самое легкое — нужно сложить все цифры и поделить на число отвечавших (10). 2+2+3+4+4+4+5+5+5+5 = 39
39/10=3.9
Мода (mode) = 5
Медиана (median) = 4
Среднее (mean, average) = 3.9
каков смысл этих чисел? ваши коллеги чаще других оценок ставили вам пятерку (мода). В среднем вы сделали доклад на 4 с минусом (3.9 это почти 4). Если разделить оценку вашего труда на две равные части, то посередине окажется оценка 4.
Так как среднее не всегда точно характеризует те же ответы ваших коллег, используют и другие показатели, такие как мода и медиана.
Медиана полезна, когда много больших или маленьких ответов, например, вам поставили много единиц и несколько пятерок
1 1 1 1 1 1 5 5 5 5 . в среднем вы сделали доклад на 1+1+1+1+1+1+5+5+5+5=26, 26/10=2.6, то есть на 3 с минусом. Но настолько многим не понравился ваш доклад, что медиана оценки его эффективности равна 1. То есть большинство оценило вас в 1! Ясно, что и мода в данном случае равна 1. Значит, доклад совсем не удался. 🙂 А может быть, вы просто неверно оценили целевую аудиторию, ведь нескольким людям доклад показался отличным.
Задание 4
Несколько женщин, кормящих детей сцеженным молоком, принимали новый чай для лактации в течение недели. В начале и в конце недели они посчитали количество сцеженного молока. В начале недели это было 670, 810, 1200 и 500 граммов. В конце недели это были 650, 810, 1250 и 690 граммов соответственно.
Посчитайте, пожалуйста, среднее количество молока и медиану до и после приема нового чая. Насколько увеличилось среднее количество молока?
Ответ.
для получения среднего нужно сложить все числа и поделить на их количество. Цифр 4, значит на 4.
670+810+1200+500=3180. 3180/4 = 795
650+810+1250+690=3400. 3400/4 = 850
значит, молока стало в среднем на 55 граммов больше
медиана
Для получения медианы расположим объем сцеженного молока в возрастающем порядке и найдем число, которое стоит посередине. Т.к. у нас четыре ответа, посередине нет числа и нужно будет найти среднее между двумя средними числами.
670, 810, 1200 и 500
расположим в возрастающем порядке
500 670 810 1200
значит, медиана равна (670+810)/2 = 740
650, 810, 1250 и 690
расположим в возрастающем порядке
650 690 810 1250
значит, медиана равна (690+810)/2 = 750
И медиана выросла (на 10 г), и среднее (на 55 г)
при этом лишь у двух женщин количество молока выросло, у одной не изменилось, и у одной даже уменьшилось.
Итак, вам уже, наверное, понятно, что, кроме самых простых случаев, среднее и медиана (не говоря уже о моде) не очень-то точно характеризуют ту величину, для которой их считают (например, средняя температура по палате не очень-то характеризует температуру каждого из больных, а средний прирост молока после применения чая не дает нам информацию, что количество молока могло уменьшиться).
Именно поэтому ввели дополнительные характеристики для меняющейся (т.н. «случайной») величины — дисперсия, а также более полное и подробное описание — «распределение случайной величины».
Автор — Мария Сорокина, IBCLC, создатель сайта «Грудное вскармливание».
Оригинал статьи
Формула средней средней моды — Что такое формула средней средней моды? Примеры
Формула средней срединной моды сообщает нам меры центральной тенденции. В этой статье мы узнаем о формуле среднего медианного режима вместе с решенными примерами.
Что такое формула среднего медианного режима?
Среднее также известно как среднее арифметическое заданных данных. Медиана — это самое среднее значение данных сгруппированных данных, если данные сгруппированы и расположены в порядке возрастания. Мода — это значение, которое больше всего встречается в данных. Формулы среднего, медианы и моды поясняются ниже отдельно для группы данных.
Формула среднего
Формула среднего определяется как сумма наблюдений, деленная на общее количество наблюдений. Это будет полезно при решении большинства тем, связанных со средним арифметическим. Формула среднего значения данных наблюдений может быть выражена следующим образом:
Формула среднего значения = (Сумма наблюдений) ÷ (Общее количество наблюдений)
Точно так же у нас есть формула среднего значения для сгруппированных данных. Что выражается как
х = Σ f х /Н
где
- x = среднее значение набора заданных данных.
- f = частота отдельных данных
- N = сумма частот
Следовательно, среднее значение всех точек данных называется средним.
Формула медианы
Чтобы найти медиану, нам нужно расположить данные либо в порядке возрастания, либо в порядке убывания. Теперь, после упорядочивания данных, получите общее количество наблюдений в данных. Если число нечетное, медиана равна (n+1)/2.
Точно так же у нас есть формула медианы для сгруппированных данных. Медианная формула для сгруппированных данных имеет следующий вид:
- n = общая частота
- F = кумулятивная частота класса перед медианным классом
- f m = Частота медианы класса
- i = ширина класса
- л м = нижняя граница медианы класса
Формула режима
Значение или число, которое чаще всего встречается в наборе данных, является режимом. В тех случаях, когда нам нужно найти наиболее часто встречающееся значение, мы находим значение режима для набора заданных данных. Для данных без повторяющихся значений режим вообще отсутствует. Значение режима зависит от данного набора данных.
Формула режима = L + h \(\dfrac{(f_{m} — f_{1})}{(f_{m} — f_{1}) + (f_{m} — f_{2})} \)
, где
- «L» — нижний предел модального класса.
- ‘h’ — размер интервала класса.
- ‘\(f_m\)’ — частота модального класса.
- ‘\(f_1\)’ — частота класса, предшествующего модальному классу.
- ‘\(f_2\)’ — частота класса, следующего за модальным классом.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запишитесь на бесплатный пробный урок
Примеры формулы среднего среднего режима
Пример 1: Используя формулу средней моды, найдите моду данных {14,16,16,16,17,16,18}
Решение:
Поскольку существует только одно повторяющееся значение, это унимодальный список.
Согласно формуле средней средней моды,
Режим = {16}
Ответ: Режим {14,16,16,16,17,16,18} – 16
Пример 2: Возраст членов общественного центра указан ниже: {42, 38, 29 , 37, 40, 33, 41}. Используя формулу среднего среднего режима, вычислите медиану заданных данных.
Решение:
Найти медиану заданного множества.
Дано: Набор возрастов для разных участников: {42, 38, 29, 37, 40, 33, 41}
Упорядочивание набора в порядке возрастания: {29, 33, 37, 38, 40, 41, 42}
Используя формулу медианы,
Медиана = (7 + 1)/2 член 90 017 = 4 -е терм
= 38
Ответ: Медиана заданных данных = 38
Пример 3: Используя формулу среднего среднего значения, найдите среднее значение первых пяти натуральных чисел, используя формулу среднего.
Решение:
Первые пять натуральных чисел = 1, 2, 3, 4, 5
Используя формулу среднего медианного режима
Среднее значение = {Сумма наблюдений} ÷ {Общее количество наблюдений}
Среднее значение = (1 + 2 + 3 + 4 + 5) ÷ 5 = 15/5 = 3
Ответ: Среднее значение первых пяти натуральных чисел { 1, 2, 3, 4, 5 } равно 3.
Часто задаваемые вопросы о формуле среднего медианного режима
Что такое формула среднего значения в формуле среднего среднего режима?
В формуле среднего значения средней моды формула среднего значения задается как среднее значение всех наблюдений. Он выражается как Среднее = {Сумма наблюдений} ÷ {Общее количество наблюдений}.
Как рассчитать среднее значение с помощью формулы среднего среднего значения?
Если задан набор из n наблюдений, то среднее значение можно легко рассчитать, используя общую формулу среднего среднего режима , то есть Среднее = {Сумма наблюдений} ÷ {Общее количество наблюдений}.
Что такое формула медианы в формуле среднего медианного режима?
В формуле среднего медианного режима формула медианы дается как для четного, так и для нечетного числа наблюдений (n). Если число наблюдений четное, то формула медианы такова: [медиана = ((n/2) -й -й термин + ((n/2) + 1) -й -й термин)/2] и если n = нечетное, то формула медианы будет [медиана = {(n + 1)/2} -й -й термин].
Что такое значение режима в формуле среднего среднего режима?
В формуле среднего медианного режима для заданных данных модой является значение, которое встречается в данных максимальное количество раз. Другими словами, значение с наибольшей частотой будет модальным значением данных.
Среднее значение, мода и медиана. Показатели центральной тенденции. Когда использовать с различными типами переменных и асимметричных распределений
Введение
Мера центральной тенденции — это отдельное значение, которое пытается описать набор данных, определяя центральное положение в этом наборе данных.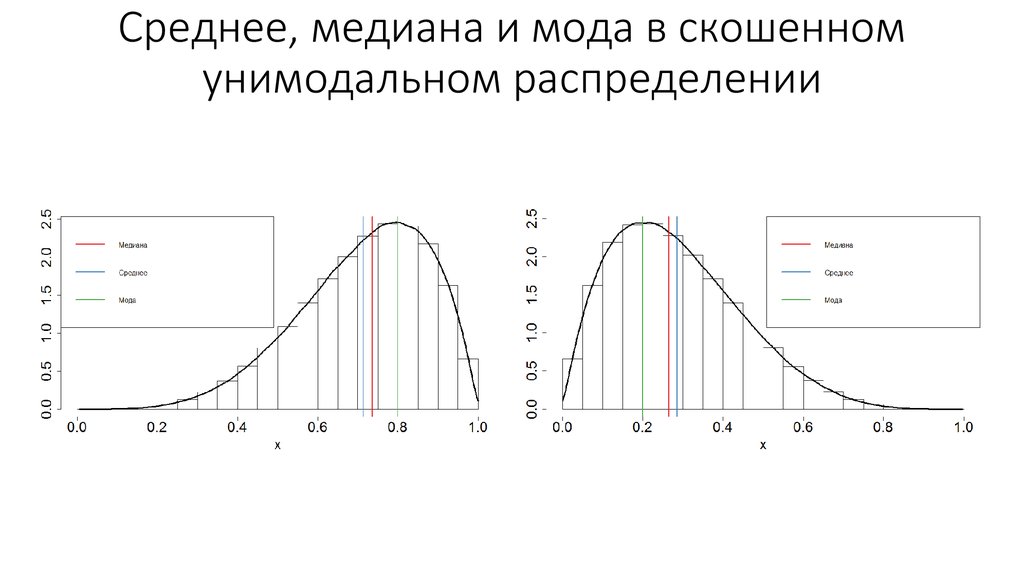
Таким образом, меры центральной тенденции иногда называют мерами центрального положения. Они также классифицируются как сводная статистика. Среднее значение (часто называемое средним), скорее всего, является мерой центральной тенденции, с которой вы лучше всего знакомы, но есть и другие, такие как медиана и мода.
Среднее значение, медиана и мода являются действительными мерами центральной тенденции, но в различных условиях одни меры центральной тенденции становятся более подходящими для использования, чем другие. В следующих разделах мы рассмотрим среднее значение, моду и медиану и узнаем, как их вычислить и при каких условиях их лучше всего использовать.
Среднее (арифметическое)
Среднее (или среднее) является наиболее популярной и известной мерой центральной тенденции. Его можно использовать как с дискретными, так и с непрерывными данными, хотя чаще всего он используется с непрерывными данными (см. наше руководство по типам переменных для типов данных). Среднее значение равно сумме всех значений в наборе данных, разделенной на количество значений в наборе данных.
Итак, если у нас есть \( n \) значений в наборе данных, и они имеют значения \( x_1, x_2, \) …\(, x_n \), среднее значение выборки обычно обозначается \( \overline{x} \ ) (произносится как «х бар»), это:
$$ \overline{x} = {{x_1 + x_2 + \dots + x_n}\over{n}} $$
Эта формула обычно записывается немного по-другому, используя заглавную букву греческого языка, \( \ сумма \), произносится как «сигма», что означает «сумма…»:
$$ \overline{x} = {{\sum{x}}\over{n}} $$
У вас может быть заметил, что приведенная выше формула относится к выборочному среднему. Итак, почему мы назвали его выборочным средним? Это связано с тем, что в статистике выборки и совокупности имеют очень разные значения, и эти различия очень важны, даже если в случае среднего значения они рассчитываются одинаково. Чтобы подтвердить, что мы вычисляем среднее значение генеральной совокупности, а не среднее значение выборки, мы используем строчную греческую букву «му», обозначаемую как \( \mu \):
$$ \mu = {{\sum{x}}\over{n}} $$
Среднее значение, по сути, является моделью вашего набора данных.
Это значение является наиболее распространенным. Однако вы заметите, что среднее значение не часто является одним из фактических значений, которые вы наблюдали в своем наборе данных. Однако одним из его важных свойств является то, что он сводит к минимуму ошибку в прогнозировании любого значения в вашем наборе данных. То есть это значение дает наименьшую ошибку из всех других значений в наборе данных.
Важным свойством среднего значения является то, что оно включает каждое значение в вашем наборе данных как часть расчета. Кроме того, среднее значение является единственным показателем центральной тенденции, когда сумма отклонений каждого значения от среднего всегда равна нулю.
Когда не следует использовать среднее значение
Среднее значение имеет один главный недостаток: оно особенно чувствительно к влиянию выбросов. Это значения, которые необычны по сравнению с остальным набором данных, поскольку они особенно малы или велики по числовому значению. For example, consider the wages of staff at a factory below:
| Staff | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Salary | 15k | 18k | 16k | 14k | 15k | 15k | 12k | 17k | 90k | 95k |
The mean salary for these ten staff is $30.
7k . Однако изучение необработанных данных показывает, что это среднее значение может быть не лучшим способом точно отразить типичную зарплату работника, поскольку зарплата большинства работников находится в диапазоне от 12 до 18 тысяч долларов. Две большие зарплаты искажают среднее значение. Следовательно, в этой ситуации мы хотели бы получить более точную меру центральной тенденции. Как мы узнаем позже, использование медианы было бы лучшим показателем центральной тенденции в этой ситуации.
Другой случай, когда мы обычно предпочитаем медиану среднему (или моде), — это когда наши данные искажены (т. е. частотное распределение наших данных искажено). Если мы рассмотрим нормальное распределение — поскольку оно чаще всего оценивается в статистике — когда данные совершенно нормальны, среднее значение, медиана и мода идентичны. Более того, все они представляют наиболее типичное значение в наборе данных. Однако по мере искажения данных среднее значение теряет способность обеспечивать наилучшее центральное расположение данных, поскольку искаженные данные уводят его от типичного значения.
Однако медиана лучше всего сохраняет эту позицию и не так сильно подвержена влиянию искаженных значений. Это объясняется более подробно в разделе об асимметричном распределении далее в этом руководстве.
Медиана
Медиана — это средний балл для набора данных, упорядоченных по порядку величины. На медиану меньше влияют выбросы и искаженные данные. In order to calculate the median, suppose we have the data below:
| 65 | 55 | 89 | 56 | 35 | 14 | 56 | 55 | 87 | 45 | 92 |
Сначала нам нужно переставить эти данные в порядке величины (сначала наименьший):
| 14 | 35 | 45 | 55 | 55 | 56 | 56 | 65 | 87 | 89 | 92 |
Our median mark is the middle mark — in в данном случае 56 (выделено жирным шрифтом).
Это средний балл, потому что до него 5 баллов, а после него 5 баллов. Это прекрасно работает, когда у вас нечетное количество баллов, но что происходит, когда у вас четное количество баллов? Что, если бы у вас было всего 10 баллов? Что ж, вам просто нужно взять две средние оценки и усреднить результат. Итак, если мы посмотрим на пример ниже:
| 65 | 55 | 89 | 56 | 35 | 14 | 56 | 55 | 87 | 45 |
We again rearrange that data into order of magnitude (smallest first):
| 14 | 35 | 45 | 55 | 55 | 56 | 56 | 65 | 87 | 89 |
Only now we have to take the 5th and 6th наберите в нашем наборе данных и усредните их, чтобы получить медиану 55,5.
Мода
Мода является наиболее частым показателем в нашем наборе данных. На гистограмме он представляет самый высокий столбец гистограммы или гистограммы. Таким образом, вы можете иногда рассматривать этот режим как наиболее популярный вариант. Пример режима представлен ниже:
Обычно этот режим используется для категориальных данных, когда мы хотим знать, какая категория является наиболее распространенной, как показано ниже: видом транспорта в данном конкретном наборе данных является автобус. Однако одна из проблем с режимом заключается в том, что он не уникален, поэтому он оставляет нас с проблемами, когда у нас есть два или более значения, которые имеют самую высокую частоту, как показано ниже:
Теперь мы застряли в том, какой режим лучше всего описывает центральную тенденцию данных. Это особенно проблематично, когда у нас есть непрерывные данные, потому что у нас, скорее всего, не будет ни одного значения, которое встречается чаще, чем другое.
Например, рассмотрим измерение веса 30 человек (с точностью до 0,1 кг). Насколько вероятно, что мы найдем двух или более людей с ровно одинаковым весом (например, 67,4 кг)? Ответ, вероятно, очень маловероятен — многие люди могут быть близки, но при такой небольшой выборке (30 человек) и большом диапазоне возможных весов вы вряд ли найдете двух людей с абсолютно одинаковым весом; то есть с точностью до 0,1 кг. Вот почему этот режим очень редко используется с непрерывными данными.
Еще одна проблема с этим режимом заключается в том, что он не дает нам очень хорошего показателя центральной тенденции, когда наиболее распространенная метка находится далеко от остальных данных в наборе данных, как показано на диаграмме ниже:
На приведенной выше диаграмме режим имеет значение 2. Однако мы можем ясно видеть, что режим не является репрезентативным для данных, которые в основном сосредоточены в диапазоне значений от 20 до 30. Было бы ошибкой использовать моду для описания центральной тенденции этого набора данных.
Асимметричные распределения, среднее и медиана
Мы часто проверяем, нормально ли распределены наши данные, потому что это распространенное предположение, лежащее в основе многих статистических тестов. Пример нормально распределенного набора данных представлен ниже:
Когда у вас есть нормально распределенная выборка, вы можете правомерно использовать как среднее значение, так и медиану в качестве меры центральной тенденции. Фактически, в любом симметричном распределении среднее значение, медиана и мода равны. Однако в этой ситуации среднее предпочтительнее в качестве наилучшей меры центральной тенденции, потому что это мера, которая включает все значения в наборе данных для ее расчета, и любое изменение в любой из оценок повлияет на значение иметь в виду. Это не относится к медиане или моде.
Однако, когда наши данные искажены, например, как в приведенном ниже наборе данных с перекосом вправо:
Мы обнаруживаем, что среднее значение перетаскивается в направлении перекоса.
В этих ситуациях медиана обычно считается лучшим показателем центрального расположения данных. Чем более асимметрично распределение, тем больше разница между медианой и средним значением, и тем больший упор следует делать на использование медианы, а не среднего. Классическим примером приведенного выше распределения с асимметрией вправо является доход (зарплата), где работники с более высоким доходом дают ложное представление о типичном доходе, если оно выражено в виде среднего, а не медианного значения.
Если речь идет о нормальном распределении и тесты на нормальность показывают, что данные ненормальны, обычно вместо среднего используется медиана. Однако это скорее эмпирическое правило, чем строгое указание. Иногда исследователи хотят указать среднее значение асимметричного распределения, если медиана и среднее не отличаются заметно (субъективная оценка) и если это позволяет упростить сравнение с предыдущими исследованиями.
Краткий обзор того, когда использовать среднее значение, медиану и моду
Пожалуйста, используйте следующую сводную таблицу, чтобы узнать, как лучше всего измерить центральную тенденцию по отношению к различным типам переменных.