Как разделить 636 на 6 в столбик: Деление в столбик 636/9 (636 делить на 9) с остатком для 3 класса — на однозначное, двузначное число, для 4 класса

Как разделить в столбик 636:6 — Знания.site

Ответы 1

Надеюсь, что видно хорошо

Знаешь ответ? Добавь его сюда!

Последние вопросы

• Литература

  5 часов назад

  Как сделать план

• Геометрия

  7 часов назад

  ПОМОГИТЕ

• Обществознание

  11 часов назад

  ужассссссссссссссссссс

  я из аккаунта этого вылетаю

• Алгебра

  12 часов назад

  СРОЧНО!! Разложите на множители!

  3x³-5x²y+9x-15

• Другие предметы

  13 часов назад

  Какая из библейских историй вам запомнилась?Чему учит каждая из них?

• Литература

  14 часов назад

  Краткий пересказ повести мелентьева одни сутки войны

• Математика

  15 часов назад

  Помогите пожалуйста сделать букву а

• Математика

  18 часов назад

  Помогите пожалуйста сделать букву а

• Другие предметы

  19 часов назад

  что делать если я бибизяна?

• Математика

  20 часов назад

  Модно эту шлюху выебать с неграми жоско в рот .

• Биология

  20 часов назад

  Васе надо выебать 245 волосатых мужиков. Ежедневно он ебёт на одно и то же количество мужиков больше по сравнению с предыдущим днём. Известно, что за первый день Вася выебал 11 мужиков в попки . Определите, сколько всего надо выебать Вася в последний день, если со всеми он справился за 1 дней.

• Математика

  20 часов назад

  Васе надо выебать 245 волосатых мужиков. Ежедневно он ебёт на одно и то же количество мужиков больше по сравнению с предыдущим днём. Известно, что за первый день Вася выебал 11 мужиков в попки . Определите, сколько всего надо выебать Вася в последний день, если со всеми он справился за 1 дней.

• Физика

  1 день назад

  Доброй ночи, помогите пожалуйста с заданием по физике, электростатика.

  Между зарядами -q и +9q расстояние равно 8 см. На каком расстоянии от первого заряда находится точка, в которой напряженность поля равна нулю?

• Математика

  1 день назад

  В равнобедренной трапеции ABCD с основаниями AD и BC O-точка пересечения диагоналей, угол CAD равен 36°. Чему равен угол AOD? Ответ дайте в градусах

• Алгебра

  1 день назад

  ПОМОГИТЕ РЕШИТЬ

Разделить длинный столбец в Excel — английский

mohamedzaki636 8 сентября 2020 г., 9:00

#1

у меня есть столбец, содержащий 5000 ячеек, есть ли способ быстро разделить этот столбец на 10 других столбцов и не выполнять это руководство

anon73440385

8 сентября 2020 г. , 9:53

#2

разделить длинный столбец в excel

Не знаю как сделать в Excel , но есть решение для Calc — см. ниже.

anon73440385 8 сентября 2020 г., 9:36

#3

Привет,

Предположения (для описания)

• Текущие данные находятся в диапазоне A1:A5000 (5000 строк)
• Вы хотите получить значения в 10 столбцах (в результате 5000/10 = 500 строк)
• Целевой диапазон начинается с
  B1 (следовательно, всего B1:K500

Выполнить следующие действия:

• Перейти в ячейку B1
• Добавьте следующую формулу в B1 : =СМЕЩ($A$1;(СТОЛБЦ()-1)+(СТРОКА()-1)*10-1;0)
• Перетащите формулу из B1 -> K1
• Введите B1:K500 в поле имени (самое левое в строке формул) и нажмите ВВОД (будет выбран диапазон B1:K500 )
• Тип CTRL+D
• Дополнительно Выберите столбцы B – D и Данные -> Вычислить -> Формула для значения

Обратите внимание Формулу необходимо адаптировать, если

• начальная ячейка целевого диапазона равна , а не B1 и/или
• первая ячейка текущих данных равна
  вместо A1 и/или
• количество столбцов, в которые должны быть распределены данные, равно , а не 10

(т.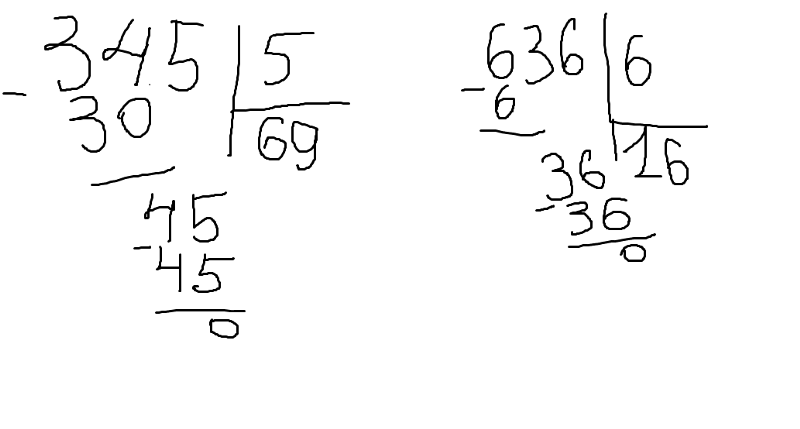 е. в любом случае предположения не выполняются)

Надеюсь поможет.

мохамедзаки636 8 сентября 2020 г., 10:11

#4

большое спасибо, это очень полезно

mohamedzaki636 9 сентября, 2020, 16:16

#5

Этот способ разделить его по горизонтали, есть ли способ решить вопрос по вертикали

анон73440385 10 сентября 2020 г., 8:10

#6

Что вы подразумеваете под этим ( 1 через 10 в B1:B10 ; 11 через 20 в C1:C10 и так далее на)? Если — да, то это, конечно, возможно, но имейте в виду, что из-за ограничения в 1024 столбца (ограничение в 16k в версии 7 все еще экспериментальная функция) вы довольно скоро достигнете предела (формула: =СМЕЩ($A$1;(СТОЛБЦ()-2)*10+(СТРОКА())-1;0) и диапазон: B1:SG10 (добавьте формулу к B1 , скопируйте [ CTRL +C ] формулу, выберите диапазон с помощью Name Box и вставьте [ CTRL+V ] формулу в диапазон).

мохамедзаки636 10 сентября 2020 г., 21:21

#7

да, это то, что я имею в виду
еще раз спасибо

AlexKemp закрыто 1 июня 2021 г., 4:58

#8

Умножение и деление Pick n Mix 1

Начало работы

Целью этого занятия является изучение ряда стратегий, которые ваши учащиеся уже используют для решения задач на умножение и деление. Это позволит вам более глубоко оценить, на каких стратегиях следует сосредоточиться, а также определить студентов в вашей группе как «экспертов» в конкретных стратегиях.

Задача 1 (Копирайтер 2):
Ванесса проезжает на велосипеде по 38 километров каждый день в течение пяти дней. Сколько километров она прошла к концу пяти дней?

Попросите учащихся придумать ответ в уме, если они могут, и записать свою стратегию на бумаге. Некоторым учащимся может понадобиться использовать запись, чтобы уменьшить нагрузку на память. Студентов, которые решают задачу быстро, можно расширить, попросив проверить свои расчеты с помощью другой стратегии. Дайте учащимся необходимое время на размышление. Затем попросите их поделиться своими решениями со своим партнером по обучению. Возможны следующие ответы:

Обратите внимание, что принято сначала записывать множитель, поэтому уравнения следует записывать в виде 5 x 38 =  .

Округление и компенсация:

5 x 38
38 округляется до 40, поэтому задача становится 5 x 40 = 200, затем из произведения вычитается 10 (5 x 2), чтобы получить 5 x 38 = 190.

Полностью стратегию можно записать как 5 x 38 = 5 x 40 – 5 x 2.

Посмотрите, как это сделать, используя Видео 1.

Пропорциональная корректировка: 
5 x 38
Вместо этого решите 10 x 19, используя удвоение и деление пополам (путем удвоения 5 и деления пополам 38).

Полная стратегия может быть записана как 5 x 38 = 10 x 19

Посмотрите, как это сделать, используя Видео 2.

Разделение разрядного значения: 5, добавить 8 х 5.

Стратегию можно записать в виде 5 х 38 = 5 х 30 + 5 х 8 или в рабочей форме:

Посмотрите, как это сделать, используя Видео 3.

По мере появления различных стратегий попросите учащихся объяснить, почему они решили решить задачу таким образом. Примите все стратегии, предложенные на этом этапе, запишите их, чтобы обдумать позже в модуле (возможно, в книге по моделированию, в цифровом документе или на плакате). Имейте в виду, что некоторые учащиеся могут предпочесть складывать, а не умножать.

Например:

                      

Вы можете обсудить эффективность умножения по сравнению с повторным сложением.

Чтобы получить похожие задачи, измените числа в Задаче 1 (Копирайтер 2), например:

Ванесса проезжает на велосипеде по 46 километров каждый день в течение четырех дней. Сколько километров она проехала за четыре дня?

Эти задачи также можно изменить, чтобы отразить соответствующие знания из других областей учебной программы (например, 6 детей пробежали 5 км на региональном чемпионате по кроссу, какое расстояние они пробежали вместе? 4 команды соревновались в 20-километровой гонке вака-ама, как далеко они путешествовали каждый день?)

Задача 2 (копирайтер 3):
В восьмёрки Кубка Маади вошли 256 гребцов, не считая водителей (рулевых).

Сколько можно составить экипажей из восьми гребцов?

Попросите учащихся придумать ответ в уме, если они могут, и записать свою стратегию на бумаге. Дайте учащимся необходимое время на размышление. Затем попросите их поделиться своими решениями со своим партнером по обучению. Возможны следующие ответы:

Разбиение разряда (дробление):
184 ÷ 8
Я знаю, что 160 ÷ 8 = 20. Это 20 экипажей.
Осталось 24 гребца. 24 ÷ 8 =3

Ответ: 20 + 3 = 23.

Посмотрите, как это сделать, используя Видео 4.

Факторизация (пропорциональное регулирование): 

Деление на 8 похоже на разделив на 2, затем на 2, затем на 2, так что половина 184 будет 92, а половина 92 будет 46, и снова разделив на 2, я получу 23, поэтому ответ будет 23.

Посмотрите, как это сделать, используя Видео 5.

Округление и компенсация: 
Если бы было 200 гребцов, это было бы 25 экипажей, потому что 4 x 25 = 100, поэтому 8 x 25 = 2 00. 184 На 16 гребцов меньше. То есть два экипажа. Таким образом, ответ 25 – 2 = 23.

По мере появления различных стратегий попросите учащихся объяснить, почему они решили решить задачу таким образом. Примите все стратегии, предложенные на этом этапе, запишите их, чтобы обдумать позже в рамках модуля (возможно, в книге по моделированию). Следите за повторяющимся вычитанием или частичным использованием умножения, например:

10 x 8 = 80

80 + 80 = 160, 20 x 8 = 160

160 + 8 = 168, 168 + 8 = 176, 176 + 8 = 184

Итак 2 Можно сделать 3 экипажа

Посмотреть как это сделать с помощью Видео 6.

Попросите учащихся подумать над стратегиями, которые обсуждались на занятии, и оценить, над какими стратегиями им лично нужно поработать, возможно, используя сигналы большим пальцем — большой палец вверх — уверенный и компетентный в стратегии , большой палец в сторону — полууверенно, большой палец вниз — еще не уверен. Используйте эту информацию, чтобы спланировать свое последующее обучение из раздела изучения, описанного ниже.

Чтобы предоставить другие связанные примеры, измените числа в Задаче 2 (Копирайтер 3), например:

В чемпионате по гребле на четверках на Кубке Маади заявлено 212 гребцов, не считая водителей (рулевых).

Сколько можно составить экипажей из четырех гребцов?

Изучение

В течение следующих двух-трех дней изучите следующие стратегии, четко обозначив стратегию, на которой вы концентрируетесь как учитель, и причину использования выбранной стратегии. Например, В задаче 7 x 29аккуратные цифры были бы полезной стратегией, так как 29 близко к 30.  Предлагайте учащимся также поделиться и обосновать использование своей стратегии. Если у вас есть множество стратегий, используемых разными учащимися, вы можете рассмотреть возможность реализации подхода tuakana-teina , при котором учащиеся работают совместно и учатся у своих сверстников.

Следующие вопросы приведены в качестве примеров для продвижения определенных стратегий. Если учащиеся не уверены в стратегии, вам, возможно, придется придумать некоторые из ваших собственных вопросов, чтобы удовлетворить потребности учащихся.

Для обсуждения стратегии можно использовать следующие вопросы:

• Какое точное число или числа, близкие к одному из факторов задачи, вы могли бы использовать?
• Что нужно сделать, чтобы убрать этот номер? Почему?
• Почему эта стратегия полезна для этой проблемы?
• Какие знания помогут вам решить такую ​​задачу?

Разделение разряда (умножение) 
У Мани есть 54 доллара, но ему нужно в 7 раз больше этой суммы, чтобы купить новый горный велосипед, который он хочет. Сколько денег стоит велосипед?
Стратегия разрядной стоимости включает умножение единиц и десятков по отдельности, а затем объединение частичных произведений. Эта стратегия использует распределительное свойство умножения, так как 54 делится на 50 + 4. В приведенной выше задаче ученик может сказать следующее:
Я умножил 7 х 50 и получил 350, затем я умножил 7 х 4 и получил 28. Я добавил 350 и 28, чтобы получить 378.

Для обсуждения стратегии можно использовать следующие вопросы:

• Как вы можете использовать свои знания о разрядности для решения этой проблемы?
• Почему эта стратегия полезна для этой проблемы?

Если кажется, что учащиеся не понимают концепцию разделения, покажите задачи физически, используя материалы с оценочными значениями, такие как блоки с оценочными значениями, BeaNZ и канистры или игрушечные деньги. Некоторым учащимся может быть полезно записывать и отслеживать свои мысли. Расширение стратегии позиционной стоимости включает использование стандартной письменной формы для умножения.

При необходимости используйте следующие вопросы для дальнейшей практики:

• 3 x 135
• 9 х 66
• 6 х 132
• 8 х 79

Разбивка (деление) разряда
Писи подрабатывает на рынке, расфасовывая папайю в пакеты по 6 штук. Если нужно расфасовать 864 папайи, сколько пакетов он сможет сделать?
Стратегия разделения по разрядным значениям для деления включает в себя «разбиение на части» известных фактов и вычитание их из ответа. Разбиение по разрядным значениям является основой письменной формы или алгоритма деления. В приведенном выше случае учащийся может подумать:
100 x 6 = 60, поэтому 100 мешков будут 600. 864 – 600 = 264. Остается 264. уберите еще 120 папайи, и я получу 24, то есть 4 лота из 6. Итак, я убрал 100 лотов, затем 20, затем 20, затем 4… ответ 144.

Это мышление может быть записано как:

Если кажется, что учащиеся не понимают концепцию разделения, покажите проблемы физически, т. е. с использованием блоков позиционных значений. Студентам будет полезно записывать и отслеживать свои мысли, а также уменьшать нагрузку на память. Расширение стратегии стоимости места включает использование стандартной письменной формы для деления.

При необходимости используйте следующие вопросы для дальнейшей практики:

• 760 ÷ 5
• 516 ÷ 4
• 992 ÷ 8
• 3808 ÷ 7
• 522 ÷ 3
• 2505 ÷ 9

Округление и компенсация (умножение) 
Фанаты нетбола Southern Sting едут в Крайстчерч, чтобы посмотреть матч по нетболу против Canterbury Tactix.

Каждый автобус полный, в нем 48 человек, всего 9 автобусов.

Сколько поклонников Стинга направляется в Крайстчерч?

Стратегия округления и компенсации включает в себя округление числа в вопросе, чтобы упростить его решение. В приведенном выше вопросе 48 можно округлить до 50 (прибавив 2). Тогда задача принимает вид 9 x 50 = 450. Чтобы компенсировать округление, из «округленного» уравнения необходимо вычесть две партии по 9 человек (18).

Если кажется, что учащиеся не понимают концепцию аккуратных чисел, используйте оборудование с порядковыми значениями или большой точечный массив, чтобы показать задачи физически. Некоторым учащимся может быть полезно записывать и отслеживать свои мысли. Запись может выглядеть так:

9 x 48 = 9 x 50 – 9 x 24                            9 x 40 = 10 x 48 – 1 x 48

= 450 – 18                                                                                                                               = 43 2
 

Посмотрите, как это сделать, используя видео Семь и восемь.

При необходимости используйте следующие вопросы для дальнейшей практики, все еще используя тот же контекст шины:

• 7 x 29
• 6 х 38
• 5 х 57
• 3 х 69
• 4 х 97
• 8 х 36

Обратите внимание, что проблемы, изложенные здесь, используют стратегию очистки, а не уборки. Если один из факторов чуть больше аккуратного числа (например, 42), то более полезной стратегией может оказаться стандартное разбиение на разряды.

Округление и компенсация (Отдел)

Каждую неделю Сара использует девять билетов на автобус для поездок по городу. Она выигрывает 162 билета на радиоконкурсе. На сколько недель ей хватит билетов?
Округление и компенсация деления включает в себя поиск числа, близкого к делимому (начальной сумме), и работу с этим числом, чтобы найти ответ. На приведенный выше вопрос студент может сказать:

Я знаю, что 20 умножить на 9 равно 180. 162 на 18 меньше 180, то есть 2 x 9.

Билетов ей хватит на 20 – 2 = 18 недель .

Если кажется, что учащиеся не понимают концепцию округления и компенсации, используйте материалы с порядковыми значениями или большой точечный массив для физического представления задач. Студенты могут счесть полезным записывать и отслеживать свои мысли, особенно если они сначала частично делят дивиденды.

Посмотрите, как это сделать, используя Видео 7.

Используйте тот же контекст автобусных билетов, чтобы ставить задачи, где округление и компенсация являются разумной стратегией.

• 343 ÷ 7
• 224 ÷ 8
• 597 ÷ 3
• 392 ÷ 4
• 1764 ÷ 18

Пропорциональная корректировка (факторизация) 
На фестивале Капа Хака участвуют 32 школы, по 25 учащихся в каждой группе, сколько всего учащихся в группах?
Пропорциональная корректировка предполагает использование знаний о коэффициентах и ​​множителях для создания более простых уравнений с одинаковым ответом. Факторы пропорционально корректируются, чтобы облегчить работу с одним (или обоими) факторами. В приведенной выше задаче множители можно скорректировать следующим образом:

Или, используя удвоение и деление пополам:

Следующие вопросы можно использовать для обсуждения стратегии:

• На что можно умножить одно из этих чисел? для облегчения работы?
• Что вам нужно сделать с другим номером, чтобы продукт (ответ) оставался прежним?
• Почему эта стратегия полезна для этой проблемы?
• Какие знания помогут вам решить такую ​​задачу?

Если кажется, что учащиеся не понимают концепцию пропорциональной корректировки, используйте большой точечный массив, чтобы показать проблемы физически. Некоторым учащимся может быть полезно записывать и отслеживать свои мысли.

Посмотрите, как это сделать, используя Видео 8.

При необходимости используйте следующие вопросы для дальнейшей практики:

• 25 x 200 (умножьте и разделите на пять)
• 27 x 3 (в 3 и 3 раза)
• 33 x 18 (в 3 и 3 раза)
• 44 x 25 (умножить и разделить на четыре)
• 24 x 125 (умножить и разделить на восемь)

Пропорциональная регулировка (раздел)
Рыболовная компания собирает в общей сложности 912 пипи за полгода.

Сколько пипи собиралось каждый месяц?

При делении пропорциональная корректировка включает изменение обоих чисел в уравнении на один и тот же коэффициент. Следовательно, числа, используемые для пропорциональной корректировки задачи, должны быть множителями обоих чисел в уравнении (делимого и делителя). Например:
Если я разделю 912 на 3 и 6 на 3, мое уравнение станет 304 ÷ 2 с тем же ответом. Половина от 304 — это 152. Таким образом, каждый месяц собиралось 152 пипи.

Для обсуждения стратегии можно использовать следующие вопросы:

• Какой общий множитель обоих чисел можно использовать для облегчения задачи?
• Почему эта стратегия полезна для этой проблемы?
• Какие знания помогут вам решить такую ​​задачу?

Если кажется, что учащиеся не понимают концепцию пропорциональной регулировки, используйте оборудование, чтобы показать проблемы физически. Некоторым учащимся может быть полезно записывать и отслеживать свои мысли.

При необходимости используйте следующие вопросы для дальнейшей практики. Подумайте, как эти вопросы могут отразить культурное разнообразие и учебные интересы вашего класса.

• 636 ÷ 12 = 212 ÷ 4 = 106 ÷ 2 = 53
• 480 ÷ 15 = 96 ÷ 3 = 32
• 1962 ÷ 18 = 981 ÷ 9 = 109
• 1498 ÷ 14 = 749 ÷ 7 = 107
• 1728 ÷ 16 = 864 ÷ 8 = 108

Факторизация (умножение и деление)
У Стефани 492 дополнительных шарика, чтобы разделить поровну между шестью ее друзьями. Сколько шариков достанется каждому?

Стратегия факторизации включает использование факторов для упрощения задачи. В этом случае шесть можно разложить на множители как 2 x 3. Это означает, что деление на два, а затем на три дает тот же чистый эффект, что и деление на 6. Точно так же умножение на два, а затем на три дает тот же чистый эффект, что и умножение на 6. Применяя факторизацию к приведенной выше задаче, учащийся может подумать:

6 равно 2 x 3. Итак, я делю 49 пополам.2, затем третий результат. Если я разделю 492 на 2, то получу 246. 246 разделить на 3 будет 82. Ответ будет 82.

Следующие вопросы можно использовать для обсуждения стратегии:

• Как вы можете использовать свои знания о факторах Для решения этой проблемы?
• Почему для этой задачи полезна стратегия факторизации?

Если учащиеся не понимают концепцию факторизации, покажите задачи физически. Некоторым учащимся может быть полезно записывать и отслеживать свои мысли.

При необходимости используйте следующие вопросы для дальнейшей практики. Подумайте, как эти вопросы могут отразить культурное разнообразие и учебные интересы вашего класса.

• 144 ÷ 4 (÷2, ÷2)
• 270 ÷ 6 (÷3, ÷2)
• 612 ÷ 9 (÷3, ÷3)
• 532 ÷ 8 (÷2, ÷2, ÷2)
• 348 ÷ 12 (÷2, ÷2, ÷3)
• 4320 ÷ 27 (÷3, ÷3, ÷3)
• 135 х 12 (х2, х2, х3)
• 43 х 8 (х2, х2, х2)
• 27 х 16 (х2, х2, х2, х2)

Каждый день следуйте той же структуре урока, что и вводная сессия, когда учащиеся делятся своими решениями на начальные вопросы и обсуждают, почему эти вопросы подходят для стратегии, которую они подробно изучают. Завершайте каждое занятие, предлагая учащимся сделать несколько утверждений о том, когда эта стратегия будет полезной и почему (например, «Значение места полезно, когда требуется ограниченное переименование» или «Факторизация полезна, когда один из факторов можно переименовать в виде ряда). меньших факторов»).