Лучший ответ по мнению автора
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
Пользуйтесь нашим приложением
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92, а также чему он равен. Это будет темой последнего раздела этого сообщения в блоге. Это будет темой последнего раздела этого сообщения в блоге.Но прежде чем мы углубимся в эту идею, давайте подытожим другое содержание лекций. Лекция 4AЯ начинаю лекцию 4A с решения задач с экспоненциальными уравнениями. Расчет 1, Урок 4A: Экспоненциальные задачи, линейное и экспоненциальное моделирование ВВП, композиция функцийОбщий смысл решения таких задач таков. Учитывая две точки данных и , мы стремимся найти числа и такие, что график экспоненциальной функции проходит через эти точки. Это означает, что мы хотим, чтобы и то, и другое было правдой. Деление первого уравнения на второе дает , предполагая . Затем это уравнение решается путем извлечения корня из обеих частей. Другим важным моментом в лекции 4А является идея моделирования данных. Рассматриваются реальные данные о валовом внутреннем продукте (ВВП) США. Затем я графически сравниваю, какая модель лучше «подходит» для данных — линейная или экспоненциальная. Считается, что экспоненциальная модель лучше, потому что ее остатки (ошибки) более случайны. Это очень важная перспектива, если вы хотите использовать математические модели в реальной жизни. Последний пункт лекции 4А — композиция функций. Композиция функций означает, что мы применяем две функции в последовательности . Имея две функции и соответствующие домены и кодомены, мы можем сформировать новую функцию. Эта функция определяется формулой . Другими словами, вывод подключается к . Это важная концепция как для более глубокого понимания функций, так и для идеи обратной функции. Лекция 4Б Это подводит нас к лекции 4B, где я начинаю описывать обратные функции и их свойства. Сначала более подробно дается идея композиции функций на примере. Отсюда определяются обратные функции для взаимно однозначных функций. Учитывая взаимно-однозначную (инъективную) функцию, ее обратная функция определяется так, чтобы удовлетворять двум свойствам относительно композиции. Оно должно удовлетворять всем в области . И оно должно удовлетворять всем в области (которая находится в диапазоне 0, Еще один факт, который я подчеркиваю в этой лекции, заключается в том, что функции, которые не являются взаимно однозначными, иногда можно сделать таковыми путем соответствующего ограничения их доменов. Я также использую функцию под названием «Управление» в Mathematica , чтобы сделать анимацию графика увеличения. Это соответствует горизонтальному переносу (сдвигу) «родительской» функции. Отсюда я решаю физическую задачу о высоте объекта под действием силы тяжести, используя функцию, обратную квадратичному. Как уже упоминалось, метод завершения квадрата используется для преобразования квадратного числа в вершинную форму. Затем область определения сужается и по квадратичной формуле находится соответствующая обратная функция. 92 при произвольном значении x для измерения (мгновенной) скорости изменения функции в этой точке. Начните с выбора произвольного значения . Тогда пусть будет ненулевым числом. Это стандартное обозначение для изменения x . Мы действительно воображаем, что независимая переменная (вход) для функции меняется с на . Если , то вход увеличивается и . Если , то вход убывает. Для простоты предположим, что . График не является линией, поэтому он не имеет постоянного наклона. Однако среднюю скорость изменения на закрытом интервале все же можно определить. Он определяется как наклон линии, соединяющей точки и . Эта линия называется секущей к графику . Его наклон равен . Для можно сделать следующее упрощение этого выражения. . Наглядное изображение секущей линии, приближающейся к касательнойПоследнее равенство верно до тех пор, пока , что мы и предполагаем. То, что мы только что сделали, можно визуализировать, как показано ниже. Наклон секущей к графику между и равен . В этом визуальном элементе наклон упрощается до . По мере приближения к 0 этот наклон становится все ближе и ближе к 3. В этом визуальном элементе наклон упрощается до . По мере приближения к 0 этот наклон становится все ближе и ближе к 3.Так что же тогда является производной ? Это предел наклонов этих секущих линий, когда они «стремятся» к нулю. Этот предел, , если он существует , тогда равен определяется как наклон касательной к графику при заданном значении . Другими словами, в данной точке на графике касательной является линия, проходящая через эту точку с наклоном, равным только что описанному пределу . Производная — это пределНо что такое предел? Мы уточним ограничения в следующем посте. На данный момент в данной ситуации просто представьте, что значения as становятся все ближе и ближе к нулю, фактически не равняясь нулю (потому что тогда мы будем делить на ноль). С тех пор, как этот предел можно найти, подумав о значениях, когда он близок к нулю. Как происходит это мышление? Проще говоря, поскольку это «хорошая» (непрерывная) функция (предполагая «фиксированную»), мы можем просто подключиться, чтобы получить ответ. |

 02.16
02.16 Затем вы можете использовать одно из исходных уравнений для решения .
Затем вы можете использовать одно из исходных уравнений для решения .
 2 в этом посте.
2 в этом посте.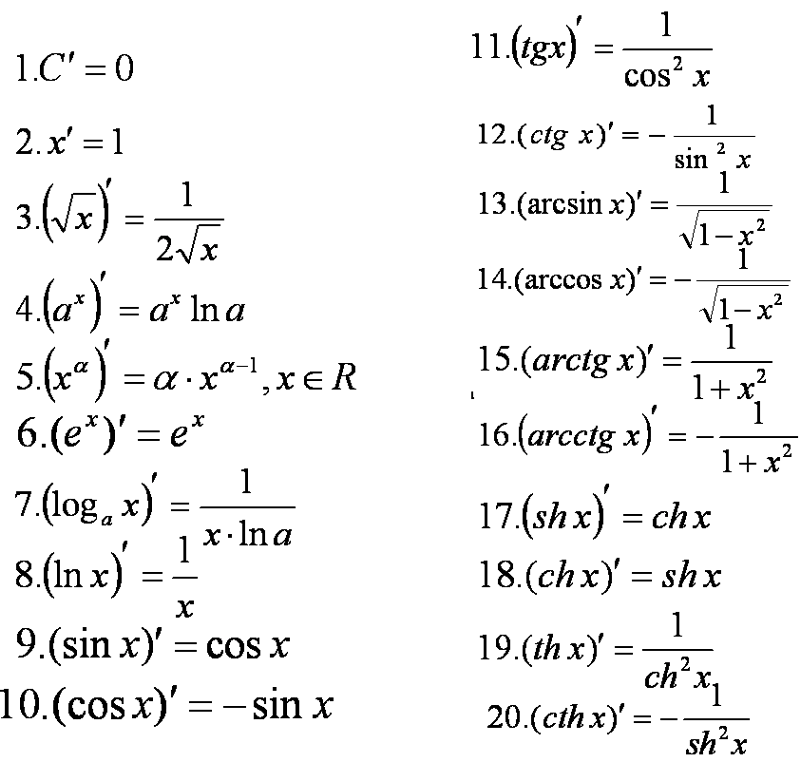 Это также описывается как наклон касательной к графику в этой точке.
Это также описывается как наклон касательной к графику в этой точке.