Неопределенный интеграл — #2 от пользователя Amir — Физика — Спроси!
eneev (Eneev Magomed)
#1
Скажите пж, используются ли на практике неопределенные интегралы?
Amir (Amir Tomashpayev)
#2
Он понадобится к примеру тогда, когда в условии дана изначально функция, а для решения потребуется первообразная. Вообще в любом случае стоит потренироваться решать неопределённые интегралы, потому что это разовьёт навык.
6 лайка
Damir (Yekibayev Damir)
#3
Amir Tomashpayev:
Вообще в любом случае стоит потренироваться решать неопределённые интегралы, потому что это разовьёт навык.
Полностью согласен
4 лайка
Anton (Anton Morgunov)
#4
Eneev Magomed:
используются ли на практике неопределенные интегралы?
каждый день использую
3 лайка
NotAshurovAltair (Альтаир Аканов)
#5
Вообще, интегралы тебе точно понадобится. Неопределённый интеграл ты тоже изучай. Я просто сам встречался когда определённый интеграл лучше решить через неопределённый. Например, метод интегрирования способом Фейнмана (подробнее трюк Фейнмана посмотри на ютубе, канал: Hmath). Трюк Фейнмана, это когда у тебя есть определённый интеграл, в нём какой-то коэффициент (которым наиболее удобно решать) заменяешь на другую переменную (пусть будет t). Теперь у тебя есть функция I(t)=\int f(t, x)dx. Находишь частную производную от I по t и решаешь интеграл. Теперь у тебя есть производная I по t. Интегрируешь по t. У тебя получилась какая-то функция +C. Эту константу можно найти через самый начальный интеграл: просто t приравниваешь к какому то коэффициенту k, такому, при котором этот интеграл равен нулю или при котором подынтегральная функция равна нулю (если у тебя получилась неопределенность типа: 0/0, 0×\infty, \infty/\infty, то используй правило Лопиталя (в Демидовиче есть такая тема).
5 лайка
NotAshurovAltair (Альтаир Аканов)
#6
А и, таким образом ты решил определенный интеграл через общий случай.
А и, почитай книжки по вышмату, такие как Thomas calculus или Демидовича(у него есть свой сборник задач), ещё прочитай планы подготовки по своему предмету, их составляли дельные люди
2 лайка
NotAshurovAltair (Альтаир Аканов)
А ещё, обычно учат неопределённый интеграл, после определенный. В темах об неопределенных интегралах обычно рассказываются методы интегрирования
2 лайка
Alisher (Alisher Yerkebayev)
#8
Альтаир:
Находишь частную производную от I по t и решаешь интеграл.
{\displaystyle n+1}}.
8 лайка
Определенный интеграл. Примеры решений
И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.
В общем виде определенный интеграл записывается так: Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой .
отрезком интегрирования.Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.
Что такое определенный интеграл? Я бы мог вам рассказать про диаметр разбиения отрезка, предел интегральных сумм и т.д., но урок носит практический характер. Поэтому я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле никогда не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: .
3) Подставляем значение нижнего предела в первообразную функцию: .
4) Рассчитываем (без ошибок!) разность , то есть, находим число.
Готово.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса.
Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики. Для того чтобы определенный интеграл вообще существовал, необходимо чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так: ???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будетнесобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.
– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
5.5: Неопределенные интегралы и правило подстановки
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5481
Цели обучения
- Применение основных формул интегрирования.
- Объясните значение теоремы о чистом изменении.
- Используйте теорему о чистых изменениях для решения прикладных задач.
- Применить интегралы от нечетных и четных функций.
В этом разделе мы используем некоторые основные формулы интегрирования, изученные ранее, для решения некоторых ключевых прикладных задач. Важно отметить, что эти формулы представлены в терминах неопределенных интегралов. Хотя определенные и неопределенные интегралы тесно связаны между собой, следует помнить о некоторых ключевых различиях. Определенный интеграл — это либо число (когда пределы интегрирования — константы), либо отдельная функция (когда один или оба предела интегрирования — переменные). Неопределенный интеграл представляет собой семейство функций, каждая из которых отличается на константу. По мере того, как вы будете лучше знакомиться с интегрированием, вы почувствуете, когда использовать определенные интегралы и когда использовать неопределенные интегралы.
Теорема о чистом изменении
Теорема о чистом изменении рассматривает интеграл скорости изменения . В нем говорится, что при изменении количества новое значение равно первоначальному значению плюс интеграл скорости изменения этого количества. Формула может быть выражена двумя способами. Второй более знаком; это просто определенный интеграл.
Теорема о чистом изменении
Новое значение изменяющейся величины равно первоначальному значению плюс интеграл скорости изменения: 9b_aF'(x)dx=F(b)−F(a). \label{Net2} \]
Вычитание \(F(a)\) из обеих частей уравнения \ref{Net1} дает уравнение \ref{Net2}.
Значение теоремы о чистом изменении заключается в результатах. Чистое изменение может быть применено к площади, расстоянию и объему, и это лишь некоторые из приложений. Чистое изменение учитывает отрицательные величины автоматически, без необходимости писать более одного интеграла. Чтобы проиллюстрировать это, давайте применим теорему о чистом изменении к скорость функция, результатом которой является смещение.
Мы рассмотрели простой пример этого в разделе «Определенный интеграл». Предположим, что автомобиль движется прямо на север (в положительном направлении) со скоростью 40 миль в час между 14:00 и 14:00. и 16:00, затем машина движется на юг со скоростью 30 миль в час между 16:00 и 16:00. и 17:00 Мы можем изобразить это движение, как показано на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): График показывает зависимость скорости от времени для заданного движения автомобиля.Как и раньше, мы можем использовать определенные интегралы для расчета чистого перемещения, а также общего пройденного расстояния. 95_430\,дт=80+30=110. \nonumber \]
Таким образом, между 14:00 и 17:00 машина проехала в общей сложности 110 миль.
Подводя итог, чистое смещение может включать как положительные, так и отрицательные значения. Другими словами, функция скорости учитывает как расстояние вперед, так и расстояние назад. Чтобы найти чистое смещение, проинтегрируйте функцию скорости по интервалу. С другой стороны, общее пройденное расстояние всегда положительно. Чтобы найти общее расстояние, пройденное объектом независимо от направления, нам нужно проинтегрировать абсолютное значение функции скорости. 92}{2}−5(3)\right]−0=\frac{27}{2}−15=\frac{27}{2}−\frac{30}{2}=−\frac{3 {2}. \nonumber \]
Чистое водоизмещение равно \( −\frac{3}{2}\) м (рис. \(\PageIndex{2}\)).
Рисунок \(\PageIndex{2}\): График показывает зависимость скорости от времени для частицы, движущейся с линейной функцией скорости.Пример \(\PageIndex{3}\): определение общего пройденного расстояния
Используйте пример \(\PageIndex{2}\) для нахождения общего расстояния, пройденного частицей в соответствии с функцией скорости \(v(t) =3t−5\) м/с за интервал времени \([0,3].\)
Решение
Общее пройденное расстояние включает как положительные, так и отрицательные значения. Следовательно, мы должны проинтегрировать абсолютное значение функции скорости, чтобы найти общее пройденное расстояние.
Чтобы продолжить пример, используйте два интеграла, чтобы найти общее расстояние. Сначала найдите \(t\)-пересечение функции, так как именно там происходит деление интервала. Приравняйте уравнение к нулю и решите относительно \(t\). Таким образом,
\[ \begin{align*} 3t−5 &=0 \\[4pt] 3t &=5 \\[4pt] t &=\frac{5}{3}. \end{выравнивание*}\] 94}{4}\right]−0 \\[4pt] &=10−\frac{16}{4} \\[4pt] &=6. \end{align*} \nonumber \]
Таким образом, моторная лодка использует \(6\) галлонов бензина за \(2\) часа.
Пример \(\PageIndex{5}\): Начало главы: Iceboats
Как мы видели в начале главы, лучших гонщиков на ледяных лодках могут развивать скорость, в пять раз превышающую скорость ветра. Однако Эндрю — средний ледоход, поэтому он развивает скорость, равную только удвоенной скорости ветра.
Рисунок \(\PageIndex{3}\): (кредит: модификация работы Картера Брауна, Flickr)Предположим, однажды утром Эндрю выводит свою лодку на лед, когда все утро дует легкий бриз со скоростью \(5\) в час. Однако, когда Эндрю настраивает свою ледяную лодку, ветер начинает усиливаться. В течение первых получаса его катания на лодке скорость ветра увеличивается в соответствии с функцией \(v(t)=20t+5.\). Во вторые полчаса прогулки Эндрю остается стабильным со скоростью \(15\) миль в час. Другими словами, скорость ветра определяется как
\[ v(t)=\begin{cases}20t+5, & \text{для } 0≤t≤\frac{1}{2}\\15, & \text{for} \frac{1}{2}≤t≤1\end{cases} \nonumber \] 91_{1/2} \\[4pt]
&=\left(\frac{20}{4}+5\right)−0+(30−15) \\[4pt]
&=25.Эндрю находится в 25 милях от начальной точки через 1 час.
Упражнение \(\PageIndex{3}\)
Предположим, что вместо того, чтобы оставаться устойчивым в течение вторых получасов прогулки Эндрю, ветер начинает стихать в соответствии с функцией \(v(t)=−10t+ 15.\) Другими словами, скорость ветра определяется как
\[ v(t)=\begin{cases}20t+5, & \text{for } 0≤t≤\frac{1}{2} \\−10t+15, &\text{для } \frac{1}{2}≤t≤1\end{случаев}. \номер\]
В этих условиях, как далеко от исходной точки находится Андрей через 1 час?
- Подсказка
Не забывайте, что ледяная лодка Эндрю движется в два раза быстрее ветра.
- Ответить
\(17,5\) ми
Интегрирование четных и нечетных функций
Мы видели в разделе «Функции и графики», что четная функция — это функция, в которой \(f(−x)=f(x)\) для всех \(x\) в области — то есть график кривой не изменится при замене \(x\) на \(−x\).
Интегралы четных функций, когда пределы интегрирования от \(−a\) до \(a\), включают две равные площади, потому что они симметричны относительно оси \(y\). Интегралы нечетных функций, когда пределы интегрирования равны \([−a,a],\), оцениваются как нуль, потому что площади выше и ниже оси \(x\) равны.
Интегралы четных и нечетных функций 98−2)\,dx\) и убедиться в справедливости формулы интегрирования четных функций.
Решение
Симметрия показана на графиках на рисунке \(\PageIndex{4}\). На графике (а) показана область под кривой и над осью \(х\). Нам нужно сильно увеличить этот график, чтобы увидеть регион. На графике (b) показана область над кривой и под осью \(x\). Знаковая область этой области отрицательна. Оба представления иллюстрируют симметрию относительно оси \(y\) четной функции.
Так как \( 2⋅\frac{500}{3}=\frac{1000}{ 3},\) мы проверили формулу для четных функций на данном конкретном примере.
Рисунок \(\PageIndex{4}\): На графике (a) показана положительная площадь между кривой и осью \(x\), тогда как на графике (b) показана отрицательная площадь между кривой и \(x\) \)-ось. Оба вида показывают симметрию относительно оси \(y\).Пример \(\PageIndex{7}\): интегрирование нечетной функции
Вычисление определенного интеграла от нечетной функции \(−5 \sin x\) на интервале \([−π,π].\) 94\,дх.\)
- Подсказка
Интегрировать четную функцию.
- Ответить
\(\dfrac{64}{5}\)
Ключевые понятия
- Теорема о чистом изменении утверждает, что при изменении количества конечное значение равно начальному значению плюс интеграл скорости изменения.
9b_aF'(x)\,dx=F(b)−F(a) \nonumber \]Глоссарий
- Теорема о чистых изменениях
- если мы знаем скорость изменения количества, теорема о чистых изменениях говорит, что будущее количество равно первоначальному количеству плюс интеграл скорости изменения количества
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- нет
- Теги
На этой странице нет тегов.
Неопределенные интегралы — исчисление 2
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 … 25 26 Следующая →
Исчисление 2 Помощь » Интегралы » Нахождение интегралов » Неопределенные интегралы
Найдите неопределенный интеграл следующей функции:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы интегрировать эту функцию, используйте подстановку u. Сделайте
, затем подставьте их в уравнение, чтобы получить
.
Интеграл
затем подставьте u обратно в уравнение
.
+C необходим, потому что интеграл не определен.
Сообщить об ошибке
Вычислить заданный неопределенный интеграл
.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы интегрировать эту функцию, используйте подстановку u. Сделайте
, затем подставьте их в уравнение, чтобы получить
.
Интеграл
затем подставьте u обратно в уравнение
.
+C необходим, потому что интеграл не определен.
Сообщить об ошибке
Вычислить заданный неопределенный интеграл
.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы интегрировать эту функцию, используйте подстановку u.
, затем подставьте их в уравнение, чтобы получить
.
Интеграл от
, поэтому мы имеем
.
+C необходим, потому что интеграл не определен.
Сообщить об ошибке
Вычислите следующий неопределенный интеграл.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы вычислить интеграл, нам нужно использовать интегрирование по частям. Определение интегрирования по частям:
Здесь важно выбрать правильные члены u и dv из нашего исходного интеграла. В конечном итоге мы хотим, чтобы термины «ушли», когда мы возьмем его производную. Здесь мы замечаем, что из двух наших функций в нашем интеграле и производная x равна 1, что в конечном итоге очень просто интегрировать. Следовательно, будет нашим термином, а будет нашим термином dv.
Теперь вычислите члены и , необходимые для выполнения уравнения интегрирования по частям.
(вы можете установить константу интегрирования c=0)
Теперь, когда у нас есть нужные нам члены, мы можем подставить их в приведенную выше формулу интегрирования по частям.
—
Обратите внимание: хотя нам все еще нужно интегрировать еще раз, этот новый интеграл состоит только из одной функции, которую легко интегрировать, в отличие от двух функций, которые у нас были раньше. Также обратите внимание, что член x из исходного интеграла «ушел», что упрощает вычисление результирующего интеграла.
Упрощение этого термина теперь становится
.
Сообщить об ошибке
Если
Что такое
?
Возможные ответы:
Правильный ответ:
Объяснение:
Хотя интеграл выглядит сложно, его можно значительно упростить.
Используя это тождество, теперь можно упростить интеграл до
, который очень просто интегрировать.
Сообщить об ошибке
Решите следующее для .
Предположим, что постоянная интегрирования равна нулю.
Возможные ответы:
Правильный ответ:
Объяснение:
В этой задаче мы можем попытаться получить все термины с с одной стороны и все термины с с другой.
Теперь мы можем интегрировать обе стороны, используя определение и степенное правило.
и
Сообщить об ошибке
Решите следующее для .
Допустим константа интегрирования Объяснение:
Переместите все выражения с в одну сторону, а все – в другую.
Теперь интегрируйте обе стороны, используя правило степени и определение натурального логарифма.
Степенное правило для состояний интегралов,
и определение натурального логарифма,
.
Применяя эти правила, мы можем решить проблему.
Сообщить об ошибке
Вычислите следующий интеграл.
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно использовать следующее удостоверение:
Теперь наш интеграл становится равным
.
Обратите внимание, что внутри косинуса становится 4, потому что мы уже имели 2 в исходном выражении.
Можно разделить на два интеграла
.
Что становится
.
Сообщить об ошибке
Найдите неопределенный интеграл от .
Возможные ответы:
Ничего из вышеперечисленного
Правильный ответ:
Объяснение:
Мы можем найти неопределенный интеграл от используя правило степени для интегралов, которое гласит, что
для всех и с произвольной константой интегрирования .
Применение этого правила к
.
Сообщить об ошибке
Найдите неопределенный интеграл от .
Возможные ответы:
Ничего из вышеперечисленного
Правильный ответ:
Объяснение:
Мы можем найти неопределенный интеграл от , используя правило степени для интегралов, которое гласит, что
для всех и с произвольной константой интегрирования .
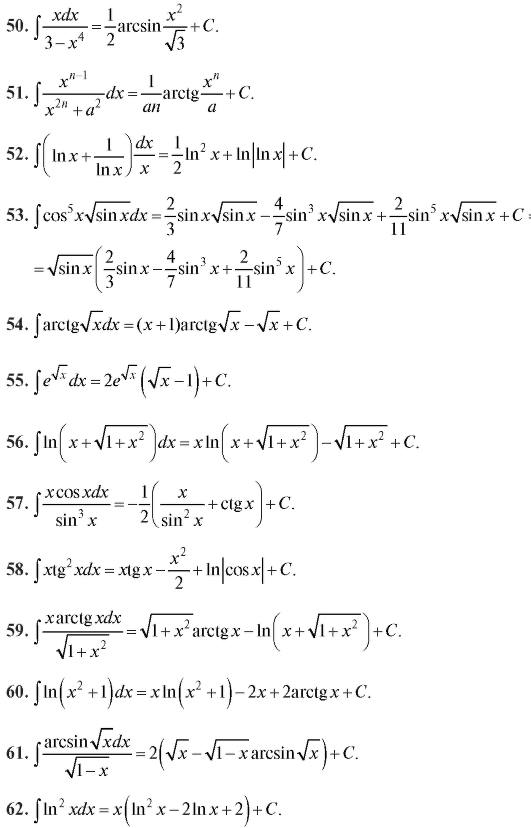{\displaystyle n+1}}.
Верхний
предел интегрирования стандартно
обозначается буквой
.
Отрезок
называется 
Вы, естественно, выберете правильный подход к данной проблеме, не слишком задумываясь об этом. Однако до тех пор, пока эти концепции не закрепятся в вашем уме, тщательно подумайте, нужен ли вам определенный интеграл или неопределенный интеграл, и убедитесь, что вы используете правильную запись, основанную на вашем выборе. 92 — 3x\справа) \, dx = −\frac{10}{3} \nonumber \]
Поскольку это эквивалентные формулы, какую из них мы используем, зависит от приложения.
\end{align*}\]
Графики четных функций симметричны относительно оси \(y\). нечетная функция — это функция, в которой \(f(-x)=-f(x)\) для всех \(x\) в области, а график функции симметричен относительно начала координат.
У нас есть 92_{0}=\frac{512}{3}−4=\frac{500}{3} \nonumber \]
Чистое изменение может быть положительным числом, отрицательным числом или нулем.
Сделайте
Обратите внимание, что термин dv — это не только dx, но и связанная с ним функция. Если бы это был наш термин, то это был бы наш термин dv.
Помните об этой важной триггерной идентичности.
