Как решать комбинаторные задачи 6 класс объяснение: Решение комбинаторных задач | Методическая разработка по алгебре (6 класс) по теме:

Содержание

Решение комбинаторных задач | Методическая разработка по алгебре (6 класс) по теме:

Конспект урока по теме

«Решение комбинаторных задач»

МБОУ СОШ № 20 п. Железнодорожный

учитель 1 математики квалификационной

категории Суворова Л.В.

Класс: 6

Предмет: математика.

Продолжительность: 40 минут

Тип урока: объяснение нового материала

Цели:

Образовательные:

— создать представление о комбинаторике как разделе математики;

— формировать умение решать комбинаторные задачи путем перебора возможных вариантов с помощью дерева вариантов или путем перестановки закодированных элементов;

— познакомить учащихся с решением комбинаторных задач и с использованием правила умножения;

— показать применение знаний, полученных на уроках математики, на практике.

Развивающие:

— развивать логическое мышление, устную математическую речь, внимание, память и воображение через интеллектуальные задания;

— развивать умение решать комбинаторные задачи по правилу умножения;

— развивать творческий потенциал и самооценку через творческие задания.

Воспитательные:

— продолжить воспитание познавательного интереса к предмету и повышение мотивации к учению по средствам ИКТ;

— способствовать воспитанию самостоятельности и умению работать в парах.

Учебники и дидактические материалы:

— Виленкин Н.Я. и др. «Математика 6 класс» — М.: Мнемозина, 2008

— Дорофеев и др. «Математика 6 кл.» — М.: Просвещение, 1996

— Макарычев Ю.Н. и др. «Элементы статистики и теории вероятностей. Алгебра 7-9 классы» — М.: Просвещение, 2008

— Мордкович А.Г. и др. «События. Вероятности. Статистическая обработка данных. 7-9 кл.» — М.: Мнемозина, 2003

— Ткачева М.В., Федорова Н.Е. «Элементы статистики и вероятность. 7-9 кл.» — М.: Просвещение, 2006

ХОД УРОКА:

Организационный момент.

СЛАЙД 1.

СЛАЙД 2.

Сегодня на уроки мы повторим понятие стохастической линии. А как она называется вы узнаете, отгадав ребус на слайде (Комбинаторика). Мы вспомним из математики 5 класса решение комбинаторных задач путем перебора вариантов и построения дерева возможных вариантов и познакомимся с новым способом – правилом умножения.

СЛАЙД 3.

Нам часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов как это действие осуществить. Разные пути или варианты, которые приходится выбирать человеку, складываются в самые разнообразные комбинации.

Комбинаторика – это раздел математики, посвященный решению задач на перебор различных вариантов, удовлетворяющих каким-либо условиям. Здесь изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Латинское слово combinare означает «соединять, сочетать».

В комбинаторных задачах обычный вопрос: сколькими способами, сколько вариантов… Рождение комбинаторики как раздела математики связано с трудами великих французских математиков XVII века Блеза Паскаля и Пьера Ферма.

Существует очень много задач, в которых рассматриваются различные ситуации выбора. Однако, несмотря на все разнообразие комбинаторных задач, можно выделить среди них группы однотипных. В этих задачах речь идет о разных предметах, приводятся разные ситуации, но ход их решения одинаков, и именно поэтому такие задачи можно объединить в отдельные группы. С такими задачами мы встречались с вами в 5 классе.

СЛАЙД 4.

Например: Сколько трехзначных чисел можно составить из цифр 0, 2, 4, если цифры в записи числа не повторяются?

Составим схему рассуждений.

Первая цифра 2 4

Вторая цифра 0 4 0 2

Третья цифра 4 0 2 0

Решение: 204, 240, 402,420 – 4 числа.

Способы решения таких задач перебором возможных вариантов используются при наличии нескольких решений. При записи возможных вариантов, их схемы изображаются, как дерево с разветвленными ветвями, которое так и называется «дерево возможных вариантов».

Решим эту задачу другим способом.

На первом месте может быть только две цифры (2 или 4), на втором – две из оставшихся, а на третьем – одна. Таким образом, 2 ∙ 2 ∙ 1 = 4

Рассмотрим другие задачи.

СЛАЙД 5.

Задача 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 7?

Решение.

Первые цифры искомых чисел: 1, 2, 4, 5, 7, так как в двузначном числе на первом месте может стоять любая цифра, кроме 0. Так как нужно составить четные двузначные числа, то второй цифрой искомых чисел могут быть: 0, 2, 4.

Составим таблицу: 5 строк (цифры 1, 2, 4, 5, 7) и 3 столбца (цифры 0, 2, 4) соответственно.

Заполняем клетки: первая цифра числа равна метке строки, а вторая цифра – метке столбца. По строкам и столбцам мы перечисляем все возможные варианты, значим, искомых чисел будет столько же, сколько клеток в таблице, то есть 3 ∙ 5 = 15.

Ответ: из цифр 0, 1, 2, 4, 5, 7 можно составить 15 четных двузначных чисел.

Учитель: В этой задаче мы осуществили полный перебор всех возможных вариантов (комбинаций). Поэтому подобные задачи называются комбинаторными.

СЛАЙД 6.

Задача 2. На завтрак в школьной столовой любой ученик может выбрать булочку, ватрушку, кекс или сочник, а запить их он может соком, чаем или компотом. Сколько вариантов завтрака предлагается в школьной столовой?

Решение. Собираем все варианты в таблицу.

Булочка (Б)

Ватрушка (В)

Пирожок (П)

Сок (С)

С Б

С В

С П

Чай (Ч)

Ч Б

Ч В

Ч П

В таблице 2 строки и 3 столбца, которые образуют 6 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоит один из возможных вариантов завтрака. Значит, всего вариантов столько, сколько клеток в таблице, то есть 6. Напиток можно выбрать двумя способами (сок или чай), а еду тремя способам.

Ответ: 2 ∙ 3 = 6 столовая предлагает 6 вариантов завтрака.

СЛАЙД 7.

Задача 3. У Тани есть розовая, желтая, красная кофта и черная, зеленая, синяя юбки. Сколько различных нарядов можно составить из них?

Решение: Составим дерево возможных вариантов.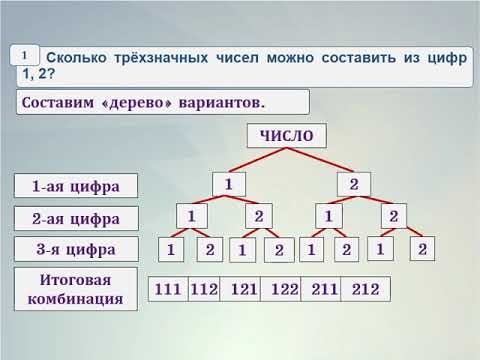

При этом возможные варианты, объекты в нем записываются

кодом. При записи объектов кодом используются буквы или

цифры. Сколько ветвей у дерева в схеме, столько решений

у задачи.

РЧ, РЗ, РС; ЖЧ, ЖЗ, ЖС; КЧ, КЗ, КС.

Кофту можно выбрать тремя способами и юбку тремя способам.

3 · 3 = 9 (нарядов)

Учитель: Что вы заметили при решении этих задач?

(Задачи разные, но решения совершенно одинаковые).

— Совершенно верно. А основаны они на общем правиле умножения

СЛАЙД 8.

Задача 4. Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?

СЛАЙД 9.

Правило умножения:

Если объект a можно выбрать m способами, а объект b можно выбрать k

способами, то выбор пары (a, b) можно осуществить m · k способами.

СЛАЙД 10.

Примеры задач:

1. Мастер должен обшить 12 стульев обшивкой красного, коричневого и зеленого цвета. Сколькими способами он может это сделать? (12 стульев и 3 цвета, значит 12 ∙ 3 = 36)

2. Сколькими способами можно выбрать гласную и согласную буквы из слова «правило»?

(3 гласных и 4 согласных, значит 3 ∙ 4 = 12)

3. На первой полке стоит 5 книг, а на второй 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй? (5 ∙ 10 = 50)

4. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя – как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z любые цифры, а X – не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9 ∙ 10 ∙ 10 = 900 вариантов.

СЛАЙД 11.

Закрепление:

№ 53 6 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 720 способов; 2 ∙ 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 240 способов

№ 410 10 ∙ 9 ∙ 8 ∙ 7 = 1540 номеров

№ 517 25 ∙ 24 = 600 способов

№ 915 27; 57; 87; 387; 357; 537; 837

СЛАЙД 12.

Итоги урока:

Вопросы ученикам:

Какие задачи называют комбинаторными?

Какие задачи называют задачами на перестановки?

В чем состоит правило умножения при решении комбинаторных задач?

Продолжите предложение по нашей теме

— Мы знаем … (как решать комбинаторные задачи по правилу умножения)

— Мы умеем … (проводить анализировать и делать выводы)

— Мы можем применить … (правило умножения при решении комбинаторных задач)

Рефлексия: А теперь оцените результаты своей деятельности на уроке.

Какое впечатление у вас об уроке? Что вам понравилось, а что нет?

Что было интересного и что еще нужно изменить? Что у вас получилось, и что нет?

Над чем еще вам нужно поработать и что повторить?

СЛАЙД 13.

Домашнее задание: № 24, № 262, № 355, № 462

Спасибо за урок.

Комбинаторные задачи. 6-й класс

Цели:

Образовательная – ознакомить учащихся с методами решения комбинаторных задач; научить применять методы полного перебора всех возможных вариантов и умножения.
Развивающая – развивать логическое мышление, интерес к изучению математики. грамотную математическую речь.
Воспитательная – воспитывать внимание и аккуратность в оформлении заданий.

Тип урока: изучение нового материала

Оборудование: доска, учебники, компьютер, проектор, презентация к уроку (образец в приложении)

План урока:

1. Организационный момент. Приветствие.
2. Изучение нового материала.
3. Рефлексия. Закрепление.
4. Итоги урока.

ХОД УРОКА

1. Приветствие.

2. Цели для учащихся:

изучить понятие «комбинаторика»,
рассмотреть методы решения комбинаторных задач,
научиться применять методы решения в различных ситуациях,
развить внимание и аккуратность в оформлении заданий.

А) Введение понятия комбинаторика. (Приложение 1, слайд 2)

Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.

Б) Что значит решить комбинаторную задачу. (Приложение 1, слайд 3)

Решить комбинаторную задачу

– это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.
В разделе представлены комбинаторные задачи на размещение, сочетание, перестановки с повторением и без повторения элементов. Используется естественный, доступный детям всех возрастов метод решения комбинаторных задач с помощью непосредственного перебора возможных вариантов (комбинаций).

В) Решение задачи методом полного перебора всех возможных вариантов.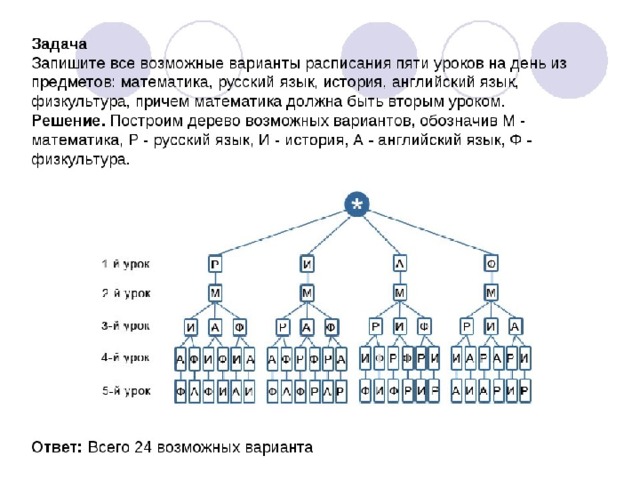 (Приложение 1, слайд 4)

Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?

Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
11; 14; 17; (начали с 1)
41; 44; 47; (начали с 4)

71; 74; 77; (начали с 7)

Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел.

Ответ: 9 чисел.

3. Решение задач методом полного перебора на доске и в тетрадях. (Приложение 1, слайд 5)

Сколько трёхзначных чисел можно составить, используя цифры 3 и 5?
В школе проводятся соревнования по хоккею. В качестве призов решили использовать мячи, ракетки, клюшки и шайбы. Сколько различных призов можно составить из этих предметов, если каждому победителю решено давать по 2 разных предмета?
В четверг в первом классе должно быть 3 урока: русский язык, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?

4. Решение задач с помощью дерева возможных вариантов на доске и в тетрадях. (Приложение 1, слайд 6)

Существует общий подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян.

5. Задача. (Приложение 1, слайд 7)

Рассмотрим задачу о составлении трехзначных чисел из цифр 1; 4; 7. Для её решения построим схему-дерево возможных вариантов, которое наглядно показывает решение задачи.

6. Решение задач с использованием дерева возможных вариантов на доске и в тетрадях. (Приложение 1, слайд 8)

В костюмерной танцевального кружка имеются жёлтые и зелёные кофты, а также синие и чёрные юбки. Сколько можно из них составить различных костюмов.
Сколькими способами три друга могут разделить между собой 2 банана, 2 груши и 2 персика так, чтобы каждый получил по два каких-нибудь плода?
Служитель зоопарка должен дать зайцу два различных овоща. Запишите все такие пары, если имеются морковь, свекла и капуста.
Из 4 ребят надо выделить двоих для дежурства по классу. Сколькими способами это можно сделать?
Наташа хочет сделать аппликацию на платье из двух цветных вертикальных полос. Из скольких вариантов придётся выбирать Наташе, если у неё есть материя жёлтого, красного и синего цвета?

7. Правило умножения в комбинаторных задачах. (Приложение 1, слайд 9)

Для комбинаторной задачи с умножением можно построить дерево вариантов, но такое дерево строить станет намного сложнее, именно поэтому используется метод умножения, чтобы запись была короче.
Рассмотрим этот метод на примере одной задачи:

На обед в школьной столовой предлагается 2 супа, 3 вторых блюда и 4 разных сока. Сколько различных обедов можно составить по предложенному меню?

Суп 2 Вторые блюда 3 Сок 4

Решение: 2 x 3 x 4 = 24

Ответ: Можно составить 24 варианта различных обедов.

8. Решение задач с использованием дерева возможных вариантов на доске и в тетрадях. (Приложение 1, слайд 10)

В костюмерной танцевального кружка имеются жёлтые и зелёные кофты, а также синие и чёрные юбки. Сколько можно из них составить различных костюмов.
Сколькими способами три друга могут разделить между собой 2 банана,2 груши и 2 персика так, чтобы каждый получил по два каких-нибудь плода?
Служитель зоопарка должен дать зайцу два различных овоща. Запишите все такие пары, если имеются морковь, свекла и капуста.
Из 4 ребят надо выделить двоих для дежурства по классу. Сколькими способами это можно сделать?
Наташа хочет сделать аппликацию на платье из двух цветных вертикальных полос. Из скольких вариантов придётся выбирать Наташе, если у неё есть материя жёлтого, красного и синего цвета?

9. Перестановки в комбинаторных задачах. (Приложение 1, слайд 11)

В комбинаторике часто приходиться решать задачу о том, сколькими способами можно расположить в ряд или, как говорят математики, упорядочить все элементы некоторого множества. Каждое из таких расположений называют перестановкой.

Задача. В турнире участвуют четыре человека. Сколькими способами могут быть распределены места между ними?

Решение: первое место может занять любой из 4 участников. При этом второе место может занять любой из трёх оставшихся, третье – любой из двух оставшихся, а на четвёртом месте остаётся последний участник.

Значит, места между участниками могут быть распределены следующим образом

4 • 3 • 2 • 1 = 24.

Ответ: 24 способами.

10. Решите задачу на перестановки. (Приложение 1, слайд 12)

Задача. Андрей, Борис и Василий входят в комнату по одному. Сколько у них есть способов это сделать?

Решение. Пусть первым войдёт Андрей, но тогда вторым может войти Борис или Василий, то есть имеются две возможности. Аналогично есть две возможности, если первым войдёт Борис и если первым войдёт Василий. Таким образом 6 возможностей.

Ответ: 6 способов.

11. Итог урока

Вспомним цели нашего урока:

изучить понятие «комбинаторика»,
рассмотреть методы решения комбинаторных задач,
научиться применять методы решения в различных ситуациях,
развить внимание и аккуратность в оформлении заданий.

– Как мы их реализовали? (Приложение 1, слайд 13)

Комбинаторные задачи 6 класс доклад, проект

Слайд 1Текст слайда:

Правило умножения для комбинаторных задач Математика 6 класс И.И. Зубарева, А.Г.Мордкович

учитель математики школы №80 с углубленным изучением
английского языка Лапшина Ирина Ивановна

Слайд 2Текст слайда:

Комбинаторика – это область математики, изучающая вопрос, сколько разных комбинаций (наборов) можно составить из элементов заданного множества. При этом нужные комбинации подчиняются определенным требованиям, что приводит к различным методам решения задач по комбинаторике.

Комбинаторика

Слайд 3Текст слайда:

Готфрид Лейбниц

Истоки этой науки были положены знаменитым немецким математиком и философом Готфридом Лейбницем.

(1646-1716)

Слайд 4Текст слайда:

Правило умножения

Пусть объект А выбирается n способами, объект В выбирается m способами ( независимо от выбора объекта А), то
пару объектов (А,В) можно выбрать n • m способами.
Все очень просто – каждый из n способов выбора объекта А комбинируется с каждым из m способов выбора объекта В, то есть количество способов просто умножается друг на друга.

Слайд 5Текст слайда:

№492

1способ:
составить дерево возможных вариантов
2 способ:
решить задачу, используя правило умножения

Собрание для проведения тайного голосования по важному вопросу избрало счетную комиссию, в состав которой вошли Антонов, Борисова и Ващенко. Члены счетной комиссии должны распределить обязанности: председатель, заместитель, секретарь. Сколькими способами они могут это сделать?

Слайд 6Текст слайда:

Председатель

Заместитель

Секретарь

комиссия

Полученная
комбинация

АБВ

АВБ

БАВ

БВА

ВАБ

ВБА

1 способ

Слайд 7Текст слайда:

2способ

3•2•1= 6

Слайд 8Текст слайда:

№493

Сколько двузначных чисел можно составить
из цифр 0,1,2,3,4?

4•5= 20

на первом месте может находится любая цифра, кроме нуля

Слайд 9Текст слайда:

№494

1)Сколько трехзначных чисел можно составить из
цифр1,3,5,7 ?

2) Сколько трехзначных чисел можно составить из цифр
1,3,5,7,если известно, что цифры не должны
повторяться?

4•4•4= 64

4•3•2= 24

Слайд 10Текст слайда:

№495

Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов-белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны свой флаг?

3•2•1= 6

Слайд 11Текст слайда:

№496

Несколько стран решили использовать для своего государственного флага символику в виде четырех вертикальных полос одинаковой ширины разных цветов -жёлтого, синего, красного, зеленого. Сколько стран могут использовать такую символику при условии, что у каждой страны свой флаг?

4•3•2•1= 24

Слайд 12Текст слайда:

№497

Руководство некоторой страны решило сделать свой государственный флаг таким: на одноцветном прямоугольном полотне в одном из углов помещается квадратик другого цвета. Цвета решено выбрать из 3 возможных : красного ,белого, зеленого. Сколько вариантов такого флага существует?

3•2•4= 24

Слайд 13Текст слайда:

№497.

= 24

Слайд 14Текст слайда:

№498

В списке учеников 6-го класса 15 девочек и 13 мальчиков. Нужно выбрать двух дежурных по классу Сколькими способами это можно сделать: а) при условии, что пару дежурных обязательно должны составлять мальчик и девочка;
б) без указанного условия

15•13= 195

28∙27=756

Среди756 учеников есть одинаковые пары

Сколько существует способов расположения девочек в паре?

2∙1=2

756:2=378

Слайд 15Текст слайда:

№499а)

В списке учеников 6 класса 15 девочек и 13 мальчиков.Нужно выделить группу из 3 человек для посещения заболевшего ученика этого класса. Сколькими способами это можно сделать, если

а) все члены группы девочки;

Ответ: 455 способов

1)15∙14∙13=2730(способов)-выбрать с повторением тройки девочек

2)3∙2∙1=6(способов)-расположения девочек по порядку в каждой тройке

3)2730:6=455(способов)-выбрать без учета порядка тройку девочек

Слайд 16Текст слайда:

№499б)

В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно выделить группу из 3 человек для посещения заболевшего ученика этого класса. Сколькими способами это можно сделать, если:

б) все члены группы- мальчики;

1)12∙11∙10=1320(способов)-выбрать с повторением тройку мальчиков

2)3 ∙ 2∙1=6(способов)-расположения мальчиков по порядку в каждой тройке

3)1320:6= 220(способов)- выбрать без учета порядка тройку мальчиков

Ответ: 220 способов

Слайд 17Текст слайда:

№499в

В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно выделить группу из 3 человек для посещения заболевшего ученика этого класса. Сколькими способами это можно сделать, если:

в) в группе 1 девочка и 2 мальчика;

1)12∙11=132(способа)-выбрать с повторением пару мальчиков

2)2∙1=2(способа)-расположения мальчиков по порядку в каждой паре

3)132:2=66(способ)-выбрать без учета порядка пару мальчиков

4)15 ∙ 66=990(способ)-выбрать без учета порядка 1девочку и 2 мальчиков

Ответ: 990 способа

Слайд 18Текст слайда:

№499 г)

В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно выделить группу из 3 человек для посещения заболевшего ученика этого класса. Сколькими способами это можно сделать, если:

г) в группе 2 девочки и 1 мальчик;

1)15∙14=210(способов)-выбрать с повторением пару девочек

2)2∙1=2(способа)-расположения девочек по порядку в каждой паре

3)210:2=105(способов)-выбрать без учета порядка пару девочек

4)105 ∙ 12=1260(способа)-выбрать без учета порядка 2девочек и 1 мальчика

Ответ: 1260 способов

Слайд 19Текст слайда:

При решении этой задачи надо учесть, что 1 мальчик из класса болен, т.е. выбор будет осуществляться не из 13 мальчиков, а из 12 мальчиков

Слайд 20Текст слайда:

№500а,б

В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно выделить группу из 3 человек для посещения заболевшей ученицы этого класса. Сколькими способами это можно сделать, если:

а) все члены группы девочки;

(14∙13 ∙ 12):6=364(способа)-выбрать без учета порядка тройку девочек

б) все члены группы- мальчики;

(13∙12 ∙ 11):6=286(способа)-выбрать без учета порядка тройку девочек

Слайд 21Текст слайда:

№500в)г)

в) в группе 1 девочка и 2 мальчика;

(13∙12):2 ∙ 14= 1092(способа)-выбрать без учета порядка 1 девочку и 2 мальчиков

г) в группе 2 девочки и 1 мальчик;

(14∙13 ):2 ∙ 13=1183(способа)-выбрать без учета порядка 2девочки и 1 мальчикадевочек

Слайд 22Текст слайда:

№501

а) Сколько двузначных чисел можно составить из
цифр 1,2,3,4,5

б) Сколько двузначных чисел можно составить
из цифр 1,2,3,4,5 при условии, что цифры не
должны повторяться?

5∙5= 25 двузначных чисел можно составить с повторением цифр

5∙4 = 20 двузначных можно составить без повторения цифр

Слайд 23Текст слайда:

№502

а) Сколько трехзначных чисел можно составить
из цифр 2,4,5?

3 ∙3∙3= 27 трехзначных чисел можно составить с
повторением цифр

б) Сколько трехзначных чисел можно составить
из цифр 2,4,5, при условии, что цифры не
должны повторяться?

3 ∙ 2 ∙ 1=6 трехзначных чисел можно составить без повторения цифр

Слайд 24Текст слайда:

Ответ б)

Ответ а)

№503

а) Сколько трехзначных
чисел можно составить
из цифр 0,7,9?

б) Сколько трехзначных
чисел можно составить
из цифр 0,7,9, при
условии, что цифры не
должны повторяться?

помощь

Слайд 25Текст слайда:

На первое
место
нельзя
поставить цифру 0

Слайд 26Текст слайда:

№503а

2 ∙

3 ∙

=18

0,7,9

Слайд 27Текст слайда:

1 цифра

2 цифра

3 цифра

2 ∙2∙1= 4

№503а

Слайд 28Текст слайда:

№506

В 6 а классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура. Сколько всего можно составить вариантов расписания на четверг?

Сколько имеется вариантов расписания при условии, что физкультура- последний урок?

Сколько имеется вариантов расписания при условии, что физкультура- последний урок, а математика -первый?

5 ∙4∙3∙2∙1 = 120

4 ∙3∙2∙1∙1 = 24

1 ∙3∙2∙1∙1 = 6

Слайд 29Текст слайда:

№508

В чемпионате России по футболу в высшей лиге участвуют 16 команд. Перед началом чемпионата газета «Спорт« провела
интернет-вопрос читателей, задав им два вопроса:
1) Какие три команды станут призерами чемпионата, т.е. займут первое, второе и третье места?
2)Какие две команды займут два последних места?

а) Сколько вариантов состава призеров чемпионата?

б) Сколько вариантов состава неудачников чемпионата?

16 ∙15∙14 = 3360

16 ∙15 = 240

Слайд 30Текст слайда:

№509а

В двух урнах имеется по семь шаров, в каждой — семи различных цветов: красного, оранжевого, жёлтого, зеленого, голубого, синего и фиолетового. Из каждой урны одновременно вынимают по одному шару.
а) Сколько существует комбинаций, при которых
вынутые шары одного цвета?

Итого

7∙1=7

Слайд 31Текст слайда:

№509б

В двух урнах имеется по семь шаров, в каждой — семи различных цветов: красного, оранжевого, жёлтого, зеленого, голубого, синего и фиолетового. Из каждой урны одновременно вынимают по одному шару.
б ) Сколько существует комбинаций, при которых
вынутые шары разных цветов?

1)7∙6=42 (способа)-выбрать с повторением пару шаров

2) 2∙1=2(способа)-расположения шаров по порядку
в каждой паре

42:2 =21(способ)-выбрать без учета порядка два шара разного цвета

Слайд 32Текст слайда:

№509в

в) Сколько существует различных комбинаций вынутых шаров(комбинации типа»белый-красный»и «красный -белый» считаются одинаковыми)?

(7∙6):2 =21(способ)-выбрать без учета порядка два шара разного цвета

7∙1=7(способов) –выбрать пару одинакового цвета

Итого: 21+7 =28(способов)–различных пар шаров

Слайд 33Текст слайда:

Самостоятельная работа

1. Сколько двузначных чисел можно составить из цифр 1,2,6 при условии, что:
а) цифры могут повторяться;
б) цифры не должны повторяться?

1. Сколько двузначных чисел можно составить из цифр 2,5,4,7 при условии, что:
а) цифры могут повторяться;
б) цифры не должны повторяться?

Вариант 1

Вариант 2

Слайд 34Текст слайда:

Самостоятельная работа

Вариант 1

Вариант 2

2. Сколько трехзначных чисел можно составить из цифр 0,1,2,6 при условии, что:
а) цифры могут повторяться;
б) цифры не должны повторяться?

2. Сколько трехзначных чисел можно составить из цифр 0,5,4,8,6 при условии, что:
а) цифры могут повторяться;
б) цифры не должны повторяться?

Слайд 35Текст слайда:

Самостоятельная работа

Вариант 1

Вариант 2

3. В списке баскетбольной команды 20 человек. Из них 12 играют в нападении, а 8 — в защите
а) Сколькими способами из этих игроков можно составить тройку нападающих?
б) Сколькими способами из этих игроков можно составить пару защитников?

3. В списке футбольной команды 22 человека. Из них 9 играют в нападении, а 7 — в защите
а) Сколькими способами из этих игроков можно составить четверку нападающих?
б) Сколькими способами из этих игроков можно составить пару защитников?

Разбор задач

Взаимопроверка

Слайд 36Текст слайда:

Разберем решение задач:

1. Сколько двузначных чисел можно составить из цифр 1,2,6 при условии, что:

1. Сколько двузначных чисел можно составить из цифр 2,5,4,7 при условии, что:

а) цифры могут повторяться

б) цифры не повторяются?

3∙3=9

3∙2=6

4∙4=16

б) цифры не повторяются?

4∙3=12

Вариант 1

Вариант 2

Слайд 37Текст слайда:

Решение

2. Сколько трехзначных чисел можно составить из цифр 0,1,2,6 при условии, что:

Вариант 1

Вариант 2

2. Сколько трехзначных чисел можно составить из цифр 0,5,4,8,6 при условии, что:

а) цифры могут повторяться

3∙4∙4=48

4∙5∙5 =100

б) цифры не повторяются?

3∙3∙2 =18

4∙4∙3 =48

Слайд 38Текст слайда:

Решение

Вариант 1

Вариант 2

3.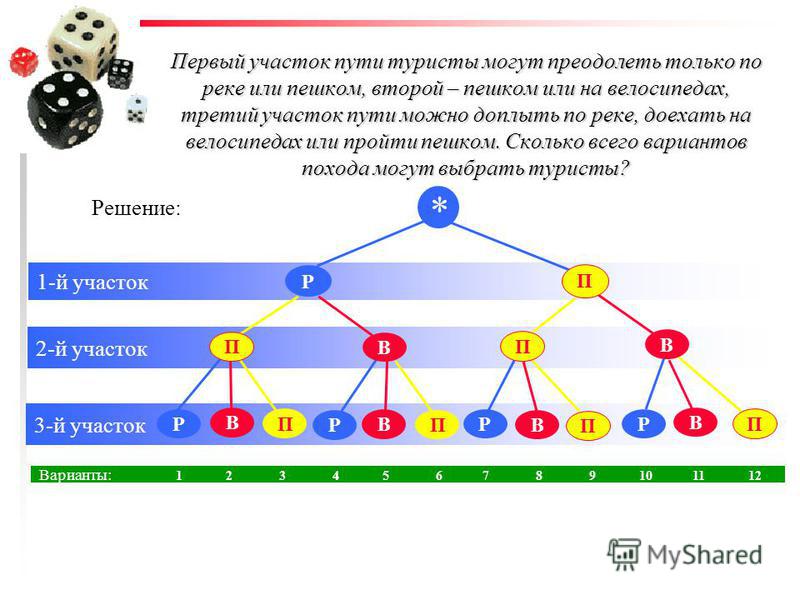 В списке баскетбольной команды 20 человек. Из них 12 играют в нападении, а 8 — в защите.

3. В списке футбольной команды 22 человека. Из них 9 играют в нападении, а 7 — в защите

а) Сколькими способами из этих игроков можно составить тройку нападающих?

б) Сколькими способами из этих игроков можно составить пару защитников?

а) Сколькими способами из этих игроков можно составить четверку нападающих?

б) Сколькими способами из этих игроков можно составить пару защитников?

(12∙11∙10):6=48

(8∙7):2=28

(9∙8∙7∙6):24 =945

(7∙6):2=21

Слайд 39Текст слайда:

Ответы

а)3∙3=9

б)3∙2=6

а)3∙4∙4=48

б)3∙3∙2 =18

а)(12∙11∙10):6=48

б)(8∙7):2=28

а)4∙4 =16

б)4∙3 =12

а)4∙5∙5 = 100

б)4∙4∙3 =48

а)(9∙8∙7 ∙6):24 = 945

а)(7∙6):2 = 21

Слайд 40Текст слайда:

Домашнее задание

№504,№505,№507

Слайд 41Текст слайда:

Используемые ресурсы:

1. Портрет Лейбница http://ru.wikipedia.org/wiki/

2.Слайд 6,13 http://school-collection.edu.ru

https://www.google.ru/

http://images.yandex.ru/

4. Книга

3. Незнайка, Знайка.Буратино

5. Источник шаблона презентации:
Татарников Виталий Викторович учитель физики МОУ СОШ №20 п. Баранчинский, г. Кушва, Свердловской обл. Рисунок для фона http://17986.globalmarket.com.ua/data/530378_3.jpg

http://pedsovet.su/

6.И.И. Зубарева, А.Г. Мордкович. Математика. 6 класс. Учебник

Методы решения комбинаторных задач — Сайт учителя математики Кобец Анны Викторовны

Методы решения комбинаторных задач

Перебор возможных вариантов

Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.

Задача 1.
Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?

Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

Задача 2.
В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.

Ответ:
Вариант 1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант 2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант 3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант 4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант 5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант 6: 1) Громов, 2) Иванов, 3) Орлов.

Задача 3.
В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?

Ответ:
1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 8) Оля — Олег, 9) Наташа — Петя, 10) Наташа — Коля, 11) Наташа — Витя, 12) Наташа — Олег, 13) Света — Петя, 14) Света — Коля, 15) Света — Витя, 16) Света — Олег.

Дерево возможных вариантов

Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода — дерево возможных вариантов.

Задача 4.
Какие трехзначные числа можно составить из цифр 0, 2, 4?

Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.

Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.

Задача 5.
Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап — на байдарках, велосипедах или пешком. И третий этап пути — пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?

Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе — А, на байдарках — Б, велосипедах — В, пешком — Х, на канатной дороге — К.

Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.

Задача 6.
Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.

Решение. Построим дерево возможных вариантов, обозначив М — математика, Р — русский язык, И — история, А — английский язык, Ф — физкультура.

Ответ: Всего 24 возможных варианта:

Р
М
И
А
Ф

Р
М
И
Ф
А

Р
М
А
И
Ф

Р
М
А
Ф
И

Р
М
Ф
И
А

Р
М
Ф
А
И

И
М
Р
А
Ф

И
М
Р
Ф
А

И
М
А
Р
Ф

И
М
А
Ф
Р

И
М
Ф
Р
А

И
М
Ф
А
Р

А
М
Р
И
Ф

А
М
Р
Ф
И

А
М
И
Р
Ф

А
М
И
Ф
Р

А
М
Ф
Р
И

А
М
Ф
И
Р

Ф
М
Р
И
А

Ф
М
Р
А
И

Ф
М
И
Р
А

Ф
М
И
А
Р

Ф
М
А
Р
И

Ф
М
А
И
Р

Задача 7.
Саша ходит в школу в брюках или джинсах, к ним одевает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки.
а) Сколько дней Саша сможет выглядеть по-новому?
б) Сколько дней при этом он будет ходить в кроссовках?
в) Сколько дней он будет ходить в рубашке в клетку и джинсах?

Решение. Построим дерево возможных вариантов, обозначив Б — брюки, Д — джинсы, С — серая рубашка, Г — голубая рубашка, З — зеленая рубашка, Р — рубашка в клетку, Т — туфли, К — кроссовки.

Ответ: а) 16 дней; б) 8 дней; в) 2 дня.

Составление таблиц

Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.

Задача 8.
Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?

Решение. Составим таблицу: слева первый столбец — первые цифры искомых чисел, вверху первая строка — вторые цифры.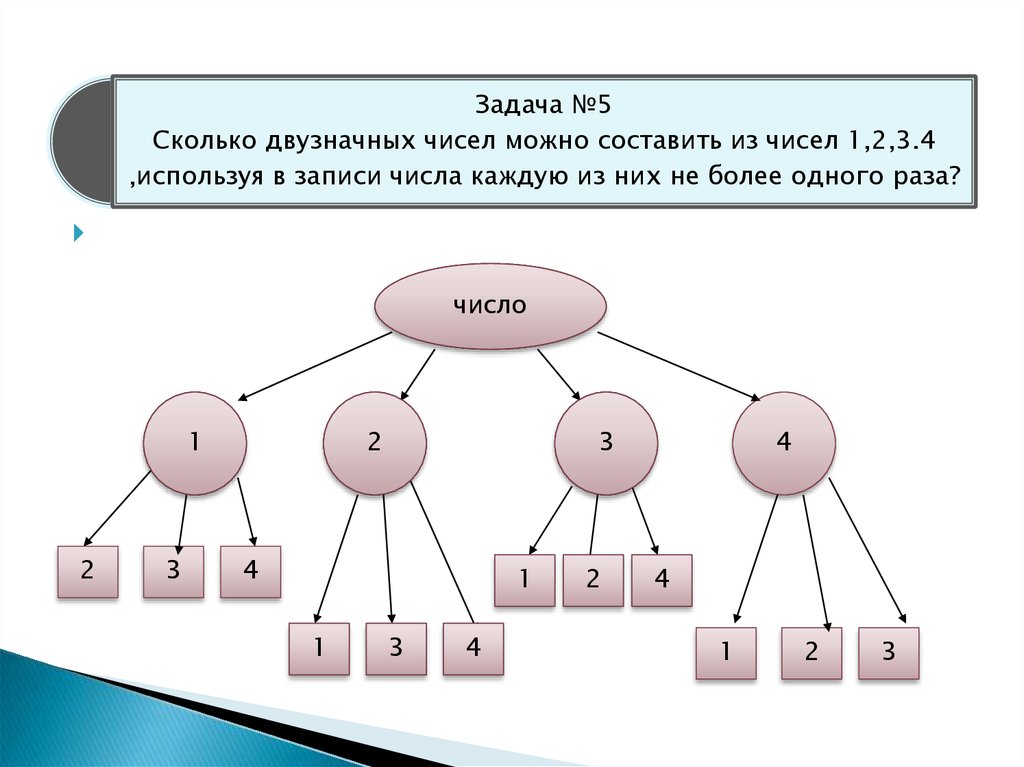

Ответ: 28.

Задача 9.
Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Решение. Составим таблицу: слева первый столбец — имена девочек, вверху первая строка — имена мальчиков.

Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы.

Правило умножения

Этот метод решения комбинаторных задач применяется, когда не требуется перечислять все возможные варианты, а нужно ответить на вопрос — сколько их существует.

Задача 10.
В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий и зеленый цвета, причем были представлены все возможные варианты. Сколько команд участвовали в турнире?

Решение.
Трусы могут быть белого, красного, синего или зеленого цвета, т. е. существует 4 варианта. Каждый из этих вариантов имеет 4 варианта цвета майки.

4 х 4 = 16.

Ответ: 16 команд.

Задача 11.
6 учеников сдают зачет по математике. Сколькими способами их можно расположить в списке?

Решение.
Первым в списке может оказаться любой из 6 учеников,
вторым в списке может быть любой из оставшихся 5 учеников,
третьим — любой из оставшихся 4 учеников,
четвертым — любой из оставшихся 3 учеников,
пятым — любой из оставшихся 2 учеников,
шестым — последний 1 ученик.

6 х 5 х 4 х 3 х 2 х 1 = 720.

Ответ: 720 способами.

Задача 12.
Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 4, 6, 7?

Решение.
Первой в двузначном числе может быть 5 цифр (цифра 0 не может быть первой в числе), второй в двузначном числе может быть 4 цифры (0, 2, 4, 6, т.к. число должно быть четным).
5 х 4 = 20.

Ответ: 20 чисел.

Методы решения комбинаторных задач

Репетиторы ❯ Математика ❯ Методы решения комбинаторных задач

Автор: Ирина П. , онлайн репетитор по математике

●

10.02.2012

●

Раздел: Математика

При решении многих практических задач приходится использовать комбинации элементов, выбирать из данной совокупности те, которые имеют определенные свойства, и размещать их в определенном порядке. Такие задачи называются комбинаторными. Раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями, называется комбинаторикой. Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский язык означает – «сочетать», «соединять».

Выбранные группы элементов называют соединениями. Если все элементы соединения разные, то получаем соединения без повторений, которые и рассмотрим ниже.

Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения.

Выбор правила	Выбор правила
Правило суммы	Правило произведения
Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор объекта либо А, либо В можно осуществить m + n способами.	Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары А и В можно осуществить m · n способами.

Задача 1.

В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?

Решение.

Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).

Ответ: 24.

Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема.

Рассмотрим решение нескольких задач на разные виды соединений без повторений.

Задача 2.

Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.

Решение.

Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A₇³ = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.

Ответ: 210.

Задача 3.

Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?

Решение.

На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:

A₁₀⁷– A₉⁶ = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.

Ответ: 544 320.

Задача 4.

Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?

Решение.

Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р₈. Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р₅ способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р₈· Р₅= 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.

Ответ: 8! · 5!

Задача 5.

В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?

Решение.

Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:

С₁₆⁴ · С₁₂³ = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.

Ответ: 400 400.

Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.

Остались вопросы? Не знаете, как решать комбинаторные задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Конспект урока по математике «Правило умножения для комбинаторных задач» 6 класс

Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 15»

Конспект урока по теме:

«Правило умножения для комбинаторных задач »

Выполнила:

учитель математики

Галкина А. В.

Губаха 2010

Конспект урока составлен по учебнику: И.И. Зубарева, А.Г. Мордкович Математика 6

Цели:

1. Развивающая – развитие у учащихся умение самостоятельно формулировать правила, развитие логического мышления.

2. Обучающая – сформировать представление о комбинаторных задачах; научить строить дерево возможных вариантов.

3. Воспитательная – приучать учащихся к самостоятельной работе, воспитание взаимопомощи.

Задачи: формировать умения решать задачи по данной теме.

Оборудование: доска, мел, учебник, компьютер , проектор.

План урока:

Организационный момент

2. Подготовка к восприятию нового материала

3. Объяснение нового материала

4. Закрепление новых знаний

5. Домашнее задание

6. Итог урока

Ход

Урока

Деятельность Учителя	Деятельность Ученика	проектор	Доска
Организационный момент (0,5 мин)	-Здравствуйте! Настраиваемся на работу на уроке! Пожалуйста, садитесь!	Здравствуйте! [садятся за парты]	1 слайд	22. 12.10
Подготовка к восприятию нового материала (8 мин)	Начало нашего урока пройдет в несколько нестандартном виде. Вначале мы с вами побываем на уроке истории и узнаем о том, что за наука такая комбинаторика и откуда она к нам пришла. Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в 17 веке. Долгое время она лежала вне основного русла развития математики. С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов — во время работы. Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника. Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д. Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж.Кардано, Н.Тарталье (1499-1557), Г.Галилею (1564-1642) и французским ученым Б. Паскалю (1623-1662) и П.Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г.Лейбниц в своей работе “ Об искусстве комбинаторики ”, опубликованной в 1666 году. Он также впервые ввел термин “комбинаторика”. Значительный вклад в развитие комбинаторики внес Л.Эйлер. В современном обществе с развитием вычислительной техники комбинаторика “добилась” новых успехов.	[слушают учителя]	2 слайд
Объяснение нового материала (15 мин)	Ну вот мы и узнали о комбинаторике, но прежде чем приступить к решению задач по данной теме нам нужно познакомиться с некоторыми основными понятиями этой науки. В задачах по комбинаторике часто применяется такое понятие как факториал (в переводе с английского “factor” — “множитель”). Итак, произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут: n!=1 2 3 … (n-1) n Пример: В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: Сочетания – сколько можно образовать сочетаний из n элементов по m. Размещения – сколько можно образовать размещений из n элементов по m Перестановки – это соединения, состоящие из одних и тех же элементов, отличающиеся только порядком расположения Вот этих понятий нам будет достаточно для решения задач. Ну а теперь можем смело приступать к решению комбинаторных задач. На доске вы видите несколько табличек на которых написаны начальные буквы областей знаний, где применяется наука комбинаторика. Разберем пару задач. Первой решим задачу, которая скрывается под буквой М: Как вы думаете какая область применения скрывается под этой буквой? Светлана: Правильно! Математика! Вот условие: Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7? Используя каждую из них не более одного раза? Решение: (решаем) Проведенный перебор вариантов проиллюстрирован на так называемом дереве возможных вариантов. Ответ на поставленный в задаче вопрос мы нашли, используя комбинаторное правило умножения. Ну что ж, молодцы давайте рассмотрим следующую карточку. Пусть это будет буква У: Ваня, как ты думаешь какая здесь задача? Это задача на управление, в данном случае в школе. Условие задачи: Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)? Решаем:	[записывают в тетради] [смотрят на доску] Математика (предполагает)	3 слайд 4 слайд 5 слайд 6 слайд 7 слайд 8 слайд 9 слайд 10 слайд 11 слайд 12 слайд	n!=1 2 3 …(n-1) n
Закрепление новых знаний (16 мин)	Ну а теперь вы сами попробуете решить любую задачу с моей помощью. Даша к доске. Какую букву выбираешь? Как ты думаешь какую науку скрывает эта буква? Молодец! Правильно! Вот условие задачи: Решаем 2 способами. Спасибо! Молодец! Садись! Ну что ж вы все сегодня хорошо поработали на уроке. (оценки)	(Даша идет к доске) Даша выбирает букву Л Я думаю логику	13 слайд	(Даша пишет решение)
Домашнее задание (3 мин) Итог урока (2 мин)	Откройте, пожалуйста, дневники, запишите домашнее задание. Итак, что нового вы сегодня для себя открыли на нашем уроке? Женя, Какие задачи называются комбинаторными? правильно! Молодец! Дима, что означает слово «комбинаторика»? Правильно! Молодец! Спасибо за урок! До свидания!	[открывают дневники и записывают домашнее задание] [отвечают на вопрос] Задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций, получили название комбинаторных. Комбинаторика означает “соединять, сочетать”. До свидания!		№ 497

Не сбрасывайте их со счетов – помогаем учащимся успешно решать комбинаторные задачи |

Элиз Локвуд, ответственный редактор Орегонского государственного университета

Введение
Решение задач на счет — одно из моих любимых занятий. Мне нравится задача осмысления проблемы, работа по правильному моделированию того, что я пытаюсь посчитать, и тот факт, что я могу рассуждать об удивительно больших числах. Однако я не всегда так относился к решению задач на счет. На протяжении большей части моей математической карьеры счет был загадкой — набором малопонятных формул и уравнений, от которых я просто страдал. Будучи студентом, я изо всех сил пытался понять разницу между порядком, имеющим значение или не имеющим значения, что представляют соответствующие факториалы в запутанных формулах и почему меня должно волновать, сколько фулл-хаусов можно выбрать из колоды карт. Мои учителя в то время, возможно, разделяли мнение Аннина и Лая: «Учителей математики часто спрашивают: «Какая самая сложная тема для преподавания?» Наш ответ — учить учащихся считать» (2010, стр. 403). .

В какой-то момент во время учебы в аспирантуре (благодаря влиятельному профессору, который любил считать) я свернул за угол и стал больше интересоваться пониманием счета. Многократно практикуясь, я начал улучшать свои способности решать задачи на счет. С тех пор я сосредоточил свои исследовательские интересы на том, чтобы узнать все, что я могу, о счете студентов бакалавриата: что они делают, когда подходят к задачам счета, почему у них возникают трудности и как мы можем помочь им решать такие задачи более эффективно.

Модель комбинаторного мышления учащихся
В этом посте я представляю модель комбинаторного мышления учащихся, которая помогла мне разобраться в счетной деятельности учащихся. Я также предлагаю примеры, иллюстрирующие аспекты модели, и заканчиваю конкретными рекомендациями по обучению учащихся решению задач на счет.

Модель (первоначально представленная в Локвуде, 2013 г., а затем уточненная в Локвуде, Суинъярде и Каумане, 2015 г.) состоит из трех компонентов: формул/выражений, процессов подсчета и наборов результатов, а также взаимосвязей между этими компонентами ( см. рис. 1 ниже). 94)\). Процессы подсчета относятся к фактическим пошаговым процедурам, в которых кто-то участвует (мысленно или физически) при решении задачи подсчета. Это может включать в себя применение принципа умножения или внедрение разбивки случаев. Набор из исходов для данной задачи относится к желаемым исходам этой проблемы — элементам, которые фактически подсчитываются. Эти результаты могут быть каким-то образом закодированы (например, в виде строк чисел или букв), и этот компонент может состоять из различных способов кодирования и структурирования результатов.

В качестве простого примера для разработки этих компонентов и выделения взаимосвязей между формулами/выражениями, процессами счета и наборами результатов рассмотрим следующую задачу: Сколько последовательностей из трех букв состоит из букв a, b, c, d, e, f могут быть образованы, если повторение не допускается и мы должны включать букву e? (Эта проблема была представлена в Tucker, 2002).

Прежде чем решать задачу, мы можем подумать, как будут выглядеть результаты. Это трехбуквенные последовательности (так, abe отличается от eab ), которые содержат букву e, где повторение не разрешено (результаты вроде abc или aaa не допускаются). Чтобы подсчитать все такие последовательности, трехэтапный процесс подсчета для решения задачи будет заключаться в том, чтобы сначала выбрать позицию, в которой должны стоять и (есть 3 варианта), а затем выбрать, какая из 5 оставшихся букв ( a, b, c, d, f ) может перейти в следующую доступную позицию, а затем выбрать, какая из 4 оставшихся букв (четырех, которые ранее не были выбраны) может перейти в последнюю доступную позицию. Этот процесс дает формулу/выражение $3 \cdot 5\cdot 4$, что равно 60.

Важно отметить, что описанный выше процесс подсчета структурирует результаты особым образом. В частности, он группируется в соответствии с расположением и , как следует из следующего списка результатов на рисунке 2:

Рисунок 2. Одна организация набора результатов

приводят к различным структурам множества результатов. Например, даже если это может быть не столь элегантное решение, другим процессом может быть организация результатов в соответствии с первой буквой. В частности, мы начинаем с выбора того, какая буква будет первой, и если это не e мы рассматриваем два случая: поместить e на вторую позицию (затем прокручивая оставшиеся буквы в третьей позиции) и затем помещая e на третью позицию (затем прокручивая оставшиеся буквы во второй позиции). должность). Если e — это первая буква, мы циклически перебираем каждую из оставшихся букв для второй и третьей позиции. Таким образом, мы могли бы рассматривать последовательности с разными соответствующими первыми буквами, в результате чего результаты были бы структурированы, как на рисунке 3. Выражение, отражающее этот процесс, имеет вид $5 \cdot 2 \cdot 4 + 1\cdot 5 \cdot 4$, что также равно 60. Смысл этого примера в том, что разные способы структурирования или организации набора результатов могут отражать разные соответствующие процессы подсчета, и, наоборот, разные процессы подсчета могут привести к разным способам организации результатов.

Рисунок 3. Альтернативная организация набора результатов

Итак, зачем нам эта модель и эти компоненты? Я утверждаю, что очень важно, чтобы учащиеся сосредоточились на наборе результатов (Lockwood, 2014) и, в частности, на размышлениях о взаимосвязи между процессами подсчета и наборами результатов. Есть несколько причин, почему эти отношения так важно понять. Во-первых, если учащиеся не настроены на набор результатов (и вместо этого сосредотачиваются в первую очередь на процессах счета и формулах/выражениях), то правила, определяющие, какую формулу использовать, становится труднее анализировать. Подсчет может превратиться в упражнение, заключающееся в простом манипулировании формулами и неясном понимании того, что подсчитывается. Кроме того, некоторые распространенные ошибки, такие как пересчет, трудно обнаружить и исправить без четкого понимания результатов и того, как процессы подсчета связаны с этими результатами. В качестве примера того, почему эта взаимосвязь важна, рассмотрим следующую аналогичную задачу, связанную с последовательностями из трех букв (также найденную в Tucker, 2002): Сколько 3-буквенных последовательностей, составленных из букв a, b, c, d, e, f, можно составить, если мы должны включить букву e, и повторение букв разрешено?

Здесь общий процесс подсчета следующий: Сначала поместите e в одну из трех позиций. Затем для каждого размещения и мы можем утверждать, что, поскольку повторение разрешено, теперь мы можем поместить любую из оставшихся 6 букв в оставшиеся две позиции. Этот процесс предлагает формулу/выражение $3 \cdot 6 \cdot 6$. Этот процесс подсчета, кажется, имеет смысл, и действительно, это очень распространенная реакция среди студентов. Однако это неверный ответ, так как этот процесс слишком много раз подсчитывает некоторые результаты. Чтобы увидеть это, мы должны внимательно рассмотреть результаты и, в частности, то, как результаты генерируются и организуются в процессе подсчета.

Давайте подумаем о следующем: предположим, что на первом этапе процесса мы поместили и на третью позицию, а затем на оставшихся этапах выбора одной из 6 букв, которые должны быть на оставшихся двух позициях, мы выбрал и , а затем и . Это дает пароль eae . Однако рассмотрим другой способ завершения этого процесса: мы могли бы сначала поместить e на первую позицию, а затем на этапе 6 $\cdot$ 6 мы могли бы выбрать и , а затем и .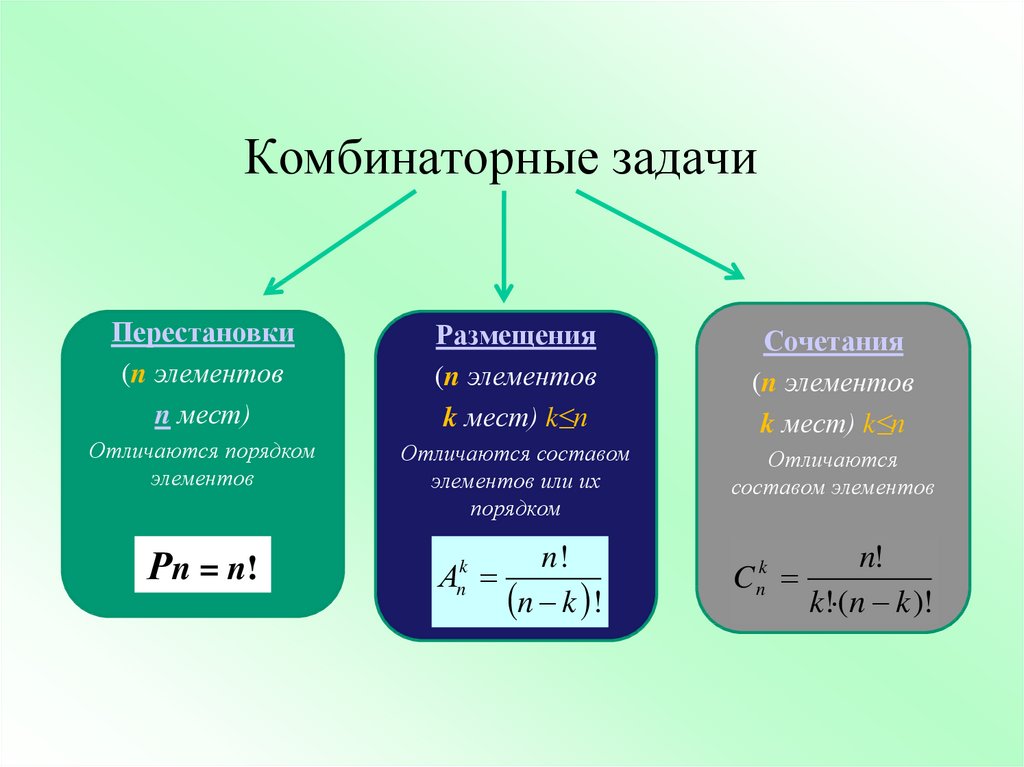 Это тоже генерирует пароль eae . Способы завершения процесса не находятся в однозначном соответствии с количеством желаемых результатов, и поэтому этот процесс приводит к пересчету.

Если учащийся не понимает, что существует взаимосвязь между процессами подсчета и результатами, как он или она может знать, когда они пересчитывают, не говоря уже о том, чтобы быть готовыми рассмотреть и исправить этот пересчет? Проблемы со счетом сложны, и может быть много разумно звучащих процессов. Без обоснования этого в наборе результатов может быть трудно сказать, может ли (и почему) данный процесс переоценить.

Практические выводы
Проблема пересчета — лишь один пример того, почему важны все три компонента модели и почему мы должны побуждать учащихся рассматривать наборы результатов и то, как они соотносятся с процессами подсчета. В свете этого ниже я предлагаю несколько советов по обучению счетам (особенно для студентов старших курсов, хотя тот же совет можно применить и к обучению счету на любом уровне).

1) Предложите учащимся сосредоточиться на наборе результатов. Основной вывод моего исследования на данный момент состоит в том, что есть ценность в том, чтобы учащиеся сосредоточились на наборе результатов. Есть несколько практических способов сделать это. Во-первых, в широком смысле учителя должны стремиться рассматривать счет как деятельность по определению мощности набора, в частности, набора желаемых результатов, указанных в задаче на подсчет. Хотя это кажется рудиментарным, у нас есть свидетельства того, что учащиеся не всегда рассматривают счет таким образом — вместо этого счет может быть вопросом сопоставления формул, слепого угадывания типов задач и т. д. Например, когда их спрашивают о проблеме порядка в проблема, один из моих студентов однажды сказал: «Я не знаю, я как бы схожу с ума из-за тех, которые конкретно не говорят, что порядок имеет значение или не имеет значения». По иронии судьбы, если бы студенты были более настроены на наборы результатов, я считаю, что это помогло бы им в их стремлении найти заданный тип задачи или применить формулы.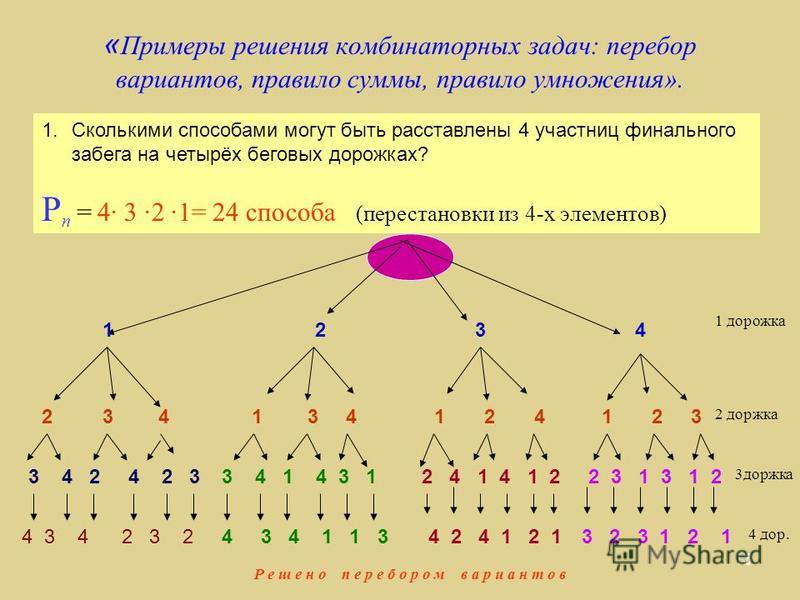 Возможно, если бы мы всегда поощряли учащихся формулировать характер того, что они считают, задавая такие вопросы, как «Что вы пытаетесь считать?» Ваши результаты более уместно моделировать как наборы вещей или их расположение? — учащиеся могут быть более склонны рассматривать счет как деятельность, связанную с результатами. Этот подход к счету, ориентированный на множество, изложен в Lockwood (2014), а также упоминается в Hadar & Hadass (19).81), Мамона Даунс и Даунс (2004 г.) и Батанеро, Наварро-Пелайо и Годино (1997 г.).

Во-вторых, есть еще один способ, с помощью которого учащиеся могут активно работать с результатами: предложить учащимся составить частичные списки результатов. Появляется все больше свидетельств того, что фактическое участие в составлении списков является полезной стратегией для студентов (English, 1991; Halani, 2012), и даже была продемонстрирована статистическая значимость (Lockwood & Gibson, в печати). Таким образом, практический совет заключается в том, чтобы учащиеся участвовали в составлении списка.

В некоторых случаях перечисление действительно может предложить ответ на задачу счета, и, более того, это помогает учащимся понять, что такое результат. Например, рассмотрим задачу домино, в которой говорится: Домино — это маленькая тонкая прямоугольная плитка с точками на одной из широких граней. Это лицо разделено на две половины, и на каждой из этих половинок может быть от 0 до 6 точек. Предположим, вы хотите сделать набор костяшек костяшек (т. е. по одному из всех возможных костяшек костяшек). Сколько различимых доминошек вы бы сделали для полного набора? В этой задаче я видел, как студенты перед перечислением предлагают ответ типа $7! \cdot 7!$, что не имеет особого смысла в контексте задачи. Решая подобную задачу, учащиеся могут понять природу результатов, которые мы хотим считать различимыми. Кроме того, стоит отметить, что частичное перечисление также полезно, особенно в задаче, в которой результаты могут быть трудно увидеть/признать похожими. Частичный список помогает, потому что, опять же, он может сориентировать учащихся в отношении того, что считается, и часто учащиеся могут экстраполировать более общее решение или стратегию даже из неполного списка.

2) Подчеркните взаимосвязь между процессами подсчета и наборами результатов. По мере того как учащиеся будут составлять списки, идея о наличии связи между их процессами счета и их набором результатов должна укрепляться. Как мы отмечали выше, эта взаимосвязь может быть ключевой, помогая учащимся обнаруживать и решать проблемы порядка и пересчета, которые являются двумя распространенными трудностями, с которыми сталкиваются учащиеся. Также важно отметить, что не обязательно преуменьшать значение выражений и формул, поскольку они являются важными аспектами подсчета, обеспечивающими упрощенные способы эффективного решения задач. Проблема в том, что мы склонны придавать им слишком большое значение, и учащиеся рассматривают их просто как формулу для запоминания, а не как обобщение и/или формализацию процесса подсчета, который имеет смысл и фактически каким-то образом структурирует набор результатов. На практике подчеркивание этой взаимосвязи может заключаться в том, чтобы давать учащимся задания, связанные с перечислением, или давать им задачи, не связанные с простым применением формулы.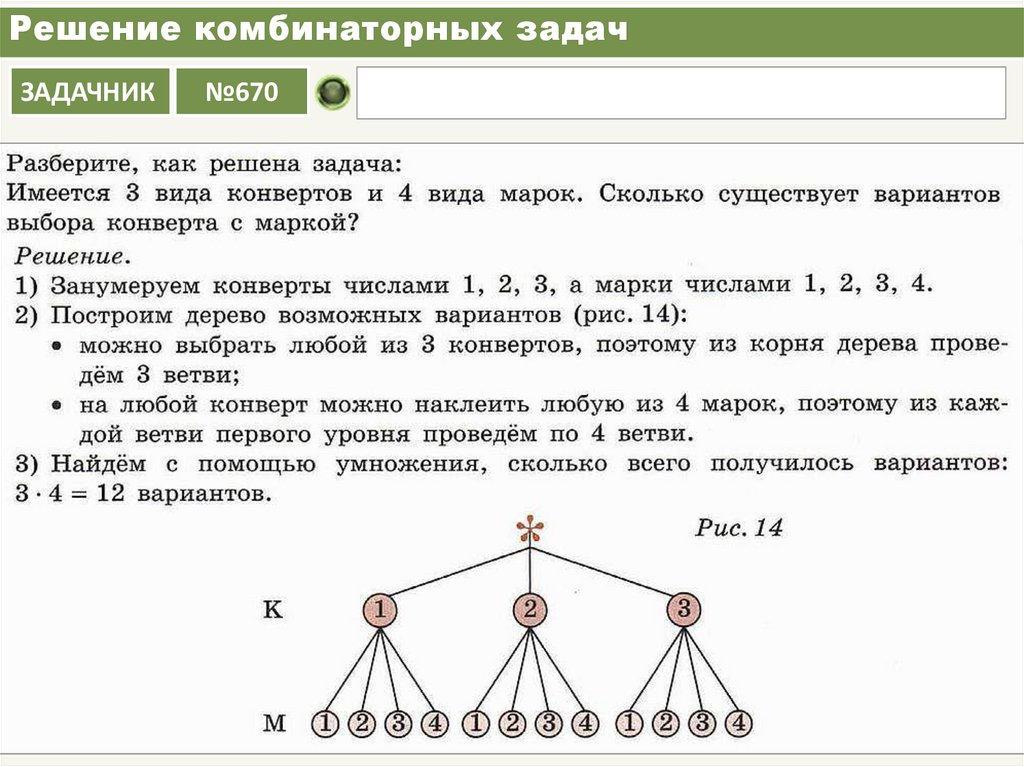 Хорошими примерами являются задача домино и задачи с последовательностями из трех букв, а также следующая задача Language Book (также адаптированная из Tucker, 2002): Y У вас есть 5 разных испанских книг, 6 разных французских книг и 4 разных японских книги. Сколькими способами можно выбрать две книги на разных языках?

3) Напомните учащимся, что задачи на счет — это весело и дают прекрасную возможность для критического мышления. Поскольку не существует четко прописанных алгоритмов для решения каждой задачи (в отличие от решения страницы, полной задач на интегрирование по частям), учащиеся могут испытывать трудности со счетом. Тем не менее, учителя должны стараться разделять мнение о том, что счет на самом деле является интеллектуальной задачей и может доставлять удовольствие. Прекрасным примером этого являются недавние видеоролики, в которых учащиеся математического класса средней школы пытаются решить задачу на счет (https://www.youtube.com/watch?v=SrWt_XvWLUk). Эти дети не беспокоятся о формулах или получении правильного ответа — они заняты критическим мышлением и решением проблем и, кажется, получают от этого удовольствие!

Для старшекурсников рассмотрите следующую задачу: Предположим, вы хотите надеть 8 одинаковых белых носков и 8 одинаковых красных ботинок на своего домашнего осьминога, у которого 8 различимых ног. Вы можете делать это в любом порядке, главное, чтобы для любой ноги носок был впереди ботинка. Сколькими способами можно надеть обувь и носки на осьминога? Если учащимся будет предоставлено время и пространство для размышлений и изучения счета как забавной возможности для решения задач, учащимся может быть удобнее заниматься результатами, а не просто пытаться применить заученную, но не совсем понятую формулу.

Ссылки:

Аннин С.А. и Лай К.С. (2010). Распространенные ошибки при подсчете задач. Учитель математики, 103(6), 402-409.

Батанеро, К., Наварро-Пелайо, В., и Годино, Дж. (1997). Влияние неявной комбинаторной модели на комбинаторное мышление учащихся средней школы. Образовательные исследования по математике, 32, 181-199.

English, LD (1991). Комбинаторные стратегии для детей младшего возраста. Образовательные исследования по математике, 22, 451-47.

Хадар, Н., и Хадасс, Р. (1981). Путь к решению комбинаторных задач усеян ловушками. Образовательные исследования по математике, 12, 435-443.

Халани, А. (2012). Способы мышления учащихся о наборах решений перечислительной комбинаторики: категория одометра. В электронных материалах Пятнадцатой группы специальных интересов MAA по исследованиям в области математического образования для студентов. (стр. 59-68) Портленд, Орегон: Портлендский государственный университет.

Локвуд, Э. (2013). Модель комбинаторного мышления учащихся. Журнал математического поведения, 32, 251–265. Дои: 10.1016/j.jmathb.2013.02.008.

Локвуд, Э. (2014). Комплексно-ориентированный подход к решению задач на счет. Для изучения математики, 34 (2), 31-37.

Локвуд Э. и Гибсон Б. (в печати). Комбинаторные задачи и список результатов: изучение продуктивного списка среди студентов бакалавриата. Чтобы появиться в образовательных исследованиях по математике.

Локвуд, Э., Суиньярд, К.А., и Коман, Дж. С. (2015). Шаблоны, наборы результатов и комбинаторное обоснование: два студента заново изобретают формулы счета. Международный журнал исследований в области математического образования бакалавриата, 1 (1), 27–62. Дои: 10.1007/s40753-015-0001-2.

Махер, К.А., Пауэлл, А.Б., и Аптегроув, Э.Б. (ред.). (2011). Комбинаторика и рассуждение: представление, обоснование и построение изоморфизмов. Нью-Йорк: Спрингер.

Мамона-Даунс, Дж. и Даунс, М. (2004). Реализация приемов решения задач: построение биекций для задач перечисления. Образовательные исследования по математике, 56, 235-253.

Такер, А. (2002). Прикладная комбинаторика (4-е изд.). Нью-Йорк: Джон Уайли и сыновья.

Эта запись была размещена в Практики оценивания, Практики в классе, Исследования и помечена как комбинаторная модель, комбинаторика, счет, формулы, результаты. Добавьте постоянную ссылку в закладки.

Математика | Бесплатный полнотекстовый | Преподавание комбинаторных принципов с использованием отношений с помощью метода Placemat

1. Введение

Как математическая дисциплина комбинаторика возникла где-то в 17 веке и часто использовалась в связи с азартными играми и привилегированными слоями в западных обществах. На самом деле история комбинаторики, вероятно, восходит к древним временам. В 1858 году во время посещения города Луксор в Египте шотландский торговец антиквариатом Александр Райнд купил папирус из Древнего Египта, датированный примерно 1800 годом до нашей эры и исписанный математическими символами. Позже, когда этот папирус был приобретен Британским музеем и иероглифы были переведены, оказалось, что проблемы нет. 79на папирусе был комбинаторным [1,2]. Томас Киркман был одним из пионеров современной комбинаторики в XIX веке и прославился комбинаторной задачей «15 школьниц» [3]. Своими оригинальными работами Киркман также внес свой вклад в дискретную геометрию и теорию групп. Сегодня комбинаторика представляет собой обширный и самостоятельный раздел математики, имеет важное значение в развитии математического мышления и служит основой для решения различных вероятностных задач. В основном это касается задач, связанных с заказом или выборкой. За последнее десятилетие она достаточно быстро развивалась в связи с появлением и взаимосвязью с информатикой. Многие задачи других дисциплин (например, теории графов и теории групп) решаются комбинаторно (например, задача о коммивояжере, задача о четырех цветах и т. д.).

Хотя комбинаторика не содержит сложных математических структур, многие комбинаторные задачи страдают из-за явной сложности вычислений, а многие реальные проблемы могут быть решены только с использованием «вычислительных мощностей». Класс комбинаторных задач, которые могут быть решены алгоритмически за полиномиальное время, называется Р (т. е. практически решаемые задачи). Более широкий класс задач включает задачи, известные как NP, которые включают комбинаторные задачи, в которых мы можем проверить, что решение существует за полиномиальное время, но для нахождения решения требуется экспоненциальное количество времени. Благодаря использованию соответствующих алгоритмов даже NP-полные задачи могут быть решены эффективно, хотя они представляют собой самые сложные задачи в классе NP. Классификация задач на практически решаемые и практически неразрешимые является одним из крупнейших открытий в теории сложности [4].

Таким образом, каждую комбинаторную задачу можно охарактеризовать по ее сложности. В этом контексте мы можем понимать сложность проблемы как усилия, необходимые для ее решения. Однако это определение сложности может привести к тому, что мы назовем проблему более сложной только потому, что она неправильно определена. Различные комбинаторные задачи привели к нахождению соответствующих методов (алгоритмов), и большой бум комбинаторики был вызван использованием компьютеров. Измерение сложности данной задачи трудом имеет смысл для одного и того же алгоритмического решения. Тогда о сложности проблемы можно судить по объему работы, которая потребовалась для вычисления решения с помощью алгоритма.

Однако существуют различные практические комбинаторные задачи, которые не решаются алгоритмически, и отсутствие алгоритма для решения проблемы может быть доказано математически, т. е. алгоритмическое решение может существовать. Само по себе наличие алгоритма решения той или иной задачи не гарантирует ее практической разрешимости. Практически решаемые задачи решаются с помощью так называемых детерминированных алгоритмов. Каждый шаг алгоритма уникален и зависит только от непосредственных данных. Если решение существует, мы знаем, как к нему прийти, или мы можем прийти к оптимальному решению для большего числа решений. Детерминированный алгоритм для практически неразрешимых задач требует больше времени, чем доступно. Поэтому эти задачи могут быть решены только с помощью так называемых рандомизированных алгоритмов, которые, например, могут быть использованы для нахождения частичного решения задачи или, по крайней мере, ряда решений в зависимости от специфики задачи. Эти алгоритмы можно представить себе как те, которые случайным образом выбирают следующий шаг на основе непосредственных данных и в соответствии с некоторыми возможными стратегиями. Таким образом, для одной и той же входной задачи этот алгоритм выполняет несколько разных вычислений и даже может выдать неверный результат. Наша цель состоит в том, чтобы создать для алгоритма такие условия, при которых вероятность неправильного расчета сведена к минимуму.

На практике рандомизированные алгоритмы используются даже для решения практически решаемых комбинаторных задач. Существует много задач с очень малой вероятностью неверного результата от использования рандомизированных алгоритмов, либо такая вероятность допустима для расчета. Причиной отказа от использования детерминированного алгоритма в этом случае является, например, время, необходимое для завершения расчета по сравнению с рандомизированным алгоритмом, который занимает лишь часть времени. Для таких задач соответствующие детерминированные алгоритмы практически непригодны (например, проверка простоты в контексте теории чисел, где нет другого способа проверить длинные простые числа, кроме как с помощью рандомизированного алгоритма). Доказательство силы и смысла использования рандомизированных алгоритмов уходит глубоко в основы математики, и, возможно, наиболее заметной областью применения являются различные задачи оптимизации, например, в теории графов или теории вероятностей, где часто бывает, что результат попасть можно только случайно. К известным комбинаторным задачам теории графов из класса NP-полных относятся, например, задачи принятия решений, такие как «раскрашиваем ли k-раскрашиваемый неориентированный граф?», «содержит ли (не)ориентированный граф (не)ориентированная схема Гамильтона?», «Содержит ли ориентированный граф полный подграф с k вершинами?» или «Содержит ли неориентированный граф k вершин?» [5,6].

Идеи комбинаторики могут проявляться во многих формах, во всех обычных ситуациях, таких как игра между детьми, в повседневной жизни и во многих областях работы или в различных школьных предметах. Вначале преподавание математики в основном сосредоточено на различных отношениях между объектами, но не касается специально комбинаторных задач [7].

Капур [8] заявил, что есть несколько причин, по которым комбинаторика важна и должна преподаваться в школе. Один из них заключается в том, что комбинаторика не требует предварительных расчетов, чтобы эти темы можно было изучать на раннем этапе; это не зависит от мастерства учащегося в исчислении. Другая заключается в том, что комбинаторика может быть использована для обучения учащихся «счету», оценке, обобщению и систематическому мышлению. Комбинаторика может применяться во многих других областях, таких как программирование, физика и инженерия, биология, социальные науки, менеджмент и даже в широко используемых и популярных компьютерных приложениях. Комбинаторика может привести учащихся к пониманию сильных и слабых сторон математики. Кроме того, важную роль в расчетах играет комбинаторика.

Исследования Сяхпутры [9] были сосредоточены на определении трудностей студентов в задачах комбинаторики и создании математической модели из данных задач. По результату задачи и анализу комбинаторного мышления учащихся можно прогнозировать, что учащиеся в целом не поняли поставленную задачу. Студенты не привыкли к процессу перечисления при подсчете. Более того, почти все студенты не составили математическую модель задачи. Студенты всегда использовали самую быструю формулу для решения данной задачи.

По опыту преподавания Спира [10], студенты не имеют никакой подготовки к комбинаторному мышлению, так как их учат, что решение комбинаторных задач состоит в основном из прямых вычислений по заданным формулам и с использованием мультипликативного принципа. Затем они часто спрашивают: «Зависит ли решение от порядка элементов в наборе?», «Должен ли я использовать комбинации или варианты?», «Могу ли я использовать один и тот же элемент из набора по порядку большее количество раз?» и т. д. В своем исследовании он описал несколько идей, связанных с принципами биекции, которые он нашел полезными в реальном обучении и которые могут изменить способ мышления студентов и преподавания комбинаторики.

При обучении комбинаторике могут использоваться различные методики. В исследовании Мамоны-Даунса и Даунса [11] авторы применили одну методику, которая хорошо показывает, как умственная обработка знакомых знаний не часто бывает в форме, подходящей для применения при решении задач. Учащиеся могут знать, что взаимное соответствие между двумя конечными множествами означает, что количество элементов в каждом из них равно, но они не смогут использовать этот факт для создания метода решения для определения количества элементов в заданном множестве, т. е. если их попросить найти количество элементов данного набора, один из возможных методов, который можно использовать, — это найти другой эквивалентный набор, с помощью которого можно легко построить биекцию.

Книга [12] представляет собой общее введение в перечислительную комбинаторику с упором на биективные методы. Представлено систематическое развитие математических аппаратов, необходимых для решения задачи перечисления, и их использование для анализа многих комбинаторных структур.

2. Математическая основа

Рассмотрим взаимно непересекающиеся подмножества X1,⋯,Xn, n≥2, конечного множества X, X=X1∪X2∪⋯∪Xn. Тогда X=X1+X2+⋯+Xn и отношение называется правилом сумм. Справедливость отношения можно показать с помощью математической индукции по n. Если сначала n=2 и X1={a1,⋯,ak}, X2={b1,⋯,bm}, то при условии X1∩X2=∅ следует, что X1∪X2={a1,⋯,ak,b1, ⋯,бм}. Тогда |X|=|X1∪X2|=|X1|+|X2|. Второй шаг аналогичен. Кроме того, для любых конечных множеств X1,⋯,Xn, n≥2 верно, что |X1×X2×⋯×Xn|=|X1|·|X2|·⋯·|Xn| и это отношение называется правилом произведения [13]. Отношение также можно показать с помощью математической индукции по n. Для n=2 и множеств X1={a1,⋯,ak} и X2={b1,⋯,bm} верно, что X1×X2={(a1,b1),⋯,(a1,bm) ,(a2,b1),⋯,(a2,bm),⋯,(ak,b1),⋯,(ak,bm)}. Таким образом, набор содержит k m-й, следовательно, X1×X2=k·m=X1·X2. Если аргумент уже применим к n > 2, покажем, что он применим и к n+1. Теперь определим количество элементов в множестве X1×X2×⋯×Xn×Xn+1. Пусть Xn+1≠∅ и |Xn+1|=s≥1. Тогда Xn+1={c1,⋯,cs}. Теперь определим для каждого ∈{1,⋯,s} Yi=X1×X2×⋯×Xn×{ci}. Тогда |Yi|=|X1×X2×⋯×Xn|, и по предположению индукции верно, что |Yi|=|X1|·|X2|·⋯·|Xn|. Далее, поскольку X1×X2×⋯×Xn×Xn+1=∪i=1sYi и множества Y1,⋯,Ys взаимно не пересекаются, из правила сумм следует, что |X1×X2×⋯×Xn×Xn+1 |=∑i=1s|Yi|=|X1|·|X2|·⋯·|Xn| [14].

Пусть A, B — конечные множества, а |A|=n и |B|=m. Тогда |BA|=|B||A|=mn (мы обозначаем BA как множество всех отображений A→B). Это отношение можно показать с помощью математической индукции по n для полностью натуральных чисел m. Если сначала n=0, то A=∅ и теорема верна, поскольку BA=∅. Пусть теорема верна для некоторого n≥0 и |A|=n+1, а A={a1,⋯,an,an+1}. Если B=∅, то BA=∅. Если m≥1 и B={b1,⋯,bm}, определим для k∈{1,2,⋯,m} Yk={f∈BA:f(an+1)=bk}. Множества Yk,k=1,⋯,m взаимно не пересекаются и BA=∪k=1mYk. Ограничения отображений f∈Yk на множество A−{an+1} различаются попарно, и они дают все отображения {a1,⋯,an}→B. Из предположения индукции можно сделать вывод, что |Yk|=mn. Тогда |BA|=∑k=1m|Yk|=m·mn=mn+1=|B||A|. При A={1,2,⋯,n} и |B|=m элементы множества BA называются вариациями с повторением n-го класса, состоящего из m элементов (множества B). Для этих отображений на практике используется указание Vn′m=mn.

Для конечных множеств A и B с |A|=n и |B|=m число всех инъективных отображений из A в B равно m·(m−1)·⋯·(m−n+ 1)=∏i=0n−1(m−i). Если символ IBA используется для обозначения количества инъекций A→B и сначала пусть n = 0, а A=∅, то имеется только одна инъекция A→B. В произведении ∏i=0n−1(m−i) нет членов, и такое произведение понимается как 1. Пусть теперь теорема верна для некоторого n≥0. Пусть |A|=n+1, а A={a1,⋯,an,an+1}. Если B=∅, то BA=∅. Пусть m≥1 и B={b1,⋯,bm}, и определим для k∈1,2,⋯,m множество Yk={f∈BA:f(an+1)=bk и f является инъекцией} . Множества Yk,k=1,⋯,m взаимно не пересекаются, и каждая инъекция A→B принадлежит одному из них. Поэтому |Y1|+|Y2|+⋯+|Ym|=IBA. Определим |Yk| для любого к. Ограничения отображений f∈Yk на множество A−{an+1} снова представляют собой инъекции A−{an+1}→B−{bk}. Каждая инъекция происходит только один раз между этими ограничениями, поэтому |Yk|=IB−{bk}A−{an+1}. По предположению индукции |Yk|=∏i=0n−1(m−i−1)=∏i=1n(m−i). Отсюда IBA=m∏i=1n(m−i)=∏i=0n(m−i) [14]. Вливаниями из множества A={1,2,⋯,n} в множество B, где |B|=m, называются вариации без повторения (и просто вариации или нет) n-го класса, состоящего из m элементов (из набор Б). Для этих отображений на практике используется обозначение Vn(m). Выражение m·(m−1)·⋯·(m−n+1) можно упростить, используя факториал Vn(m)=m!(m−n)! [15]. Вариации n-го класса элементов множества B являются биективными отображениями A→B, и их число равно n·(n−1)·⋯·2·1=n!. Они называются перестановками (множества B) и обозначаются как P(n)=n! [16].

Предположим, что существует конечное множество A, где |A|=n. Комбинации (без повторения) k-го класса (или даже k-комбинации), состоящие из n элементов, являются k-элементными подмножествами множества A. Они обозначаются как Ck(n) [17] и подсчитываются k-комбинаций n элементов множества A есть Ckn=nk=n!n−k!k!=nn−1⋯n−k+1kk−1⋯1 [18]. Чтобы показать это, предположим, что множество K={0,1,⋯,k−1}. Мы будем исследовать инъективные отображения K→A, то есть на множестве IAK. На этом наборе мы можем создать бинарное отношение R fRg⟺f({0,1,⋯,k−1})=g({0,1,⋯,k−1}). Тогда отношение R является отношением эквивалентности, и каждый класс эквивалентности C на множестве IAK однозначно определяется одним k-элементным подмножеством M, на котором отображения из множества C отображают множество {0,1,⋯,k −1}. Если мы заменим кодовый домен A на M в этих отображениях, мы получим все перестановки множества M. Следовательно, |C|=k!. Каждый класс эквивалентности на IAK имеет k! элементы. Следовательно, k!nk=n!n−k!=IAK и количество k-элементных подмножеств множества A равно (nk)=IAKk!=n!(n−k)!k! [14].

Для A=1,2,⋯,n и |B|=m в множестве BA всех вариаций с повторением n-го класса в m-элементном множестве B можно установить отношение эквивалентности R как следует. Пусть f,g∈BA. Определим fRg⟺f−1x=g−1x для каждого элемента x∈A. Таким образом, два варианта с повторением эквивалентны тогда и только тогда, когда одни и те же элементы повторяются в них обоих одинаковое число раз. Комбинации с повторением n-го класса, составленные из m элементов множества B, являются классами эквивалентности R на множестве BA. Они обозначаются как Cn′(m). Если B — m-элементное множество и n∈ℕ, то количество всех комбинаций с повторением n-го класса в множестве B равно Cn′(m)=(m+n−1n). Комбинации с повторением n-го класса в множестве B являются элементами разложения множества BA, индуцированного отношением эквивалентности fRg⟺|f−1({x})|=|g−1({x} )|. Пусть B=1,2,⋯,m. В каждом классе эквивалентности R (сочетания с повторением) выделим слово, в котором элементы множества B упорядочены по размеру, и укажем это слово с сочетанием с повторением. Пусть c1c2⋯cn — комбинация с повторением n-го класса множества B, а c1≤c2≤⋯≤cn. Сопоставим этой последовательности новую последовательность d1d2⋯dn, поставив f(ci)=di=ci+i−1, i=1,2,⋯,n. Выполняется di∈{1,2,⋯,m+n−1} и d1 Следовательно, количество комбинаций с повторением равно (m+n−1n) [14].

Рассмотрим два множества, A и B, при этом |A|=n=|B|. Пусть множество A разбивается на множества A1,A2,⋯,Am размера |Ai|=ni, i=1,2,⋯,m. Допустим пустые множества между множествами Ai и рассмотрим биекции A→B, а две биекции f, g будем считать эквивалентными, если для каждого элемента y∈B существует индекс i∈{1,2,⋯,m }, так что оба элемента f−1 и g−1 принадлежат одному и тому же множеству Ai. Классы эквивалентности этих биекций обозначаются как перестановки с повторением n1 элементов первого типа, n2 элементов второго типа, … nm элементов m-го типа. Обозначим их Pn1,⋯,nm′(n). Для конечных множеств A и B, где |A|=n, |B|=m и B={b1,b2,⋯,bm} количество отображений f:A→B таких, что для каждого элемента bi i =1,2,⋯,m, верно, что |f−1({bi})|=ni, где n _i — целые неотрицательные числа, сумма которых n1+n2+⋯+nm=n равна n!n1!·⋯·nm!. Если мы рассматриваем (ai1,ai2,⋯,ain) как случайную перестановку множества A, определенную как порядок, мы можем определить отображение A→B так, что первые n1 элементов множества A отправляются в b1, вторые n2 элементов на b2 и т. д. Однако первые n1 элементов можно переставлять независимо друг от друга, и отображение не изменится. Таким же образом мы можем переставлять и другие наборы. Отсюда получаем, что n1!,⋯,nm! перестановки отображают одно и то же отображение, и каждое отображение, такое что |f−1({bi})|=ni для каждого элемента bi∈B, получается таким же образом. Следовательно, число этих отображений равно n!n1!·⋯·nm! [14].

3. Методика исследования и обсуждения

Проведено педагогическое исследование по проверке эффективности инновационного подхода к обучению по программе по новой методике — с использованием отображений и отношений, причем отношения и отображения взяты отдельно. Цель эксперимента состояла в том, чтобы определить, улучшил ли семинар по отбору, где учебный план объяснялся по новой методике, результаты студентов как в понимании математической концепции «комбинаторики», так и в повышении успешности решения задач, ориентированных на комбинаторные принципы. Обучение комбинаторным принципам по предложенному нами методу проводилось в течение 2 месяцев с субсидией на 2 учебных часа в неделю. Обучение проходило в форме комбинированного обучения. Студентам был предоставлен учебный материал для домашнего задания, который содержал базовые теоретические знания о последнем обучении в классе и основные примеры. Эти учебные материалы были предоставлены учащимся за неделю до начала преподавания темы в классе на сайте школы в разделе электронного обучения. Штурм вопросов проходил в классе в начале встречи, а затем ответы на вопросы студентов давались в форме дискуссии под руководством преподавателя. Цель обсуждения состояла в том, чтобы студенты получили концептуальное понимание основных комбинаторных понятий. Впоследствии студенты решали различные задачи по комбинаторике. Мы использовали форму совместного обучения с использованием метода обучения Placemat [19].,20,21]. Для нужд эксперимента авторы исследования подготовили преподавателя, который преподавал комбинаторные принципы на семинаре, используя новый метод в EXG.

Эксперимент неоднократно проводился среди талантливых детей по математике в выбранной средней школе в Жилине, Словацкая Республика, в течение четырех последовательных учебных лет с 2016/2017 по 2019/2020. Эксперимент проводился одинаково каждый учебный год. Всего в эксперименте приняли участие 104 студента. Студенты были разделены на экспериментальную и контрольную группы. Экспериментальную группу (ЭКГ) составили 44 студента, отдавшие предпочтение семинару по отбору. 60 студентов, отдавших предпочтение классическому (алгоритмическому) подходу преподавания выбранного предмета, составили контрольную группу (КГ). В ходе эксперимента обе группы студентов обучались выбранной части учебного плана по математике, при этом студенты ЭГП также обучались данному учебному плану по новой методике, а студенты КГ преподавали тот же учебный план только стандартным образом.

Перед началом эксперимента необходимо было проверить эквивалентность обеих групп учащихся — ЭГ и КГ — в знаниях по математике. Мы проверили эквивалентность обеих групп учащихся, выполнив тест по учебной программе по комбинаторике. Тест (предтест) включал в себя три задания из вышеуказанной учебной программы, при этом результаты предварительного теста оценивались баллами от А (лучший) до Е (худший). Результаты, достигнутые студентами обеих групп (ЭКГ и КГ) в предварительном тестировании, представлены на рис. 1.

На рисунке 1 показано, что учащиеся EXG и CG достигли немного разных результатов или разных оценок в предварительном тесте выбранной учебной программы по математике. Нас интересовало, являются ли эти различия в результатах тестов также статистически значимыми. Статистическую значимость различий между студентами ЭГ и КГ по результатам предтестовой математики проверяли тестом на независимость качественных характеристик с помощью статистики тестирования Y2.

Тест на независимость с помощью статистики тестирования Д ² — это тест, с помощью которого можно проверить независимость между двумя признаками качества 𝕦 и 𝕧, значения которых расположены в таблице сопряженности типа r×s, а случайная величина 𝕦 принимает значения 1, 2, …, r (r ≥2) и случайной величиной 𝕧 значения 1, 2, …, s (s ≥ 2). Обозначим pij=P𝕦=i,𝕧=j, pi·=∑j=1spij и p·j=∑i=1rpij, полагая, что pij>0 для i=1,2,⋯,r, j=1, 2,⋯,s и ∑i=1r∑j=1spij=1. Предположим, что был сделан случайный выбор диапазона n из этого распределения. Пусть nij — эмпирические частоты, т. е. nij количество тех случаев, когда встречалась выбранная пара файлов (i,j). Затем случайные величины nij становятся комбинированным полиномиальным распределением с параметром n и вероятностями pij. Верно, что n=∑i=1r∑j=1snij, ni·=∑j=1snij, i=1,2,⋯,r, n·j=∑i=1rnij, j=1,2,⋯, с, где п _i — скорость значения i символа 𝕦, n·j — скорость значения j символа 𝕧. Числа pi·, p·j представляют собой предельные вероятности, а значения ni· и n·j представляют собой предельные ставки.

Используя статистику тестирования Y ² , проверяем гипотезу H0: «характеристики 𝕦, 𝕧 независимы» против альтернативной гипотезы h2: «имеется статистически значимая зависимость между характеристиками 𝕦, ·𝕧». Статистика тестирования Y2 имеет вид Y2=2·∑i=1r∑j=1snij·lnnijeij [22].

Тестовая статистика Y2 имеет при справедливости нулевой гипотезы H ₀ · χ2- распределение с (r−1)(s−1) степенями свободы. Отклоняем нулевую гипотезу H0 на уровне значимости α, если вычисленное значение статистики тестирования Y2 больше соответствующего критического значения χ2- распределения. Ярнольд показал, что χ2≈Y2, если ожидаемые скорости eij>3 для всех i и j [23].

В нашем случае наблюдаемыми характеристиками являются две характеристики качества, 𝕦 и 𝕧, где 𝕦 указывает на результаты, достигнутые студентами ЭГ, а 𝕧 указывает на результаты, достигнутые в письменных тестах (предварительном тесте) студентами КГ.

Мы проверили нулевую гипотезу H ₀ о независимости наблюдаемых характеристик 𝕦 и 𝕧 от выбранного уровня значимости α=0,05 или о том, что различия между EXG и CG в результатах предварительного тестирования не являются статистически значимыми. Мы проверили нулевую гипотезу против альтернативной гипотезы h2: различия между EXG и CG в результатах предварительного тестирования статистически значимы.

По критерию независимости с использованием статистики тестирования Y2 мы рассчитали значение статистики тестирования для таблицы сопряженности 2 × 5 Y ² = 1,08. Для выбранного уровня значимости α=0,05 и числа степеней свободы (5−1)(2−1)=4 ищем критическое значение χ2-распределения: χ0,052(4)=9,49 (для α=0,01, критическое значение χ0,012(4)=13,28).

Поскольку расчетное значение критерия проверки Y2 меньше критического значения 9,49 при уровне значимости α=0,05, мы не можем отвергнуть проверяемую гипотезу H0. Это означает, что различия между результатами, полученными студентами ЭГ в предварительном тесте, и результатами, достигнутыми студентами КГ, не являются статистически значимыми.

После завершения эксперимента обе группы (EXG и CG) прошли 90-минутный письменный экзамен (пост-тест) по соответствующей части математики.

Задания по комбинаторному исчислению были включены в письменный экзамен:

Задание 1 — Показать, сколько раз в день электронные часы показывают возрастающую последовательность.

Решение. Время на цифровых часах можно закодировать с помощью упорядоченного секстоля натуральных чисел.

Должно быть верно, что c1

Если c1=1, то c5=5. Если c1=0, то c5=4∨c5=5.

Множество H искомых последовательностей должно быть разделено следующим образом:

В первом наборе последовательность имеет вид (12:34:5c6), что подразумевает |h2|=4 (поскольку c6 может быть только 6, 7, 8, 9).

Во втором наборе последовательности имеют вид (01:23:4c6), поэтому |H04|=5 (c6 может быть только 5, 6, 7, 8, 9).

Количество элементов в наборе H05 рассчитывается следующим образом: для (c2, c3, c4) возможны только следующие варианты:

Для c6 тогда 6, 7, 8, 9, (потому что c5=5). Каждая последовательность в H05 характеризуется упорядоченной парой [(c2, c3, c4),c6] со счетом 4·4=16 в соответствии с правилом произведения.

Итого по правилу произведения получаем H = h2 + H04 + H05 = 4 + 5 + 16 = 25. индивидуально через определенный промежуток времени). Среди них Адам, Питер и Джордж. Покажите, сколькими способами можно составить расписание стартов так, чтобы никакие два из перечисленных выше участников не стартовали подряд.

Решение. Общее количество всех возможных расписаний равно P(k). Давайте сначала определим, через сколько часов Адам начинает свой путь сразу после Петра. Эту пару можно рассматривать как одного участника, и количество таких расписаний равно P(k−1). Мы приходим к одному и тому же счету для каждой из V(2,3) упорядоченных пар Адама, Петра и Джорджа. В результате получается общее количество расписаний V(2,3)P(k−1), которое, однако, также включает те, в которых все три участника стартуют последовательно. Таким образом, количество расписаний, которые необходимо вычесть, равно P(3)P(k−2) (каждая из упорядоченных троек P(3) может быть принята за одного участника). Следовательно, общее количество равно P(k)−(V(2,3)P(k−1)−P(3)P(k−2)).

Задание 3. Укажите количество слов длины k в n-элементном алфавите, таких что (а) нет двух одинаковых последовательных символов и (б) есть палиндромы.

Решение:

(a): Первую букву можно выбрать из n вариантов, вторую из n−1 вариантов, третью также из n−1 вариантов (мы не можем выбрать соседнюю букву, но первую применима буква) и т. д. В целом n(n−1)⋯(n−1)=n(n−1)k−1.
(б): Палиндром однозначно идентифицирует первые (k+1) div 2 буквы (также известные как ⌊k+1⌋ — так называемая нижняя часть целого), и таким образом определяются остальные. Если в слове четное количество букв, (k + 1) div 2 совпадает с k div 2; если в нем нечетное количество букв, (k+1) div 2 также включает среднюю букву, которая симметрична самой себе.

Всего у нас есть n⌊k+1⌋ вариантов.

Задание 4 — Покажите количество всех четырехзначных чисел, кратных девяти, которые можно записать с использованием цифр 0, 1, 2, 5, 7, причем цифры в числе могут также повторяться.

Решение. Число делится на 9, если сумма его цифр делится на 9. В нашем случае на ум приходят только суммы цифр 9 и 18 (из данных цифр нельзя составить никакую другую).

Давайте сначала создадим экземпляры с суммой 9 и пока не будем учитывать их позиции:

Постепенно будем решать отдельные случаи.

Случай (a), количество четырехзначных чисел, которые можно записать, используя числа 7,2,0,0, равно 4!2! (это перестановки четырех элементов, где одна цифра повторяется дважды). Однако мы должны исключить числа, у которых цифра 0 стоит на первой позиции слева, т. е. 3!=6 чисел (мы делаем перестановку оставшихся трех элементов). Таким образом, случай (a) имеет 6 экземпляров (4!2!−3!=6).

Случай (b) имеет 4!2!−3!2!=12−3=9 экземпляров, поскольку цифра 1 повторяется в последовательности 2 раза, а 0 заблокирован в первой позиции.

Случай (c) имеет 4!2!−3!2!=12−3=9 экземпляров.

Случай (d) имеет 4!2!=12 экземпляров.

Таким образом, всего имеется 36 случаев суммы цифр 9.

Теперь мы создадим экземпляры с суммой 18:

В случае (a) число перестановок равно 4!2!2!=6 потому что первый элемент повторяется 2 раза и второй элемент также повторяется 2 раза.

В случае (b) количество перестановок равно 4!2!=12, так как первый элемент повторяется 2 раза.

Следовательно, всего 18 случаев суммы цифр 18.

Всего существует 54 числа, делящихся на 9, которые можно записать, используя цифры 0, 1, 2, 5, 7 и цифры в числе может повторяться.

Задание 5. Рассмотрим блоки домино, каждый блок которых разделен на две половины и каждая половина отмечена одним из значений 0,1,⋯,n. Ни одна из двух половин не может быть выделена как первая или вторая. Покажите вероятность того, что два случайно выбранных блока могут быть прикреплены друг к другу, т. е. иметь одинаковое значение хотя бы с одной стороны.

Решение. Блок со значениями i,j∈{0,1,⋯,n} может быть четко идентифицирован набором {i,j}. Поскольку возможно, что i = j (в игре домино речь идет о так называемых дублетах), в общем случае для домино-блока выполняется 1≤|{i,j}|≤2. Следовательно, общее количество блоков равно (n+11)+(n+12)=(n+22), поскольку общее количество значений в наборе {0, 1, ⋯, n} равно n+1. Первый элемент (n+11) представляет количество дублетов, а второй — количество блоков с двумя разными значениями.

Тогда количество всех возможных выборов двух блоков равно:

Теперь давайте покажем количество пар блоков, которые имеют общее значение i. Помимо значения i, эти блоки также несут два других значения j и k (j≠k), причем одно из этих значений может совпадать с i.

Таким образом, мы получаем (n+12) пар блоков с общим значением i, потому что мы выбрали два элемента j, k из n+1 элементов. Поскольку значение i можно выбрать (n+1) раз, всего у нас есть (n+1)(n+12) пар костяшек домино, которые можно соединить друг с другом.

Следовательно, вероятность случайно выбранной пары с возможностью взаимной привязанности равна

Кроме того, в данном случае письменный (посттестовый) экзамен оценивался по баллам от А (лучший) до Е (худший). Были проанализированы и сопоставлены результаты пост-тестирования в обеих группах учащихся в каждом из упомянутых выше учебных лет. Результаты, достигнутые студентами обеих групп (ЭГ и КГ) в итоговом тестировании в каждом году, представлены на рис. 2, рис. 3, рис. 4 и рис. 5.

Из Рисунков 2, Рисунков 3, Рисунков 4 и Рисунков 5 мы видим, что студенты EXG и CG получили разные результаты или разные оценки на письменном экзамене (пост-тесте) по выбранной части математики в каждый год. наблюдаемый. Нас интересовало, были ли эти различия в результатах письменных экзаменов также статистически значимыми. Значимость статистических различий между учащимися ЭГ и КГ в результатах математического посттестирования в этом случае также проверялась тестами независимости качественных характеристик в каждом учебном году с использованием статистики тестирования Y2. В нашем случае в 2016/17 учебном году также имелись две качественные характеристики, 𝕦 и 𝕧, где 𝕦 указывает на результаты, достигнутые учащимися EXG в пост-тесте по выбранной математике, а 𝕧 указывает на результаты, достигнутые в пост-тесте. тест студентов CG. Кроме того, в этом случае мы проверили нулевую гипотезу H0 о независимости наблюдаемых характеристик, 𝕦 и 𝕧, на выбранном уровне значимости α=0,05. Или мы проверили H0, где различия между EXG и CG в результатах посттеста не являются статистически значимыми, против альтернативной гипотезы h2, где различия между EXG и CG посттестами являются статистически значимыми.

По критерию независимости с использованием статистики тестирования Y2 для таблицы сопряженности 2 × 5 мы вычислили значение статистики тестирования Y2=12,56. Для выбранного уровня значимости α=0,05 и числа степеней свободы (5−1)(2−1)=4 ищем критическое значение χ2-распределения: χ0,052(4)=9,49 ( при α=0,01 критическое значение χ0,012(4)=13,28).

Поскольку расчетное значение тестового критерия Y2 превышает критическое значение 9,49, мы отвергаем тестовую гипотезу α=0,05 на уровне значимости H0 в пользу альтернативной гипотезы h2. Это означает, что различия между результатами, достигнутыми учащимися ЭГ в письменном экзамене по математике, и результатами, достигнутыми учащимися КГ в показанном тесте, статистически значимы.

Основываясь на анализе результатов письменного экзамена, представленного на рис. 2, мы видим, что в то время как только 13% студентов в КГ получили оценку А по письменному экзамену, 64% студентов в EXG получили оценку . Напротив, рейтинги D и E по EXG не были получены ни одним учащимся, но по CG до 25% студентов получили этот рейтинг.

Мы также следовали аналогичному процессу при проверке статистической значимости различий между ЭГ и КГ в результатах посттестирования по выбранному разделу математики в другие учебные годы с 2017/2018 по 2019 год./2020. С помощью тестовой статистики Y ² мы рассчитали таблицы сопряженности 2 × 5 и значения тестовой статистики Y2, которые четко занесены в Таблицу 1.

критическое значение 9,49, α=0,05, во всех трех случаях мы отвергаем проверяемую гипотезу H0 в пользу альтернативной гипотезы h2. Это означает, что различия между результатами, достигнутыми учащимися EXG на письменном экзамене по выбранной части учебной программы по математике, и результатами, достигнутыми учащимися CG в показанном тесте, статистически значимы. В 2016/2017 учебном году, как и в другие учебные годы, из результатов, представленных на рис. 2, рис. 3, рис. Оценка A или B на письменном экзамене по выбранной актуарной математике, менее 60% студентов получили эту оценку в CG. Наоборот, результаты вышеперечисленных тестов в КГ значительно чаще оценивались в баллах СЕ-Е (50%, 41%, 47% и 58%) каждый год.

По результатам проведенного эксперимента можно сделать вывод, что за счет привлечения селекторного семинара (в сочетании с классическим подходом к обучению) достигнут более высокий уровень знаний, лучшее понимание различных принципов и алгоритмов, и, таким образом, студенты лучше освоил вопрос. Поэтому в дальнейших исследованиях эффективно и необходимо обратить внимание на создание новых методов обучения математике, чтобы инновационные методы обучения можно было в большей степени использовать в обучении математике.

4. Выводы

В настоящее время образование перемещается в онлайн-сферу, в результате чего смешанное обучение приобретает все большую популярность и значение. Изменение контекста образования также требует создания новых методических процедур, которые будут поддерживать учащихся, особенно в их обучении вне класса, где отсутствует присутствие учителя. Кроме того, деятельность в классе должна быть обновлена, чтобы она была больше ориентирована на применение уже приобретенных теоретических знаний. Кроме того, на основе нашего исследования было показано, что если учащиеся получают новые знания подходящим образом, они также лучше усваивают учебную программу.

На основании графического представления результатов обоих тестов можно сделать вывод, что вероятность получения более высокой оценки увеличилась от посещения отборочного семинара, где преподавание комбинаторики проходило описанным выше способом. Это показало, что предложенный новый способ обучения комбинаторике через отношения эффективен.

Следует отметить, что многие проблемы реального мира можно рассматривать с точки зрения комбинаторики, и что каждая комбинаторная задача характеризуется сложностью как одним из ее существенных признаков. С этой точки зрения мы поддерживаем усилия по изучению и развитию теории сложности, основанной на различных математических принципах. Мы делаем акцент на постановке избранных решений задач, которые являются основой для понимания самих возможностей решения комбинаторных задач. Теоретическая основа данной статьи характеризует и описывает основные комбинаторные структуры, но, учитывая ее довольно узкий охват, достаточное освещение такой широкой темы, как комбинаторика, теория сложности и теория графов, может быть найдено только в соответствующей литературе, где отдельные разделы Упомянутые в этой статье поясняются более подробно.

Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок

Узнайте, сколькими способами можно выбрать k предметов из n предметов набора. С/без повторения, с/без порядка.

Расчет:

Ck(n)=(kn)=k!(n−k)!n! n=10 k=4 C4(10)=(410)=4!(10 −4)!10!=4⋅3⋅2⋅110⋅9⋅8⋅7=210

Количество комбинаций: 210

Вариантов

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, образованная из множества n элементов. Элементы не повторяются и зависят от порядка элементов группы (поэтому расположены).

Количество вариаций можно легко подсчитать, используя комбинаторное правило произведения. Например, если у нас есть набор n = 5 чисел 1,2,3,4,5 и мы должны сделать вариации третьего класса, их V ₃ (5) = 5 * 4 * 3 = 60. Vk(n)=n(n−1)(n−2)…(n−k+1)=(n−k)!n! н! мы называем факториалом числа n, которое является произведением первых n натуральных чисел. Обозначение с факториалом только более понятное, эквивалентное. Для вычислений вполне достаточно использовать процедуру, вытекающую из комбинаторного правила произведения.

Перестановки

Перестановка является синонимом вариации n-го класса n-элементов. Таким образом, это любая упорядоченная группа из n элементов, состоящая из n элементов. Элементы не повторяются и зависят от порядка элементов в группе. P(n)=n(n−1)(n−2). ..1=n! Типичный пример: у нас есть 4 книги, и сколькими способами мы можем расположить их рядом на полке?

Вариации с повторением

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, состоящая из множества n элементов, причем элементы могут повторяться и зависят от их порядка. Типичным примером является образование чисел из цифр 2,3,4,5 и нахождение их количества. Рассчитываем их количество по комбинаторному правилу произведения: Vk′(n)=n⋅n⋅n⋅n…n=nk

Перестановки с повторением

Повторяющаяся перестановка представляет собой упорядоченную группу k-элементов из n-элементов, при этом некоторые элементы повторяются в группе. Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок. Pk1k2k3…km′(n)=k1!k2!k3!…km!n! Типичный пример — узнать, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.

Комбинации

Комбинация k-го класса из n элементов представляет собой неупорядоченную группу k-элементов, образованную из множества n элементов. Элементы не повторяются, и порядок элементов группы не имеет значения. В математике неупорядоченные группы называются множествами и подмножествами. Их количество является комбинационным числом и рассчитывается следующим образом: Ck(n)=(kn)=k!(n−k)!n! Типичный пример комбинаций: у нас 15 учеников, и мы должны выбрать троих. Сколько их будет?

Комбинации с повтором

Здесь мы выбираем k групп элементов из n элементов, независимо от порядка, и элементы могут повторяться. k логически больше n (иначе мы получили бы обычные комбинации). Их счет: Ck′(n)=(kn+k−1)=k!(n−1)!(n+k−1)! Пояснение к формуле — количество комбинаций с повторением равно количеству расположений n − 1 разделителей на n-1 + k местах. Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть? к = 6, п = 3.

Основы комбинаторики в текстовых задачах

ПИН-коды
Сколько пятизначных ПИН-кодов мы можем составить, используя четные числа?
Усвоение
Учащийся усваивает предмет для экзамена по чешскому языку на 98%, по математике на 86% и по экономике на 71%. Какова вероятность того, что он потерпит неудачу по математике, а другие преуспеют?
Пересечение) 1566
В скольких точках пересекаются девять прямых на плоскости, из которых четыре параллельны друг другу, а из остальных пяти никакие две не параллельны (а если предположить, что через каждое пересечение проходят только две прямые) ?
Блюда
Из 5 разных блюд HOD должен протестировать не менее трех разных блюд, прежде чем выставлять оценки учащимся. Сколькими способами он может выбрать блюда?
MATES
В MATES (Маленькая телевизионная хитрость) из 35 случайных чисел выпадает 5 выигрышных номеров. Сколько возможных комбинаций существует?
Произвольно 69194
На плоскости есть десять произвольных точек. Сколько кругов мы можем сделать из них?
7 героев
9 героев скачут на 9лошади позади. Сколькими способами мы можем отсортировать их сзади?
Тест из шести вопросов
В тесте шесть вопросов. На каждый есть три ответа, правильный только один. Для сдачи экзамена студенты должны правильно ответить не менее чем на четыре вопроса. Алан не выучил, поэтому обвел ответы, только угадывая. Какова вероятность th
Три кости
Игрок, бросающий три кости, задал Г. Галилею вопрос: «Стоит ли ставить на сумму 11 или на сумму 12?» Что ответил ему Галилей? Подсказка: запишите все три тройки чисел, которые можно выбросить и: всего 11 всего 12 и
Семисегментный дисплей
Электронные устройства иногда используют тип цифр ниже, где каждая цифра состоит из нескольких коротких полос. Например, семерка использует три маленькие полоски. Какое самое большое трехзначное число можно составить, если использовать двадцать полосок?
Вероятность 3219
В последние годы в марте 12 дней шли дожди. Какова вероятность того, что 18 марта шел дождь?
Следующие
Следующие данные представляют собой количество ящиков кофе или фильтров, проданных четырьмя торговыми представителями в ходе недавнего конкурса продаж. продавец; Гурман; Единая чашка; фильтры; Тотал Коннор; 142; 325; 30; 497 Пейдж ; 42; 125; 40; 207 Брайс ; 9; 100; 10; 119 Mall
Равносторонний 75284
Даны 6 отрезков длиной 3 см, 4 см, 5 см, 7 см, 8 см и 9 см. Сколько равносторонних треугольников можно составить из них? Перечислите все варианты.
Четырехзначные коды
С учетом цифр 0-7. Если повторение запрещено, сколько возможны четырехзначные коды, которые больше 2000 и делятся на 4?
Блоки
Существует девять интерактивных основных строительных блоков организации. Сколько существует комбинаций из двух блоков?
Аккорды
Сколько 4-тональных аккордов (аккорд = одновременно звучащие разные тона) можно сыграть в пределах 7 тонов?

комбинаторика | математика | Британика

Комбинаторика

Просмотреть все СМИ

Ключевые люди:: Пол Эрдёш Андрей Окуньков

Связанные темы:: теория графов перестановки и комбинации ортогональный массив Латинский квадрат дизайн

Просмотреть весь связанный контент →

Сводка

Прочтите краткий обзор этой темы

комбинаторика , также называемая комбинаторной математикой , область математики, связанная с проблемами выбора, расположения и работы в конечной или дискретной системе. Включена тесно связанная область комбинаторной геометрии.

Одной из основных задач комбинаторики является определение числа возможных конфигураций ( например, графики, конструкции, массивы) заданного типа. Даже когда правила, определяющие конфигурацию, относительно просты, перечисление иногда может представлять огромные трудности. Математику, возможно, придется довольствоваться приближенным ответом или, по крайней мере, хорошей нижней и верхней оценкой.

В математике обычно говорят, что сущность «существует», если математический пример удовлетворяет абстрактным свойствам, определяющим сущность. В этом смысле может быть неочевидно, что существует хотя бы одна конфигурация с определенными заданными свойствами. Эта ситуация порождает проблемы существования и построения. Снова имеется важный класс теорем, гарантирующих существование определенного выбора при соответствующих гипотезах. Помимо их внутреннего интереса, эти теоремы могут быть использованы как теоремы существования в различных комбинаторных задачах.

Наконец, есть проблемы с оптимизацией. Например, функция f , экономическая функция, присваивает числовое значение f ( x ) любой конфигурации x с определенными заданными свойствами. В этом случае задача состоит в том, чтобы выбрать конфигурацию x ₀, которая минимизирует f ( x ) или делает его ε = минимальным, то есть для любого числа ε > 0 f ( x ₀ ) ф ( x ) + ε, для всех конфигураций x с указанными свойствами.

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

История

Ранние разработки

Некоторые типы комбинаторных задач привлекали внимание математиков с древних времен. Магические квадраты, например, квадратные массивы чисел со свойством, что строки, столбцы и диагонали в сумме дают одно и то же число, встречаются в И Цзин, китайская книга, датируемая 12 веком до н.э. Биномиальные коэффициенты, или целые коэффициенты в разложении ( a + b ) ⁿ, были известны индийскому математику XII века Бхаскаре, который в своей книге Līlavati («Изящный») посвященный красивой женщине, дал правила их расчета вместе с наглядными примерами. «Треугольник Паскаля», треугольный массив биномиальных коэффициентов, преподавал персидский философ 13-го века Насир ад-Дин ах-Туси.

На Западе можно считать, что комбинаторика началась в 17 веке с Блеза Паскаля и Пьера де Ферма, оба из Франции, которые открыли многие классические комбинаторные результаты в связи с развитием теории вероятностей. Термин «комбинаторный» впервые был использован в современном математическом смысле немецким философом и математиком Готфридом Вильгельмом Лейбницем в его Dissertatio de Arte Combinatoria («Диссертация о комбинированных искусствах»). Он предвидел применение этой новой дисциплины ко всему спектру наук. Швейцарский математик Леонард Эйлер, наконец, стал ответственным за развитие школы подлинной комбинаторной математики, начиная с 18 века. Он стал отцом теории графов, когда решил проблему Кенигсбергского моста, а его знаменитая гипотеза о латинских квадратах не была решена до 19 века.59.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

В Англии Артур Кейли в конце 19 века внес важный вклад в перечислительную теорию графов, а Джеймс Джозеф Сильвестр открыл множество комбинаторных результатов. Британский математик Джордж Буль примерно в то же время использовал комбинаторные методы в связи с развитием символической логики, а также комбинаторные идеи и методы Анри Пуанкаре, получившие развитие в начале ХХ века в связи с проблемой n тел привели к возникновению дисциплины топологии, которая занимает центральное место в математике. Многие комбинаторные задачи ставились в XIX веке как чисто развлекательные задачи и получили такие названия, как «задача восьми ферзей» и «задача Киркмана о школьницах». С другой стороны, изучение тройных систем, начатое Томасом П. Киркманом в 1847 году и продолженное Якобом Штайнером, немецким математиком швейцарского происхождения, в 1850-х годах, стало началом теории дизайна. К числу самых ранних книг, посвященных исключительно комбинаторике, относятся «9» немецкого математика Ойгена Нетто.0003 Lehrbuch der Combinatorik (1901; «Учебник комбинаторики») и Combinatory Analysis (1915–16) британского математика Перси Александра Мак-Магона, которые дают представление о комбинаторной теории в том виде, в каком она существовала до 1920 года. век

Многие факторы способствовали ускорению темпов развития комбинаторной теории с 1920 г. Одним из них было развитие статистической теории планирования экспериментов английскими статистиками Рональдом Фишером и Фрэнком Йейтсом, давшее начало многим проблемы комбинаторного интереса; методы, изначально разработанные для их решения, нашли применение в таких областях, как теория кодирования. Теория информации, возникшая примерно в середине века, также стала богатым источником комбинаторных задач совершенно нового типа.

Другим источником возрождения интереса к комбинаторике является теория графов, важность которой заключается в том, что графы могут служить абстрактными моделями для многих различных схем отношений между множествами объектов. Его приложения распространяются на исследование операций, химию, статистическую механику, теоретическую физику и социально-экономические проблемы. Теорию транспортных сетей можно рассматривать как главу теории ориентированных графов. Одна из самых сложных теоретических задач, задача четырех цветов (см. ниже), относится к области теории графов. У него также есть приложения к таким другим разделам математики, как теория групп.

Развитие вычислительной техники во второй половине 20 века является главной причиной интереса к конечной математике вообще и комбинаторной теории в частности. Комбинаторные задачи возникают не только при численном анализе, но и при проектировании компьютерных систем и при применении компьютеров к таким задачам, как хранение и поиск информации.

Статистическая механика — один из старейших и наиболее продуктивных источников комбинаторных задач. С середины 20 в. прикладными математиками и физиками проделана большая важная комбинаторная работа, например, работа над моделями Изинга (см. ниже «Проблема Изинга»).

В чистой математике комбинаторные методы успешно использовались в таких различных областях, как вероятность, алгебра (конечные группы и поля, теория матриц и решеток), теория чисел (разностные множества), теория множеств (теорема Шпернера) и математическая логика. (теорема Рамзи).

В отличие от широкого круга комбинаторных задач и множества методов, разработанных для их решения, отсутствует центральная объединяющая теория. Однако объединяющие принципы и перекрестные связи стали появляться в различных областях комбинаторной теории. Поиск лежащего в основе паттерна, который может каким-то образом указать, как переплетаются различные части комбинаторики, — задача, стоящая перед математиками в последней четверти 20-го века.

Как решить задачи оптимизации в исчислении — Matheno.com

Нужно решить задачи оптимизации в исчислении? Давайте разберем их и разработаем стратегию, которую вы сможете использовать, чтобы решать их самостоятельно.

Обзор

Задачи оптимизации всегда будут просить вас максимизировать или минимизировать какое-то количество, описав ситуацию словами (вместо того, чтобы сразу дать вам функцию максимизировать/минимизировать). Типичные фразы, указывающие на проблему с оптимизацией, включают:

Найдите самый большой ….
Найдите минимум….
Какие размеры дадут наибольшее…?

Каждая из этих фраз должна заставить вас задуматься: «Я ищу максимальное (или минимальное) значение».

Большинство учащихся не понимают, что вам нужно пройти два отдельных этапа.

Прежде чем вы сможете искать это максимальное/минимальное значение, вам сначала нужно разработать функцию, которую вы собираетесь оптимизировать. Таким образом, для полного решения этих проблем существует два отдельных этапа — то, что большинство студентов изначально не осознают [Ссылка].

Первый этап вообще не связан с исчислением, в то время как второй этап представляет собой просто задачу на макс/мин, которую вы недавно научились решать:

Этап I. Разработайте функцию. Вы должны сначала преобразовать описание ситуации в функцию — и, что особенно важно, функцию, которая зависит только от одной единственной переменной.

Этап II. Максимизируйте или минимизируйте эту функцию. Теперь максимизируйте или минимизируйте функцию, которую вы только что разработали. Вы будете использовать свои обычные инструменты исчисления, чтобы найти критические точки, определить, являются ли они максимальными или минимальными, и так далее. 93$.) Какие размеры (высота и радиус) минимизируют стоимость металла, необходимого для изготовления банки?

Этап I. Разработка функции

Шаг 1.
В задачах оптимизации всегда начинайте с наброска ситуации . Всегда. По крайней мере, этот шаг означает, что вы смотрите не на чистый лист бумаги; вместо этого вы начали создавать свое решение.

Задача требует от нас минимизировать стоимость металла, используемого для изготовления банки, поэтому мы показали каждый кусок металла отдельно: круглую верхнюю часть банки, цилиндрическую сторону и круглое дно. Мы обозначили высоту банки h и его радиус r . Мы ищем значения h и r (в пересчете на V ), которые минимизируют стоимость изготовления банки.

Шаг 2.

Чаще всего вы будете использовать свои знания геометрии.

Нарисовав картинку, следующим шагом будет написать уравнение для величины, которую мы хотим оптимизировать . Чаще всего для этого шага вы будете использовать свои повседневные знания по геометрии. В этой задаче, например, мы хотим минимизировать стоимость изготовления банки, а это значит, что мы хотим использовать 92 + 2 \pi r h
\end{align*}

Вот и все; Вы сделали шаг 2! Вы написали уравнение для величины $(A_\text{total})$, которую хотите минимизировать, относительно соответствующих величин ( r и h ).

ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ

Проблемы оптимизации и полные решения

Шаг 3.
Вот ключевой момент, который нужно знать о том, как решать проблемы оптимизации: вам почти всегда придется использовать подробную информацию, приведенную в задаче. до перепишите уравнение, которое вы разработали на шаге 2, чтобы оно использовало одну переменную.

Например, приведенное выше уравнение для $A_\text{total}$ имеет две переменные: r и h . Мы должны устранить одного из них, чтобы продолжить. Выбор того, что оставить, а что исключить, произволен; для нашего решения здесь мы решили сохранить r . (С тем же успехом мы могли бы выбрать ч и развивать наше решение по этому пути. Мы пришли бы к тому же конечному результату.) Поскольку мы решили работать с 92 + \frac{2V}{r}$$
Теперь мы пишем $A(r)$, чтобы подчеркнуть, что A является функцией только одной переменной r , и мы опустили нижний индекс « total» из $A_\text{total}$, так как он нам больше не нужен.

Это также завершает этап I нашей работы: за эти три шага мы разработали функцию, которую теперь собираемся минимизировать!

Заметьте, кстати, что до сих пор в нашем решении мы вообще не использовали Исчисление. Так будет всегда, когда вы решаете проблему оптимизации: вы не используете исчисление, пока не дойдете до стадии II.

Этап II: максимизируйте или минимизируйте свою функцию

Многие учащиеся не осознают, что задача оптимизации на самом деле является задачей макс/мин.

Многие учащиеся не понимают, что задача оптимизации на самом деле является задачей макс/мин; это просто тот случай, когда вам сначала нужно разработать функцию, которую вы собираетесь максимизировать или минимизировать, как мы это сделали на этапе I выше. После этого оставшиеся шаги точно такие же, как и для задач на макс/минимум, которые вы недавно научились решать. 92 + \dfrac{710}{r}\,.$ Найдите значение r , которое минимизирует эту площадь».

Вероятно, вы автоматически найдете производную $A'(r)$ (которую эквивалентно можно записать как $\dfrac{dA}{dr})$, затем найдете критические точки, а затем определите, представляет ли каждая из них максимум или минимум для функции и так далее. Это именно то, что мы сейчас собираемся сделать на Этапе II. Следовательно, вы уже знаете, как выполнить все следующие шаги; единственная новая часть задач максимизации — это то, что мы сделали на этапе I выше. 93 &= \frac{V}{2\pi} \\[8px] r &= \sqrt[3]{\frac{V}{2\pi}}
\end{align*} \] Таким образом, у нас есть только одна критическая точка для исследования, $r = \sqrt[3]{\dfrac{V}{2\pi}}\,.$

Шаг 5.
Затем мы должны обосновать, что Критическая точка, которую мы нашли, представляет собой минимум для площади поверхности банки (в отличие от максимума или седловой точки). Мы могли бы рассуждать физически или использовать тест первой производной, но мы думаем, что в этом случае проще всего использовать тест второй производной. Давайте быстро вычислим вторую производную, начиная с первой производной, которую мы нашли выше: 9\prime(r) > 0 \right)$. То есть график A(r) против r всегда выпуклый. Следовательно, эта единственная критическая точка дает нам минимума (в отличие от максимума или седловой точки), что нам и нужно:

Минимальная площадь поверхности возникает, когда {V}{2\pi}}\,. \quad \triangleleft$

Шаг 6.
Теперь, когда мы нашли критическую точку, соответствующую минимальной площади поверхности банки (тем самым минимизируя стоимость), давайте 9{1/3}}\,\sqrt[3]{\frac{V}{\pi}} \\[8px] &= 2 \sqrt[3]{\frac{V}{2\pi}} = 2r
\end{align*} \] поскольку напомним, что идеальный радиус равен $r = \sqrt[3]{\dfrac{V}{2\pi}}\,.$ Следовательно, идеальная высота h ровно в два раза больше идеального радиуса.

Подводя итог, мы заключаем, что оптимальные размеры для банки с закрытой крышкой, которая должна содержать объем жидкости V , составляют
\[ \begin{align*}
\text{radius } r &= \sqrt[3 ] {\ dfrac {V} {2 \ pi}} \ quad \ cmark \\ [8px] \text{высота} h &= 2\sqrt[3]{\dfrac{V}{2\pi}} \quad \cmark
\end{align*} \]

Шаг 7. Последняя проверка

Вы потеряете очки, если не ответите на заданный вопрос.

Поскольку решения по оптимизации могут быть длинными, мы рекомендуем, прежде чем закончить, вернуться и проверить, какое количество/количества запросила проблема, и убедиться, что вы предоставили это — , особенно на экзамене, где вы проиграете баллы, если вы не ответите точно на вопрос, который был задан. Например, задача 9.0003 мог бы запросить значение наименьшей возможной площади поверхности A или минимальную стоимость.

Вместо этого в данном случае задача гласила: «Какие размеры (высота и радиус) минимизируют стоимость металла для изготовления банки?» Мы обеспечили эти два измерения, и на этом мы закончили. $\checkmark$

Резюме: стратегия решения проблем

Теперь мы проиллюстрировали шаги, которые мы используем для решения каждой отдельной проблемы оптимизации, с которой мы сталкиваемся, и они всегда работают.

СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ: Оптимизация

Стратегия состоит из двух Больших Этапов. Первый вообще не связан с исчислением; второй идентичен тому, что вы сделали для задач max/min.

Этап I: Разработка функции.

Ваша первая задача — разработать функцию, представляющую количество, которое вы хотите оптимизировать. Он может зависеть только от одной переменной. Шаги:

Нарисуйте картину физической ситуации.
Также обратите внимание на любые физические ограничения, определяемые физической ситуацией.
Напишите уравнение , которое связывает количество, которое вы хотите оптимизировать, с точки зрения соответствующих переменных.
При необходимости используйте другую предоставленную информацию, чтобы переписать уравнение с одной переменной.

Этап II: максимизация или минимизация функции.

Теперь вам нужно решить стандартную задачу на макс/мин.

Возьмем производную вашего уравнения относительно вашей единственной переменной. Затем найдите критические точки.
При необходимости определите максимальные и минимальные значения.
Не забудьте проверить конечные точки , если они есть.
Обоснуйте свои максимумы или минимумы , рассуждая о физической ситуации, или с помощью теста первой производной, или теста второй производной.
Наконец, проверьте, правильно ли вы ответили на заданный вопрос : Перечитайте задачу и убедитесь, что вы предоставляете запрошенные значения: значение x или y ; или координаты; или максимальная площадь; или кратчайшее время; что бы ни спрашивали.

Хотите посмотреть, как мы решаем другие примеры задач?

Хотите посмотреть, как мы используем эту стратегию для решения других примеров задач? Перейдите на нашу страницу Оптимизация, чтобы увидеть больше примеров с бесплатными комплексными решениями.

А пока, для вас:

Какими советами вы можете поделиться о том, как решить проблемы оптимизации?
Какие у вас есть вопросы? Проблемы с оптимизацией могут быть сложными для начала, и мы будем рады помочь!
Как мы можем сделать сообщения, подобные этому, более полезными для вас?

Пожалуйста, зайдите на наш форум и напишите!

[Спасибо С. Кэмпбеллу за его конкретное исследование обучения студентов оптимизации:

«Трудности студентов колледжа с прикладными задачами оптимизации в вводном исчислении», неопубликованная магистерская диссертация, Университет штата Мэн, 2013 г.]

Обучение с подкреплением для комбинаторной оптимизации | by Or Rivlin

Стратегии обучения для решения сложных задач оптимизации с использованием глубокого обучения с подкреплением и графовых нейронных сетей.

источник

С самого начала человечества, миллионы лет назад, все инновации в технологии и каждое изобретение, которые улучшали нашу жизнь и нашу способность выживать и процветать на земле, были изобретены хитрыми умами разумных людей. От огня до колеса и от электричества до квантовой механики наше понимание мира и сложности окружающих нас вещей возросло до такой степени, что нам часто трудно понять их интуитивно.

Сегодня конструкторы самолетов, автомобилей, кораблей, спутников, сложных структур и многих других начинаний в значительной степени полагаются на способность алгоритмов улучшать их, часто тонкими способами, которые люди просто никогда не смогли бы достичь. Помимо дизайна, оптимизация играет решающую роль в повседневных вещах, таких как сетевая маршрутизация (интернет и мобильная связь), логистика, реклама, социальные сети и даже медицина. В будущем, по мере того как наша технология будет продолжать совершенствоваться и усложняться, способность решать сложные проблемы огромного масштаба, вероятно, будет пользоваться гораздо большим спросом и потребует прорывов в алгоритмах оптимизации.

источник

Вообще говоря, задачи комбинаторной оптимизации — это задачи, связанные с поиском «наилучшего» объекта из конечного набора объектов. В этом контексте «лучший» измеряется заданной функцией оценки, которая сопоставляет объекты с некоторой оценкой или стоимостью, и цель состоит в том, чтобы найти объект, который заслуживает наименьшей стоимости. Большинство практически интересных задач комбинаторной оптимизации (далее COP) также очень сложны в том смысле, что количество объектов в наборе увеличивается чрезвычайно быстро из-за даже небольшого увеличения размера задачи, что делает непрактичным исчерпывающий поиск.

Чтобы прояснить ситуацию, мы сосредоточимся на конкретной проблеме, хорошо известной задаче коммивояжера (TSP). в этой задаче у нас N городов, и наш продавец должен посетить их все. Однако путешествие между городами сопряжено с некоторыми затратами, и мы должны найти тур, который минимизирует общую накопленную стоимость при путешествии по всем городам и возвращении в начальный город. Например, на изображении ниже показан оптимальный тур по всем столицам США:

источник

Эта проблема естественным образом возникает во многих важных приложениях, таких как планирование, службы доставки, производство, секвенирование ДНК и многие другие. Поиск лучших туров иногда может иметь серьезные финансовые последствия, побуждая научное сообщество и предприятия вкладывать много усилий в поиск лучших методов решения таких проблем.

При построении тура для экземпляра TSP с K городами мы исключаем город на каждом этапе процесса построения тура, пока городов не останется. На первом этапе у нас есть K городов на выбор для начала тура, на втором этапе у нас есть варианты K-1, затем варианты K-2 и так далее. Количество возможных туров, которые мы можем построить, является произведением количества вариантов, которые у нас есть на каждом этапе, поэтому сложность этой задачи имеет вид O(K!) . Для небольших чисел это может показаться не таким уж плохим. Допустим, у нас есть задача о 5 городах, количество возможных туров равно 5!=120. Но для 7 городов он увеличивается до 5040, для 10 городов уже 3628800 а для 100 городов это целых 9.332622e+157, что на много порядков больше, чем количество атомов во Вселенной. Практические случаи TSP, которые возникают в реальном мире, часто имеют много тысяч городов и требуют очень сложных алгоритмов поиска и эвристик, которые десятилетиями разрабатывались в обширной литературе, чтобы решить их в разумные сроки (которые могут быть часами). . К сожалению, многие COP, которые возникают в реальных приложениях, имеют уникальные нюансы и ограничения, которые не позволяют нам просто использовать современные решатели для известных проблем, таких как TSP, и требуют от нас разработки методов и эвристик, специфичных для этой проблемы. Этот процесс может быть длительным и трудным и может потребовать работы экспертов в предметной области для обнаружения некоторой структуры в комбинаторном пространстве поиска конкретной проблемы.

Благодаря поразительным успехам глубокого обучения во многих областях в последние годы возможность позволить машине научиться решать нашу проблему самостоятельно звучит очень многообещающе. Автоматизация процесса разработки алгоритмов для сложных COP могла бы сэкономить много денег и времени и, возможно, могла бы дать лучшие решения, чем методы, разработанные человеком (как мы видели в таких достижениях, как AlphaGo, которые превзошли тысячи лет человеческого опыта). ).

Первая попытка решить эту проблему была предпринята в 2016 году в статье под названием « Изучение алгоритмов комбинаторной оптимизации на графах » . В этой статье авторы обучили своего рода графовую нейронную сеть (я обсуждаю графовые нейронные сети в другой статье), названную structure2vec , для жадного построения решений для нескольких жестких COP и достигли очень хороших коэффициентов аппроксимации (соотношение между произведенной стоимостью и оптимальным Стоимость).

Основная идея такова: состояние задачи можно выразить в виде графа, на котором нейронная сеть строит решение. На каждой итерации процесса построения решения наша сеть наблюдает за текущим графом и выбирает узел для добавления к решению, после чего граф обновляется в соответствии с этим выбором, и процесс повторяется до тех пор, пока не будет получено полное решение.

источник

Авторы обучили свою нейронную сеть с использованием алгоритма DQN и продемонстрировали способность обученной модели обобщать гораздо более крупные экземпляры проблем, чем она была обучена. Их модель хорошо обобщалась даже на экземпляры с 1200 узлами (при обучении на экземплярах примерно со 100 узлами) и могла давать за 12 секунд решения, которые иногда были лучше, чем то, что коммерческий решатель мог найти за 1 час. Большим недостатком их метода было то, что они использовали «вспомогательную» функцию, чтобы помочь нейронной сети найти лучшие решения. Эта вспомогательная функция была разработана человеком и специфична для конкретной проблемы, чего мы хотели бы избежать.

Такое использование представления состояния на основе графа имеет большой смысл, так как многие COP могут быть очень естественно выражены таким образом, как в этом примере графа TSP:

источник

Узлы представляют города и ребра содержат междугородние расстояния. Очень похожий граф можно построить без атрибутов ребер (если мы по какой-то причине не предполагаем знание расстояний). В последние годы наблюдается невероятный рост популярности моделей нейронных сетей, которые работают с графами (с учетом или без знания структуры), особенно в области обработки естественного языка, где Модели в стиле Transformer стали современными во многих задачах.

Существует множество отличных статей, подробно объясняющих архитектуру Transformer, поэтому я не буду слишком углубляться в нее, а дам очень краткий обзор. Архитектура преобразователя была представлена исследователями Google в известной статье под названием « Attention Is All You Need » и использовалась для решения проблем последовательности, возникающих в НЛП. Разница в том, что в отличие от рекуррентных нейронных сетей, таких как LSTM, которые явно подают последовательность входных векторов, преобразователь получает вход как набор объектов, и необходимо использовать специальные средства, чтобы помочь ему увидеть порядок в « последовательность». Трансформатор использует несколько уровней, которые состоят из подуровня самоконтроля с несколькими головками, за которым следует полностью подключенный подуровень.

источник

Связь с графами становится очевидной в слоях внимания, которые на самом деле являются своего рода механизмом передачи сообщений между входными «узлами». Каждый узел наблюдает за другими узлами и уделяет внимание тем, которые кажутся ему более «значимыми». Это очень похоже на процесс, который происходит в Graph Attention Networks , и на самом деле, если мы используем маску для блокировки узлов, передающих сообщения несмежным, мы получаем эквивалентный процесс.

В своей статье « Внимание! Научитесь решать проблемы маршрутизации », авторы решают несколько задач комбинаторной оптимизации, в которых задействованы агенты маршрутизации на графах, включая уже известную задачу коммивояжёра. Они обрабатывают входные данные как граф и передают его в модифицированную архитектуру Transformer, включающую узлы графа, а затем последовательно выбирают узлы для добавления в тур, пока не будет построен полный тур. Обработка входных данных как графа является более «правильным» подходом, чем передача ему последовательности узлов, поскольку это устраняет зависимость от порядка, в котором города заданы во входных данных, пока их координаты не меняются. Это означает, что как бы мы ни переставляли города, выходные данные данной графовой нейронной сети останутся прежними, в отличие от последовательного подхода.

В архитектуре, представленной в документе, граф встраивается кодировщиком в стиле преобразователя, который создает вложения для всех узлов и один вектор встраивания для всего графа. Для получения решения отдельной сети декодера каждый раз задается специальный вектор контекста , который состоит из вложений графа, последнего и первого городов, а также вложений непосещенных городов, и выводит распределение вероятностей на непосещенные города, из которых выбирается следующий город для посещения. Декодер последовательно производит города, пока тур не будет завершен, а затем выдается вознаграждение в зависимости от продолжительности тура.

Авторы обучают свою модель с помощью алгоритма обучения с подкреплением под названием REINFORCE, который представляет собой алгоритм, основанный на политическом градиенте. Псевдокод их версии можно увидеть здесь:

источник

Они используют сеть развертывания для детерминистической оценки сложности экземпляра и периодически обновляют сеть развертывания параметрами сети политик. Используя этот метод, авторы достигают отличных результатов по ряду задач, превосходящих другие методы, упомянутые мною в предыдущих разделах. Однако они по-прежнему тренируют и оценивают свой метод на небольших экземплярах, до 100 узлов. Хотя эти результаты являются многообещающими, такие случаи ничтожны по сравнению с реальными.

Совсем недавно был сделан важный шаг к проблеме реального мира в статье « Изучение эвристики на больших графах с помощью глубокого обучения с подкреплением ». В этой статье авторы обучили сверточную сеть графов для решения больших экземпляров задач, таких как минимальное покрытие вершин (MVC) и задача максимального покрытия (MCP). Они использовали популярный жадный алгоритм для этих задач, чтобы обучить нейронную сеть встраиванию графа и прогнозированию следующего узла для выбора на каждом этапе, а затем дополнительно обучили ее с помощью алгоритма DQN.

источник

Они оценили свой метод на графах с миллионами узлов и добились результатов, которые лучше и быстрее, чем текущие стандартные алгоритмы. Хотя они использовали созданную вручную эвристику для обучения своей модели, будущие работы могут устранить это ограничение и научиться решать огромные проблемы Tabula Rasa.

В целом, я думаю, что поиск структуры в задачах с обширными пространствами поиска является важным и практичным направлением исследований для обучения с подкреплением. Многие критики RL утверждают, что до сих пор он использовался только для решения игр и простых задач управления, и что до переноса его на задачи реального мира еще очень далеко.

Решение комбинаторных задач | Методическая разработка по алгебре (6 класс) по теме:

Комбинаторные задачи. 6-й класс

Комбинаторные задачи 6 класс доклад, проект

Методы решения комбинаторных задач — Сайт учителя математики Кобец Анны Викторовны

Методы решения комбинаторных задач

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Курсы по математике 10 класс

Курсы по математике 9 класс

Математика 11 класс

Курсы по геометрии 7 класс

Курсы по алгебре 7 класс

Алгебра 8 класс

Курсы по геометрии 8 класс

Курсы французского языка для начинающих

Конспект урока по математике «Правило умножения для комбинаторных задач» 6 класс

Не сбрасывайте их со счетов – помогаем учащимся успешно решать комбинаторные задачи |

Математика | Бесплатный полнотекстовый | Преподавание комбинаторных принципов с использованием отношений с помощью метода Placemat

1. Введение

2. Математическая основа

3. Методика исследования и обсуждения

4. Выводы

Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок

Расчет:

Количество комбинаций: 210

Вариантов

Перестановки

Вариации с повторением

Перестановки с повторением

Комбинации

Комбинации с повтором

Основы комбинаторики в текстовых задачах

комбинаторика | математика | Британика

Прочтите краткий обзор этой темы

История

Ранние разработки

Как решить задачи оптимизации в исчислении — Matheno.com

Обзор

Этап I. Разработка функции

Этап II: максимизируйте или минимизируйте свою функцию

Резюме: стратегия решения проблем

Этап I: Разработка функции.

Этап II: максимизация или минимизация функции.

Обучение с подкреплением для комбинаторной оптимизации | by Or Rivlin

Стратегии обучения для решения сложных задач оптимизации с использованием глубокого обучения с подкреплением и графовых нейронных сетей.

Добавить комментарий Отменить ответ