Как решить систему с тремя неизвестными
Линейная система с тремя неизвестными имеет несколько методов решения. Обнаружить решение системы дозволено с поддержкой правила Кремера через определители, способом Гаусса либо применяя легкой метод подстановки. Способ подстановки является основным для решения систем линейных уравнений небольшого порядка. Он заключается в поочередном выражении из всякого уравнения системы одной незнакомой переменной, подстановки ее в следующее уравнение и облегчение получаемых выражений.
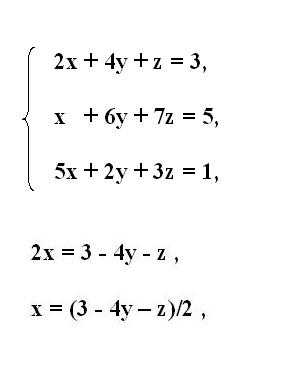
Инструкция
1. Запишите начальную систему уравнений третьего порядка. Из первого уравнения системы выразите первую неведомую переменную х. Для этого перенесите члены, содержащие другие переменные за знак равенства. Перенесенным членам поменяйте знак на противоположный.
2. Если при множителе с выражаемой переменной присутствует показатель чудесный от единицы, поделите на его значение все уравнение. Таким образом, вы получите переменную х, выраженную через остальные члены уравнения.
3. Подставьте во второе уравнение взамен х то выражение, которое вы получили из первого уравнения. Упростите полученную запись, произведя сложение либо вычитание сходственных членов. Подобно предыдущему шагу выразите из второго уравнения следующую неведомую переменную у. Также перенесите все другие члены за знак равенства и поделите все уравнение на показатель при у.
4. В последнее третье уравнение подставьте взамен 2-х незнакомых переменных х и у выраженные значения из первого и второго уравнений системы. Причем в выражении х также замените переменную у. Упростите полученное уравнение. В нем в качестве неведомой величины останется лишь третья переменная z. Выразите ее из уравнения, как описано выше, и высчитайте ее значение.

5. В выражение у из второго уравнения подставьте знаменитое значение переменной z. Подсчитайте значение переменной у. Дальше в выражение переменной х подставьте значения переменных у и z. Вычислите х. Запишите полученные значения х, у и z – это и есть решение системы с тремя неизвестными .
Система из 3 уравнений с тремя незнакомыми может и не иметь решений, невзирая на довольное число уравнений. Дозволено пытаться решить ее с подмогой способа подстановки либо с поддержкой способа Крамера. Способ Крамера помимо решения системы дозволяет оценить, является ли система разрешимой, до того, как разыскать значения незнакомых.

Инструкция
1. Способ подстановки заключается в последовательном выражении одной неведомой через две других и подстановке полученного итога в уравнения системы. Пускай дана система из 3 уравнений в всеобщем виде:a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3Выразите из первого уравнения x: x = (d1 – b1y – c1z)/a1 – и подставьте во второе и третье уравнения, после этого из второго уравнения выразите y и подставьте в третье. Вы получите линейное выражение для z через показатели уравнений системы. Сейчас идите “обратно”: подставьте z во второе уравнение и обнаружьте y, а после этого z и y подставьте в первое и обнаружьте x. Процесс в всеобщем виде отображен на рисунке до нахождения z. Дальше запись в всеобщем виде будет слишком массивной, на практике, подставив числа, вы достаточно легко обнаружите все три неведомые.
2. Способ Крамера заключается в составлении матрицы системы и вычислении определителя этой матрицы, а также еще 3 вспомогательных матриц. Матрица системы составляется из показателей при неведомых членах уравнений. Столбец, содержащий числа, стоящие в правых частях уравнений, именуется столбцом правых частей. В матрице системы он не применяется, но применяется при решении системы.
3. Пускай, как и прежде, дана система из 3 уравнений в всеобщем виде:a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3Тогда матрицей этой системы уравнений будет дальнейшая матрица:| a1 b1 c1 || a2 b2 c2 || a3 b3 c3 |Прежде каждого обнаружьте определитель матрицы системы. Формула нахождения определителя: |A| = a1b2c3 + a3b1c2 + a2b3c1 – a3b2c1 – a2b1c3 – a1b3с2. Если он не равен нулю, то система разрешима и имеет исключительное решение. Сейчас надобно обнаружить определители еще 3 матриц, которые получаются из матрицы системы путем подставления столбца правых частей взамен первого столбца (эту матрицу обозначим Ax), взамен второго (Ay) и третьего (Az). Вычислите их определители. Тогда x = |Ax|/|A|, y = |Ay|/|A|, z = |Az|/|A|.
Само по себе уравнение с тремя неизвестными имеет уйма решений, следственно почаще каждого оно дополняется еще двумя уравнениями либо условиями. В зависимости от того, каковы начальные данные, во многом будет зависеть ход решения.

Вам понадобится
- – система из 3 уравнений с тремя незнакомыми.
Инструкция
1. Если два из 3 уравнений системы имеют лишь две неведомые из 3, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными . Ваша цель при этом – превратить его в обыкновенное уравнение с одной незнакомой. Если это удалось, последующее решение достаточно примитивно – подставьте обнаруженное значение в другие уравнения и обнаружьте все остальные неведомые.
2. Некоторые системы уравнений дозволено решить вычитанием из одного уравнения иного. Посмотрите, нет ли вероятности умножить одно из выражений на число либо переменную так, дабы при вычитании сократились сразу две незнакомые. Если такая вероятность есть, воспользуйтесь ею, скорее каждого, дальнейшее решение не составит труда. Не забывайте, что при умножении на число нужно умножать как левую часть, так и правую. Верно также, при вычитании уравнений нужно помнить о том, что правая часть должна также вычитаться.
3. Если предыдущие методы не помогли, воспользуйтесь всеобщим методом решений всяких уравнений с тремя неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Сейчас составьте матрицу показателей при х (А), матрицу незнакомых (Х) и матрицу свободных членов (В). Обратите внимание, умножая матрицу показателей на матрицу неведомых, вы получите матрицу, равную матрице свободных членов, то есть А*Х=В.
4. Обнаружьте матрицу А в степени (-1) заблаговременно разыскав определитель матрицы, обратите внимание, он не должен быть равен нулю. Позже этого умножьте полученную матрицу на матрицу В, в итоге вы получите желанную матрицу Х, с указанием всех значений.
5. Обнаружить решение системы из 3 уравнений дозволено также с поддержкой способа Крамера. Для этого обнаружьте определитель третьего порядка ?, соответствующий матрице системы. После этого ступенчато обнаружьте еще три определителя ?1, ?2 и ?3, подставляя взамен значений соответствующих столбцов значения свободных членов. Сейчас обнаружьте х: х1=?1/?, х2=?2/?, х3=?3/?.
jprosto.ru
Как решить уравнение с тремя неизвестными
Автор КакПросто!
Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.

Статьи по теме:
Вам понадобится
- — система из трех уравнений с тремя неизвестными.
Инструкция
Если два из трех уравнений системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными. Ваша цель при этом – превратить его в обычное уравнение с одной неизвестной. Если это удалось, дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные. Некоторые системы уравнений можно решить вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из выражений на число или переменную так, чтобы при вычитании сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными. Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных членов (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, равную матрице свободных членов, то есть А*Х=В.
Найдите матрицу А в степени (-1) предварительно отыскав определитель матрицы, обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.
Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.
Источники:
- решений уравнений с тремя неизвестными
Совет полезен?
Распечатать
Как решить уравнение с тремя неизвестными
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Система трех уравнений с тремя неизвестными
Присоединим к уравнениям
15x + 10y + 8z = 164, (1)
x + y + z = 16 (2)
третье уравнение:
z = 2y. (3)
Получили систему трех уравнений с тремя неизвестными.
Прежде всего заметим, что все свойства, о которых говорилось в § 48, остаются справедливыми и для системы уравнений с тремя (и более) неизвестными. Поэтому для решения данной системы применимы те же способы, что и для решения системы двух уравнений с двумя неизвестными.
1. Способ алгебраического сложения.
Так как уравнение (3) уже не содержит x, то исключим x из системы уравнений (1) и (2). Для этого умножим обе части уравнения (2) на 15. Получим систему:
Коэффициенты при x равны. Вычтем из первого уравнения второе, тогда получим:
5y + 7z = 76.
Получили уравнение с двумя неизвестными y и z. Вместе с уравнением (3) оно образует систему двух уравнений с двумя неизвестными:
Решив ее одним из способов, изложенных в § 80, найдем:
y = 4; z = 8.
Подставив эти значения в (1) или (2) уравнение, найдем: x = 4.
Итак, если данная система трех уравнений с тремя неизвестными имеет решение, то это решение будет следующей тройкой чисел:
x = 4; y = 4; z = 8.
Подставляя эти значения в данную систему, можно убедиться, что полученная тройка чисел является решением системы.
2. Способ подстановки.
Для данной системы этот способ более удобен, так как в уравнении (3) неизвестное z уже выражено через y. Сделав подстановку в уравнении (1) и (2), получим:
или
(4) (5)
Решим эту систему любым способом, изложенным в § 80, например способом алгебраического сложения.
Умножим уравнение (5) на 15 и вычтем из него уравнение (4):
19y = 76.
Отсюда найдем: y = 4.
Подставив найденное значение y в уравнение (5), найдем: x = 4. Наконец, подставив значение y в (3), найдем: z = 8. Получили то же решение, что и первым способом.
Решим еще систему способом алгебраического сложения:
Исключим одно из неизвестных, например z. Для этого сложим первое и второе уравнение, получим:
3x + y = 13.
Умножим теперь второе уравнение на 2 и сложим с третьим, получим:
5x + 6y = 26.
Оба полученных уравнения образуют систему уравнений с двумя неизвестными:
Решим ее одним из известных способов, найдем: x = 4, y = 1. Подставив эти значения в одно из данных уравнений, например в первое, найдем: z = 2. Итак, если данная система имеет решение, то оно может быть только такое: x = 4; y = 1; z = 2. Подставив эти значения во второе и третье уравнения, убедимся, что они действительно дают решение данной системы.
mthm.ru
Глава А5. Система трех уравнений с тремя неизвестными
Глава П5. Решение и исследование системы трех уравнений первой степени с тремя неизвестными
Рассмотрим систему уравнений
, , (1)
с неизвестными x, y, z (коэффициенты , , …, и свободные члены , , предположим данными). Введем обозначения
, , , .
Определитель , составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
Полезно заметить, что определители , , получаются из определителя при помощи замены соответственно его первого, второго и, наконец, третьего столбца столбцом свободных членов данной системы. Если , то система (1) имеет единственное решение; оно определяется формулами
, , .
Предположим теперь, что определитель системы равен нулю: . Если в случае хотя бы один из определителей , , отличен от нуля, то система (1) совсем не имеет решений.
В случае, когда и одновременно , , , система (1) также может совсем не иметь решений; но если система (1) при этих условиях имеет хотя бы одно решение, то она имеет бесконечно много различных решений. Однородной системой трех уравнений первой степени с тремя неизвестными называется система вида
, , (2)
то есть система уравнений, свободные члены которых равны нулю. Очевидно, что такая система всегда имеет решение: x=0, y=0, z=0; оно называется нулевым. Если , то это решение является единственным. Если же , то однородная система (2) имеет бесконечно много ненулевых решений.
a-geometry.narod.ru
Система 3 уравнений с 3 неизвестными как решить?
Дальше не бред, а можно решить методом сложения (умножить 1 уравнение на -19, а второе на 5 и сложить, останется одна переменная зет, ее найдешь, затем найдешь у, затем х. Учись сразу решать методом исключения переменных (метод Гаусса) . Сначала исключаем переменную х. Первое уравнение переписываешь ( за первое лучше взять второе х+3у-зет=1). Затем умножаешь его на -2 и складываешь со вторым (чтобы переменная х ушла) , записываешь. Вместо третьего уравнения тоже записываешь сумму (первое умножаешь на -7 и складываешь с третьим) . Затем первое и второе уравнения переписываешь, а вместо третьего записываешь сумму (второе умножаешь на -19, третье на 5 и складываешь, чтобы переменная у ушла) . В третьем уравнении остается одна переменная зет, ее находишь. Затем ее значение подставляешь во второе уравнение и находишь у. Затем значения зет и у подставляешь в первое уравнение и находишь х. Таким методом можно решать системы не только трех уравнений, но и больше.
Не просто сложения, а алгебраического сложения!
Математика… японская… 😀
touch.otvet.mail.ru
