Как решать уравнения квадратные 7 класс: Алгебра 7-9 классы. 19. Квадратные уравнения. Разложение квадратного трехчлена на множители

Алгебра 7-9 классы. 19. Квадратные уравнения. Разложение квадратного трехчлена на множители

Подробности

Категория: Алгебра 7-9 классы

 

ОСНОВНЫЕ ПОНЯТИЯ

 

Определение 1. Квадратным уравнением называют уравнение вида

где коэффициенты а, b, с — любые действительные числа, причем а ≠ 0.

Коэффициенты а, b, с различают по названиям: а — первый, или старший, коэффициент; b — второй коэффициент, или коэффициент при х; с — свободный член.

 

Определение 2. Квадратное уравнение называют приведенным, если его старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1

.

Так, уравнение

— неприведенное квадратное уравнение (старший коэффициент равен 2), а уравнение

— приведенное квадратное уравнение.

Кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.

Определение 3. Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля. Неполное квадратное уравнение — это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b, с равен нулю.

Обратите внимание: об ах² речи нет, этот член всегда присутствует в квадратном уравнении.

Опрелеление 4. Корнем квадратного уравнения

называют всякое значение переменной х, при котором квадратный трехчлен

обращается в нуль; такое значение переменной х называют также корнем квадратного трехчлена.

Можно сказать и так: корень квадратного уравнения

— это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство 0 = 0.

Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.

Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Рассмотрим несколько таких уравнений.

Пример 1. Решить неполные квадратные уравнения:

Решение.

а) Имеем

Поэтому либо х = 0, либо 2х — 7 = 0, откуда находим х = 3,5. Итак, уравнение имеет два корня: х₁ = 0, х₂ = 3,5.

б) Имеем

Уравнение имеет два корня: х₁ = 0, х₂ = 5.

в) Имеем

Ранее,  мы уже говорили о том, что уравнение вида х² = а, где а > О, имеет два корня:  и . Значит, для уравнения х² = 16 получаем х₁ = 4, x₂ = — 4 (мы учли, что ).

Допускается более экономная запись:

 

г) Имеем

Уравнение имеет два корня: И в этом случае можно записать короче

д) Имеем

Так как выражение Зx²неотрицательно при любых значениях х, то уравнение Зx² = — 10 не имеет корней. Иными словами, нет ни одного числа, подстановка которого вместо переменной х обратила бы это уравнение в верное числовое равенство.

Иногда в таких случаях уточняют: нет действительных корней. Дело в том, что в математике, кроме действительных чисел, рассматриваются так называемые мнимые числа; мнимые корни у этого уравнения есть.

е) Если 5x² = 0, то x² = 0, откуда x = 0 единственный корень уравнения.
Этот пример показывает, как решаются неполные квадратные уравнения:

1. Если уравнение имеет вид

ах² = 0, то оно имеет один корень х = 0.

2. Если уравнение имеет вид , то используется метод разложения на множители: ; значит, либо x = 0, либо ах + b = 0. В итоге получаем два корня:

3. Если уравнение имеет вид , то его преобразуют к виду и далее . В случае, когда — отрицательное число, уравнение не имеет корней (значит, не имеет корней и исходное уравнение ). В случае, когда

— положительное число, т. е., где m > 0, уравнение х² = m имеет два корня: (в этом случае, как мы условились выше, допускается более короткая запись:
).

Неполное квадратное уравнение, как мы только что видели, может иметь два корня, один корень, ни одного корня. То же можно сказать и о полном квадратном уравнении. Почему?

Мы с вами знаем, что графиком функции является парабола. Корнями квадратного уравнения служат абсциссы точек пересечения параболы с осью

х. Парабола может пересекать ось х в двух точках, может касаться оси х, т. е. иметь с ней лишь одну общую точку, может вообще не пересекаться с осью х (рис. 92, а, б, в). Это значит, что квадратное уравнение может иметь либо два корня, либо один корень, либо вообще не иметь корней.

Конечно, неплохо знать, сколько корней имеет квадратное уравнение, но еще лучше уметь находить эти корни. Если уравнение неполное, то, как мы видели выше, особых проблем не возникает. А если мы имеем полное квадратное уравнение? Ниже на примере одного такого уравнения напомним, какими способами мы пользовались до сих пор, когда приходилось встречаться с квадратным уравнением.

Пример 2. Решить уравнение х² — 4х + 3 = 0.

Решение.

I способ. Рассмотрим квадратный трехчлен х2 — 4х + 3 и разложим его на множители, используя способ группировки; предварительно представим слагаемое — 4х в виде — х — Зх. Имеем

Значит, заданное уравнение можно переписать в виде (х — 1) (х — 3) = 0, откуда ясно, что уравнение имеет два корня; х₁ = 1, х₂ = 3; при х = 1 обращается в нуль множитель х — 1, а при х = 3 обращается в нуль множитель х — 3.

II способ. Рассмотрим квадратный трехчлен х² — 4х + 3 и разложим его на множители, используя метод выделения полного квадрата; предварительно представим слагаемое

3 в виде 4-1. Имеем

Воспользовавшись формулой разности квадратов, получим

Рассуждая, как и в I способе, находим, что .

III способ. Построим график функции :

1) Имеем   Значит, вершиной параболы является точка (2; -1), а осью параболы — прямая х = 2.

2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 1 и х = 3. Имеем ; построим на координатной плоскости точки (1; 0) и (3; 0).

3) Через точки (1; 0), (2; -1), (3;0) проводим параболу (рис. 93).

 

Корнями уравнения х² — 4х +  3 = 0 служат абсциссы точек пересечения параболы с осью х. Таких точек две: (1; 0) и (3; 0). Итак, х₁ = 1, х₂ = 3.

IV способ. Преобразуем уравнение к виду х² — 4х — 3. Построим в одной системе координат графики функций у = х² и у = 4х — 3 (рис. 94). Они пересекаются в точках А( 1; 1) и B(3; 9). Корнями уравнения служат абсциссы точек А и B, поэтому х₁ = 1, х₂ = 3.

V  способ. Преобразуем уравнение к виду x² + 3 = 4х. Построим в одной системе координат графики функций у = х² + 3 и у = 4х

(рис. 95). Они пересекаются в точках А (1; 4) и B (3; 12). Корнями уравнения служат абсциссы точек А и B, таким образом,

VI    способ. Преобразуем уравнение к виду и далее , т. е. . Построим в одной системе координат параболу у = (х — 2)² и прямую у = 1 (рис. 96). Они пересекаются в точках А (1; 1) и B(3; 1). Корнями уравнения служат абсциссы точек А и B, следовательно, .

VII  способ. Разделив почленно обе части уравнения на х, получим

и далее

Построим в одной системе координат гиперболу прямую у = х — 4. Они пересекаются в точках

А (1; -3) и (3; — 1) (рис. 97). Корнями уравнения служат абсциссы точек А и B, значит,

Итак, мы решили уравнение х² — 4х + 3 = 0 семью способами. Тем не менее знание этих способов не есть, как говорится, панацея от всех бед. Ведь наши успехи в решении квадратных уравнений зависели до сих пор от наличия одного из двух благоприятных обстоятельств:

1) квадратный трехчлен удавалось разложить на множители;

2) графики, которые мы использовали для графического решения уравнения, пересекались в «хороших» точках.

Надеяться на такие подарки судьбы математики, естественно, не могли. Они искали универсальный способ, пригодный для решения любых квадратных уравнений, и нашли его.

Сколько существует способов решения квадратного уравнения?

Сколько существует способов решения квадратного уравнения? Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи до окончания вуза.         В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Прежде чем рассмотреть способы решения квадратных уравнений, вспомним определение: Квадратным уравнением называется уравнение вида аx² + bx + c = 0, где х- переменная, а,b и с-некоторые числа, причем, а ≠ 0. Если в квадратном уравнении аx² + bx + c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением. Способы решения неполных квадратных уравнений: Если c = 0, то уравнение примет вид ax² + bx = 0. x(ax + b) = 0 , x = 0 или ax + b = 0, x = -b : a. Если b = 0, то уравнение примет вид ax² + c = 0, x² = -c / a, x₁ͅͅͅ͵₂ = ± Если b = 0 и c = 0 , то уравнение примет вид ax² = 0, x = 0 Остановимся на рассмотрении способов решения полных квадратных уравнений. Первый способ известен из курса алгебры 7 класса — решение квадратного уравнения по формуле: ах²+ bх + с = 0, а ≠ 0, Х 1,2 = ,где х₁ и х₂-корни уравнения. 2 способ. Разложение левой части на множители. х2 — 2х — 8 = 0. Разложим левую часть на множители: х2 — 2х — 8 = х2 — 4х +2х -8 = х(х -4 ) + 2(х -4) = (х + 2)(х -4). (х + 2)(х -4)=0. Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = -2, а также при х = 4. Это означает, что число — 2 и 4 являются корнями уравнения х2 — 2х — 8 = 0. 3 способ. Решение квадратных уравнений по теореме Виета. Вспомним формулировку теоремы Виета: Сумма корней приведенного квадратного уравнения х2+ рх + q = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т. е. Теорема, обратная теореме Виета. Если р, q, x1, x2 таковы, что х1 + х₂ = — р, х1 · х2 = q, то х1 и х2 – корни уравнения х2+ рх + q = 0. 4 способ. Метод выделения полного квадрата. Поясним этот метод на примере. Решим уравнение х2 + 6х – 40 = 0 Выделим в левой части полный квадрат. Для этого запишем выражение х2 + 6х в следующем виде: х2 + 6х = х2 + 2· х ·3. В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3. поэтому чтобы получить полный квадрат, нужно прибавить 9, так как х2 + 2· х ·3 + 9 = (х + 3)2 . Преобразуем теперь левую часть уравнения х2 + 6х – 40 = 0, прибавляя к ней и вычитая 9. Имеем: х2 + 6х – 40 = х2 + 2х ·3 + 9 – 9 – 40 = (х + 3)2 – 49. Таким образом, данное уравнение можно записать так: (х + 3)2 –49 = 0, т.е. (х + 3)2 = 49. Следовательно, х + 3 = 7, х1= 4, или х +3 = -7 , х2 = -10. 5 Способ. Способ переброски коэффициентов. Рассмотрим квадратное уравнение ах2 + bх + с = 0, а ≠ 0. Умножая обе его части на а, получаем уравнение а2 х2 + а bх + ас = 0. Пусть ах = у, откуда х =y/a; тогда приходим к уравнению у2 + by + ас = 0, равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = и х2 = . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Например, решим уравнение 2х2-9x+9 = 0. Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у2 – 9y +18 = 0. Согласно теореме Виета = > => Ответ: 1,5; 3. 6 способ: графический. Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = — px — q. Построим графики зависимости у = х2 и у = — px — q. График первой зависимости — парабола, проходящая через начало координат. График второй зависимости – прямая. Возможны следующие случаи: — прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения; — прямая и парабола могут касаться (одна общая точка), т.е. уравнение имеет одно решение; — прямая и парабола не имеют общих точек, т. е. квадратное уравнение не имеет корней. 7 способ: геометрический. Опять же обратимся к примеру: решить уравнение у2+ 6у – 16 = 0. y 3 Преобразуем уравнение: у2 + 6у = 16 y у² 3у 3 3у 9 Уравнение у2 + 6у – 16 +9 – 9 = 0 равносильно исходному. у²+ 6у + 9 = 16 + 9,у²+6у+9=25.На геометрическом языке площадь квадрата со стороной , равной 5, равна сумме площадей его частей, т.е. у²+3у+3у+9.Откуда после примения формулы сокращенного умножения и получаем, что( у + 3)² = 25, у+3=±5 у1 = 2, у2 = – 8. Значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений , например, при решении задач нередко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений. Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников.

NCERT Solutions для класса 7 Математика Глава 4

Страница № 73:

Вопрос 1:

Проверьте, являются ли следующие квадратичные уравнения:

Ответ:

. форма .

Следовательно, данное уравнение является квадратным уравнением.

Форма.

Следовательно, данное уравнение является квадратным уравнением.

Это не форма.

Следовательно, данное уравнение не является квадратным уравнением.

Форма.

Следовательно, данное уравнение является квадратным уравнением.

Форма .

Следовательно, данное уравнение является квадратным уравнением.

Это не форма.

Следовательно, данное уравнение не является квадратным уравнением.

Не по форме.

Следовательно, данное уравнение не является квадратным уравнением.

Это форма .

Следовательно, данное уравнение является квадратным уравнением.

Видео Решение квадратных уравнений (Страница: 73 , Q.No.: 1)

NCERT Решение математических квадратных уравнений 7 класса 73 , Вопрос 1

Страница № 73:

Вопрос 2:

следующие ситуации в виде квадратных уравнений.

(i) Площадь прямоугольного участка составляет 528 м ² . Длина участка (в метрах) более чем в два раза превышает его ширину. Нам нужно найти длину и ширину участка.

(ii) Произведение двух последовательных положительных целых чисел равно 306. Нам нужно найти целые числа.

(iii) Мать Рохана старше его на 26 лет. Произведение их возраста (в годах) через 3 года будет равно 360. Мы хотели бы найти нынешний возраст Рохана.

(iv) Поезд проходит расстояние 480 км с постоянной скоростью. Если бы скорость была на 8 км/ч меньше, то на преодоление того же расстояния ушло бы на 3 часа больше.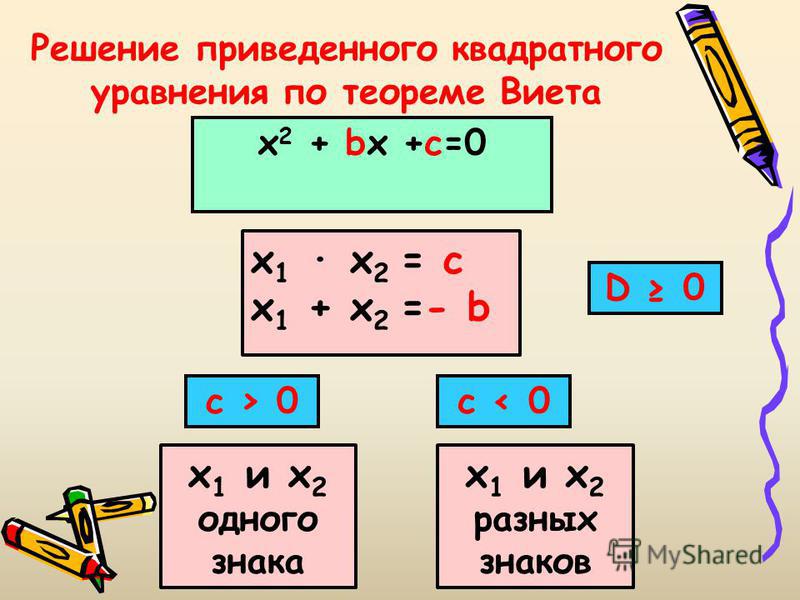 Нам нужно найти скорость поезда.

Ответ:

(i) Пусть ширина участка будет х м.

Отсюда длина участка равна (2 х + 1) м.

Площадь прямоугольника = длина × ширина

∴ 528 = x (2 x + 1)

(ii) Пусть последовательные целые числа будут x и x + 1.

66. Известно, что их произведение равно 306.

∴

(iii) Пусть возраст Рохана равен x .

Следовательно, возраст его матери = 9 лет0084 x + 26

Через 3 года

Возраст Рохана = x + 3

Возраст матери = x + 26 + 3 = x + 29

через 3 года 360.

(iv) Пусть скорость поезда x км/ч.

Время, необходимое для проезда 480 км =

Во втором условии, пусть скорость поезда = км/ч

Также известно, что поезд проедет то же расстояние за 3 часа.

Следовательно, время, затраченное на прохождение 480 км = часы

Скорость × Время = Расстояние

⇒ 480+3x-3840x-24=480
⇒3x-3840x=24
⇒x3x2-04 ⇒x2-8x-1280=0

Видео Решение квадратных уравнений (Страница: 73 , Q.

No.: 2)

NCERT Решение математических квадратных уравнений 7 класса 73 , Вопрос 2

Страница № 76:

Вопрос 1:

Найдите корни следующих квадратных уравнений методом факторизации:

Ответ:

Корни этого уравнения являются значениями, для которых = 0

∴ = 0 Ор. это уравнение – значения, для которых = 0

∴ = 0 или = 0

, т.е. x = −2 или x =

. = 0 или = 0

т. е. x = или x =

Корни этого уравнения являются значениями, для которых = 0

Следовательно,

, т. Е.

Корни этого уравнения являются значениями, для которых = 0

,

, т.е.

Видео Решение квадратных уравнений (Страница: 76 , Q.No.: 1)

NCERT Решение математических квадратных уравнений 7 класса 76 , Вопрос 1

Страница № 76:

Вопрос 2:

) У Джона и Дживанти вместе 45 шариков. Оба они потеряли по 5 шариков каждый, и произведение количества шариков, которое у них теперь есть, равно 124. Выясните, сколько шариков у них было в начале.

(ii) Кустарное производство производит определенное количество игрушек в день. Себестоимость производства каждой игрушки (в рупиях) составила 55 минус количество игрушек, произведенных за день. В определенный день общая стоимость производства составила 750 рупий. Найдите количество игрушек, произведенных в этот день.

Ответ:

(i) Пусть количество шариков Джона равно x .

Следовательно, количество шариков Дживанти = 45 − x

После потери 5 шариков

Количество шариков Джона = x — 5

Количество шариков Дживанти = 45 — x — 5 = 40 — x

Произведение их шариков равно 7

6

124.

Либо = 0, либо x — 9 = 0

, т. е. x = 36 или x = 9

. 9

Если количество шариков Джона = 9,

Тогда количество шариков Дживанти = 45 − 9 = 36

(ii) Пусть количество произведенных игрушек равно x .

∴ Себестоимость производства каждой игрушки = Rs (55 − x )

При условии, что общее производство игрушек = Rs 750

Либо = 0, либо x — 30 = 0 9000 т. е. x = 25 или x = 30

Следовательно, количество игрушек будет либо 25, либо 30.

Видео Решение квадратных уравнений (Страница: 76 , Q.No.: 2)

NCERT Решение математических квадратных уравнений для 7 класса 76 , Вопрос 2

Номер страницы 76:

Вопрос 3:

Найдите два числа, сумма которых равна 27, а произведение равно 182.

Ответ:

Пусть первое число быть x , а второе число 27 — x .

Следовательно, их произведение = x (27 − x )

Известно, что произведение этих чисел равно 182.

Либо = 0, либо x — 14 = 0

т.е. x = 13 или x = 14

Если первое число = 13, то

Другое число = 27 — 13 = 14

4 Если первое число, то 90 — квадратные уравнения 76 , Вопрос 3

Страница № 76:

Вопрос 4:

Найдите два последовательных натуральных числа, сумма квадратов которых равна 365.

Ответ:

Пусть последовательные положительные целые числа равны x и x + 1. x — 13 = 0, то есть, x _{= — 14 или x = 13}

, поскольку целые числа положительны, x может быть только 13.

∴ x + 10085 + 1. + 10085 + 1. . = 13 + 1 = 14

Следовательно, два последовательных натуральных числа будут равны 13 и 14.

Видео Решение квадратных уравнений (Страница: 76 , Q.No.: 4)

NCERT Решение математических квадратных уравнений 7 класса 76 , Вопрос 4

Страница № 76:

Вопрос 5:

Высота прямоугольного треугольника на 7 см меньше его основания. Найдите две другие стороны, если гипотенуза равна 13 см.

Ответ:

Пусть основание прямоугольного треугольника равно х см.

Его высота = ( x − 7) см

Либо x — 12 = 0, либо x + 5 = 0, т. е. x _{= 12 или x = -5}

Следовательно, основание данного треугольника равно 12 см, а высота этого треугольника будет (12 − ​​7) см = 5 см.

Видео Решение квадратных уравнений (Страница: 76 , Q.No.: 5)

NCERT Решение математических квадратных уравнений 7 класса 76 , Вопрос 5

Страница № 76:

Вопрос 6:

Кустарное производство производит определенное количество гончарных изделий в день. Было замечено, что в определенный день стоимость производства каждого изделия (в рупиях) в 3 раза превышала количество изделий, произведенных в этот день. Если общие издержки производства в этот день были 90 рупий, найти количество произведенных изделий и стоимость каждого изделия.

Ответ:

Пусть произведено х изделий.

Следовательно, себестоимость каждого изделия = рупий (2 х + 3)

Дано, что общий объем производства составляет 90 рупий. x _{= 6}

Поскольку количество произведенных изделий может быть только положительным целым числом, поэтому x может быть только 6.

Следовательно, количество произведенных изделий = 6

Стоимость каждого изделия = 2 × 6 + 3 = 15 рупий

Видео Решение квадратных уравнений (Страница: 76 , Q.

No.: 6)

NCERT Решение для 7 класса математические квадратные уравнения 76 , Вопрос 6

Страница № 87:

Вопрос 1:

Найдите корни следующих квадратных уравнений, если они существуют, методом заполнения квадрата:

Ответ:

Видео Решение квадратных уравнений0007

Страница № 87:

Вопрос 2:

Найдите корни квадратных уравнений, данных в вопросе 1 выше, применяя квадратную формулу.

Ответ:

Видео для квадратичных уравнений (Страница: 87, Q.No.: 2)

Решение NCERT для класса 7 Математика — квадратичные уравнения 87, Вопрос 2

Страница. № 88:

Вопрос 3:

Найдите корни следующих уравнений:

Ответ:

Видео Решение квадратных уравнений (Страница: 88 , Q.No.: 3)

NCERT Решение математических квадратных уравнений 7 класса Страница 80 8 0 7 900 3 900 :

Вопрос 4:

Сумма обратных величин возраста Рехмана (в годах) 3 года назад и 5 лет спустя равна. Найдите его настоящий возраст.

Ответ:

Пусть нынешний возраст Рехмана будет х лет.

Три года назад его возраст составлял ( x − 3) лет.

Через пять лет его возраст составит ( x + 5) лет.

Дано, что сумма обратных величин возраста Рехмана 3 года назад и 5 лет спустя равна.

Однако возраст не может быть отрицательным.

Таким образом, настоящий возраст Рехмана составляет 7 лет.

Видео Решение квадратных уравнений (Страница: 88 , Q.No.: 4)

NCERT Решение математических квадратных уравнений 7 класса 88 , Вопрос 4

Страница № 88:

Вопрос 5:

В контрольной работе сумма оценок Шефали по математике и английскому языку равна 30. Если бы она получила на 2 балла больше по математике и на 3 балла меньше по английскому языку, произведение их оценок было бы 210. Найдите ее отметки по двум предметам.

Ответ:

Пусть оценки по математике будут х .

Тогда оценки на английском языке будут 30 − x .

По заданному вопросу

Если по математике 12 баллов, то по английскому языку будет 30 − 12 = 18

Если по математике 13 баллов, то по английскому языку будет 30 − 13 = 17 баллов

Видео Решение квадратных уравнений (Страница: 88 , Q.No.: 5)

NCERT Решение математических квадратных уравнений для 7 класса 88 , Вопрос 5

Номер страницы 88:

Вопрос 6:

Диагональ прямоугольного поля составляет 60 метров больше чем более короткая сторона. Найдите стороны поля, если длинная сторона на 30 м больше короткой.

Ответ:

Пусть меньшая сторона прямоугольника равна х м.

Тогда большая сторона прямоугольника = ( x + 30) m

Однако сторона не может быть отрицательной. Следовательно, длина меньшей стороны будет

90 м.

Следовательно, длина большей стороны будет (90 + 30) м = 120 м

Видео Решение квадратных уравнений (Страница: 88 , Q.

No.: 6)

NCERT Решение для 7 класса по математике — квадратное уравнения 88 , Вопрос 6

Страница № 88:

Вопрос 7:

Разница квадратов двух чисел равна 180. Квадрат меньшего числа в 8 раз больше большего числа. Найдите два числа.

Ответ:

Пусть большее и меньшее число будут x и y соответственно.

Согласно заданному вопросу,

Однако большее число не может быть отрицательным, так как 8-кратное большее число будет отрицательным и, следовательно, квадрат меньшего числа будет отрицательным, что невозможно.

Следовательно, большее число будет только 18.

Следовательно, это числа 18 и 12 или 18 и −12.

Видео Решение квадратных уравнений (Страница: 88 , Q.No.: 7)

NCERT Решение математических квадратных уравнений 7 класса 88 , Вопрос 7

Страница № 88:

Вопрос 8:

Поезд проехал 360 км с постоянной скоростью. Если бы скорость была на 5 км/ч больше, то то же самое путешествие заняло бы на 1 час меньше. Найдите скорость поезда.

Ответ:

Пусть скорость поезда х км/час.

Время, необходимое для преодоления 360 км/ч

Согласно заданному вопросу,

Однако скорость не может быть отрицательной.

Следовательно, скорость поезда 40 км/ч

Видео Решение квадратных уравнений (Страница: 88 , Q.No.: 8)

NCERT Решение математических квадратных уравнений 7 класса 88 , Вопрос 8

Страница № 88:

Вопрос 9:

Два водопроводных крана вместе могут наполнить резервуар за несколько часов. Крану большего диаметра требуется на 10 часов меньше, чем меньшему, чтобы заполнить бак отдельно. Найдите время, за которое каждый кран в отдельности сможет наполнить бак.

Ответ:

Пусть время, за которое меньшая труба наполняет бак, равно x часов.

Время, затрачиваемое большей трубой = ( x − 10) ч

Часть резервуара, заполненная меньшей трубой за 1 час =

Часть резервуара, заполненная большей трубой за 1 час =

Дано, что бак можно наполнить за час по обеим трубам вместе. Следовательно,

Время, затраченное меньшей трубой, не может быть = 3,75 часа. Как и в этом случае, время, затрачиваемое большей трубой, будет отрицательным, что логически невозможно.

Таким образом, время, затраченное на меньшую и большую трубы по отдельности, составит 25 и 25 − 10 = 15 часов соответственно.

Видео Решение квадратных уравнений (Страница: 88 , Q.No.: 9)

NCERT Решение математических квадратичных уравнений для 7 класса 88 , Вопрос 9

Страница № 88:

Вопрос 10:

Экспрессу требуется на 1 час меньше, чем пассажирскому поезду, чтобы проехать 132 км между Майсором и Бангалором (без учета учитывать время остановки на промежуточных станциях). Найдите среднюю скорость двух поездов, если средняя скорость экспресса на 11 км/ч больше скорости пассажирского поезда.

Ответ:

Пусть средняя скорость пассажирского поезда равна х км/ч.

Средняя скорость экспресса = ( x + 11) км/ч

Известно, что время, необходимое экспрессу для прохождения 132 км, на 1 час меньше, чем пассажирскому поезду для преодоления того же пути.

Скорость не может быть отрицательной.

Следовательно, скорость пассажирского поезда будет 33 км/ч, а значит, скорость экспресса будет 33 + 11 = 44 км/ч.

Видео Решение квадратных уравнений (Страница: 88 , Q.No.: 10)

NCERT Решение математических квадратных уравнений для 7 класса 88 , Вопрос 10

Номер страницы 88:

Вопрос 11:

Сумма площадей двух квадратов равна 468 м ² . Найдите стороны двух квадратов, если разница их периметров равна 24 м.

Ответ:

Пусть стороны двух квадратов равны х м и х м. Следовательно, их периметр будет равен 4 x и 4 y соответственно, а их площади будут равны x ² и y ² соответственно.

Указано, что

4 x — 4 y = 24

x — y = 6

x = y + 6

9008 9008 . квадрат не может быть отрицательным.

Следовательно, стороны квадратов равны 12 м и (12 + 6) м = 18 м

Видео Решение квадратных уравнений (Страница: 88 , Q.№: 11)

NCERT Решение математических квадратных уравнений для 7 класса 88 , Вопрос 11

Номер страницы 88:

Вопрос 1:

Найдите характер корней следующих квадратных уравнений.

Если настоящие корни есть, найди их;

(I) 2 x ² −3 x + 5 = 0

(II)

(III) 2 x ² − 6 x + 3 = 0

Ответ:

Мы знаем что для квадратного уравнения топор ² + бх + в = 0, дискриминант равен b ² − 4 ac.

(А) Если б ² − 4 ак > 0 → два различных действительных корня

(B) If b ² − 4 ак = 0 → два равных действительных корня

(C) If b ² − 4 ак < 0 → нет реальных корней

(I) 2 x ² −3 х + 5 = 0

Сравнивая это уравнение с ax ² + bx + c = 0, получаем

a = 2, b = −3, c = 5

Дискриминант = b ² − 4 ac = (− 3) ² − 4 (2) (5) = 9 − 40

= −31

Как b ² − 4 ac < 0,

Следовательно, для данного уравнения невозможен действительный корень.

(II)

Сравнивая это уравнение с ax ² + bx + c = 0, получаем

дискриминант

= 48 — 48 = 0

Как b ² − 4 ac = 0,

Следовательно, у данного уравнения существуют действительные корни и они равны друг другу.

И корни будут а также .

Следовательно, корни а также.

(III) 2 х ² − 6 х + 3 = 0

Сравнивая это уравнение с ax ² + bx + c = 0, получаем

a = 2, b = −6, c = 3

Дискриминант = b ² − 4 ac = (− 6) ² − 4 (2) (3)

= 36 — 24 = 12

Как b ² − 4 ac > 0,

Следовательно, для этого уравнения существуют различные действительные корни следующим образом.

Следовательно, корни или же .

Страница № 91:

Вопрос 2:

Найдите значения k для каждого из следующих квадратных уравнений так, чтобы они имели два одинаковых корня.

(i) 2 x ² + KX + 3 = 0

(ii) KX ( x — 2) + 6 = 0

Ответ:

Мы знаем, что если уравнение ax ² + bx + c = 0 имеет два равных корня: его дискриминантный
( B ² — 4 AC ) составит 0,

(I) 2 x ² + KX + 3 = 0

. Сравнение уравнения с AX ² + BX + C = 0, мы получаем

A = 2, B = K , C = 3

Discinanne = 4 B. − 4 ac = ( k ) ² − 4(2) (3)

= k ² − 24

For equal roots,

Discriminant = 0

k ² − 24 = 0

k ² _{= 24}

( II) KX ( x — 2) + 6 = 0

или KX ² — 2 KX + 6 = 0

Сравнение этого уравнения с AX ² + 545454545454545454545. + c = 0, получаем

A = K , B = −2 K , C = 6

Дискриминантный = B ² — AC = (– 4 K) 2 AC = (444444. − 4 ( k ) (6)

= 4 k ² − 24 k

For equal roots,

b ² − 4 ac = 0

4 к ² − 24 к = 0

4 к ( k − 6) = 0

Либо 4 k = 0, либо k = 6 = 0

k = 0 или k = 6

, тогда 5

в уравнении не будет членов « x ² » и « x ».

Следовательно, если это уравнение имеет два одинаковых корня, k должно равняться только 6.

Видео Решение квадратных уравнений (Страница: 91 , Q.No.: 2)

NCERT Решение математических уравнений 7 класса — квадратные уравнения 91 , Вопрос 2

Страница № 91:

Вопрос 3:

Можно ли спроектировать манговую рощу прямоугольной формы, длина которой вдвое больше ширины, а площадь 800 м ² ?

Если да, найдите его длину и ширину.

Ответ:

Пусть ширина манговой рощи будет l .

Длина манговой рощи будет 2 л .

Площадь манговой рощи = (2 л ) ( л )

= 2 л ²

Comparing this equation with al ² + bl + c = 0, we obtain

a = 1 b = 0, c = 400

Дискриминантная = B ² — 4 AC = (0) ² — 4 × (1) × ( — 400) = 1600

здесь, B ² — 4 AC > 0. 2 — 4 AC > 0. 2 — 4 AC > 0.

Следовательно, уравнение будет иметь действительные корни. И, следовательно, можно спроектировать желаемую прямоугольную манговую рощу.

Однако длина не может быть отрицательной.

Следовательно, ширина манговой рощи = 20 м

Длина манговой рощи = 2 × 20 = 40 м

Видео Решение квадратных уравнений (Страница: 91 , Q.

№: 3) 7 математические квадратные уравнения 91 , Вопрос 3

Страница № 91:

Вопрос 4:

Возможна ли следующая ситуация? Если да, то определите их настоящий возраст. Сумма возрастов двух друзей равна 20 годам. Четыре года назад произведение их возраста в годах равнялось 48.

Ответ:

Пусть возраст одного друга будет х лет.

Возраст другого друга будет (20 − x ) лет.

4 года назад, 1 год ^й друг = ( х — 4) лет

И, 2 года ^й друг = (20 — х — 4)

= (184 х ) лет

Учитывая, что

( х — 4) (16 — х ) = 48

16 х — 64 — х ² + 4 x = 48

— x ² + 20 x — 112 = 0

x ² — 200084 x x ^{. Уравнение с AX 2 + BX + C = 0, мы получаем}

A = 1, B = −20, C = 112

DISSINANT = 4444 = 112

= 444449 2 = 112

= 444449 2 = 112

= 44444 40085 = 112

= 44444 = 112

= 4444.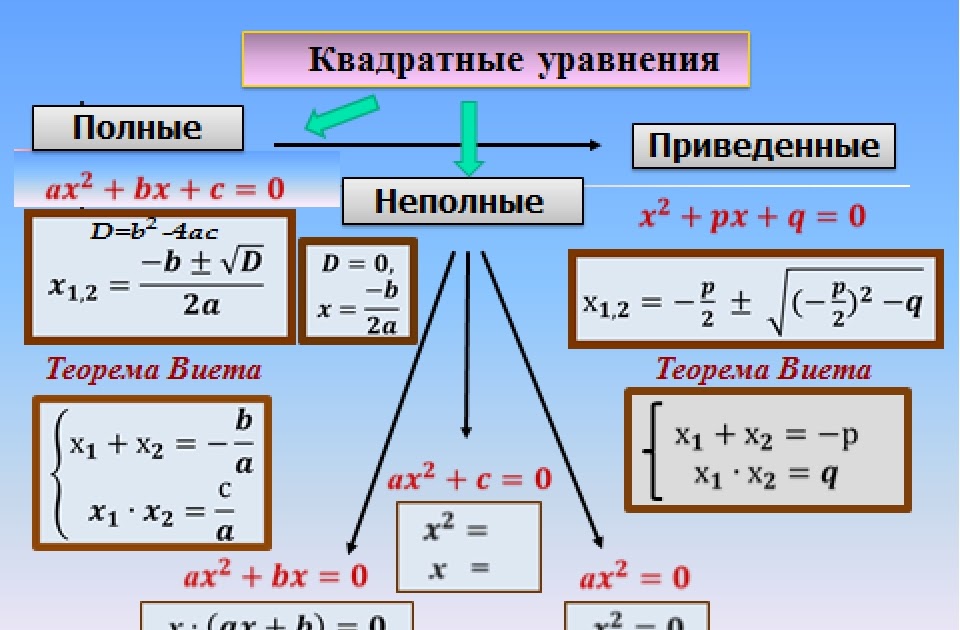 − 4 ac = (− 20) ² − 4 (1) (112)

= 400 − 448 = −48

As b ² − 4 ac < 0,

Следовательно, для этого уравнения не может быть никакого реального корня, и, следовательно, эта ситуация невозможна.

Видео Решение квадратных уравнений (Страница: 91 , Q.No.: 4)

NCERT Решение математических квадратных уравнений 7 класса 91 , Вопрос 4

Страница № 91:

Вопрос 5:

Возможно ли спроектировать прямоугольный парк периметром 80 и площадью 400 м ² ? Если да, то найдите его длину и ширину.

Ответ:

Пусть длина и ширина парка l и b .

Периметр = 2 ( L + B ) = 80

L + B = 40

OR, B = 40 — L

. = л (40 − л ) = 40 л − л ²

40 L — L ² = 400

L ² — 40 L + 400 = 0

СПОРТИ BL + C = 0, мы получаем

A = 1, B = −40, C = 400

Дискриминантный = B ² — 4 AC = (–4072 — 4 AC = (–4072 ² — 40084 AC = (–4072 — 40084 AC = (–4072 2 −4 (1) (400)

= 1600 − 1600 = 0

As b ² − 4 ac = 0,

Следовательно, это уравнение имеет одинаковые действительные корни. А значит, такая ситуация возможна.

Корень этого уравнения,

Следовательно, длина парка, l = 20 м

И ширина парка, b = 40 − l Решение = 40 0 ​​0 2 0 0 9 = 20 0 9 m для квадратных уравнений (Страница: 91 , Q.No.: 5)

NCERT Решение для класса 7 по математике — квадратные уравнения 91 , Вопрос 5

2.3 Квадратичная формула | Уравнения и неравенства

Предыдущий 2.2 Заполнение квадрата

Следующий 2.4 Замена

92 + т +1 &= 0\\ t&= \dfrac{-1 \pm \sqrt{1-4(1)(1)}}{2(1)}\\ &= \dfrac{-1 \pm \sqrt{-3}}{2}\\ \text{Нет реального решения} \конец{выравнивание*}

Предыдущий 2. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт