Информатика — Задачи на вероятность из ЕГЭ по математике.
1. Что такое вероятность
Вот три задачи.
А. В корзине лежат елочные игрушки – 4 шарика разных цветов, красный, синий, зеленый и золотой. Вера наугад достает шарик из корзины. С какой вероятностью она достанет золотой шарик?
Б. В мешке лежат теннисные мячи разных сортов: 45 белых , 35 жёлтых и 20 светло-голубых. С какой вероятностью случайно вынутый из мешка мяч окажется желтым?
В. Для экзамена по информатике есть 30 билетов, в 27 из них встречается вопрос по алгоритмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по алгоритмам.
Во всех этих задачах описаны однотипные ситуации. А именно.
1. Совершается определенное действие (можно сказать и так: происходит событие):
А) Вера достает шарик из корзины.
Б) Кто-то достает мячик из мешка.
В) Школьник тащит билет.
!!! Все исходы – равно возможны (можно сказать – «равновероятны»).
А) Исход – какой шарик достала Вера. Количество исходов – 4.
Б) Исход – какой мячик достали. Количество исходов – 45+35+20 = 100.
В) Исход – какому билет вытянул школьник. Количество исходов – 30.
3. Некоторые исходы считаются «успешными» (в смысле задачи :), по жизни в таком «успехе» может ничего особенного не быть). Нам важно, сколько есть «успешных» исходов.
А) Успешный исход –Вера достала золотой шарик.
Количество успешных исходов – 1.
Б) Успешный исход – достали желтый мячик.
Количество успешных исходов – 35.
В) Успешный исход – школьник вытянул билет без вопроса по алгоритмам.
Количество успешных исходов – 30-27 = 3.
Так вот.
Вероятность успеха (иными словами – вероятность того, что произойдет один из исходов, которые мы считаем успешными) – это отношение числа успешных исходов к общему числу возможных исходов.
Схематично это можно записать так (знак # заменяет слово «количество»):
# успешных исходов
Вероятность = ——————————-
# всех исходов
Понятно, что вероятность не может быть меньше 0 или больше 1.
4. Таким образом, в задачах получаем такие ответы:
А) 1/4 = 0,25
Б) 35/100 = 0,35
В) 3/30 = 0,1
Вот, собственно говоря, и все. В заключение – два важных замечания.
Замечание 1: В основе определения вероятности – предположение о том, что все исходы равноправны (равно возможны). Например, в задаче В школьник не должен знать, что написано в билетах, а Вера не должна подсматривать. В условиях задач на это указывают слова «наугад», «по жребию», и т.п. Иногда таких слов в условии нет, равноправность исходов подразумевается по смыслу (например, в задаче В).
Замечание 2. Разбираясь, что считать исходом в конкретной задаче, нужно следить за тем, чтобы исходы было (по смыслу задачи) равноправны (равновероятны). Например, некто мог бы в задаче Б считать исходом цвет вытащенного мячика. Тогда исходов было бы 3 (белый, желтый, светло-зеленый), из них один успешный. Но эти исходы не равноправны – ведь мячиков разное число.
Упражнение. Вот известный анекдот.
Какова вероятность того, что первый человек, которого ты встретишь, выйдя из дома, будет королева Великобритании
Ответ. Есть 2 исхода – либо королева, либо не королева. Успешный исход – 1. Значит вероятность равна ½ = 0,5 = 50%.
Разберитесь – где в рассуждении ошибка.
2. Как решать задачи
Вероятность находим так.
- Разбираемся, что в задаче является исходом и сколько их.
!!! Следим за тем, чтобы исходы были равновероятными.
2. Разбираемся в том, какие исходы считаются успешными. Находим количество успешных исходов.
3. Находим вероятность – делим количество успехов на количество всех возможных исходов.
При этом не ошибаемся в арифметике и записываем ответ ДЕСЯТИЧНОЙ дробью.
4. Радуемся, что решили задачу 🙂
3. Еще два примера
3.1. На чемпионате по гимнастике выступают 50 спортсменов, среди них 6 спортсменов из Китая. Спортсменам по жребию дали номера – от 1-го до 50-го. Найдите вероятность того, что под номером 37 будет выступать гимнаст из прыгун из Китая.
В этой задаче исход – это спортсмен, которому достался 37-й номер. Всего исходов – 50. То, что говорится о 37-м номере, а не о, скажем, первом нас не смущает. У всех спортсменов равные шансы получить этот номер! Успешных исходов – 6 (спортсмены из Китая). Дальше – сами 🙂
3.2. Завод выпускает часы. В среднем на 1800 качественных часов приходится 200 часов со скрытыми дефектами. Найдите вероятность того, что купленные часы, сделанные на этом заводе, окажутся с дефектом.
В этой задаче – одна тонкость и одна ловушка (несложная).
Тонкость связана со словами «в среднем». По-хорошему, количество исходов, — это количество доступных покупателю часов этого завода. Количество «успехов» — количество доступных ему дефектных часов. Ни того, ни другого мы не знаем. Так в жизни бывает часто.
И часто поступают так.
1) Выбирают наугад достаточно большую группу часов, обозначим ее размер N.
2) Считают количество дефектных часов (т.е. успешных исходов) в этой группе, обозначим его G.
3) Вычисляем вероятность успеха по формуле (P – вероятность):
P = G/N
То есть, мы считаем, что вероятность успеха среди всех исходов (примерно) такая же, как и в выбранном наугад подмножестве всех исходов. Такое предположение выглядит разумно и может быть обосновано (если аккуратно разбираться, что значит «наугад», насколько большое подмножество нужно выбирать и насколько вероятность успеха для множества всех исходов может отличаться от вероятности, подсчитанной по подмножеству).
Слова «в среднем» и означают, что нужно применить такой подход. При этом в выбранном множестве исходов будет 1800 «неуспехов» (качественных часов 🙂 ) и 200 «успехов (дефектных часов). Ловушка в том, что общее количество исходов N здесь не указано. Его нужно подсчитать: N = 1800+200 = 2000. Таким образом, вероятность здесь считается по формуле P = G/N = 200/2000 = 0,1 = 10%/
Ответ: 0,1
4. События, их пересечения, объединения и дополнения.
Вот письмо посетителя сайта http://ege-go.ru/math-ege/b10math/comment-page-1/#comment-1262 : «Помогите, пожалуйста, решить такую задачу.
Задача. В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате чай закончится, равна 0,4. Вероятность того, что к концу дня чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
Я рассуждаю, что исходя из того, что вероятность не может превышать 1:
1-0,2=0,8 — вероятность, того что чай останется в обоих автоматах. А в ответе 0,4. Не могу понять, где я ошибаюсь.»
Комментарий. Спасибо за письмо! Задача действительно трудная. А трудность в том, чтобы разобраться, что означают слова «вероятность того, что к концу дня в автомате чай закончится»; «вероятность того, что к концу дня чай закончится в обоих автоматах»; «вероятность того, что к концу дня чай останется в обоих автоматах». Я чуть позже разберу задачу на сайте подробно Пока пишу коротко.
Ты ошибаешься вот в чем. Формула 1-0,2=0,8 означает, что события «к концу дня чай закончился в обоих автоматах» и «к концу дня чай остался в обоих автоматах» являются взаимно дополнительными, то есть в любой день происходит ровно одно из этих событий и они никогда не происходят одновременно. На самом деле, одновременно эти события, конечно произойти не могут, но может не произойти ни одно из них: в одном автомате чай может закончиться, а в другом – нет. Поэтому вероятность того, что к концу дня чай останется в обоих автоматах, заведомо меньше, чем 1-0,2=0,8. Насколько меньше – нужно разбираться.
Решение. Возьмем какой-то день. Для удобства, присвоим автоматам имена A и В. К концу дня может случиться ровно одно из четырех событий (говорят: эти события образуют полную систему)
1) Чай закончился в обоих автоматах (обозначение: А+В+)
2) Чай закончился в автомате А, но остался в автомате В (обозначение: А+В-)
3) Чай закончился в автомате В, но остался в автомате А (обозначение: А-В+)
4) Чай остался в обоих автоматах (обозначение: А-В-).
Обозначим вероятности этих событий соответственно: Р(А+В+), Р(А+В-), Р(А-В+), Р(А-В-).
Так, как перечисленные события образуют полную систему, то
Р(А+В+) + Р(А+В-) + Р(А-В+) + Р(А-В-) = 1 (1)
Событие «чай закончился в автомате А» — это объединение двух дополнительных событий Р(А+В+) и Р(А+В-). Поэтому
Р(А+В+) + Р(А+В-) = 0,4 (2)
Аналогично, для автомата В получаем:
Р(А+В+) + Р(А-В+) = 0,4 (3)
Наконец, по условию,
Р(А+В+) = 0,2 (4)
Нужную нам вероятность Р(А-В-) находим, решая систему (1)-(4).
Р(А-В-) = Р(А+В+) + Р(А+В-) + Р(А-В+) + Р(А-В-) –
— (Р(А+В+) + Р(А+В-) ) — (Р(А+В+) + Р(А+В-) ) +
+ Р(А+В+) =
= 1 -0,4 -0,4 +0,2 = 0,4.
Ответ:0,4
Замечание. Чтобы решать такие задачи, нужно уметь свободно рассуждать о событиях – множествах возможных элементарных исходов. В нашей задаче элементарные исходы – это дни. Например, событие А+В- — это множество всех дней, в которые чай в автомате А закончился, а в автомате В – нет. Про подсчет количества элементов в объединении и пересечении множеств – см. http://ege-go.ru/temy/sets/ .
ege-go.ru
Задачи по теории вероятностей. Решение задания В10
1. Задание B5 (№ 285924) из Открытого банка заданий для подготовки к ЕГЭ по математике.
На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Решение.
Заметим, что поскольку порядок докладов определяется жеребьевкой, вероятность того, что восьмым окажется доклад ученого из России такая же, как вероятность того, что доклад ученого из России окажется первым. То есть эта вероятность не зависит от номера выступления.
Вероятность события определятся по формуле:
,
где
k — число событий, которые нас «устраивают», на языке теории вероятностей они называются благоприятными исходами.
n — число всех возможных событий, или число всех возможных исходов.
В нашей задаче на семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании, то есть всего 10 человек.
Значит, число всех возможных исходов равно 10. Из России приехали 3 ученых, значит, число благоприятных исходов, то есть тех событий, которые нас устраивают, равно 3.
Следовательно, вероятность того, что восьмым окажется доклад ученого из России равна 3/10=0,3
Ответ: 0,3
2. Задание B5 (№ 285925) Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение. «Зафиксируем» Руслана Орлова. Теперь осталось найти вероятность того, что в паре с ним окажется бадминтонист из России. Если мы исключили Руслана Орлова из списка спортсменов (мы его «зафиксировали»), то нам осталось выбрать ему пару из 25 спортсменов, из которых 9 участников из России.
То есть число всех возможных исходов равно 25, а число благоприятных исходов равно 9.
Следовательно, p=9/25=0,36
Ответ: 0,36
3. Задание B5 (№ 285922) Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение. Заметим, что доклад профессора М. окажется запланированным на последний день конференции с той же вероятностью, что и доклад любого другого участника конференции. Поэтому вопрос задачи можно переформулировать так: с какой вероятностью любой участник конференции выступит в последний день.
1. Найдем, какое количество докладчиков должно выступить в последний день конференции.
Так как всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями, на два последних дна запланировано
75-17х3=24 доклада.
Значит, на последний день запланировано 12 докладов, то есть количество благоприятных исходов равно 12.
Число всех возможных исходов равно 75, так как всего запланировано 75 докладов.
Итак, р=12/75=0,16
Ответ: 0,16.
4. Задание B5 (№ 283471) В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
Решение. Чтобы решить эту задачу, нам нужно вспомнить правило умножения вероятностей. Так как результат каждого бросания монеты не зависит от результата бросания монеты в другие разы, мы имеем дело с независимыми событиями.
Вероятность того, что произойдут независимые события А и В, равна произведению вероятностей события А и события В.
В нашей задаче орел не выпадет ни разу, если в результате бросания монеты каждый раз будет выпадать решка. Вероятность выпадения решки в каждом случае равна 1/2. Значит, вероятность того, что решка выпадет в результате всех четырех бросаний равна
ххх=1/16=0,0625
Ответ: 0,0625
5. Во время вероятностного эксперимента монету бросили 1000 раз, 532 раза выпал орел. На сколько частота выпадения решки в этом эксперименте отличается от вероятности этого события?
Частота события x — отношение N(x) / N числа N(x) наступлений этого
события в N испытаниях к числу испытаний N.
Если орел выпал 532 раза, то решка выпала 1000-532=468
Частота этого события равна
Вероятность выпадения решки равна 0,5
Следовательно, частота выпадения решки в этом эксперименте отличается от вероятности этого события на |0,5-0,468|=0,032
Ответ: 0,032
И, в заключение, предлагаю вам посмотреть ВИДЕОУРОК с решением задачи:
Вася выбирает трехзначное число. Найти вероятность того, что оно делится на 6. Ответ округлите до сотых.
Вероятно, Ваш браузер не поддерживается. Попробуйте скачатьFirefox или
Chrome
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Теория вероятности в задачах ЕГЭ-2016.
Теория вероятностей в задачах ЕГЭ-2016
(Слайд 1)
Для того, чтобы решать задачи по теории вероятностей нужно иметь своего рода вероятностное мышление, которое формируется поэтапно, по мере углубления в этот своеобразный раздел математики. Теория вероятностей — это математическая наука, изучающая закономерности случайных явлений то есть другими словами, в котором изучаются случайные явления и выявляются закономерности при массовом их повторении.
В задачах ЕГЭ в основном встречаются три вида задач: Простейшие задачи, на определение вероятности – как правило они не вызывают трудностей у учащихся. Задачи, решаемые с помощью графа и Задачи на правила вероятностей, которые вызывают затруднения, возможно ещё и потому, что дети не обладают данной теорией.
Прежде чем приступить к задачам, вспомним теорию. Задачи, на определение вероятности решаются методом логического перебора: когда выписываются все возможные исходы (а), выбираются благоприятные (b) и находится отношение p = b:a (Слайд 2) Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания из урны извлекается одна карточка. Какова вероятность того, что число на взятой карточке окажется делящимся на 5? (6/30=1/5)
(Слайд 3) В фирме такси в данный момент свободно 10 машин: 5 чёрных, 1 жёлтая и 4 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси. (1/10)
(Слайд 4) Задачи на графы. Иногда условие удобнее расположить в виде графа – дерева, который позволяет найти количество всех возможных исходов, выбрать благоприятные и вычислить вероятность.
Давайте решим несколько таких задач:
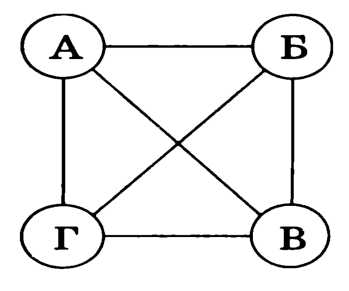
1) Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?
Решение: решим задачу с помощью так называемого полного графа с четырьмя вершинами А, Б, В, Г, обозначенными по первым буквам имён каждого из 4 мальчиков. В полном графе проводятся все возможные рёбра. В данном случае отрезки-рёбра обозначают шахматные партии, сыгранные каждой парой мальчиков. Из рисунка видно, что граф имеет 6 рёбер, значит, и партий было сыграно 6.
2) Антон, Борис и Василий купили 3 билета на футбольный матч на 1, 2 и 3-е места первого ряда. Сколькими способами они могут занять имеющиеся три места?
Решение: на 1-е место может сесть любой из троих друзей, на 2-е – любой из двоих оставшихся, а на 3-е – последний. Сказанное изобразим с помощью дерева, помещая в вершины графа первые буквы имён друзей А, Б, В:

3) Пенсионер совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Какова вероятность, что он придёт в пункт G.
А
С В
F E D G H
Решение: Возьмём любое число исходов, причём, чем больше, тем точнее.
N=1000.
MB=1000:2=500 (т.к. две развилки)
МG=500:2=250 (т.к. две развилки)
Находим вероятность Р=250/1000=0,25.
4) Сколько различных трёхзначных чётных чисел можно записать с помощью цифр 1, 2, 3.
1 2 3
1 2 3 1 2 3 1 2 3
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
Выбираем чётные (благоприятные): 9.
5) В урне 3 чёрных и 4 белых шара. Вынимают один из них, перемешивают и вынимают другой. Какова вероятность достать 2 белых шара, 2 чёрных, шары разных цветов. 7 шаров
Белый 4/7 черный 3/7
Белый 3/6 черный3/6 белый 4/6 черный 2/6
Решение: Исходы: 2 белых шара: 4/7*3/6=2/7
Шары разных цветов: 3/7*4/6+4/7*3/6=4/7
2 чёрных шара: 3/7*2/6=1/7
В данной задаче ещё и используются правила:
Сложение и умножение вероятностей.
Событие называют противоположным событию А, если оно происходит только тогда, когда не происходит событие А. Обозначается . Сумма вероятностей противоположных событий равна 1.
Два события называются несовместными, если в одном и том же испытании, они не могут произойти одновременно, т.е. наступление одного из них исключает наступление другого.
Теорема о сумме вероятностей: Если событие С означает, что наступает одно из двух несовместных событий А или В, то вероятность события С равна сумме вероятностей событий А и В.
Два события называются независимыми, если наступление одного из них, не влияет на вероятность наступления другого события.
Теорема о произведении вероятностей: Если событие С означает совместное наступление двух независимых событий А и В, то вероятность события С равна произведению вероятностей событий А и В.
Решим несколько задач на правила: 1). Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что пассажиров в автобусе наберётся менее двадцати человек, составляет 0,94. Вероятность того, что пассажиров будет менее пятнадцати – 0,56. Найти вероятность того, что число пассажиров в автобусе будет от пятнадцати до девятнадцати человек. Решение: Итак, пусть событие A будет заключаться в том, что автобусом решило воспользоваться менее 20 человек, т.е. P(A) = 0,94. Событие B – пассажиров в автобусе меньше 15 человек и, следовательно, P(B) = 0,56. Событие C – пассажиров в автобусе от 15 до 19 человек, и требуется вычислить вероятность этого события P(C). Но события B и C вместе (надо говорить, объединение событий) составляют событие A, при этом они не пересекаются, т.е. совместно события B и C не могут произойти. Поэтому имеем, P(A)=P(B)+P(C), откуда P(C) = P(A) — P(B) = 0.94 — 0.56 = 0,38.
2). Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,95. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой.
Решение:
Обозначим события:
А – выбранная батарейка не исправна.
В – выбранная батарейка исправна.
С – система контроля забраковала батарейку.
Применяя формулу полной вероятности получим искомую вероятность события С:
Р(С) = Р(А)Р(С/А) + Р(В)Р(С/В) = 0,03×0,95 + 0,97×0,04 = 0,0673
Здесь вероятность события В вычисляется как Р(В) = 1 – Р(А) = 1 – 0,03 = 0,97.
Итак, Ответ: 0,0673.
Я хочу предложить такую цепь рассуждений, которая, по моему мнению, может помочь решить эту задачу тем ученикам или учителям, которые не могут прочитать учебник в силу его отсутствия или понять формулу полной вероятности.
Можно представить, что имеется 10000 изготовленных батареек, из которых 300 не исправны, а 9700 исправны. И вот все эти батарейки отправили на контроль. Ясно, что система из трех неисправных батареек забракует 300×0,95 = 285 штук. Из 300 неисправных 285 система забракует и из 9700 исправных будет забраковано 388 и того система не пропустит 285+388=673 из 10000. И отсюда легко получим тот же ответ, разделив 673 на 10000.
3). Стрелок стреляет по мишени с вероятностью попадания 0,6. Если он промахивается один раз, можно выстрелить второй. Какова вероятность поражения мишени в таких условиях стрельбы?
Решение: Предлагаем аналогичную цепь рассуждений. Пусть всего мишеней, в которую стреляли один раз 1000. Стрелок попал 600 раз. 400 раз он промахнулся, поэтому будет стрелять ещё столько же раз. Попадёт 400*0,6=240 раз. Получается всего стрелок поразил мишень 600+240=840 раз. Находим вероятность: 840/1000=0,84.
4). В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. Решение. Рассмотрим события А = кофе закончится в первом автомате, В = кофе закончится во втором автомате. Тогда A·B = кофе закончится в обоих автоматах, A + B = кофе закончится хотя бы в одном автомате. По условию P(A) = P(B) = 0,3; P(A·B) = 0,12. События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения: P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48. Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52. Ответ: 0,52.
5). Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным. Решение: Анализ пациента может быть положительным по двум причинам: А) пациент болеет гепатитом, его анализ верен; B) пациент не болеет гепатитом, его анализ ложен. Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем: Ответ: 0,0545.
Ссылка на видео урок по теории вероятности. https://youtu.be/ptW5gpk3vRM
infourok.ru
Теория вероятности в задачах ЕГЭ
Выступление
на методическом объединении учителей математики по теме
«Задачи раздела «Вероятность»
в КИМ ЕГЭ»
Подготовила учитель математики
МБОУ «Лицей №4» г.Рузаевка
Овчинникова Т.В.
2016
ЕГЭ по математике является обязательным и по праву считается одним из самых сложных. Как и в прошлом году будет разделение экзаменов на базовый и профильный уровни.
Изменений структуры и содержания экзаменационной работы базового уровня в КИМ ЕГЭ 2016 года в сравнении с 2015 годом нет.
В профильном уровне из первой части исключены два задания: задание практико-ориентированной направленности базового уровня сложности и задание по стереометрии повышенного уровня сложности. Максимальный первичный балл уменьшился с 34 до 32 баллов.
ФИПИ опубликовал образцы Демонстрационных вариантов ЕГЭ 2016 по математике.
В этом году задания Демонстрационного варианта базового уровня соответствуют прошлогодним практически полностью, за исключением незначительных редакционных правок, облегчающих прочтение текста задачи. Более существенным изменением является добавление в экзаменационную работу раздела Справочные материалы, что ранее было характерно только для ОГЭ в 9-ом классе.
Демонстрационные варианты носят исключительно ознакомительный характер. Они дают возможность изучить структуру КИМ: количество заданий, их форму, уровень сложности и дают представление о требованиях к оформлению ответов.
Задания демонстрационных вариантов не используются на экзаменах, но они имеют аналогичную структуру, ознакомление с которой позволяет выпускникам выработать стратегию подготовки к ЕГЭ.
В 2012 году в ЕГЭ по математике впервые появилось задание по теории вероятностей. С тех пор их число и разнообразие прототипов, опубликованных на сайте ФИПИ, значительно возросло. Появились задачи на сумму и произведение событий. Для этого типа задач формулы не главное. Гораздо важнее понять и хорошо сформулировать событие, о котором спрашивается в условии задачи.
Наибольшие затруднения при выполнении части 1 у выпускников вызывают задачи раздела «Вероятность». Решения некоторых типов задач я бы хотела вам предложить.
Определение вероятности
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместимых событий, которые могут произойти в результате одного испытания или наблюдения:
Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2k.
Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6k.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Всего 4 варианта: о; о о; р р; р р; о.
Благоприятных 2: о; р и р; о.
Вероятность равна 2/4 = 1/2 = 0,5.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение.
Игральные кости – это кубики с 6 гранями. На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому варианту выпадения очков соответствует 6 вариантов выпадения очков на втором кубике.
Т.е. всего различных вариантов 6×6 = 36.
Варианты (исходы эксперимента) будут такие:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
и т.д. …………………………
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8.
2; 6 3; 5; 4; 4 5; 3 6; 2. Всего 5 вариантов.
Найдем вероятность: 5/36 = 0,138 ≈ 0,14.
В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.
Решение:
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна 11/55 =1/5 = 0,2.
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные − из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Решение.
Всего участвует 20 спортсменок, из которых 20 – 8 – 7 = 5 спортсменок из Китая.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5/20 = 1/4 = 0,25.
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение:
В последний день конференции запланировано
(75 – 17 × 3) : 2 = 12 докладов.
Вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12/75 = 4/25 = 0,16.
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение:
Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России.
Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.
Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при первом броске выпало 2 очка.
Решение.
В сумме на двух кубиках должно выпасть 8 очков. Это возможно, если будут следующие комбинации:
2 и 6
6 и 2
3 и 5
5 и 3
4 и 4
Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка.Такой вариант 1.
Найдем вероятность: 1/5 = 0,2.
В чемпионате мира участвует 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе.
Решение:
Всего команд 20, групп – 5. В каждой группе – 4 команды.
Итак, всего исходов получилось 20, нужных нам – 4, значит, вероятность выпадения нужного исхода 4/20 = 0,2.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: р1 = 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: р2 = 0,55 · 0,01 = 0,0055.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна
р = р1 + р2 = 0,0135 + 0,0055 = 0,019.
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3.Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: р = 0,52 · 0,3 = 0,156.
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Решение:
Результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы.
Вероятность каждого попадания равна 0,8. Значит, вероятность промаха равна 1 – 0,8 = 0,2.
1 выстрел: 0,8
2 выстрел: 0,8
3 выстрел: 0,8
4 выстрел: 0,2
5 выстрел: 0,2
По формуле умножения вероятностей независимых событий, получаем, что искомая вероятность равна:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:
Найдем вероятность того, что неисправны оба автомата.
Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна
1 − 0,0025 = 0,9975.
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение:
Вероятность того, что Джон промахнется, если схватит пристрелянный револьвер равна: 0,4 · (1 − 0,9) = 0,04
Вероятность того, что Джон промахнется, если схватит непристрелянный револьвер равна: 0,6 · (1 − 0,2) = 0,48
Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52.
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение:
Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов:
Р(1) = 0,6;
Р(2) = Р(1) · 0,4 = 0,24;
Р(3) = Р(2) · 0,4 = 0,096;
Р(4) = Р(3) · 0,4 = 0,0384;
Р(5) = Р(4) · 0,4 = 0,01536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени.
В классе 26 человек, среди них два близнеца – Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Решение:
Пусть один из близнецов находится в некоторой группе.
Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников. Вероятность того, что второй близнец окажется среди этих 12 человек, равна P = 12 : 25 = 0,48.
multiurok.ru
