1. Основные понятия векторной алгебры; примеры решения задач.
Основные понятия включают в себя: понятие вектора, разложение вектора по другим векторам, модуль вектора, скалярное произведение, векторное произведение и смешанное произведение, а также их приложения для решения задач.
Пример 1. Задание. Разложить вектор по векторам
Прежде чем привести решение задачи напомним понятие линейной зависимости системы векторов.
Рассмотрим систему векторов и составим равенство вида:
–постоянные величины.
Если это равенство выполняется только
при одновременном равенстве нулю всех 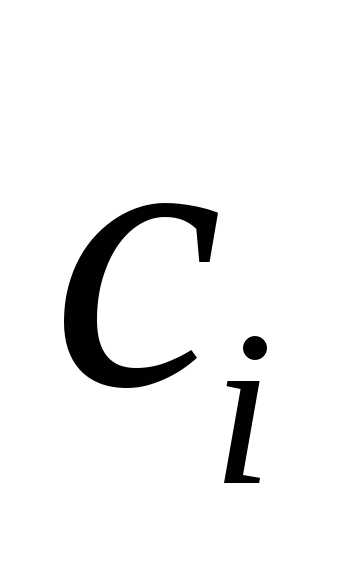 ,
,
, тогда система векторов называется линейно независимой , в противном случае – система векторов линейно зависима, то есть один вектор можно представить в виде линейной комбинации других векторов.
.
Разделим левую и правую части равенства
на 
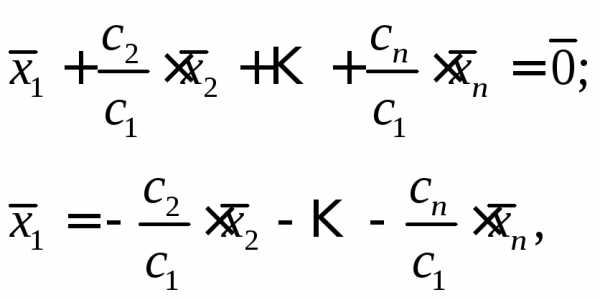
то есть вектор 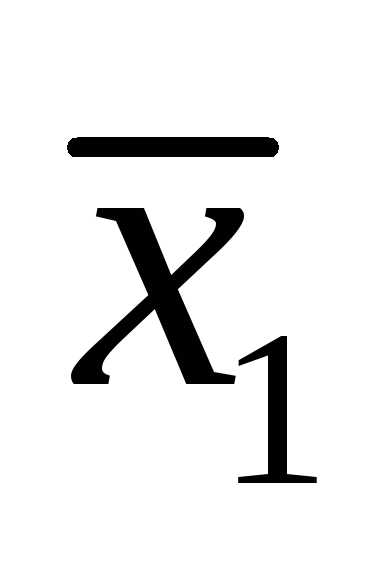 представлен в виде линейной комбинации.
представлен в виде линейной комбинации.
Решение.
Разложить вектор  по векторам
по векторам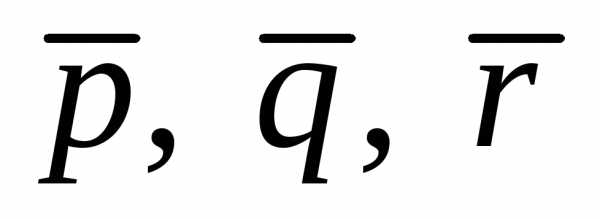 это значит представить его в виде
линейной комбинации– искомые числа.
это значит представить его в виде
линейной комбинации– искомые числа.
Представим линейную комбинацию в координатной форме
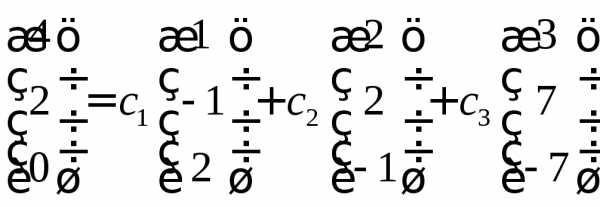
И получим систему линейных уравнений
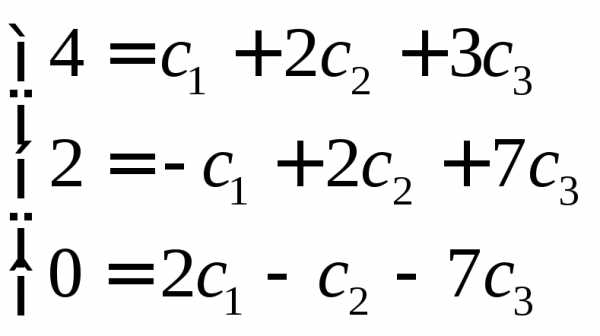
Решение системы имеет вид:
Следовательно:
Пример 2.
Напомним понятие длины вектора (модуля вектора)
Если , то
–называется длиной вектора.
Рассмотрим свойство
скалярного произведения:
,
то есть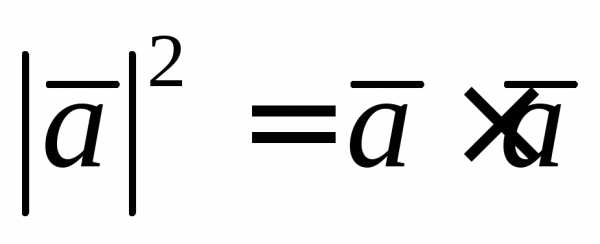 .
.
Задание.
Найти длину вектора 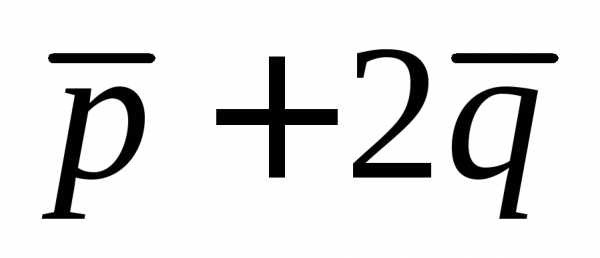 ,
если
,
если
Решение. Имеем
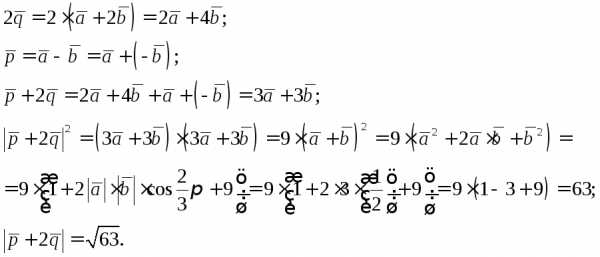
Пример 3.
Напомним определение
коллинеарности двух векторов 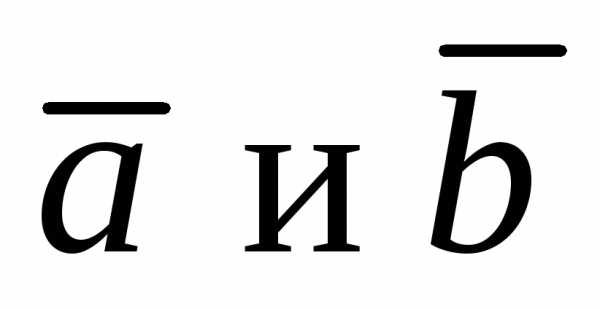 отличных от нуля: два вектора
отличных от нуля: два вектора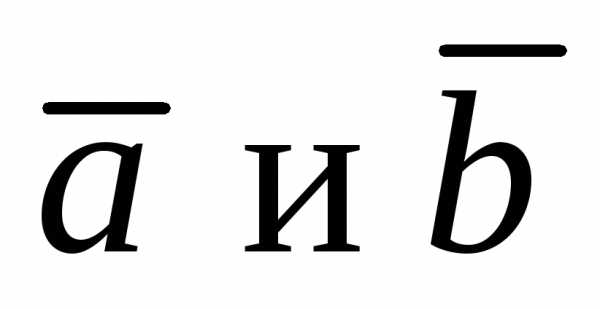 называются коллинеарными, если
называются коллинеарными, если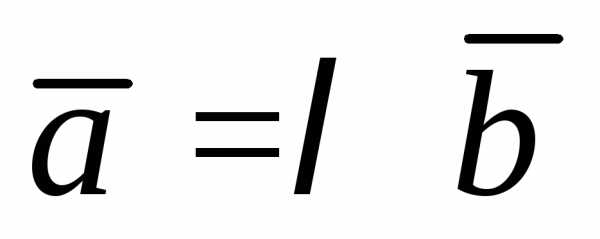 ,
где
,
где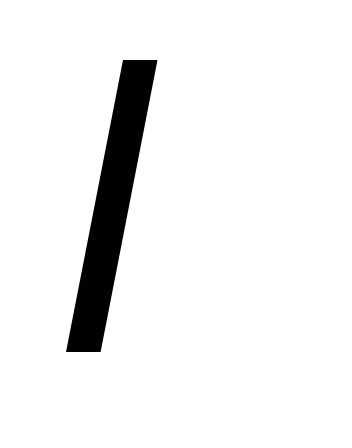 – некоторый постоянный множитель.
– некоторый постоянный множитель.
Задание.
Найти вектор 
Решение.
Запишем условие
коллинеарности двух векторов
и полученный вектор подставим в условие
подставим в условие
Следовательно .
Пример 4.
Напомним определение скалярного произведения векторов:
.
Задание.
Вычислить проекцию
вектора  на направление вектора
на направление вектора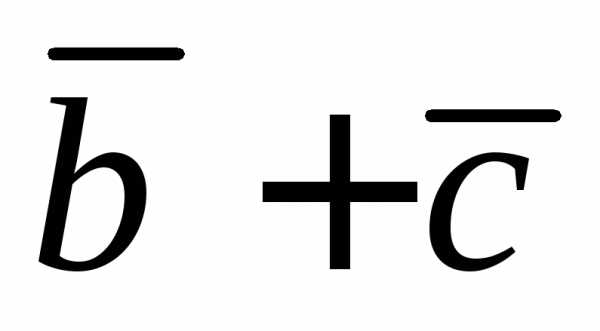 ,
если
,
если
Решение.
Обозначим , тогда
, отсюда
Ответ: 
Пример 5.
Пусть
.
Напомним, что векторное произведение
двух векторов и
и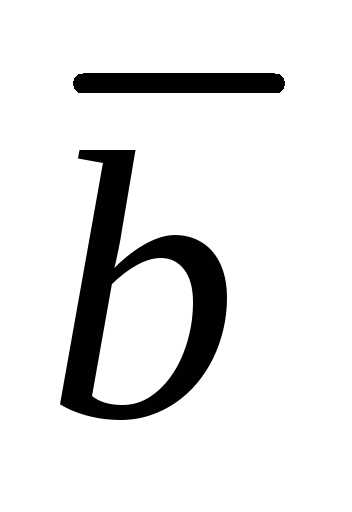
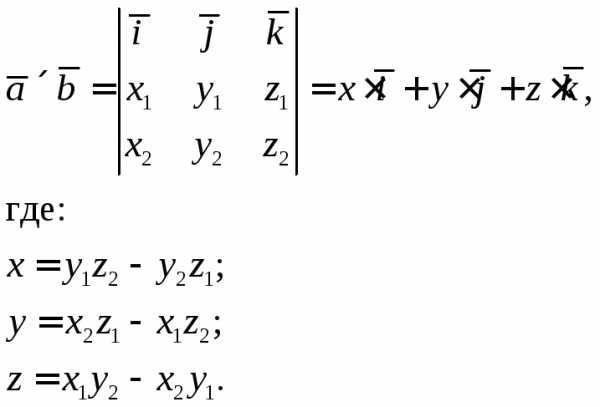
Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.
Задание.
Найти площадь треугольника
Решение.
Построим
параллелограмм  на векторах(рис. 1):
на векторах(рис. 1):
рис. 1 
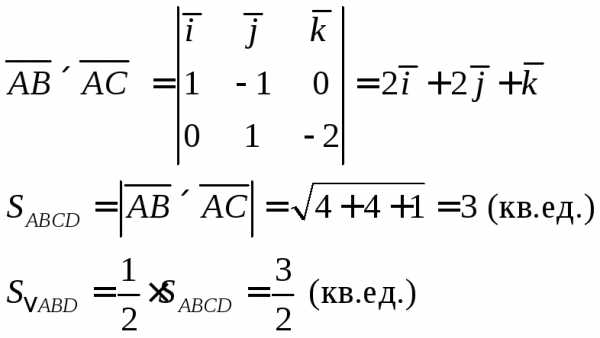
Пример 6.
Задание.
Найти вектор 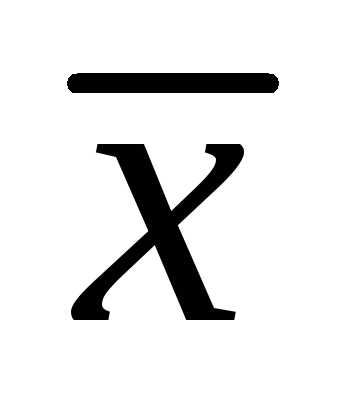 ,
перпендикулярный векторами образующий с осью
,
перпендикулярный векторами образующий с осью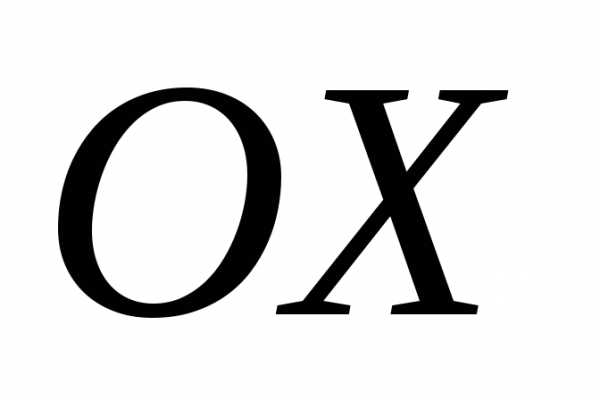 тупой угол, если
тупой угол, если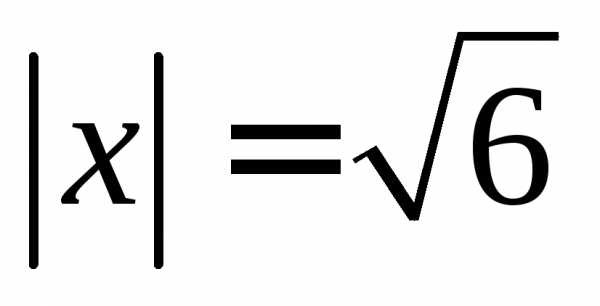 .
.
Решение
Если
,
тогда вектор перпендикулярен векторам
перпендикулярен векторам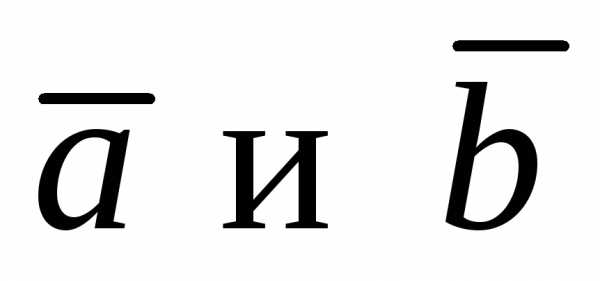 .
.
Найдем вектор  :
: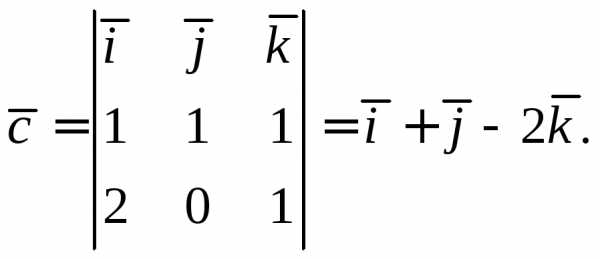
Так как 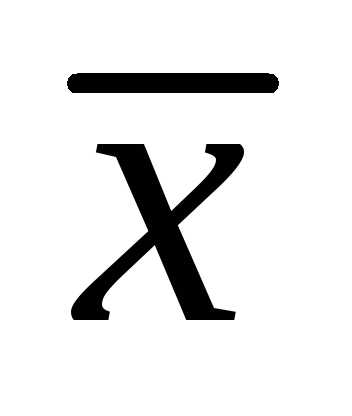 тоже перпендикулярен
тоже перпендикулярен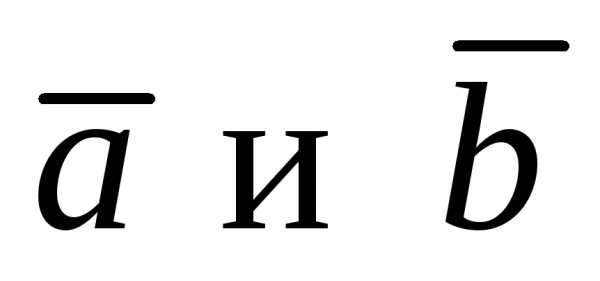 ,
следовательно вектора
,
следовательно вектора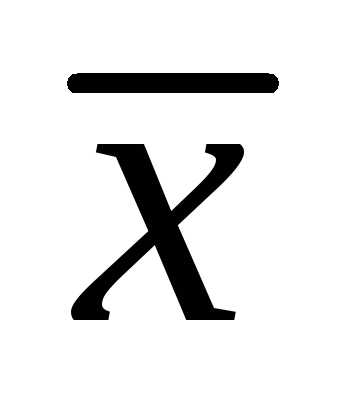 и
и — коллинеарны. Запишем условие
коллинеарности векторов:
— коллинеарны. Запишем условие
коллинеарности векторов: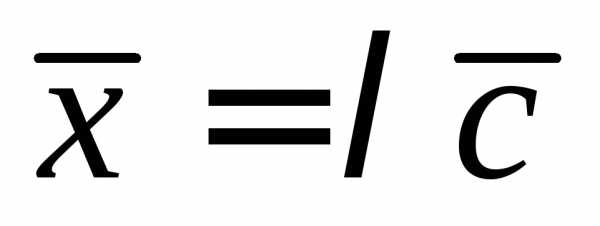 ,
,
По условию 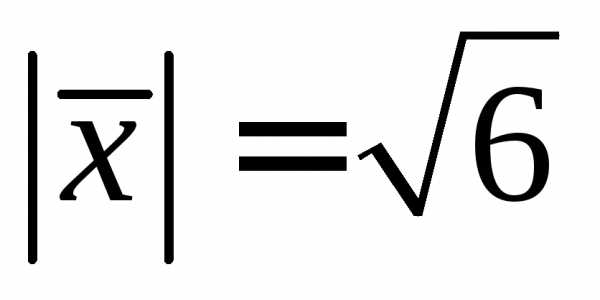 ,
то есть
,
то есть
Так как вектор 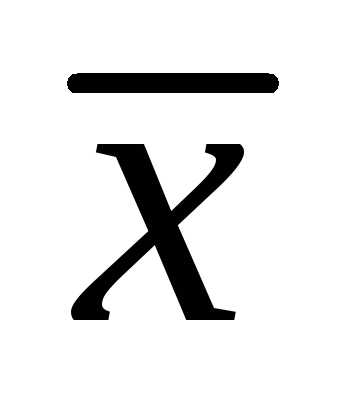
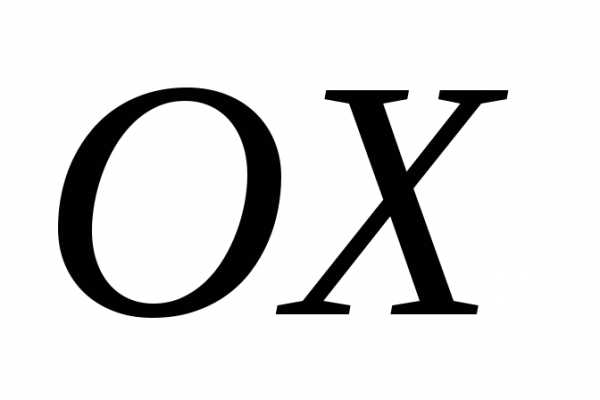 тупой угол, то его проекция на ось
тупой угол, то его проекция на ось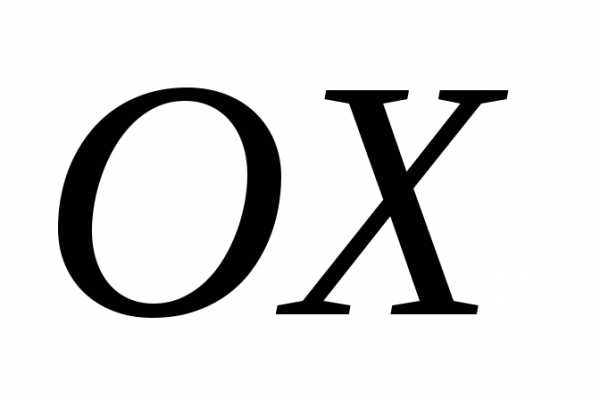 должна быть отрицательной.
должна быть отрицательной.Отсюда
Пример 7.
Рассмотрим вектор
.
Вектор образует с осями координат углы
образует с осями координат углы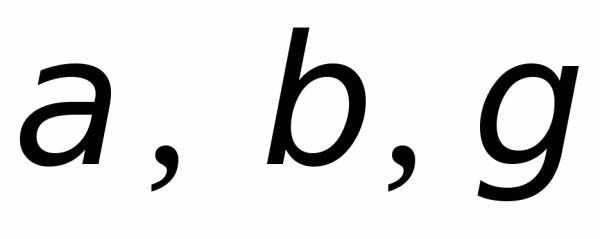 ,
аназываются направляющими косинусами,
при этом
,
аназываются направляющими косинусами,
при этом
Задание.
Найти направляющие
косинусы вектора силы
,
приложенной в точке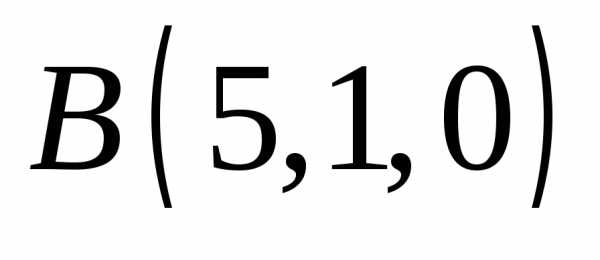 ,
и момент этой силы относительно точки
,
и момент этой силы относительно точки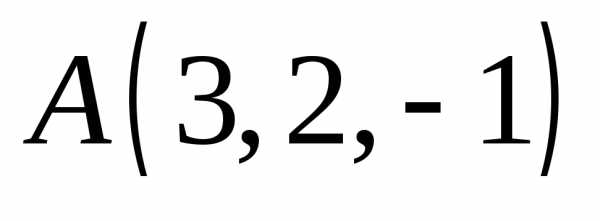 .
.
Решение.
Найдем направляющие косинусы вектора силы:
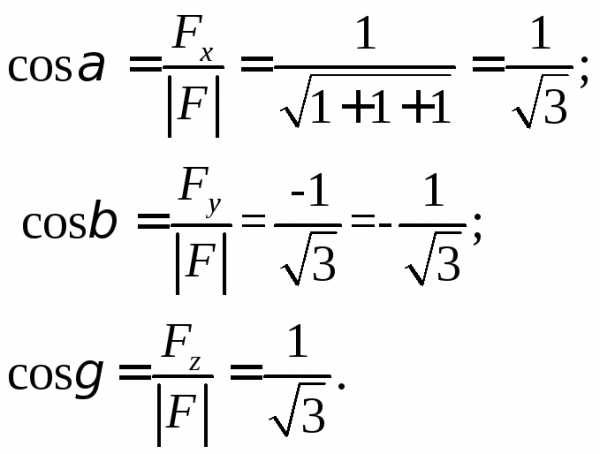
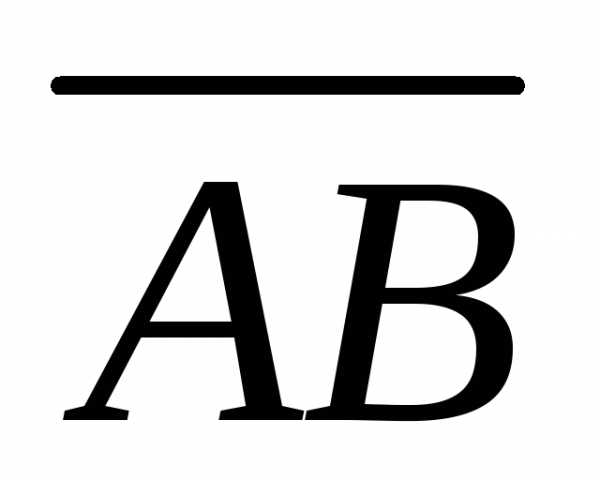 на вектор
на вектор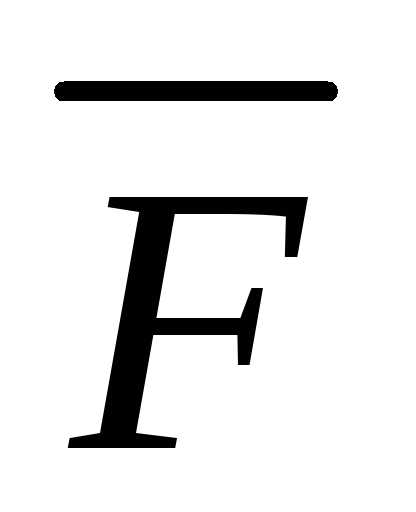 .
Имеем
.
Имеем 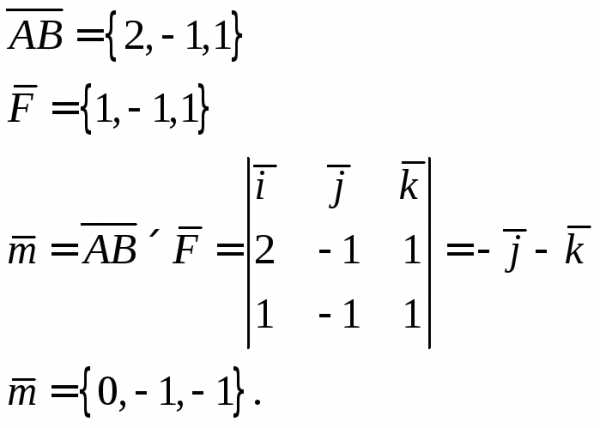
Пример 8.
Напомним формулу смешанного произведения трех векторов
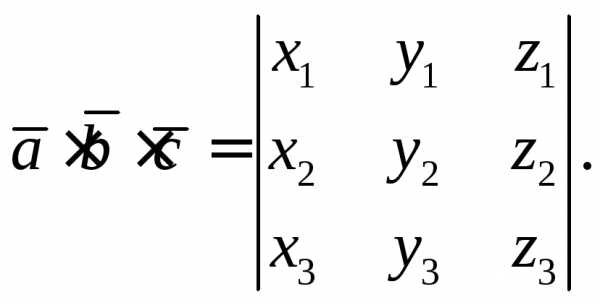
Известно, что
модуль смешанного произведения  равен объему параллелепипеда, построенного
на этих векторах.
равен объему параллелепипеда, построенного
на этих векторах.
Задача.
Найти длину высоты
пирамиды, опущенной из вершины  (рис. 2), если ее вершины
(рис. 2), если ее вершины
Решение.
рис. 2
Найдем векторы:
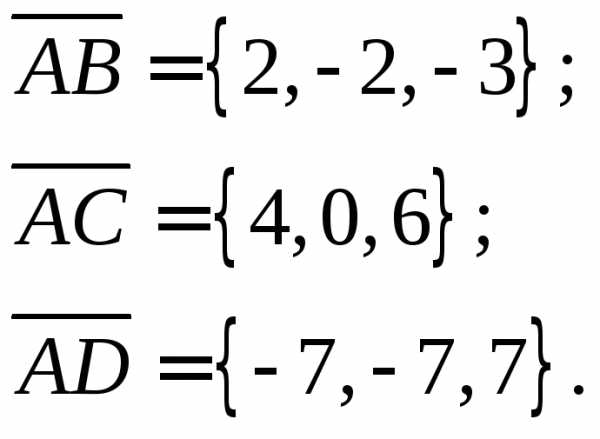
Объем пирамиды, построенной на векторах , равен одной шестой модуля смешанного произведения этих векторов.
, где 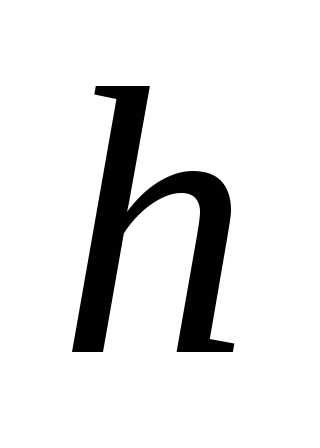 – высота пирамиды, а площадь прямоугольника,
построенного на векторах
– высота пирамиды, а площадь прямоугольника,
построенного на векторах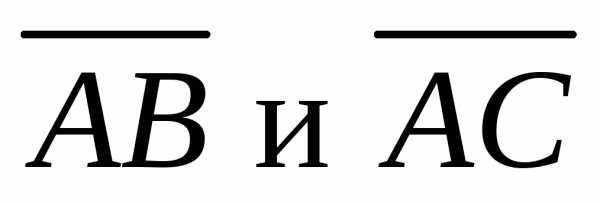 равна одной второй векторного произведения.
равна одной второй векторного произведения.
Вычислим смешанное произведение векторов
Отсюда  пирамиды
пирамиды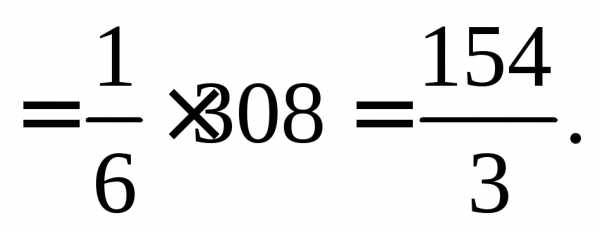
Вычислим векторное произведение векторов:
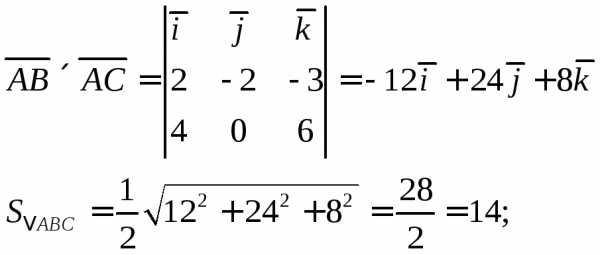
Найдем высоту пирамиды:
studfiles.net
3.2.4. Примеры решения задач по теме «Векторное и смешанное произведени
Задача 1.
Найти модуль вектора [A
Указание
Векторное произведение коллинеарных векторов равно нулю, поэтому
[A, а] = 0.
Операция векторного умножения некоммутативна,
[B, А] = — [A, B]
Решение
Используя свойства векторного произведения, получим:
[A – 3B, 2A + b] = 2[A, A] – 6[B, A] + [A, b] – 3[B, b] = 2·0 + 6[A, b] + [A, b] – 3·0 =
= 7[A, b].
Следовательно, |[A – 3B, 2A + b ]| = 7|[A, b]| = 7 |A| |B| sin φ = 7·6·7·0,5 =147.
Ответ: |[A – 3B, 2A + b]| = 147.
Задача 2.
Известно, что |A| = 2, |B| = 10 и |[A, B]| = 12. Найти скалярное произведение Ab.
Указание
Поскольку |[A, B]| = |A| |B| sin J, можно найти sin J, а затем с помощью основного тригонометрического тождества вычислить cos J.
Решение
Поскольку |[A, B]| = |A| |B| sin J, где J – угол между векторами A И B, получаем:
12 = 2·10·sin J, откуда sin J = 0,6. Тогда cos2J = 1 – sin2
Если угол между векторами A И B острый, то cos J = 0,8, и Ab = 2·10·0,8 = 16; если же этот угол тупой, то cos J = -0,8, и Ab = -16.
Ответ: Ab = +16.
Задача 3.
Найти координаты векторного произведения векторов A = {3; 2; 1} и
B = {-1; 1; -2}.
Указание
Воспользуйтесь формулами для координатной записи векторного произведения:
Решение
Ответ: [A,B] = {-5; 5; 5}.
Задача 4.
Даны точки А(1; -1; 2), В(5; -6; 2), С(1; 3; -1). Найти площадь треугольника АВС.
Указание
Рассмотрите векторы
Модуль векторного произведения [AB, AC] равен площади параллелограмма АВМС, построенного на них как на смежных сторонах, а площадь треугольника АВС равна половине площади АВМС.
Решение
Рассмотрим векторы
Модуль векторного произведения [AB, AC] равен площади параллелограмма АВМС, построенного на них как на смежных сторонах, а площадь треугольника АВС равна половине площади АВМС.
Рис. 7
Ответ: 12,5.
Задача 5.
Даны векторы A = {4; -1; 2} и B = {1; 1; -3}. Найти координаты векторного произведения [A – 4B, B].
Указание
Воспользуйтесь тем, что
Решение
Ответ: {1; 14; 5}.
Задача 6.
Даны векторы A = {2; -1; 1}, B = {3; 3; 4} и С = {2; 0; 2}. Найти координаты вектора D, если известно, что он перпендикулярен векторам A и B, а скалярное произведение Dc = -8.
Указание
Векторное произведение [A, B] перпендикулярно обоим сомножителям,
То есть [A, B] перпендикулярен А и B.
Решение
Векторное произведение [A, B] перпендикулярно обоим сомножителям,
То есть [A, B] перпендикулярен А и B.
Следовательно, вектор D || [A,B], поэтому координаты вектора D Пропорциональны координатам [A,B].
Пусть D = {-7K; -5K; 9K}, тогда Dc = -7K ·2 + 9K ·2 = 4K = -8.
Следовательно, K = -2, и D = {14; 10; -18}.
Ответ: D = {14; 10; -18}.
Задача 7.
Вычислить объем тетраэдра, вершины которого находятся в точках
А(2; 2; 2), В(3; 1; 5), С(0; 4; 3), D(5; 0; 7).
Указание
Модуль смешанного произведения векторов AB, AC, AD равен объему параллелепипеда, построенного на этих векторах как на смежных ребрах.
Решение
Модуль смешанного произведения векторов AB, AC, AD равен объему параллелепипеда, построенного на этих векторах как на смежных ребрах. У треугольной пирамиды ABCD высота равна высот параллелепипеда, а площадь основания вдвое меньше площади основания параллелепипеда. Поэтому

Рис. 8
Ответ: .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Тема 1.6.Применение векторов к решению задач
школьного курса геометрии
Литература: [1], § 10, стр. 32-34.
Основные сведения
Векторная алгебра может быть весьма успешно использована при решении широкого класса содержательных геометрических (аффинных и метрических) задач. Аффинные задачи характеризуются тем, что все участвующие в них объекты и отношения определяются отношением отрезков, площадей, параллельностью. В метрических же задачах – длинами отрезков, величинами углов.
Как правило, векторное решение геометрической задачи позволяет автоматически, или после несложного анализа полученных формул и уравнений, сделать интересные обобщения доказываемых геометрических фактов.
Алгоритм применения векторов при решении геометрических задач состоит из следующих этапов:
Выясняем, является ли рассматриваемая задача аффинной или же метрической.
Если задача аффинная, то, как правило, выбираем произвольный базис или вводим в рассмотрение наименьшее количество векторов, через которые можно выразить все интересующие нас векторы. Если же задача метрическая, то выбираем ортонормированный базис.
Все, что дано в задаче, записываем с помощью векторов.
Все, что необходимо найти или доказать, записываем с помощью векторов.
С помощью алгебраических преобразований из того, что дано, получаем, что необходимо.
Из приведенного алгоритма видно, что если задачу можно перевести на язык векторов, то она решается с помощью векторов. И для успешного использования векторной алгебры к решению геометрических задач необходимо уметь переводить геометрические факты на язык векторов или на язык координат.
Ниже, в таблице, приведены часто встречающиеся примеры.
На языке геометрических фактов | На языке векторов | На языке координат векторов |
Прямые а и b параллельны. | Векторы | Координаты
векторов
и |
Точки А,В и С лежат на одной прямой. | Координаты
векторов
и | |
Точка С лежит между точками А и В. | | Координаты
векторов
и |
Точки А и В симметричны относительно точки 0. | | Соответствующие
координаты векторов |
Угол между прямыми а и в:
|
|
Задание: Для ускорения усвоения этого метода рекомендуем после решения каждой из рассматриваемых задач продумать, какая информация, чем была заменена в процессе работы, и продолжить заполнение таблицы.
Пример 1. Доказать, что медианы треугольника пересекаются в одной точке (центре тяжести треугольника) и делятся ею в отношении 2:1, считая от вершины.
Решение. Пусть
медианыAD
и BE
пересекаются в точке О. Докажем, что
третья медиана СМ тоже проходит через
точку О. Из приведенной выше таблицы
видно, что это все равно, что доказать
коллинеарность векторов  и
и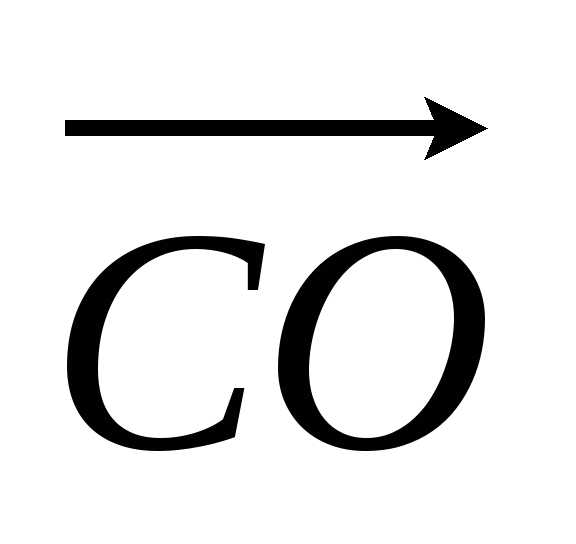 .
Эта задача аффинная.
.
Эта задача аффинная.
Пусть  =
=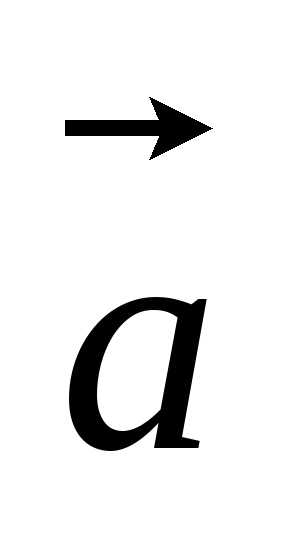 ,
,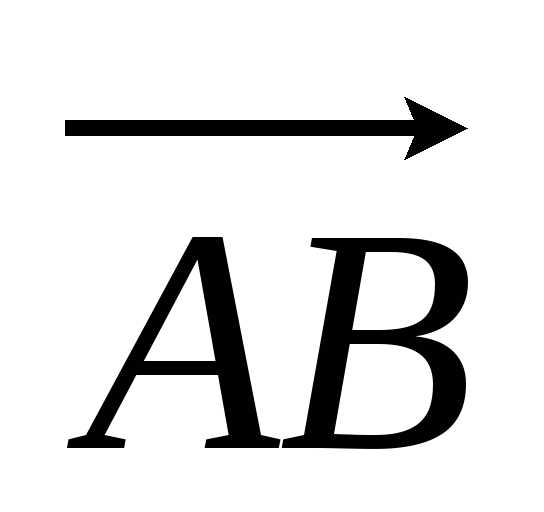 =
=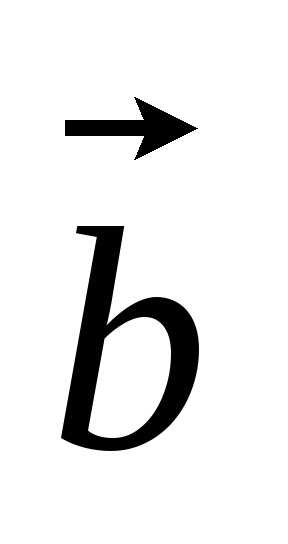 .
Замечаем, что векторы
.
Замечаем, что векторы 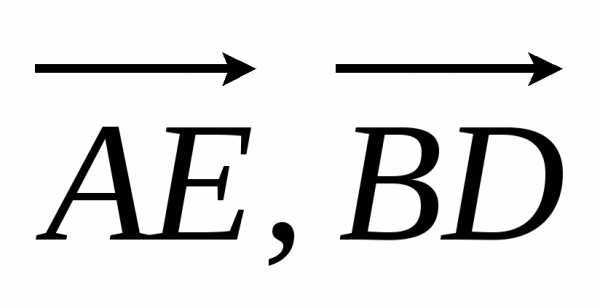 и
и  можно выразить через векторы
можно выразить через векторы и
и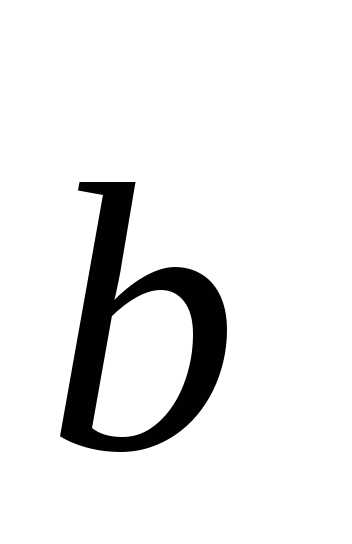 :
:
.
.
.
Так
как 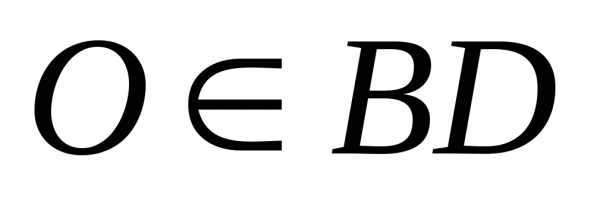 ,
то,
,
то,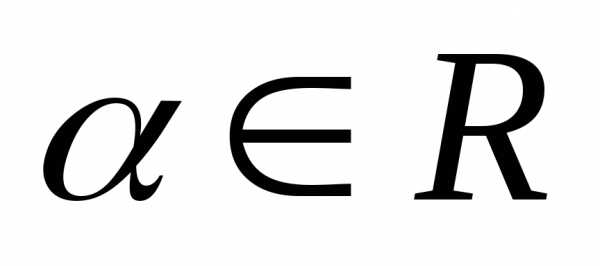 .
.
Аналогично,  ,
поэтому:
,
поэтому:
, 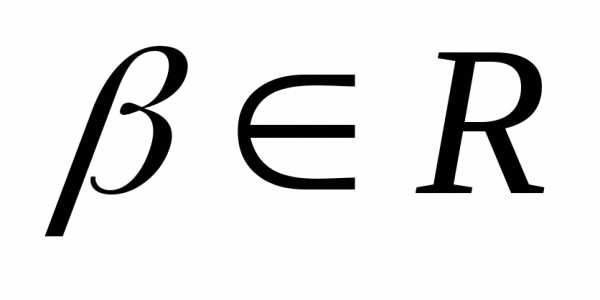 .
.
Найдем
вектор 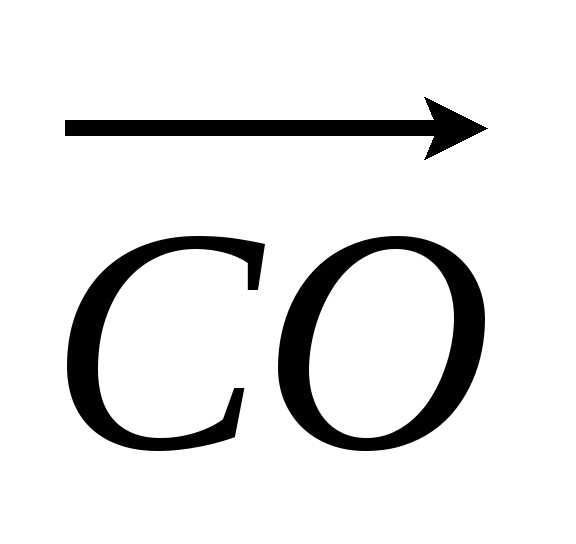 .
С одной стороны:
.
С одной стороны:
.
С другой стороны:
.
Значит, .
Так
как векторы  и
и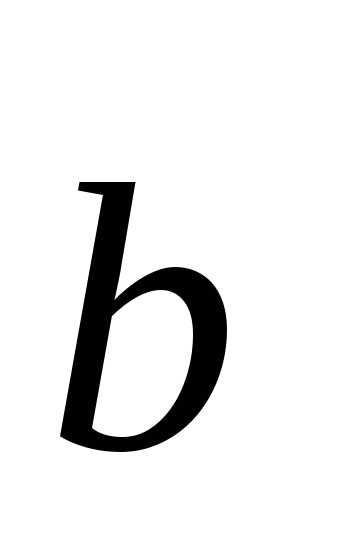 линейно независимы, то отсюда:
линейно независимы, то отсюда:
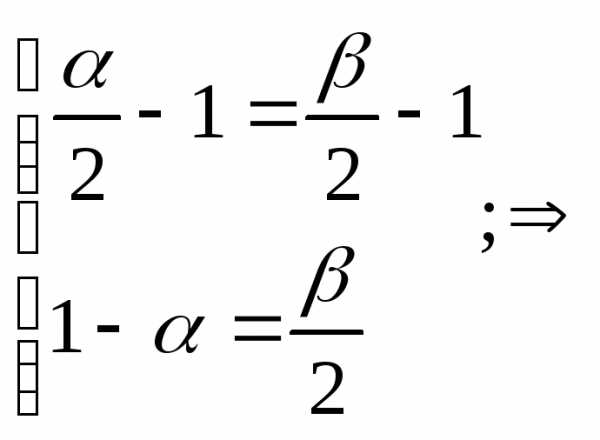
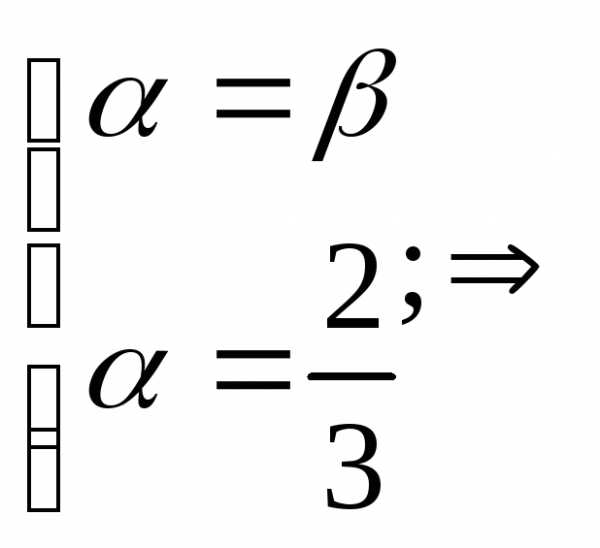
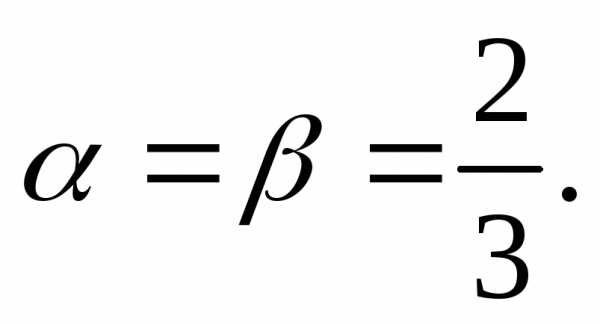
Значит, 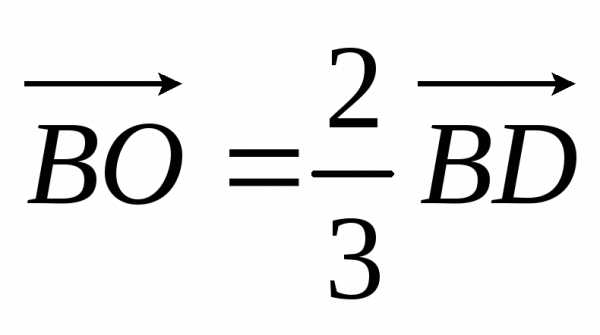 ,
,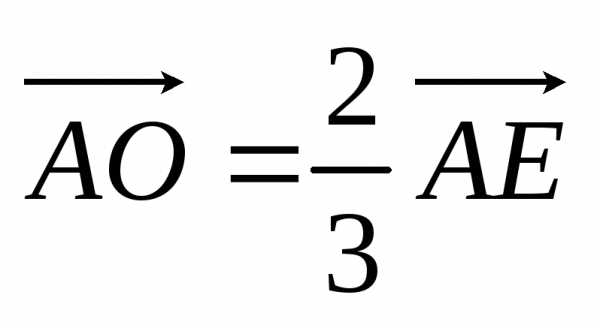 ,
,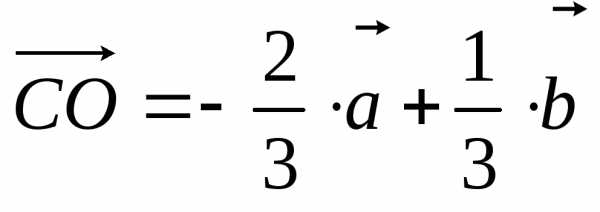 .
.
Сравнив
векторы 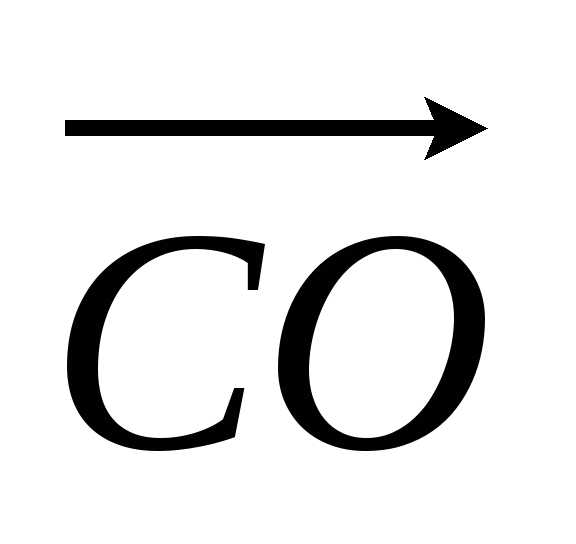 и
и ,
заключаем:
,
заключаем: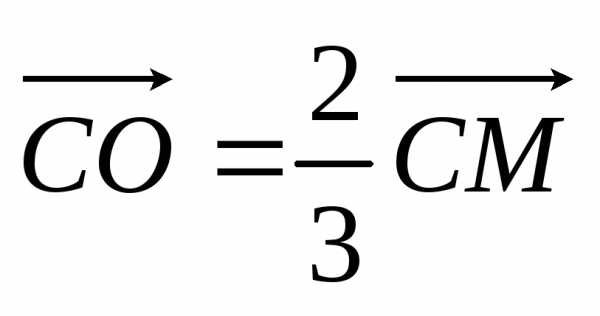 .
.
Следовательно, третья часть медианы СМ тоже проходит через точку О.
Пример 2. Доказать, что прямые, содержащие высотытреугольника пересекаются в одной точке.
Решение.Пусть
высоты АD
и ВН пересекаются в точке О. Обозначим 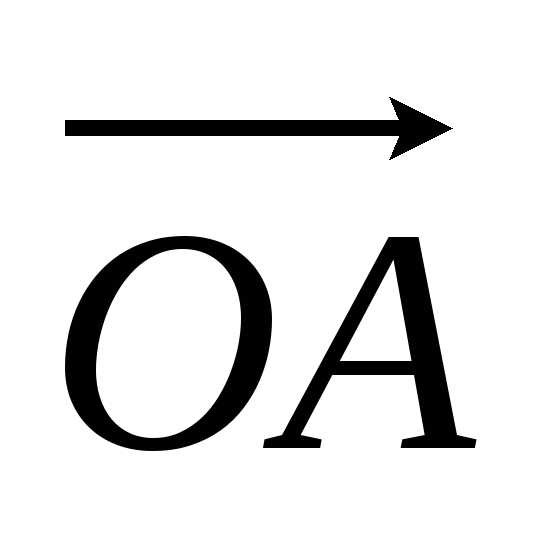
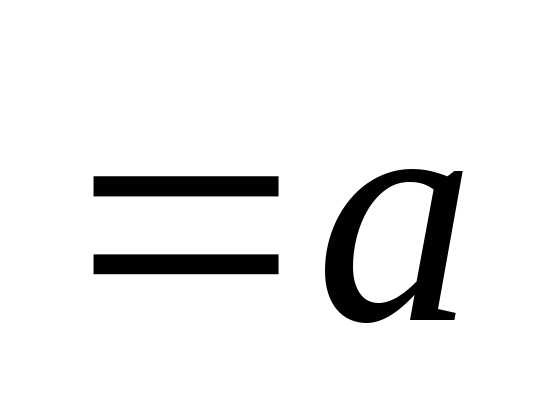 ,
, 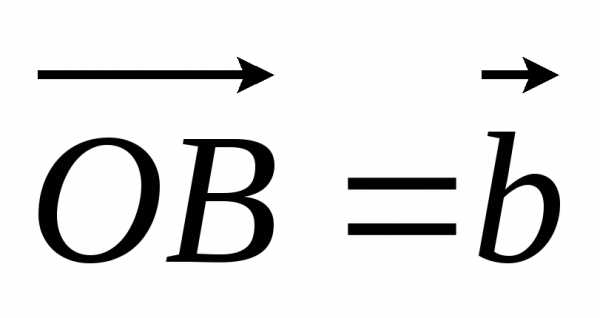 ,
,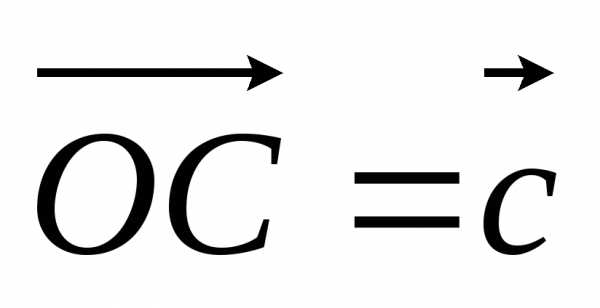 .Тогда
,,.
.Тогда
,,.
, то есть, . , т.е..
Вычтя из первого подчеркнутого равенства второе, получим , т.е.или. Следовательно,. Значит, и третья высота треугольника проходит так же через точку О.
Задачи
С помощью векторов докажите следующие утверждения: а) если диагонали четырехугольника в точке пересечения делятся пополам, то этот четырехугольник – параллелограмм; б) сумма квадратов длин диагоналей параллелограмма равна сумме квадратов всех его сторон; в) диагонали ромба взаимно перпендикулярны; г) средняя линия треугольника параллельна основанию и длина ее равна половине длины основания.
Доказать, что в треугольнике ABC угол ABC прямой тогда и только тогда, когда AC2=AB2+BC2.
Доказать, что сумма квадратов длин диагоналей трапеции равна сумме квадратов длин ее непараллельных сторон, сложенной с удвоенным произведением длин оснований.
В кубе найти величину угла: а) между диагональю и скрещивающейся с ней диагональю грани; б) между скрещивающимися диагоналями соседних граней; в) между диагональю куба и пересекающейся с ней диагональю грани.
Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей и учетверенного квадрата расстояния между серединами этих диагоналей (теорема Эйлера).
Доказать, что в правильном тетраэдре противоположные ребра взаимно перпендикулярны.
Доказать, что в четырехугольнике ABCD имеет место равенство: , гдеM, N –соответственно середины сторон AD и BC. Пользуясь этим равенством, докажите, что средняя линия трапеции параллельна основаниям и равна их половине.
studfiles.net
| 1. |
Выражение вектора в треугольнике (1)
Сложность: лёгкое |
1 |
| 2. |
Выражение вектора в параллелограмме (1)
Сложность: лёгкое |
1 |
| 3. |
Выражение вектора в треугольнике (2)
Сложность: среднее |
1 |
| 4. |
Выражение вектора в параллелограмме (2)
Сложность: среднее |
1 |
| 5. |
Вопросы о проекции вектора
Сложность: среднее |
1 |
| 6. |
Проекция вектора
Сложность: среднее |
2 |
| 7. |
Проекция вектора силы
Сложность: среднее |
2 |
| 8. |
Векторы в задаче на движение
Сложность: сложное |
4 |
www.yaklass.ru

 и
и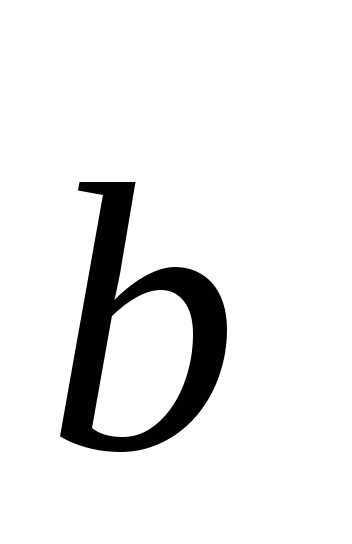 коллинеарны или
коллинеарны или =t
=t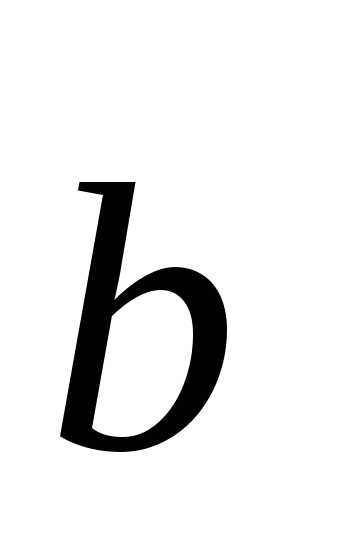 (здесь
(здесь и
и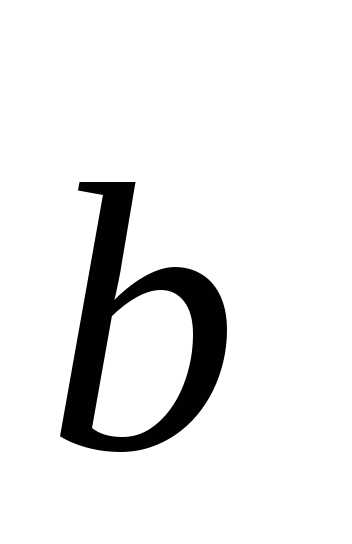 — направляющие векторы прямых а иb
соответственно)
— направляющие векторы прямых а иb
соответственно)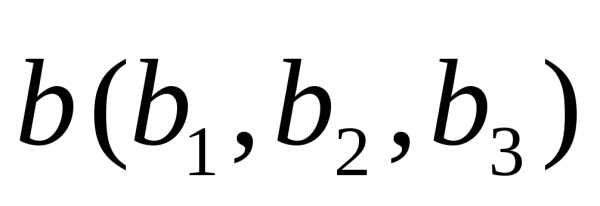 пропорциональны, т.е.
пропорциональны, т.е.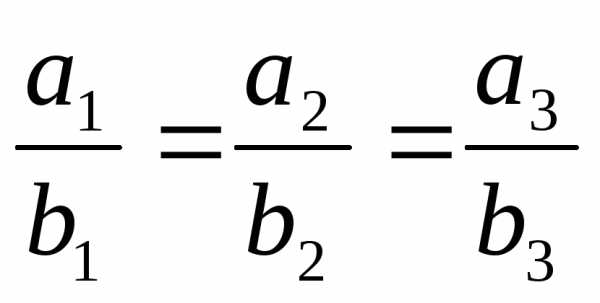 .
.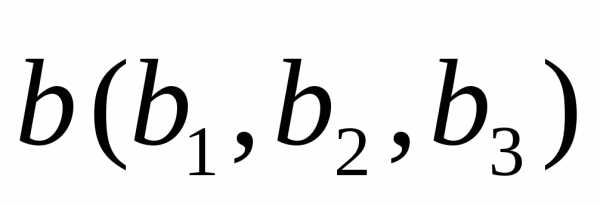 пропорциональны, т.е.
пропорциональны, т.е.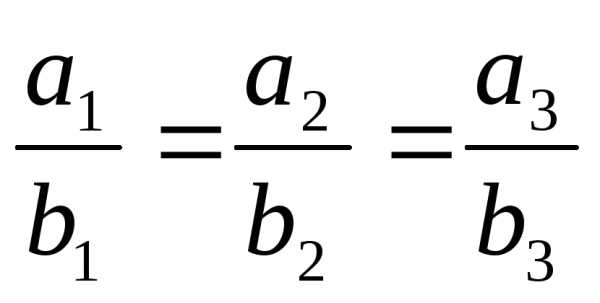 .
.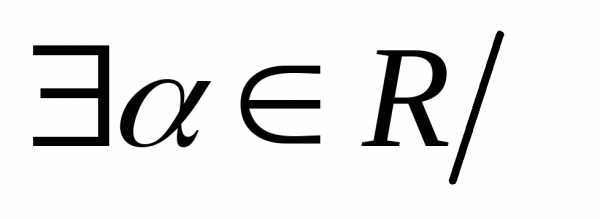 ,
, 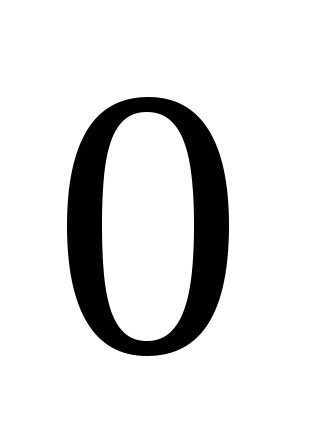 <
< <
<
 пропорциональны, т.е.
пропорциональны, т.е.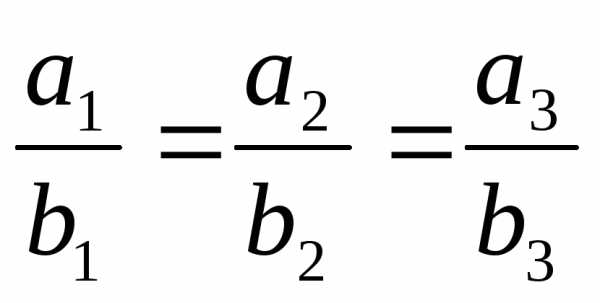 .
. или
или 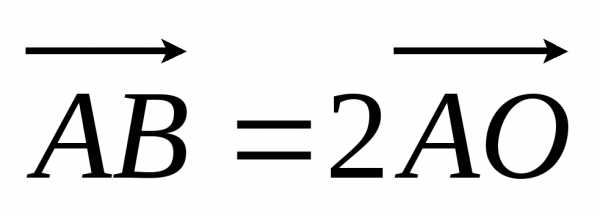
 и
и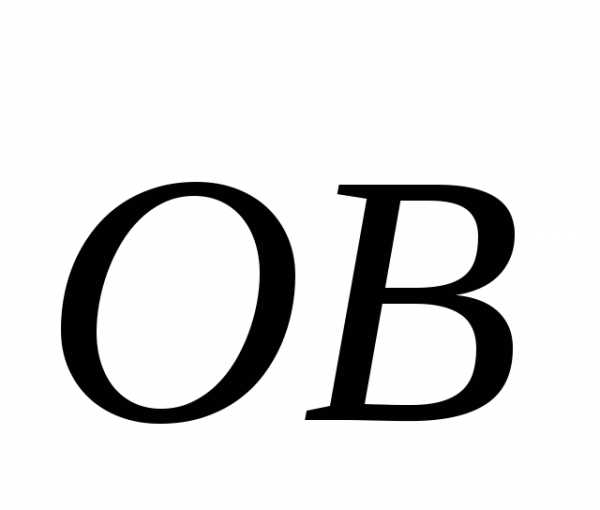 равны.
равны.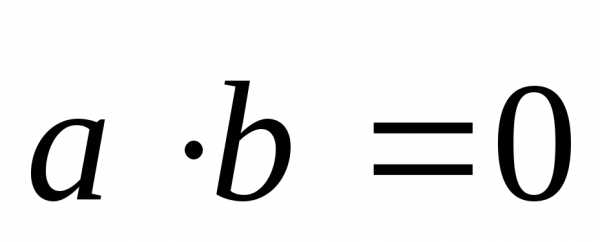 ;
;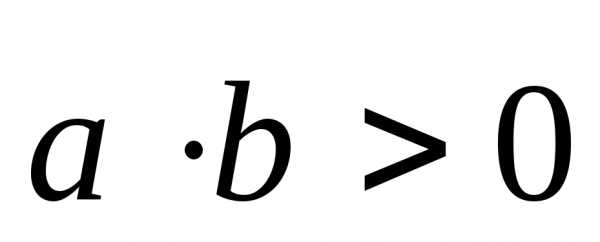 ;
;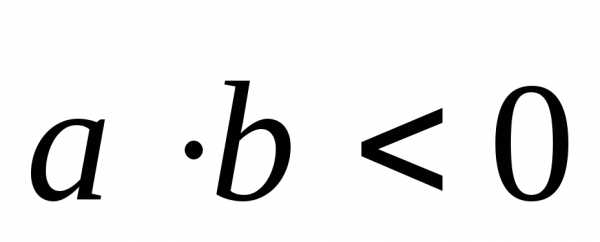 ;
;