В-1.1 1) -92; 2) 100; 3) 30; 4) 49; 5) -18; 6) 62; 7) -77; 8) 5; 9) 0; 10) -38; 11) -88; 12) 0. | В -1.2 1) 0; 2) 64; 3) 0; 4) -84; 5) 72; 6) -35; 7) 100; 8) -38; 9) 1; 10) 80; 11) -20; 12) -90. | В-1.3 1) 5; 2) 62; 3) 35; 4) -82; 5) 100; 6) 0; 7) 0; 8) -22; 9) -16; 10) -98; 11) 14; 12) -52. | В-1.4 1) 2; 2) 0; 3) 10; 4) -3; 5) -24; 6) 80; 7) -48; 8) 78; 9) -65; 10) -94; 11) 100; 12) 0. | В -1.5. 1) 64; 2) 100; 3) 5; 4) -98; 5) 0; 6) 58; 7) -63; 8) -36; 9) 0; 10) -32; 11) -24; 12) 96. | В-1.6 1) 5; 2) -56; 3) 10; 4) -92; 5) -42; 6) 72; 7) 0; 8) -11; 9) 68; 10) 100; 11) -38; 12) 0. | В-1.7 1) 0; 2) -19; 3) 86; 4) -66; 5) 6; 6) 52; 7) -74; 8) 100; 9) -30; 10) -84; 11) 42; 12) 0. | В- 1.8 1) 0; 2) 34; 3) -42; 4) 0; 5) 32; 6) 56; 7) -24; 8) -94; 9) 100; 10) 2; 11) -58; 12) -72. | В-1.9 1) 0; 2) 34; 3) -42; 4) 0; 5) 32; 6) 56; 7) -24; 8) -94; 9) 100; 10) 2; 11) -58; 12) -72. | В-1.10. 1) 4; 2) 98; 3) 100; 4) -96; 5) 0; 6) 0; 7) -64; 8) 38; 9) -33; 10) -66; 11) 78; 12) -24. | В-1.11 1) 0; 2) 8; 3) 83; 4) -71; 5) -37; 6) 42; 7) 100; 8) 0; 9) -48; 10) -39; 11) -88; 12) 92. | В-1.12 1) 0; 2) 8; 3) 83; 4) -71; 5) -37; 6) 42; 7) 100; 8) 0; 9) -48; 10) -39; 11) -88; 12) 92. | В-1.13 1) 54; 2) -97; 3) 0; 4) 3; 5) -98; 6) 25; 7) 0; 8) -46; 9) 100; 10) -41; 11) -84; 12) 26. | В-1.14. 1) -90; 2) 0; 3) -36; 4) 3; 5) -74; 6) 66; 7) -11; 8) 0; 9) 100; 10) -32; 11) 22; 12) 77. | В -1.15. 1) -29; 2) 0; 3) 86; 4) 49; 5) -32; 6) 0; 7) -92; 8) -27; 9) 100; 10) 50; 11) -68; 12) 3. | В-1.16. 1) -25; 2) -37; 3) 76; 4) 0; 5) 32; 6) -24; 7) 0; 8) -92; 9) 6; 10) -63; 11) 45; 12) 100. | В-1.10. 1) 54; 2) -86; 3) 100; 4) -64; 5) 1; 6) 27; 7) 34; 8) 0; 9) 0; 10) -37; 11) -26; 12) -39. | В-1.18. 1) 58; 2) 85; 3) 100; 4) 52; 5) 6; 6) 0; 7) -30; 8) 0; 9) -52; 10) -14; 11) -82; 12) -26. | В-1 .19. 1) 86; 2) 42; 3) -37; 4) 100; 5) -57; 6) -86; 7) 0; 8) -51; 9) 46; 10) 5; 11) 0; 12) -58 | В-1.20. 1) 100; 2) 30; 3) 25; 4) -69; 5) 78; 6) -55; 7) 7; 8) -94; 9) -88; 10) 0; 11) -45; 12) 0. | В-1.21. 1) 52,92; 2) -12,6; 3) 60; 4) 9,8; 5) 3; 6) 0; 7) -3,6; 8) -101,41; 9) -8,8; 10) -49,74; 11) 79,23; 12) 69,55. | В-1.22. 1) -125,7; 2) -23,42; 3) 4; 4) 5,95; 5) 28,9; 6) -20,3; 7) 97,41; 8) 0; 9) 13,92; 10) -137,68; 11) 50; 12) -10,2. | В-1.23. 1) -7,3; 2) 32,4; 3) -18,8; 4) -142,35; 5) -103,2; 6) 0; 7) 10,95; 8) 5,73; 9) 50; 10) 97,14; 11) 7; 12) -25,7. | В-1.24. 1) -106,2; 2) -65,18; 3) 80; 4) -12,58; 5) 3,48; 6) -2,1; 7) -47,6; 8) 3,9; 9) 99; 10) 77,71; 11) 0; 12) 85,99. | В-1.25. 1) -19,3; 2) 47,17; 3) 107,95; 4) -75,68; 5) 5,9; 6) -8,02; 7) -22,4; 8) 9; 9) 20; 10) 0; 11) -4,4; 12) 1,55. | В-1.26. 1) 30; 2) -26,7; 3) -24,72; 4) 6,52; 5) -10,4; 6) 9; 7) -288,1; 8) -77,38; 9) 0; 10) 5,83; 11) 4,41; 12) 21,3. | В-1.27. 1) 30; 2) -26,7; 3) -24,72; 4) 6,52; 5) -10,4; 6) 9; 7) -288,1; 8) -77,38; 9) 0; 10) 5,83; 11) 4,41; 12) 21,3. | В-1.28. 1) 60; 2) -62,6; 3) 96; 4) 3,83; 5) -53,36; 6) 7,09; 7) 12,54; 8) -122,8; 9) 67,3; 10) 0; 11) -3,4; 12) -166,18. | В-1.29. 1) 3; 2) -6,4; 3) 5,26; 4) -155,6; 5) -23,34; 6) -27,9; 7) 4,87; 8) 80; 9) 0; 10) 96,79; 11) 28,6; 12) -66,12. | В-1.30. 1) 63,1; 2) 0; 3) 95,93; 4) -152,4; 5) -14,8; 6) -71,1; 7) 3,82; 8) 40; 9) -94,37; 10) 8,94; 11) 4; 12) -13,7. |
infourok.ru
Вычитание. Видеоурок. Математика 6 Класс
Мы знаем, что с помощью знака равенства разными способами записываются эквивалентные выражения.
Например, (действительно, если на складе лежало мячей и мячей оттуда забрали, то на складе ничего не осталось).
С другой стороны, (действительно, мы определяли противоположное число так, что ). Как видим, , то есть вычитание равносильно сложению с противоположным числом: .
Но тогда для вычитания мы можем пользоваться уже известными нам правилами сложения с одинаковыми или разными знаками.
Рассмотрим примеры.
1.
Но эту же разность, , еще можно считать суммой двух чисел и : . Так как знаки разные, надо от большего модуля отнять меньший и поставить знак числа с большим модулем, в данном случае – плюс.
2.
Эту разность можно считать суммой двух отрицательных чисел: . Так как знаки одинаковые, то складываем модули и ставим знак минус: .
3.
Это сумма положительного числа и отрицательного : . От большего модуля отнимаем меньший и ставим знак числа с большим модулем, то есть минус: .
Получается, нам не нужны новые правила, чтобы вычитать из одного числа другое. Достаточно знать правила сложения чисел с разными знаками.
1.
Оба слагаемых одного знака. Складываем модули, ставим знак минус: .
2.
Слагаемые разных знаков. Нужно от большего модуля отнять меньший и поставить впереди знак числа с большим модулем. То есть знак минус: 3.
Вычитание числа можно заменить прибавлением противоположного числа . Или, если короче, два минуса перед числом дают плюс: .
4.
Выполняем действие в скобках, результат будет отрицательным. Два минуса перед числом дают плюс. Слагаемые имеют разные знаки, значит, вычитаем из большего модуля меньший, ставим знак плюс в ответе:
по-другому. Знак минус перед скобкой относится к каждому слагаемому в скобках, то есть меняет его знак. Раскрываем скобки, меняя знак каждого слагаемого. Первое и последнее слагаемые легко складываются. Они разных знаков, вычитаем из большего модуля меньший. Ответ тот же самый:
Расстояние между точками на координатной прямой
Рассмотрим такой пример. Найдём расстояние между точками, соответствующими числам и на координатной прямой. Несложно увидеть, что оно равно : (рис. 1).
Рис. 1. Расстояние между данными точками
То есть чтобы найти расстояние между точками на числовой прямой, совсем не обязательно строить координатную прямую, отмечать точки. Нужно просто из большего числа вычесть меньшее.
Убедимся, что это правило верно независимо от того, какой знак у чисел, соответствующих этим точкам. Найдем расстояние между точками, координаты которых – числа с разными знаками, например, между и . Расстояние от до равно сумме расстояний от этих чисел до нуля. Но получается, для вычисления расстояния мы используем третье число , которого не было в условии (рис. 2).
Рис. 2. Расстояние между точками и
Это не очень удобно. Давайте попробуем обойтись только теми числами, которые есть в условии задачи. Пользуясь тем, что прибавление числа эквивалентно вычитанию противоположного (или, коротко, два минуса подряд дают плюс), мы можем переписать нашу сумму: .
Здесь уже участвуют только те два числа, что были в условии. Но это снова разность двух чисел: из большего мы вычитаем меньшее. То есть чтобы найти расстояние между двумя числами с разными знаками, нужно из большего (положительного) вычесть меньшее (отрицательное).
Нам осталось рассмотреть последний случай: расстояние между точками, координаты которых – отрицательные числа. Найдем расстояние между Расстояние от нуля до равно , до равно . Чтобы найти расстояние между точками, нужно из вычесть : . Мы снова использовали числа, которых не было в условии (рис. 3).
Рис. 3. Расстояние между числами и
Сделаем эквивалентную замену: .
У нас получилась разность двух исходных чисел. Причем первое число () больше второго (). То есть чтобы найти расстояние между отрицательными числами, нужно из большего вычесть меньшее.То есть во всех трех случаях получилось одно и то же правило. Давайте его еще раз повторим: чтобы найти расстояние между двумя точками на числовой прямой, нужно из большей координаты вычесть меньшую: – расстояние между и .
Если мы не знаем, какое число больше, а какое меньше ( или ), то мы не можем записать просто или , ведь так мы можем получить отрицательное значение расстояния.
Чем отличаются эти два выражения? Только знаком. Например, и . Действительно: То есть эти разности – противоположные числа, а значит, их модули равны. Таким образом, мы можем сказать коротко: расстояние между точками на координатной прямой равно модулю разности их координат: .
Давайте потренируемся. Без построения числовой прямой найти расстояние между двумя числами.
1. и
Из большего числа вычитаем меньшее. Из двух отрицательных чисел больше то число, модуль которого меньше:
2. и
Из большего числа вычитаем меньшее. Положительное число всегда больше отрицательного:
interneturok.ru
Отрицательные числа
Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.
Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).
Например, −10 градусов холода:
Обычные же числа, которые мы рассматривали ранее, такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).
При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.
Координатная прямая
Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:
Здесь показаны числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.
Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.
Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом ∞. Отрицательное направление будет обозначаться символом −∞, а положительное символом +∞. Тогда можно сказать, что на координатной прямой располагаются все числа от минус бесконечности до плюс бесконечности:
(−∞; +∞)
Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.
Например, точка А(2) читается как «точка А с координатой 2» и будет обозначаться на координатной прямой следующим образом:
Здесь A — это имя точки, 2 — координата точки A.
Пример 2. Точка B(4) читается как «точка B с координатой 4» и будет обозначаться на координатной прямой так:
Здесь B — это имя точки, 4 — координата точки B.
Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:
Здесь M — это имя точки, −3 — координата точки M .
Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O
Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.
Существуют такие словосочетания, как «чем левее, тем меньше» и «чем правее, тем больше». Наверное, вы уже догадались о чём идёт речь. При каждом шаге влево, число будет уменьшаться в меньшую сторону. И при каждом шаге вправо число будет увеличиваться. Стрелка, направленная вправо, указывает на положительное направление отсчёта.
Сравнение отрицательных и положительных чисел
Правило 1. Любое отрицательное число меньше любого положительного числа.
Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.
Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3
Видно, что −5 лежит левее, а 3 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что любое отрицательное число меньше любого положительного числа. Отсюда следует, что
−5 < 3
«Минус пять меньше, чем три»
Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.
Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.
Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1
Видно, что −4 лежит левее, а −1 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Отсюда следует, что
−4 < −1
Минус четыре меньше, чем минус единица
Правило 3. Ноль больше любого отрицательного числа.
Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3
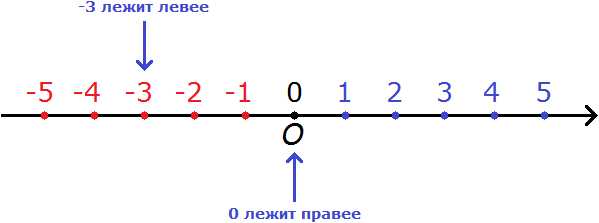
Видно, что 0 лежит правее, а −3 левее. А мы говорили, что «чем правее, тем больше». И правило говорит, что ноль больше любого отрицательного числа. Отсюда следует, что
0 > −3
Ноль больше, чем минус три
Правило 4. Ноль меньше любого положительного числа.
Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:

Видно, что на координатной прямой 0 располагается левее, а 4 правее. А мы говорили, что «чем левее, тем меньше». И правило говорит, что ноль меньше любого положительного числа. Отсюда следует, что
0 < 4
Ноль меньше, чем четыре
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Математика 6 класс. Тест на сложение и вычитание отрицательных чисел
Действия с отрицательными числами (наравне с линейными уравнениями) — наиболее важная тема из всех изучаемых в курсе математики за 6 класс. Более того, если ученик, штурмующий высоты ЕГЭ, путается в элементарных арифметических действиях на первом же занятии с репетитором — неудовлетворительный результат на экзамене можно исключить только при гигантском объеме занятий в течение года. Поэтому крайне важно не запускать математику на самых ранних этапах. Решайте с Вашим ребенком тематические тесты с моего сайта. Они позволят в некотором приближении распознать зарождающиеся проблемы.
Я хочу отправить результаты на почту Меня зовут
и я хочу отправить свои результаты
на e-mail
В приведенном тесте проверяются только навыки сложения и вычитания целых чисел и десятичных дробей. При необходимости репетитору по математике легко составить подобные упражнения с обыкновенными дробями, увеличив количество действий в одном примере до трёх — четырёх. Далее можно усложнять номера различными комбинациями видов дробей (обыкновенная с десятичной дробью в одном примере), а также вовлекая в процесс следующие действия: умножение и деление.
Хочу особо подчеркнуть, что без основных арифметических навыков изучение алгебры невозможно. Грамотный репетитор по математике не станет форсировать события материалами старшей школы, пока не приведет в порядок азы арифметики. Если ко мне для подготовки к ЕГЭ в 10-11 классе приходит нулевой ученик, то чаще всего я начинаю работу с числовых операций, выражений. Этот процесс нельзя вести параллельно с изучением производных, логарифмов и синусов с косинусами. Такие попытки, как правило, обречены на неудачу. Более того, после стратегических ошибок репетитора дети перестают верить в свои способности и начинают еще больше ненавидеть математику.
С уважением, Колпаков Александр. Занятия в Строгино по авторским материалам.
ankolpakov.ru
В-1 1) 0; 2) -84; 3) -58; 4) 4; 5) 18; 6) -90; 7) -19; 8) -16; 9) 56; 10) -78; 11) -55; 12) 0. | В-2. 1) 0; 2) -57; 3) 0; 4) -48; 5) 5; 6) -92; 7) -68; 8) -46; 9) 40; 10) -66; 11) -75; 12) 24. | В-3 1) 0; 2) -22; 3) 0; 4) -93; 5) -68; 6) 97; 7) -87; 8) -70; 9) -61; 10) 12; 11) -28; 12) 2. | В-4. 1) 3; 2) 0; 3) -62; 4) 0; 5) -42; 6) -94; 7) -42; 8) 14; 9) 61; 10) -33; 11) -73; 12) -60 | В-5. .1) -51; 2) 11; 3) -87; 4) 73; 5) -73; 6) 2; 7) -95; 8) -96; 9) -38; 10) -52; 11) 0; 12) 0. | В-6. 1) 0; 2) -14; 3) -78; 4) -95; 5) 0; 6) -44; 7) 7; 8) -53; 9) 19; 10) -47; 11) -29; 12) 11. | В-7. 1) 0; 2) -61; 3) 0; 4) -86; 5) 98; 6) -13; 7) -35; 8) 3; 9) -42; 10) 15; 11) -69; 12) -99. | В-8 1) 0; 2) -7; 3) -98; 4) -84; 5) 48; 6) -58; 7) -27; 8) -99; 9) 4; 10) 68; 11) -60; 12) 0. | В-9 1) 0; 2) -78; 3) 57; 4) 16; 5) -57; 6) -49; 7) -51; 8) 3; 9) 0; 10) -58; 11) -43; 12) -57. | В-10. .1) -99; 2) 4; 3) -33; 4) 0; 5) 34; 6) 0; 7) -85; 8) -87; 9) 27; 10) -21; 11) -35; 12) -42. | В-11 1) -59; 2) -17; 3) 7; 4) 91; 5) 44; 6) 0; 7) -78; 8) 0; 9) -28; 10) -79; 11) -19; 12) -99 | В-12 1) -83; 2) 13; 3) 0; 4) 0; 5) -48; 6) -71; 7) -64; 8) -99; 9) 2; 10) -42; 11) 64; 12) -47. | В-13 1) 0; 2) -85; 3) 23; 4) -65; 5) -65; 6) -95; 7) -99; 8) 5; 9) -46; 10) -68; 11) 0; 12) 45. | В-14 1) -55; 2) 0; 3) -65; 4) 52; 5) -49; 6) -44; 7) 0; 8) 4; 9) -72; 10) 11; 11) -63; 12) -89. | В-15 1) -64; 2) -86; 3) 51; 4) -63; 5) 0; 6) -59; 7) 3; 8) -96; 9) -91; 10) 15; 11) 0; 12) -41. | В-16 1) -88; 2) -89; 3) 0; 4) 0; 5) -45; 6) -83; 7) 2; 8) 15; 9) -13; 10) 69; 11) -40; 12) -64. | В-17 1) 11; 2) -4; 3) 0; 4) 36; 5) -70; 6) -58; 7) 3; 8) 0; 9) -88; 10) -32; 11) -99; 12) -35 | В-18. 1) -83; 2) 87; 3) 0; 4) -56; 5) -99; 6) 0; 7) -79; 8) -57; 9) 16; 10) -68; 11) -88; 12) 5 | В-19. 1) 2; 2) -47; 3) -96; 4) -26; 5) 63; 6) 0; 7) 0; 8) -64; 9) -51; 10) -85; 11) 24; 12) -35 | В-20. 1) -53; 2) -77; 3) -50; 4) -29; 5) 11; 6) 79; 7) -27; 8) 0; 9) -93; 10) 4; 11) 0; 12) -80 | В-21 1) 24,3; 2) -6,9; 3) 61,86; 4) -90,8; 5) -3; 6) -165; 7) -13,57; 8) -25,99; 9) -15,9; 10) -27; 11) 0,15; 12) -0,56. | В-22 1) -68,6; 2) -4; 3) 101,91; 4) 550; 5) -0,21; 6) -101,4; 7) 9,75; 8) -1,98; 9) -20; 10) 30,2; 11) -10,2; 12) -90,72. | В-23 1) -12; 2) -104,25; 3) 29,3; 4) 18,3; 5) 0,65; 6) -38,45; 7) 88,03; 8) -4; 9) -25,5; 10) -18,2; 11) -0,48; 12) -114. | В-24 1) -92,5; 2) -95,01; 3) 124,2; 4) 4,85; 5) -16,18; 6) -4; 7) -6; 8) -1,97; 9) 97,61; 10) -32,9; 11) -0,36; 12) 25,2. | В-25 1) 8,62; 2) -90,9; 3) 50,62; 4) -0,28; 5) -3; 6) -10,56; 7) -27,5; 8) -2; 9) -14,91; 10) 8,3; 11) -55; 12) 6,3. | В-26 1) -126,16; 2) 10,92; 3) -18; 4) 0,45; 5) -96; 6) -1,4; 7) -0,09; 8) -32,5; 9) 4,6; 10) 40,2; 11) -88,34; 12) -42,1. | В -27 1) 12,2; 2) 0,18; 3) -15,3; 4) 26,78; 5) -71; 6) -59,88; 7) -0,32; 8) -35,4; 9) -48; 10) -8; 11) -107,48; 12) -15,9. | В-28 1) -0,6; 2) 74,19; 3) 88,6; 4) 4,42; 5) -18; 6) -88; 7) -7,58; 8) 2,58; 9) -0,18; 10) -102,55; 11) 20,2; 12) -260. | В-29 1) -205; 2) 14,64; 3) -0,72; 4) 410; 5) -19,2; 6) 32,4; 7) -94,04; 8) -15; 9) -15,3; 10) -120,12; 11) 0,85; 12) 5,5. | В-30 .1) -149,49; 2) 37,48; 3) 96; 4) 13,43; 5) 0,32; 6) -0,24; 7) -14; 8) -480; 9) -7,5; 10) 56,4; 11) -6,4; 12) -77,08. |
infourok.ru
Сложение и вычитание целых чисел
В этом уроке мы изучим сложение и вычитание целых чисел, а также правила для их сложения и вычитания.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
−3, −2, −1, 0, 1, 2, 3
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой. Как показывает практика, ошибки сделанные из-за отрицательных чисел, расстраивают обучающихся больше всего.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться, это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа, и где положительные.
Рассмотрим простейшее выражение: 1 + 3. Значение данного выражения равно 4:
1 + 3 = 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3.
Значение данного выражения равно −2
1 − 3 = −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Вообще, надо запомнить, что если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
−2 + 4 = 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2.
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Знак плюса в выражении −2 + 4 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
−1 − 3 = −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Знак минуса в выражении −1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
−2 + 2 = 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Знак плюса в выражении −2 + 2 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Удобнее воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками. −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
−2 + 5 = 5 − 2 = 3
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3+−2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа модуль, которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
3 − 7 = 7 − 3 = −4
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:

После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
5 − 3 = 2
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
5 + (−3)
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
(+3) − (+1)
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) вычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
(+3) − (+1) = (+3) + (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
(+3) − (+7)
Заменим вычитание сложением:
(+3) − (+7) = (+3) + (−7)
Дальнейшее вычисление не составляет труда:
(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
(−4) − (+5)
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
(−4) − (+5) = (−4) + (−5)
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
−4 − 5 = −(4 + 5) = −9
или ещё короче:
−4 − 5 = −9
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
(−3) − (+5) − (+7) − (+9)
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
или ещё короче:
−3 − 5 − 7 − 9 = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
(−10) + (+6) − (+15) + (+11) − (+7)
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
−50 + 40
Решение
−50 + 40 = −10
Задание 2. Найдите значение выражения:
25 + (−5)
Решение
25 + (−5) = 20
Задание 3. Найдите значение выражения:
−20 + 60
Решение
−20 + 60 = 40
Задание 4. Найдите значение выражения:
20 + (−8)
Решение
20 + (−8) = 12
Задание 5. Найдите значение выражения:
30 + (−50)
Решение
30 + (−50) = −20
Задание 6. Найдите значение выражения:
27 + (−19)
Решение
27 + (−19) = 8
Задание 7. Найдите значение выражения:
−17 + (−12) + (−8)
Решение
Задание 8. Найдите значение выражения:
−6 − 4
Решение
−6 − 4 = −6 + (−4) = −10
Задание 9. Найдите значение выражения:
−6 − (−4)
Решение
−6 − (−4) = −6 + 4 = −2
Задание 10. Найдите значение выражения:
−15 − (−15)
Решение
−15 − (−15) = −15 + 15 = 0
Задание 11. Найдите значение выражения:
−11 − (−14)
Решение
−11 − (−14) = −11 + 14 = 3
Задание 12. Найдите значение выражения:
−3 + 2 − (−1)
Решение
Задание 13. Найдите значение выражения:
−5 − 6 − 3
Решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Сложение чисел с разными знаками. Видеоурок. Математика 6 Класс
Посмотрите на эту шестеренку (см. рис. 1).

Рис. 1. Шестеренка часов
Это не стрелка, которая непосредственно показывает время и не циферблат (см. рис. 2). Но без этой детали часы не работают.
Рис. 2. Шестеренка внутри часов
А что обозначает буква Ы? Ничего, кроме звука Ы. Но без нее не будут «работать» многие слова. Например, слово «мЫшь». Так и отрицательные числа: они не показывают никакого количества, но без них механизм вычислений был бы существенно труднее.
Мы знаем, что сложение и вычитание равноправные операции, и их можно выполнять в любом порядке. В записи в прямом порядке мы можем посчитать: , а начать с вычитания нет, так как мы не договорились еще, а что же такое .
Понятно, что увеличить число на , а потом уменьшить на означает в итоге уменьшение на три. Почему бы так и не обозначить этот объект и так и считать: прибавить – значит вычесть . Тогда .
Число может означать, например, яблока. Новое число не обозначает никакого реального количества. Само по себе оно ничего не означает, как буква Ы. Это просто новый инструмент для упрощения вычислений.
Назовем новые числа отрицательными. Теперь мы можем вычитать из меньшего числа большее. Технически всё равно нужно вычесть из большего числа меньшего, но в ответе поставить знак минус: .
Рассмотрим ещё один пример: . Можно сделать все действия подряд: .
Однако из первого числа легче вычесть третье, а потом прибавить второе число:
Отрицательные числа можно определить и по-другому.
Для каждого натурального числа, например , введем новое число, которое обозначим , и определим, что оно обладает следующим свойством: сумма числа и равна : .
Число будем называть отрицательным, а числа и – противоположными. Таким образом, мы получили бесконечное количество новых чисел, например:
– противоположное для числа ;
– противоположное числу ;
– противоположное числу ;
– противоположное числу ;
Вычтем из меньшего числа большее: . Прибавим к данному выражению : . Получили ноль. Однако согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять : . Следовательно, выражение можно обозначить как .
То есть теперь мы можем вычитать из меньшего числа большее. Результатом будет отрицательное число:
У каждого положительного числа существует число-близнец, которое отличается только тем, что перед ним стоит знак минус Такие числа называются противоположными (см. рис. 3).

Рис. 3. Примеры противоположных чисел
Свойства противоположных чисел
1. Сумма противоположных чисел равна нулю: .
2. Если из нуля вычесть положительное число, то результатом будет противоположное отрицательное число: .
1. Оба числа могут быть положительными, и складывать их мы уже умеем: .
2. Оба числа могут быть отрицательными.
Мы уже прошли сложение таких чисел на предыдущем уроке, но убедимся, что понимаем, что с ними делать. Например: .
Чтобы эту сумму найти, складываем противоположные положительные числа и и ставим знак минус.
3. Одно число может быть положительным, а другое – отрицательным.
Прибавление отрицательного числа мы, если это нам удобно, можем заменять на вычитание положительного: .
Ещё один пример: . Опять сумму записываем как разность. Вычесть из меньшего большее число можно, вычитая из большего меньшее, но поставив знак минус.
Слагаемые можем менять местами: .
Ещё один аналогичный пример: .
Во всех случаях в итоге получается вычитание.
Чтобы коротко сформулировать эти правила, давайте вспомним еще один термин. Противоположные числа, конечно, не равны друг другу. Но было бы странно не заметить у них общего. Это общее мы назвали модулем числа. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного – противоположному, положительному. Например: , .
Чтобы сложить два отрицательных числа, нужно сложить их модули и поставить знак минус:
Чтобы сложить отрицательное и положительное число, нужно из большего модуля вычесть меньший модуль и поставить знак числа с большим модулем:
1.
Оба числа отрицательные, следовательно, складываем их модули и ставим знак минус:
2.
Два числа с разными знаками, следовательно, из модуля числа (больший модуль) вычитаем модуль числа и ставим знак минус (знак числа с большим модулем):
3.
Два числа с разными знаками, следовательно, из модуля числа (больший модуль) вычитаем модуль числа и ставим знак минус (знак числа с большим модулем): .
4.
interneturok.ru
