Как решаются матричные уравнения: Умножение матриц онлайн

Содержание

Студопедия — Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.

Studopedia.info — Студопедия — 2014-2023 год . (0.014 сек.) русская версия | украинская версия

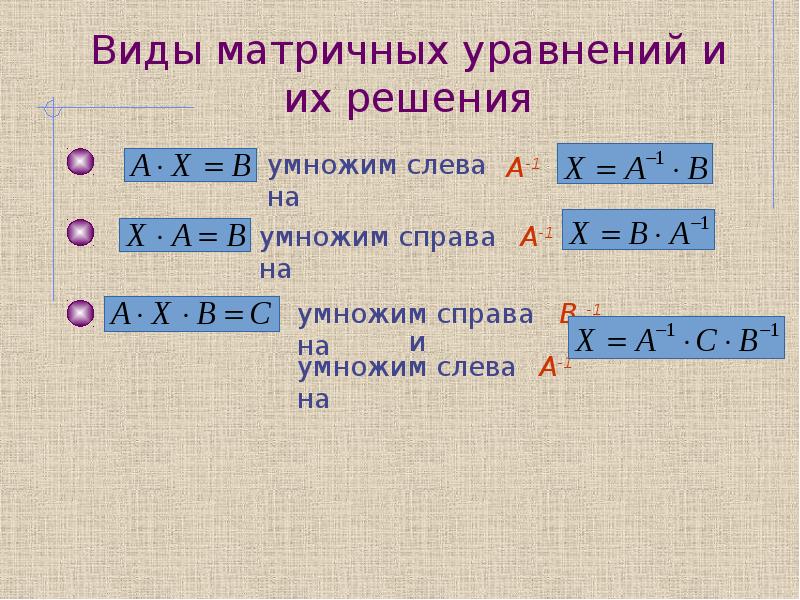
12345678910Следующая ⇒

Решения матричных уравнений

Матричные уравнения могут иметь вид:

АХ = В, ХА = В, АХВ = С,

где А,В,С — задаваемые матрицы, Х- искомая матрица.

Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.

Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.

Тогда:

Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.

3) Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Ранг матрицы — Размерность образа dim (im (A)) линейного оператора, которому соответствует матрица.

Обычно ранг матрицы A обозначается () или . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английскогоязыка, в то время как первый — для немецкого, французского и ряда других языков.

4) Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b ₁, b ₂,…, b_n и x ₁, x ₂,…, x_n, либо набор c ₁, c ₂,…, c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модулянад этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

5)Ме́тод Га́усса ^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные

12345678910Следующая ⇒

Дата добавления: 2015-09-07; просмотров: 654. Нарушение авторских прав; Мы поможем в написании вашей работы!

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета…

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где…

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса…

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар…

Этапы трансляции и их характеристика Трансляция (от лат. translatio — перевод) — процесс синтеза белка из аминокислот на матрице информационной (матричной) РНК (иРНК…

Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни…

Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана. ..

Билиодигестивные анастомозы Показания для наложения билиодигестивных анастомозов: 1. нарушения проходимости терминального отдела холедоха при доброкачественной патологии (стенозы и стриктуры холедоха) 2. опухоли большого дуоденального сосочка…

Сосудистый шов (ручной Карреля, механический шов). Операции при ранениях крупных сосудов 1912 г., Каррель – впервые предложил методику сосудистого шва. Сосудистый шов применяется для восстановления магистрального кровотока при лечении…

Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность · Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов…

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

%PDF-1.5 % 1 0 obj > /Metadata 3 0 R /Pages 4 0 R /StructTreeRoot 5 0 R /Type /Catalog >> endobj 6 0 obj /CreationDate (D:20130719105816+04’00’) /Creator /ModDate (D:20140312122942+04’00’) /Producer /Title >> endobj 2 0 obj > /Font > >> /Fields [] >> endobj 3 0 obj > stream application/pdf

Вартан Тагиров

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

2013-07-19T10:58:16+04:00Microsoft® Word 20102014-03-12T12:29:42+04:002014-03-12T12:29:42+04:00Microsoft® Word 2010uuid:885adc5b-e7d0-484e-8622-030b999f8737uuid:7a0354d3-b91b-436b-9a9d-b8d8ac18f7f8 endstream endobj 4 0 obj > endobj 5 0 obj > endobj 7 0 obj > endobj 8 0 obj > endobj 9 0 obj > endobj 10 0 obj > /MediaBox [0 0 595.

32 841.92] /Parent 4 0 R /Resources > /ProcSet [/PDF /Text] /XObject > >> /StructParents 0 /Tabs /S /Type /Page /Annots [62 0 R] >> endobj 11 0 obj > /MediaBox [0 0 595.32 841.92] /Parent 4 0 R /Resources > /ProcSet [/PDF /Text] >> /StructParents 1 /Tabs /S /Type /Page >> endobj 12 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 66 0 R /Group > /Tabs /S /StructParents 2 >> endobj 13 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 70 0 R /Group > /Tabs /S /StructParents 3 >> endobj 14 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 71 0 R /Group > /Tabs /S /StructParents 4 >> endobj 15 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 72 0 R /Group > /Tabs /S /StructParents 5 >> endobj 16 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.

32 841.92] /Contents 73 0 R /Group > /Tabs /S /StructParents 6 >> endobj 17 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 74 0 R /Group > /Tabs /S /StructParents 7 >> endobj 18 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 76 0 R /Group > /Tabs /S /StructParents 8 >> endobj 19 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 77 0 R /Group > /Tabs /S /StructParents 9 >> endobj 20 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 79 0 R /Group > /Tabs /S /StructParents 10 >> endobj 21 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 80 0 R /Group > /Tabs /S /StructParents 11 >> endobj 22 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.

32 841.92] /Contents 81 0 R /Group > /Tabs /S /StructParents 12 >> endobj 23 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 82 0 R /Group > /Tabs /S /StructParents 13 >> endobj 24 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 83 0 R /Group > /Tabs /S /StructParents 14 >> endobj 25 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 84 0 R /Group > /Tabs /S /StructParents 15 >> endobj 26 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 85 0 R /Group > /Tabs /S /StructParents 16 >> endobj 27 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 86 0 R /Group > /Tabs /S /StructParents 17 >> endobj 28 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.

32 841.92] /Contents 87 0 R /Group > /Tabs /S /StructParents 18 >> endobj 29 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 88 0 R /Group > /Tabs /S /StructParents 19 >> endobj 30 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 89 0 R /Group > /Tabs /S /StructParents 20 >> endobj 31 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 90 0 R /Group > /Tabs /S /StructParents 21 >> endobj 32 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 91 0 R /Group > /Tabs /S /StructParents 22 >> endobj 33 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 92 0 R /Group > /Tabs /S /StructParents 23 >> endobj 34 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.

32 841.92] /Contents 93 0 R /Group > /Tabs /S /StructParents 24 >> endobj 35 0 obj > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 94 0 R /Group > /Tabs /S /StructParents 25 >> endobj 36 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 96 0 R /Group > /Tabs /S /StructParents 26 >> endobj 37 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 97 0 R /Group > /Tabs /S /StructParents 27 >> endobj 38 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 98 0 R /Group > /Tabs /S /StructParents 28 >> endobj 39 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 99 0 R /Group > /Tabs /S /StructParents 29 >> endobj 40 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.

32 841.92] /Contents 100 0 R /Group > /Tabs /S /StructParents 30 >> endobj 41 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 101 0 R /Group > /Tabs /S /StructParents 31 >> endobj 42 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 102 0 R /Group > /Tabs /S /StructParents 32 >> endobj 43 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 103 0 R /Group > /Tabs /S /StructParents 33 >> endobj 44 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 104 0 R /Group > /Tabs /S /StructParents 34 >> endobj 45 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.32 841.92] /Contents 105 0 R /Group > /Tabs /S /StructParents 35 >> endobj 46 0 obj > /ExtGState > /ProcSet [/PDF /Text /ImageB /ImageC /ImageI] >> /MediaBox [0 0 595.

32 841.92] /Contents 106 0 R /Group > /Tabs /S /StructParents 36 >> endobj 47 0 obj > endobj 48 0 obj > endobj 49 0 obj > endobj 50 0 obj > stream HWK6WxH#͌@]\».n{d)uv @a14@0ǟo޿|ٵhm4UDCIDmzUǅ.PT&1jIpVQs*xG(

Использование матриц для решения систем уравнений | безграничная алгебра |

Матрицы

Матричные уравнения

Матрицы можно использовать для компактного написания и работы с системами нескольких линейных уравнений.

Цели обучения

Определите, как матрицы могут представлять систему уравнений

Основные выводы

Ключевые моменты

Если
AAA
представляет собой матрицу
m×nm \times nm×n
, а
xxx
обозначает вектор-столбец (т. е.
n×1n \times 1n×1
матрица) из
nnn
переменных
x1,x2,…,xnx_1, x_2,…, x_nx1,x2,… ,xn
, а
bbb
представляет собой вектор-столбец
m×1m \times 1m×1
, тогда матричное уравнение:
Ax=bAx=bAx=b
.

Ключевые термины

матрица : прямоугольное расположение чисел или термов, имеющее различное применение, такое как преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.

Матрицы можно использовать для компактной записи и работы с системами уравнений. Как мы узнали из предыдущих разделов, матрицами можно манипулировать так же, как и обычным уравнением. Это очень полезно, когда мы начинаем работать с системами уравнений. Полезно понять, как организовать матрицы для решения этих систем.

Написание системы уравнений с матрицами

Эту систему можно решить методом исключения или замены, но можно и с помощью матричной операции. Прежде чем мы приступим к настройке матриц, важно сделать следующее:

Убедитесь, что все уравнения написаны одинаково, то есть все переменные должны быть в одном порядке.
Убедитесь, что одна часть уравнения состоит только из переменных и их коэффициентов, а другая часть — только из констант.

Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц:

XXX

матрица, представляющая переменные системы, и

BBB

— матрица, представляющая константы. Используя умножение матриц, мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как:

A⋅X=B\displaystyle A\cdot X=BA⋅X=B

Чтобы решить систему линейных уравнений с помощью обратной матрицы, пусть

AAA

будет матрицей коэффициентов, пусть

XXX

будет матрицей переменных, и пусть

BBB

— постоянная матрица.

Учитывая систему:

x+8y=72x−8y=−3\displaystyle \начать{выравнивать} х+8у&=7 \\ 2x-8y&=-3 \end{align}x+8y2x−8y=7=−3

Матрица коэффициентов:

A=[182−8]A=\begin{bmatrix} 1 и 8\\ 2 и -8 \end{bmatrix}A=[128−8]

Переменная матрица:

X=[xy]\displaystyle X=\begin{bmatrix} х\\у \end{bmatrix}X=[xy]

Постоянная матрица:

B=[7−3]\displaystyle B=\begin{bmatrix} 7\\-3 \end{bmatrix}B=[7−3]

9{-1} \right)(A−1)

существует, эта формула решит систему.

Если матрица коэффициентов необратима, система может быть несовместной и не иметь решения или быть зависимой и иметь бесконечно много решений.

Матрицы и операции со строками

Две матрицы эквивалентны по строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.

Цели обучения

Объясните, как использовать операции со строками и почему они создают эквивалентные матрицы

Key Takeaways

Key Points

Элементарная операция со строками — это любое из следующих действий: переключение строк (перестановка двух строк матрицы), умножение строк (умножение строки матрицы на ненулевую константу) , или сложение строк (добавление к одной строке матрицы некоторого числа, кратного другой строке).
Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраическим путем из уравнений системы.

Ключевые термины

пространство строк : Набор всех возможных линейных комбинаций его векторов-строк.
эквивалент строки : В линейной алгебре, когда одна матрица может быть заменена другой с помощью последовательности элементарных операций над строками.

Элементарные операции с рядами (ERO)

В линейной алгебре две матрицы эквивалентны по строкам, если одну можно заменить на другую с помощью последовательности элементарных операций со строками. Или два

m×nm \times nm×n

матрицы эквивалентны по строкам тогда и только тогда, когда они имеют одинаковое пространство строк. Пространство 90 163 строк 90 164 матрицы представляет собой набор всех возможных линейных комбинаций ее векторов-строк. Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраическим путем из уравнений системы. Две матрицы одинакового размера эквивалентны по строкам тогда и только тогда, когда соответствующие однородные системы имеют одинаковый набор решений или, что то же самое, матрицы имеют одно и то же нулевое пространство. Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно его обозначают тильдой (~).

Элементарной операцией со строками является любой из следующих трех ходов:

Переключение строк (своп): поменять местами две строки матрицы.
Умножение строк (масштаб): умножение строки матрицы на ненулевую константу.
Добавление строки (поворот): добавление к одной строке матрицы числа, кратного другой строке.

Создание эквивалентных матриц с использованием элементарных операций со строками

Поскольку матрица по существу представляет собой коэффициенты и константы линейной системы, операции с тремя строками сохраняют матрицу. Например, замена двух строк просто означает изменение их положения в матрице. Кроме того, при решении системы линейных уравнений методом исключения умножение строк будет таким же, как умножение всего уравнения на число для получения аддитивных инверсий, чтобы переменная сокращалась. Наконец, добавление строк также совпадает с методом исключения, когда для получения переменной выбирают добавление или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод решения системы уравнений.

Пример 1. Покажите, что эти две матрицы эквивалентны по строкам:

A=(1−10211)B=(301031)\displaystyle A=\begin{pmatrix} 1 & -1 & 0 \\ 2 & 1 & 1 \end{pmatrix}\quad B=\begin{pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \end{pmatrix }A=(12−1101)B=(300311)

Начните с

AAA

, добавьте вторую строку к первой:

A=(301211)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 2 & 1 & 1 \end{pmatrix}A=(320111)

Затем умножьте вторую строку на 3, а затем вычтите первую строку из второй:

A=(301332)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 3 & 3 & 2 \end{pmatrix}A=(330312)

Наконец, вычтите первую строку из второй:

A= (301031)\displaystyle A=\begin{pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \end{pmatrix}A=(300311)

Вы можете видеть, что

A=BA=BA=B

, чего мы достигли с помощью серии элементарных операций над строками.

Сокращение строк: решение системы линейных уравнений

При сокращении строк линейная система:

x+3y−2z=53x+5y+6z=72x+4y+3z=8\displaystyle х+3у-2г=5 \\ 3х+5у+6з=7\\ 2x+4y+3z=8x+3y−2z=53x+5y+6z=72x+4y+3z=8

Представляется расширенной матрицей:

A=(13−2535672438)\displaystyle A=\begin{pmatrix} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \end{pmatrix}A=⎝

⎛132354−263578⎠

⎞

Эта матрица затем модифицируется с помощью элементарных операций со строками до тех пор, пока она не примет форму сокращенного эшелона строк.

Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.

Существует несколько конкретных алгоритмов сокращения строк расширенной матрицы, простейшими из которых являются исключение Гаусса и исключение Гаусса-Жордана. Это вычисление можно выполнить вручную (используя три типа ERO) или на калькуляторе с помощью матричной функции ‘rref’ (уменьшенная ступенчатая форма строки).

Окончательная матрица имеет сокращенную ступенчатую форму и представляет собой систему

A=(100−1501080012)\displaystyle A=\begin{pmatrix} 1 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{pmatrix}A=⎝

⎛100010001 −1582⎠

⎞

Упрощение матриц с помощью операций со строками

Используя элементарные операции, метод исключения Гаусса приводит матрицы к форме эшелонирования строк.

Цели обучения

Используйте элементарные операции со строками, чтобы представить матрицу в упрощенной форме

Ключевые выводы

Ключевые моменты

Поскольку элементарные операции со строками сохраняют пространство строк матрицы, пространство строк эшелонированной формы строк такое же, как и исходное матрица.
Существует три типа операций с элементарными строками: поменять местами две строки, умножить строку на ненулевой скаляр и добавить к одной строке скаляр, кратный другому.
На практике системы обычно не рассматриваются в терминах уравнений, а вместо этого используется расширенная матрица (которая также подходит для компьютерных манипуляций).

Ключевые термины

расширенная матрица : Матрица, полученная путем сложения столбцов двух данных матриц, обычно с целью выполнения одних и тех же элементарных операций над строками на каждой из данных матриц.

С помощью конечной последовательности элементарных операций над строками, называемой методом исключения Гаусса, любая матрица может быть преобразована в ступенчатую форму строк. Это преобразование необходимо для решения системы линейных уравнений.

Прежде чем перейти к более подробному рассмотрению, необходимо упомянуть несколько ключевых терминов:

Расширенная матрица : расширенная матрица — это матрица, полученная путем сложения столбцов двух заданных матриц, обычно с целью выполнения одни и те же элементарные операции над строками на каждой из заданных матриц.
Форма верхнего треугольника : Квадратная матрица называется верхнетреугольной, если все элементы ниже главной диагонали равны нулю. Треугольная матрица — это либо нижняя треугольная, либо верхняя треугольная. Матрица, имеющая как верхнюю, так и нижнюю треугольную форму, является диагональной матрицей.
Элементарные операции со строками : Перестановка строк, добавление строк или умножение строк.

Исключение Гаусса

Напишите расширенную матрицу для линейных уравнений.
Используйте элементарные операции со строками над расширенной матрицей
[A∣b][A|b][A∣b]
, чтобы преобразовать
AAA
в форму верхнего треугольника. Если на диагонали стоит ноль, меняйте местами строки, пока на его месте не окажется ненулевое значение.
Используйте обратную замену, чтобы найти решение.

Пример 1. Решите систему методом исключения Гаусса:

2x+y−z=8−3x−y+2z=−11−2x+y+2z=−3\displaystyle 2x+y-z=8\\ -3x-y+2z=-11\\ -2x+y+2z=-32x+y-z=8-3x-y+2z=-11-2x+y+2z=-3

Запишите расширенную матрицу:

[21-18-3-12 −11−212−3]\left[\begin{array}{rrr|r} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & — 3 \end{array} \right] ⎣

⎡2−3−21−11−1228−11−3⎦

⎤

Используйте элементарные операции со строками, чтобы уменьшить матрицу до уменьшенной форма эшелона ряда:

[10020103001−1]\left[\begin{array}{rrr|r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \end{массив } \right] ⎣

⎡10001000123−1⎦

⎤

Используя элементарные операции со строками для получения сокращенной ступенчатой формы строк (‘rref’ в калькуляторе), решение системы в последнем столбце:

x=2,y=3,z=-1x=2, y=3, z=-1x=2,y=3,z=-1

Лицензии и атрибуты

Контент под лицензией CC, совместно используемый ранее

Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права

Лицензионный контент CC, конкретное указание авторства

Решающие системы с инверсиями. Предоставлено : Openstax. Расположен по адресу : https://openstax.org/books/college-алгебра/pages/7-7-solving-systems-with-inverses. Лицензия : CC BY-SA: Attribution-ShareAlike
Матричное уравнение. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
матрица. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Эквивалентность строк. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Матрица (математика). Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
система линейных уравнений. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/System_of_linear_equations. Лицензия : CC BY-SA: Attribution-ShareAlike
эквивалент строки. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Исключение Гаусса. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Форма эшелона строк. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Треугольная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Дуг Дэниелс и Стивен Кокс, сокращенная форма строки. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Элементарные операции со строками. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Дополненная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
дополненная матрица. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike

Решение систем уравнений с использованием матриц — Промежуточная алгебра

Системы линейных уравнений

Цели обучения

К концу этого раздела вы сможете:

Записывать расширенную матрицу для системы уравнений
Использовать операции со строками над матрицей
Решение систем уравнений с использованием матриц

Прежде чем начать, пройдите этот тест на готовность.

Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
Оценить, когда и
Если вы пропустили эту проблему, просмотрите (рисунок).

Напишите расширенную матрицу для системы уравнений

Решение системы уравнений может быть утомительной операцией, где простая ошибка может нанести ущерб поиску решения. Доступен альтернативный метод, использующий основные процедуры исключения, но с более простыми обозначениями. Метод предполагает использование матрицы. Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах.

Матрица

Матрица представляет собой прямоугольный массив чисел, расположенных в строках и столбцах.

Матрица с 90 539 m 90 164 строк и 90 539 n 90 164 столбцов имеет порядок Матрица слева внизу имеет 2 строки и 3 столбца, поэтому она имеет порядок Мы говорим, что это матрица 2 на 3.

Каждое число в матрице называется элементом или записью в матрице.

Мы будем использовать матрицу для представления системы линейных уравнений. Мы записываем каждое уравнение в стандартной форме, а коэффициенты переменных и константы каждого уравнения становятся строкой в матрице. Тогда каждый столбец будет коэффициентом одной из переменных в системе или констант. Вертикальная черта заменяет знаки равенства. Полученную матрицу назовем расширенной матрицей системы уравнений.

Обратите внимание, что первый столбец состоит из всех коэффициентов x  , второй столбец содержит все коэффициенты y , а третий столбец содержит все константы.

Запишите каждую систему линейных уравнений в виде расширенной матрицы:

ⓐⓑ

ⓐ Второе уравнение не имеет стандартной формы. Перепишем второе уравнение в стандартной форме.

Заменим второе уравнение его стандартной формой. В расширенной матрице первое уравнение дает нам первую строку, а второе уравнение дает нам вторую строку. Вертикальная черта заменяет знаки равенства.

ⓑ Все три уравнения имеют стандартную форму. В расширенной матрице первое уравнение дает нам первую строку, второе уравнение дает нам вторую строку, а третье уравнение дает нам третью строку. Вертикальная черта заменяет знаки равенства.

Запишите каждую систему линейных уравнений в виде расширенной матрицы:

ⓐⓑ

ⓐ

ⓑ

Запишите каждую систему линейных уравнений в виде расширенной матрицы:

ⓐⓑ

ⓐ

ⓑ

Когда мы решаем системы уравнений с использованием матриц, важно иметь возможность переключаться между системой и матрицей. В следующем примере нас просят взять информацию из матрицы и написать систему уравнений.

Запишите систему уравнений, соответствующую расширенной матрице:

Мы помним, что каждая строка соответствует уравнению и что каждая запись является коэффициентом переменной или константой. Вертикальная черта заменяет знак равенства. Поскольку эта матрица представляет собой , мы знаем, что она преобразуется в систему трех уравнений с тремя переменными.

Напишите систему уравнений, соответствующую расширенной матрице:

Использование операций со строками над матрицей

После того, как система уравнений будет представлена в расширенной матричной форме, мы будем выполнять операции над строками, которые приведут нас к решению.

Для решения методом исключения не имеет значения, в каком порядке мы располагаем уравнения в системе. Точно так же в матрице мы можем поменять местами строки.

При решении методом исключения мы часто умножаем одно из уравнений на константу. Поскольку каждая строка представляет собой уравнение, и мы можем умножить каждую часть уравнения на константу, аналогичным образом мы можем умножить каждую запись в строке на любое действительное число, кроме 0.

При исключении мы часто добавляем кратное одной строке к другой ряд. В матрице мы можем заменить строку на ее сумму, кратную другой строке.

Эти действия называются операциями со строками и помогут нам использовать матрицу для решения системы уравнений.

Операции со строками

В матрице следующие операции могут выполняться над любой строкой, и результирующая матрица будет эквивалентна исходной матрице.

Поменяйте местами любые два ряда.
Умножить строку на любое действительное число, кроме 0.
Добавить ненулевое кратное одной строки к другой строке.

Выполнение этих операций несложно, но все арифметические действия могут привести к ошибке. Если мы используем систему для записи операций со строками на каждом шаге, гораздо проще вернуться и проверить нашу работу.

Мы используем заглавные буквы с нижними индексами для представления каждой строки. Затем мы показываем операцию слева от новой матрицы. Чтобы показать перестановку строк:

Чтобы умножить строку 2 на:

Чтобы умножить строку 2 на и добавить к строке 1:

Выполните указанные операции над расширенной матрицей:

9 0002 ⓐ Поменять местами ряды 2 и 3.

ⓑ Умножить строку 2 на 5.

ⓐ Меняем местами 2 и 3 ряды.

ⓑ Умножаем 2 ряд на 5.

Выполнить указанные операции над расширенной матрицей:

ⓐ Поменять местами строки 1 и 3.

ⓑ Умножить строку 3 на 3.

Выполнить указанные операции над расширенной матрицей: 9 0005

ⓐ Поменять местами ряды 1 и 2,

ⓑ Умножить 1-ю строку на 2,

ⓒ 2-ю строку умножить на 3 и прибавить к 1-й строке. использовать для достижения цели. Это именно то, что мы сделали, когда мы сделали исключение. Мы решили, на какое число умножить строку, чтобы при сложении строк исключалась переменная.

Учитывая эту систему, что бы вы сделали, чтобы устранить х ?

Следующий пример делает то же самое, но с матрицей.

Выполните необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице:

Чтобы сделать 4 равными 0, мы могли бы умножить строку 1 на и затем добавить ее к строке 2.

Выполнить необходимую операцию со строками, чтобы первая запись в строке 2 была равна нулю в расширенной матрице:

Решение систем уравнений с использованием матриц

Чтобы решить систему уравнений с использованием матриц, мы преобразуем расширенную матрицу в матрицу в виде строк-ступеней, используя операции со строками. Для непротиворечивой и независимой системы уравнений ее расширенная матрица имеет форму эшелона строк, когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нули.

Форма Row-Echelon

Для непротиворечивой и независимой системы уравнений ее расширенная матрица находится в строка-эшелон формы , когда слева от вертикальной линии каждая запись на диагонали равна 1, а все записи ниже диагонали — нулями.

Как только мы приведем расширенную матрицу к ступенчатой форме, мы можем написать эквивалентную систему уравнений и прочитать значение по крайней мере одной переменной. Затем мы подставляем это значение в другое уравнение, чтобы продолжить решение для других переменных. Этот процесс проиллюстрирован в следующем примере.

Как решить систему уравнений с помощью матрицы

Решите систему уравнений, используя матрицу:

Решение:

Решите систему уравнений, используя матрицу:

Решение:

Шаги суммированы здесь .

Решить систему уравнений с помощью матриц.

Напишите расширенную матрицу для системы уравнений.
С помощью операций со строками значение записи в строке 1 столбца 1 равно 1.
Используя операции со строками, получить нули в столбце 1 ниже 1.
Используя операции со строками, сделайте запись в строке 2 столбца 2 равной 1.
Продолжайте процесс до тех пор, пока матрица не будет иметь форму строки-эшелона.
Напишите соответствующую систему уравнений.
Используйте подстановку, чтобы найти оставшиеся переменные.
Запишите решение в виде упорядоченной пары или тройки.
Убедитесь, что решение соответствует исходным уравнениям.

Вот изображение, показывающее порядок расположения единиц и нулей в правильных позициях для эшелонированной формы.

Мы используем ту же процедуру, когда система уравнений состоит из трех уравнений.