§ Квадратные неравенства с одним корнем или без корней
Как решать квадратные неравенства. Метод интервалов Квадратные неравенства с одним корнем или без корней
Прежде чем перейти к разбору решений не совсем типичных квадратных неравенств, потренируйтесь в
решении обычных квадратных неравенств,
у которых при решении соответствующего квадратного уравнения получаются два корня.
Квадратные неравенства, у которых получается один корень
Рассмотрим неравенство, в котором при решении квадратного уравнения методом интервалов получается только один корень. Например, требуется решить следующее квадратное неравенство:
x2 − 2x + 1 ≤ 0
Используем метод интервалов для решения квадратного неравенства.
Сразу переходим к
п.3
правила из урока
«Метод интвервалов», так как
п.1
и
п.2
уже выполнены. То есть, приравняем левую часть неравенства к нулю и
решим полученное квадратное уравнение.
x
x1;2 =
| −(−2) ± √(−2)2 − 4 · 1 · 1 |
| 2 · 1 |
x1;2 =
| 2 ± √4 − 4 |
| 2 |
x1;2 =
| 2 ± √0 |
| 2 |
x1;2 =
x1 = x2 = 1
У нас получилось, что оба корня имеют одно одинаковое значение равное единице. Другими словами, значение корня повторяется два раза. Отметим это значение на числовой оси согласно п.5 из правила метода интервалов.
Теперь по п.6 отметим знаки внутри интервалов. Но в отличии от решения обычных квадратных неравенств с двумя различными корнями здесь появляется важный нюанс.
Запомните!
Если значение корня в уравнении повторяется четное количество раз, то при расставлении знаков
в интервалах при переходе через этот корень знак не меняется.
В нашем случае значение корня повторяется два раза «x1 = x2 = 1». Значит, при переходе через это значение знак не поменяется. С учетом выше сказанного проставим знаки в интервалах справа налево, начиная со знака «+».
Теперь по исходному неравенству «x2 − 2x + 1 ≤ 0» определяем, какие интервалы мы запишем в ответ. Исходя из знак неравенства делаем вывод, что нас интересуют отрицательные интервалы.
Таких интервалов на нашем рисунке нет, но неравенство нестрогое, значит, только число «1» является решением неравенства. Запишем ответ.
Ответ: x = 1
Убедимся в правильности нашего решения, подставив «x = 1» в исходное неравенство.
x
12 − 2 · 1 + 1 ≤ 0
0 ≤ 0 (верно)
Квадратные неравенства, не имеющие корней (нет решений)
Рассмотрим квадратные неравенства, у которых при решении соответствующего
квадратного уравнения не получается ни одного
корня. Пусть требуется решить следующее квадратное неравенство.
Пусть требуется решить следующее квадратное неравенство.
x2 + 2x + 7 ≤ 0
П.1 и п.2 для решения этого квадратного неравенства методом интервалов уже выполнен, поэтому сразу перейдем к п.3, то есть к решению соответсвующего квадратного уравнения.
x2 + 2x + 7 ≤ 0
x2 + 2x + 7 = 0
x1;2 =
| 2 ± √22 − 4 · 7 · 1 |
| 2 · 1 |
x1;2 =
| 2 ± √4 − 28 |
| 2 |
x 1;2 =
| 2 ± √−24 |
| 2 |
Нет действительных корней
При решении квадратного уравнения мы получили, что действительных корней нет. Но это вовсе не означает, что исходное квадратное неравенство невозможно решить.
Запомните!
Если при решении квадратного уравнения для неравенства получилось, что действительных корней нет, значит, ответом квадратного
неравенства будет: «нет действительных решений».
Так и запишем в ответ.
Ответ: нет действительных решений.
При написании ответа для квадратного неравенства важно помнить, что изначально мы решаем именно неравенство, поэтому речь идет именно о «решениях», а не о «корнях».
Помните, что решением любых неравенств, как правило, являются области решений (множество чисел), а в уравнениях — это конкретные числа, которые мы называем корнями уравнений.
Стоит запомнить для себя: уравнения — корни, неравенства — решения.
В завершении урока разберем еще одно квадратное неравенство, при решении которого получается только один корень.
x2 − 6x + 9 > 0
x2 − 6x + 9 = 0
x1;2 =
| 6 ± √62 − 4 · 1 · 9 |
| 2 · 1 |
x1;2 =
| 6 ± √36 − 36 |
| 2 |
x1;2 =
| 6 ± √0 |
| 2 |
x1;2 =
| 6 ± 0 |
| 2 |
x1;2 =
x1 = x2 = 3
Корень повторяется два раза, значит, знак при переходе через
число «3» не меняется.
Выберем нужные интервалы. В исходном неравенстве « x2 − 6x + 9 > 0 », значит, нам нужны интервалы со знаком «+».
Ответ: x 3
Как решать квадратные неравенства. Метод интервалов Квадратные неравенства с одним корнем или без корней
Как решать неравенства с двумя корнями. Иррациональные неравенства. Примеры решения задач
Цели:
- Общеобразовательная: систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения неравенств.
- Развивающая: развивать у учащихся умение слушать лекцию, конспективно записывая ее в тетрадь.
- Воспитательная: формировать познавательную мотивацию к изучению математики.
Ход урока
I. Вводная беседа:
Мы с вами закончили тему “Решение иррациональных уравнений” и сегодня начинаем учиться решать иррациональные неравенства.
Сначала давайте вспомним, какие виды неравенств вы умеете решать и какими методами?
Ответ : Линейные, квадратные, рациональные, тригонометрические. Линейные решаем, исходя из свойств неравенств, тригонометрические сводим к
простейшим тригонометрическим, решаемым с помощью тригонометрического круга, а
остальные, в основном, методом интервалов.
Линейные решаем, исходя из свойств неравенств, тригонометрические сводим к
простейшим тригонометрическим, решаемым с помощью тригонометрического круга, а
остальные, в основном, методом интервалов.
Вопрос : На каком утверждении основан метод интервалов?
Ответ : На теореме, утверждающей, что непрерывная функция, не обращающаяся в ноль на некотором интервале, сохраняет свой знак на этом интервале.
II. Давайте рассмотрим иррациональное неравенство типа >
Вопрос : Можно ли применить для его решения метод интервалов?
Ответ : Да, так как функция y = – непрерывна на D(y).
Решаем такое неравенство методом интервалов .
Вывод: мы довольно легко решили данное иррациональное неравенство методом интервалов, фактически сведя его к решению иррационального уравнения.
Давайте попробуем решить этим методом другое неравенство.
3) f(x) непрерывна на D(f)
4) Нули функции:
- Долго искать D(f).

- Трудно вычислять контрольные точки.
Возникает вопрос: “Нет ли других способов решения этого неравенства?”.
Очевидно, есть, и сейчас мы с вами с ними познакомимся.
III. Итак, тема сегодняшнего урока: “Методы решения иррациональных неравенств”.
Урок будет проходить в виде лекции, так как в учебнике нет подробного разбора всех методов. Поэтому наша важная задача: составить подробный конспект этой лекции.
IV. О первом методе решения иррациональных неравенств мы с вами уже поговорили.
Это – метод интервалов , универсальный метод решения всех типов неравенств. Но он не всегда приводит к цели коротким и простым путем.
V. При решении иррациональных неравенств можно использовать те же идеи,
что и при решении иррациональных уравнений, но так как простая проверка решений
невозможна (ведь решениями неравенств являются чаще всего целые числовые
промежутки), то необходимо использовать равносильность.
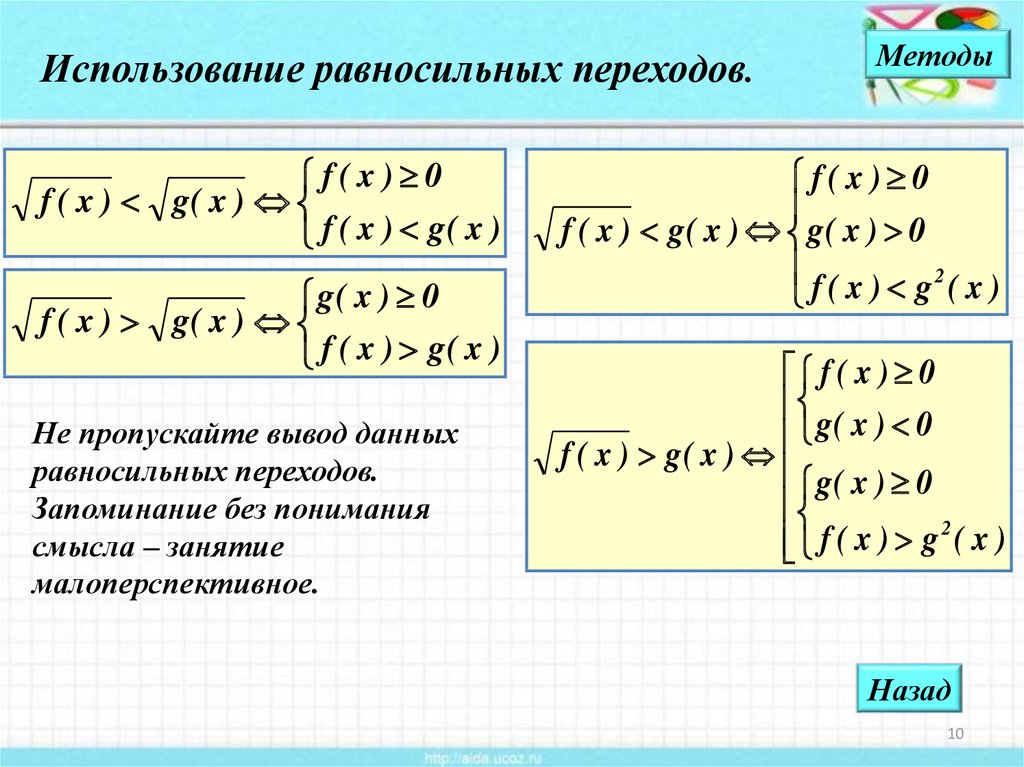
Приведем схемы решения основных типов иррациональных неравенств методом равносильных переходов от одного неравенства к системе неравенств.
2. Аналогично доказывается, что
Запишем эти схемы на опорной доске. Над доказательствами 3 и 4 типа подумайте дома, на следующем уроке мы их обсудим.
VI. Решим новым способом неравенство.
Исходное неравенство равносильно совокупности систем.
VII. И существует еще третий метод, часто помогающий решать сложные иррациональные неравенства. Мы с вами о нем уже говорили применительно к неравенствам с модулем. Это метод замены функций (замены множителей) . Напомню вам, что суть метода замены заключается в том, что разность значений монотонных функций можно заменить разностью значений их аргументов.
Рассмотрим иррациональное неравенство вида
то есть –
По теореме, если p(x) возрастает на некоторм промежутке, которому принадлежат a и b , причем a >b , то неравенства p(a) – p(b ) > 0 и a – b > 0 равносильны на D(p) , то есть
VIII. Решим методом замены множителей неравенство.
Решим методом замены множителей неравенство.
Значит, данное неравенство равносильно системе
Таким образом, мы увидели, что применение метода замены множителей для сведения решения неравенства к методу интервалов существенно сокращает объем работы.
IX. Теперь, когда мы разобрали три основных метода решения уравнений, давайте выполним самостоятельную работу с самопроверкой.
Нужно выполнить следующие номера (по учебнику А. М. Мордковича): 1790(а) – решить_ методом_ равносильныхпереходов,_ 1791(а) – решить методом замены множителей.Для решения иррациональных неравенств предлагается использовать способы, ранее разобранные при решении иррациональных уравнений:
- замена переменных;
- использование ОДЗ;
- использование свойств монотонности функций.
Завершением изучения темы является контрольная работа.
Анализ контрольной работы показывает:
- типичные ошибки слабых учащихся помимо арифметических и алгебраических – неверные равносильные переходы к системе неравенств;
- метод замены множителей успешно используется только сильными учащимися.

Цели:
- Общеобразовательная: систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения неравенств.
- Развивающая: развивать у учащихся умение слушать лекцию, конспективно записывая ее в тетрадь.
- Воспитательная: формировать познавательную мотивацию к изучению математики.
Ход урока
I. Вводная беседа:
Мы с вами закончили тему “Решение иррациональных уравнений” и сегодня начинаем учиться решать иррациональные неравенства.
Сначала давайте вспомним, какие виды неравенств вы умеете решать и какими методами?
Ответ : Линейные, квадратные, рациональные, тригонометрические. Линейные решаем, исходя из свойств неравенств, тригонометрические сводим к простейшим тригонометрическим, решаемым с помощью тригонометрического круга, а остальные, в основном, методом интервалов.
Вопрос : На каком утверждении основан метод интервалов?
Ответ : На теореме, утверждающей, что непрерывная функция, не
обращающаяся в ноль на некотором интервале, сохраняет свой знак на этом
интервале.
II. Давайте рассмотрим иррациональное неравенство типа >
Вопрос : Можно ли применить для его решения метод интервалов?
Ответ : Да, так как функция y = – непрерывна на D(y).
Решаем такое неравенство методом интервалов .
Вывод: мы довольно легко решили данное иррациональное неравенство методом интервалов, фактически сведя его к решению иррационального уравнения.
Давайте попробуем решить этим методом другое неравенство.
3) f(x) непрерывна на D(f)
4) Нули функции:
- Долго искать D(f).
- Трудно вычислять контрольные точки.
Возникает вопрос: “Нет ли других способов решения этого неравенства?”.
Очевидно, есть, и сейчас мы с вами с ними познакомимся.
III. Итак, тема сегодняшнего урока: “Методы решения иррациональных неравенств”.
Урок будет проходить в виде лекции, так как в учебнике нет подробного разбора
всех методов. Поэтому наша важная задача: составить подробный конспект этой
лекции.
Поэтому наша важная задача: составить подробный конспект этой
лекции.
IV. О первом методе решения иррациональных неравенств мы с вами уже поговорили.
Это – метод интервалов , универсальный метод решения всех типов неравенств. Но он не всегда приводит к цели коротким и простым путем.
V. При решении иррациональных неравенств можно использовать те же идеи, что и при решении иррациональных уравнений, но так как простая проверка решений невозможна (ведь решениями неравенств являются чаще всего целые числовые промежутки), то необходимо использовать равносильность.
Приведем схемы решения основных типов иррациональных неравенств методом равносильных переходов от одного неравенства к системе неравенств.
2. Аналогично доказывается, что
Запишем эти схемы на опорной доске. Над доказательствами 3 и 4 типа подумайте дома, на следующем уроке мы их обсудим.
VI. Решим новым способом неравенство.
Исходное неравенство равносильно совокупности систем.
VII. И существует еще третий метод, часто помогающий решать сложные иррациональные неравенства. Мы с вами о нем уже говорили применительно к неравенствам с модулем. Это метод замены функций (замены множителей) . Напомню вам, что суть метода замены заключается в том, что разность значений монотонных функций можно заменить разностью значений их аргументов.
Рассмотрим иррациональное неравенство вида
то есть –
По теореме, если p(x) возрастает на некоторм промежутке, которому принадлежат a и b , причем a >b , то неравенства p(a) – p(b ) > 0 и a – b > 0 равносильны на D(p) , то есть
VIII. Решим методом замены множителей неравенство.
Значит, данное неравенство равносильно системе
Таким образом, мы увидели, что применение метода замены множителей для
сведения решения неравенства к методу интервалов существенно сокращает объем
работы.
IX. Теперь, когда мы разобрали три основных метода решения уравнений, давайте выполним самостоятельную работу с самопроверкой.
Нужно выполнить следующие номера (по учебнику А. М. Мордковича): 1790(а) – решить_ методом_ равносильныхпереходов,_ 1791(а) – решить методом замены множителей.Для решения иррациональных неравенств предлагается использовать способы, ранее разобранные при решении иррациональных уравнений:
- замена переменных;
- использование ОДЗ;
- использование свойств монотонности функций.
Завершением изучения темы является контрольная работа.
Анализ контрольной работы показывает:
- типичные ошибки слабых учащихся помимо арифметических и алгебраических – неверные равносильные переходы к системе неравенств;
- метод замены множителей успешно используется только сильными учащимися.
В данном уроке мы рассмотрим решение иррациональных неравенств, приведем различные примеры.
Тема: Уравнения и неравенства. Системы уравнений и неравенств
Урок: Иррациональные неравенства
При решении иррациональных неравенств довольно часто необходимо возводить обе части неравенства в некоторую степень, это довольно ответственная операция. Напомним особенности.
Обе части неравенства можно возвести в квадрат, если обе они неотрицательны, только тогда мы получаем из верного неравенства верное неравенство.
Обе части неравенства можно возвести куб в любом случае, если исходное неравенство было верным, то при возведении в куб мы получим верное неравенство.
Рассмотрим неравенство вида:
Подкоренное выражение должно быть неотрицательным. Функция может принимать любые значения, необходимо рассмотреть два случая.
В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) больше отрицательного выражения, значит, неравенство выполняется всегда.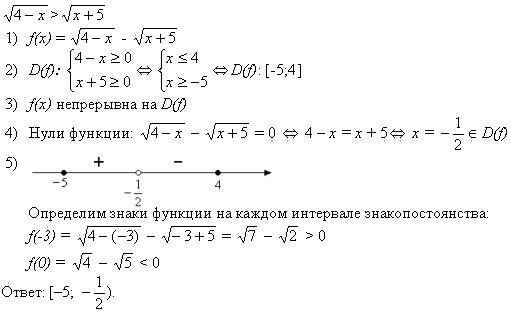
Итак, имеем следующую схему решения:
В первой системе мы не защищаем отдельно подкоренное выражение, т. к. при выполнении второго неравенства системы подкоренное выражение автоматически должно быть положительно.
Пример 1 — решить неравенство:
Согласно схеме, переходим к эквивалентной совокупности двух систем неравенств:
Проиллюстрируем:
Рис. 1 — иллюстрация решения примера 1
Как мы видим, при избавлении от иррациональности, например, при возведении в квадрат, получаем совокупность систем. Иногда эту сложную конструкцию можно упростить. В полученной совокупности мы имеем право упростить первую систему и получить эквивалентную совокупность:
В качестве самостоятельного упражнения необходимо доказать эквивалентность данных совокупностей.
Рассмотрим неравенство вида:
Аналогично предыдущему неравенству, рассматриваем два случая:
В первом случае обе части неравенства неотрицательны, имеем право возвести в квадрат. Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) меньше отрицательного выражения, значит, неравенство противоречиво. Вторую систему рассматривать не нужно.
Во втором случае правая часть отрицательна, и мы не имеем права возводить в квадрат. В таком случае необходимо смотреть на смысл неравенства: здесь положительное выражение (квадратный корень) меньше отрицательного выражения, значит, неравенство противоречиво. Вторую систему рассматривать не нужно.
Имеем эквивалентную систему:
Иногда иррациональное неравенство можно решить графическим методом. Данный способ применим, когда соответствующие графики можно достаточно легко построить и найти их точки пересечения.
Пример 2 — решить неравенства графически:
а)
б)
Первое неравенство мы уже решали и знаем ответ.
Чтобы решить неравенства графически, нужно построить график функции, стоящей в левой части, и график функции, стоящей в правой части.
Рис. 2. Графики функций и
Для построения графика функции необходимо преобразовать параболу в параболу (зеркально отобразить относительно оси у), полученную кривую сместить на 7 единиц вправо. График подтверждает, что данная функция монотонно убывает на своей области определения.
График подтверждает, что данная функция монотонно убывает на своей области определения.
График функции — это прямая, ее легко построить. Точка пересечения с осью у — (0;-1).
Первая функция монотонно убывает, вторая монотонно возрастает. Если уравнение имеет корень, то он единственный, по графику легко его угадать: .
Когда значение аргумента меньше корня, парабола находится выше прямой. Когда значение аргумента находится в пределах от трех до семи, прямая проходит выше параболы.
Имеем ответ:
Эффективным методом решения иррациональных неравенств является метод интервалов.
Пример 3 — решить неравенства методом интервалов:
а)
б)
согласно методу интервалов, необходимо временно отойти от неравенства. Для этого перенести в заданном неравенстве все в левую часть (получить справа ноль) и ввести функцию, равную левой части:
теперь необходимо изучить полученную функцию.
ОДЗ:
Данное уравнение мы уже решали графически, поэтому не останавливаемся на определении корня.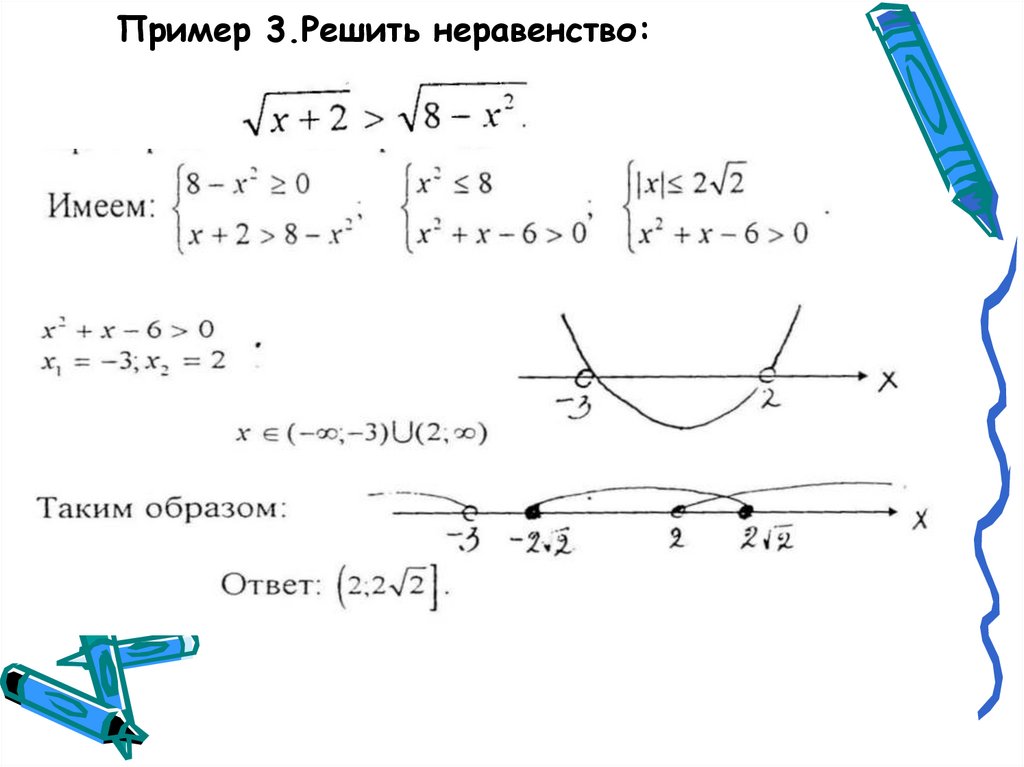
Теперь необходимо выделить интервалы знакопостоянства и определить знак функции на каждом интервале:
Рис. 3. Интервалы знакопостоянства к примеру 3
Напомним, что для определения знаков на интервале необходимо взять пробную точку и подставить ее в функцию, полученный знак функция будет сохранять на всем интервале.
Проверим значение в граничной точке:
Очевиден ответ:
Рассмотрим следующий тип неравенств:
Сначала запишем ОДЗ:
Корни существуют, они неотрицательны, обе части можем возвести в квадрат. Получаем:
Получили эквивалентную систему:
Полученную систему можно упростить. При выполнении второго и третьего неравенств первое истинно автоматически. Имеем::
Пример 4 — решить неравенство:
Действуем по схеме — получаем эквивалентную систему.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Всякое неравенство, в состав которого входит функция, стоящая под корнем, называется иррациональным . Существует два типа таких неравенств:
В первом случае корень меньше функции g
(x
), во втором — больше.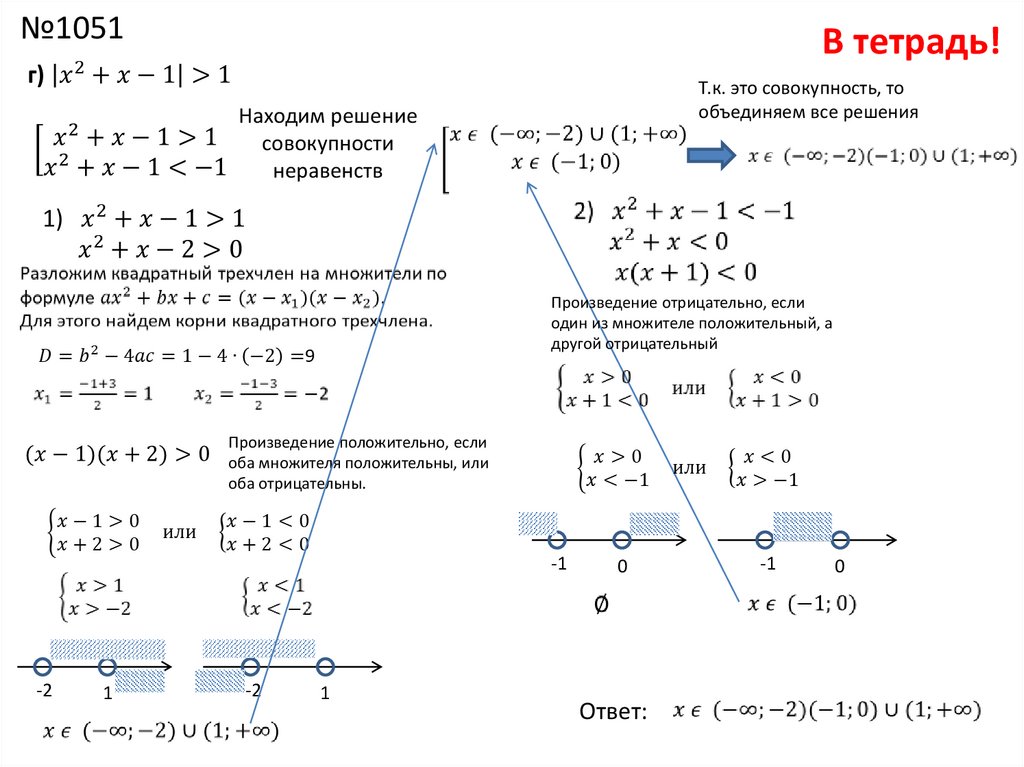 Если g
(x
) — константа , неравенство резко упрощается. Обратите внимание: внешне эти неравенства очень похожи, но схемы решения у них принципиально различаются.
Если g
(x
) — константа , неравенство резко упрощается. Обратите внимание: внешне эти неравенства очень похожи, но схемы решения у них принципиально различаются.
Сегодня научимся решать иррациональные неравенства первого типа — они самые простые и понятные. Знак неравенства может быть строгим или нестрогим. Для них верно следующее утверждение:
Теорема. Всякое иррациональное неравенство вида
Равносильно системе неравенств:
Неслабо? Давайте рассмотрим, откуда берется такая система:
- f (x ) ≤ g 2 (x ) — тут все понятно. Это исходное неравенство, возведенное в квадрат;
- f (x ) ≥ 0 — это ОДЗ корня. Напомню: арифметический квадратный корень существует только из неотрицательного числа;
- g (x ) ≥ 0 — это область значений корня. Возводя неравенство в квадрат, мы сжигаем минусы. В результате могут возникнуть лишние корни. Неравенство g (x ) ≥ 0 отсекает их.
Многие ученики «зацикливаются» на первом неравенстве системы: f
(x
) ≤ g
2 (x
) — и напрочь забывают два других. Результат предсказуем: неправильное решение, потерянные баллы.
Результат предсказуем: неправильное решение, потерянные баллы.
Поскольку иррациональные неравенства — достаточно сложная тема, разберем сразу 4 примера. От элементарных до действительно сложных. Все задачи взяты из вступительных экзаменов МГУ им. М. В. Ломоносова.
Примеры решения задач
Задача. Решите неравенство:
Перед нами классическое иррациональное неравенство : f (x ) = 2x + 3; g (x ) = 2 — константа. Имеем:
Из трех неравенств к концу решения осталось только два. Потому что неравенство 2 ≥ 0 выполняется всегда. Пересечем оставшиеся неравенства:
Итак, x ∈ [−1,5; 0,5]. Все точки закрашены, поскольку неравенства нестрогие .
Задача. Решите неравенство:
Применяем теорему:
Решаем первое неравенство. Для этого раскроем квадрат разности. Имеем:
2x 2 − 18x + 16 2x 2 − 18x + 16 x 2 − 10x x (x − 10) x ∈ (0; 10).
Теперь решим второе неравенство. Там тоже квадратный трехчлен :
Там тоже квадратный трехчлен :
2x
2 − 18x
+ 16 ≥ 0;
x
2 − 9x
+ 8 ≥ 0;
(x
− 8)(x
− 1) ≥ 0;
x
∈ (−∞; 1]∪∪∪∪}
Решение радикальных неравенств: методы и примеры
Любые алгебраические выражения или уравнения могут содержать неравенств для демонстрации отношения порядка между ними. Здесь мы обсудим неравенства в радикальных функциях (содержащих квадратные корни) и научимся их решать.
Радикальные неравенства: Определение и формула
Неравенство, в котором переменные находятся в пределах подкоренной и известно как радикальное неравенство .
Другими словами, подкоренное неравенство — это неравенство, в котором переменная или переменные находятся внутри подкоренного символа (подкоренного). Следующая формула описывает формат, в котором вы можете увидеть радикальное неравенство: Переменная x внутри радикала представляет подкоренное число. Этот формат одинаков для всех остальных знаков неравенства
Помните, что подкоренное число — это значение внутри подкоренного символа.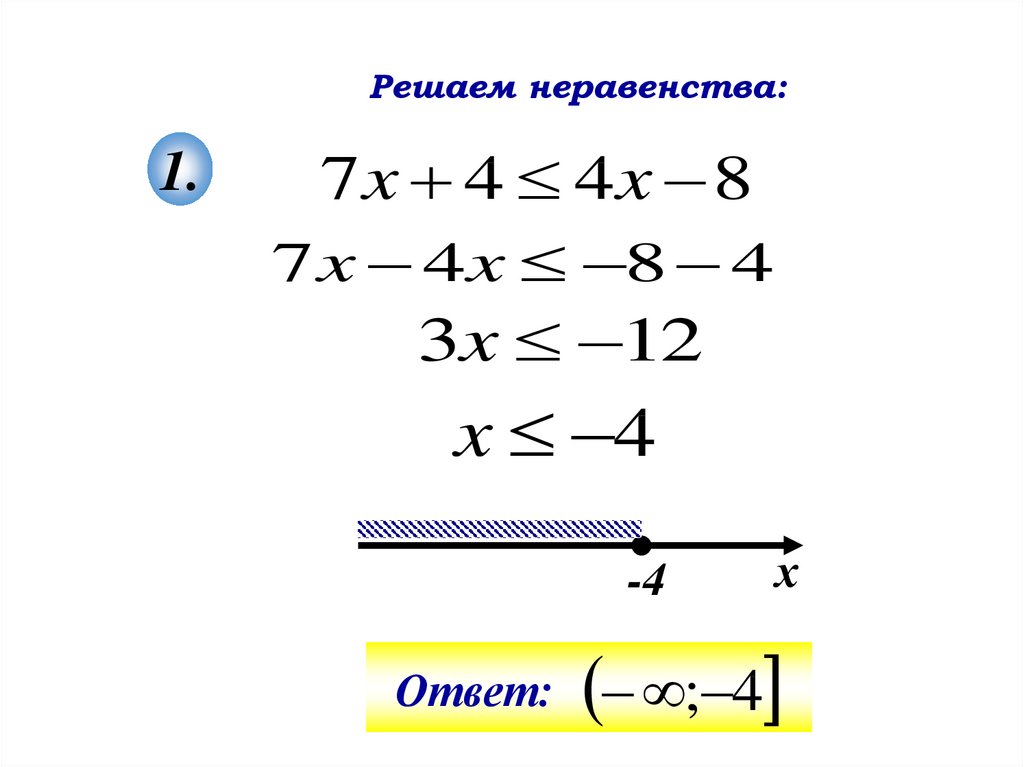 То есть это значение, за которое мы берем корень.
То есть это значение, за которое мы берем корень.
Давайте рассмотрим несколько примеров, чтобы понять, как мы можем идентифицируют это неравенство.
.
Здесь мы видим переменную x внутри корня. И это уравнение выражается со знаком неравенства.
Аналогично, ниже приведены некоторые другие примеры радикального неравенства.
Определение радикальных неравенств: Метод и правила
Ниже приведены два способа определения радикальных неравенств:
- С помощью алгебры
- С помощью графиков
С помощью алгебры
Мы можем решать радикальные неравенства всех типов с помощью алгебры. Некоторые радикальные неравенства также имеют переменные вне радикала, и мы также можем использовать алгебру для их вычисления. Для решения радикальных неравенств можно использовать следующие шаги:
Шаг 1 : Проверить индекс радикала.
- Если индекс четный, то окончательное вычисленное значение подкоренного числа не может быть отрицательным и должно быть положительным.
 Это называется ограничением домена . Здесь для радикального неравенства n — индекс, а x — подкоренное число.
Это называется ограничением домена . Здесь для радикального неравенства n — индекс, а x — подкоренное число.
Шаг 2 : Если индекс четный, подкоренное число считается положительным. Найдите переменную x в подкоренном члене.
- Итак, мы будем решать переменную x для этого подкоренного числа, когда оно больше или равно нулю. То есть считаем подкоренное и подкоренное неравенство и вычисляем переменную x. Однако если индекс нечетный, то подкоренное число рассматривается как .
Поскольку главный квадратный корень никогда не бывает отрицательным, неравенства, которые упрощаются до формы , где d — отрицательное число, не имеют решений.
Шаг 3 : Решите исходное выражение неравенства алгебраически (как вы это делаете с уравнениями), а также удалите радикал из выражения.
- Мы удалим радикал, взяв индекс и используя его как показатель степени членов в обеих частях неравенства.
 (т. е. ). Здесь обратите внимание, что при использовании индекса в качестве показателя радикального члена он аннулирует радикальный символ, тем самым устраняя его.
(т. е. ). Здесь обратите внимание, что при использовании индекса в качестве показателя радикального члена он аннулирует радикальный символ, тем самым устраняя его.
Помните, что если значение индекса не указано, оно всегда считается равным 2.
Шаг 4 : Проверьте значения, чтобы проверить решение.
- Чтобы проверить значения x, мы рассмотрим некоторые случайные значения, которые удовлетворяют неравенству. А также рассмотрим некоторые значения вне равенства, чтобы можно было подтвердить правильность нашего решения.
Давайте рассмотрим пример, чтобы правильно понять это.
Решить
Решение : Чтобы решить это радикальное неравенство, давайте выполним все шаги.
Шаг 1: Сначала мы проверяем индекс данного радикального неравенства. Поскольку значение индекса не задано, значение индекса равно 2.
Шаг 2: Поскольку индекс четный, подкоренная часть квадратного корня будет больше или равна нулю.
Шаг 3: Теперь мы решим радикальное неравенство алгебраически, а также удалим радикальный символ, чтобы упростить его. Во-первых, мы изолируем радикал.
Теперь мы удалим радикальный символ, взяв индекс в качестве показателя степени в обеих частях неравенства.
Здесь мы получили два неравенства для значения x из уравнения и . Поэтому мы объединяем их оба и записываем в виде сложного неравенства. Итак, наш окончательный ответ:
Здесь обратите внимание, что 1 — это нижнее значение интервала, а 5 — это верхнее значение интервала.
Шаг 4: Наконец, мы проверим некоторые значения x, чтобы проверить наше решение и подтвердить его. Давайте рассмотрим вне нашего диапазона x и внутри нашего диапазона x.
| Not possible as is not a real number | It satisfies the inequality | This value doesn’t satisfy the inequality |
We can see that the value of x удовлетворяет радикальному неравенству. Таким образом, решение проверяет и удовлетворяет данному радикальному неравенству.
Таким образом, решение проверяет и удовлетворяет данному радикальному неравенству.
Использование графов
Мы также можем решать радикальные неравенства с помощью графов. Мы будем следовать данным шагам, чтобы использовать этот метод:
Шаг 1 : Для радикального неравенства , где также может быть, рассмотрим обе функции от и .
Шаг 2 : Постройте график, отображающий обе функции из шага 1. с учетом знака неравенства. Кроме того, найдите точку x, в которой обе функции пересекаются на графике, если применимо.
- То есть, если неравенство имеет знак больше, то найти значения x выше другой функции. А если неравенство имеет знак меньше, то идентифицируйте x ниже другой функции.
Шаг 4 : Подтвердите и проверьте значения x.
- Аналогично предыдущему методу рассматриваются случайные значения x, удовлетворяющие неравенству, а также не удовлетворяющие полученному диапазону x.

Давайте разберемся с этим на примере.
Решить
Решение :
Шаг 1: Считаем и .
Шаг 2: Теперь мы строим график для обеих функций из шага 1.
График радикального неравенства, Мули-Хавия — StudySmarter Originals
Здесь график с красной линией относится к функции, а график с зеленой линией имеет функцию . Мы построили график таким образом, что можем четко определить значения по оси x от 0 до 30. Точно так же мы можем четко отметить значения по оси y.
Шаг 3: Теперь мы идентифицируем значения x, для которых первый график лежит выше второго графика, так как у нас есть знак неравенства больше в исходном уравнении неравенства. Мы также можем видеть, что значение x пересекает оба графика в точке . Это означает, что первый график лежит выше второго графика для
. Решением этого радикального неравенства является .
Примечание. Домен . Таким образом, домен не оказывает никакого влияния на решение.
Решение радикальных неравенств примеры
Здесь представлены некоторые другие примеры радикального неравенства с использованием обоих методов.
Решить алгебраически и графически.
Решение : Сначала решаем методом алгебры.
Шаг 1: Сначала мы проверяем индекс данного радикального неравенства. Здесь 3.
Шаг 2: Поскольку индекс нечетный, считаем:
Шаг 3: Теперь решим исходное неравенство. Так как данное неравенство не имеет других операций, шаг выделения пропускаем.
Таким образом, значения x на шагах 2 и 3 равны .
Шаг 4: Теперь мы проверяем наше решение, чтобы подтвердить его.
Отсюда видно, что данное радикальное неравенство для значений выполняется.
Теперь решим это же радикальное неравенство графическим методом.
Шаг 1: Рассматриваем и
Шаг 2: строим графики для двух функций, учтенных в шаге 1.
графическая форма радикального неравенства, Мули-Хавия — StudySmarter Originals
На приведенном выше графике красная линия представляет функцию, а синяя линия представляет функцию.
Шаг 3: Определяем значения x, для которых первый график лежит над графиком . И значение x пересекает оба графика в точке . Таким образом, первый график лежит над вторым графиком для значений .
И значение x пересекает оба графика в точке . Таким образом, первый график лежит над вторым графиком для значений .
Следовательно, решение данного радикального неравенства есть .
Решение радикальных неравенств. Ключевые выводы
- Неравенство, в котором переменные находятся в пределах подкоренной части, называется радикальным неравенством.
- Подкоренное число — это значение внутри подкоренного символа.
- Есть два способа определения радикальных неравенств: с помощью алгебры и с помощью графиков.
Видео с вопросами: Решение радикальных неравенств с одной переменной с использованием факторизации
Стенограмма видео
Алгебраически найдите набор решений неравенства квадратный корень из 𝑥 в квадрате плюс восемь 𝑥 плюс 16 больше или равно трем.
Итак, первое, что мы хотим сделать, если хотим решить это неравенство, это удалить знак квадратного корня. Мы делаем это, возводя в квадрат обе части нашего неравенства.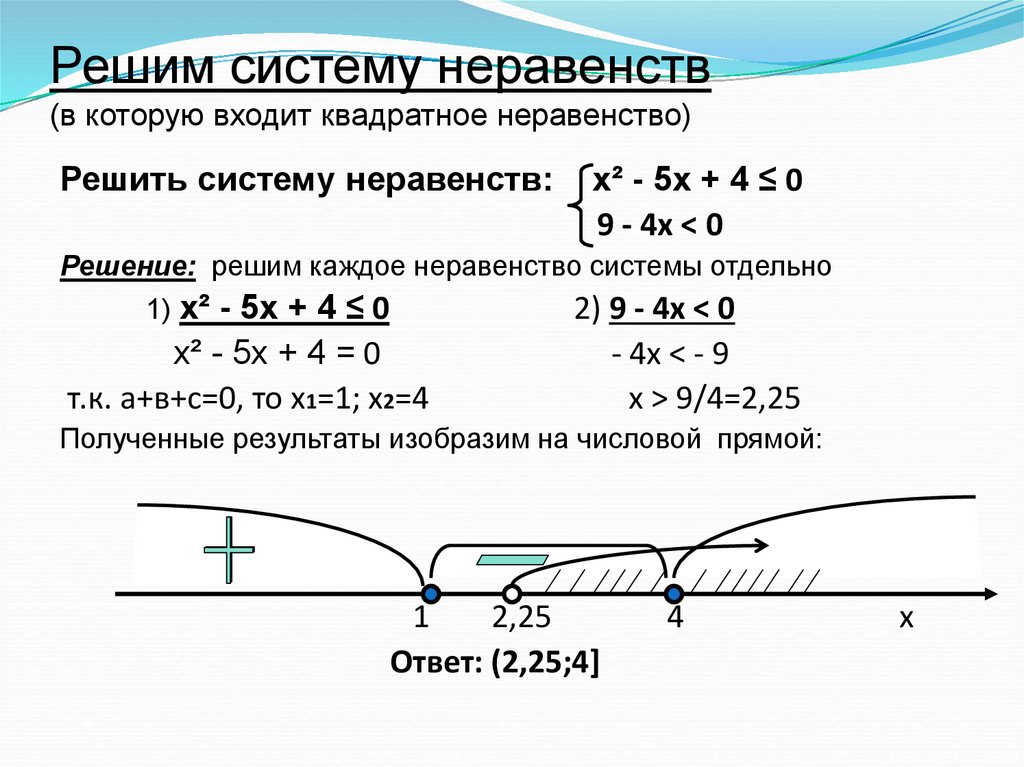 И когда мы это сделаем, у нас останется 𝑥 в квадрате плюс восемь 𝑥 плюс 16 больше или равно девяти. Это потому, что если возвести в квадрат три, получится девять. И если мы возведем квадратный корень в квадрат, то мы просто получим значение, находящееся внутри этого квадратного корня.
И когда мы это сделаем, у нас останется 𝑥 в квадрате плюс восемь 𝑥 плюс 16 больше или равно девяти. Это потому, что если возвести в квадрат три, получится девять. И если мы возведем квадратный корень в квадрат, то мы просто получим значение, находящееся внутри этого квадратного корня.
Теперь нам нужно найти критические значения. И для этого мы собираемся решить квадратное уравнение. Но мы хотим, чтобы квадратное равнялось нулю. Итак, что мы собираемся сделать в первую очередь, так это вычесть девять из каждой стороны нашего неравенства. И когда мы это сделаем, мы получим 𝑥 в квадрате плюс восемь 𝑥 плюс семь. И это потому, что 16 минус девять будет семь больше или равно нулю. Хорошо, отлично. Итак, в той форме, в которой мы хотели. Итак, теперь мы будем действовать так, как будто оно равно нулю. Итак, мы собираемся убрать неравенство. И мы собираемся сделать это, потому что мы хотим решить квадратное уравнение, чтобы найти наши критические значения.
Итак, если я хочу решить неравенство вида 𝑥 в квадрате плюс восемь 𝑥 плюс семь равно нулю, то мы делаем это разными способами. Мы могли бы использовать квадратную формулу, мы могли бы использовать завершение квадрата. Однако для этого, просто потому, что он самый простой, мы собираемся учитывать. И чтобы разложить на множители, нам нужно найти два значения, произведение которых равно положительной семерке, а сумма которых равна положительной восьмерке, потому что это коэффициент нашего 𝑥. Ну, два коэффициента, которые мы собираемся использовать, это один и семь. И это потому, что один, умноженный на семь, равен семи. Итак, наш продукт дает нам положительную семерку. А одна прибавка семь равно восьми, положительной восьмерке.
Мы могли бы использовать квадратную формулу, мы могли бы использовать завершение квадрата. Однако для этого, просто потому, что он самый простой, мы собираемся учитывать. И чтобы разложить на множители, нам нужно найти два значения, произведение которых равно положительной семерке, а сумма которых равна положительной восьмерке, потому что это коэффициент нашего 𝑥. Ну, два коэффициента, которые мы собираемся использовать, это один и семь. И это потому, что один, умноженный на семь, равен семи. Итак, наш продукт дает нам положительную семерку. А одна прибавка семь равно восьми, положительной восьмерке.
Итак, мы знаем, что это наши факторы. Итак, это означает, что теперь мы можем переписать наш квадрат, используя круглые скобки. Итак, у нас есть 𝑥 плюс один, умноженный на 𝑥 плюс семь равно нулю. Итак, теперь нам нужно выяснить, какими будут значения 𝑥. И для этого нам нужно установить каждую из наших скобок равными нулю. И это потому, что если у нас есть нулевой результат, это означает, что одна из наших скобок должна быть нулевой. И это потому, что ноль, умноженный на что-либо, дает нам ноль.
И это потому, что ноль, умноженный на что-либо, дает нам ноль.
Итак, если мы начнем с 𝑥 плюс единица равна нулю и вычтем единицу из каждой части уравнения, мы получим 𝑥 равно отрицательной единице. И точно так же, если мы сделаем то же самое с другим уравнением, у нас есть 𝑥 плюс семь равно нулю, мы получим 𝑥 равно отрицательной семерке. Хорошо, отлично. Итак, мы нашли наши критические значения: 𝑥 равно отрицательной единице, а 𝑥 равно отрицательной семерке.
Итак, если мы быстро набросаем наш квадратик, у нас будет вот такая фигура. Вот мы и получили U-образную параболу. И это потому, что у нас положительный 𝑥 в квадрате. И затем у нас есть пересечение оси 𝑥 в отрицательных семи и отрицательных единицах, которые являются нашими критическими значениями. Так что у нас также может быть наш 𝑦-перехват. Нам это не нужно, если этот вопрос стоило показать, если мы делаем скетч. И мы знаем, что будет семь. И это потому, что если бы у нас было 𝑦 равно 𝑥 в квадрате плюс восемь, 𝑥 плюс семь и 𝑥 равно нулю, то это ноль в квадрате, то есть ноль плюс восемь, умноженный на ноль, что равно нулю плюс семь. И это означает, что это просто дало бы нам семь. Хорошо, отлично.
И это означает, что это просто дало бы нам семь. Хорошо, отлично.
Но как это поможет нам с нашим неравенством? Ну, если вы посмотрите на наше неравенство, нас интересует, где наш квадрат больше или равен нулю. Поэтому нам не нужен этот раздел, который находится под осью 𝑥. Нам нужна только часть нашего графика, которая находится выше оси 𝑥. Итак, как мы можем представить это? Ну, мы могли бы написать это, используя знаки неравенства, потому что мы могли бы сказать, что 𝑥 меньше или равно отрицательной семерке. Поскольку нам нужны все значения, которые меньше отрицательной семерки или 𝑥 больше или равно отрицательной единице, мы хотим, чтобы все было справа от отрицательной единицы. Вот что мы запишем, используя знаки неравенства.
Таким образом, мы могли бы также показать это в системе обозначений. И мы делаем это, потому что вопрос просил нас найти алгебраически множество решений неравенства. Итак, мы делаем это со всеми действительными числами. Итак, это наш ℝ минус, и это означает, что кроме этого у нас есть значения между отрицательной семеркой и отрицательной единицей.




 Это называется ограничением домена . Здесь для радикального неравенства n — индекс, а x — подкоренное число.
Это называется ограничением домена . Здесь для радикального неравенства n — индекс, а x — подкоренное число.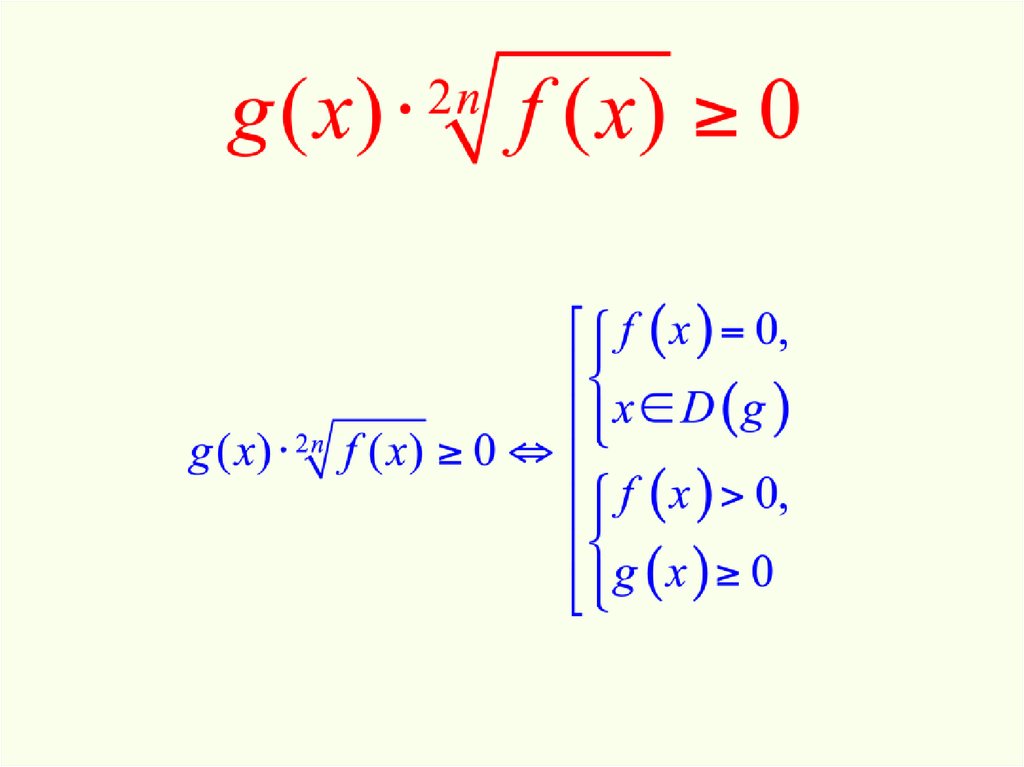 (т. е. ). Здесь обратите внимание, что при использовании индекса в качестве показателя радикального члена он аннулирует радикальный символ, тем самым устраняя его.
(т. е. ). Здесь обратите внимание, что при использовании индекса в качестве показателя радикального члена он аннулирует радикальный символ, тем самым устраняя его.