Математический анализ. (Виленкин)
Математический анализ. (Виленкин)
ОглавлениеПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств.  8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2.  Метод разложения на множители. Метод разложения на множители.3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 4. Извлечение корня из произведения и степени. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.  6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений.  8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 2. Выражение степенных сумм 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения.  § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости. 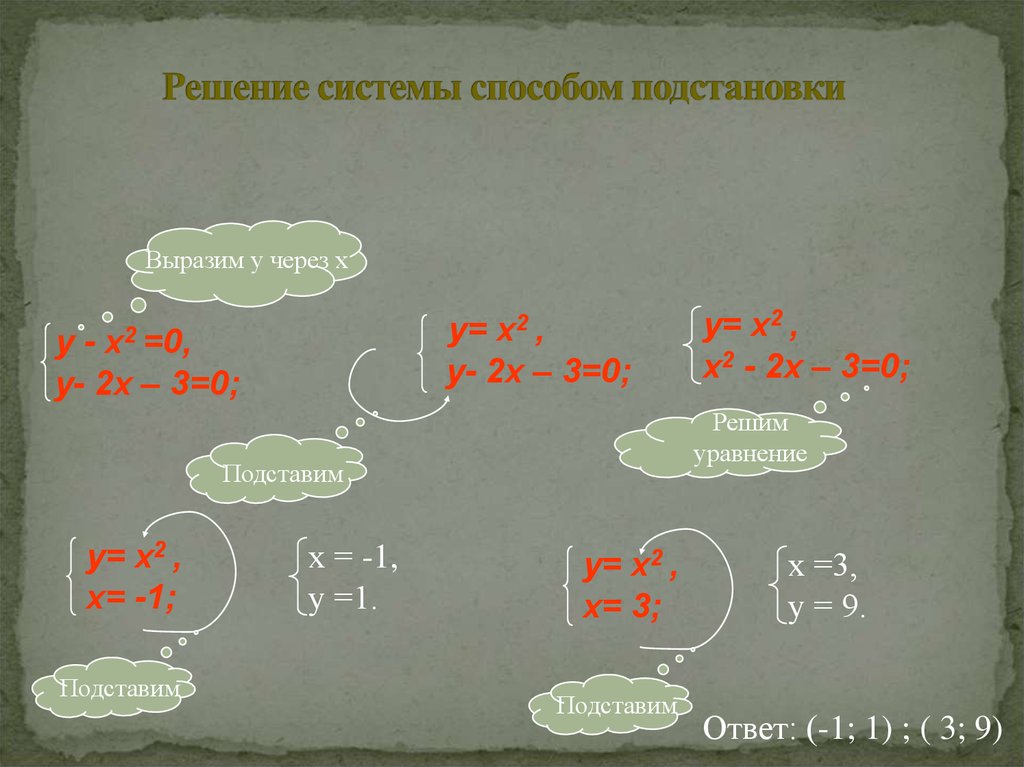 § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 4. Краткие исторические сведения. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2.  Комбинаторные задачи. Продолжение Комбинаторные задачи. Продолжение§ 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения |
1.Подготовительный Цель: актуализировать опорные знания решения линейных уравнений с двумя переменными, решения систем линейных уравнений с двумя переменными Метод: репродуктивный Прием: беседа, объяснение | |||||||||||||||||||||
Деятельность учителя | Деятельность ученика | Развитие познавательных УУД | |||||||||||||||||||
На предыдущих уроках мы учились решать системы линейных уравнений. Вспомним: Система двух линейных уравнений с двум переменными это — ……………..; Что мы называем решением системы уравнений?; Какими способами мы умеем решать системы уравнений? 2. а) 2х + у = 6; б) – 2у + 17х = 15; в) 4х – 9у = 1; г) ху = — 2; д) 7х – 2у = 6; е) 3у – 5х = 4. 3.Является ли решение системы , пара чисел (- 1; 1), (2; — 1), (6; 2,5) | Слушают учителя. Отвечают на поставленные вопросы: Математическая модель, состоящая из двух линейных уравнений с двумя переменными; Пара чисел (х; у), которая одновременно является решением первого и второго уравнений системы; Метод подбора и графический метод. 2. Выражают переменную у через х: а) 2х + у = 6 у = 6 – 2х; б) – 2у + 17х = 15 у = 7,5 + 8,5; в) 4х – 9у = 1 у = ; г) ху = — 2 у = — ; д) 7х – 2у = 6 у = 3 + 3,5х; е) 3у – 5х = 4 у = . 3. Производят проверку: Рассмотрим пару (-1; 1): , (-1; 1) – не является; Рассмотрим пару (2;1): , , (2; — 1) не является; Рассмотрим пару (6; 2,5): (6; 2,5) является | осознавать познавательную задачу, слушать извлекать нужную информацию; осознанное построение речевого высказывания в устной форме; анализ опорных знаний и умений; умение осознанного и произвольного построения речевых высказываний в устной форме; использование знаков – символических средств для решения учебных задач; понимать информацию в модельной форме; осознавать познавательную задачу читать и слушать, извлекая нужную информацию; осуществлять для решения учебных задач операции анализа, сравнения; представлять информацию в развернутом виде; устанавливать причино – следственные связи, делать вывод; | |||||||||||||||||||
2. Цель: возбудить интерес учащихся к изучению нового способа решение систем линейных уравнений Метод: исследовательский Прием: беседа, практическая работа, объяснение | |||||||||||||||||||||
Решите систему уравнений графическим способом: Определили координаты точки пересечения графиков уравнений? | Решают систему уравнений графическим методом: Выразим у через х в каждом уравнении: 2) построим в одной системе координат график каждого уравнения:
Графическим методом определить координаты точки пересечения графиков уравнения неудобно, не достаточно места в тетради для определения точки пересечения. | решения различных задач; представлять информацию в сжатом или развернутом виде; использовать задания на самостоятельное обобщение на основе собственных практических наблюдений; использовать знаково – символичные средства для выполнять учебно – познавательные действия в материализованной и умственной форме; умение выбирать наиболее простые способы решения задач; понимать информацию в изобразительной , схематичной форме; использовать знаково – символические средства для решения задачи; уметь определить условия по заданным исходным данным и конечному результату; уметь самостоятельно найти способы решения проблемы поискового или творческого характера | |||||||||||||||||||
Ориентировочный этап – поиск алгоритма Цель: введения алгоритма решение систем линейных уравнений способом подстановки Метод: частично – поисковый, объяснительно — иллюстративный Прием: разрешение проблемной ситуацией беседа, объяснение | |||||||||||||||||||||
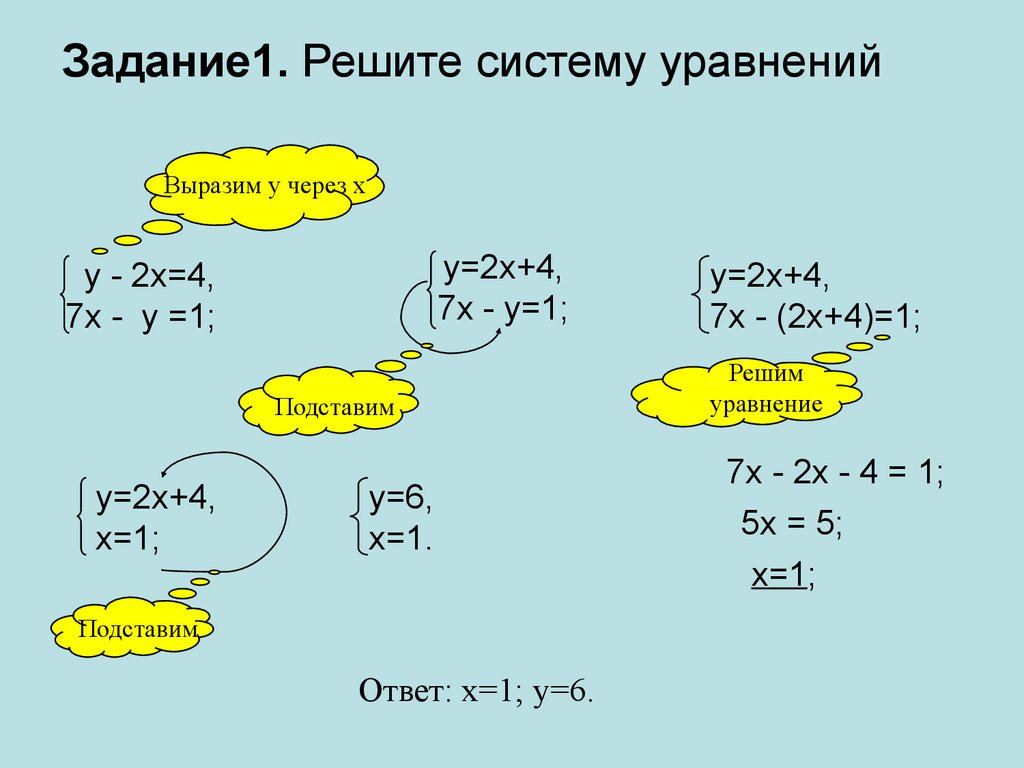
Решим систему уравнений : Выразим из первого уравнения переменную у через х, получим у = 4 – 2х. Это выражение подставим во второе уравнение вместо переменной у. Теперь второе уравнение содержит только одну переменную х. Решим это уравнение. Подставим значение в первое уравнение системы Подстановкой значений х = 1, у = 2 Пара чисел (1; 2) являются единственным решением системы. В эту систему можно, убедится, что такая пара чисел и есть решение системы. | Решают систему уравнений: Решают уравнение: подставляют в первое уравнение систему х = 1 | использовать знако – символические средства для решения различных задач; осознавать познавательную задачу, читать и слушать, извлекая нужную речевого высказывания в устной и письменной форме; устанавливать причинно – следственные связи; поиск и выделение необходимой информации; умение собирать необходимые факты для выдвижения гипотезы и ее обоснование; использовать знако – символические средства для решения различных задач; | |||||||||||||||||||
— обоснования алгоритма Метод: объяснительно – иллюстративный Прием: беседа, объяснение. | |||||||||||||||||||||
Систему линейных уравнений с двумя переменными была решена методом подстановки. Мы следовали определенному алгоритму: Первый шаг, нашего действия был какой?; Вторым шагом, что мы делали? ; Третьим действием, что у нас происходило? Ну и последнее, что в данном алгоритме мы делали? Запишите с учебника на стр. 165, алгоритм решения систем уравнений методом подстановки. | первым шагом мы выражали из одного уравнения системы одну переменную через другую; вторым шагом подставляли полученное выражение вместо переменной в другое уравнение; решали полученное уравнение с одной переменной; последним четвертым шагом мы находили соответствующее значение второй переменной. Записывают алгоритм с учебника | выделение необходимой информации; умение строить логические цепи рассуждений; умение структурировать знания; умение выбирать эффективные способы решения задач; умение осознанного и произвольного построения речевого высказывания в устной и письменной форме; представлять информацию в развернутом виде | |||||||||||||||||||
Этап усвоение алгоритма Цель: отработка алгоритма решение систем линейных уравнений методом подстановки Метод: частично – поисковый, репродуктивный Прием: решение практических задач, беседа | |||||||||||||||||||||
Способом подстановки по алгоритму можно, решить систему линейных уравнений которую мы решали графическим методом. Решить систему линейных уравнений методом подстановки по алгоритму: Какой метод удобнее применить к данной системе графический или метод подстановки | Решают, систему линейных уравнений методом подстановки проговаривая каждый шаг алгоритма: Выразим из первого уравнения у через х: у= 7х; Подставим во второе уравнение вместо у выражение 7х, получим систему: Решим второе уравнение, которое содержит только одну переменную: 3х – 7х + 12 = 0 –4х = – 12 х = 3 подставим в равенство у = 7х вместо х число 3, найдем соответствующее значение у: у =73 у = 21 пара (3; 21) – решение данной системы. К данной системе удобнее применить метод подстановки. | усвоение общего способа действий; использование знако символьные средства для решения различных учебных задач; построение речевого высказывания в устной и письменной форме; рефлексия способов и условий действий; выполнять учебно-познавательные действия в материализованной и умственной форме; построение логической цепи рассуждений; усвоение общего способа действий | |||||||||||||||||||
Этап применение алгоритма при решении задач Метод: частично – поисковый Прием: практическая работа, объяснение | |||||||||||||||||||||
Учитель вызывает к доске, контролируя работу отвечающих и выполняющих задание в тетрадях. Решить систему уравнений методом подстановки: а) б) | Решение систем уравнений: Ответ: пара (2;3) является решением Решение: б) Ответ: пара (1; 4) является решением системы | Построение логической цепи рассуждения; осуществлять для решения учебных задач операции анализа; усвоение общего способа действий; представлять информацию в развернутом виде; выбор наиболее эффективных способов решения задач; структурирование знаний Построение логической цепи рассуждения; осуществлять для решения учебных задач операции анализа; усвоение общего способа действий; представлять информацию в развернутом виде; выбор наиболее эффективных способов решения задач; структурирование знаний; выдвижение гипотез и их обоснование; | |||||||||||||||||||
Этап записи домашнего задания | |||||||||||||||||||||
Запомнить алгоритм решения систем уравнений методом подстановки, № 1132(а), № 1133 (а,б), 1141 (б) | Записывают в дневники Выслушивают краткие объяснения | Находить самостоятельно нужную информацию в материалах учебника информацию | |||||||||||||||||||
Рефлексия | |||||||||||||||||||||
Какой новый способ решения системы уравнений вы узнали? — сформулируйте алгоритм решения систем уравнений способом подстановки | Способ подстановки Формулируют алгоритм | Представлять информацию в развернутом виде. | |||||||||||||||||||
Решение трех уравнений с тремя переменными путем замены
Решение трех уравнений с тремя переменными путем заменыРешение линейной системы линейных Уравнения с тремя переменными подстановкой
Метод подстановки включает алгебраические подстановка одного уравнения в переменную другого.
Это будет примерное уравнение, используемое в инструкциях:
Уравнение 1) x 6y 2z = -8
Уравнение 2) -x + 5y + 3z = 2
Уравнение 3) 3x — 2y 4z = 18
Шаги для решения систем линейных уравнений через замена:
- Решить одно из уравнений для одной из его переменных. Из трех переменных нет неправильного выбора, поэтому выберите решение для любой переменной.
то есть: x= 6y +2z -8
- Далее,
подставьте значение из первой переменной, для которой вы решили, в другую
уравнение и решить для следующей переменной.

то есть: -(6y + 2z -8) +2y-5z = -30
-y + z + 8 = 2
г = у 6
- Замена значение из двух переменных, которые вы решили, и подставьте его в оставшееся уравнение и решить для последней оставшейся переменной. Этот шаг должен позволить вам решить для действительного числа.
то есть: 3(6y + 2y 8) 2y 4 (y 6) = 18
18y 36 = 18
18y = 54
y = 3
5 найдя последнюю переменную, подставьте значение самой последней найденную вами переменную (в примере y=3) в ответ другие уравнения с оставшимися переменными (на примере z = y 6, х = 6). Примечание: Предпочтительно, подставьте значение к наиболее упрощенному уравнению.
то есть: z = 3 6
z = -3
- После
решения для другой переменной, вы должны иметь оставшиеся части
головоломка для последнего уравнения.

то есть: x = 6(3) + 2(-3) 8
x = 18 6 8
x = 4
- Следовательно, в конце концов, вы успешно нашли ответы на систему линейных уравнений с тремя переменными.
Ответ = (4, 3, -3)
ПРАКТИЧЕСКИЕ ЗАДАЧИ
5
5 Практика 2 и
5
5
отточите свои навыки замены!
Удачи!
- -2x + у + 6z = 1
3x + 2y + 5z = 16
7x + 3y 4z = 11
- x 3y + 6з = 21
3x + 2y -5z = -30
2x 5y + 2z = -6
- x 6y 2z = -8
-x + 5y + 3y = 2
3x 2y 4z = 18
Задача-вызов
Подсказка: оставайтесь непредвзятыми
3x + 3y +z = 30
10x — 3y — 7z = 17 + 3Z = -49
9
Как решать системы подстановкой?
Системы решения путем замены
Шэрон П.
4x+2y=-2
y=6x-5
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Тамара Дж. ответил 18.03.13
Репетитор
4.9 (51)
Репетиторство по математике — алгебра и исчисление (все уровни)
Смотрите таких репетиторов
Смотрите таких репетиторов
Система состоит из следующих уравнений: 4x + 2y = -2 и y = 6x — 5
Чтобы решить систему методом подстановки, возьмем одно из уравнений и решим его для любой переменной (x= или y =), затем подставьте это в другое уравнение. Здесь мы видим, что второе уравнение уже решено для одной из переменных, этой переменной является y. Таким образом, мы подставляем то, чему равен y в терминах x, в первое уравнение, таким образом имея возможность решить для x. После того, как мы нашли x, мы используем его значение для решения для y.
Здесь мы видим, что второе уравнение уже решено для одной из переменных, этой переменной является y. Таким образом, мы подставляем то, чему равен y в терминах x, в первое уравнение, таким образом имея возможность решить для x. После того, как мы нашли x, мы используем его значение для решения для y.
с Y = 6x — 5 , затем
4x + 2 y = -2 Заменитель 6x — 5 для y
4x + 2 ( 6x — 5 ) = -2 Умножение внутри каждого внутри. Священные скобки по 2
4x + 2 · 6x + 2 · -5 = -2
4x + 12x -10 = -2 Комбинируйте, как термины с левой стороны уравнения
16x -10 = -2 Добавить 10 в обе части уравнения
16x — 10 + 10 = -2 + 10
16x = 8 разделите обе стороны уравнения на 16 для решения для x
16x/16 = 8/16
x = 1/2
найдите y, подставьте значение x в любое из двух исходных уравнений:
y = 6 x — 5 , x = 1/2
y = 6( 8 1/2) 5
y = 3 — 5
y = -2
Голосовать за 0 Понизить
Подробнее
Отчет
Курт Т. ответил 18.03.13
ответил 18.03.13
Репетитор
4,8 (155)
Репетиторство по математике и подготовка к экзаменам
См. таких репетиторов
Смотрите таких репетиторов
В этом случае вы можете подставить (6x-5) вместо y в первое уравнение, найти x и подставить новое значение x в оба уравнения, чтобы убедиться, что вы получите тот же ответ для y…
4x + 2 (6x — 5) = -2
4x + 12x — 10 = -2
16x = 8
x = 1/2
Теперь подставьте 1/2 вместо x в обоих уравнениях…
4 ( 1/2) + 2y = -2
2 + 2y = -2
2y = -4
y = -2
y = 6 (1/2) — 5
y = 3 — 5
г = -2
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.



 Выразите переменную у через х:
Выразите переменную у через х: Мотивационный этап
Мотивационный этап Возможно есть другой способ?
Возможно есть другой способ?