Как считать примеры со степенями: Свойства степеней, действия со степенями

alexxlab / / Разное

Степень числа. Квадрат и куб числа 5 класс онлайн-подготовка на Ростелеком Лицей

Определение степени

 

Мы с вами знаем, что если дана сумма одинаковых слагаемых, например,

 

 ,

то её можно записать как , или, например,

Мы видим, что первое число в правых частях равенств показывает, сколько элементов мы складывали, а второе – какие элементы мы складывали.

Было бы неплохо, если бы для умножения тоже существовала более компактная запись. Например, для того чтобы упростить запись такого выражения

Такая запись есть. Она называется четвертой степенью числа 3. Почему четвертой? Потому что троек у нас 4 штуки.

Так выглядит данная запись:

Читается как «три в четвертой степени» или «три в четвертой».

Такая запись читается как «икс в пятой степени» или «икс в пятой».

 

Квадрат и куб

 

 

У второй и третьей степеней есть свои названия.

 

Когда мы n умножим на n, получим n во второй степени. Но также мы можем сказать, что получили n в квадрате. Если у нас есть квадрат со стороной, равной n, то его площадь равна .

Если а умножим на себя два раза, то получим a в третьей степени:

Обычно про такую запись говорят не a в третьей степени, а a в кубе. Ведь объем кубика со стороной a равен .

Пример 1. 

Пример 2.

Пример 3.

Есть ли первая степень? Да, есть. Если степень равна 1, значит, у нас есть один сомножитель. Например,

 

Нулевая степень

Нулевая степень означает, что мы рассматриваем 0 сомножителей.

Принято считать, что нулевая степень любого числа равна 1.

 

 

Решение примеров со степенями

 

 

Пример 4. Представьте произведение в виде степени.

 

1)       

У элементов степени есть специальные названия. То, что мы возводим в степень, называется основанием степени. В нашем примере это 1. Число, обозначающее степень, называется показателем. В нашем примере это 4.

2)             

3)           

Пример 5. Представьте степень в виде произведения.

1) 

2) 

3) 

Пример 6. Вычислите сумму квадратов чисел 5 и 4.

Что такое сумма квадратов? Данная запись выглядит так:

То есть сначала мы возводим каждое число в степень, а затем складываем.

Стоит отличать данную запись от следующей:

В таком случае мы сначала складываем, а потом возводим в степень.

Пример 7. Вычислите куб разности чисел 2 и 1.

Сначала нам необходимо найти разность, а потом полученное число возвести в третью степень:

Совершенно другой результат мы получим при вычислении разности кубов, то есть если мы сначала возведем числа в третью степень, а затем выполним вычитание.

 

Возведение в квадрат чисел, оканчивающихся на 5

Возведем число 35 в квадрат:

Возьмем первую цифру нашего числа – 3 – и умножим ее на следующую, то есть ту, которая идет после нее в натуральном ряду – 4. Получим 12. Теперь просто припишем к 12 число 25:

Мы получили число тысяча двести двадцать пять.

1)

2)

Почти то же самое работает и для трехзначных чисел. Только теперь мы берем не цифру, которая стояла перед цифрой 5, а число. Например,

Получили одиннадцать тысяч двадцать пять.

 

 

Заключение

 

 

Мы познакомились с такими понятиями, как квадрат и куб числа, кроме того, дали чуть более сложное определение степени; узнали, что такое показатель степень, основание степени; научились преобразовывать произведение одинаковых чисел в степень и наоборот.

 

 

Список рекомендованной литературы

  1. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика, 5 класс (в 2 частях). ООО «ИОЦ МНЕМОЗИНА».
  2. Мерзляк А. Г., Полонский В. Б., Якир М. С. Математика. 5 класс – М.: Вентана-Граф.

 

Рекомендованные ссылки на ресурсы сети Интернет

  1. Теоретический материал (Источник)
  2. Учебник Н. Я. Виленкина. Математика 5 класс (Источник)
  3. Презентация (Источник)

 

Домашнее задание

  1. Представьте в виде степени произведение:

а)

б)

в)

г)

  1. Запишите выражение в виде степени и вычислите значение:

а) 2 в квадрате

б) 3 в пятой степени

в) 7 в кубе

  1. Представьте степень в виде произведения:

а)

б)

в)

г)

 

n (x в степени n). Вы можете считать, что x и n малы и переполнения не происходит.

Пример — 

 мощность(3,4) = 81
power(2,-3) = 0,125
Решения
  1. Наивный итеративный подход
  2. Метод «разделяй и властвуй»
  3. Оптимизированный подход «разделяй и властвуй»
числа состоит в том, чтобы умножить это число ровно n раз.

Что, если n отрицательно, например, pow(2,-3) = 0,125 93).

Шаги решения
  1. Объявить и инициализировать переменную для хранения мощности, скажем, power = 1 .
  2. Запустить цикл от 1 до экспоненты, увеличивая счетчик цикла на 1 на каждой итерации.
  3. Для каждой итерации внутри цикла умножьте степень на число.
  4. Для отрицательного показателя степени верните 1/степень В противном случае верните степень
Псевдокод 
 число с плавающей запятой (основание, число){
    логическое значение Отрицательное = Ложь
    если (выражение < 0) {
        отрицательный = Истина
    }
    поплавковая мощность = 1
    for(int i = 1 to abs(expo)){
        мощность = мощность * база
    }
    если (отрицательно) {
       возврат (1/сила)
    }
    вернуть власть
}
Анализ сложности

Временная сложность — O(n) или O(показатель степени)

Пространственная сложность — O(1)

Критические идеи для размышления
6 Будет ли работать алгоритм, если вход отрицательный ?
  • Будет ли алгоритм работать, если входной показатель степени отрицательный?
  • Можете ли вы придумать лучший подход к ее решению?
    • 2.
    Метод «разделяй и властвуй»

    Метод «разделяй и властвуй» каждый раз возводит число в квадрат, а не умножает его на само число.

    Теперь, если мы попытаемся визуализировать этот процесс рекурсивно, то это будет выглядеть так: мощность (базовая, экспо) = мощность (базовая, экспо/2) * мощность (базовая, экспо/2) если показатель степени нечетный: power(base, expo) = base * power(base, expo/2)*power(base, expo/2)

    Шаги решения
    1. Проверить, равен ли показатель степени 0, затем вернуть 1, иначе
    2. В зависимости от четности или нечетности рекурсивно вызвать степенную функцию, как определено выше.
    Псевдокод 
     число с плавающей запятой (внутренняя база, целая экспо) {
    если (экспо равно 0)
        вернуть 1
    если (экспо% 2 == 0)
       сила возврата(база, экспо / 2) * мощность(база, экспо / 2)
    еще {
       если (выражение > 0)
           return (мощность(база, экспо/2) * мощность(база, экспо/2))* база
       еще
           return (мощность(база, экспо/2) * мощность(база, экспо/2))/база
    }
}
    Анализ сложности

    Временная сложность — O(n) или O(экспонента) (Почему?)

    Пространственная сложность — O(log(n)) (Думай!) Критическая идея

    5 90 с Думайте

    • Можете ли вы указать повторяющиеся вычисления?
    • Будет ли этот алгоритм работать для отрицательного значения показателя степени?
    3.
    Оптимизированный подход «разделяй и властвуй»

    Если вы посмотрите на предыдущую рекурсивную диаграмму подхода «разделяй и властвуйте», вы обнаружите, что на каждом шаге мы пересчитываем мощность базы на каждом уровне, т.е. считается одна и та же мощность дважды.

    Таким образом, вместо того, чтобы дважды рекурсивно вызывать степенную функцию, мы могли бы просто возвести степенную функцию в квадрат один раз. Таким образом, мы могли бы оптимизировать временную сложность.

    Псевдокод 
     число с плавающей запятой (внутренняя база, внутр. экспо) {
    если (экспо равно 0)
        вернуть 1
    температура = мощность (база, экспо/2)
    если (экспо% 2 == 0)
       температура возврата * температура
    еще{
       если (выражение > 0)
           возврат temp * temp * base
       еще
           температура возврата * температура / база
    }
}
    Анализ сложности

    Временная сложность: O(log n) или O(log expo)

    Пространственная сложность: O(log n) или O(log expo) из-за рекурсивного пространства стека 

      Критические идеи для размышления 
    •  Можете ли вы придумать лучший подход, чем этот?
    •  Пробный запуск этого алгоритма на нескольких примерах.
     Сравнение различных решений 
     Предлагаемые задачи для решения 
    •  Вычисление квадратного корня из числа
    •  Рассчитать значение nCr
     Вот и все для этого блога. Надеюсь, вы сегодня узнали что-то новое.
      Приятного программирования, наслаждайтесь алгоритмами! 
     Использование логарифмов для вычисления произвольных корней и степеней – World Mental Calculation 
     Этот сложный метод использует свойства логарифмов (с основанием 10), чтобы представить общий метод вычисления любого корня или степени. Например, с помощью этого метода можно эффективно рассчитать с точностью до 4 знаков следующее: 95\) прямое умножение проще.
      
     Однако для самых экстремальных корней и способностей этот метод работает хорошо. Это один из успешных методов, использованных в неожиданной задаче Кубка мира по умственным вычислениям 2016 года, который заключался в вычислении:
    .
     \(\sqrt[4]{2016} – \sqrt[6]{2016} + \sqrt[7]{2016}\)
     Математика: 
     Для простоты все логарифмы и экспоненты должны быть основаны на 10.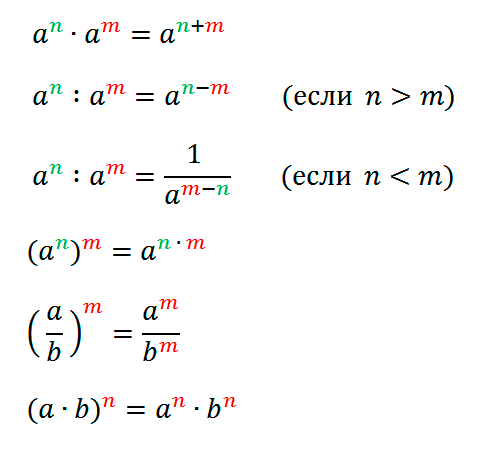 Десятичные ответы должным образом округлены.
     Логарифм  9{\ журнал (п)} \)
     Итак, если у нас есть сложный для вычисления корень или степень, мы можем сначала вычислить его логарифм, используя правила (1)-(4), а затем мы можем найти его антилогарифм, который и будет нашим окончательным ответом.
       
       
     Подготовка: 
    •  Вам нужно знать, как считать логарифмы и вычислять антилогарифмы
    •  Вам нужно будет запомнить достаточно значений логарифмов (например, \(\log 2 = 0,30103\))
      Метод: 9\pi) = \pi * \log \pi\)
     Используя наш алгоритм вычисления логарифмов, мы аппроксимируем \(\log \pi\) следующим образом:
     \(\log{3,14159} = \log{\frac{22}{7} - 0,04\%} = \log{11} + \log{2} - \log{7} - 0,00432*0,04\)
      
     Примечание: 0,04% от быстрого приближения \(\frac{\frac{22}{7} – \pi}{\pi}\)
     \(\log{3,14159} = 1,04139 + 0,30103 - 0,84510 - 0,00017 = 0,49715\)
      
     Самая сложная часть в этом расчете — слепое умножение 3,14159.
     
    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *