Тема 3 Нормальные формы
3.1 Разложение булевых функций по переменным
3.2 Алгебра Жегалкина
Выше мы показали, что любая булева функция может быть задана с помощью таблицы истинности. В настоящем разделе излагается переход от табличного перехода задания функции к аналитическому.
3.1 Разложение булевых функций по переменным. Пусть G – параметр, равный 0 или 1. Введем обозначение.
Проверкой легко установить, что XG=1, тогда и только тогда, когда X=G. Отсюда следует, конъюнкция равна 1 (здесь G равен 0 или 1) тогда и только тогда, когда . Например, конъюнкция (в которой G2=G1=0, G3=G4=1) равна 1 только в случае, когда X1=X2=0, X3=X4=1.
Теорема 1. Всякая булева функция F(X1,X2,…,Xn) может быть представлена в следующей форме:
(1)
Где 1≤K≤N, в дизъюнкции берется по всем наборам значений переменных.
Это представление носит название разложения функции по переменным . Например, при n=4, k=2 разложение (1) имеет вид:
.
Докажем справедливость разложения (1). Для этого возьмем произвольный набор значений переменных . Покажем, что левая и правая части соотношения (1) принимают при нем одно и то же значение. Действительно, так как XG=1 тогда и только тогда, когда X=G, то среди 2К конъюнкции правой части (1) в единицу обращается только одна, в которой . Все остальные конъюнкции равны нулю.
Поэтому . В качестве следствия из разложения (1) получаем следующие два специальных разложения.
Разложение по переменной XN:
(2)
Если булева функция не есть константа 0, то справедливо разложение
Разложение по всем переменным:
, (3)
Где дизъюнкция берется по всем наборам , при которых значение функции равно 1.
Разложение (3) называется совершенной дизъюнктивной нормальной формой (сокращенная запись СДНФ) функции.
Разложение (3) дает способ построения СДНФ. Для этого в таблице истинности отмечает все строки , в которых . Для каждой такой строки образуем конъюнкцию и затем все полученные конъюнкции соединяем знаком дизъюнкции.
Таким образом, существует взаимно однозначное соответствие между таблицей истинности функции и ее СДНФ. А это значит, что СДНФ для булевой функции единственна.
Единая булева функция, не имеющая СДНФ, есть константа 0.
Пример 1. Найти совершенную дизъюнктивную форму для функции .
Составим таблицы истинности для данной функции:
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 | 0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
Отсюда получаем: ==.
Важную роль в алгебре логики играет следующее разложение булевых функций.
Теорема 2. Всякая булева функция Может быть представлена в следующей форме:
(4)
Где 1≤k≤n, а конъюнкция берется По всем 2K наборам значений переменных.
Действительно, пусть – произвольный набор значений переменных. Покажем, что любая и правая части соотношения (4) принимают при нем одно и то же значение. Так как только тогда, когда , то среди 2k дизъюнкций правой части (4) в 0 обращается только одна, в которой . Все остальные дизъюнкции равны 1.
Поэтому ==.
Непосредственно из разложения (4) следуют следующие разложения булевых функций:
(5)
, (6)
Последнее разложение носит название совершенной конъюнктивной нормальной формы (СКНФ). Разложение (6) дает способ построения СКНФ. Для этого в таблице истинности отмечаем все строки , в которых . Для каждой такой строки образуем дизъюнкцию и затем все полученные конъюнкции соединяем знаком конъюнкции.
Таким образом, существует взаимно однозначное соответствие между таблицей истинности функции и ее СКНФ. А это значит, что СКНФ для булевой функции единственна.
Единственная булева функция, не имеющая СКНФ, есть константа 1.
Пример 2. Найти совершенную конъюнктивную нормальную форму для функции .
Составим таблицу истинности для данной функции.
|
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
Отсюда получаем СКНФ
.
Формула вида (краткая запись ), где — конъюнкции называется Дизъюнктивной нормальной формой.
В силу приведенного определения ДНФ будут, например, выражения: , .
Как отмечено в пункте 2.2, все логические операции можно свести к трем: конъюнкции, дизъюнкции и отрицания. Причем, ввиду закона де Моргана, знак отрицания можно предполагать отнесенным только к переменным.
Теперь, используя дистрибутивный закон, раскрываем скобки и получаем дизъюнктивную нормальную форму. Итак, справедлива следующая теорема.
Теорема 3. Для любой формулы алгебры логики существует равносильная ей дизъюнктивная нормальная форма.
Доказательство данной теоремы дает способ построения дизъюнктивной нормальной формы для любой формулы алгебры логики.
Пример 3. Найти дизъюнктивную нормальную форму для следующей формулы:
.
Исключая знак по закону и применяя законы де Моргана и двойного отрицания, получаем:
Затем, применяя закон дистрибутивности, раскроем скобки
Последнее выражение есть дизъюнктивная нормальная форма.
Форма вида
(краткая запись ), где — дизъюнкции называется Конъюнктивной нормальной формой (сокращенно КНФ).
В силу приведенного определения КНФ будут, например, выражения:
, .
Как показано выше, для любой формулы алгебры логики существует равносильная ей дизъюнктивная форма. Используя дистрибутивный закон , из данной ДНФ легко получить КНФ.
Итак, справедлива следующая теорема.
Теорема 4. Для любой формулы алгебры логики существует равносильная ей конъюнктивная нормальная форма.
Доказательство данной теоремы дает способ построения конъюнктивной нормальной формы для любой формулы алгебры логики.
Пример 4. Найти дизъюнктивную и конъюнктивную нормальные формы для следующей формулы: .
Используя закон , исключаем знак .
Получаем формулу .
Используя закон де Моргана, получаем формулу .
Раскрывая скобки, получаем дизъюнктивную нормальную форму
.
Чтобы получить конъюнктивную нормальную форму, применим к формуле
Дистрибутивный закон, получаем:
Последнее выражение является конъюнктивной нормальной формой.
Так как и , то полученная КНФ равносильна следующей КНФ:
.
Среди всех нормальных формул данной формулы выделим совершенную нормальную форму как дизъюнктивную, так и конъюнктивную. Учитывая разложение (3), нетрудно заметить, что совершенная дизъюнктивная нормальная форма формулы алгебры логики, содержащей ровно n различный переменных, есть ее дизъюнктивная нормальная форма, в которой:
1) все конъюнкции попарно различны;
2) каждая конъюнкция содержит ровно n переменных;
3) в каждой конъюнкции встречаются все n переменных.
На примере 1 мы рассмотрели один из способов построения СДНФ, основанный на составлении таблицы истинности. Следующий способ построения СДНФ основан на применении законов алгебры логики.
Пример 5. Найти совершенную дизъюнктивную форму формулы .
Используя, что , получаем . Ввиду законов де Моргана и двойного отрицания имеем:
Получили дизъюнктивную нормальную форму. Данная ДНФ равносильна формуле .
Раскрывая скобки, получаем:
.
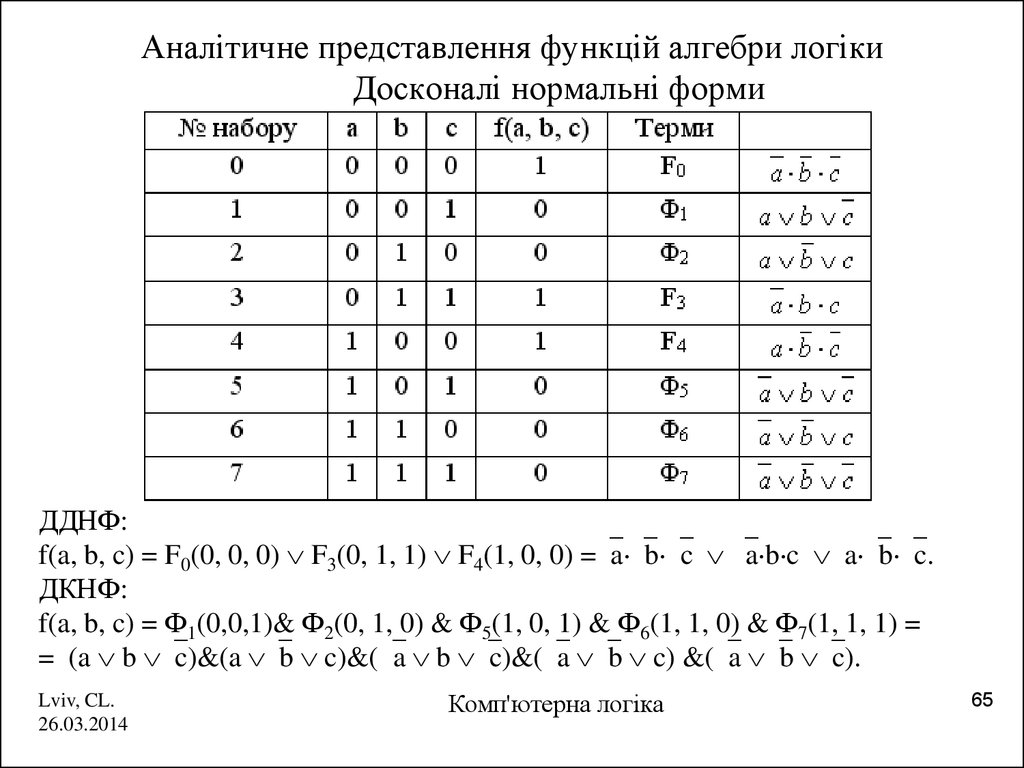
Используя закон идемпотентности, получаем требуемую СДНФ:
.
Учитывая разложение (6), нетрудно заметить, что совершенная конъюнктивная нормальная форма формулы алгебры логики, содержащей ровно N различных переменных, есть ее конъюнктивная нормальная форма, в которой:
1) все дизъюнкции попарно различны;
2) каждая дизъюнкция содержит ровно n членов;
3) в каждой дизъюнкции встречаются все n переменных.
На примере 2 мы рассмотрели один из способов построения СКНФ, основанный на составлении таблицы истинности. Следующий способ построения СКНФ основан на применении законов алгебры логики.
Пример 6. Найти совершенную конъюнктивную нормальную форму формулы
.
Используя, что , получаем
.
Данная формула является конъюнктивной нормальной формой. Она равносильна формуле
.
Используя закон дистрибутивности, получаем:
Применяя закон идемпотентности, получаем требуемую совершенную конъюнктивную нормальную форму
.
Формула алгебры логики называется Тождественно истинной, если она при всех значениях входящих в нее переменных принимает значение истинно.
Примерами тождественно истинных формул являются формулы:
Формула алгебры логики называется Тождественно ложной, если она при всех значениях, входящих в нее переменных, принимает значение Ложь.
Примерами тождественно ложных формул являются формулы:
,
Формула алгебры логики называется Выполнимой, если она при некоторых значениях, входящих в нее переменных, принимает значение Истинно.
Примерами выполнимых формул являются следующие формулы:
, .
В алгебре логики можно поставить следующую задачу: указать способ (алгоритм), позволяющий для каждой формулы алгебры логики выяснить, является она тождественно истинной или нет. Поставленная задача носит название Проблемы разрешения.
Рассмотрим следующие два способа решения этой задачи.
Способ 1 (табличный).
Для того, чтобы определить, является ли данная формула тождественно истинной или нет, достаточно составить ее таблицу истинности.
Однако данный способ, хотя и дает принципиальное решение проблемы разрешимости, он довольно громоздкий.
Способ 2 основан на приведении формул к нормальной форме.
Теорема 4. Формула алгебры логики тогда и только тогда является тождественно истинной, когда каждая дизъюнкция в ее конъюнктивной нормальной форме содержит некоторую переменную вместе с ее отрицанием.
Действительно, если каждая дизъюнкция в конъюнктивной нормальной форме содержит переменную вместе с ее отрицанием, то все дизъюнкции равны 1, ибо , . Отсюда следует, что КНФ является тождественно истинной.
Пусть теперь данная формула является тождественно истинной, и пусть есть некоторая дизъюнкция в КНФ данной формулы. Допустим, что данная дизъюнкция не содержит переменной вместе с ее отрицанием. В таком случае мы может каждой переменной, не стоящей под знаком отрицания, дать значение 0, а каждой переменной, стоящей под знаком отрицания – значение 1.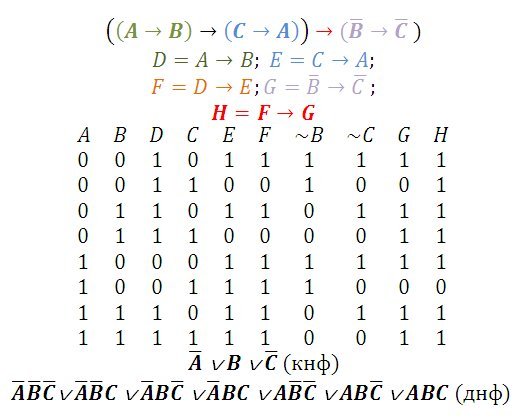
После указанной подстановки все дизъюнкции станут равны 0, следовательно, формула не является тождественно истинной. Получили противоречие.
Пример 7. Выяснить, будет ли тождественно истинной формула
Используя, что , получаем
.
Применяя закон дистрибутивности, получаем КНФ:
.
Так как каждая дизъюнкция содержит некоторую переменную вместе с ее отрицанием, то формула тождественно истинна.
Аналогично предыдущей теореме доказывается теорема:
Теорема 5. Формула алгебры логики тогда и только тогда является тождественно ложной, когда каждая конъюнкция в ее дизъюнктивной форме содержит некоторую переменную вместе с ее отрицанием.
3.2 Алгебра Жегалкина. Множество булевых функций, рассматриваем вместе с операциями конъюнкции и сложения (по модулю два), будем называть алгеброй Жегалкина.
Непосредственно проверкой (с помощью таблиц истинности) устанавливаются следующие законы:
— закон коммутативности;
— закон ассоциативности;
— закон дистрибутивности;
В алгебре Жегалкина роль совершенных нормальных форм булевой алгебры играют полиномы Жегалкина.
Полиномом Жегалкина называется полином вида
Причем в каждом наборе все координаты различны, а суммирование ведется по некоторому множеству таких не совпадающих наборов, А – константа 0 или 1.
Например, выражение является полиномом Жегалкина, а выражения и нет, так как в первом выражении имеется конъюнкция, содержащая две переменные y, а второе выражение содержит два одинаковых слагаемых и .
Если в произвольной форме алгебры Жегалкина раскрыть скобки и произвести все возможные упрощения по указанным выше законам и закону идемпотентности, то получится формула, являющаяся полиномом Жегалкина.
Рассмотрим теперь взаимосвязь, существующую между операциями булевой алгебры и алгебры Жегалкина. Непосредственной проверкой устанавливается
(1)
Ранее мы показали, что любая булева функция может быть выражена в виде формулы через отрицание, конъюнкцию и дизъюнкцию. Согласно законам (1) получаем, что любая булева функция может быть выражена в виде формулы алгебры Жегалкина.
Следовательно, существование полинома Жегалкина доказано для любой булевой функции.
Число различных слагаемых (конъюнкций) полинома Жегалкина от переменных равно числу всех подмножеств из n элементов, т. е. 2n. Число различных полиномов, которых можно образовать из этих конъюнкций, равно числу всех подмножеств множества данных конъюнкций, т. е. . Следовательно, число всех полиномов Жегалкина от n переменных равно числу всех булевых функций от n переменных. Отсюда следует единственное представление булевой функции посредством полинома Жегалкина. Итак, справедлива следующая теорема.
Теорема 6. Каждая булева функция может быть единственным образом выражена при помощи полинома Жегалкина.
Пример 8. Выразить в виде полинома Жегалкина.
1 способ. Ищем требуемый полином методом неопределенных коэффициентов: .
При X=y=0 имеем: d=1;
При X=0, y=1 имеем: a=0;
При X=1, y=0 имеем: b=1;
При X=1, y=0 имеем: 1=a+b+c+d =a+1+0+1=a, т.
е. а=1.
Отсюда
2 способ.
| < Предыдущая | Следующая > |
|---|
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 4 из 6Следующая ⇒ Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Пример КНФ: ( )( )( ). Пусть ДНФ F имеет вид F= , где – элементарные конъюнкции. Процедура приведения ДНФ к КНФ: 1. Применить к F правило двойного отрицания F= и привести к ДНФ , где – элементарные конъюнкции. Тогда F= = = . 2. С помощью правил де Моргана освободиться от второго отрицания и преобразовать отрицания элементарных конъюнкций в элементарные дизъюнкции . Тогда F= = × ×…× = × ×…× 5. Двойственность. Функция f*( ,…, ) называется двойственной к функции f ( ,…, ), если f*( ,…, )= ( ,…, ). Отношение двойственности между функциями симметрично, т. ( ,…, )= ( ,…, )=f*( ,…, ). Функция, двойственная к самой себе, называется самодвойственной. Принцип двойственности: если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула F* будет представлять функцию f*, двойственную f. Принцип двойственности в булевой алгебре: если в формуле F, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу F*, представляющую функцию f*, двойственную f. Пример 1. Доказать справедливость обобщенного склеивания методом эквивалентных преобразований. Выполним эквивалентные преобразования: ×1 .
Пример 2. Получить СДНФ функции, используя эквивалентные соотношения: f (x,y,z,u)=xy Ú xz Ú zu.
f( x,y,z,u) = .
Пример 3. Упростить булевы формулы: а) ( , , ) ; б) f (x,y,z) .
а) ( , , ) ×1 ; б) f (x,y,z) 0× Ú 0×z Ú x×0Ú xyz Ú Ú xzz .
Пример 4. Представить булеву формулу в базисе {&,Ø} и {Ú,Ø}. а) ; б) .
Пример 5. Упростить СДНФ функции f (x,y,z,u)
Для эффективного упрощения СДНФ используем метод Блейка-Порецкого. Метод заключается в попарном склеивании всех элементарных конъюнкций СДНФ между собой, а также полученных в процессе склеивания элементарных конъюнкций меньшего числа переменных и затем – поглощении конъюнкциями меньшего числа переменных конъюнкций большего числа переменных. Рассмотрим метод Блейка-Порецкого “в действии”, для чего пронумеруем элементарные конъюнкции СДНФ: 1 2 3 4 5 6 7 Выполним все возможные попарные склеивания элементарных конъюнкций в СДНФ (под результатом склеивания проставим номера склеиваемых конъюнкций): 1,6 1,7 2,3 2,4 2,5 3,7 4,6 4,7 5,6 Выполним все возможные попарные склеивания полученных элементарных конъюнкций трех переменных: 1,6 1,7 2,3 2,4 2,4 2,5 4,7 4,6 4,7 3,7 5,6 4,6 Очевидно, что дальнейшее склеивание в данном примере невозможно. Объединим символом Ú все полученные дизъюнкции элементарных конъюнкций. Таким образом, в результате попарного склеивания получили: f (x,y,z,u) . Выполним теперь в этом выражении поглощение, в результате чего получим: f (x,y,z,u)=
Пример 6. Привести к ДНФ формулу: f (x,y,z)= .
f (x,y,z) .
Пример 7. Привести формулу к КНФ: f (x,y,z) . f (x,y,z) .
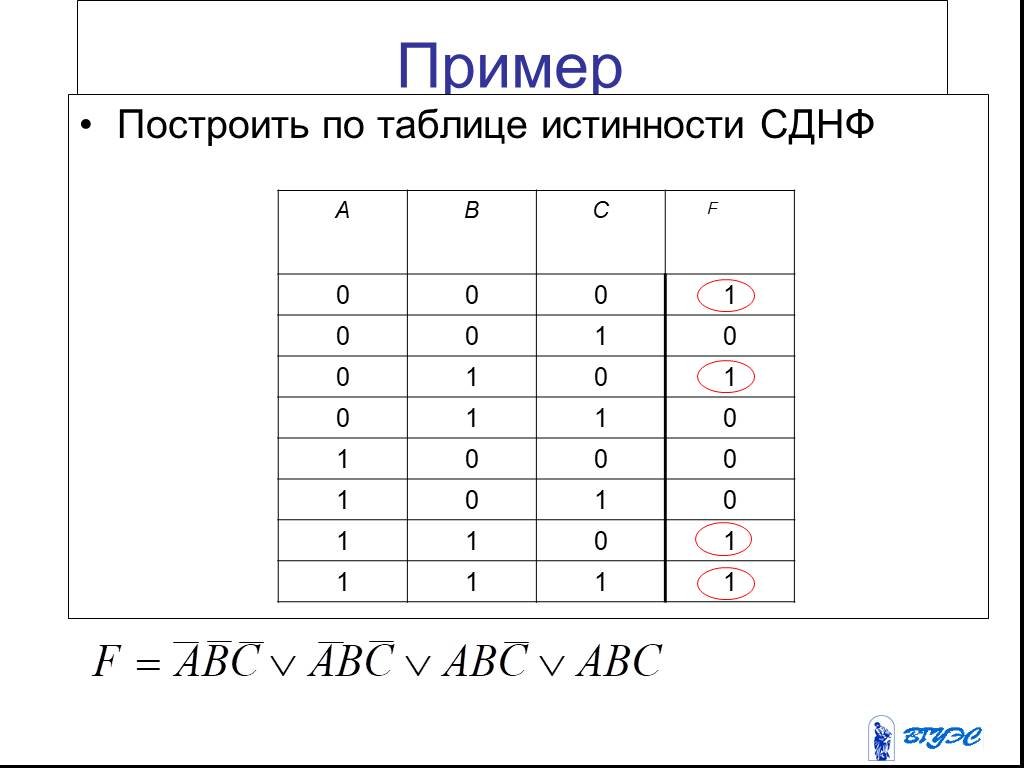
Пример 8. Получить СКНФ функции f (x,y,z,u) из примера 2.
В примере 2 для заданной функции f (x,y,z,u)=xyÚxzÚzu была получена СДНФ: f (x,y,z,u) . Воспользуемся этими данными для получения СКНФ, для чего определим единичное множество функции f (x,y,z,u), т.е. множество наборов, на которых f =1:{(1111),(1101),(1110),(1100),(1011),(1010), (0111),(0011)}. Всего наборов функции четырех переменных 24=16. Определим теперь нулевое множество для f (x,y,z,u), т.е. множество наборов, на которых f =0: {(0000),(0001),(0010),(0100),(0101),(0110),(1000), (1001)}. f (x,y,z,u) .
Пример 9. Доказать справедливость принципа двойственности в булевой алгебре, исходя из общего принципа двойственности.
Найдем для каждой операции булевой алгебры ( ; &, Ú, Ø) двойственные им операции. а) Пусть f (x,y)=x×y. Тогда f*(x,y) xÚy. б) Пусть f (x,y)=xÚy. Тогда f*(x,y) x×y. в) Пусть f (x) . Тогда f*(x) . Таким образом, конъюнкция двойственна дизъюнкции, дизъюнкция – конъюнкции, а отрицание самодвойственно. Наконец, константы 0 и 1 принадлежат множеству логических функций , поэтому 0 и 1 могут содержаться в булевой формуле и являются двойственными друг к другу: если ( ,…, )=0, то f*( ,…, ) ( ,. Отсюда следует справедливость принципа двойственности в булевой алгебре.
Пример 10. Пусть f (x,y,z) . Найти ДНФ двойственной функции f*(x,y,z), исходя из: а) определения двойственности функции; б) принципа двойственности в булевой алгебре.
а) f*(x,y,z) xz; б) f*(x,y,z) xz.
Вопросы для самопроверки и упражнения. 1. Доказать методом эквивалентных преобразований справедливость соотношений п.11, п.12, п.13. 2. Упростить СДНФ импликации и функции Шеффера, используя эквивалентные соотношения. 3. Логическая функция ( , , ) представлена формулой ( , , ) . Упростить формулу и получить СДНФ, используя: а) табличное представление функции f ; б) расщепление (обратное склеивание). 4. Для функций, заданных в виде ДНФ, получить СДНФ, используя эквивалентные преобразования, и упростить СДНФ, использую метод Блейка-Порецкого, описанный в примере 5. а) f (x,y,z) ; г) f (x,y,z) ; б) f (x,y,z) ; д) f (x,y,z) . в) f (x,y,z) ; 5. Привести формулы к ДНФ: а) ( , , ) ; б) ( , , ) ; в) ( , , ) ; г) ( , , ) . 6. Для функций ( , , ), заданных в упражнении 5: 1) получить КНФ, используя правило приведения ДНФ к КНФ; 2) найти СДНФ и СКНФ, используя табличное представление функции. 7. Подтвердить самодвойственность функции f (x,y,z)= , используя принцип двойственности в булевой алгебре. 8. Для функции ( , , ) найти ДНФ двойственной функции f*( , , ), исходя из: 1) определения двойственной функции; 2) принципа двойственности в булевой алгебре: а) ( , , ) ; б) ( , , ) ; в) ( , , ) . 9. Методом эквивалентных преобразований подтвердить справедливость правил 9, 12 §1.2 логически правильных рассуждений. 10. Убедиться в неправильности рассуждений а)–в), приведенных в §1.2: а) стандартным методом; б) методом эквивалентных преобразований.
⇐ Предыдущая123456Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Определение реакций опор и моментов защемления
е. если f* двойственна к f, то f двойственна к f*:
Отсюда по правилу построения СКНФ из нулевого множества функции:
.., ) 1. Аналогично, если f =1, то f*=0.
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.) логика — Преобразование CNF в DNF
спросил
Изменено 3 года назад
Просмотрено 675 раз
$\begingroup$
У меня есть формула
$(L\Leftrightarrow (A\vee J))$
и я должен превратить ее в DNF и CNF. Когда я использую правила де Моргана и так далее, формула выглядит как
$(L\Стрелка вправо (A\vee J))\клин ((A\vee J)\Стрелка вправо L)$
$(\lnot L\vee (A\vee J))\клин ((\lnot A\wedge \lnot J)\vee L)$
CNF довольно просто его
$(\lnot L \vee A\vee J)\wedge (L\vee \lnot A)\wedge (L\vee \lnot J)$
Но как мне сделать из этой формулы ДНФ?
- логика
- исчисление высказываний
- конъюнктивная нормальная форма
- дизъюнктивная нормальная форма
$\endgroup$
5
$\begingroup$
Простой способ вычислить ДНФ, логически эквивалентную формуле $L \Leftrightarrow (A \lor J)$, состоит в том, чтобы посмотреть на ее таблицу истинности и «построить» формулу, соответствующую «дизъюнкции» строк, для которых $ L \Leftrightarrow (A \lor J)$ верно.
$\begin{массив}{ccccc} A & J & L & A \lor J & L \Leftrightarrow (A \lor J) \\ \mathtt{t} & \mathtt{t} & \mathtt{t} & \mathtt{t} & \mathtt{t} \\ \mathtt{t} & \mathtt{t} & \mathtt{f} & \mathtt{t} & \mathtt{f} \\ \mathtt{t} & \mathtt{f} & \mathtt{t} & \mathtt{t} & \mathtt{t} \\ \mathtt{t} & \mathtt{f} & \mathtt{f} & \mathtt{t} & \mathtt{f} \\ \mathtt{f} & \mathtt{t} & \mathtt{t} & \mathtt{t} & \mathtt{t} \\ \mathtt{f} & \mathtt{t} & \mathtt{f} & \mathtt{t} & \mathtt{f} \\ \mathtt{f} & \mathtt{f} & \mathtt{t} & \mathtt{f} & \mathtt{f} \\ \mathtt{f} & \mathtt{f} & \mathtt{f} & \mathtt{f} & \mathtt{t} \\ \end{массив}$
Формула $L \Leftrightarrow (A \lor J)$ верна в строке 1 (что соответствует формуле $A \land J \land L$), строке 3 (что соответствует формуле $A \land \ lnot J \land L$), строка 5 (соответствует формуле $\lnot A \land J \land L$) и строка 8 (соответствует формуле $\lnot A \land \lnot J \land \ не L$). Следовательно, ДНФ, логически эквивалентная $L \Leftrightarrow (A \lor J)$, есть
\begin{уравнение*}
(A \land J \land L) \lor (A \lnot J \land L) \lor (\lnot A \land J \land L) \lor (\lnot A \land \lnot J \land \lnot л).
\end{уравнение*}
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Логика — Преобразование DNF в CNF
спросил
Изменено 9 месяцев назад
Просмотрено 36 тысяч раз
$\begingroup$
Я не понимаю, как преобразовать DNF в CNF. В бланке для ответов, который мне дала моя учительница, она сразу же преобразовала его без каких-либо объяснений. Любая помощь будет здорово.
Мой учитель преобразовал $F: (A \wedge \neg B) \vee (B \wedge D)$ в CNF-форму $(A \vee B) \wedge (\neg B \vee D)$. Как это происходит? Есть ли способ преобразовать его без рисования таблиц истинности?
- логика
- исчисление высказываний
- конъюнктивная нормальная форма
- дизъюнктивная нормальная форма
$\endgroup$
0
$\begingroup$
Закон Де Моргана гласит: $\neg(a + b) \equiv \neg a\neg b $ и $\neg(ab) \equiv \neg a + \neg b$.
$$\begin{equation} \begin{aligned}A\neg B + BD \equiv & \neg(\neg(A\neg B)\neg(BD)) \text{ Де Морган снаружи} \\ \equiv & \neg((\neg A + B)(\neg B + \neg D)) \text{ Внутри Де Моргана} \\ \equiv & \neg(\neg A \neg B + \neg A \neg D + B \neg D) \text{ Дистрибутивность} \\ \equiv & \neg(\neg A \neg B + \neg A \neg D (\neg B + B) + B \neg D) \text{ Дополнение} \\ \neg & \neg(\neg A \neg B + \neg A \neg D \neg B + \neg A \neg D B + B \neg D) \text{ Распределение} \\ \equiv & \neg(\neg A \neg B(1 + \neg D) + B \neg D (1 + \neg A)) \text{ Распределение} \\ \equiv & \neg(\neg A \neg B + B \neg D) \ text{ Аннигилятор} \\ \equiv & (A + B)(\neg B + D) \text{ Снаружи Де Моргана}\end{aligned}\end{equation} $$
Вы также можете изучить К-карты.
$\endgroup$
5
$\begingroup$
Я думаю, что есть более простой способ, чем принятый ответ:
$$\begin{equation} \begin{aligned}A\neg B \vee BD \equiv & (A \vee B)(A \vee D)(\neg B \vee B)(\neg B \vee D) \text{ Дистрибутивность} \\ \equiv & (A \vee B)(A \vee D) 1 (\neg B \vee D) \text{ Tertium non datur} \\ \equiv & (A \vee B)(A \vee D)(\neg B \vee D) \text{ Нейтральный элемент $\wedge$} \\ \equiv & (A \vee B)(\neg B \vee D) \text{ средний термин лишний*} \end{выравнивание}\end{уравнение} $$
* $A\vee D$ ложно только в том случае, если и A, и D ложны, но тогда весь термин в любом случае ложен, потому что он сводится к $(B)(A \vee D)(\neg B)$.