Парабола: формулы, примеры решения задач
Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы имеет вид:
,
где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.
На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.
В математическом анализе принята другая запись уравнения параболы:
y = ax²,
то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c, в
котором 
График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.
Фокус параболы имеет координаты
Директриса параболы определяется уравнением .
Расстояние r от любой точки параболы до фокуса определяется формулой .
Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.
Пример 1. Определить координаты фокуса параболы
Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:
Находим координаты фокуса параболы:
Пример 2. Составить уравнение директрисы параболы
Решение. Находим p:
Получаем уравнение директрисы параболы:
Нет времени вникать в решение? Можно заказать работу!
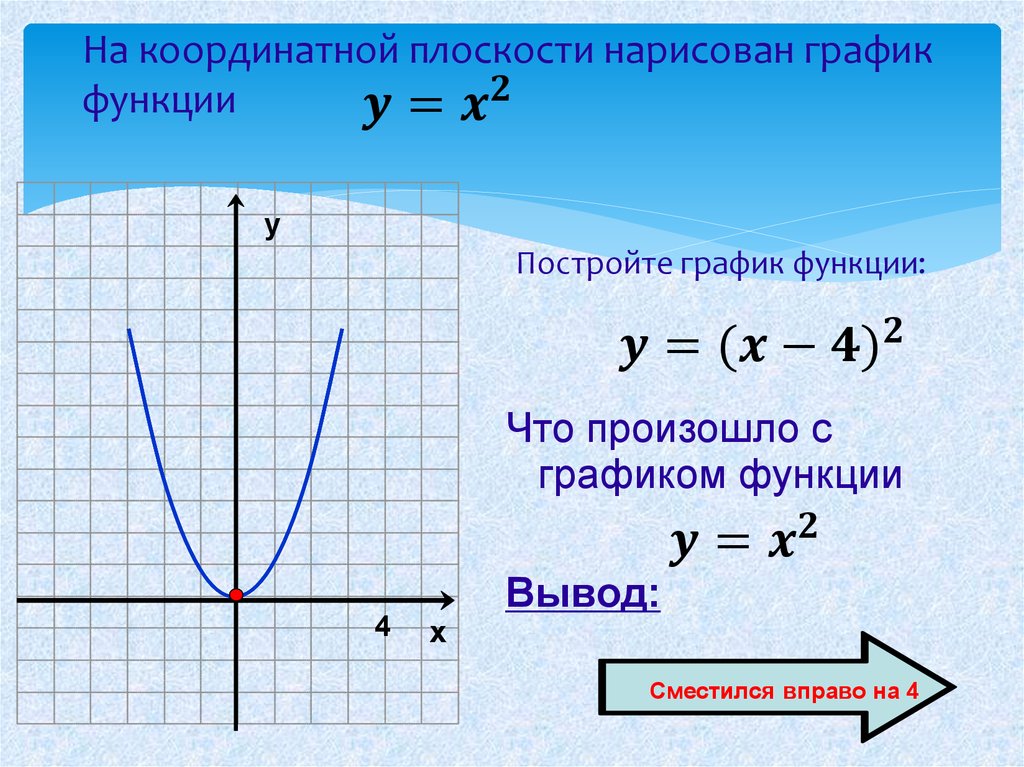
Пример 3.
Составить уравнение параболы, если
расстояние от фокуса до директрисы равно 2.
Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:
Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.
Парабола обладает следующим оптическим свойством: все лучи, исходящие
из источника света, находящегося в фокусе параболы, после отражения оказываются направленными
параллельно её оси. Это свойство параболы используется при изготовлении прожекторов,
автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения
(фигур, получающихся при вращении параболы вокруг оси).
Пучок параллельных лучей,
двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Кривые второго порядка
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Эллипс
Гипербола
Как написать уравнение параболы в вершинной форме
Алгебра2, ПараболаАлия М.
спросил 20.09.13Например, если бы мне дали графическую параболу, как бы я понял, как записать уравнение в вершинной форме/
Подписаться І 5
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Прити С.
ответил 20.09.13
Репетитор
5,0 (554)
Алгебра 2 Знание и опыт с более чем 10-летним опытом преподавания
Об этом репетиторе ›
Об этом репетиторе › 92+2
Голосовать за 0 голос против
Подробнее
Отчет
Роберт Дж. ответил 20.09.13
Репетитор
4.6 (13)
Сертифицированный учитель исчисления и физики средней школы AP
См. таких репетиторов 92 + к
Голосовать за 0 голос против
Подробнее
Отчет
Шад С.
ответил 24.09.13
Репетитор
4,8 (5)
Двуязычный учитель математики с 15-летним стажем.
Смотрите таких репетиторов
Смотрите таких репетиторов
Некоторые примеры формулы
Формат уравнения, показывающего, где находится вершина
Пример. Эта парабола имеет вершину в точке (3,4).
y = 2(x — 3) 2 + 4
3
г = (х–1)² + 1
Как найти «а»???
Выберите точку на графике, отличную от вершины. Допустим, вы видите, что линия проходит через (1,5), а вершина находится в (3,4)…
Сначала вершина дает вам это…
y = a (x — 3) 2 + 4
Подставьте значения (1,5) в это уравнение.
5 = a (1 — 3) 2 + 4
Найдите
9000 2 5 = а*(-2) 2 + 4
5 = 4a + 4
1 = 4a
1/4 = a
Итоговое уравнение:
у = 1/4*(х — 3) 2 + 4
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Как найти уравнение параболы
Обновлено 19 ноября 2018 г.
Автор Lisa Maloney
В реальном мире парабола — это дуга, которую описывает мяч, когда вы его бросаете, или характерная форма спутниковой антенны. С математической точки зрения, парабола — это форма, которую вы получаете, когда разрезаете твердый конус под углом, параллельным одной из его сторон, поэтому она известна как одно из «конических сечений».
Самый простой способ найти уравнение параболы — использовать знания о специальной точке, называемой вершиной, которая расположена на самой параболе.
Распознавание формулы параболы
Если вы видите квадратное уравнение с двумя переменными вида y = ax 2 + bx + c , где a ≠ 0, то поздравляем! Вы нашли параболу. Квадратное уравнение иногда также называют формулой «стандартной формы» параболы.
Но если вам показывают график параболы (или дают небольшую информацию о параболе в текстовом формате или в формате «словной задачи»), вы захотите записать свою параболу в так называемой вершинной форме, которая выглядит так:
y = a(x — h) 2 + k (если парабола раскрывается вертикально)
x = a(y — k) 2 + h (если парабола раскрывается вертикально) по горизонтали)
Что такое вершина параболы?
В обеих формулах координаты (h,k) представляют собой вершину параболы, то есть точку, в которой ось симметрии параболы пересекает линию самой параболы.
Или, другими словами, если бы вы сложили параболу пополам прямо посередине, вершина была бы «вершиной» параболы, прямо там, где она пересекала бы сгиб бумаги.
Нахождение уравнения параболы
Если вас попросят найти уравнение параболы, вам либо сообщат вершину параболы и хотя бы еще одну точку на ней, либо вы получить достаточно информации, чтобы понять их. Получив эту информацию, вы сможете найти уравнение параболы в три шага.
Давайте решим пример задачи, чтобы увидеть, как это работает. Представьте, что вам дана парабола в виде графика. Вам говорят, что вершина параболы находится в точке (1,2), что она открывается вертикально и что еще одна точка параболы — (3,5). Каково уравнение параболы?
В первую очередь вам нужно решить, какую форму уравнения вершин вы будете использовать. Помните, что если парабола открывается вертикально (что может означать, что открытая сторона буквы U направлена вверх или вниз), вы будете использовать это уравнение:
y = a(x — h) 2 + k
И если парабола раскрывается горизонтально (что может означать, что открытая сторона буквы U обращена вправо или влево), вы будете использовать это уравнение:0003
Поскольку парабола в примере раскрывается вертикально, воспользуемся первым уравнением.
Затем подставьте координаты вершины параболы (h, k) в формулу, которую вы выбрали на шаге 1. Поскольку вы знаете, что вершина находится в точке (1,2), вы подставите h = 1 и k = 2, что дает вам следующее:
y = a(x — 1) 2 + 2
Последнее, что вам нужно сделать, это найти значение a . Для этого выберите любую точку ( x,y ) на параболе, если эта точка не является вершиной, и подставьте ее в уравнение.
В этом случае вы уже получили координаты другой точки вершины: (3,5). Таким образом, вы подставите x = 3 и y = 5, что даст вам:
5 = a(3 — 1) 2 + 2
Теперь все, что вам нужно сделать, это решить это уравнение для и . Небольшое упрощение дает вам следующее:
5 = a(2) 2 + 2 , что можно еще упростить до:
5 = a(4) + 2 , что в очередь становится:
3 = a(4) и, наконец:
a = 3/4
Теперь, когда вы нашли значение a , подставьте его в уравнение закончи пример:
y = (3/4)(x — 1) 2 + 2 — уравнение параболы с вершиной (1,2) и содержащей точку (3,5).