Как составить уравнение по графику: Как для графика составить уравнение 🚩 составление уравнения для графика 🚩 Математика

2 — 2
f'(x0) = 9 — 2 = 7
y = 7(x-3)+3 = 7x-21+3=7x-18
Да, все верно у вас получилось.

18.04.17

Содержание Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на

ответы майл ру помогите решить задачу какое наименьшее количество карандашей надо прибавить к 146 уже имеющимя карандашам, чтобы получившееся

Решено

В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.

Решено

в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?

Высота правильной треугольной пирамиды равно…

Пользуйтесь нашим приложением

Как найти уравнение нормали к графику функции в заданной точке

Как найти уравнение нормали к графику функции в заданной точке?

На данном уроке мы узнаем, как найти уравнение нормали к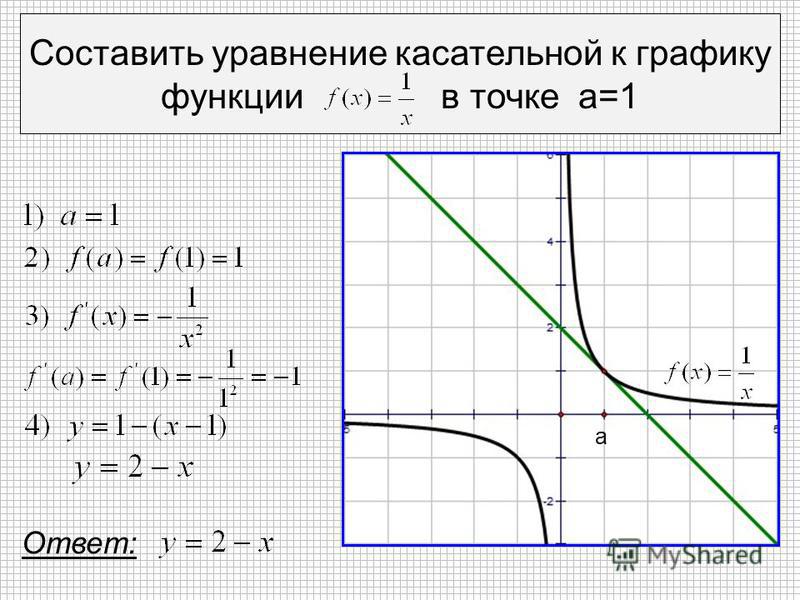

графику функции  в точке  и разберём многочисленные примеры, которые касаются этой задачи. Для качественного усвоения  материала нужно понимать геометрический смысл производной и уметь их находить хотя бы на уровне следующих статей:

Как найти производную? Производная сложной функции и Простейшие задачи с производными.

Перечисленные уроки позволят «чайникам» быстро сориентироваться в теме и поднять свои навыки дифференцирования практически с полного нуля. По существу, сейчас последует развёрнутое продолжение параграфа об уравнении касательной 3-й статьи из вышеприведенного списка. Почему продолжение? Уравнение нормали тесно связано с уравнением касательной. Помимо прочего я рассмотрю задачи о том, как построить уравнения этих линий в ситуациях, когда функция задана неявно

либо параметрически.

Но сначала освежим воспоминания: если функция  дифференцируема в точке  (т.е. если существует конечная производная ), то уравнение касательной к графику функции в точке  можно найти по следующей формуле:

Это самый распространенный случай, с которым мы уже столкнулись на уроке Простейшие задачи с производными. Однако дело этим не ограничивается: если в точке  существует бесконечная производная: , то касательная будет параллельна оси  и её уравнение примет вид . Дежурный пример: функция  с производной , которая обращается в бесконечность вблизи критической точки . Соответствующая касательная выразится уравнением:  (ось ординат).

Если же производной  не существует (например, производной от  в точке ), то, разумеется, не существует и

общей касательной.

Как различать последние два случая, я расскажу чуть позже, а пока что вернёмся в основное русло сегодняшнего урока:

Что такое нормаль? Нормалью к графику функции  в точке  называется прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке (понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.

Как найти уравнение нормали? Из курса аналитической геометрии напрашивается очень простой алгоритм: находим уравнение касательной и представляем его в общем виде . Далее «снимаем» нормальный вектор  и составляем уравнение нормали по точке  и направляющему вектору .

Этот способ применять можно, но в математическом анализе принято пользоваться готовой формулой, основанной на взаимосвязи угловых коэффициентов перпендикулярных прямых. Если существует конечная и отличная от нуля производная , то уравнение нормали к графику функции  в точке  выражается следующим уравнением:

Особые случаи, когда  равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:

Пример 1

Составить уравнения касательной и нормали к графику кривой  в точке, абсцисса которой равна .

В практических заданиях часто требуется найти и касательную тоже. Впрочем, это очень только нА руку – лучше будет «набита рука» =)

Решение: Первая часть задания хорошо знакома, уравнение касательной составим по формуле:

В данном случае:

Найдём производную: Здесь на первом шаге вынесли константу за знак производной, на втором – использовали

правило дифференцирования сложной функции.

Теперь вычислим производную в точке :

Получено конечное число и это радует. Подставим  и  в формулу :

Перебросим  наверх левой части, раскроем скобки и представим уравнение касательной в общем виде: Вторая часть задания ничуть не сложнее. Уравнение нормали составим по формуле: Избавляемся от трёхэтажности дроби и доводим уравнение до ума:  – искомое уравнение.

Ответ:

Здесь можно выполнить частичную проверку. Во-первых, координаты точки  должны удовлетворять каждому уравнению:

 – верное равенство.

 – верное равенство.

И, во-вторых, векторы нормали  должны быть ортогональны. Это элементарно проверяется с помощью скалярного произведения: , что и требовалось проверить.

Как вариант, вместо нормальных векторов можно использовать направляющие векторы прямых.

! Данная проверка оказывается бесполезной, если неверно найдена производная  и/или производная в точке . Это «слабое звено» задания – будьте предельно внимательны!

Чертежа по условию не требовалось, но полноты картины ради: Забавно, но фактически получилась и полная проверка, поскольку чертёж выполнен достаточно точно =) Кстати, функция  задаёт верхнюю дугу эллипса.

Следующая задача для самостоятельного решения:

Пример 2

Составить уравнения касательной и нормали к графику функции  в точке .

Примерный образец чистового оформления задания в конце урока.

Теперь разберём два особых случая:

1) Если производная в точке  равна нулю: , то уравнение касательной упростится: То есть, касательная будет параллельна оси .

Соответственно, нормаль будет проходить через точку  параллельно оси , а значит её уравнение примет вид .

2) Если производная в точке  существует, но бесконечна: , то, как отмечалось в самом начале статьи, касательная станет вертикальной: . И поскольку нормаль проходит через точку  параллельно оси , то её уравнение выразится «зеркальным» образом:

Всё просто:

Пример 3

Составить уравнения касательной и нормали к параболе  в точке . Сделать чертёж.

Требование выполнить чертёж я не добавлял – так было сформулировано задание в оригинале. Хотя это редкость.

Решение: составим уравнение касательной . В данном случае  

Казалось бы, расчёты пустяковые, а в знаках запутаться более чем реально:

Таким образом:

Поскольку касательная параллельна оси  (Случай №1), то нормаль, проходящая через ту же точку , будет параллельна оси ординат:

Чертёж – это, конечно же, дополнительные хлопоты, но зато добротная проверка аналитического решения:

Ответ: ,

В школьном курсе математики распространено упрощённое определение касательной, которое формулируется примерно так: «Касательная к графику функции – это прямая, имеющая с данным графиком единственную общую точку». Как видите, в общем случае это утверждение некорректно. Согласно геометрическому смыслу производной, касательной является именно зелёная, а не синяя прямая.

Следующий пример посвящён тому же Случаю №1, когда :

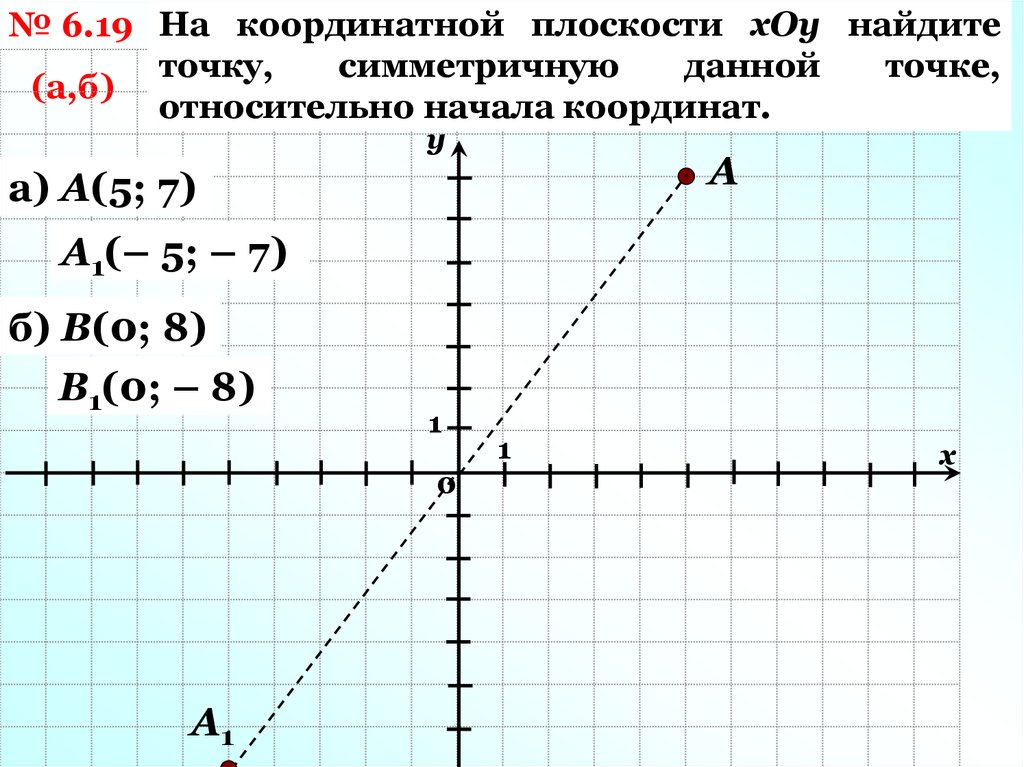
Пример 4

Написать уравнение касательной и нормали к кривой  в точке .

Краткое решение и ответ в конце урока

Случай №2, в котором  на практике встречается редко, поэтому начинающие могут особо не волноваться и с лёгким сердцем пропустить пятый пример. Информация, выделенная курсивом, предназначена для читателей с высоким уровнем подготовки, которые хорошо разобрались с определениями производной и касательной, а также имеют опыт нахождения производной по определению:

Пример 5

Найти уравнения касательной и нормали к графику функции  в точке

Решение: в критической точке знаменатель производной  обращается в ноль, и поэтому здесь нужно вычислить односторонние производные  с помощью определения производной (см. конец статьи Производная по определению): Обе производные бесконечны, следовательно, в точке  существует общая вертикальная касательная: Ну, и очевидно, что нормалью является ось абсцисс. Формально по формуле: Для лучшего понимания задачи приведу чертёж: Ответ:

Я рад, что вы не ушли бороздить просторы Интернета, потому что всё самое интересное только начинается! Чтобы осилить материал следующего параграфа, нужно уметь находить производную от неявно заданной функции:

Как найти уравнение касательной и уравнение нормали, если функция задана неявно?

Формулы касательной и нормали остаются прежними, но меняется техника решения:

Пример 6

Найти уравнения касательной и нормали к кривой  в точке .

Решение: судя по уравнению, это какая-то линия 3-го порядка, какая именно – нас сейчас совершенно не интересует.

В уравнении присутствует зловред , и поэтому перспектива выразить функция в явном виде  выглядит весьма туманной.

Но этого и не требуется! Есть куда более остроумное решение. Уравнение касательной составим по той же формуле .

Из условия известны значения , кстати, не помешает убедиться, что они действительно удовлетворяют предложенному уравнению: Получено верное равенство, значит, с точкой  всё в порядке.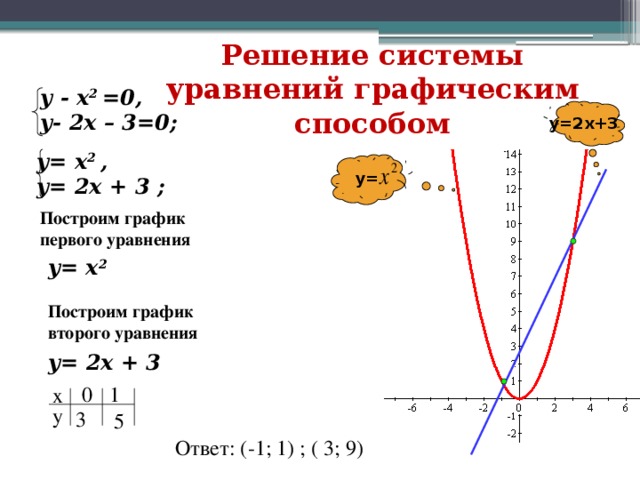

Осталось вычислить . Сначала по стандартной схеме найдём производную от функции, заданной неявно:

Перепишем результат с более подходящим для нашей задачи обозначением:

На 2-м шаге в найденное выражение производной подставим :

Вот так-то!

Осталось аккуратно разобраться с уравнением:

Составим уравнение нормали:

Ответ:

Готово! А поначалу представлялось всё непросто. Хотя производная здесь, конечно,  – место уязвимое. Миниатюра для самостоятельного решения:

Пример 7

Найти уравнение нормали к линии  в точке

Хватит уже вымучивать касательную =)

В данном случае легко выяснить, что это окружность  центром в точке  радиуса  и даже выразить нужную функцию . Но зачем?! Ведь найти производную от неявно заданной функции на порядок легче! Она тут чуть ли не самая примитивная.

Краткое решение и ответ в конце урока.

Как найти уравнение касательной и уравнение нормали, если функция задана параметрически?

Ещё проще. Но для этого нужно потренироваться в нахождении производной от параметрически заданной функции. А так – почти халява:

Пример 8

Составить уравнения касательной и нормали к циклоиде , проведенные в точке, для которой .

Чертёж циклоиды можно найти на странице S и V, если линия задана параметрически (так получилось, что эта статья была создана раньше). Там даже изображена точка касания.

Решение: абсцисса и ордината точки касания рассчитываются непосредственно из параметрических уравнений кривой:

Найдём 1-ую производную от параметрически заданной функции:

И вычислим её значение при  :

Уравнение касательной составим по обычной формуле с поправкой на несколько другие обозначения:

Уравнение нормали:

Ответ:

В заключение предлагаю познакомиться с ещё одной интересной линией:

Пример 9

Составить уравнение нормали к полукубической параболе , проведенной в точке, для которой .

Это пример для самостоятельного решения. Напоминаю, что графики параметрически заданных функций можно построить, например, с помощью моего расчётного геометрического макета.

Ну а наш урок подошёл к концу, и я надеюсь, что изложенный материал прошёл для вас не по касательной, а нормально =)

Спасибо за внимание и успехов!

Решения и ответы:

Пример 2: Решение: уравнение касательной составим по формуле: В данном случае: Таким образом: Уравнение нормали составим по формуле : Ответ:

Пример 4: Решение: уравнение касательной составим по формуле: В данной задаче: Таким образом: В точке  касательная параллельна оси , поэтому соответствующее уравнение нормали: Ответ:

Пример 7: Решение: в данной задаче: . Найдём производную: Или: Подставим в выражение производной : Искомое уравнение нормали: Ответ:

Пример 9: Решение: в данном случае: Найдём производную и вычислим её значение при : Уравнение нормали: Ответ:

Взято с сайта http://www. mathprofi.ru

Как создавать уравнения на основе графика

••• BananaStock/BananaStock/Getty Images

Обновлено 24 апреля 2017 г.

Автор: Кэтрин Уайт изображается линией при нанесении на координатную плоскость. Хотя важно научиться рисовать линейное уравнение, когда оно задано в алгебраической форме, работа в обратном направлении, чтобы написать уравнение, когда есть график, поможет улучшить ваше понимание концепции. Практикуясь в том, как связать график и уравнение друг с другом, вы также развиваете способность распознавать способы, которыми текстовые задачи и графики связаны друг с другом. Кроме того, эти навыки могут применяться в науке и статистике, где на основе собранных данных можно составлять уравнения и использовать их для прогнозирования будущих ситуаций.

Определите две отдельные точки на графике и обозначьте их как пары координат, используя отметки на осях Y и X в качестве направляющих. Например, если вы должны провести воображаемую линию от точки, которую вы выбрали, вниз к оси X, и она должна попасть в значение отрицательное три, x часть точки будет -3. Если бы вы провели воображаемую горизонтальную линию от точки к оси Y, и она попала бы в плюс четыре, точка была бы помечена (-3, 4).

Назовите одну из ваших точек «точкой один», а другую — «точкой два», чтобы не перепутать их.

Используйте формулу наклона, чтобы вычислить наклон или «крутизну» линии. Вычтите координату y точки два из координаты y точки один. Вычтите координату x точки два из координаты x точки один. Разделите первое число на второе число. Если числа не делятся без остатка, оставьте их в виде уменьшенной дроби. Отметьте это число как свой уклон.

Выберите любую из двух точек и обведите ее. С этого момента вы будете игнорировать другой пункт.

Запишите уравнение в форме «точка-наклон». Слева напишите букву «y» минус координата y вашей обведенной точки. Если координата отрицательна и у вас есть два знака минус, измените их на один знак плюс. Слева напишите наклон, умноженный на набор скобок. Внутри круглых скобок напишите букву «x» минус координата x обведенной точки. Снова замените два минуса на плюс. Например, вы можете получить y — 4 = 5 (x + 3).

Если в указаниях требуется уравнение в форме пересечения наклона, вы должны получить только y. Сделайте это, распределив наклон (умножьте его как на x, так и на число в скобках). Затем добавьте или вычтите число с левой стороны, чтобы изолировать «у». В примере y — 4 = 5(x + 3) вы получите y = 5x + 23,9.0003

• Чтобы облегчить себе математическую работу, попробуйте определить точки, в которых используются круглые целые числа, и избегайте дробей или десятичных знаков. Неважно, с какой точки вы начинаете вычислять наклон, если вы используете один и тот же порядок как для координат x, так и для координат y.

Статьи по теме

Ссылки

• Бесплатная помощь по математике: Учебное пособие по форме наклона точки

Советы

• Чтобы облегчить себе математическую работу, попробуйте определить точки, в которых используются круглые целые числа, и избегайте дробей или десятичных знаков.
• Неважно, с какой точки вы начинаете вычислять наклон, если вы используете один и тот же порядок для координат x и координат y.

Об авторе

Кэтрин Уайт более 11 лет занимается репетиторством по целому ряду предметов от детского сада до колледжа. Ее письмо отражает ее способности к обучению, а также ее веру в то, что все концепции можно сделать понятными и доступными. Уайт получил степень бакалавра искусств по истории в Уэслианском университете Иллинойса.

Photo Credits

BananaStock/BananaStock/Getty Images

как написать уравнение, используя только график?

Графические решения

Мэрайя С.

спросил 19.10.12

Я не понимаю, как написать уравнение, используя только график. нет ни цифр ни чего. просто диагональная линия через середину. пожалуйста помоги!!

Подписаться І 7

Еще

Отчет

5 ответов от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Джеймс П. ответил 19.10.12

Репетитор

4.9 (49)

Репетитор по математике в районе Woodbridge/DC/NOVA – VT Math Student

Смотрите таких репетиторов

Смотрите таких репетиторов

Чтобы упростить то, что уже было сказано, самый простой способ найти уравнение линии — это найти точки пересечения x и y. Одна точка будет (a, 0), а другая будет (0, b), где a и b — числовые значения. Наклон просто m = b/a. Когда у вас есть точка пересечения с осью y (0, b), вы можете использовать форму y = mx + b, чтобы найти уравнение для линии. Следовательно, с используемой нотацией вы можете представить это как y=(b/a)x + b, где b — значение из (0, b), а a — значение из (a, 0).

Голосовать за 1 Понизить

Подробнее

Отчет

Джон Р. ответил 19.10.12

Репетитор

4.6 (55)

Джон Р.: учитель математики, естественных наук и истории

Смотрите таких репетиторов

Смотрите таких репетиторов

     Не видя графика, я не могу помочь вам получить точный ответ, но могу дать несколько советов, которые могут вам помочь.

1. Поскольку вы заявили, что график представляет собой диагональную линию, я знаю, что вы ищете линейное уравнение . Линейные уравнения можно записать в виде y = mx + b .

Чтобы получить точное уравнение, нам нужно найти значения m и b (вы сохраните y и x в окончательном ответе).

2. Знак на 9Значение 0117 м (наклон линии) определяется тем, идет ли она вверх или вниз при движении вправо. Если линия идет вверх вправо, m положительно. Если линия идет вниз вправо, m отрицательно.

3. Предполагая, что вы видите оси X и Y с решетками (жирные вертикальные и горизонтальные линии с небольшими метками, равномерно расположенными вдоль них), вы можете найти значение м (наклон линии). Наклон определяется путем подсчета того, насколько линия смещается вверх или вниз на расстоянии, смещающемся справа налево.

Например, вы можете обнаружить, что в одной точке линии вы находитесь на одну отметку выше оси X и на две отметки правее оси Y. Двигаясь вдоль линии, вы можете обнаружить, что находитесь на четыре отметки выше оси X и на четыре отметки выше оси Y. Наклон определяется путем сравнения изменения высоты (от 1 отметки до 4 отметок) и изменения длины (от 2 до 4). Отношение 3 (4-1) к 2 (4-2), поэтому уклон (м) равен 3/2.

4. Если вы видите, где линия пересекает ось Y (жирная вертикальная линия), значит, у вас есть значение b.

5. Если вы не видите, где линия пересекает ось Y, вы все равно можете найти значение b. Просто найдите точку на линии. Подставьте значения x и y точки вместе с наклоном (m) в формулу пересечения наклона (y=mx+b) и найдите b.

6.  Запишите форму пересечения наклона уравнения со значениями, которые вы нашли для m и b.

     Еще один небольшой совет:  Если у вас есть хэши на осях X и Y, но числа не написаны, предположим, что каждый хэш представляет 1,

 

Голосовать за 1 Понизить

Подробнее

Отчет

Парвиз Ф. ответил 30.08.13

Репетитор

4,8 (4)

Профессор математики в муниципальных колледжах

См. таких репетиторов

Посмотреть таких репетиторов

Просто найдите координаты 2 точек и из них вычислите уклон: y = mx +b

 

           y1= mX1 + b

 

            тогда b = y1-mx1 , у вас есть уравнение.

         Точки пересечения просты в использовании, потому что 1 координатная точка всегда равна 0. целое число.

Голосовать за 0 Понизить

Подробнее

Отчет

Ариэль М. ответил 20.10.12

Репетитор

4,8 (40)

Физика, математика, английский язык, история

Смотрите таких репетиторов

Смотрите таких репетиторов

Похоже, вы говорите, что диагональная линия пересекает ось x-y в начале координат (или в нулевой точке, где пересекаются оси x и y). Если да, то мой ответ будет таким. Есть определенные графики, которые являются базовыми или общими, и поэтому вы можете знать их уравнение, не зная о них ничего, кроме их графика.

Линия, пересекающая начало координат на диагонали, скажем, начинающаяся в положительном квадранте x и y (I) и входящая в отрицательный квадрант x и y (III), является графиком y=x. Предполагается, что наклон равен m = 1, и, поскольку линия пересекает y в точке y = 0, общее уравнение линии (y = mx + b) можно упростить до y = x. 92.

Подводя итог, зная, что центр графика находится в начале координат, и зная общие уравнения линий, парабол, окружностей и т. д., вы обычно можете вывести уравнение без какой-либо другой информации.

Голосовать за 0 Понизить

Подробнее

Отчет

Тамара Дж. ответил 19.10.12

Репетитор

4.9 (51)

Репетиторство по математике – алгебра и исчисление (все уровни)

См. таких репетиторов

Смотрите таких репетиторов

Вы должны быть в состоянии найти его, используя форму пересечения наклона:   y = mx + b   , где m – наклон линии, а b – точка пересечения с осью y.

Чтобы найти уклон, м, выберите 2 точки на графике (x ₁  , y ₁ ) и (x ₂ , y ₂ ) и используйте следующую формулу:

     m = (y ₂ — y ₁ ) / (x ₂ — x ₁ ,

) точка на графике, где x=0. Чтобы найти его, ищите, где линия пересекается с осью Y (здесь x = 0).

Например, скажем, где искать уравнение графика линии, которая имеет две точки (3, 1) и (0, 7). Мы хотим использовать форму пересечения наклона, y = mx + b …

    Наклон:   m = (7 — 1) / (0 — 3) = (6) / (-3) = -2 ,   таким образом, m = -2

Поскольку точка (0, 7) является точкой, где x=0, то мы знаем, что точка пересечения с осью y находится в этой точке. Таким образом, b = 7.

Следовательно, уравнение этой прямой выглядит следующим образом:

    y = mx + b     ===>     y = -2x + 7

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.