Web in Math: Как строить графики функций в Wolfram
Как строить графики функций в Wolfram | Alpha
Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20
Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5
В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если мы не будем задавать область значений х?
Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:
Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.
Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.
Источник by Sam Blake
Больше информации по использованию Wolfram|Alpha вы найдете в блоге
Следующее Предыдущее Главная страница
Подписаться на: Комментарии к сообщению (Atom)
Графики | Функции
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажеромПоскольку функции — это отношения, у них есть графики.
В этом уроке мы покажем, как визуально представить функцию.
График функции — это визуальное представление функции на плоскости, которое помогает понять различные свойства функции.
Графики функций можно строить по-разному, но процесс всегда похож — надо строить кривую, которая соответствует функции.
Вспомним, какие сущетсвуют типы графиков функций:
Линейная
Квадратичная
Кубическая
Рациональная
Логарифмическая
Давайте выясним, как строить графики на примере линейной функции.
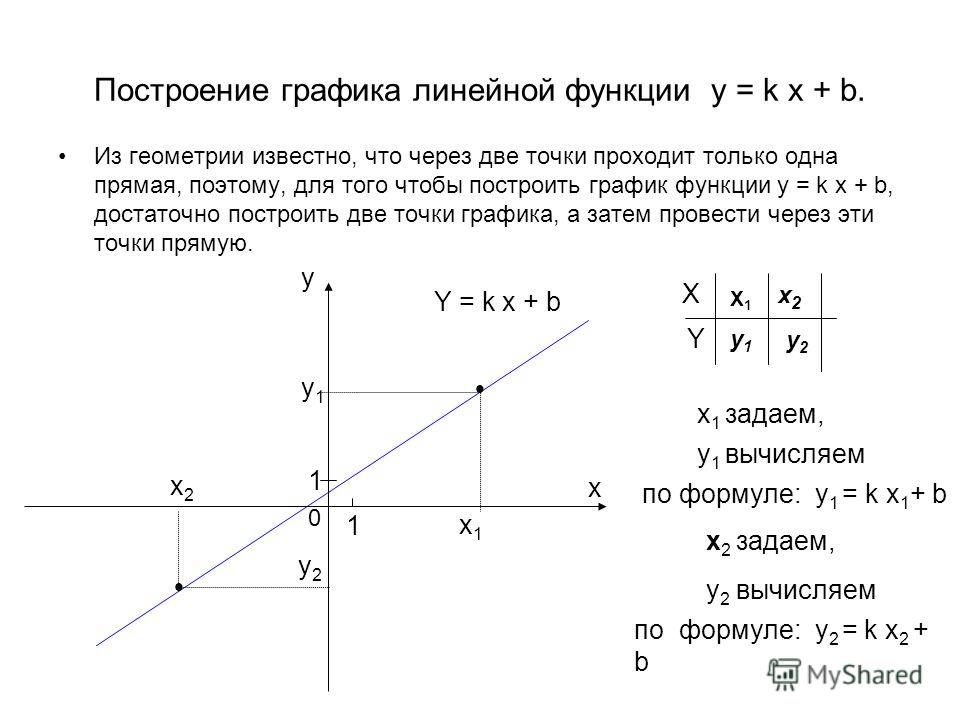
Шаг 1. Сначала построим график функции . Для этого создадим таблицу значений, взяв несколько случайных чисел для , скажем, и . Затем подставим каждое из них в , чтобы вычислить значения :
Таким образом, две точки на прямой — это и . Если построить их на графике и соединить прямой линией, то мы получим ее график:
Посмотрим еще на такой пример — это часть графика функции Floor:
Представим, что
— график функции с областью
.
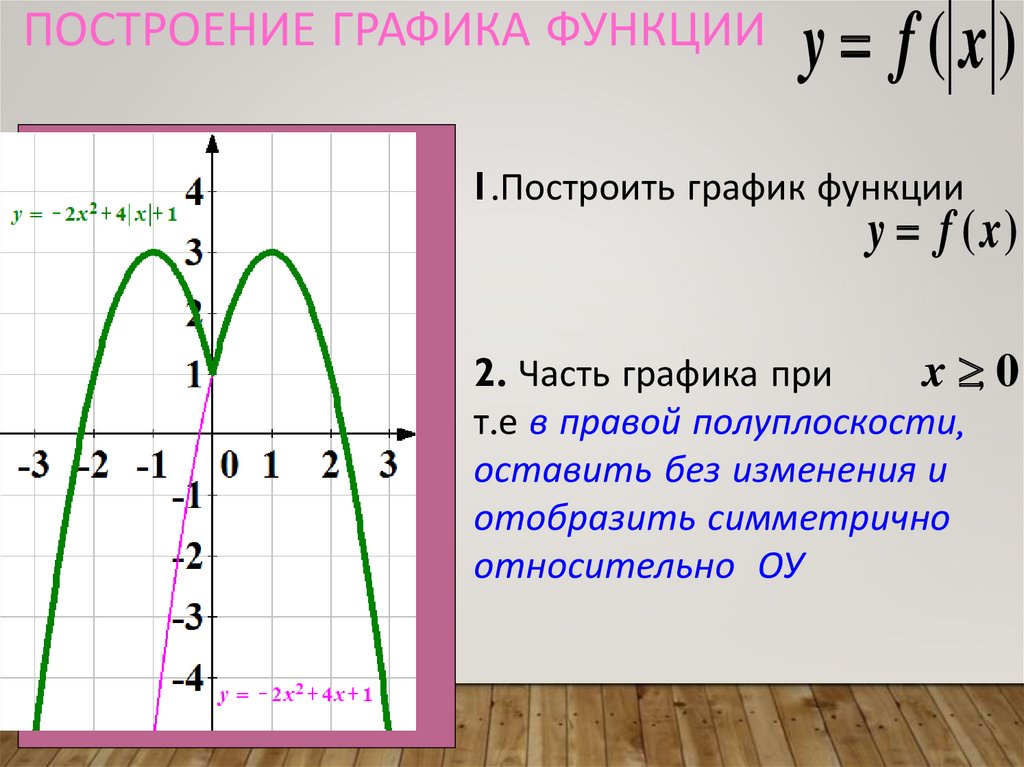
В таком случае будет являться графиком функции при одном условии: всякий раз, когда , вертикальная прямая должна пересекаться в одной точке. Это называется тестом вертикальной линии для функции.
Часто функции представляют в виде диаграммы. Например, когда у функции маленькое множество в качестве своей области и маленькое множество в качестве своего кодомена.
Допустим, есть такая функция:
, определенная как и
Линии, которые соединяют элемент слева на рисунке с элементом справа — это связь между элементами области и элементами кодомена. Ее интерпретируют как правило для . Например, мы интерпретируем линию между и , как означающую :
Теперь посмотрим на еще один пример:
Элементы области и кодомена могут быть перечислены в любом порядке. Иногда подобное представление облегчает понимание функций, определенных на
— состоящих из натуральных чисел. Такое представление можно использовать и для некоторых больших множеств.
Выводы
В этом уроке мы вспомнили тему графиков и узнали, как работать с графиками функций. Эти знания пригодятся далее в курсе, когда мы будем изучать разные типы функций и их визуальные представления.
Остались вопросы? Задайте их в разделе «Обсуждение»
Вам ответят команда поддержки Хекслета или другие студенты.
Для полного доступа к курсу нужен базовый план
Базовый план откроет полный доступ ко всем курсам, упражнениям и урокам Хекслета, проектам и пожизненный доступ к теории пройденных уроков. Подписку можно отменить в любой момент.
Получить доступ
130
курсов
1000
упражнений
2000+
часов теории
3200
тестов
Как построить график функции
Обновлено 4 декабря 2020 г.
Автор: John Papiewski
Построение графика математических функций не так уж сложно, если вы знакомы с функцией, которую изображаете.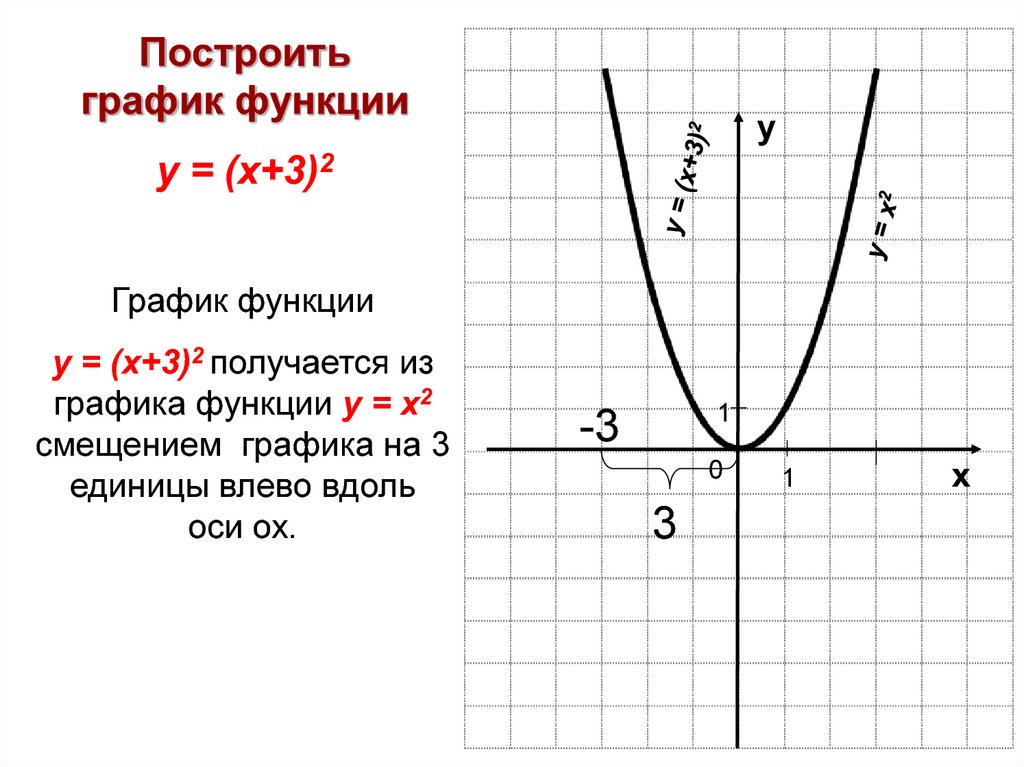
Каждый тип функции, будь то линейная, полиномиальная, тригонометрическая или какая-либо другая математическая операция, имеет свои особенности и особенности. Подробная информация об основных классах функций обеспечивает отправные точки, подсказки и общие рекомендации по их построению.
TL;DR (слишком длинный; не читал)
Чтобы построить график функции, рассчитайте набор значений оси y на основе тщательно выбранных значений оси x , а затем нанесите результаты на график.
Графики линейных функций
Линейные функции являются одними из самых простых для построения графиков; каждый просто прямая линия. Чтобы построить линейную функцию, вычислите и отметьте на графике две точки, а затем проведите прямую линию, проходящую через них обе. Формы «точка-наклон» и « y »-перехват дают вам сразу одну точку; а y -линейное уравнение пересечения имеет точку (0, y ), а точка-наклон имеет произвольную точку ( x , y ).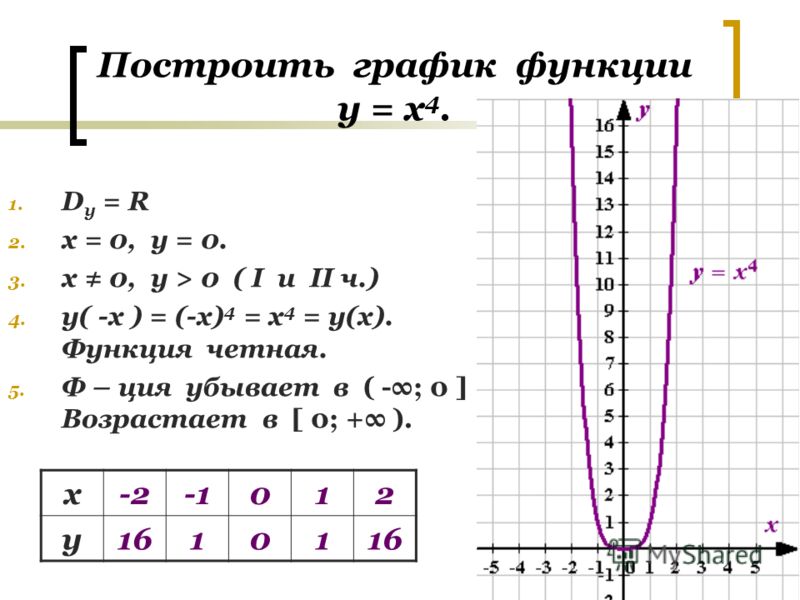
Чтобы найти еще одну точку, вы можете, например, установить y = 0 и найти x . Например, чтобы построить график функции:
y = 11x + 3
3 — это точка пересечения y , поэтому одна точка равна (0, 3).
Установка y на ноль дает вам следующее уравнение:
0 = 11x + 3
Вычесть 3 из обеих частей:
0 — 3 = 11x + 3 — 3
Упростить:
-3 = 11x
Разделить обе части на 11:
\frac{-3}{11} = \ frac{11x}{11}
Упростить:
\frac{-3}{11} = x
Итак, ваша вторая точка равна (-0,273, 0)
При использовании общей формы вы устанавливаете y = 0 и найдите x , а затем установите x = 0 и найдите y , чтобы получить два очка. Чтобы построить график функции, x − y = 5, например, установка x = 0 дает y -5, а установка y = 0 дает x из 5. Две точки — это (0, −5) и (5, 0).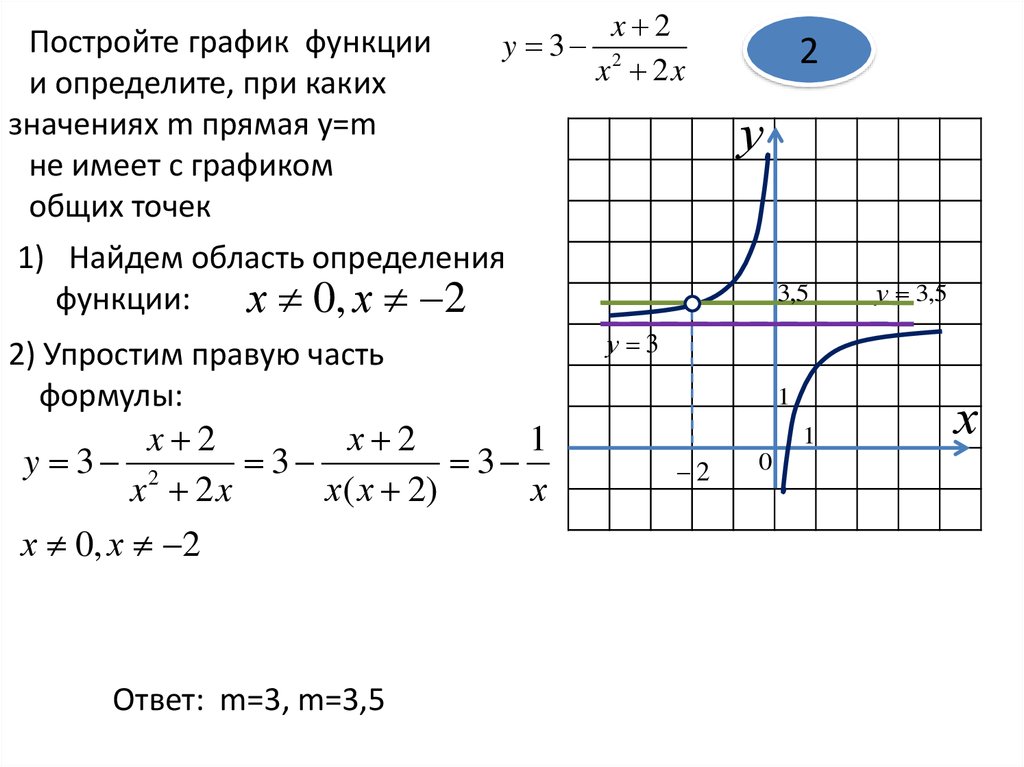
График тригонометрических функций
Тригонометрические функции, такие как синус, косинус и тангенс, являются циклическими, и график, построенный с помощью триггерных функций, имеет регулярно повторяющийся волнообразный рисунок. Например, функция
y = \sin(x)
начинается с 9.0011 y = 0, когда x = 0 градусов, затем плавно увеличивается до значения 1, когда x = 90, уменьшается обратно до 0, когда x = 180, уменьшается до −1 когда x = 270, и возвращается к 0, когда x = 360. Паттерн повторяется бесконечно. Для простых функций sin( x ) и cos( x ) y никогда не выходит за пределы диапазона от −1 до 1, а функции всегда повторяются через каждые 360 градусов. Функции тангенса, косеканса и секанса немного сложнее, хотя они также следуют строго повторяющимся шаблонам.
Более обобщенные триггерные функции, такие как
y = A × \sin(Bx + C)
, предлагают свои сложности, хотя при изучении и практике вы сможете определить, как эти новые термины влияют на функцию.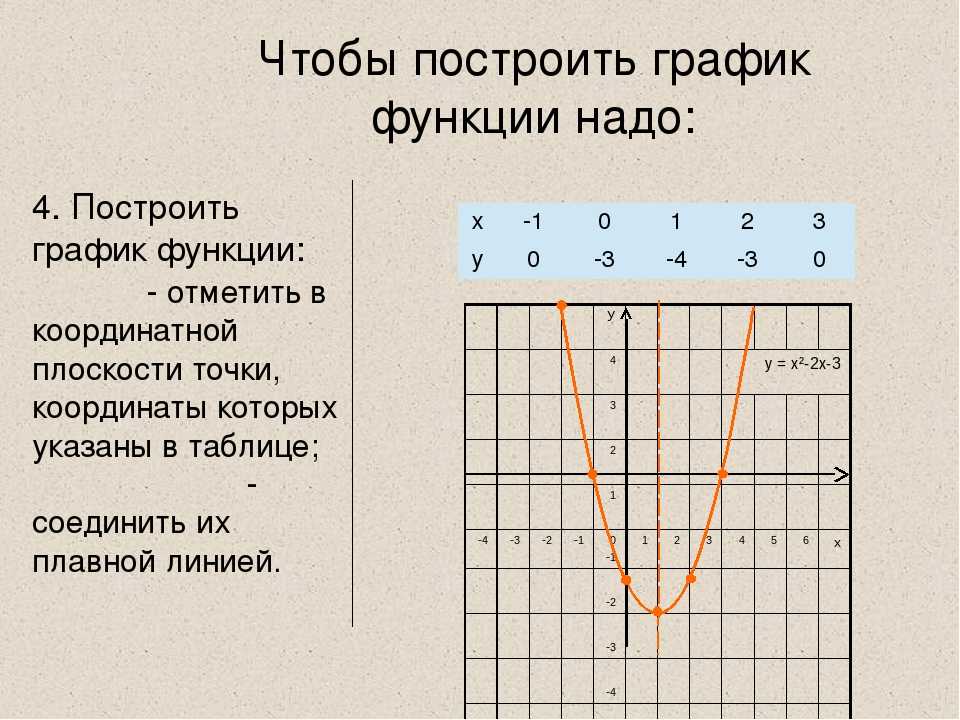
Например, константа A изменяет максимальное и минимальное значения, поэтому она становится A и отрицательной A вместо 1 и −1. Постоянное значение B увеличивает или уменьшает скорость повторения, а константа C сдвигает начальную точку волны влево или вправо.
Графики с помощью программного обеспечения
Помимо построения графиков вручную на бумаге, вы можете автоматически создавать графики функций с помощью компьютерного программного обеспечения. Например, многие программы для работы с электронными таблицами имеют встроенные возможности построения графиков. Чтобы построить график функции в электронной таблице, вы создаете один столбец со значениями x , а другой, представляющий ось y , представляет собой вычисленную функцию столбца значений x . Когда вы заполните оба столбца, выберите их и выберите функцию точечной диаграммы программного обеспечения.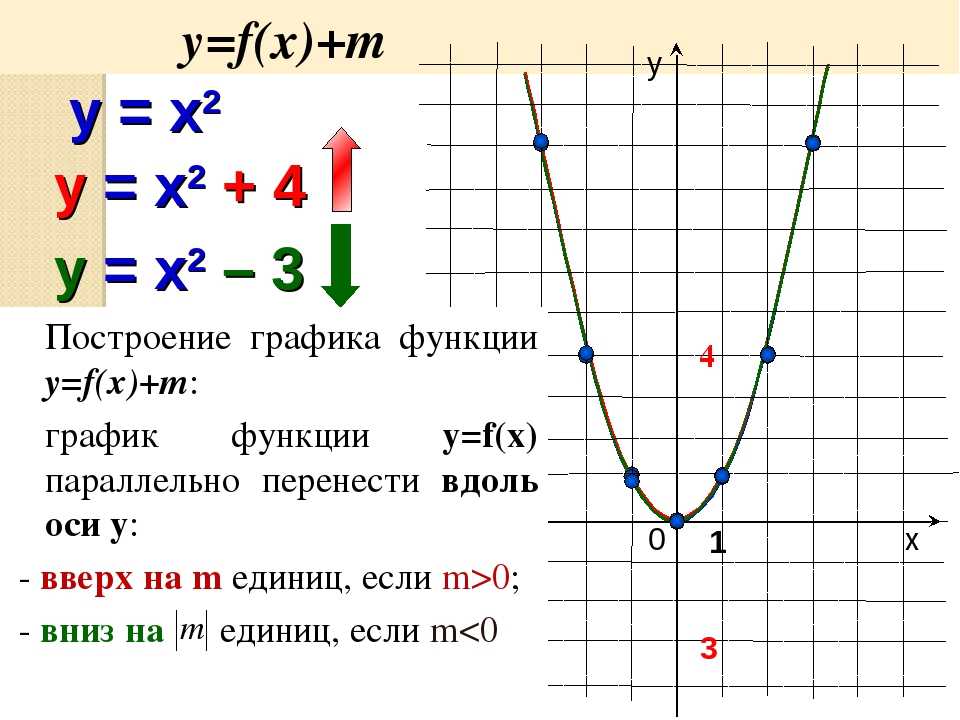
Точечная диаграмма отображает ряд дискретных точек на основе ваших двух столбцов. При желании вы можете сохранить график в виде отдельных точек или соединить каждую точку, создав непрерывную линию. Перед печатью графика или сохранением электронной таблицы пометьте каждую ось соответствующим описанием и создайте главный заголовок, описывающий назначение графика.
OpenAlgebra.com: Графические функции с использованием преобразований
Один из способов построения графиков функций — это простое построение точек. В этом разделе мы рассмотрим метод, используемый для быстрого построения графиков, связанных с некоторыми основными функциями. Здесь мы сосредоточимся на жестких преобразованиях , то есть преобразованиях, которые не изменяют форму графика.
Вертикальные переводы: [ Интерактивный график ]
Если k является любым положительным вещественным числом, то
График базовой функции f ( x ) = sqrt( x ) выглядит следующим образом:
Используя этот базовый график и вертикальные переносы, описанные выше, мы можем нарисовать f ( x ) = sqrt( x ) + 2, сдвинув все точки вверх на 2 единицы.
Точно так же на графике g ( x ) = sqrt( x ) − 3 сдвиньте все точки вниз на 3 единицы.
Горизонтальные переводы: [ Интерактивный график ]
Если h является любым положительным действительным числом, то
Используя график f ( x ) = sqrt( x ) и горизонтальное перемещение, описанное выше, мы можем изобразить f ( x ) = sqrt( x + 4 ), сдвигая все очков осталось 4 единицы. Точно так же на графике 90 152 g 90 153 ( 90 152 x 90 153 ) = sqrt ( 90 152 x 90 153 − 3 ), сдвинув все точки вправо на 3 единицы.
Отражения: [Интерактивный график]
Для любой функции f ( x ),
Используя график f ( x ) = sqrt( x ), нарисуйте график f ( x ) = −sqrt( x ) , отражая все точки вокруг x -ось.
Точно так же график f ( x ) = sqrt(− x ) отражает все точки относительно оси y
Для первой функции f ( x ) = −sqrt( x ) все значения y отрицательные, что приводит к отражению относительно оси x . Для второй функции f ( x ) = sqrt(− x ) все значения x должны быть отрицательными, что приводит к отражению относительно оси y .
Нарисуйте график .
-1 указывает на отражение графика функции возведения в квадрат f ( x 92 по оси x . Обязательно изобразите функцию возведения в квадрат пунктирной кривой, потому что она будет использоваться в качестве ориентира, а не ответа. Затем отразите все точки на оси x и нарисуйте окончательный график сплошной кривой.
Общие этапы построения графиков функций с помощью преобразований :
1. Определите и нарисуйте базовую функцию с помощью пунктирной кривой.