Как умножить матрицу на матрицу 3х3: Умножение матриц онлайн

Виды матриц:

Матрица — это таблица, состоящая из определенного количества строк и столбцов, заполненная элементами.

Например, матрица А имеет две строки и три столбца, значит ее размер 2х3, а матрица В — три строки и два столбца, значит ее размер обозначим как 3х2. Важно: первое число при написании размера матрицы всегда количество строк, а второе — количество столбцов. Элементы матрицы — это те числа, которыми заполнена матрица.

Матрицы С и D имеют размеры 3х3 и 2х2. В том случае, когда количество строк матрицы равняется количеству ее столбцов, матрица называется квадратной. Значит матрица C — квадратная матрица третьего порядка, а матрица D — квадратная матрица второго порядка.

Матрица, которая содержит только одну строчку или один столбец называется вектором. В таких матрицах можно выделить вектор-строка и вектор-столбец.

Так, матрица K — это вектор-строка, а матрица F — вектор-столбец.

Квадратная матрица, у которой в главной диагонали стоят ненулевые элементы, а все остальные — это нули называется диагональная матрица. Матрица L — диагональная матрица третьего порядка. Если ненулевые элементы равны только единицам, то это единичная матрица, она всегда обозначается буквой Е. В нашем случае матрица Е — тоже единичная матрица третьего порядка.

Если все элементы матрицы нули, то это нулевая матрица. Например, матрица V — нулевая матрица третьего порядка.

Если в данной матрице поменять строки и столбцы местами, то получится транспонированная матрица данной. Например, дана матрица М, каждую строчку этой матрицы перенесем в соответствующий столбец матрицы, стоящей на рисунке рядом. Вторая матрица — это транспонированная матрица матрицы М.

При решении задач по высшей математике достаточно часто возникает необходимость вычислить определитель квадратной матрицы.

Определитель (число) можно найти только для квадратной матрицы, т.е. для той, у которой количество строк равняется количеству столбцов.

Определитель матрицы обозначается:

Определитель квадратной матрицы можно искать двумя способами:

1. Правило треугольников (правило Саррюса)

• для матрицы 2х2:

• для матрицы 3х3:

Рассмотрим на примере правило Саррюса:

• для матрицы 2х2:

• для матрицы 3х3:

2. Теорема Лапласа или одно из свойств определителя «Разложение определителя по элементам некоторого ряда».

Определитель матрицы равен сумме произведений элементов некоторого ряда (любой строки или столбца) на соответствующие им алгебраические дополнения.

Алгебраическое дополнение матрицы есть у каждого элемента этой матрицы, для его определения надо (-1) возвести в степень суммы номеров строки и столбца и умножить все это минор этой матрицы, т.е. на определитель матрицы, получающейся из исходной матрицы путем вычёркивания i -й строки и j -го столбца.

Рассмотрим на примере нахождение алгебраического дополнения элементов матрицы:

Пусть дана матрица А:

Найдем алгебраические дополнения для двух элементов:

1. для элемента, который стоит в первой строке, первом столбце

2. для элемента, который стоит в третьей строке, втором столбце

А теперь используя алгебраическое дополнение матрицы найдем определитель матрицы А , используя теорема Лапласа:

Пусть дана матрица А:

Разложим по первой строке:

Обратите внимание еще раз, как раскладывалась матрица, как находилось алгебраическое дополнение матрицы:

В последнем примере определитель матрицы равен нулю. В таких случаях матрицу называют

вырожденная матрица. Во всех выше представленных примерах, определитель отличен от нуля, значит матрица невырожденная.

1. Сложение и вычитание матриц:

Сложение и вычитание матриц — одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицы одинаковых размеров, т. е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.

Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами:

Сумма двух матриц:

Разность двух матриц:

2. Умножение матрицы на число:

Умножение матрицы на число — процесс, заключающийся в умножении числа на каждый элемент матрицы.

Например, пусть дана матрица А:

Умножим число 3 на матрицу А:

3. Умножение двух матриц:

Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы.

Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца.

Можно представить все это в виде схемы:

После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц, можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д.

Посмотрим как это выглядит на схеме:

Посмотрим как это выглядит на примере:

Даны две матрицы:

Найдем произведение этих матриц:

Как найти определитель матрицы 3Х3: 12 шагов

‘). insertAfter(«#intro»),$(‘

‘).insertBefore(«.youmightalsolike»),$(‘

‘).insertBefore(«#quiz_container»),$(‘

‘).insertBefore(«#newsletter_block_main»),ha(!0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a

В этой статье:

Поиск определителя

Как упростить задачу

Дополнительные статьи

Источники

Определители матриц часто используются в вычислениях, в линейной алгебре и аналитической геометрии. Вне академического мира определители матриц постоянно требуются инженерам и программистам, в особенности тем, кто работает с компьютерной графикой. Если вы уже знаете, как найти определитель матрицы размерностью 2×2, то из инструментов для нахождения определителя матрицы 3×3 вам будут необходимы только сложение, вычитание и умножение.

Шаги

1. 1

   Запишите матрицу размерностью 3 x 3. Запишем матрицу размерностью 3 x 3, которую обозначим M, и найдем ее определитель |M|. Далее приводится общая форма записи матрицы, которую мы будем использовать, и матрица для нашего примера:

   • M=(a11a12a13a21a22a23a31a32a33)=(153247462){\displaystyle M={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}={\begin{pmatrix}1&5&3\\2&4&7\\4&6&2\end{pmatrix}}}

2. 2

   Выберите строку или столбец матрицы.

   Эта строка (или столбец) будет опорной. Результат будет одинаков, независимо от того, какую строку или какой столбец вы выберете. В данном примере давайте возьмем первую строку. Чуть позже вы найдете несколько советов касательно того, как выбирать строку или столбец, чтобы упростить вычисления.
   • Давайте выберем первую строку матрицы M в нашем примере. Обведите числа 1 5 3. В общей форме обведите a₁₁ a₁₂ a₁₃.

3. 3

   Зачеркните строку или столбец с первым элементом. Обратитесь к опорной строке (или к опорному столбцу) и выберите первый элемент. Проведите горизонтальную и вертикальную черту через этот элемент, вычеркнув таким образом столбец и строку с этим элементом. Должно остаться четыре числа. Будем считать эти элементы новой матрицей размерностью 2 x 2.

   • В нашем примере, опорной строкой будет 1 5 3. Первый элемент находится на пересечении первого столбца и первой строки. Вычеркните строку и столбец с этим элементом, то есть первую сроку и первый столбец. Запишите оставшиеся элементы в виде матрицы 2 x 2:
   •  1  5 3
   •  2  4 7
   •  4  6 2

4. 4

   Найдите определитель матрицы 2 x 2. Запомните, что определитель матрицы (abcd){\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}} вычисляется как ad — bc. ^{[1] X Источник информации} Опираясь на это, вы можете вычислить определитель полученной матрицы 2 x 2, которую, если хотите, можете обозначить как X. Умножьте два числа матрицы X, соединенных по диагонали слева направо (то есть так: \ ). Затем вычтите результат умножения двух других чисел по диагонали справа налево (то есть так: / ). Используйте эту формулу, чтобы вычислить определитель матрицы, которую вы только что получили.

   • В нашем примере определитель матрицы (4762){\displaystyle {\begin{pmatrix}4&7\\6&2\end{pmatrix}}} = 4*2 — 7*6 = -34.
   • Этот определитель называется минором элемента, который мы выбрали в нашей первоначальной матрице.^{[2] X Источник информации} Другими словами, мы только что нашли минор a₁₁.

5. 5

   Умножьте полученный ответ на выбранный элемент матрицы M. Вспомните, какой элемент из опорной строки (или столбца) мы использовали, когда вычеркивали другие элементы строки и столбца, чтобы получить новую матрицу. Умножьте этот элемент на полученный минор (определитель матрицы 2×2, которую мы обозначили X).

   • В нашем примере мы выбирали элемент a₁₁, который равнялся 1. Умножим его на -34 (определитель матрицы 2×2), и у нас получится 1*-34 = -34.

6. 6

   Определите знак полученного результата. Далее вам понадобится умножить полученный результат на 1, либо на -1, чтобы получить алгебраическое дополнение (кофактор) выбранного элемента. Знак кофактора будет зависеть от того, в каком месте матрицы 3×3 стоит элемент. Запомните эту простую схему знаков, чтобы знать знак кофактора:

   • + — +
   • — + —
   • + — +
   • Поскольку мы работали с элементом a₁₁, для которого стоит знак +, то мы будем умножать полученное значение на +1 (то есть оставим его как есть). Алгебраическое дополнение нашего элемента будет равно -34.
   • Вы также можете найти знак алгебраического дополнения по формуле (-1)^{i+j, где i и j — номер столбца и строки выбранного элемента соответственно. [3] X Источник информации}

7. 7

   Повторите все вышеописанные действия со вторым элементом опорной строки (или столбца). Вернитесь к исходной матрице размерностью 3×3 и строке, которую мы обвели в самом начале вычислений. Повторите все действия с этим элементом:

   • Вычеркните строку и столбец с этим элементом. В нашем примере мы должны выбрать элемент a₁₂ (равный 5). Вычеркнем первую строку (1 5 3) и второй столбец (546){\displaystyle {\begin{pmatrix}5\\4\\6\end{pmatrix}}} матрицы.
   • Запишите оставшиеся элементы в виде матрицы 2×2. В нашем примере матрица будет иметь вид (2742){\displaystyle {\begin{pmatrix}2&7\\4&2\end{pmatrix}}}
   • Найдите определитель этой новой матрицы 2×2. Воспользуйтесь вышеприведенной формулой ad — bc. (2*2 — 7*4 = -24)
   • Умножьте полученный определитель на выбранный элемент матрицы 3×3. -24 * 5 = -120
   • Проверьте, нужно ли умножить результат на -1. Воспользуемся формулой (-1)^ij, чтобы определить знак алгебраического дополнения. Для выбранного нами элемента a₁₂ в таблице указан знак «-», аналогичный результат дает и формула. То есть мы должны изменить знак: (-1)*(-120) = 120.

8. 8

   Повторите с третьим элементом. Далее вам понадобится найти еще одно алгебраическое дополнение. Вычислите его для последнего элемента опорной строки или опорного столбца. Далее приводится краткое описание того, как вычисляется алгебраическое дополнение для a₁₃ в нашем примере:

   • Зачеркните первую строку и третий столбец, чтобы получить матрицу (2446){\displaystyle {\begin{pmatrix}2&4\\4&6\end{pmatrix}}}
   • Ее определитель равен 2*6 — 4*4 = -4.
   • Умножьте результат на элемент a₁₃: -4 * 3 = -12.
   • Элемент a₁₃ имеет знак + в приведенной выше таблице, поэтому ответ будет -12.

9. 9

   Сложите полученные результаты. Это последний шаг. Вам необходимо сложить полученные алгебраические дополнения элементов опорной строки (или опорного столбца). Сложите их вместе, и вы получите значение определителя матрицы 3×3.

   • В нашем примере определитель равен -34 + 120 + -12 = 74.

   Реклама

1. 1

   Выбирайте в качестве опорной строки (или столбца) ту, что имеет больше нулей. Помните, что в качестве опорной вы можете выбрать любую строку или столбец. Выбор опорной строки или столбца не влияет на результат. Если вы выберете строку с наибольшим количеством нулей, вам придется выполнять меньше вычислений, поскольку вам будет необходимо вычислить алгебраические дополнения только для ненулевых элементов. Вот почему:

   • Допустим, вы выбрали 2 строку с элементами a₂₁, a₂₂, and a₂₃. Чтобы найти определитель, вам будет необходимо найти определители трех различных матриц размерностью 2×2. Давайте назовем их A₂₁, A₂₂, and A₂₃.
   • То есть определитель матрицы 3×3 равен a₂₁|A₂₁| — a₂₂|A₂₂| + a₂₃|A₂₃|.
   • Если оба элемента a₂₂ и a₂₃ равны 0, то наша формула становится намного короче a₂₁|A₂₁| — 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| — 0 + 0 = a₂₁|A₂₁|. То есть необходимо вычислить только алгебраическое дополнение одного элемента.

2. 2

   Используйте сложение строк, чтобы упростить матрицу. Если вы возьмете одну строку и прибавите к ней другую, то определитель матрицы не изменится. То же самое верно и для столбцов. Подобные действия можно выполнять несколько раз, кроме того, вы можете умножать значения строки на постоянную (перед сложением) для того, чтобы получить как можно больше нулей. Подобные действия могут сэкономить массу времени.

   • Например, у нас есть матрица из трех строк: (9−1231075−2){\displaystyle {\begin{pmatrix}9&-1&2\\3&1&0\\7&5&-2\end{pmatrix}}}
   • Чтобы избавиться от 9 на месте элемента a₁₁, мы можем умножить вторую строку на -3 и прибавить результат к первой. Новая первая строка будет [9 -1 2] + [-9 -3 0] = [0 -4 2].
   • То есть мы получаем новую матрицу (0−4231075−2){\displaystyle {\begin{pmatrix}0&-4&2\\3&1&0\\7&5&-2\end{pmatrix}}} Попробуйте проделать то же самое со столбцами, чтобы получить на месте элемента a₁₂ нуль.

3. 3

   Помните, что вычислять определитель треугольных матриц намного проще. Определитель треугольных матриц вычисляется как произведение элементов на главной диагонали, от a₁₁ в верхнем левом углу до a₃₃ в нижнем правом углу. Речь в данном случае идет о треугольных матрицах размерностью 3×3. Треугольные матрицы могут быть следующих видов, в зависимости от расположения ненулевых значений:^{[4] X Источник информации}

   • Верхняя треугольная матрица: Все ненулевые элементы находятся на главной диагонали и выше нее. Все элементы ниже главной диагонали равны нулю.
   • Нижняя треугольная матрица: Все ненулевые элементы находятся ниже главной диагонали и на ней.
   • Диагональная матрица: Все ненулевые элементы находятся на главной диагонали. Является частным случаем вышеописанных матриц.

   Реклама

Советы

• Описанный метод распространяется на квадратные матрицы любого ранга. Например, если вы используете его для матрицы 4×4, то после «вычеркивания» будут оставаться матрицы 3×3, для которых определитель будет вычисляться вышеупомянутым способом. Будьте готовы к тому, что вычислять определитель для матриц таких размерностей вручную — очень трудоемкая задача!
• Если все элементы строки или столбца равны 0, то определитель матрицы тоже равен 0.

Реклама

Источники

Об этой статье

На других языках

Как найти определитель матрицы 3Х3 — Wiki How Русский

Определители матриц часто используются в вычислениях, в линейной алгебре и аналитической геометрии. Вне академического мира определители матриц постоянно требуются инженерам и программистам, в особенности тем, кто работает с компьютерной графикой. Если вы уже знаете, как найти определитель матрицы размерностью 2×2, то из инструментов для нахождения определителя матрицы 3×3 вам будут необходимы только сложение, вычитание и умножение.

Эту страницу просматривали 112 378 раз.

Реклама

Программа Python для умножения двух матриц

В этом примере мы научимся умножать матрицы двумя разными способами: вложенным циклом и вложенным списком.

Чтобы понять этот пример, вы должны знать следующие темы программирования на Python:

В Python мы можем реализовать матрицу как вложенный список (список внутри списка).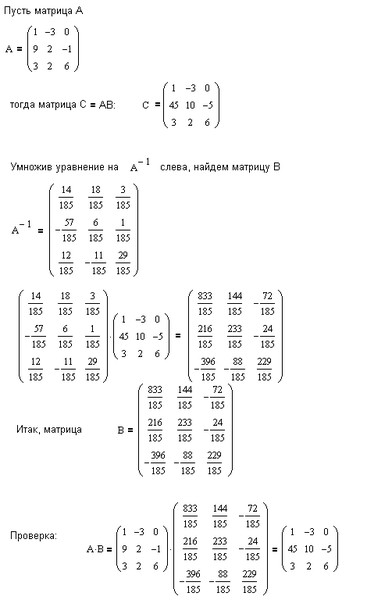

Каждый элемент можно рассматривать как строку матрицы.

Например, X = [[1, 2], [4, 5], [3, 6]] будет представлять собой матрицу 3x2 .

Первую строку можно выбрать как X[0] . И элемент в первой строке, первом столбце можно выбрать как X[0][0] .

Умножение двух матриц X и Y определено, только если количество столбцов в X равно количеству строк Y .

Если X является матрицей n x m , а Y является матрицей m x l , то XY определен и имеет размерность n x l (но YX не определен). Вот несколько способов реализовать матричное умножение в Python.

Исходный код: Умножение матриц с использованием вложенного цикла

 # Программа для умножения двух матриц с использованием вложенных циклов
#матрица 3х3
Х = [[12,7,3],
    [4 ,5,6],
    [7 ,8,9]]
#матрица 3х4
Y = [[5,8,1,2],
    [6,7,3,0],
    [4,5,9,1]]
# результат 3x4
результат = [[0,0,0,0],
         [0,0,0,0],
         [0,0,0,0]]
# перебираем строки X
для i в диапазоне (len (X)):
   # перебираем столбцы Y
   для j в диапазоне (len (Y [0])):
       # перебираем строки Y
       для k в диапазоне (len (Y)):
           результат[i][j] += X[i][k] * Y[k][j]
для r в результате:
   печать (р)
 

Выход

  [114, 160, 60, 27]
[74, 97, 73, 14]
[119, 157, 112, 23] 
 

В этой программе мы использовали вложенные циклы for для перебора каждой строки и каждого столбца. Сумму произведений суммируем в результате.

Этот метод прост, но требует больших вычислительных ресурсов, поскольку мы увеличиваем порядок матрицы.

Для больших операций с матрицами мы рекомендуем оптимизированные программные пакеты, такие как NumPy, которые в несколько (порядка 1000) раз быстрее, чем приведенный выше код.

Исходный код: Умножение матриц с использованием понимания вложенных списков

 # Программа для умножения двух матриц с использованием понимания списков
#матрица 3х3
Х = [[12,7,3],
    [4 ,5,6],
    [7 ,8,9]]
#матрица 3х4
Y = [[5,8,1,2],
    [6,7,3,0],
    [4,5,9,1]]
# результат 3x4
результат = [[сумма(a*b для a,b в zip(X_row,Y_col)) для Y_col в zip(*Y)] для X_row в X]
для r в результате:
   печать (р)
 

Вывод этой программы такой же, как и выше. Чтобы понять приведенный выше код, мы должны сначала узнать о встроенной функции 9.0011 zip() и список аргументов распаковки с помощью оператора *.

Мы использовали вложенный список для перебора каждого элемента в матрице. Сначала код кажется сложным и нечитаемым. Но как только вы освоите понимание списков, вы, вероятно, уже не вернетесь к вложенным циклам.

Как сделать умножение матриц и обратное в MS Excel « Microsoft Office :: WonderHowTo

• Автор Шон Конати
• 03.05.10 5:18

Это видео об умножении, определении и обращении матрицы в Excel. Сначала мы должны взять две матрицы в Excel. Если взять две матрицы 3х3 и перемножить их, то в результате получится матрица 3х3. Сначала мы должны выбрать ячейки 3×3 в Excel и затем дать формулу = mmult (а затем выбрать первую матрицу, она автоматически примет номера строк и ячеек, затем выберите вторую матрицу). Тогда он даст ответ. Затем, если вы хотите найти определитель матрицы A, введите формулу = mdeterm (выберите матрицу A). Гнездо нажмите Enter. Вы получите определитель A. Затем, если вы хотите найти обратную A, введите формулу = minverse (выберите матрицу A) и нажмите cntl + shft + enter. Вы получите обратное. Если вы хотите умножить три матрицы за раз, вы должны указать эту формулу. То есть =mmult(выберите матрицу A, выберите матрицу B). Это умножит AxB. Затем дайте формулу =mmult(mmult(matrix A selection, B selection), (matrix c selection) ). Тогда вы получите AxBxC. У вас есть возможность выбрать матрицу AxB, а затем матрицу C, чтобы получить матрицу AxBxC. Итак, это формула для создания матрицы в Excel.

Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Начните свою карьеру с нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам обучения от базового до продвинутого по функциям, формулам, инструментам и многому другому.