Как вычислить арккосинус: arcsin, arccos, arctg arcctg, .

Внеклассный урок — Арккосинус

Арккосинус

Арккосинус  в переводе с латинского означает дуга и косинус. Это обратная функция.

 

Арккосинус числа а – это такое число в отрезке от 0 до π, косинус которого равен а. При этом | a | ≤ 1. Обозначается так: arccos a.

 

Говоря иначе:

arccos a = t. Следовательно, cos t = a. Условия: модуль а не больше 1;  t не меньше 0, но не больше π (| a | ≤ 1;  0 ≤ t  ≤ π)

Пример-пояснение: Найдем arccos √2/2 (см. рисунок).

Решение.

Выражение arccos √2/2 показывает, что косинус угла t равен √2/2 (cos t = √2/2).

Далее просто находим точку этого косинуса на числовой окружности, что и является ответом:

число √2/2, являющееся значением оси х, соответствует точке π/4 на числовой окружности.
Значит, arccos √2/2 = π/4.

 

Обратите внимание:

если cos π/4 = √2/2, то arccos √2/2 = π/4.

То есть в первом случае по точке на числовой окружности определяем значение косинуса, а во втором – наоборот, по значению косинуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арккосинус.

Обобщим: косинус – это точка на оси х, а арккосинус – это соответствующая ей точка на окружности.

Формулы:

t = ± arccos a  +  2πk,     где k – любое целое число arccos (-a) = π – arccos a,    где 0 ≤ a ≤ 1

 

Пример 1: Вычислить арккосинус 1/2.

Решение.

Итак, а = 1/2. Значит, наша формула arccos a = t обретает конкретику:

arccos 1/2 = t.

Это означает, что косинус угла t равен 1/2:

cos t = 1/2.

При этом наша точка t находится на отрезке [0; π].

Находим значение t. Для этого смотрим на числовую окружность. Мы видим, что число 1/2 является абсциссой точки π/3 – то есть является косинусом угла π/3. Иначе говоря:

t = π/3.

Подставляем значение t в выражение cos t = 1/2:

cos π/3 = 1/2. При этом π/3 входит в отрезок [0; π].

Совершаем обратное действие: если cos π/3 = 1/2, то:

arccos 1/2 = π/3.

Без объяснений процесс решения будет таким:

arccos 1/2 = t

cos t = 1/2,  t ∈ [0; π]

t = π/3,  π/3 ∈ [0; π]

arccos 1/2 = π/3

Пример решен.

Обратите внимание: косинусом π/3 является 1/2, а арккосинусом 1/2 является π/3. Движение в обратную сторону. Косинусом числа является точка на оси координат, а арккосинусом – точка на числовой окружности.

                                              √3
Пример 2: Найти arccos – ——
                                               2

 Решение.

                 √3
arccos (– ——) = t
                  2

                √3
cos t = – ——,    t ∈ [0; π]
                 2

                      √3
cos 5π/6 = – ——,    5π/6  ∈ [0; π]
                       2

                √3        5π
arccos – —— = ——
                 2          6

Пример решен.

Акцентируем ваше внимание: косинусом 5π/6 является -√3/2, а арккосинусом -√3/2 является 5π/6.

 

Как посчитать арксинус без калькулятора

Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса

В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.

Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».

Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.

Для четкого понимания рассмотрим пример.

Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .

Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °

Основные значения arcsin, arccos, arctg и arctg

Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.

Таблица синусов основных углов предлагает такие результаты значений углов:

sin ( — π 2 ) = — 1 , sin ( — π 3 ) = — 3 2 , sin ( — π 4 ) = — 2 2 , sin ( — π 6 ) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1

Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.

Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.

в р а д и а н а х

Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:

cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1

Следуя из таблицы, находим значения арккосинуса:

a r c cos ( — 1 ) = π , arccos ( — 3 2 ) = 5 π 6 , arcocos ( — 2 2 ) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0

в р а д и а н а х

Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.

α		— 3	— 1	— 3 3	0	3 3	1	3
a r c t g a к а к у г о л	в р а д и а н а х	— π 3	— π 4	— π 6	0	π 6	π 4	π 3
	в г р а д у с а х	— 60 °	— 45 °	— 30 °	0 °	30 °	45 °	60 °
a r c t g a к а к ч и с л о		— π 3	— π 4	— π 6	0	π 6	π 4	π 3

Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса

a r c sin , a r c cos , a r c t g и a r c c t g

Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.

Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .

Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.

Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.

Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.

Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.

Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .

Нахождение значения arcsin, arccos, arctg и arcctg

Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).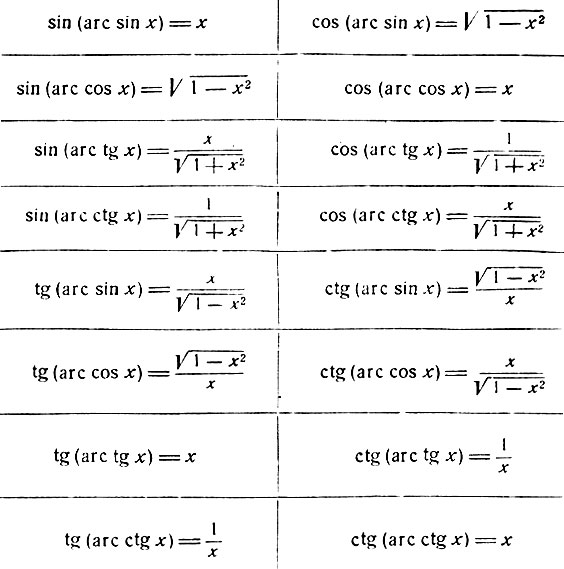

При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:

a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .

Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.

Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.

При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.

Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.

Простейшие тригонометрические уравнения

Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:

Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1<а < 1, то должно получиться две точки, которым соответствуют два противоположных угла:

Получается, что каждому значению числа а соответствует некоторый угол α. А если есть соответствие, то есть и функция:

В математике ее называют арккосинусом. Записывается она так:

Вертикальная прямая может пересекать единичную окружность в двух разных точках. Им соответствуют разные углы. Принято считать, что арккосинус – это значение того угла, который лежит в первой или второй четверти, то есть ему соответствует точка, лежащая выше оси Ох. Тогда другая точка пересечения будет соответствовать углу (– arccosa):

Выходит, что арккосинус может принимать только значения из отрезка [0; π]. Дадим определение арккосинуса:

Задание. Вычислите арккосинус числа 1/2.

Решение. Мы помним, что косинус угла π/3 равен 1/2:

Следовательно, arccos 1/2 – это и есть угол π/3:

Обратим внимание, что если число а равно 1 или (– 1), то его арккосинус равен нулю в первом случае и π во втором:

В тех случаях, когда а > 1 либо а <– 1, то соответствующая прямая не пересечет единичную окружность. Это значит, что эти значения не входят в область определения арккосинуса:

Получается, что область определения арккосинуса – это промежуток [– 1; 1].

Для вычисления арккосинусов от отрицательных величин удобно пользоваться формулой

Действительно, если отложить на координатной прямой числа а и (– а), то вертикальные прямые, проходящие через них, пересекут окружность в некоторых точках А и С:

Дополнительно обозначим буквой В точку с координатами (1; 0) и буквой D точку с координатами (– 1; 0). Эти точки располагаются на пересечении оси Ох и единичной окружности.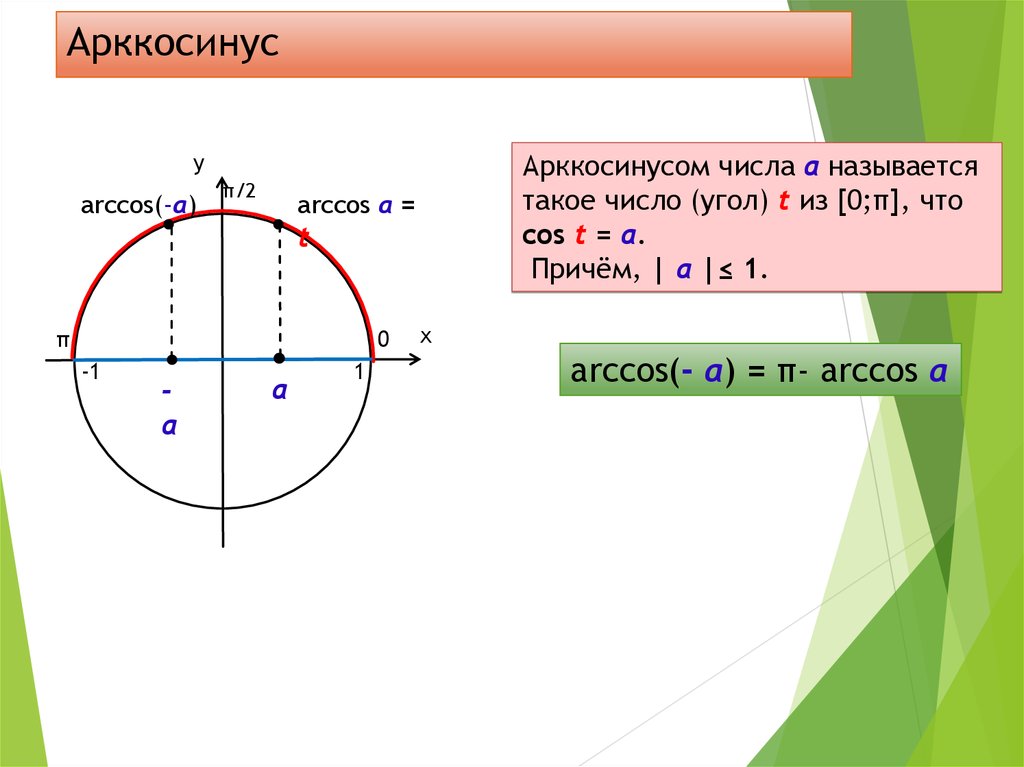 Тогда можно записать, что

ведь эти два угла образуют вместе развернутый угол ВОD, равный π. С другой стороны, из симметрии очевидно, что углы ∠COD и ∠АОВ равны друг другу, значит, ∠COD = ∠АОВ = arccosa. Тогда

Но ∠СОВ – это арккосинус от (– а), поэтому

Задание. Вычислите arccos (– 1/2).

Решение. Используем только что полученную формулу:

Арксинус

Арккосинус – это ф-ция, обратная косинусу. Аналогично можно вести и другие обратные тригонометрические ф-ции. Пусть нам требуется узнать, синус какого угла равен числу а. Так как синус – это координата у точки на единичной окружности, то достаточно провести горизонтальную линию у = а:

Прямая может пересечь окружность сразу в двух точках. За арксинус принимают угол, соответствующей точке, расположенной правее оси Оу. Вторая же точка соответствует углу π – arcsin α:

Арксинус может быть вычислен и для отрицательного значения а. В этом случае точка пересечения прямой и окружности будет располагаться в IV четверти, а соответствующий ему угол окажется отрицательным:

При значениях а, равных (– 1) и 1, точка пересечения будет только одна. В этих случаях арксинус окажется равным либо углу π/2, либо углу (– π/2):

Таким образом, арксинус может принимать значения из отрезка [– π/2; π/2], а вычислить его можно для чисел а, принадлежащих отрезку [– 1; 1]. Если же число а выходит за пределы этого промежутка, то горизонтальная прямая не пересекает единичную окружность, а потому ф-ция арксинуса становится неопределенной:

Получается, что областью определения арксинуса является промежуток [– 1; 1], а областью значений – промежуток [– π/2; π/2].

Дадим определение арксинусу:

Задание. Чему равен arcsin0,5?

Решение. Мы знаем, что sinπ/6 = 1/2 = 0,5. Следовательно, арксинус 0,5 равен π/6.

Для вычисления арксинусов отрицательных углов используется формула

Справедливость этой формулы очевидна из картинки:

Задание.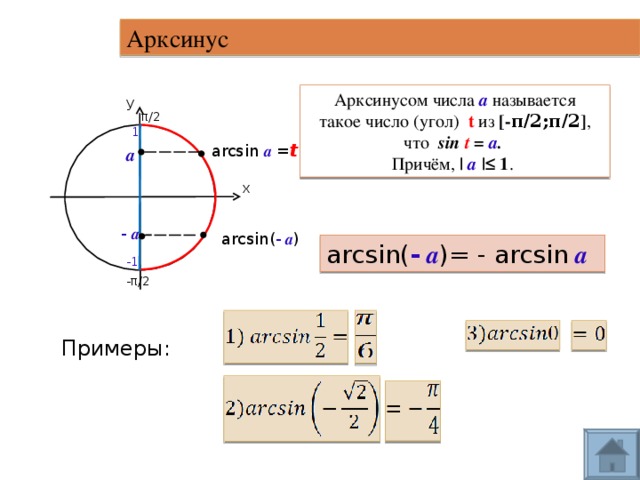 Вычислите arcsin (– 0,5).

Решение. Используем формулу для арксинуса отрицательного числа:

Арктангенс

Введем ф-цию, обратную тангенсу. Она называется арктангенс.

Напомним, что величину тангенса на координатной плоскости можно получить, если продолжить угол до его пересечения с вертикальной прямой х = 1. Аналогично, чтобы определить арктангенс некоторого числа а, надо отметить на этой прямой точку с координатами (1; а) и соединить её с началом координат:

Несложно видеть, что, какое бы число а нами не было выбрано, мы с помощью построения всегда сможем соединить точку А с началом координат и получить некоторый угол arctga. Это значит, что область определения арктангенса – это вся числовая прямая, то есть промежуток (– ∞; + ∞).

Ещё раз уточним, что вводимые нами функции arcos, arcsin, arctg называются ОБРАТНЫМИ тригонометрическими функциями. C их помощью можно определить угол, если известно значение его синуса, косинуса или тангенса. Образно говоря, обратные триг-кие функции играют в тригонометрии ту же роль, что и квадратные корни при исследовании квадратных ур-ний. Как без квадратных корней невозможно решать квадратные ур-ния, так и без знания об обратных триг-ких функций нельзя решать уже тригом-кие уравнения.

Теперь вернемся к понятию арктангенса. При положительном значении числа а угол arctga будет принадлежать I четверти. Если же а – отрицательное число, то угол arctga окажется также отрицательным и будет принадлежать IV четверти:

Получается, что величина arctgа может принадлежать промежутку (– π/2; π/2). Обратите внимание, что в данном случае у промежутка круглые скобки. Действительно для углов (– π/2) и π/2 тангенс не определен, а потому арктангенс не может принимать эти два значения.

Задание. Чему равен arctg 1?

Решение. Из таблицы тангенсов мы знаем, что tgπ/4 = 1. Это значит, что

Для вычисления арктангенсов отрицательных чисел используют формулу

В ее справедливости можно убедиться, взглянув на рисунок:

Задание. Вычислите arctg (– 1).

В принципе можно ввести ещё ф-цию, обратную котангенсу – арккотангенс. Однако для решения тригонометрических уравнений, как мы убедимся далее, она не требуется, а поэтому в рамках школьного курса математики ее можно не изучать.

В заключение приведем таблицы, которые помогают вычислять значение обратных тригон-ких функций:

Решение уравнения cosx = a

Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:

По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь

Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:

Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:

Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:

Здесь мы использовали тот факт, косинус – четная функция, то есть

Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:

Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть

Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:

Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство.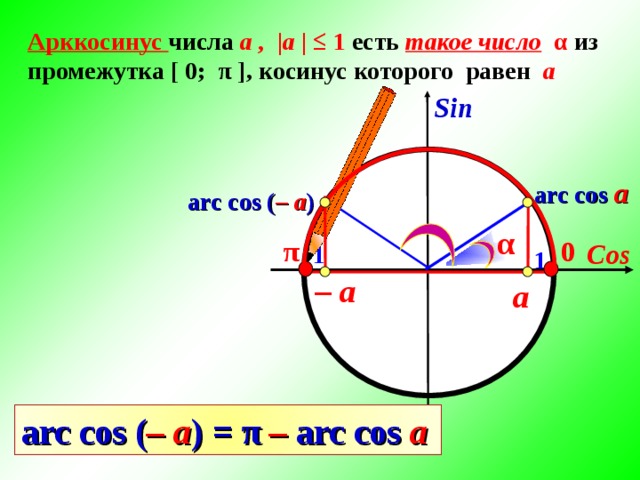 Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение

При n = 5 получим корень

При n = – 10 у нас получится решение

Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:

Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень

Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:

Объединить же обе серии можно одной записью:

Напомним, что мы решали ур-ние

и получили для него решение

Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид

где а – некоторое число, его решением будут все такие х, что

Для краткости запись «n– целое число» заменяют эквивалентной записью

Напомним, что буквой Z обозначают множество целых чисел.

Задание. Решите ур-ние

Решение. Вспомним, что

Задание. Решите ур-ние

Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:

Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.

Задание. Укажите три наименьших положительных корня ур-ния

Решение. Так как

то все решения образуют две серии:

Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.

Для первой серии:

Для второй серии:

Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):

Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4

Ответ: π/4, 7π/4 и 9π/4.

Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния

На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния

являются точки, в которых график пересекает ось Ох:

Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок [– 1; 1].

Решение уравнения sinx = a

Ур-ние cosx = a называют простейшим тригонометрическим уравнением, ведь, ведь для его решения не требуется проводить никаких преобразований. Аналогично простейшими являются ур-ния sinx = a, tgx = a и ctgx = a.

Ситуация с ур-нием sinx = a аналогична ситуации с косинусом.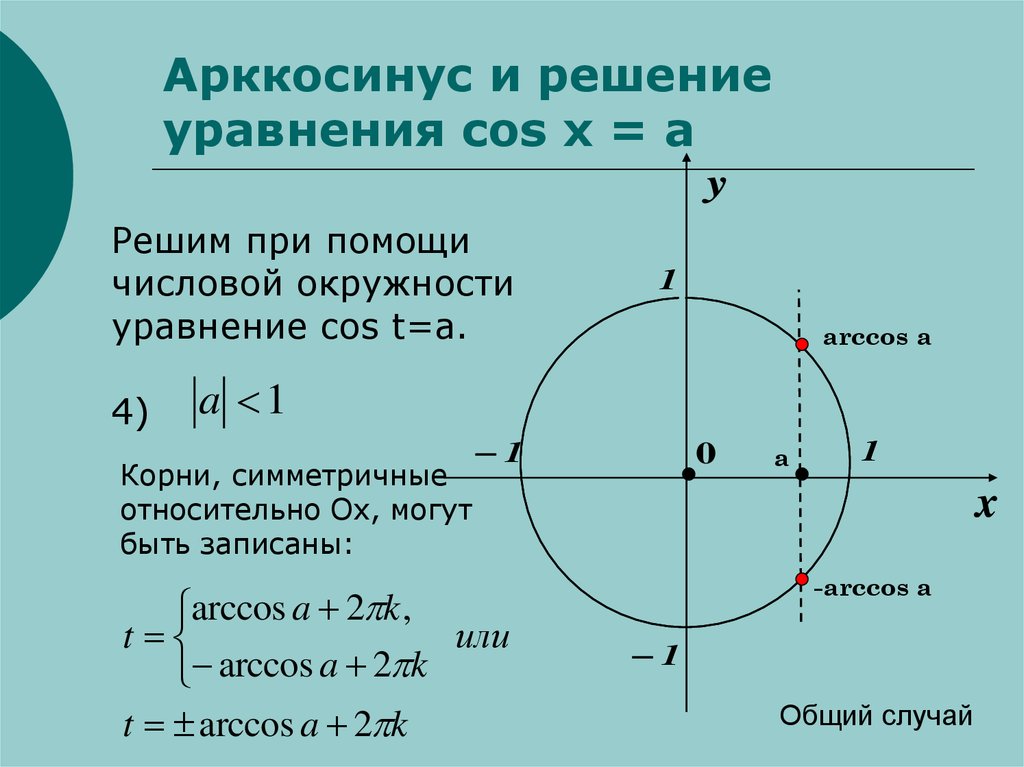 Если число а не принадлежит промежутку [– 1; 1], то корней у ур-ния не будет. Если же число а будет принадлежать этому промежутку, то у ур-ния окажется бесконечное число решений.

Рассмотрим случай, когда 0<а< 1. Тогда решениями ур-ния окажутся числа arcsina и π – arcsina:

В свою очередь каждое из этих двух решений порождает свою собственную бесконечную серию решений

Однако, как и в случае с косинусом, существует способ записать одной формулой сразу оба этих решения. Для этого перепишем первую серию таким образом:

Действительно, если n окажется четным, то, то выражение (– 1) n ,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1) n окажется равным (– 1), и мы получим вторую серию.

Задание. Решите ур-ние

Задание. Запишите корни ур-ния

Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.

Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:

Ответ: 7π/3 и 8π/3.

Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние

Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:

Наконец, решениями ур-ния

Решение уравнений tgx = a и ctgx = a

Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):

Таким образом, у ур-ния tgx = a существует очевидное решение

Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:

Задание. Решите ур-ние

Задание. Запишите формулу корней ур-ния

Далее рассмотрим ур-ние вида

Задание. Решите ур-ние

Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии

Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.

Как найти арксинус: формула, свойства, функция

Обратные тригонометрические функции называют по соответствующим им тригонометрическим функциям. Формулировка наименования заключается в приписывании приставки «арк», что является производным от латинского слова «дуга» (arcus).

Такая методика объясняется тем, что в геометрии функцию, обратную тригонометрической, связывают с длиной, которую имеет дуга единичной окружности, равной какому-то отрезку, либо с углом, стягивающим данную дугу.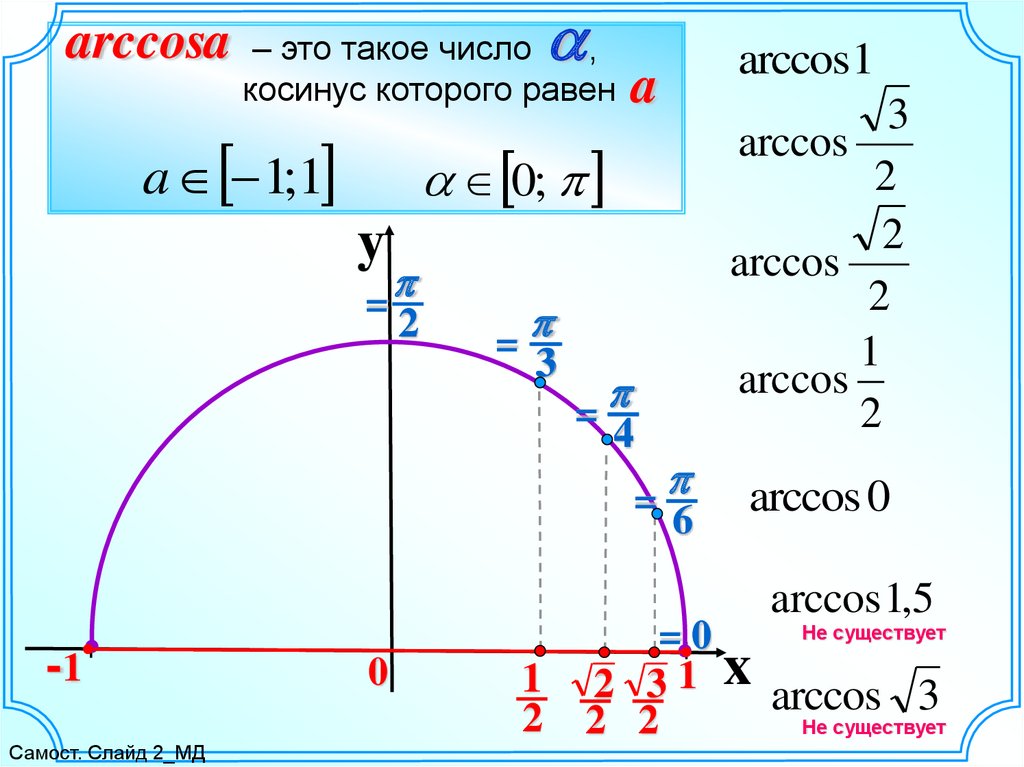 \arcsin \alpha +\pi n,

Арксинус числа х — значение для угла у, определенного в радианах, для которого \(\sin y=x,\quad —>\leqslant y\leqslant >,\quad |x|\leqslant 1\) .

Зачем нужен арксинус

С помощью аркфункций, в том числе — арккосинуса, арктангенса, арккотангенса, арксинуса — определяют углы треугольника. Подобное действие доступно при наличии информации о сторонах данной геометрической фигуры.

В том случае, когда имеется некий прямоугольный треугольник, обратные тригонометрические функции от отношений сторон позволяют определить угол. Например, длина катета составляет «а». Этот катет определяется, как противолежащий для угла \(\alpha\) , то:

\(\alpha =\arcsin(a/c)=\arccos(b/c)=\operatorname (a/b)=\operatorname (c/a)=\operatorname (c/b)=\operatorname (b/a)\)

Получение функции arcsin с пояснением на примерах

Предположим, что существует некая функция:

Записанная функция обладает областью определения. В ее рамках она приобретает кусочно-монотонный вид. По этой причине обратное выражение y=\arcsin x нельзя причислить к функциям.

В результате целесообразно проанализировать отрезок, где наблюдается строгое возрастание функции, и все значения относятся к ряду из области значений:

Функция \(y=\sin x \) на отрезке \(\left[->;>\right]\) обладает следующей особенностью: какое-либо из значений этой функции возможно только при одном значении аргумента. По этой причине на данном интервале может существовать обратная функция с формулой \(y=\arcsin x.\)

График обратной функции является симметричным графику функции \(y=\sin x\) в рамках интервала \(\left[->;>\right]\) по отношению к прямой y=x. Можно наблюдать симметричность в расположении графиков функций, которые являются взаимно обратными, по отношению к биссектрисе первого и третьего координатных углов на плоскости координат Oxy.

Определим значение выражение:

По определению обратной тригонометрической функции можно сделать вывод, что запись означает угол с синусом, равным 0,4. В данном выводе заключается смысл понятия арксинус.

Требуется найти, что означает \(\arcsin 0,5\) .

Если знать определение, эта простая обратная тригонометрическая функция является обозначением угла с синусом, равным 0,5. Таким синусом обладает угол в 30°. Таким образом:

Общий ответ можно высчитать не в градусах, а в радианах:

Свойства функции arcsin

Рассмотрим функцию \(y=\arcsin x\) . Она является непрерывной в тригонометрии и ограничивается на протяжении всей своей области определения. Данная функция строго возрастает.

Калькулятор — arccos(2) — Solumaths

Arccos, расчет онлайн

Резюме:

Функция arccos позволяет вычислить арккосинус числа. Функция arccos является обратной функцией функции косинуса.

arccos online

---

Описание:

Функция арккосинуса является обратной функцией функция косинуса, это вычисляет арккосинус числа онлайн .

Число, к которому вы хотите применить функцию арккосинуса, должно принадлежать диапазону [-1,1].

1. Расчет арккосинуса

Чтобы вычислить арккосинус числа, просто введите число и примените функция arccos . Таким образом, для вычисление арккосинуса числа, следующего за 0,4, вы должны ввести arccos(`0.4`) или сразу 0.4, если кнопка arccos уже есть, результат 1.1592)`.

2. Таблица замечательных значений
9005-6 arccos(sqrt(sqrt) 2)/2`) `

arccos(`-1`)	`pi`
arccos(`-sqrt(3)/2`)	`5*pi/6`
`3*pi/4`
arccos(`-1/2`)	`2*pi/3`
arccos(`0`)		`2*pi/3` pi/2`
arccos(`1/2`)	`pi/3`
arccos(`sqrt(2)/2`)	`pi/4`
arccos(`sqrt(3)/2`)	`pi/6`
arccos(`1`)	`0`

Syntax :

arccos(x), где x — число.

Иногда используются другие обозначения: acos

---

Примеры:

arccos(`1`) возвращает 0

---

Производная арккосинуса :

Чтобы дифференцировать функцию арккосинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арккосинуса 92)`

---

Предел арккосинуса :

Калькулятор предела позволяет вычислить пределы функции арккосинуса.

предел арккосинуса(x) is limit(`»arccos»(x)`)

---

Обратная функция арккосинуса :

обратная функция арккосинуса – это функция косинуса, отмеченная как cos.

---

---

Графический арккосинус :

Графический калькулятор может отображать функцию арккосинуса в заданном интервале.

---

Расчет онлайн с арккосинусом

См. также

Список связанных калькуляторов:

• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус: арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
• Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
• Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
• Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
• Тангенс: тангенс. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

---

Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции

 

Arccos(x) Calculator | Калькулятор арккосинуса

Arccos(x) Калькулятор | Калькулятор арккосинуса

Главная›Калькуляторы›Математические калькуляторы› Калькулятор Arccos

Калькулятор Arccos(x). Калькулятор арккосинуса.

арккос
Угол в градусах:
°
Угол в радианах:
рад
Расчет:

Калькулятор косинуса ►

Определение арккосинуса

Функция арккосинуса является обратной функцией cos(x).

Arccos ( x ) = COS ^-1 ( x )

Например, если косинус 60 ° составляет 0,5:

Cos (60 °) = 0,5

, то дуга. 0,5 равно 60°:

arccos(0,5) = cos ^-1 (0,5) = 60°

Таблица Arccos

x	arccos(x)
	градусов	радиан
-1	180°	№
-0,8660254	150°	5π/6
-0,7071068	135°	3π/4
-0,5	120°	2π/3
0	90°	№/2
0,5	60°	№/3
0,7071068	45°	№/4
0,8660254	30°	№/6
1	0°	0

 

---

См.