Как находится длина окружности формула. Как вычислить диаметр окружности: формула и пояснения
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
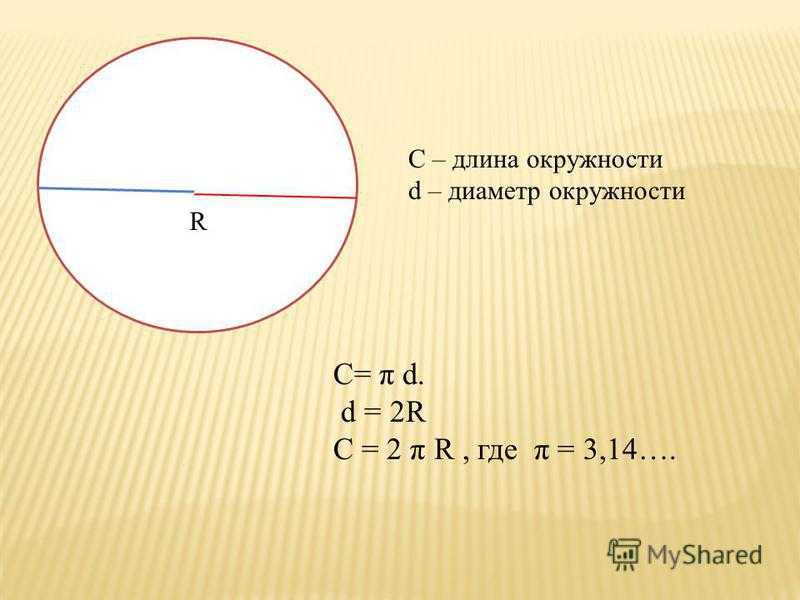
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах
Она измеряется в квадратных единицах
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два .
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r .
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. В школьной математике она считается заранее известной табличной величиной, равной 3,14!
Теперь перепишем предыдущую формулу, чтобы найти длину окружности через её диаметр, помня, в чём состоит его разница по отношению к радиусу.
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
«Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ:
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых.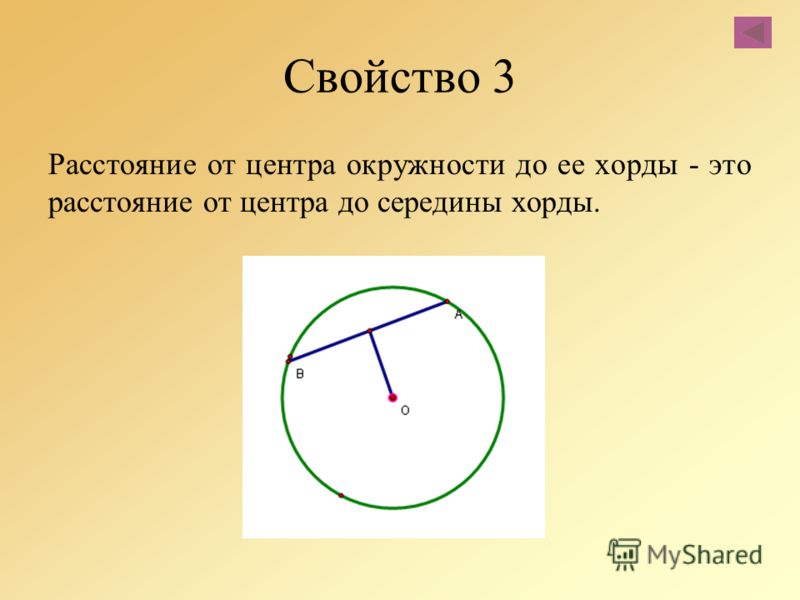 В результате такого действия получается число 18. Результат получен.
В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.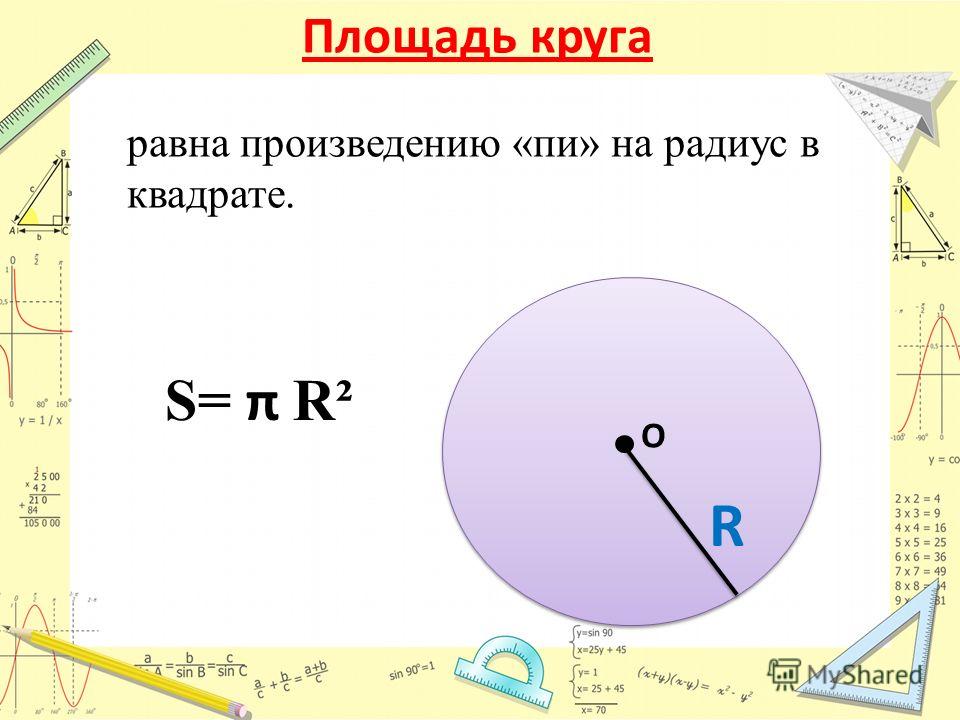 2»).
2»).
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Инструкция
Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например, круга равен двадцати сантиметрам, то его
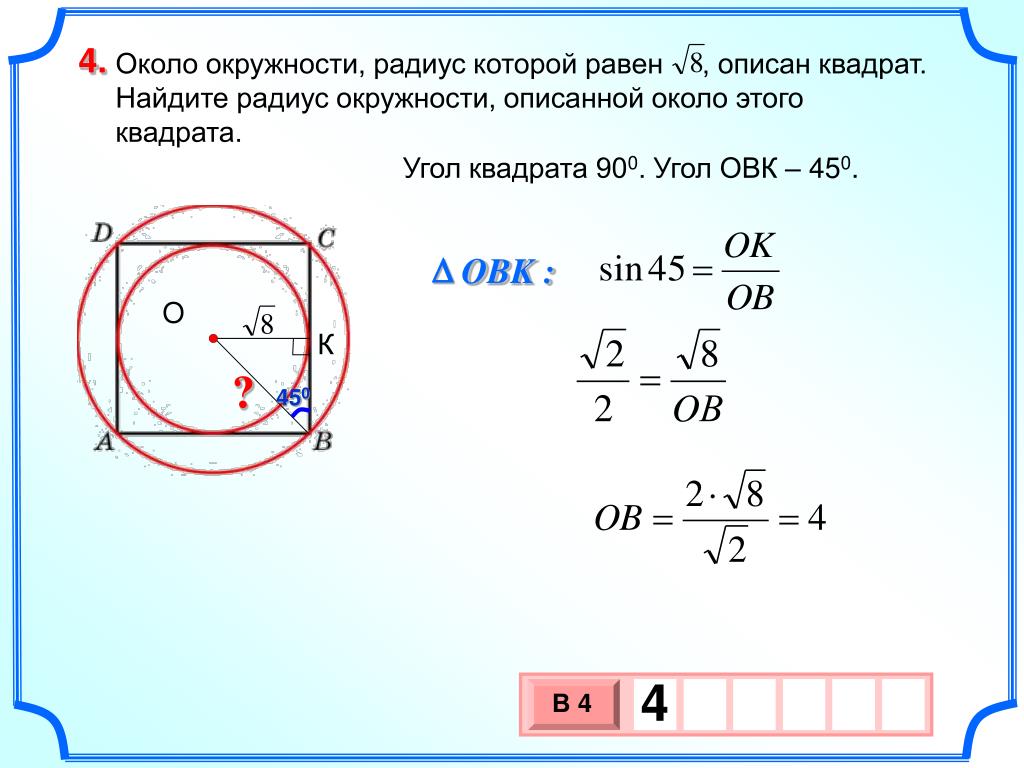
Если надо найти площадь квадрата (S) по диаметру вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.
Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². 2 / 4 + 20*10/2», а нажать клавишу Enter.
2 / 4 + 20*10/2», а нажать клавишу Enter.
Источники:
- как найти площадь окружности по диаметру
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Используйте какой-либо , чтобы рассчитать длину диаметра, если сделать это в уме не получается. Например, можно воспользоваться тем, который встроен в поисковую систему Nigma или Google — он математические операции, вводимые на «человеческом» . Например, если известная длина окружности составляет четыре метра, то для нахождения диаметра можно «по-человечески» попросить поисковик: «4 метра разделить на пи». Но если вы введете в поле поискового запроса, например, «4/пи», то поисковик поймет и такую постановку задачи. В любом случае ответом будет «1.27323954 метра».
Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.
Применительно к Земле не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».
Официальный диаметр Земли
Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.
Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.
Вычисление диаметра Земли
Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.
Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.
Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).
В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах. Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.
На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по – 40 007,86. Эратосфен лишь немного ошибся.
Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.
Источники:
- Как измерили Землю в 2019
В процессе выполнения строительных работ в быту или на производстве может появиться необходимость в измерении диаметра трубы, которая уже вмонтирована в систему водоснабжения или канализации. Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.
Отсюда возникает необходимость разобраться с тем, как определить диаметр трубы. Выбор конкретного способа выполнения измерений зависит от размеров объекта и от того, доступно ли расположение трубопровода.
Определение диаметра в бытовых условиях
До того, как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:
- рулетка или стандартная линейка;
- штангенциркуль;
- фотоаппарат — его задействуют при необходимости.
Если трубопровод доступен для проведения замеров, а торцы труб можно без проблем измерить, тогда достаточно иметь в распоряжении обычную линейку или рулетку. При этом следует учитывать, что используют такой метод, когда к точности предъявляются минимальные требования.
В этом случае выполняют измерение диаметра труб в такой последовательности:
- Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.
- Потом отсчитывают количество делений, соответствующих размеру диаметра.
Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров.
Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:
- Раздвигают его ножки и прикладывают к торцу изделия.

- Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.
- Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.
Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.
Когда трубопровод недоступен для обмера и является частью уже функционирующей конструкции водоснабжения или газовой магистрали, поступают следующим образом: штангенциркуль прикладывают к трубе, к ее боковой поверхности. Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.
Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14.
Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате.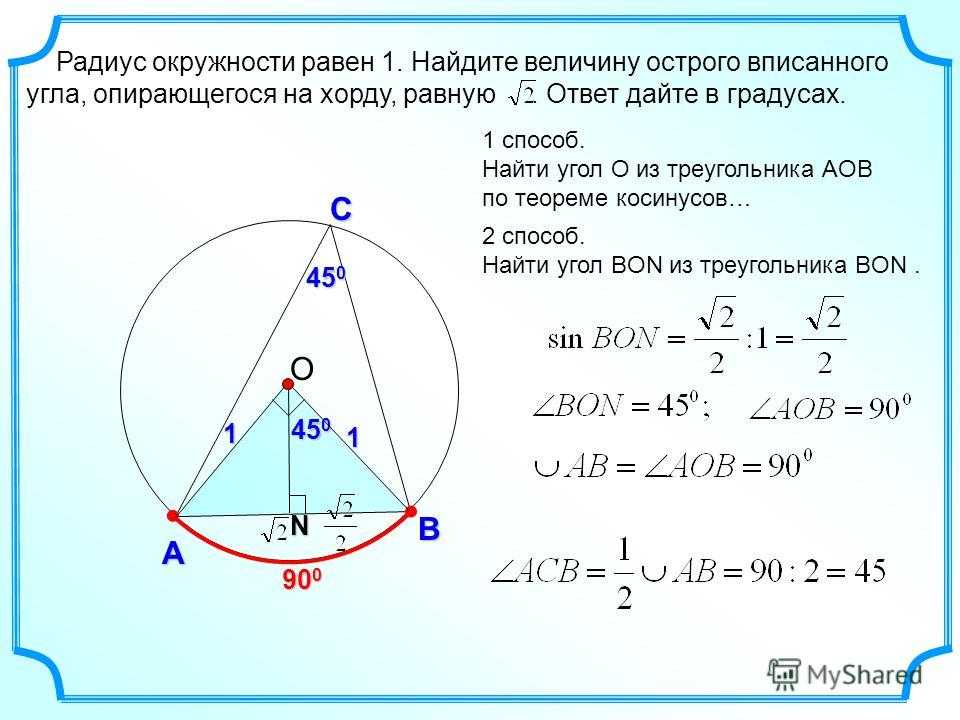 Потом подставляют известные величины в формулу d=l:π, где:
Потом подставляют известные величины в формулу d=l:π, где:
d – определяемый диаметр;
l – длина измеренной окружности.
К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.
Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.
К примеру, это может быть коробок спичек, длина которого равна 5 сантиметрам. Потом этот участок трубопровода фотографируют. Последующие вычисления выполняют по фотографии. На снимке измеряют видимую толщину изделия в миллиметрах. Потом нужно перевести все полученные величины в реальные параметры трубы с учетом масштаба произведенной фотосъемки.
Измерение диаметров в производственных условиях
На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю.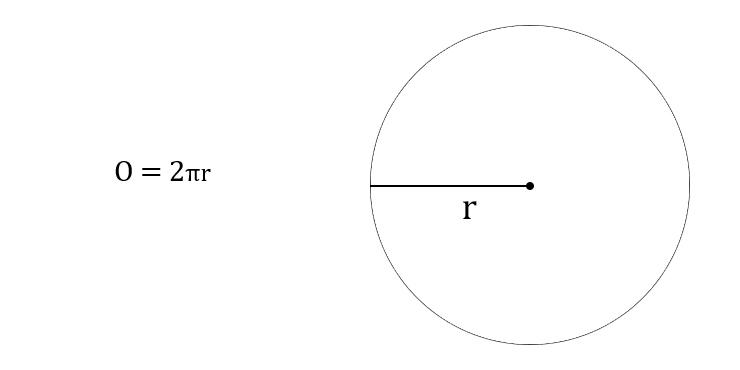 Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Документация должна содержать определенную информацию, касающуюся труб:
- номинальные размеры;
- номер и дата ТУ;
- марка металла или вид пластика;
- номер товарной партии;
- итоги проведенных испытаний;
- хим. анализ выплавки;
- тип термической обработки;
- результаты рентгеновской дефектоскопии.
Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:
- наименование производителя;
- номер плавки;
- номер изделия и его номинальные параметры;
- дату изготовления;
- эквивалент углерода.
Длины труб в производственных условиях определяют мерной проволокой. Также не возникает сложностей с тем, как измерить диаметр трубы рулеткой.
Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров.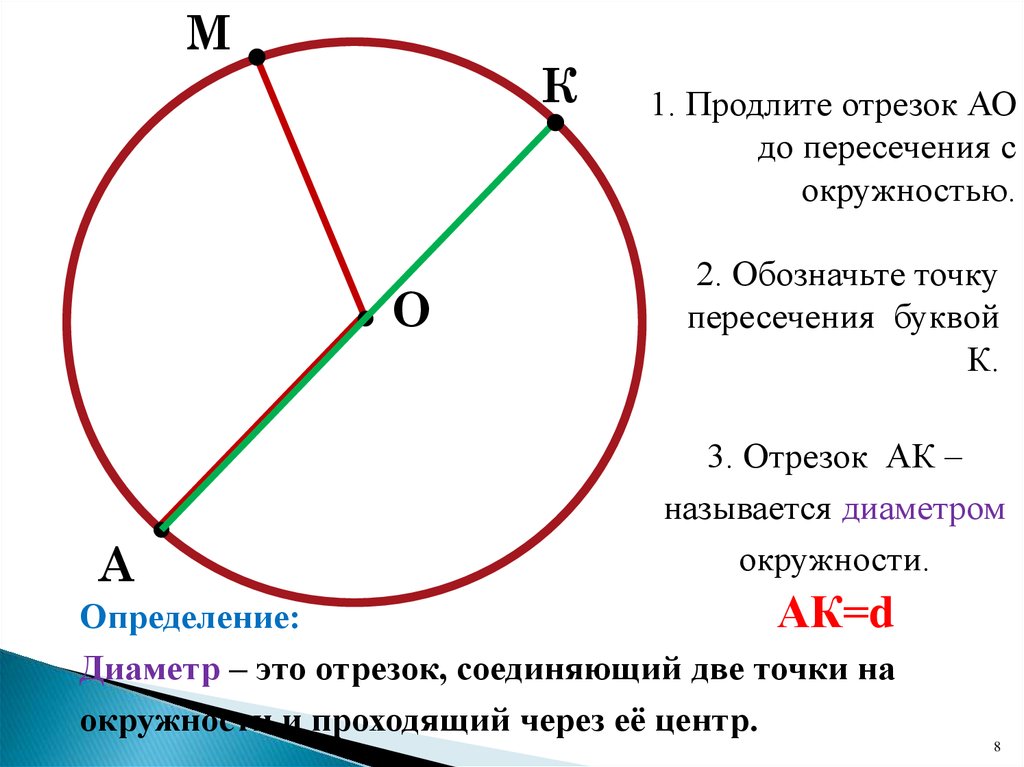 Для второго класса –100 миллиметров.
Для второго класса –100 миллиметров.
У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:
Δр – толщина материала рулетки;
0,2 миллиметра– припуск на прилегание инструмента к поверхности.
Допускается отклонение величины внешнего диаметра от заявленной производителем:
- для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
- для больших труб – 0,7%.
В последнем случае для проверки трубной продукции пользуются ультразвуковыми измерительными приборами. Для определения толщины стенок задействуют штангенциркули, у которых деление на шкале соответствует 0,01 миллиметра. Минусовой допуск не должен превышать 5% номинальной толщины. При этом кривизна не может быть более 1,5 миллиметра на 1 погонный метр.
Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов.
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π
≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π
,
Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52
дм.
(π
≈ 3,14
).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .
как найти длину окружности зная диаметр. Диаметр в формулах вычисления
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415
.
Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415
.
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE{P} = 2 \cdot \pi \cdot r \]
\[ \LARGE{P} = \pi \cdot d \]
\(P \) – периметр (длина окружности).
\(r \) – радиус.
\(d \) – диаметр.
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
В декартовой системе координат \(xOy \)
мы также можем ввести уравнение любой окружности. 0}{n}}=\frac{2τ}{2τ»} \)
0}{n}}=\frac{2τ}{2τ»} \)
Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:
\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)
Из последних двух равенств получим, что
\(\frac{C}{C»}=\frac{2τ}{2τ»} \)
\(\frac{C}{2τ}=\frac{C»}{2τ»} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\(\frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\(\frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\(C=2πτ \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Вконтакте
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы.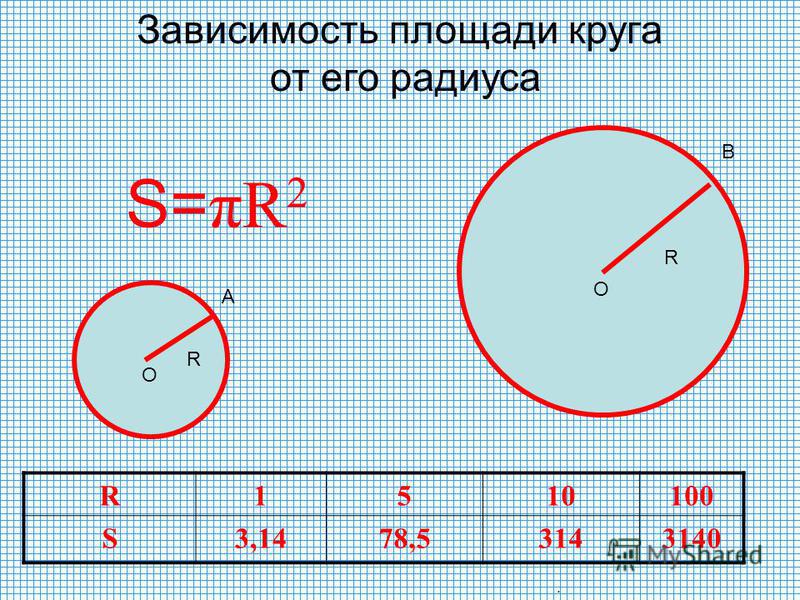 Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом.
 При этом отрезок АВ – диаметр.
При этом отрезок АВ – диаметр. - Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски.
Чему равна длина окружности ее. Как найти длину окружности: через диаметр и радиус
Окружностью называют кривую линию, которая ограничивает собой круг.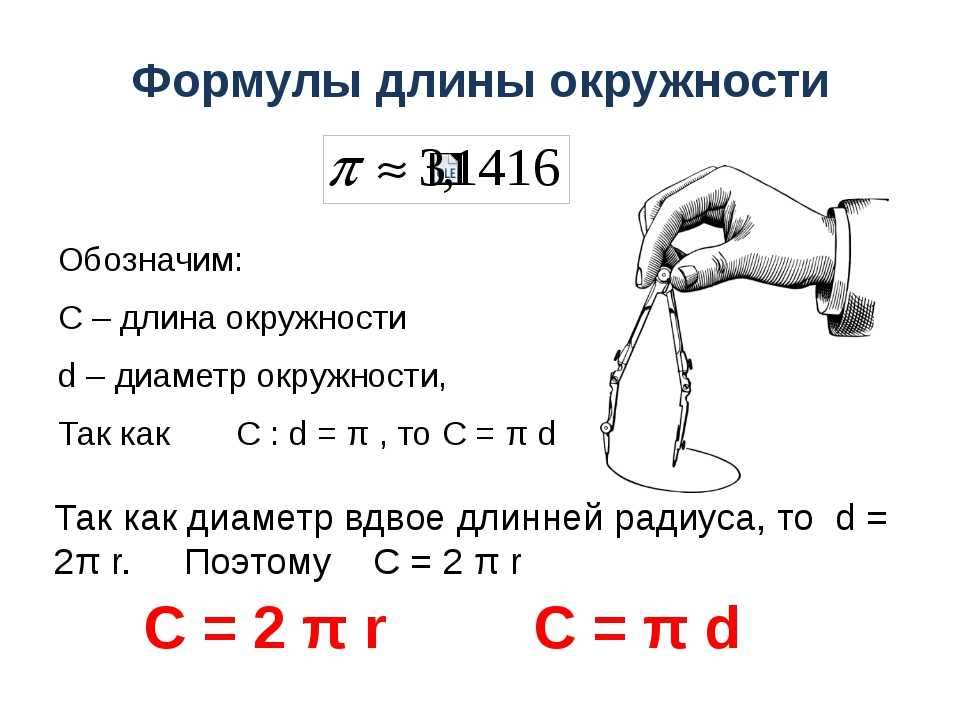 В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр.
 Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое.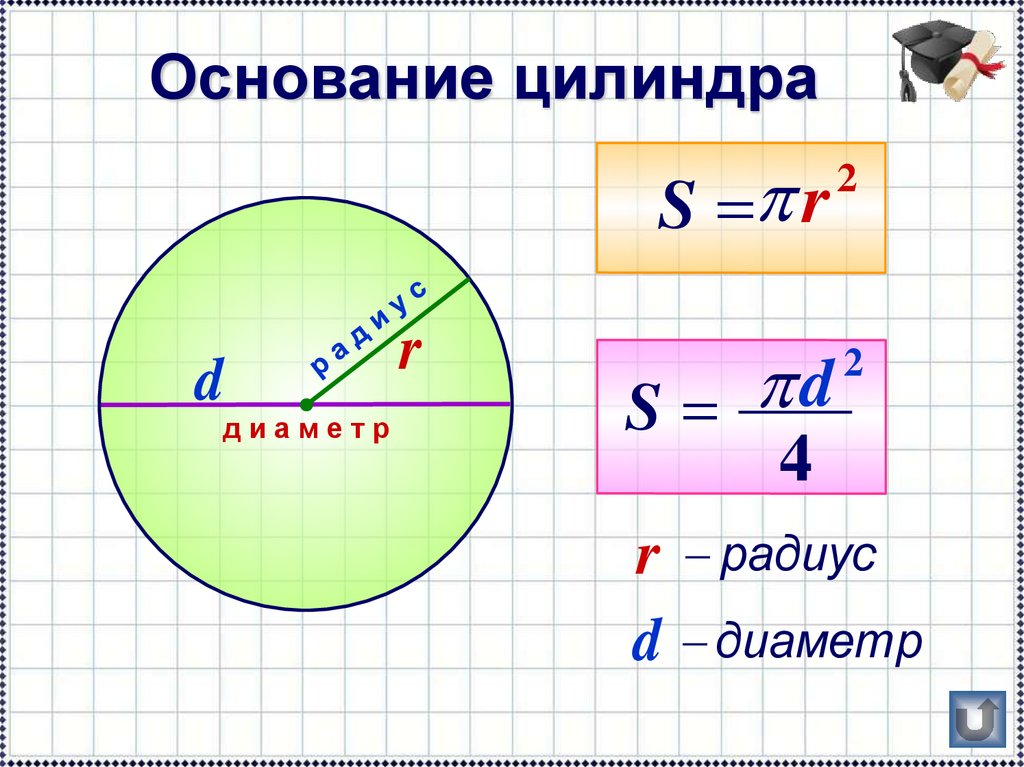 Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).

Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила.
Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Вконтакте
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре.
 Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности.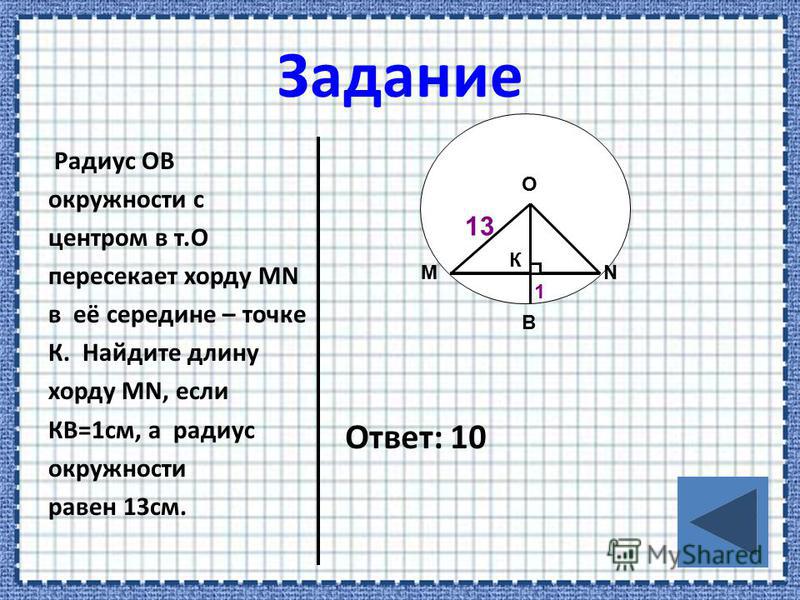 Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром.
 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два .
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r .
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь.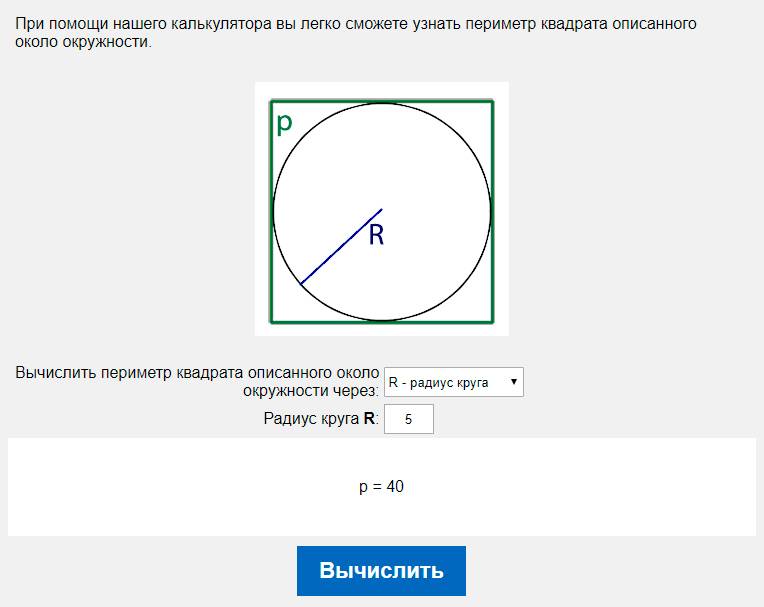 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр. Пусть d = 815 метров.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
через диаметр и радиус. Терминология, основные формулы и характеристика фигуры. Вычислить площадь круга
- если известен диаметр окружности, то формула выглядит так L = ПD
- если известен радиус окружности, то формула имеет следующий вид L = 2Пr.

Формула длины окружности
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе. Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.
Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.
Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.

Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга. Она вас, при решении геометрических задач, еще не раз выручит.
Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,
Решение уравнений:
Геометрическая прогрессия:
Комбинаторика:
Решить химическое уравнение
Арифметическая прогрессия.
Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности
Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.
r — это радиус
D — диаметр
Приблизительно 3,14
Но окружность — это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.14.
Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.
Длину окружности можно найти одним из представленных способов:
То окружности, например: крышки на бак, люка, зонтовой крыши, котлована, округлого оврага и так далее, вы можете, замерив длину окружности, быстро высчитать ее диаметр.Для этого только надо применить формулу длины окружности.L = п DЗдесь:L – длина окружности,п – число Пи, равное 3.14,D – диаметр окружности.Переставьте в формуле длины окружности искомое в левую часть и получите:D = L/п
Разберем практическую задачу. Предположим, вам необходимо изготовить крышку на круглый дачный колодец, доступа к которому в данный момент нет. Не сезон, и неподходящие погодные условия. Но у вас есть данные по длине его окружности. Предположим, это 600 см.В указанную формулу подставляем значения:D = 600/3,14 = 191.08 см.Итак, 191 см составляет диаметр вашего колодца.Увеличивайте диаметр до 2-х метров с учетом припуска за края. Устанавливайте циркуль на радиус 1 м (100 см) и вычерчивайте окружность.
Не сезон, и неподходящие погодные условия. Но у вас есть данные по длине его окружности. Предположим, это 600 см.В указанную формулу подставляем значения:D = 600/3,14 = 191.08 см.Итак, 191 см составляет диаметр вашего колодца.Увеличивайте диаметр до 2-х метров с учетом припуска за края. Устанавливайте циркуль на радиус 1 м (100 см) и вычерчивайте окружность.
Полезный совет
Окружности сравнительно больших диаметров в домашних условиях удобно вычерчивать циркулем, который быстро можно изготовить. Делается это так. В рейку вбивается два гвоздя на расстоянии друг от друга, равному радиусу окружности. Один гвоздь неглубоко вбейте в заготовку. А другой используйте, вращая рейку, в качестве маркера.
Чтобы вычислить объем трубы, измерьте ее длину, а также внутренний и внешний радиусы. Определите площади поперечных сечений по внешнему и внутреннему радиусу, рассчитайте объемы. Это будет внутренний и внешний объем трубы. После этого вычислите объем материала, из которого сделана труба, простым вычитанием. Если известен материал, из которого сделана труба и ее можно взвесить, рассчитайте ее объем через плотность.
Если известен материал, из которого сделана труба и ее можно взвесить, рассчитайте ее объем через плотность.
Вам понадобится
- рулетка, штангенциркуль, таблица плотностей некоторых веществ, весы.
Инструкция
Определение объема трубы геометрическим методомС помощью рулетки или любым другим способом измерьте длину трубы, включая все ее изгибы. Затем штангенциркулем или другим подходящим прибором найдите и внутренний диаметр трубы и вычислите радиусы, поделив каждый диаметр на 2. Некоторые трубы маркированы в дюймах. Чтобы перевести это значение в , умножьте дюймы на 0,0254. Чаще всего в дюймах указывается внутренний диаметр. Рассчитайте полный объем трубы по внешнему радиусу. Для этого число 3,14 умножьте на квадрат внешнего радиуса, измеренного в метрах и измеренную в метрах длину трубы V=3,14 R² l. Объем получите в кубических метрах.
Рассчитайте внутренний объем трубы. Делайте это таким же образом, как и для внешнего объема, только при расчете используйте значение радиуса трубы V=3,14 r² l. Так можно определить объем вещества, которое может в трубе. Это может быть вода, газ и т.д. Чтобы найти объем материала, из которого сделана труба, от внешнего объема отнимите внутренний. Чтобы не делать лишних расчетов, в том случае, если не нужно рассчитывать внешний и внутренний объемы, найдите объем тела трубы сразу. Для этого разницу внешнего и внутреннего радиусов возведите в квадрат, умножьте на число 3,14 и длину трубы V=3,14 (R-r)² l.
Так можно определить объем вещества, которое может в трубе. Это может быть вода, газ и т.д. Чтобы найти объем материала, из которого сделана труба, от внешнего объема отнимите внутренний. Чтобы не делать лишних расчетов, в том случае, если не нужно рассчитывать внешний и внутренний объемы, найдите объем тела трубы сразу. Для этого разницу внешнего и внутреннего радиусов возведите в квадрат, умножьте на число 3,14 и длину трубы V=3,14 (R-r)² l.
Определение объема тела трубы через плотностьУзнайте из специальной таблицы плотность материала, из которого сделана труба (сталь, чугун, пластик, стекло и т.д.) в кг/м³. Затем взвесьте трубу на весах, выразив ее массу в килограммах. Для того чтобы получить объем тела трубы, ее массу поделите на плотность V=m/ρ. Результат получите в кубических метрах. Во всех случаях, когда нужно перевести кубические метры в кубические сантиметры, полученный результат умножайте на 1000000.
Кругом называют плоскую геометрическую фигуру, а линию, ее ограничивающую, принято называть окружностью. Основное свойство круга заключается в том, что каждая точка на этой линии находится на одинаковом расстоянии от центра фигуры. Отрезок с началом в центре круга и окончанием на любой из точек окружности называется радиусом, а отрезок, соединяющий две точки окружности и проходящий через центр — диаметром.
Основное свойство круга заключается в том, что каждая точка на этой линии находится на одинаковом расстоянии от центра фигуры. Отрезок с началом в центре круга и окончанием на любой из точек окружности называется радиусом, а отрезок, соединяющий две точки окружности и проходящий через центр — диаметром.
Инструкция
Используйте число Пи для нахождения длины диаметра по известной длине окружности. Эта константа выражает постоянное соотношение между этими двумя параметрами круга — независимо от размеров круга, деление длины его окружности на длину диаметра всегда дает одно и то же число. Из этого вытекает, что для нахождения длины диаметра следует длину окружности разделить на число Пи. Как правило, для практических вычислений длины диаметра достаточно точности до сотых единицы, то есть до двух знаков после запятой, поэтому число Пи можно считать равным 3,14. Но так как эта константа является числом иррациональным, то имеет бесконечное число знаков после запятой. Если возникнет необходимость в более точном определении , то нужное число знаков для числа пи можно найти, например, по этой ссылке — http://www. math.com/tables/constants/pi.htm .
math.com/tables/constants/pi.htm .
При известной площади круга (S) для нахождения длины диаметра (d) удваивайте квадратный корень из отношения площади к числу Пи: d=2∗√(S/π).
При известной длине стороны описанного возле круга прямоугольника, длина диаметра будет равна этой известной величине.
При известных длинах сторон (a и b) прямоугольника, вписанного в круг, длину диаметра (d) можно вычислить, найдя длину диагонали этого прямоугольника. Поскольку диагональ здесь является гипотенузой в прямоугольном треугольнике, катеты которого образуют стороны известной длины, то по теореме Пифагора длину диагонали, а вместе с ней и длину диаметра описанной окружности, можно рассчитать, найдя квадратный корень из суммы квадратов длин известных сторон: d=√(a² + b²).
При выполнении различных работ, как в домашнем хозяйстве, так и на производстве, может возникнуть необходимость установить диаметр трубы. Рассчитать диаметр любой трубы правильной формы можно при помощи несложных вычислений, в основе которых лежат элементарные знания из школьной геометрии.
Вам понадобится
- — измерительная рулетка;
- — штангенциркуль;
- — калькулятор;
- — лист бумаги и карандаш.
Инструкция
Чтобы внешний диаметр небольшого размера, воспользуйтесь измерительным инструментом, например, штангенциркулем. Раздвиньте губки инструмента, чтобы раствор его был больше, чем сечение трубы. Приложите штангенциркуль к и сожмите губки инструмента так, чтобы они плотно охватили . По шкале определите, каков диаметр измеренной трубы. Штангенциркуль обеспечивает точность измерения трубы до десятых долей миллиметра.
Для измерения внутреннего диаметра трубы используйте верхние губки штангенциркуля. Вставьте губки внутрь трубы и раздвиньте их, чтобы губки плотно прилегали к противоположным внутренним краям трубы. По измерительной шкале определите внутренний диаметр трубы. Учитывайте, что стандартный штангенциркуль позволяет измерить трубы диаметром до 150 мм.
Если вам необходимо измерить диаметр трубы, не имея доступа к ее срезу, используйте строительную рулетку или нитку (в зависимости от размеров трубы). Измерьте при помощи нитки или рулетки длину окружности трубы (ее обхват). Затем произведите расчет внешнего диаметра трубы по формуле:
Измерьте при помощи нитки или рулетки длину окружности трубы (ее обхват). Затем произведите расчет внешнего диаметра трубы по формуле:
D = L / p, где L – длина окружности трубы, p = 3,14 (число «пи»).
Например, при длине окружности 400 мм внешний диаметр трубы составит:
D = 400 / 3,14 = 127,4 мм.
Внутренний диаметр трубы рассчитайте по формуле:
D’ = D – 2 * t, где D – внешний диаметр трубы, а t – толщина стенки.
Так, для рассмотренного выше примера, при толщине стенок трубы 3 мм, внутренний диаметр трубы составит:
D’ = 127,4 – 2 * 3 = 121,4 мм.
Если у вас имеется отрезок трубы, причем известны площадь поверхности и длина отрезка, то диаметр рассчитайте, применив формулу площади боковой поверхности цилиндра:
D = p * N / S, где N – длина трубы, S – площадь поверхности, p = 3,14.
D’ = D – 2 * t, где D – внешний диаметр трубы, а t – толщина ее стенки.
Отрезок, соединяющий две несовпадающие точки, лежащие на одной окружности, называют «хордой», а хорда, проходящая через центр этой окружности, имеет и еще одно название — «диаметр». Такая хорда имеет максимально возможную для этой окружности длину, которую можно вычислить несколькими способами, используя базовые определения и соотношения.
Такая хорда имеет максимально возможную для этой окружности длину, которую можно вычислить несколькими способами, используя базовые определения и соотношения.
Инструкция
Самый простой способ определения диаметра (D) окружности можно применять в том случае, когда известен радиус (R) . По радиус — это отрезок, соединяющий круга с любой точкой, лежащей на окружности. Из этого вытекает, что диаметр составляют два отрезка, каждого из которых равна радиусу: D=2*R.
Используйте для вычисления диаметра (D) соотношение, называемое числом Пи, если вам известна длина периметра (L). Периметр, применительно к , принято называть длиной окружности, а Пи выражает постоянное соотношение между диаметром и длиной окружности — в евклидовой геометрии деление периметра круга на его диаметр всегда равно числу Пи. Значит, для нахождения диаметра длину окружности вам нужно разделить на эту константу: D=L/π.
Из корень из результата деления площади на число Пи и удвоить полученное значение: D=2*√(S/π).
Если возле круга описан прямоугольник и длина его стороны известна, то ничего вычислять не потребуется — таким прямоугольником может быть только квадрат, а длина его стороны будет равна диаметру круга.
В случае же вписанного в круг прямоугольника длина диаметра будет совпадать с длиной его диагонали. Для ее нахождения при известных ширине (H) и высоте (V) прямоугольника можно воспользоваться теоремой Пифагора, так как треугольник, образованный диагональю, шириной и высотой будет прямоугольным. Из теоремы вытекает, что длина диагонали прямоугольника, а значит и диаметра окружности, равна квадратному корню из суммы квадратов ширины и высоты: D= √(H²+V²).
Источники:
- площадь круга через диаметр
Расчет объема какого-либо тела – это одна из классических задач прикладной науки. Подобные вычисления часто требуются в инженерной деятельности. Чтобы найти объем трубы , достаточно произвести ряд математических действий.
Вам понадобится
- — Калькулятор.

Инструкция
Измерьте внутренний или внешний диаметр трубы, а также длину окружности сечения.
Найдите радиус трубы – R. Если требуется вычислить внутренний объем, необходимо найти внутренний радиус. Чтобы рассчитать объем, который занимает тело, рассчитывать нужно внешний радиус. Поделите диаметр на два. R=D/2. Также можно использовать длину сечения: R=L/6,28318530. Здесь L – это длина окружности, а число – удвоенное Пи.
Вычислите площадь сечения трубы. Значение радиуса возведите в квадрат, помножьте его на Пи. Площадь сечения будет выражаться в тех же единицах, что и значение радиуса. Например, радиус представлен в сантиметрах. В этом случае площадь сечения будет выражена в квадратных сантиметрах. Формула, по которой рассчитывается площадь сечения: S = R2*Пи, где S – это искомая площадь, а R2 — радиус.
Найдите объем трубы. Для этого помножьте длину трубы на площадь ее сечения. Формула: V=S*L, где V – это объем трубы, S – площадь сечения, L – длина.
Аналогичным образом найдите объем всех труб (если они имеют разные диаметры).
Обратите внимание
Необходимо убедиться, что длина трубы и значение радиуса выражаются в одинаковых единицах измерения. В противном случае вы получите неверное значение. Обычно все вычисления производятся в сантиметрах и квадратных сантиметрах.
Полезный совет
Если при вычислениях вы пользуетесь калькулятором, в его память можно занести удвоенное число Пи. Тогда можно будет довольно быстро вычислять значения нескольких объемов – если вам нужно найти объем труб с различными диаметрами. Также в память калькулятора или компьютера можно внести готовые формулы, чтобы в дальнейшем быстро производить необходимые расчеты. Если вам часто приходится работать с математическими формулами, можно скачать в интернете специальную программу.
Источники:
- Внутренний объем погонного метра трубы в литрах — таблица в 2018
При проведении построений различных геометрических фигур иногда требуется определить их характеристики: длину, ширину, высоту и так далее. Если речь идет о круге или окружности, то часто приходится определять их диаметр. Диаметр представляет собой отрезок прямой, который соединяет две наиболее удаленных друг от друга точки, расположенные на окружности.
Если речь идет о круге или окружности, то часто приходится определять их диаметр. Диаметр представляет собой отрезок прямой, который соединяет две наиболее удаленных друг от друга точки, расположенные на окружности.
Вам понадобится
- — измерительная линейка;
- — циркуль;
- — калькулятор.
Инструкция
В самом простом случае определите диаметр по формуле D = 2R, где R – радиус окружности с центром в точке О. Такая удобна, если вы вычерчиваете круг с заранее оговоренным . Например, если при построении фигуры вы установите раствор ножек циркуля равным 50 мм, то диаметр круга, полученного в результате, будет равен удвоенному радиусу, то есть 100 мм.
Если вам известна длина окружности, составляющей внешнюю границу круга, то используйте для определения диаметра формулу:
D = L / p, где
L – длина окружности;
p – число «пи», равное приблизительно 3,14.
Например, если длина 180 мм, то диаметр будет равняться приблизительно: D = 180 / 3,14 = 57,3 мм.
Если вы имеете предварительно вычерченный круг с радиусом, диаметром и длиной окружности, то для приблизительного диаметра используйте циркуль и измерительную линейку с делениями. Сложность заключается в том, чтобы найти на окружность две точки, максимально далеко отстоящие друг от друга, то есть такие, которые будут располагаться именно на диаметре.
При помощи линейки проведите прямую линию, чтобы она пересекала окружность в любом месте. Точки пересечения линии и окружности отметьте как А и В. Теперь Установите раствор циркуля таким образом, чтобы он был больше половины отрезка АВ.
Установите иглу циркуля в точку А и проведите дугу, пересекающую отрезок АВ или даже окружность. Теперь, не меняя раствор циркуля, установите его в точку В и проделайте то же самое. В результате вы получите точки пересечения двух окружностей по обе стороны от отрезка АВ. Соедините их по линейке прямой линией, чтобы она пересекла окружность в точках C и D. Отрезок CD и будет искомым диаметром.
Теперь измерьте диаметр при помощи измерительной линейки, приложив ее к точкам C и D. Второй способ определения диаметра: приложить ножки циркуля вначале к точкам C и D, а затем перенести раствор циркуля на измерительную шкалу линейки.
Число «пи» — это отношение длины окружности к ее диаметру. Отсюда вытекает, что длина окружности равняется «пи дэ» (C = π*D). Исходя из этого соотношения несложно вывести формулу обратной зависимости, т.е. D=С/π.
Вам понадобится
- — калькулятор.
Инструкция
Чтобы узнать диаметр окружности, зная ее длину, разделите длину окружности на число «пи» (π), равное примерно три целых и четырнадцать сотых (3,14). Значение диаметра при этом получится в тех же единицах , что и длина окружности. Эту формулу можно записать в следующем виде:D=С/π,где:С – длина окружности,π – число «пи», примерно равное 3,14.
Для более точного вычисления диаметра окружности воспользуйтесь более точным представлением числа «пи», например: 3,1415926535897932384626433832795. Конечно же вовсе необязательно использовать все этого числа, для большинства инженерных расчетов вполне достаточно 3,1416.
Конечно же вовсе необязательно использовать все этого числа, для большинства инженерных расчетов вполне достаточно 3,1416.
При вычислении диаметра окружности на основании ее длины, обратите внимание, что на (особенно, инженерных) калькуляторах имеется специальная клавиша для ввода числа «пи». Обозначается такая кнопка надписью на (над, под) ней «π» или чем-то аналогичным. Так, например, в виртуальном калькуляторе Windows соответствующая кнопка обозначена как pi. Использование специальной клавиши позволяет значительно ускорить ввод числа «пи» и избежать ошибок при его вводе. К тому же, число «пи», хранящееся в памяти калькулятора, представлено там с максимально возможной для каждого устройства точностью.
Иногда измерение длины окружности является единственным практически приемлемым способом узнать ее диаметр. Особенно это касается труб и цилиндрических конструкций, «не имеющих начала и конца».
Чтобы измерить длину окружности (поперечного сечения) цилиндрического предмета, возьмите нитку или веревку достаточной длины и обмотайте ее вокруг этого цилиндра (в один оборот). 2). Эта формула будет верной и для граничных точек расположения площади, когда k = R или k = 0. При подстановке этих значений площадь сечения S равняется либо 0, либо площади круга с радиусом шара R.
2). Эта формула будет верной и для граничных точек расположения площади, когда k = R или k = 0. При подстановке этих значений площадь сечения S равняется либо 0, либо площади круга с радиусом шара R.
Видео по теме
Необходимость определить диаметр трубы часто возникает при замене труб канализации, подборе полотенцесушителя и других домашних работах. Определить его можно самостоятельно, для этого вам понадобится лишь рулетка или штангенциркуль.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Длина окружности обозначается буквой C и вычисляется по формуле:
C = 2πR,
где R — радиус окружности.
Вывод формулы, выражающей длину окружности
Путь C и C’ — длины окружностей радиусов R и R’. Впишем в каждую из них правильный n-угольник и обозначим через P n и P» n их периметры, а через a n и a» n их стороны. Используя формулу для вычисления стороны правильного n-угольника a n = 2R sin (180°/n) получаем:
P n = n · a n = n · 2R sin (180°/n),
P» n = n · a» n = n · 2R» sin (180°/n).
Следовательно,
P n / P» n = 2R / 2R». (1)
Это равенство справедливо при любом значении n. Будем теперь неограниченно увеличивать число n. Так как P n → C, P» n → C», n → ∞, то предел отношения P n / P» n равен C / C». С другой стороны, в силу равенства (1) этот предел равен 2R / 2R». Таким образом, C / C» = 2R / 2R». Из этого равенства следует, что C / 2R = C» / 2R», т. е. отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π («пи»).
Будем теперь неограниченно увеличивать число n. Так как P n → C, P» n → C», n → ∞, то предел отношения P n / P» n равен C / C». С другой стороны, в силу равенства (1) этот предел равен 2R / 2R». Таким образом, C / C» = 2R / 2R». Из этого равенства следует, что C / 2R = C» / 2R», т. е. отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π («пи»).
Из равенства C / 2R = π получаем формулу для вычисления длины окружности радиуса R:
С = 2πR.
Длина дуги окружности
Так как длина всей окружности равна 2πR, то длина l дуги в 1° равна 2πR / 360 = πR / 180.
Поэтому длина l дуги окружности с градусной мерой α выражается формулой
l = (πR / 180) · α.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Вконтакте
Одноклассники
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Читайте также…
- Девять самых крутых животных из «Звёздных войн Маленькие зверьки из звездных войн
- Черное Солнце — символ-оберег для Ведающих Черное солнце star wars
- Пример из двух зол выбирают меньшее
- Неизвестная трехпалая раса
через диаметр и радиус.
 Терминология, основные формулы и характеристика фигуры
Терминология, основные формулы и характеристика фигурыГлавная > Двери > Как рассчитать длину зная диаметр. Как найти длину окружности: через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415 .
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE{P} = 2 \cdot \pi \cdot r \]
\[ \LARGE{P} = \pi \cdot d \]
\(P \) – периметр (длина окружности).
\(r \) – радиус.
\(d \) – диаметр.
Окружностью
будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки. 0}{n}}=\frac{2τ}{2τ»} \)
0}{n}}=\frac{2τ}{2τ»} \)
Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:
\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)
Из последних двух равенств получим, что
\(\frac{C}{C»}=\frac{2τ}{2τ»} \)
\(\frac{C}{2τ}=\frac{C»}{2τ»} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\(\frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\(\frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\(C=2πτ \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.

Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Класса учащиеся общеобразовательных школ в курсе изучают круг и окружность как геометрическую фигуру, и все, что с этой фигурой связано. Ребята знакомятся с такими понятиями, как радиус и диаметр, длина окружности или периметр , площадь круга. Именно на этой теме они узнают про загадочное число Пи – это лудольфово число, как оно называлось раньше. Число Пи иррационально, так как его представление в виде десятичной дроби бесконечно. На практике используется его усеченный вариант из трех цифр: 3.14. Эта константа выражает отношение длины любой окружности к ее диаметру.
Шестиклассники решают задачи, выводя по одной данности и числа «Пи» остальные характеристики окружности и круга. В тетрадях и на классной доске они в масштабе вычерчивают абстрактные сферы и производят мало что говорящие вычисления.
А на практике
На практике такая задача может возникнуть в ситуации, когда, например, возникает необходимость проложить трассу определенной протяженности для проведения каких-либо состязаний со стартом и финишем в одном месте. Высчитав радиус, вы сможете на плане выбрать прохождение этой трассы, с циркулем в руке рассматривая варианты с учетом географических особенностей региона. Перемещая ножку циркуля – равноудаленного центра от будущей трассы, можно уже на этом этапе предусмотреть, где на участках будут подъемы, где спуски, учитывая естественные перепады рельефа. Также сразу можно определиться и с участками, где лучше разместить трибуны для болельщиков.
Высчитав радиус, вы сможете на плане выбрать прохождение этой трассы, с циркулем в руке рассматривая варианты с учетом географических особенностей региона. Перемещая ножку циркуля – равноудаленного центра от будущей трассы, можно уже на этом этапе предусмотреть, где на участках будут подъемы, где спуски, учитывая естественные перепады рельефа. Также сразу можно определиться и с участками, где лучше разместить трибуны для болельщиков.
Радиус из окружности
Итак, предположим, что вам для проведения соревнований по автокроссу необходима круговая трасса длиной 10 000 м. Вот нужная формула для определения радиуса (R) окружности при известной её длине (C):
R=C/2п (п – число, равное 3.14).
Подставив имеющиеся значения, вы легко получаете результат:
R = 10 000:3.14 = 3 184. 71 (м) или 3 км 184 м и 71 см.
От радиуса к площади
Зная радиус окружности, легко можно определить площадь, которая будет изъята из ландшафта. Формула площади круга (S): S=пR2
При R = 3 184. 71 м она составит: S = 3.14 х 3 184. 71 х 3 184. 71 = 31 847 063 (кв. м) или почти 32 квадратных километров.
71 м она составит: S = 3.14 х 3 184. 71 х 3 184. 71 = 31 847 063 (кв. м) или почти 32 квадратных километров.
Подобные вычисления могут быть полезными при огораживании. Например, у вас имеется материал на ограду на столько-то . Взяв эту величину за периметр круга, вы легко определите его диаметр (радиус) и площадь, а, следовательно, зримо представите величину будущего огороженного участка.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
§ 117. Длина окружности и площадь круга.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).
Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.
И. Сырнева.
как найти длину окружности зная диаметр. Как найти и чему будет равна длина окружности
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка.
 Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса.
 Именно так выглядит формула для его вычисления: D=2r.
Именно так выглядит формула для его вычисления: D=2r. - Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два .
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r .
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. В школьной математике она считается заранее известной табличной величиной, равной 3,14!
Теперь перепишем предыдущую формулу, чтобы найти длину окружности через её диаметр, помня, в чём состоит его разница по отношению к радиусу. 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Формула диаметра — объяснение, решенные примеры и часто задаваемые вопросы
Длина радиуса, умноженная на два, равна диаметру окружности. Радиус круга измеряется от его центра до одной из его конечных точек, тогда как диаметр измеряется от одного конца круга до другого конца круга, проходящего через центр.
Буква D обозначает диаметр. Окружность круга имеет неограниченное количество точек, что означает, что круг имеет бесконечное количество диаметров, каждый из которых имеет одинаковую длину.
Φ — это знак диаметра, который используется в технике. В технических стандартах и чертежах этот знак часто используется. Значение Φ25 мм обозначает круг диаметром 25 мм.
Полное представление круга
(Изображение будет загружено в ближайшее время)
Формула и пример
Формула для расчета диаметра круга или идеально круглой фигуры описывает соотношение между его диаметром и радиусом. Диаметр по существу состоит из двух сегментов, каждый из которых является радиусом. Таким образом, формула диаметра: Диаметр = 2 × измерение радиуса. Вы можете записать эту формулу в сокращении как d = 2r.
Диаметр по существу состоит из двух сегментов, каждый из которых является радиусом. Таким образом, формула диаметра: Диаметр = 2 × измерение радиуса. Вы можете записать эту формулу в сокращении как d = 2r.
Тем не менее, вычислить диаметр круга легко, если мы знакомы с другими измерениями круга, т. е. с радиусом, длиной окружности или площадью. Однако расчет диаметра все же возможен, если вы не знаете ни одного из вышеуказанных размеров, но у вас есть набросок круга.
Все мы знаем, что длина окружности является одним из ее компонентов. Прежде чем мы узнаем формулу диаметра круга, давайте определим несколько понятий.
Радиус (r) — это длина отрезка, соединяющего центр окружности и конечную точку.
Окружающая граница круга называется окружностью (С). Он также известен как периметр круга. Из длины окружности и радиуса круга мы можем вычислить формулу диаметра.

1. Диаметр — Используя окружность
Из длины окружности мы можем легко получить формулу диаметра. Длина окружности вычисляется по формуле C = πd, где C = длина окружности, d = диаметр окружности и π = константа (3.141)
Диаметр = длина окружности ÷ π
2. Диаметр – с использованием радиуса
Радиус окружности – это длина отрезка от центра до конечной точки окружности, а диаметр равен удвоенному радиусу окружности.
Следовательно, D = радиус × 2.
3. Диаметр – с использованием площади круга
Площадь = π(радиус)².
Следовательно,
D = 2 \[\sqrt{\frac{A}{\pi }}\] — это формула диаметра окружности.
Пример: Джилл нарисовала круг радиусом 3 единицы. Каков диаметр круга?
Радиус данной окружности = 3 единицы
Таким образом, диаметр окружности будет = 2 × радиус
= 2 × 3 = 6 единиц.
Таким образом, диаметр окружности равен 6 единицам.
Как рассчитать диаметр
Мы можем узнать диаметр окружности следующими способами:-
A. Рассчитать диаметр окружности с помощью радиуса
Если вы уже знаете меру радиуса окружности , просто удвойте его, чтобы получить диаметр. Радиус – это расстояние от центра окружности до ее периметра. Например, если радиус круга равен 7 см, то диаметр круга равен 7 х 2, или 14 см.
B. Вычислите диаметр окружности, используя длину окружности
Если у вас есть измерение длины окружности, разделите ее на π, и вы получите диаметр. Значение π приблизительно равно 3,14, но для получения наиболее точных результатов необходимо использовать калькулятор. Например, если длина окружности равна 25 см, то диаметр равен 25 см/π, или 7,96 см.
C. Вычислите диаметр круга, используя площадь круга
Если у вас есть площадь круга, разделите результат на π и найдите его квадратный корень, чтобы получить радиус; затем умножьте на 2, чтобы получить диаметр. Это возвращает к маневрированию формулы, чтобы найти площадь круга, то есть: A = πr², чтобы получить диаметр. Вы можете преобразовать это в формулу площади диаметра круга, как показано ниже: —
Это возвращает к маневрированию формулы, чтобы найти площадь круга, то есть: A = πr², чтобы получить диаметр. Вы можете преобразовать это в формулу площади диаметра круга, как показано ниже: —
r = \[\sqrt{\frac{A}{\pi}}\] см.
Например, если площадь круга равна 12 см², разделите ее на π и извлеките квадратный корень.
Используя формулу отношения диаметра к площади, мы имеем \[\frac{12}{3,14}\] = \[\sqrt{3,82}\]
Таким образом, диаметр круга равен 1,95 x 2 = 3,90 см.
Решенные примеры
Пример 1:
Найдите диаметр круга с длиной окружности 32 см
Решение 1:
то есть
C = πd
Теперь заполните указанные детали
32 = (3,14)d
Затем разделите обе части на 3,14. Таким образом, 3.14 нейтрализуется в правой части уравнения, оставляя d. Затем разделите 32 на 3,14 = 10,19
Ответ: диаметр равен 10,19 см.
Это также означает, что радиус равен 5,09 см \[\left ( \frac{10.19}{2} \right )\]
Пример 2:
Окружность автомобильной шины Сюзанны равна 24 дюймам. Узнайте диаметр, наименьшее пройденное расстояние в футах после 3 полных оборотов шины?
Решение 2:
Учитывая, что длина окружности = 24
Используйте формулу: C = πd
24 = πd
D= \[\frac{24}{3.14}\] = 7,64 дюйма
Диаметр равно 7,64 дюйма
И самое близкое расстояние, пройденное после 3 полных оборотов = 24 x 3= 72 дюйма
Поскольку нам нужно дать ответ в футах, преобразуйте значение в футы
12 дюймов = 1 фут
Таким образом,
\[\frac{72}{12}\] = 6 футов
Вывод
Это различные способы расчета диаметра круга и его математическое представление. Узнайте, как термины используются для определения формул для расчета диаметра из решенных примеров.
Окружность круга — формулы, примеры, часто задаваемые вопросы
Окружность круга определяется как граница или внешний путь, покрываемый любым кругом. Как правило, окружность круга также называется периметром круга, который определяется как сумма всех сторон любой фигуры или длины нити, необходимой для покрытия границы круга. Окружность и площадь круга являются наиболее важными формулами для изучения круга. Длина окружности зависит только от радиуса окружности.
Что такое длина окружности?
Периметр круга — это кривая, проходящая по краю круга. Периметр круга также называют окружностью круга. Периметр круга обозначен буквой С. Он чуть больше, чем его диаметр в три раза. Это π диаметра окружности. Окружность измеряется в см, м или км. Преобразование между этими единицами может быть выполнено с помощью различных формул, таких как формула преобразования сантиметра в метр.
C = π × диаметр
Как найти длину окружности?
Правильный способ найти периметр круга — вычислить его по формуле C = 2π × r . Если известен диаметр или радиус круга, можно легко рассчитать окружность круга. Радиус круга — это отрезок линии от центра круга до любой точки на круге, а диаметр равен удвоенному радиусу круга. Длина окружности равна длине ее границы. Поскольку круг представляет собой плоскую форму, вы не используете линейку или шкалу для вычисления длины окружности. На изображении ниже r — радиус, d — диаметр, O — центр, а C — окружность.
Если известен диаметр или радиус круга, можно легко рассчитать окружность круга. Радиус круга — это отрезок линии от центра круга до любой точки на круге, а диаметр равен удвоенному радиусу круга. Длина окружности равна длине ее границы. Поскольку круг представляет собой плоскую форму, вы не используете линейку или шкалу для вычисления длины окружности. На изображении ниже r — радиус, d — диаметр, O — центр, а C — окружность.
Формула длины окружности
Формула длины окружности выражается с использованием радиуса «r», «d» (диаметр) и «π».
- C = π × d , где π(pi) = 22/7 или 3,14 (приблизительно), d — диаметр.
- C = π × 2r , где r — радиус, а диаметр в два раза больше радиуса.
- C = 2 × π × r
Формула длины полукруга
Если круг разделен на две равные части, он называется полукругом. Окружность круга определяется как общая длина его границы, которая определяется как
.
d — диаметр окружности.
Формула площади полукруга
Площадь полукруга вычисляется путем взятия половины площади круга. то есть площадь полукруга равна ½ × площади круга. формула площади полукруга дается как
Площадь полукруга = ½ × πr 2
где r — радиус окружности.
Решенные примеры длины окружности
Пример 1: Какова длина окружности диаметром 2 см?
Решение:
Дано, диаметр = 2 см
Используя формулу длины окружности,
C = π × d
Где, C = длина окружности, 3 π (pi) и d (4) и = диаметр
С = 3,14 × 2
С = 6,28 см.
Пример 2: Какова длина окружности с радиусом 3 см?
Решение:
Дано, радиус = 3 см
Используя формулу длины окружности,
C = 2 × π × r
Где, C = длина окружности, 4π r = радиус
C = 2 × 3,14 × 3
C = 18,84 см.
Пример 3: Какова длина окружности диаметром 14 см? 9
C = π × d
С = 3,14 × 14
С = 43,96 см.
Пример 4. Всегда ли длина окружности составляет 360° в углах?
Ответ:
Кривая, охватывающая окружность, представляет собой дугу в 360 градусов этой кривой. Следовательно, длина окружности — это длина 360-градусной или 360-градусной дуги этой окружности.
Пример 5. Какова длина окружности с радиусом 10 см?
Решение:
Дано, радиус = 10 см
Используя формулу длины окружности,
C = π × 2r
С = 3,14 × 2(10)
С = 62,8 см.
Пример 6. Какова длина окружности с радиусом 25 см?
Ответ:
Дано, радиус = 25 см
Используя формулу длины окружности,
C = 2 × π × r
Где, C = длина окружности, π = 3,14 см и r = 2
С = 2 × 3,14 × 25
С = 157 см.
Часто задаваемые вопросы о длине окружности
Вопрос 1: Как рассчитать диаметр по длине окружности?
Ответ:
Формула длины окружности = диаметр × π
Или, диаметр = длина окружности/π
Итак, диаметр окружности в пересчете на длину окружности будет равен отношению длины окружности к π.
Вопрос 2: Какие шаги нужно предпринять, чтобы найти длину окружности, если известна ее площадь?
Ответ:
Шаг 1: Найдите радиус, используя формулу площади круга (A = πr2).
Шаг 2: Теперь подставьте значение радиуса в формулу длины окружности (C = 2πr), чтобы получить ответ.
Вопрос 3: Какая формула используется для нахождения периметра круга, если известна его площадь?
Ответ:
Если дана площадь круга, то формула для вычисления периметра или длины окружности будет выглядеть следующим образом: C = 2√(πA) единиц.
Вопрос 4: Какова длина окружности полукруга?
Ответ:
Формула длины окружности полукруга C = (πr + 2r), где r — радиус. Мы знаем, что диаметр в два раза больше радиуса, d = 2r. Формула длины окружности полукруга принимает вид C = π(d/2) + d.
Вопрос 5: Какова длина четверти окружности?
Ответ:
Квадрантом круга называется сектор круга, секторальный угол которого равен 90°. Периметр квадранта круга равен одной четвертой длины окружности и удвоенному радиусу круга. Следовательно, периметр четверти окружности равен 75 см.
Радиус круга: определение, формула с примерами решений
Линии и окружности — это первое, чему вы учитесь рисовать, когда начинаете изучать математику в начальных классах. Однако эти простые цифры могут предложить больше, чем кажется на первый взгляд. У них есть несколько элементов и свойств, некоторые из которых мы рассмотрим в этой статье, прежде чем, наконец, узнаем, как найти радиус окружности.
Круг можно определить разными способами.
- Это совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от заданной точки на плоскости. Фиксированной точкой здесь является центр, называемый «О».
- Замкнутая двумерная фигура с площадью, т. е. граничащей с ней областью в двумерной плоскости. У него также есть периметр, который также называют окружностью, т. е. расстоянием по окружности.
- Это фигура, в которой все точки на плоскости «равноудалены» от центра, «О».
- Фокусное расстояние объектива камеры рассчитывается с использованием радиуса кривизны объектива.
- Одометры — это приборы, используемые для расчета расстояния, пройденного автомобилями. Это делается путем подсчета количества оборотов и окружности колеса, которая определяется его радиусом.
- Диаметр круглых противней используется для расчета размеров пиццы и тортов.

Некоторые важные элементы круга:
- Окружность: Это граница круга.
- Центр – Это середина круга.
- Диаметр – это линия, проходящая через центр окружности и касающаяся двух точек на окружности. Обозначается как «D» или «d». Диаметры должны быть прямыми и касаться границы круга в двух различных точках, противоположных друг другу.
- Дуга – Это изогнутая часть окружности круга. Самая большая дуга называется «большой дугой», а меньшая дуга называется «малой дугой».
- Сектор – Это сечение или часть окружности, определяемая двумя радиусами и включающая дугу окружности
- Хорда – Это прямая линия, соединяющая любые две точки на окружности.
- Касательная – это линия, соединяющая окружность окружности в точке.
- Секущая – Это любая линия, пересекающая окружность в двух различных точках.

- Кольцо – Это область, определяемая двумя концентрическими окружностями, которые напоминают кольцеобразный объект.
- Радиус: Радиус, обозначаемый буквой «R» или «r», представляет собой линию от центра круга до окружности.
Круги обладают свойствами, определяющими их качество и функции. Некоторые из них приведены ниже:
- Окружности двумерные, а не многоугольники.
- Окружности считаются конгруэнтными, если они имеют одинаковый радиус, т. е. равные радиусы
- Самая длинная хорда в окружности — это диаметр.
- Равные хорды окружности ограничивают равные углы в центре окружности
- Любой радиус, проведенный перпендикулярно хорде в окружности, делит хорду пополам
- Окружность может описывать любую фигуру – прямоугольники, треугольники, трапеции, воздушные змеи, квадраты, и т. д.
- Окружности можно вписать в квадрат, комплект и треугольник
- Хорды, находящиеся на равном расстоянии от центра, имеют одинаковую длину
- Расстояние от центра окружности до диаметра хорда) равна нулю
- Когда длина хорды увеличивается, перпендикулярное расстояние от центра окружности уменьшается
- Касательные параллельны друг другу, если они проведены в конце самой длинной хорды или диаметра
Некоторые формулы используются в геометрии для решения решений, связанных с кругами. Вот некоторые из этих формул:
Вот некоторые из этих формул:
- Площадь круга:
A = πr 2 кв. единица
- Длина окружности:
2πr единиц ИЛИ πd.
Где Диаметр = 2 x r
Следовательно, d = 2r Где «r» = радиус окружности.
Что такое радиус?- Радиус можно определить как линию от центра круга «О» до окружности круга. Это отрезок линии, представленный буквой «R» или «r».
- Длина радиуса окружности остается неизменной от средней точки до любой точки на границе. Радиус равен половине длины диаметра круга или сферы. Итак, радиус круга или сферы можно выразить как d/2, где «d» представляет собой диаметр.
- Термин «радиус» — это множественное число слова «радиус», которое используется, когда речь идет о радиусе двух или более окружностей.
- Окружность может иметь несколько радиусов внутри себя, потому что окружность окружности имеет бесконечное количество точек.
 Таким образом, круги могут иметь бесконечное количество радиусов, и все эти радиусы имеют одинаковую длину расстояния от центра круга.
Таким образом, круги могут иметь бесконечное количество радиусов, и все эти радиусы имеют одинаковую длину расстояния от центра круга.
Формулы для определения радиуса окружности
Формула радиуса получается путем деления диаметра окружности пополам. Когда точка на окружности соединяется с точным центром, образующийся отрезок называется радиусом кольца или окружности.
Радиус окружности может быть получен с использованием трех основных формул радиуса, т. е. если указаны диаметр, длина окружности или площадь. Ниже приведены формулы радиуса для окружности.
- Формула радиуса из диаметра: Как упоминалось ранее, диаметр в два раза больше радиуса окружности. Следовательно, формулу радиуса можно получить, разделив диаметр на 2. Математически диаметр обозначается буквой «D» и записывается как:
Диаметр = 2 × радиус.
Когда в задаче указан диаметр круга, формула радиуса записывается так:
радиус = диаметр/2 единицы
= D/2 единицы.
- Формула радиуса из окружности: Длина окружности обозначается буквой «C». Его можно выразить как единицы C = 2πr, где C = длина окружности, r = радиус окружности и π = 3,14159. Отношение длины окружности к 2π — это радиус. Формула радиуса, полученная из длины окружности, записывается как:
R= C/2π единиц
- Формула радиуса с площадью: Отношение между радиусом и площадью представлено формулой:
Площадь круга = πr 2 квадратных единиц.
Где r — радиус, а π — константа, 3,14159. Формула радиуса, полученная из площади круга, записывается следующим образом:
Радиус = √(Площадь/π) единиц
Пример : Если диаметр равен 24 единицам, то радиус равен 24/2 = 12 единицам. . Если длина окружности равна 44 единицам, то ее радиус можно рассчитать как 44/2π. Отсюда следует, что (44×7)/(2×22) = 7 единиц. И, если площадь круга равна 616 квадратных единиц, то радиус равен ⎷(616×7)/22 = ⎷28×7 = ⎷196 = 14 единиц.
Примеры:
В. Если диаметр баскетбольного мяча 24 см, найдите радиус мяча.
Sol : Дано, диаметр = 24см
Мы знаем, d= 2r
Следовательно, r=d/2
=24/2см
=12см2
3 9013
В. Если площадь апельсина равна 13 кв. см, найдите радиус апельсина.
Сол : Дано, площадь = 13 см кв,
Мы знаем, что площадь = 2πR²
Следовательно, R= ⎷(A/2π)
R= ⎷(13/2*3,14)см кв
= 2,03 см или 2 см прибл.
Следовательно, радиус апельсина равен 2см.
В. Если диаметр вишни равен 9 см, найдите ее радиус.
Сол : Дано, Диаметр (d) = 9 см
Мы знаем, что диаметр = 2r,
Радиус = d/2
Следовательно, радиус = 9/2 = 4,5 см
Теперь, Площадь = πr² (где r=радиус)
Следовательно, Площадь круга = 3,14 х 4,5 х 4,5 = 63,585 см кв.
Таким образом, получаем, что радиус вишни равен 4,5 см.
РАБОЧИЙ ЛИСТ
Вот рабочий лист, который поможет вам отработать свои навыки нахождения радиуса окружности.
В. Решите следующие текстовые задачи:
- Найдите радиус круга диаметром 89 см.
- Если площадь круга 152 см², найдите радиус круга.
- Найдите радиус окружности с длиной окружности 375 см.
Q. Найдите радиус окружности, исходя из предоставленного диаметра:
- D = 354 см
- D = 79 см
- D = 1001 см
- A = 200 см²
- A = 2346 см²
- A = 623 см²
Q. Найдите радиус круга, исходя из полученного периметра:
- P = 67 см
- P = 107 см
- P = 482 см
Q. Найдите окружность круга, чей Radius:
(A) 57 CM
.8. 57 CM8. 57 CM. 57 CM. 57 CM. см
57 CM. 57 CM. 57 CM. см(c) 90,09 см
В этой статье подробно объясняется и демонстрируется, как найти радиус окружности. Теперь, когда вы готовы со своими знаниями об элементах, свойствах и формулах круга и его частей, решение вопросов геометрии теперь будет проще простого, а точнее, сектора круга.
find c – Площадь в квадратных футах
Рассчитаем окружность
Калькулятор окружности
Circle calc: find c — Наш калькулятор длины окружности должен быть введен любым другим значением.
Радиус футыдюймыярдымиллиметрысантиметрыметры
Диаметр футыдюймыярдымиллиметрысантиметрыметры
Окружность футыдюймыярдымиллиметрысантиметрыметры
Район футы (ft²)дюймы (in²)ярды (ярды²)миллиметры (мм²)сантиметры (см²)метры (м²)
Бесплатный виджет калькулятора
Вы можете разместить этот виджет калькулятора на своем веб-сайте, веб-странице или в блоге.
HTML LinkDirect URLEmbed Calculator Widget
Помните, что ввод может быть только в футах (ft), дюймах (in), ярдах (yd), сантиметрах (cm), миллиметрах (mm) и метрах (m), но не в комбинации из двух разных единиц!
Окружность круга = π x d
π = 3,142 (постоянное значение)
d = диаметр (в раскрывающемся списке футы, дюймы, ярды, см, мм, м)
c относится к длине окружности, то есть к длине окружности, которую вы проводите по окружности с помощью компаса.
Вы можете вычислить его следующими способами:
Если вы знаете радиус или диаметр окружности:
Формула для нахождения длины окружности: c = 2πr = πd
Если радиус и диаметр неизвестны, то
Формула: c = 2√(πa)
Чтобы понять, как вычислить окружность, мы должны сначала начать с определения окружности. Окружность круга — это линейное расстояние вокруг внешней границы круга. Чтобы узнать длину окружности, нам нужно знать ее диаметр, который равен длине ее самой широкой части. Диаметр следует измерять в футах (футах) для расчета площади в квадратных футах и, при необходимости, конвертировать в дюймы (дюймы), ярды (ярды), сантиметры (см), миллиметры (мм) и метры (м).
Диаметр следует измерять в футах (футах) для расчета площади в квадратных футах и, при необходимости, конвертировать в дюймы (дюймы), ярды (ярды), сантиметры (см), миллиметры (мм) и метры (м).
Формула:
Длина окружности = π x d
π = 3,142
d = диаметр (раскрывающиеся футы, дюймы, ярды, см, мм, м)
Сокращения единиц площади: футов
0 8
7 8 , дюймов 2 , ярдов 2 , см 2 , мм 2 , м 2
Использование калькуляторов:
Калькуляторы математики очень интерактивны и эксклюзивны. Эти калькуляторы идеально подходят для проверки работы или решения сложных и сложных задач. Эти калькуляторы являются инструментом решения задач и не должны заменять какие-либо старые математические приемы. Геометрия — это раздел математики, который состоит из частей круга, таких как:
- Радиус
- Диаметр
- Пи
- Окружность кругов
- Площадь кругов
Значение круга:
Сам по себе круг представляет собой простую и замкнутую форму. Это множество всех точек плоскости, находящихся на одинаковом расстоянии от данной точки, называемой центром. Его также можно назвать кривой, очерченной точкой, где расстояние от данной точки остается неизменным при изменении точки. В то время как круг символически означает разные вещи для разных людей, включая такие понятия, как бесконечность, постоянство и полнота.
Это множество всех точек плоскости, находящихся на одинаковом расстоянии от данной точки, называемой центром. Его также можно назвать кривой, очерченной точкой, где расстояние от данной точки остается неизменным при изменении точки. В то время как круг символически означает разные вещи для разных людей, включая такие понятия, как бесконечность, постоянство и полнота.
Что определяет длину окружности?
Окружность круга — это линейное расстояние, измеренное вдоль его сторон. Он параллелен периметру геометрической фигуры, но термин «периметр» скорее используется для описания свойства многоугольников. Окружность часто неправильно пишется как окружность .
Расстояние по внешней стороне круга называется окружностью круга. Он считается периметром других форм, таких как квадраты. Таким образом, для фигур, состоящих из прямых линий, используется слово «периметр», а для окружности используется слово «окружность». Окружность круга может быть известна как расстояние вокруг круга или длина пути по кругу.
Не только это, но и некоторые значительные расстояния на окружности, которые необходимо рассчитать, прежде чем найти длину окружности. И они радиус (r) и диаметр (d) . Диаметр – это расстояние от одной стороны круга до другого, пересекающее центр/середину круга. Радиус равен половине диаметра.
Все эти значения связаны с математической константой π, или пи, которая представляет собой отношение длины окружности к ее диаметру и составляет почти 3,14159.. Пи или π — иррациональное число, что означает, что его нельзя точно выразить в виде дроби (хотя его часто оценивают как 22/7). Десятичное представление π никогда не заканчивается или имеет постоянно повторяющийся образец. Это также скользящее число, что означает, что оно не является основанием любого ненулевого многочлена с рациональными коэффициентами.
Аспекты окружности окружности:
Калькулятор окружности выполняет многие аспекты, такие как:
- Калькулятор отношения длины окружности к диаметру
- Длина окружности до радиуса
- Окружность области
- Радиус до окружности
- Радиус к диаметру
- Радиус до зоны
- Диаметр к окружности
- Диаметр по радиусу
- Диаметр по площади
- Площадь к окружности
- Площадь к диаметру
- Площадь по радиусу
Если вы знакомы с диаметром или радиусом круга, то вы легко сможете вычислить длину окружности. Начнем с того, что имейте в виду, что Пи — это число, представленное символом π. Пи или π почти равно 3,14. Следовательно, формула для нахождения длины окружности: Окружность окружности = π x Диаметр окружности, которую мы обычно записываем в краткой форме как C = πd. Это показывает нам, что длина окружности в три «с небольшим» раза больше диаметра.
Начнем с того, что имейте в виду, что Пи — это число, представленное символом π. Пи или π почти равно 3,14. Следовательно, формула для нахождения длины окружности: Окружность окружности = π x Диаметр окружности, которую мы обычно записываем в краткой форме как C = πd. Это показывает нам, что длина окружности в три «с небольшим» раза больше диаметра.
Вы также можете узнать длину окружности, если знаете радиус. Имейте в виду, что диаметр в два раза больше длины радиуса. Это означает, что каким бы ни был радиус, его следует умножить на 2, чтобы найти диаметр. Понятно, что C = πd. А мы знаем, что если r — радиус окружности, то d = 2r. Следовательно, C = 2πr.
Определение окружности Земли:
Используя приведенные выше вычисления, легко вычислить длину окружности Земли! Ученые установили, что диаметр Земли составляет 12 742 км. При наличии этой информации, какова окружность Земли?
Все мы знаем, что C = πd, а здесь диаметр, т.е. d = 12 742 км. Итак, мы можем быстро узнать окружность Земли как C = π x 12 742 км = 40 030 км.
Примеры:
- Реальным и оригинальным примером радиуса является ось велосипедного колеса.
- 9-дюймовая пицца является примером диаметра: когда человек делает первый надрез, чтобы разрезать круглый пирог для пиццы пополам, этот надрез и есть диаметр пиццы. Итак, 9-дюймовая пицца имеет 9-дюймовый диаметр.
Вопрос 1:
Круг имеет диаметр 10 см, какова его длина окружности?
Ответ 1:
Хотя мы знаем, что C = πd. Поскольку диаметр равен 10 см, мы имеем, что C = π x 10 см = 31,42 см.
Вопрос 2:
Круг имеет радиус 3 м, какова его длина окружности?
Ответ 2:
Мы знаем, что C = 2πr. Поскольку радиус равен 3 м, мы имеем, что C = π x 6 м = C = 18,84.
Отношение длины окружности к диаметру:
Было замечено, что, поскольку диаметр в два раза больше радиуса, отношение длины окружности к диаметру равно π, т.е. / 2R = π
Это отношение длины окружности к диаметру является описанием постоянной числа пи. Он используется в разных областях, таких как физика и математика.
Он используется в разных областях, таких как физика и математика.
Вывод:
Число представляет собой отношение длины окружности к ее диаметру. Значение составляет около 3,14159265358979323846…
Диаметр круга в два раза больше радиуса. Если диаметр или радиус круга дан, то мы можем легко найти длину окружности. Мы также можем найти диаметр и радиус круга, если дана длина окружности. Округляем до 3,14, чтобы упростить расчеты. Окружность, диаметр и радиусы рассчитываются в линейных единицах, таких как дюймы и сантиметры. У круга много разных радиусов и много разных диаметров, и каждый из них проходит через центр.
Переводные коэффициенты:
Для преобразования квадратных футов, квадратных дюймов, квадратных ярдов, квадратных сантиметров, квадратных миллиметров и квадратных метров вы можете использовать следующую таблицу преобразования.
| Квадратные футы в Квадратные ярды | умножьте футы 2 на 0,11111, чтобы получить ярды 2 |
| Квадратные футы в Квадратные метры | умножьте футы 2 на 0,092903, чтобы получить м 2 |
| Квадратные ярды в квадратные футы | умножьте ярды 2 на 9, чтобы получить футы 2 |
| Квадратные ярды в Квадратные метры | умножьте ярды 2 на 0,836127, чтобы получить м 2 |
| Квадратные метры в Квадратные футы | умножьте м 2 на 10,7639, чтобы получить футы 2 |
| Квадратные метры в Квадратные ярды | умножьте m 2 на 1,19599, чтобы получить ярды 2 |
| Квадратные метры в квадратные миллиметры | умножьте значение m 2 на 1000000, чтобы получить мм 2 |
| Квадратные метры в Квадратные сантиметры | умножьте значение m 2 на 10 000, чтобы получить см 2 |
| Квадратные сантиметры в Квадратные метры | умножьте значение см 2 на 0,0001, чтобы получить мм 2 |
| Квадратные сантиметры в Квадратные миллиметры | умножьте значение см 2 на 100, чтобы получить мм 2 |
| Квадратные миллиметры в квадратные сантиметры | умножьте значение мм 2 на 0,000001, чтобы получить см 2 |
| Квадратных миллиметров в квадратных метров | умножьте значение мм 2 на 1000000, чтобы получить m 2 |
Лучший 19 Диаметр 38 Окружность
Ниже представлена лучшая информация и знания о диаметр окружности 38 составлен и составлен командой onthihsg. com , а также другими связанными темами, такими как: диаметр окружности, диаметр 38 в дюймах, калькулятор окружности круга, диаметр 38 в см, что такое диаметр
com , а также другими связанными темами, такими как: диаметр окружности, диаметр 38 в дюймах, калькулятор окружности круга, диаметр 38 в см, что такое диаметр
Изображение с ключевым словом: диаметр 38 окружности
Самые популярные статьи о диаметре 38 окружности
Mục Lục
- 1 1. Какова длина окружности круга диаметром 38 дюймов?
- 2 2. Окружность круга диаметром 38 дюймов – CalculateMe.com
- 3 3. Каков диаметр окружности диаметром 38 футов? – Ответы
- 4 4. Каков диаметр 38-дюймовой окружности? – AnswersToAll
- 5 5. Калькулятор окружности
- 6 6. Как рассчитать диаметр по окружности – Sciencing
- 7 7. Если моя окружность составляет 38 футов, каков диаметр? – Мозг.in
- 8 8. Калькулятор длины окружности
- 9 9. Найдите длину окружности диаметром 38 см
- 10 10. Если диаметр окружности равен 12 дюймам, какова площадь …
- 11 11.
 Площадь круга Калькулятор – день Пи
Площадь круга Калькулятор – день Пи - 12 12. Буй – норвежский 12″ Диаметр 38″ Окружность
- 13 13. Если длина окружности 5 дюймов, каков диаметр …
- 14 14. Радиус, диаметр, окружность и площадь Круги
- 15 15. Базовая геометрия – университетские преподаватели
- 16 16. Какова длина окружности диаметром 12 дюймов?
- 17 17. Независимый от гестационного возраста метод оценки развития плода
- 18 18. Какова окружность 36-дюймового диаметра? – Reviews.tn
- 19 19. Окружность круга (периметр круга) | Формула – Byju’s
1. Какова длина окружности диаметром 38 дюймов?
Автор: coolconversion.com
Оценить 3 ⭐ (10835 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том Какова длина окружности круга диаметром 38 дюймов? Как найти длину окружности любого круга, зная его диаметр.
 Длина окружности диаметром 38 равна 119,4.
Длина окружности диаметром 38 равна 119,4.Совпадение с результатами поиска: Используйте приведенный выше калькулятор длины окружности, чтобы найти периметр круга, зная его диаметр или другие параметры.
Цитата из источника: …
2. Длина окружности круга диаметром 38 дюймов – CalculateMe.com
Автор: www.calculateme.com
Оценить 3 ⭐ (2968 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о длине окружности круга диаметром 38 дюймов – CalculateMe.com Длина окружности круга диаметром 38 дюймов ; 119,38 дюйма; 9,9484 фута; 9 футов 11,38 дюйма, футы и дюймы; 3,0323, м; 303,23, см …
Совпадение с результатами поиска: Диаметр круга — это расстояние от одного края до другого, проходящее через центр.
 Это в два раза больше радиуса.
Это в два раза больше радиуса.Цитата из источника: …
3. Каков диаметр окружности длиной 38 футов? – Ответы
Автор: math.answers.com
Оценить 3 ⭐ (15771 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, что такое диаметр окружности 38 футов? – Ответы 38/пи = 12,09577567 или около 12 футов.
Сопоставьте результаты поиска: если диаметр в футах, то
умножьте диаметр на пи
38 x 3,14159 = 119,38042 квадратных фута
если диаметр в дюймах, то
разделите дюймы на 12 и умножьте диаметр на пи
38 &разделять; 12 = 3,16666 x 3,14159 = 9,94835 квадратных футовЦитата из источника: …
4.
 Каков диаметр 38-дюймовой окружности? — ОтветыВсем
Каков диаметр 38-дюймовой окружности? — ОтветыВсемАвтор: answer-to-all.com
Оценить 3 ⭐ (4375 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, что такое диаметр окружности 38 дюймов? – AnswersToAll Диаметр, дюйм, см. 38,1 дюйма, 119,7 дюйма; Диаметр, Окружность. 30, 94,25; Диаметр, фут, дюйм 36′0″, 113,1 …
Совпадение с результатами поиска: Чтобы вычислить длину окружности круга диаметром 30 дюймов, используйте формулу C = 2πr, где r — радиус. Мы также можем использовать формулу C = πd, где d — диаметр круга… Какова длина окружности диаметром 30 дюймов?
Цитата из источника: …
5. Калькулятор круга
Автор: www.
 calculator.net
calculator.netОценить 3 ⭐ (19602 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о калькуляторе окружности Пожалуйста, укажите любое значение ниже, чтобы рассчитать оставшиеся значения окружности. Радиус (R). Диаметр (D). Окружность (С).
Совпадение с результатами поиска: В то время как круг символически представляет много разных вещей для многих разных групп людей, включая такие понятия, как вечность, вневременность и тотальность, круг по определению представляет собой простую замкнутую форму. Это множество всех точек на плоскости, равноудаленных от данной точки, называемой…
Цитата из источника: …
6. Как рассчитать диаметр по длине окружности – наука
Автор: sciencing.
 com
comОценить 3 ⭐ (6036 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, как рассчитать диаметр по длине окружности – наука Для любого круга, если вы разделите длину окружности на диаметр, вы получите число Пи, нестандартное число, обычно округляемое до 3,14.
Совпадение с результатами поиска: Круг — это геометрическая форма, в которой все точки вне круга находятся на одинаковом расстоянии от центра. Расстояние вокруг края круга называется окружностью. Расстояние от одной стороны окружности до другой, проходящей через центр окружности, равно диаметру…
Цитата из источника: …
7. Если моя окружность составляет 38 футов, каков диаметр? – Мозг.in
Автор: brainly.
 in
inОценить 4 ⭐ (28068 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Если моя окружность составляет 38 футов, каков диаметр? – Brainly.in ОКРУЖНОСТЬ = 2 X круг X радиус. 28 = 2Х3,14Хр. 28=6,28р. 28/6,28=р. 4,45=р. Диаметр = 2 х радиус. => 2 х ( 4,45 ). 8,9ft — диаметр …
Совпадение с результатами поиска: Пожалуйста, включите JS и отключите любой блокировщик рекламы
Цитата из источника: …
8. Калькулятор длины окружности
Автор: www.omnicalculator.com
Оценить 3 ⭐ (3105 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи по теме Калькулятор окружности Как найти длину окружности; Окружность к диаметру; ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ.
 Если вам нужно решить некоторые задачи по геометрии, …
Если вам нужно решить некоторые задачи по геометрии, …Совпадение с результатами поиска: Как и в случае со всеми нашими инструментами, калькулятор длины окружности работает во всех направлениях — он также является калькулятором длины окружности в диаметр и может использоваться для преобразования длины окружности в радиус, длины окружности в площадь, радиуса в окружность, радиус в диаметр (ох!), радиус в площадь, диаметр в c…
Цитата из источника: …
9. Найдите длину окружности диаметром 38см
Автор: brainly.in
Оценить 4 ⭐ (30027 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Summary: Статьи о нахождении длины окружности диаметром 38см ·
Совпадение с результатами поиска: ОКРУЖНОСТЬ = π × радиус × 2
Цитата из источника: …
10.
 Если диаметр круга 12 дюймов, какова площадь …
Если диаметр круга 12 дюймов, какова площадь …Автор: socratic.org
Оценить 3 ⭐ (4085 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о Если диаметр круга 12 дюймов, то какова площадь … R.=6 , C.≈38 и A.≈113 . … Чтобы найти длину окружности, вы будете использовать формулу C=2⋅π⋅r ; поэтому длина окружности C равна …
Совпадение с результатами поиска: Чтобы найти длину окружности, вы будете использовать формулу #C = 2*pi*r#; поэтому длина окружности #C# составляет #2*pi*6 ~~ 38# дюймов.
Цитата из источника: …
11. Калькулятор площади круга – число Пи
Автор: www.piday.org
Оценить 4 ⭐ (32624 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о площади круга Калькулятор — День Пи Используйте наш простой калькулятор, чтобы найти площадь, длину окружности, диаметр и радиус круга.
 Узнайте, как решать круговые задачи, с помощью нашего пошагового руководства.
Узнайте, как решать круговые задачи, с помощью нашего пошагового руководства.Совпадение с результатами поиска: Отличительной особенностью формул является то, что вы можете манипулировать ими, чтобы найти неизвестное, если вы знаете одну из других величин. Например, если мы знаем длину окружности, но не знаем радиус, вы можете решить c = 2πr относительно r и получить \(r = \frac{c}{2\pi}\). Аналогично, если вам нужен диаметр…
Цитата из источника: …
12. Буй – норвежский 12″ Диаметр 38″ Окружность
Автор: baytechrentals.com
Оценить 4 ⭐ (33475 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о буе – норвежский 12″ диаметр 38″ окружность Ярко-оранжевые буи для обозначения трубопроводов или других подводных объектов.
 Имеет прочную виниловую конструкцию, усиленную проушину и легко …
Имеет прочную виниловую конструкцию, усиленную проушину и легко …Совпадение с результатами поиска: Ярко-оранжевые буи для обозначения трубопроводов и других подводных объектов. Имеет прочную виниловую конструкцию, усиленную проушину и легкодоступное заливное отверстие. У нас есть в наличии размеры от диаметра 9 дюймов (окружность 28 дюймов) до диаметра 34 дюйма (окружность 107 дюймов).
Цитата из источника: …
13. Если длина окружности 5 дюймов, каков диаметр …
Автор: www.quora.com
Оценить 4 ⭐ (28457 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Если окружность круга 5 дюймов, то какой диаметр … Пусть C = длина окружности и D = диаметр.
 … Все связанные (38). Рекомендуется… Какова длина окружности диаметром 10 дюймов?
… Все связанные (38). Рекомендуется… Какова длина окружности диаметром 10 дюймов?Совпадение с результатами поиска: Что-то пошло не так. Подождите немного и повторите попытку.
Цитата из источника: …
14. Радиус, диаметр, длина окружности и площадь кругов
Автор: www.dummies.com
Оценить 3 ⭐ (4985 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о радиусе, диаметре, длине окружности и площади кругов Расширьте свои геометрические знания — узнайте о взаимосвязях между различными частями круга, а также о некоторых основных формулах.
Совпадение с результатами поиска: С помощью меры радиуса можно многое сказать об окружности: ее диаметр (расстояние от одной стороны до другой, проходящее через центр), ее окружность (насколько ), и его площадь (сколько квадратных дюймов, футов, ярдов, метров — сколько у вас — влезет в него).

Цитата из источника: …
15. Базовая геометрия – университетские преподаватели
Автор: www.varsitytutors.com
Оценить 4 ⭐ (21871 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи по основам геометрии – университетские преподаватели Используйте 3.14 для Пи в следующем вопросе. Если длина окружности равна 25,12 см, чему равен ее диаметр? Возможные ответы:.
Совпадение с результатами поиска: наша окружность просто . Утроение диаметра дает новый диаметр и, следовательно, новую длину окружности . Затем мы можем определить отношение между двумя окружностями.
Цитата из источника: …
16.
 Какова длина окружности диаметром 12 дюймов?
Какова длина окружности диаметром 12 дюймов?Автор: www.celebritiesbuzz.com.gh
Оценить 3 ⭐ (19446 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том Какова длина окружности круга диаметром 12 дюймов? Окружность и площади Размер в дюймах Окружность в дюймах Площадь в квадратных дюймах 12 … следовательно, длина окружности C равна 2⋅π⋅6≈38 дюймов.
Совпадение с результатами поиска: Окружность и площади Размер в дюймах Окружность в дюймах Площадь в квадратных дюймах 12 37,700 144,000 12 1/4 38,480 150,060 12 1/2 39,270 156,250 12 3/4 40,060 162,560 Нажмите, чтобы увидеть полный ответ. Аналогично, каков диаметр 12-дюймового круга? Итак, если радиус круга равен 12″, то …
Цитата из источника: …
Автор: pubmed.
 ncbi.nlm.nih.gov
ncbi.nlm.nih.govОценить 4 ⭐ (21914 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о независимом от гестационного возраста методе оценки роста плода… измерения поперечного диаметра мозжечка (ПДМ) и окружности живота (ОП) были получены между 15-38 неделями беременности.
Совпадение с результатами поиска:
В проспективном исследовании 162 пациенток измерения поперечного диаметра мозжечка (TCD) и окружности живота (AC) были получены между 15-38 неделями беременности. Соотношение между ТКД и АС рассчитывали после каждого обследования. Это соотношение оставалось постоянным в течение всего времени…
Цитата из источника: …
18. Какова окружность диаметра 36 дюймов? – Отзывы.tn
Автор: отзывов.
 тн
тнОценить 4 ⭐ (33232 Оценки)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том, что такое окружность 36 дюймов в диаметре? – Reviews.tn Ответ: Длина окружности диаметром 36 дюймов равна 113 дюймам… формула C=2⋅π⋅r ; поэтому длина окружности C равна 2⋅π⋅6≈38 дюймов.
Совпадение с результатами поиска: Аналогично, как найти длину окружности в дюймах? Вы можете рассчитать длину окружности в дюймах с помощью пи в уравнениях окружность = 2 * радиус * пи и длина окружности = диаметр * пи. Найдите центр круга и измерьте длину от его центра до точки на его …
Цитата из источника: …
19. Длина окружности (периметр окружности) | Формула – Byju’s
Автор: byjus.


 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.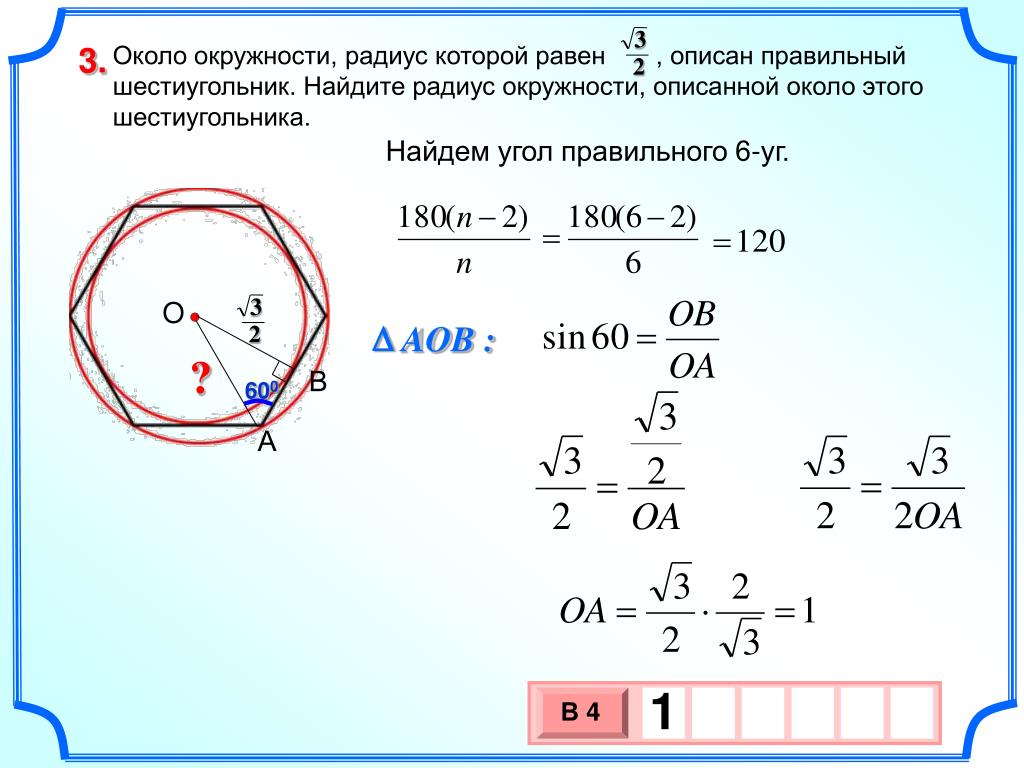

 При этом отрезок АВ – диаметр.
При этом отрезок АВ – диаметр.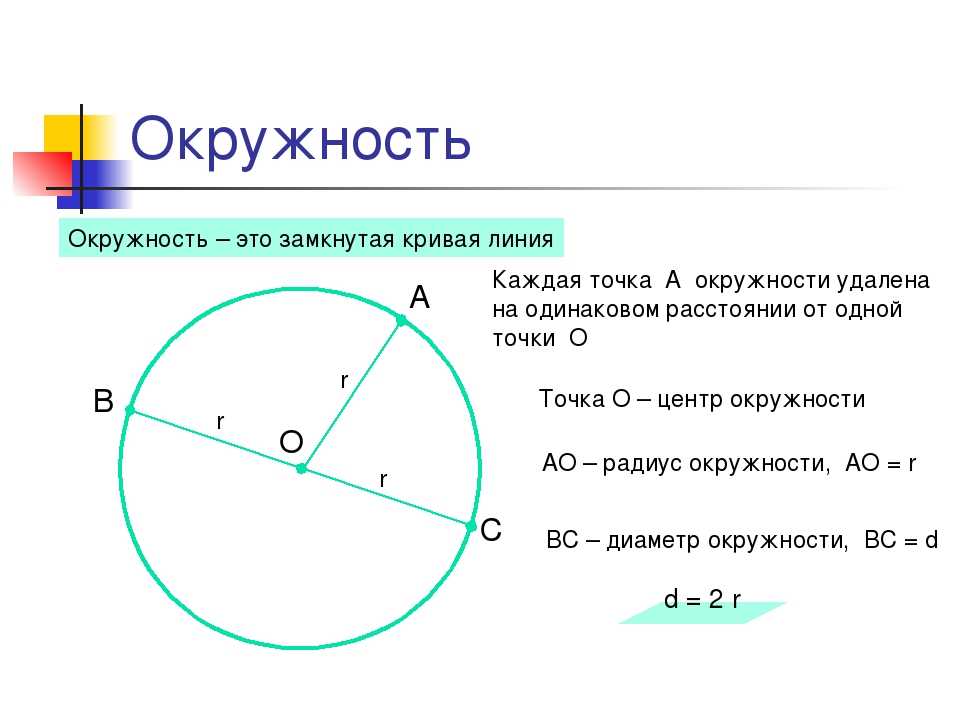 Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Так вот ту хорду, которая через него проходит, тоже называют диаметром.

 Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.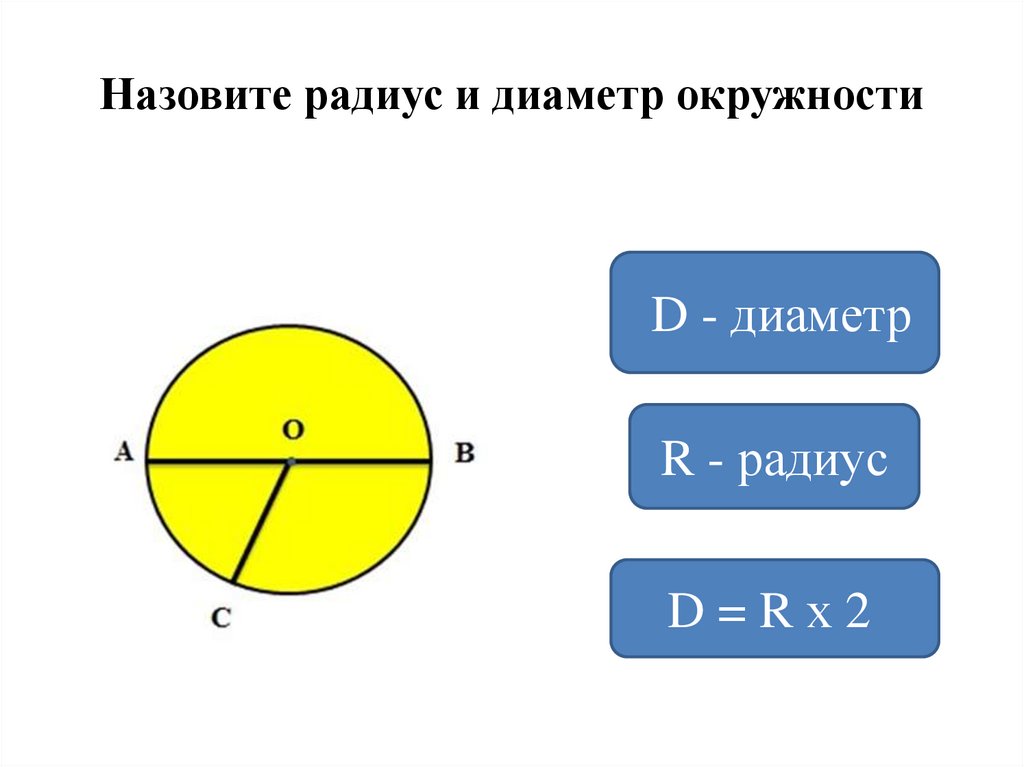 Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4. Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l. 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.