Чему равен наименьший общий знаменатель двух дробей. Калькулятор онлайн.Нахождение (вычисление) НОД и НОК
Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.
Yandex.RTB R-A-339285-1
Вычисление наименьшего общего кратного (НОК) через НОД
Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.
Определение 1
Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .
Пример 1
Необходимо найти НОК чисел 126 и 70 .
Решение
Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .
Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД
Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .
Ответ: НОК (126 , 70) = 630 .
Пример 2
Найдите нок чисел 68 и 34 .
Решение
НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .
Ответ: НОК (68 , 34) = 68 .
В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.
Нахождение НОК с помощью разложения чисел на простые множители
Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.
Определение 2
Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:
- составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
- исключаем их полученных произведений все простые множители;
- полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.
Пример 3
У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится:
Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .
Пример 4
Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.
Решение
Найдем все простые множители чисел, данных в условии:
441 147 49 7 1 3 3 7 7
700 350 175 35 7 1 2 2 5 5 7
Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .
Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7
. Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .Ответ: НОК (441 , 700) = 44 100 .
Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.
Определение 3
Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:
- разложим оба числа на простые множители:
- добавим к произведению простых множителей первого числа недостающие множители второго числа;
- получим произведение, которое и будет искомым НОК двух чисел.

Пример 5
Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители
Пример 6
Необходимо вычислить НОК чисел 84 и 648 .
Решение
Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 .
Ответ: НОК (84 , 648) = 4 536 .
Нахождение НОК трех и большего количества чисел
Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.
На этот случай есть теорема.
Теорема 1
Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .
Теперь рассмотрим, как можно применять теорему для решения конкретных задач.
Пример 7
Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .
Решение
Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .
Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .
Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .
Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .
НОК четырех чисел из условия примера равно 94500 .
Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .
Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.
Определение 4
Предлагаем вам следующий алгоритм действий:
- раскладываем все числа на простые множители;
- к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
- к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
- полученное произведение будет наименьшим общим кратным всех чисел из условия.
Пример 8
Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение
Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 .
Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.
Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.
Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .
Нахождение наименьшего общего кратного отрицательных чисел
Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.
Пример 9
НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .
Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .
Пример 10
Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .
Решение
Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.
Получим, что НОК чисел − 145 и − 45 равно 1 305 .
Ответ: НОК (− 145 , − 45) = 1 305 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Рассмотрим три способа нахождения наименьшего общего кратного.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.
Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:
Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:
2 2 · 3 2 · 5 · 7 · 11 = 13 860
Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.
Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.
Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 — взаимно простые. Поэтому
Например, три числа: 20, 49 и 33 — взаимно простые. Поэтому
НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.
Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.
Нахождение путём подбора
Второй способ заключается в нахождении наименьшего общего кратного путём подбора.
Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:
НОК (60, 30, 10, 6) = 60
В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:
- Определяем наибольшее число из данных чисел.
- Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.
Пример 2. Дано три числа 24, 3 и 18. Определяем самое большое из них — это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:
Дано три числа 24, 3 и 18. Определяем самое большое из них — это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:
24 · 1 = 24 — делится на 3, но не делится на 18.
24 · 2 = 48 — делится на 3, но не делится на 18.
24 · 3 = 72 — делится на 3 и на 18.
Таким образом, НОК (24, 3, 18) = 72.
Нахождение путём последовательного нахождения НОК
Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.
НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.
Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 8) = 4. Перемножаем данные числа:
Делим произведение на их НОД:
Таким образом, НОК (12, 8) = 24.
Чтобы найти НОК трёх и более чисел используется следующий порядок действий:
- Сначала находят НОК каких-нибудь двух из данных чисел.
- Потом, НОК найденного наименьшего общего кратного и третьего данного числа.

- Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа — 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:
Делим произведение на их НОД:
Таким образом, НОК (12, 8, 9) = 72.
При сложении и вычитании алгебраический дробей с разными знаменателями сначала дроби приводят к общему знаменателю . Это значит, находят такой один знаменатель, который делится на исходный знаменатель каждой алгебраической дроби, входящей в состав данного выражения.
Как известно, если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, отличное от нуля, то значение дроби не изменится. Это является основным свойством дроби.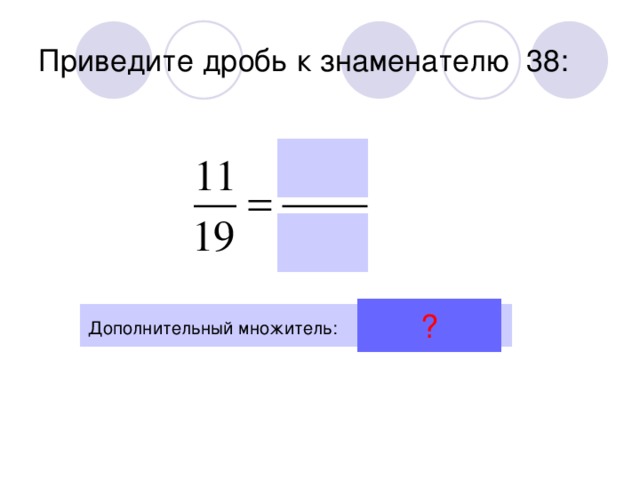 Поэтому, когда дроби приводят к общему знаменателю, по-сути умножают исходный знаменатель каждой дроби на недостающий множитель до общего знаменателя. При этом надо умножить на этот множитель и числитель дроби (для каждой дроби он свой).
Поэтому, когда дроби приводят к общему знаменателю, по-сути умножают исходный знаменатель каждой дроби на недостающий множитель до общего знаменателя. При этом надо умножить на этот множитель и числитель дроби (для каждой дроби он свой).
Например, дана такая сумма алгебраических дробей:
Требуется упростить выражение, т. е. сложить две алгебраические дроби. Для этого в первую очередь надо привести слагаемые-дроби к общему знаменателю. Первым делом следует найти одночлен, который делится и на 3x и на 2y. При этом желательно, чтобы он был наименьший, т. е. найти наименьшее общее кратное (НОК) для 3x и 2y.
Для числовых коэффициентов и переменных НОК ищется отдельно. НОК(3, 2) = 6, а НОК(x, y) = xy. Далее найденные значения перемножаются: 6xy.
Теперь надо определить, на какой множитель надо умножить 3x, чтобы получить 6xy:
6xy ÷ 3x = 2y
Значит, при приведении первой алгебраической дроби к общему знаменателю ее числитель надо умножить на 2y (знаменатель уже был умножен при приведении к общему знаменателю). Аналогично ищется множитель для числителя второй дроби. Он будет равен 3x.
Аналогично ищется множитель для числителя второй дроби. Он будет равен 3x.
Таким образом, получаем:
Далее уже можно действовать как с дробями с одинаковыми знаменателями: складываются числители, а в знаменателе пишется один общий:
После преобразований получается упрощенное выражение, представляющее собой одну алгебраическую дробь, являющуюся суммой двух исходных:
Алгебраические дроби в исходном выражении могут содержать знаменатели, представляющие собой многочлены, а не одночлены (как в приведенном выше примере). В таком случае, перед поиском общего знаменателя следует разложить знаменатели на множители (если это возможно). Далее общий знаменатель собирается из разных множителей. Если множитель есть в нескольких исходных знаменателях, то его берут единожды. Если множитель имеет разные степени в исходных знаменателях, то его берут с большей. Например:
Здесь многочлен a 2 – b 2 можно представить как произведение (a – b)(a + b). Множитель 2a – 2b раскладывается как 2(a – b). Таким образом, общий знаменатель будет равен 2(a – b)(a + b).
Таким образом, общий знаменатель будет равен 2(a – b)(a + b).
Онлайн калькулятор позволяет быстро находить наибольший общий делитель и наименьшее общее кратное как для двух, так и для любого другого количества чисел.
Калькулятор для нахождения НОД и НОК
Найти НОД и НОК
Найдено НОД и НОК: 5806
Как пользоваться калькулятором
- Введите числа в поле для ввода
- В случае ввода некорректных символов поле для ввода будет подсвечено красным
- нажмите кнопку «Найти НОД и НОК»
Как вводить числа
- Числа вводятся через пробел, точку или запятую
- Длина вводимых чисел не ограничена , так что найти НОД и НОК длинных чисел не составит никакого труда
Что такое НОД и НОК?
Наибольший общий делитель нескольких чисел – это наибольшее натуральное целое число, на которое все исходные числа делятся без остатка. Наибольший общий делитель сокращённо записывается как НОД .
Наименьшее общее кратное нескольких чисел – это наименьшее число, которое делится на каждое из исходных чисел без остатка. Наименьшее общее кратное сокращённо записывается как НОК .
Как проверить, что число делится на другое число без остатка?
Чтобы узнать, делится ли одно число на другое без остатка, можно воспользоваться некоторыми свойствами делимости чисел. Тогда, комбинируя их, можно проверять делимость на некоторые их них и их комбинации.
Некоторые признаки делимости чисел
1. Признак делимости числа на 2
Чтобы определить, делится ли число на два (является ли оно чётным), достаточно посмотреть на последнююю цифру этого числа: если она равна 0, 2, 4, 6 или 8, то число чётно, а значит делится на 2.
Пример: определить, делится ли на 2 число 34938 .
Решение: смотрим на последнюю цифру: 8 — значит число делится на два.
2. Признак делимости числа на 3
Число делится на 3 тогда, когда сумма его цифр делится на три. Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Таким образом, чтобы определить, делится ли число на 3, нужно посчитать сумму цифр и проверить, делится ли она на 3. Даже если сумма цифр получилась очень большой, можно повторить этот же процесс вновь.
Пример: определить, делится ли число 34938 на 3.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 3, а значит и число делится на три.
3. Признак делимости числа на 5
Число делится на 5 тогда, когда его последняя цифра равна нулю или пяти.
Пример: определить, делится ли число 34938 на 5.
Решение: смотрим на последнюю цифру: 8 — значит число НЕ делится на пять.
4. Признак делимости числа на 9
Этот признак очень похож на признак делимости на тройку: число делится на 9 тогда, когда сумма его цифр делится на 9.
Пример: определить, делится ли число 34938 на 9.
Решение: считаем сумму цифр: 3+4+9+3+8 = 27. 27 делится на 9, а значит и число делится на девять.
Как найти НОД и НОК двух чисел
Как найти НОД двух чисел
Наиболее простым способом вычисления наибольшего общего делителя двух чисел является поиск всех возможных делителей этих чисел и выбор наибольшего из них.
Рассмотрим этот способ на примере нахождения НОД(28, 36) :
- Раскладываем оба числа на множители: 28 = 1·2·2·7 , 36 = 1·2·2·3·3
- Находим общие множители, то есть те, которые есть у обоих чисел: 1, 2 и 2.
- Вычисляем произведение этих множителей: 1·2·2 = 4 — это и есть наибольший общий делитель чисел 28 и 36.
Как найти НОК двух чисел
Наиболее распространены два способа нахождения наименьшего кратного двух чисел. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди них такое число, которое будет общим для обоих чисел и при этом наименьшем. А второй заключается в нахождении НОД этих чисел. Рассмотрим только его.
Для вычисления НОК нужно вычислить произведение исходных чисел и затем разделить его на предварительно найденный НОД. Найдём НОК для тех же чисел 28 и 36:
- Находим произведение чисел 28 и 36: 28·36 = 1008
- НОД(28, 36), как уже известно, равен 4
- НОК(28, 36) = 1008 / 4 = 252 .

Нахождение НОД и НОК для нескольких чисел
Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел. Также для нахождение НОД нескольких чисел можно воспользоваться следующим соотношением: НОД(a, b, c) = НОД(НОД(a, b), c) .
Аналогичное соотношение действует и для наименьшего общего кратного чисел: НОК(a, b, c) = НОК(НОК(a, b), c)
Пример: найти НОД и НОК для чисел 12, 32 и 36.
- Cперва разложим числа на множители: 12 = 1·2·2·3 , 32 = 1·2·2·2·2·2 , 36 = 1·2·2·3·3 .
- Найдём обшие множители: 1, 2 и 2 .
- Их произведение даст НОД: 1·2·2 = 4
- Найдём теперь НОК: для этого найдём сначала НОК(12, 32): 12·32 / 4 = 96 .
- Чтобы найти НОК всех трёх чисел, нужно найти НОД(96, 36): 96 = 1·2·2·2·2·2·3 , 36 = 1·2·2·3·3 , НОД = 1·2·2·3 = 12 .

- НОК(12, 32, 36) = 96·36 / 12 = 288 .
Рассмотрим решение следующей задачи. Шаг мальчика составляет 75 см, а шаг девочки 60 см. Необходимо найти наименьшее расстояние, на котором они оба сделают по целому числу шагов.
Решение. Весь путь который пройдут ребята, должен делиться без остатка на 60 и на 70, так как они должны сделать каждый целое число шагов. Другими словами, в ответе должно быть число, кратное как 75 так и 60.
Сначала будем выписывать все кратные числа, для числа 75. Получаем:
- 75, 150, 225, 300, 375, 450, 525, 600, 675, … .
Теперь выпишем числа, которые будут кратны 60. Получаем:
- 60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660, … .
Теперь находим числа которые есть в обоих рядах.
- Общими кратными чисел будут числа, 300, 600, и т.д.
Самое наименьшее из них, это число 300. Оно в данном случае будет называться наименьшим общим кратным чисел 75 и 60.
Возвращаясь к условию задачи, наименьшее расстояние, на котором ребята сделают целое число шагов будет 300 см. Мальчик пройдет этот путь за 4 шага, а девочке потребуется сделать 5 шагов.
Мальчик пройдет этот путь за 4 шага, а девочке потребуется сделать 5 шагов.
Определение наименьшего общего кратного
- Наименьшим общим кратным двух натуральных чисел a и b называется наименьшее натуральное число, которое кратно как a, так и b.
Для того, чтобы найти наименьшее общее кратное двух чисел, не обязательно выписывть подряд все кратные для этих чисел.
Можно воспользоваться следующим методом.
Как найти наименьшее общее кратное
Сначала необходимо разложить данные числа на простые множители.
- 60 = 2*2*3*5,
- 75=3*5*5.
Теперь выпишем все множители которые есть в разложении первого числа (2,2,3,5) и добавим к нему все недостающие множители из разложения второго числа (5).
Получим в итоге ряд простых чисел: 2,2,3,5,5. Произведение этих чисел и будет наименьшим общим сомножителем для данных чисел. 2*2*3*5*5 = 300.
Общая схема нахождения наименьшего общего кратного
- 1. Разложить числа на простые множители.
 2
2Приведение дробей к наименьшему общему знаменателю, правило, примеры, решения. Записи с меткой «наименьший общий знаменатель»
Умножение «крест-накрест»
Метод общих делителей
Задача. Найдите значения выражений:
Задача. Найдите значения выражений:
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест».
Общий знаменатель дробей
Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Смотрите также:
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями.
 А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко.
 Метод заключается в следующем:
Метод заключается в следующем:- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным.
 Посмотрите на примеры:
Посмотрите на примеры:Как найти наименьший общий знаменатель
Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Не думайте, что таких сложных дробей в настоящих примерах не будет.
 Они встречаются постоянно, и приведенные выше задачи — не предел!
Они встречаются постоянно, и приведенные выше задачи — не предел!Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Смотрите также:
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется.
 А искомые числа, «выравнивающие» знаменатели, называются.
А искомые числа, «выравнивающие» знаменатели, называются.Для чего вообще надо приводить дроби к общему знаменателю?
Общий знаменатель, понятие и определение.
Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой.
 В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.

- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей.
 Затем приводим к этому числу знаменатели обеих дробей.
Затем приводим к этому числу знаменатели обеих дробей.Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4.
 Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК.
 Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.Смотрите также:
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей.
Взгляните:
Задача.
 Найдите значения выражений:
Найдите значения выражений:В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия.
 Заодно резко снижается вероятность ошибки.
Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий.
 Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения.
 Здесь мы не будем этого касаться.
Здесь мы не будем этого касаться.Смотрите также:
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями.
 По-другому эту операцию никак не выполнить;
По-другому эту операцию никак не выполнить; - Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто.
 Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа.
Приведение дробей к общему знаменателю
Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей.
 Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Математические выражения и задачи требуют множества дополнительных знаний. НОК — это одно из основных, особенно часто применяемое в Тема изучается в средней школе, при этом не является особо сложным в понимании материалом, человеку знакомому со степенями и таблицей умножения не составит труда выделить необходимые числа и обнаружить результат.

Определение
Общее кратное — число, способное нацело разделиться на два числа одновременно (а и b). Чаще всего, это число получают методом перемножения исходных чисел a и b. Число обязано делиться сразу на оба числа, без отклонений.
НОК — это принятое для обозначения краткое название, собранной из первых букв.
Способы получения числа
Для нахождения НОК не всегда подходит способ перемножения чисел, он гораздо лучше подходит для простых однозначных или двухзначных чисел. принято разделять на множители, чем больше число, тем больше множителей будет.
Пример № 1
Для простейшего примера в школах обычно берутся простые, однозначные или двухзначные числа. Например, необходимо решить следующее задание, найти наименьшее общее кратное от чисел 7 и 3, решение достаточно простое, просто их перемножить. В итоге имеется число 21, меньшего числа просто нет.
Пример № 2
Второй вариант задания гораздо сложнее. Даны числа 300 и 1260, нахождение НОК — обязательно.
 Для решения задания предполагаются следующие действия:
Для решения задания предполагаются следующие действия:Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7. Первый этап завершен.
Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.
Для вычисления итогового результата необходимо взять каждое число в наибольшей их представленных степеней, в уравнение. Остается только перемножить и получить ответ, при правильном заполнении задача укладывается в два действия без пояснений:
1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7.
2) НОК = 6300.

Вот и вся задача, если попробовать вычислить нужное число посредством перемножения, то ответ однозначно не будет верным, так как 300 * 1260 = 378 000.
Проверка:
6300 / 300 = 21 — верно;
6300 / 1260 = 5 — верно.
Правильность полученного результата определяется посредством проверки — деления НОК на оба исходных числа, если число целое в обоих случаях, то ответ верен.
Что значит НОК в математике
Как известно, в математике нет ни одной бесполезной функции, эта — не исключение. Самым распространенным предназначением этого числа является приведение дробей к общему знаменателю. Что изучают обычно в 5-6 классах средней школы. Также дополнительно является общим делителем для всех кратных чисел, если такие условия стоят в задаче. Подобное выражение может найти кратное не только к двум числам, но и к гораздо большему количестве — трем, пяти и так далее. Чем больше чисел — тем больше действий в задаче, но сложность от этого не увеличивается.
Например, даны числа 250, 600 и 1500, необходимо найти их общее НОК:
1) 250 = 25 * 10 = 5 2 *5 * 2 = 5 3 * 2 — на этом примере детально описано разложение на множители, без сокращения.

2) 600 = 60 * 10 = 3 * 2 3 *5 2 ;
3) 1500 = 15 * 100 = 33 * 5 3 *2 2 ;
Для того чтобы составить выражение, требуется упомянуть все множители, в этом случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.
Внимание: все множители необходимо доводить до полного упрощения, по возможности, раскладывая до уровня однозначных.
Проверка:
1) 3000 / 250 = 12 — верно;
2) 3000 / 600 = 5 — верно;
3) 3000 / 1500 = 2 — верно.
Данный метод не требует каких-либо ухищрений или способностей уровня гения, все просто и понятно.
Еще один способ
В математике многое связано, многое можно решить двумя и более способами, то же самое касается поиска наименьшего общего кратного, НОК. Следующий способ можно использовать в случае с простыми двузначными и однозначными числами. Составляется таблица, в которую вносятся по вертикали множимое, по горизонтали множитель, а в пересекающихся клетках столбца указывается произведение.
 Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.
Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.Даны числа 30, 35, 42 необходимо найти НОК, связывающий все числа:
1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т. д.
2) Кратные 35: 70, 105, 140, 175, 210, 245 и т. д.
3) Кратные 42: 84, 126, 168, 210, 252 и т. д.
Заметно, что все числа достаточно разные, единственное общее среди них число 210, вот оно и будет НОК. Среди связанных с этим вычислением процессов есть также наибольший общий делитель, вычисляющийся по похожим принципам и часто встречающийся в соседствующих задачах. Различие невелико, но достаточно значимо, НОК предполагает вычисление числа, которое делится на все данные исходные значения, а НОД предполагает под собой вычисление наибольшего значение на которое делятся исходные числа.

Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел. Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.
Шаги
Ряд кратных чисел
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.
Кратное число – это число, которое делится на данное число без остатка. Кратные числа можно посмотреть в таблице умножения..
- Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.
Запишите ряд чисел, которые кратны первому числу.
 Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.
Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.- Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.
Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел. Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.
- Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.
Разложение на простые множители
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.

- Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.
Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.
- Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20} и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10} . Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .
Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.
- Например, 2 × 42 = 84 {\displaystyle {\mathbf {2} }\times 42=84}
, 7 × 6 = 42 {\displaystyle {\mathbf {7} }\times 6=42}
и 3 × 2 = 6 {\displaystyle {\mathbf {3} }\times {\mathbf {2} }=6}
. Таким образом, простыми множителями числа 84 являются числа 2, 7, 3 и 2. Запишите их в виде выражения: .

- Например, 2 × 42 = 84 {\displaystyle {\mathbf {2} }\times 42=84}
, 7 × 6 = 42 {\displaystyle {\mathbf {7} }\times 6=42}
и 3 × 2 = 6 {\displaystyle {\mathbf {3} }\times {\mathbf {2} }=6}
. Таким образом, простыми множителями числа 84 являются числа 2, 7, 3 и 2. Запишите их в виде выражения: .
Запишите множители, общие для обоих чисел. Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).
- Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times } и зачеркните 2 в обоих выражениях.
- Общим для обоих чисел является еще один множитель 2, поэтому напишите 2 × 2 {\displaystyle 2\times 2} и зачеркните вторую 2 в обоих выражениях.
К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.
- Например, в выражении 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} зачеркнуты обе двойки (2), потому что они являются общими множителями. Не зачеркнут множитель 5, поэтому операцию умножения запишите так: 2 × 2 × 5 {\displaystyle 2\times 2\times 5}
- В выражении 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2}
также зачеркнуты обе двойки (2).
 Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3}
.
Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3}
.
Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.
- Например, 2 × 2 × 5 × 7 × 3 = 420 {\displaystyle 2\times 2\times 5\times 7\times 3=420} . Таким образом, наименьшее общее кратное 20 и 84 равно 420.
Нахождение общих делителей
Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.
- Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.

- Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.
Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.
- Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2. Таким образом, напишите 2 в первой строке и первом столбце.
Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.
- Например, 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} , поэтому запишите 9 под 18.
- 30 ÷ 2 = 15 {\displaystyle 30\div 2=15} , поэтому запишите 15 под 30.
Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.
- Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.
Разделите каждое частное на второй делитель.
 Каждый результат деления запишите под соответствующим частным.
Каждый результат деления запишите под соответствующим частным.- Например, 9 ÷ 3 = 3 {\displaystyle 9\div 3=3} , поэтому запишите 3 под 9.
- 15 ÷ 3 = 5 {\displaystyle 15\div 3=5} , поэтому запишите 5 под 15.
Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.
Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.
- Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так: 2 × 3 × 3 × 5 {\displaystyle 2\times 3\times 3\times 5} .
Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.
- Например, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90}
. Таким образом, наименьшее общее кратное 18 и 30 равно 90.

- Например, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90}
. Таким образом, наименьшее общее кратное 18 и 30 равно 90.
Алгоритм Евклида
Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят. Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.
- Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2}
ост. 3:
15 – это делимое
6 – это делитель
2 – это частное
3 – это остаток.
- Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2}
ост. 3:
- Метод простой факторизации
- Использование алгоритма Евклида
- Метод длинного деления
- GCF(33, 12) = GCF(12, 33 mod 12) = GCF(12, 9)
- GCF(12, 9) = GCF(9, 12 mod 9) = GCF(9, 3)
- GCF(9, 3) = GCF(3, 9 mod 3) = GCF(3, 0)
- GCF(3, 0) = 3 (∵ GCF(X, 0) = |X|, где X ≠ 0)
- Шаг 1: Разделите 33 (большее число) на 12 (меньшее число).
- Шаг 2: Поскольку остаток ≠ 0, разделим делитель шага 1 (12) на остаток (9).
- Шаг 3: Повторяйте этот процесс до тех пор, пока остаток не станет равным 0.
- НОД 8 и 18 = 2
- GCF 18 и 54 = 18
- GCF 54 и 72 = 18
- GCF 8 и 40 = 8
- GCF 28 и 32 = 4
- GCF 6 и 14 = 2
- GCF 42 и 60 = 6
Пример 1. Для двух чисел GCF = 3 и LCM = 132. Если одно число равно 12, найдите другое число.
Решение:
Дано: GCF (y, 12) = 3 и LCM (y, 12) = 132
∵ GCF × LCM = 12 × (y)
⇒ y = (GCF × LCM)/12
⇒ у = (3 × 132)/12
⇒ у = 33
Следовательно, другое число равно 33.
Пример 2: Произведение двух чисел равно 396. Если их НОД равен 3, какова их НОК?
Решение:
Дано: GCF = 3 и произведение чисел = 396
.
∵ LCM × GCF = произведение чисел
⇒ НОК = Продукт/GCF = 396/3
Следовательно, НОК равен 132.Пример 3. Найдите НОКФ чисел 12 и 33, если их НОКМ равен 132.
Решение:
∵ НОКМ × НГК = 12 × 33
⇒ GCF(12, 33) = (12 × 33)/132 = 3
Следовательно, наибольший общий делитель чисел 12 и 33 равен 3,9.0003- Путем перечисления общих факторов
- Длинным делением
- Путем простой факторизации
- Ассоциативный: НОК (а, б) = НОК (б, а)
- Коммутативный: МОК (a, b, c) = LCM (LCM (a, b), c) = LCM (a, LCM (b, c))
- Распределительный: LCM (ka, kb, kc) = kLCM (a, b, c)
- LCM связан с GCF:
- Использование табличного метода
- Использование метода наибольшего общего делителя (НОД)
- Использование метода простой факторизации
- Использование нескольких чисел
- Перечислите все заданные числа горизонтально в таблице через запятую.
- Начните делить числа на 2, если они полностью делятся. Напишите 2 вверху левого столбца и напишите результат горизонтально. Повторяем этот процесс до тех пор, пока в результате не получим простое(ые) число(а).
- Если какое-либо число не делится на 2, выберите следующее по величине простое число и начните делить число (числа) на это число. Запишите это число под цифрой 2 и напишите результат горизонтально. Повторяйте этот шаг, пока мы не получим 1 в последней строке.
- Чтобы получить LCM, умножьте все числа, написанные в крайнем левом столбце.
- Запишите все множители каждого числа.
- Выберите общие факторы.
- Выберите наибольшее число в качестве НОД.
- Выпишите все простые множители данных чисел.
- Выберите все простые числа. Столько, сколько они встречаются чаще всего для любого заданного числа.
- Перемножьте все простые числа, чтобы получить НОК.
- Перечислите все кратные каждого числа, пока не будет найдено первое общее кратное.
- Выберите наименьшее кратное, общее для всех заданных чисел.
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48847
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады
- уметь находить наименьшее общее кратное двух или более целых чисел
- Ответить
4, 8, 12, 16, 20
- Ответ
5, 10, 15, 20, 25
- Ответить
6, 12, 18, 24, 30
- Ответить
7, 14, 21, 28, 35
- Ответить
9, 18, 27, 36, 45
- Ответить
4, 8, 12, 16, 20
- Ответить
12, 24, 36, 48, 60
- Ответить
10, 20, 30, 40, 50
- Ответить
6, 12, 18, 24, 30
- Ответить
20, 40, 60, 80, 100
- Запишите простую факторизацию каждого числа, используя показатели степени повторяющихся множителей.
- Запишите все основания, которые встречаются в каждой из простых факторизаций.
- К каждому основанию присоедините наибольшего показателя степени , который появляется на нем в простых факторизациях.
- LCM является произведением чисел, найденных на шаге 3.
- Обратите внимание на разницу между этапом 2 для LCM и этапом 2 для GCF.
 Для GCF мы используем только основания, которые являются общими в простых факторизациях, тогда как для LCM мы используем для каждого оснований, которые появляются в простых факторизациях.
Для GCF мы используем только основания, которые являются общими в простых факторизациях, тогда как для LCM мы используем для каждого оснований, которые появляются в простых факторизациях. - Обратите внимание на разницу между шагом 3 для LCM и шагом 3 для GCF. Для GCF мы присоединяем наименьших} \\ {} & = & {4 \cdot 3 \cdot 5 \cdot 121} \\ {} & = & {7260} \end{массив}\)
- Ответить
540
- Ответить
28
- Ответить
126
- Ответить
1 960
- Ответить
6 534 000
- Ответить
24
- Ответить
40
- Ответить
12
- Ответить
18
- Ответить
30
- Ответить
12
- Ответить
63
- Ответить
72
- Ответить
720
- Ответить
120
- Ответить
216
- Ответить
144
- Ответить
105
- Ответить
231
- Ответить
126
- Ответить
4 410
- Ответить
240
- Ответить
432
- Ответить
144
- Ответить
224
- Ответить
193 050
- Ответить
8
- Ответить
36
- Ответить
\(84 \cdot 84 \cdot 84\)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Денни Бурзински и Уэйд Эллис-младший
- Лицензия
- СС BY
- Показать страницу TOC
- нет
- Теги
- общие кратные
- наименьшее общее кратное
- кратно
- Вычитание дробей с помощью полос дробей
- Вычитание дробей с помощью числовой линейки
- Вычитание дробей напрямую.
- Сложите числители
- Запишите знаменатель один раз
- с использованием фракционных полос
- Использование номеров
- Установите непосредственное
- Разделите числовую прямую между 0 и 1 на количество частей, указанное в знаменателе. Убедитесь, что каждая из частей имеет одинаковый размер.
- Начиная с 0, считать вперед количество частей, указанное в числителе.
- Отметьте точку на числовой прямой.
- Укажите прыжки в каждой числовой строке и закончите предложения с вычитанием.
- У капитана есть пицца, и он ест ее. Какая доля у него осталась?
- Патрик натер 2/3 блока сыра, чтобы сделать макароны.

Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей
). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30: 5=6), дополнительный множитель ко 2-й дроби равен 5 (30: 6=5), дополнительный множитель к 3-ей дроби равен 2 (30: 15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Страница 1 из 1 1
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Например :
Число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
Число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа . Делитель натурального числа a — это такое натуральное число, которое делит данное число a без остатка. Натуральное число, которое имеет более двух делителей, называется составным .
Делитель натурального числа a — это такое натуральное число, которое делит данное число a без остатка. Натуральное число, которое имеет более двух делителей, называется составным .
Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел — 12. Общий делитель двух данных чисел a и b — это число, на которое делятся без остатка оба данных числа a и b .
Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например , числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 — тоже их общие кратные. Среди всех jбщих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим общим кратным (НОК) .
НОК всегда натуральное число, которое должно быть больше самого большого из чисел, для которых оно определяется.
Наименьшее общее кратное (НОК). Свойства.
Коммутативность:
Ассоциативность:
В частности, если и — взаимно-простые числа , то:
Наименьшее общее кратное двух целых чисел m и n является делителем всех других общих кратных m и n .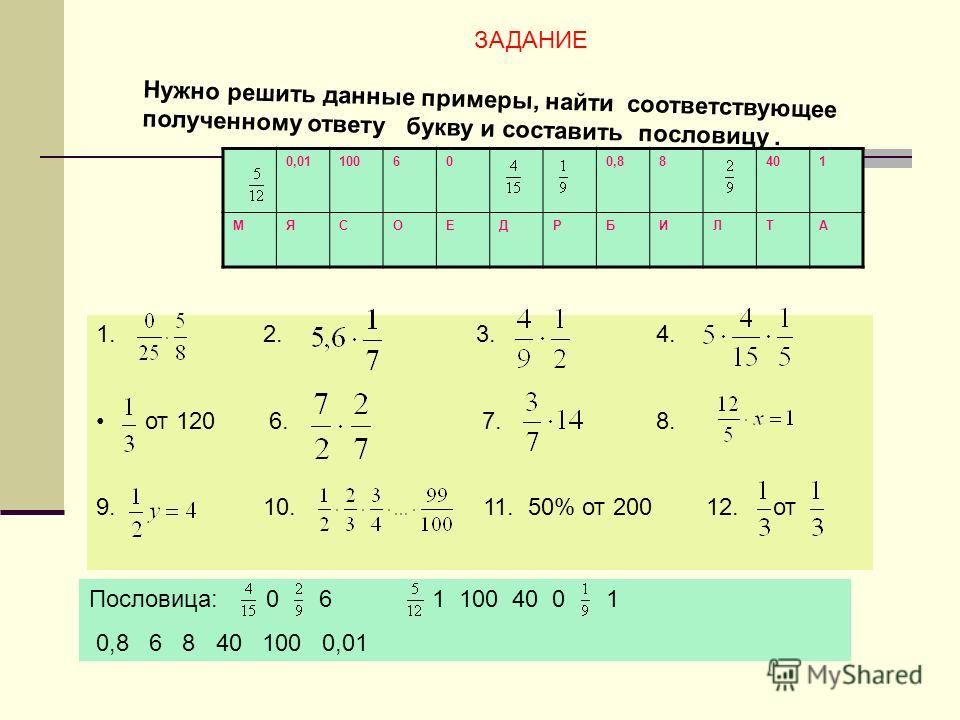 Более того, множество общих кратных m, n совпадает с множеством кратных для НОК(m, n ).
Более того, множество общих кратных m, n совпадает с множеством кратных для НОК(m, n ).
Асимптотики для могут быть выражены через некоторые теоретико-числовые функции.
Так, функция Чебышёва . А также:
Это следует из определения и свойств функции Ландау g(n) .
Что следует из закона распределения простых чисел.
Нахождение наименьшего общего кратного (НОК).
НОК(a, b ) можно вычислить несколькими способами:
1. Если известен наибольший общий делитель , можно использовать его связь с НОК:
2. Пусть известно каноническое разложение обоих чисел на простые множители:
где p 1 ,…,p k — различные простые числа, а d 1 ,…,d k и e 1 ,…,e k — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении).
Тогда НОК (a ,b ) вычисляется по формуле:
Другими словами, разложение НОК содержит все простые множители , входящие хотя бы в одно из разложений чисел a, b , причём из двух показателей степени этого множителя берётся наибольший.
Пример :
Вычисление наименьшего общего кратного нескольких чисел может быть сведено к нескольким последовательным вычислениям НОК от двух чисел:
Правило. Чтобы найти НОК ряда чисел, нужно:
— разложить числа на простые множители;
— перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;
— полученное произведение простых множителей будет НОК заданных чисел.
Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.
Простые множители числа 28 (2, 2, 7) дополнили множителем 3 (числа 21), полученное произведение (84) будет наименьшим числом, которое делится на 21 и 28 .
Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка.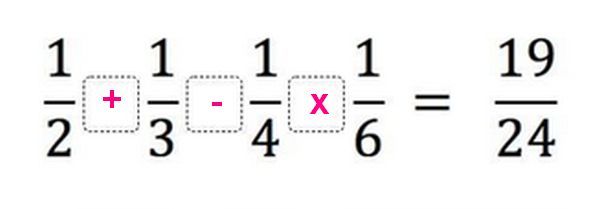 Это наименьшее произведение из возможных (150, 250, 300…), которому кратны все заданные числа.
Это наименьшее произведение из возможных (150, 250, 300…), которому кратны все заданные числа.
Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.
Правило . Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.
Еще один вариант:
Чтобы найти наименьшее общее кратное (НОК) нескольких чисел нужно:
1) представить каждое число как произведение его простых множителей, например:
504 = 2 · 2 · 2 · 3 · 3 · 7 ,
2) записать степени всех простых множителей:
504 = 2 · 2 · 2 · 3 · 3 · 7 = 2 3 · 3 2 · 7 1 ,
3) выписать все простые делители (множители) каждого из этих чисел;
4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;
5) перемножить эти степени.
Пример . Найти НОК чисел: 168, 180 и 3024.
Решение . 168 = 2 · 2 · 2 · 3 · 7 = 2 3 · 3 1 · 7 1 ,
180 = 2 · 2 · 3 · 3 · 5 = 2 2 · 3 2 · 5 1 ,
3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2 4 · 3 3 · 7 1 .
Выписываем наибольшие степени всех простых делителей и перемножаем их:
НОК = 2 4 · 3 3 · 5 1 · 7 1 = 15120.
Урок 51. приведение дробей к общему знаменателю — Математика — 5 класс
Наименьший общий знаменатель
Чему равен наименьший общий знаменатель дробей $\frac{3}{8}$ и $\frac{2}{3}$?
Выберите правильный ответ.
6 | |
48 | |
8 | |
24 |
НОЗ дробей
Наименьшим общим знаменателем дробей $\frac{5}{8}$ и $\frac{7}{12}$ является число
35
96
24
12
.
Общие знаменатели
Общим знаменателем дробей $\frac{5}{8}$ и $\frac{7}{12}$ являются числа __ и __.
12
24
35
96
Равные дроби
Соедините попарно дроби так, чтобы выполнялось равенство.
$\frac{1}{2}$
$\frac{7}{8}$
$\frac{5}{6}$
$\frac{21}{24}$
$\frac{25}{30}$
$\frac{6}{12}$
Части целого
Определите, как можно записать одну часть целого на представленных рисунках. Добавьте подписи к изображениям.
$\frac{1}{8}$
$\frac{1}{4}$
$\frac{1}{6}$
Определение общего знаменателя
Составьте правильное определение, подставив слова в пропуски.
Общим дробей может быть общее их знаменателей.
одно
знаменателем
кратное
числителем
частное
любое
Увеличение дробей
Заполните пропуски в таблице, добавив соответствующие дроби в столбцы.
| $\frac{7}{12}$ | $\frac{13}{21}$ | |
| $\frac{15}{21}$ | $\frac{39}{63}$ | |
| $\frac{35}{49}$ | $\frac{49}{84}$ |
$\frac{91}{147}$
$\frac{5}{7}$
$\frac{21}{36}$
Нахождение знаменателей
Выделите цветом общие знаменатели для дробей $\frac{9}{14}$ и $\frac{8}{21}$.
126; 106; 86; 84; 63; 42
Оранжевый
Общие знаменатели дробей
Зачеркните числа, не являющиеся общими знаменателями для дробей $\frac{5}{13}$ и $\frac{9}{17}$.
221; 217; 413; 442; 568; 663
Новый знаменатель дробей
Подчеркните числа, являющиеся общими знаменателями для дробей $\frac{6}{15}$ и $\frac{11}{18}$.
210; 270; 90; 60; 180; 150
Наименьший знаменатель двух дробей
Выберите правильный ответ.
Наименьшим общим знаменателем дробей $\frac{7}{33}$ и $\frac{3}{77}$ является число
321 231 963 967 .
Общий множитель
Заполните пропуски в таблице, добавив соответствующие дроби в столбцы.
| $\frac{2}{55}$ | $\frac{4}{49}$ | |
| $\frac{4}{288}$ | $\frac{16}{196}$ | |
| $\frac{22}{605}$ | $\frac{11}{792}$ |
$\frac{1}{72}$
$\frac{8}{220}$
$\frac{44}{539}$
Равные дроби
Соедините попарно дроби так, чтобы выполнялось равенство.
$\frac{15}{98}$
$\frac{13}{72}$
$\frac{1}{51}$
$\frac{65}{360}$
$\frac{75}{490}$
$\frac{8}{408}$
Определение общего знаменателя
Выберите общие знаменатели для дробей $\frac{1}{72}$ и $\frac{1}{56}$.
412
824
504
804
1008
Сбросить ответы Сохранить и перейти к следующему
Общий знаменатель 3 способа как его найти
SubtitleList.com +Extensions for quick download снова все вы на канал это просто математика и с вами вячеслав сегодня данном за не и хочу рассказать о том как найти наименьший общий знаменатель и так принципе можно выделить три способа наименьший общий знаменатель эта тема нашего занятия первый способ который мы будем использовать этим способом легче всего пользоваться состоит из трех шагов 1 выбираем большей знаменатель второй шаг проверяем делится ли он на остальные и третий шаг есть и делится то это есть на меньшую признана тилль третий шаг если не подходит второе то умножаем на 2 и снова проверяем и так далее имеется виду умножаем на 3 на 4 и на практике мы часто посмотрим например смотрите есть у нас дробь 5 12 и дробь и три четвёртых две дроби нужен наименьший общий знаменатель ну допустим сложить их нужно знаменателе 12 4 выбираем больше то есть 12 проверяем делится ли он на остальные то есть на 4 12 делится на 4 да значит он в общий знаменатель значит наименьший общий знаменатель это 12 он делится и на 12 и на 4 допустим еще один пример у нас есть дробь 4 15 и / 70-ых нужен наименьший общий знаменатель проверяем берем наибольшей то есть 15 проверяем делится ли он на остальные то есть на десятку 15 на 10 15 не делится значит не подходит третий шаг есть и не делится то значит нужно в два раза взять по 15 это 30 проверяем делится на 10 делится значит наименьший общий знаменатель это 30 и дополнительные множителями у этих дробей если сложить или вычесть или сравнить то 15 нужно будет умножить на 2 а 10 нужно будет умножить на 3 из-за того что в общий знаменатель 30 и другие подобные пример сейчас мы может быть ещё к ним вернёмся но пока второй способ покажу второй способ это разбить на простые множители разбить на простые множители возьмем те же дроби 11 три четвертых разобьем на простые множители число 12 и число 4 простые множители это множители это числа которые делятся только на себя ирина 112 это вот такие простые ножки как число 1 2 3 5 7 и так далее идей и не 9 уже сложно внутри уже делятся и так 12 делим на 2 это будет 66 делим внутренне тоже на 2 это будет 3 3 делится на 3 это будет 1 и так вот простые множители 12 состоит из множителей 2231 12 это 223 и 14 развивая на простые множители 4 делим на 2 будет 22 делим на 2 будет этих значит 4 это 2 2 и 1 какой же знаменатель общей общий знаменатель состоит из множителей 1 знаменателе и 2 но во втором видим все те же числа что их первым поэтому из 2 мы ничего добавлять не будем дополнительно и так наименьший общий знаменатель это 2 2 3 то есть 12 возьмем другие наши две дроби взобьем 15 и 10 на множители просто 15 делится на пять это будет 33 делятся на 3 это будет 110 делятся на 5 это 229 на 2 и таки итак 15 состоит из множителей 5 умножить на 3 умножить на 110 состоит из множителя 5 умноженное на 2 можем знать и наименьший общий знаменатель это множители 1 531 и множитель 2 5 1 есть двойки нет поэтому еще и на 2 в итоге общий знаменатель это 5 на 315 на 1-ой 15 на 2 вот такой второй способ третий способ который можем использовать это так напишу таблица кратных допустим возьмем снова наши пример есть у а знаменатель 12 и 4 построим таблицу кратных этих этим числам 2 умножить на 1 это 12 12 умножить на 2 это 24 12 умножить на 3 это 3612 на 448 41 44 на 2 во всем 4 на 13 44 16:04 на 520 так вот мы выписали кратные чистый кратные нашим знаменатель кратны это те числа которые делятся на слона на вот данные ищем общей смотрим здесь здесь вот первый встречающиеся в общий знаменатель но тут еще есть и другие конечно вот например представьте если мы продолжим вот на 66 на 424 то есть тоже вот обще есть но наименьший вообще-то 12 значит наименьшую при знаменатель это наименьшее общее кратное в данном случае это число 12 проделаем ту же схему с нашими другими знаменателями в 15 и 10 15 10 1 на 2 на клеточной кстати вот к чему вот эти цифры я пишу можно в принципе так писать эти цифры верху это то насколько мы домножаем данное число чтобы получилось вот результат эти цифры помогает нам найти дополнительные множители ну допустим опять же нам нужно сложить вот эти 512 их и три четвёртых мы нашли что знаменателю вот этим способом нашли что общий знаменатель 12 но сколько нужно домножить дроби первая дробь 12 наложилось на один из чтобы стало общая 12 значит знать это нажать 2 дробь со знаменателем 4 общий знаменатель получили 12 при умножении четверки на тройку значит вторую дробь нужно до умножать на тройку вот эти числа они в этом помогают то есть они сразу показывают дополнительным но тоже такой небольшой плюс хотя и в этом способ в способе тоже можно дополнительно множителей определить смотрите например мы разбили на множители вы выяснили какой наименьший общий знаменатель видимость каких множителей он состоит теперь смотрим первый знаменатель состоит из всех таких же множителей значит домножаем на 1 2 знаменатель состоит из 7 таких множителей помимо тройки начать дам нажать нужно на 100 на оставшийся тот которого в нем нет а в общем знаменателе есть множитель эта тройка значит четверку придется над руками нажать придется эту дробь дам нажать но натрий в любом из способов видно как можно дополнительно и множитель искать вернемся в 15 10 15 на 115 15 на 230 15 на 3 45 на 460 здесь на 110 здесь на два двадцать тридцать сорок и так мы видим в общем тридцатку тридцатка а ты здесь же слова мы видим что 15 при умножении на 2 до с 30 а 10 приложений на 3 до встретить то есть дополнительный множитель ему 15 4 15 будет 2у 70 вы дополнительно множитель 3 если проанализировать способ с разбивкой на множители простые то это тоже можно увидеть общий знаменатель состоит из множителей 531 и 215 состоит из множителей 531 не хватает двойки значит 415 на двойку дам нажать 10 состоит из множителей 521 не хватает тройки значит семь десятых нужно нажать на тройку ну что ж вот такие способы давайте покажу вам пример например с 7 18 + 4 15 и нам нужно сложить две эти дроби нужно найти наименьший общий знаменатель первым способом 18 самый большой выбираем делится ли он на 15 нет не делится не подходит значит 820 умножаем на 2 18 умножить на 2 будет 36 36 на 15 тоже не делится это не общий знаменатель 18 умножаем на 3 это 5454 на 15 не делится число готовится на 15 это 15 писать-то 15-30 45-60 75 90 мы закончили на тройке 18 умножаем на 4 это 72 на 15 тоже не делится 18 умножаем на 5 это 90 до на 15 9 значит таким способом мы нашли что наименьший общий знаменатель 90 ну давайте освоим 2 оставшиеся способа проверим например 18 мы будем разбивать на множители простые делится на 3 это 6 делится на 3 это 2 делится на два это 118 состоит из множителей 332 15 состоит из множителей в пять-то 33 это 150 опять этой наименьший общий знаменатель состоит из множителей 332 из 1 и 5 из 2 считаем треба 392 на 5 10 9 на 1090 да так и есть 90 нам подошло ну раз мы сегодня учимся находить знаменатель то все способы пробы попробуем третий способ таблица кратных 18 умножить на 118 18 умножить на 2 36 18 умножить на 350 418 ночь на 4 4 на 1044 на 832 в итоге 72 18 умножить на 590 15 умножить на 1 это будет 15-15 на 2 это 30 15-45 15 на 460 15 на 575 не влазит давайте вот так вот продолжим здесь на 6 1815 не подрассчитал 18 на 660 и 48 108 15 на 15 на 615 на 660 и 30 то есть 90 довольно вот общий и вот числа на которые придется дам нажать определяем здесь сразу видно 18 на 5 нужно будет домножить на 15 на 6 нужно притом но жить как это определить здесь в разбивке на простые множители 18 это 332 общество этим 3325 значит не хватает пятерки да вот мы до пятерку нам нужен 15 это 5 3 5 3 в общем знаменателе есть не хватает тройки двойки 3 на 2 это 6 до этого общей это число которое нужно домножить чтобы стало общий знаменатель 5 на 7 35 6 на 4 24 в итоге получается 59 девяностых он постарался интенсивно коротко так быстро рассказать вам некоторые способы в принципе вот три основных таких способа как разбить на множители на множители разбить или таблицу сделать как найти общий наименьший общий знаменатель пишите комментарии если какие-то нюансы недопоняли если что-то нужно подсказать или может где-то ошибку увидели также ставьте лайки подписывайтесь на мой канал ну и напоследок хочу вам без попробуйте для закрепления освоить эту тему даже попробуйте всеми двумя способами чтобы увидеть какой для вас более интересен какой вам больше нравится попробуйте найти общий знаменатель и вот такие дроби в первое задание это будет три пятых и 1 4 2 пример это будет двенадцать шестьдесят четвёртых и 14 сороковых и третий пример попробуйте из трех чисел две пятых 1 6 и 4 15 среди этих трёх дробей найти наименьший общий знаменатель но желаю вам успехов пишите свои ответы в комментарияхLoading
Приведение дробей к общему знаменателю
Цель урока: закрепить основное свойство дроби, научить учащихся применять это свойство на практике приведения к общему знаменателю дробей, показать связь между приведением дробей к общему знаменателю и НОКом знаменателей дробей.
Ход урока
I. Организационный момент
II. Актуализация опорных знаний
Учитель фронтально опрашивает учащихся о основном свойстве дроби. Вспоминают понятие НОКа и способы нахождения НОКа двух чисел:
Поможет нам разобраться с этой темой основное свойство дроби, которое, напомню, звучит следующим образом:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Так, например, по основному свойству дробь 2/3 можно привести к знаменателю 6, умножив и числитель, и знаменатель на 2. Эту дробь можно привести и к знаменателю 9, и 12, и к любому другому числу, кратному 3.
Напомним, что дроби можно приводить только к тем знаменателям, которые кратны исходным.
Ученики по очереди называют числа, к которым можно привести знаменатель дроби ¾.
Дробь ¾ можно привести к знаменателю 4, 8, 12 и к любому другому числу, кратному 4.
Учитель обращает внимание учеников, что можно обе дроби привести к знаменателю 12.
III. Изучение нового материала
Говорят, можно 2/3 и ¾ можно привести к общему знаменателю.
То есть если у нас есть две дроби с разными знаменателями, мы можем сделать так, чтобы знаменатели стали одинаковыми.
Приведение к общему знаменателю понадобится для сложения и вычитания обыкновенных дробей. Кроме того, сравнивать дроби с одинаковыми знаменателями очень просто.
Приведем к общему знаменателю дроби 11/12 и 17/18.
Сначала нам нужно найти такое число, которое делится на каждый из знаменателей.
Учащиеся называют свои варианты чисел.
Таких чисел очень много: 36, 72, 108 и так далее.
Затем приводим к этому числу знаменатели обеих дробей.
То есть дроби можно привести к одинаковому знаменателю 36, 72, 108, 144 и так далее. Удобнее всего выбирать наименьший из возможных общих знаменателей, так как объем вычислений в этом случае будет минимальным.
Удобнее всего выбирать наименьший из возможных общих знаменателей, так как объем вычислений в этом случае будет минимальным.
Например,
11/12=33/36. Чтобы привести 11/12 к знаменателю 36, умножим числитель и знаменатель на 3.
Кстати, число, на которое мы умножаем числитель и знаменатель, называется «дополнительным множителем».
11/12=132/144. Чтобы привести 11/12 к знаменателю 144, умножим числитель и знаменатель на 12. А это немного сложнее, чем умножать на 3.
17/18=34/36. Чтобы привести 17/18 к знаменателю 36, умножим числитель и знаменатель на 2.
17/18=136/144. Чтобы привести 17/18 к знаменателю 144, умножим числитель и знаменатель на 8. Задумались? Поэтому не усложняйте сами себе задачу. Выбирайте наименьший общий знаменатель.
Ученики делают вывод о рациональности приведения дробей к наименьшему общему знаменателю.
Для чисел 12 и 18 число 36 будет наименьшим общим кратным.
IV.Закрепление и практическое применение знаний
В математике существует много способов нахождения общего кратного чисел, а значит общего знаменателя для дробей.
Поэтому, если перед вами стоит задача приведения дробей к общему знаменателю, не торопитесь. Правильно выбранный способ может сократить ваше решение.
Приведем 7/12 и 5/48 к общему знаменателю. Вначале внимательно посмотрите на знаменатели дробей. Возможно, один из них делится на другой.
Ученики делают вывод, то знаменатель 48 делится на 12.
В этом случае дробь с большим знаменателем вообще не надо ни на что умножать. 48 и будет общим знаменателем обеих дробей. А число, полученное в результате деления 48 на 12, будет дополнительным множителем для дроби с меньшим знаменателем.
5/48=5/48
7/12=28/48
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он только в случае, когда один знаменатель делится на другой.
Существует способ, который работает для любых дробей. Суть способа заключается в нахождении наименьшего общего кратного знаменателей. Этот способ используется чаще всего.
Приведем к общему знаменателю дроби 7/410 и 5/861.
Для начала найдём НОК чисел 410 и 861.
Разложим эти числа на простые множители. На первый взгляд это может показаться сложным, но даже при минимальной тренировке вы научитесь быстро раскладывать на простые множители. Главное — помнить признаки делимости и иметь под рукой таблицу простых чисел.
Теперь записываем все множители одного из чисел, например числа 861. Потом добавляем к ним недостающие множители из разложения другого числа. В этом примере в разложении числа 410 три множителя: 2, 5 и 41. Множитель 41 уже есть в записи, а множителей 2 и 5 нет. Эти недостающие множители мы и добавим к выписанным множителям числа 861.
Наименьшее общее кратное чисел 410 и 861 равно 8610.
Теперь найдем дополнительный множитель для дроби со знаменателем 410. Для этого 8610 делим на 410. Получим 21.
Теперь найдем дополнительный множитель для дроби со знаменателем 861. Для этого 8610 делим на 861. Получим 10.
Последний этап — умножение дробей на дополнительные множители.
Если вам сложно раскладывать числа на множители, находить наименьший общий знаменатель, то следующий способ для вас.
Приведём к общему знаменателю 3/10 и 5/6.
Для этого умножаем первую дробь на знаменатель второй дроби.
3/10=18/60
А вторую — на знаменатель первой.
5/6=50/60
В результате знаменатели обеих дробей стали равными произведению исходных знаменателей.
Этот способ простой для понимания. Но приготовьтесь много считать, если используете этот способ для дробей с большими числами в числителе и знаменателе.
Учитель вместе с учениками проговаривают все возможные способы приведения, все достоинства и недостатки.
№ 275, 278, 283.
V. Подведение итогов урока. Рефлексия
Повторим главное:
Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.
Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
VI. Домашнее задание
§2, п. 10, № 299, 300.
GCF от 12 до 33
LearnPracticeDownload
GCF от 12 до 33 — это наибольшее возможное число, на которое 12 и 33 делятся точно без остатка. Множители 12 и 33 равны 1, 2, 3, 4, 6, 12 и 1, 3, 11, 33 соответственно. Существует 3 наиболее часто используемых метода нахождения НОК 12 и 33 — разложение на простые множители, алгоритм Евклида и длинное деление.
| 1. | GCF 12 и 33 |
| 2. | Список методов |
| 3. | Решенные примеры |
| 4. | Часто задаваемые вопросы |
Что такое GCF 12 и 33?
Ответ: НГК 12 и 33 равно 3.
Объяснение:
НГК двух ненулевых целых чисел, x(12) и y(33), есть наибольшее натуральное число m(3) который делит и x (12), и y (33) без остатка.
Методы определения GCF 12 и 33
Давайте рассмотрим различные методы нахождения GCF чисел 12 и 33.
GCF 12 и 33 с помощью простой факторизации
Простая факторизация 12 и 33 равна (2 × 2 × 3) и (3 × 11) соответственно. Как видно, числа 12 и 33 имеют только один общий простой делитель, т. е. 3. Следовательно, НГК чисел 12 и 33 равен 3,9.0003
GCF 12 и 33 по алгоритму Евклида
Согласно алгоритму Евклида, GCF(X, Y) = GCF(Y, X mod Y)
где X > Y, а mod — оператор по модулю.
Здесь X = 33 и Y = 12
Таким образом, значение GCF 12 и 33 равно 3,
GCF 12 и 33 путем длинного деления
GCF 12 и 33 — это делитель, который мы получаем, когда остаток становится равным 0 после повторного длинного деления.
Соответствующий делитель (3) — это НОД 12 и 33.
☛ Также проверьте:
GCF 12 и 33 Примеры
перейти к слайдуперейти к слайдуперейти к слайду
Готовы посмотреть на мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о GCF 12 и 33
Что такое GCF 12 и 33?
GCF 12 и 33 равен 3 . Чтобы вычислить наибольший общий множитель чисел 12 и 33, нам нужно разложить каждое число на множители (множители 12 = 1, 2, 3, 4, 6, 12; множители 33 = 1, 3, 11, 33) и выбрать наибольший множитель, который точно делит и 12, и 33, т. е. 3,
Чтобы вычислить наибольший общий множитель чисел 12 и 33, нам нужно разложить каждое число на множители (множители 12 = 1, 2, 3, 4, 6, 12; множители 33 = 1, 3, 11, 33) и выбрать наибольший множитель, который точно делит и 12, и 33, т. е. 3,
Какая связь между LCM и GCF 12, 33?
Следующее уравнение можно использовать для выражения отношения между НОК (наименьшим общим кратным) и НОД 12 и 33, т. е. НОД × НОК = 12 × 33.
Как найти НОД 12 и 33 с помощью простой факторизации?
Чтобы найти НОК чисел 12 и 33, мы найдем разложение данных чисел на простые множители, т. е. 12 = 2 × 2 × 3; 33 = 3 × 11,
⇒ Так как 3 — единственный общий простой делитель чисел 12 и 33. Следовательно, НОД (12, 33) = 3,
☛ Простое число
Как найти GCF 12 и 33 методом длинного деления?
Чтобы найти НОД 12, 33 с помощью метода деления в длину, 33 нужно разделить на 12. Соответствующий делитель (3), когда остаток равен 0, принимается за НОД.
Если GCF 33 и 12 равен 3, Найдите его LCM.

GCF(33, 12) × LCM(33, 12) = 33 × 12
Так как GCF 33 и 12 = 3
⇒ 3 × НОК(33, 12) = 396
Следовательно, НОК = 132
.
☛ Калькулятор GCF
Каковы методы определения GCF 12 и 33?
Существует три широко используемых метода нахождения GCF 12 и 33 .
Скачать БЕСПЛАТНЫЕ учебные материалы
GCF и LCM
Наименьшее общее кратное — 33
| Числа | ЛКМ |
|---|---|
| 33 и 1 | 33 |
| 33 и 2 | 66 |
| 33 и 3 | 33 |
| 33 и 4 | 132 |
| 33 и 5 | 165 |
| 33 и 6 | 66 |
| 33 и 7 | 231 |
| 33 и 8 | 264 |
| 33 и 9 | 99 |
| 33 и 10 | 330 |
| 33 и 11 | 33 |
| 33 и 12 | 132 |
| 33 и 13 | 429 |
| 33 и 14 | 462 |
| 33 и 15 | 165 |
| 33 и 16 | 528 |
| 33 и 17 | 561 |
| 33 и 18 | 198 |
| 33 и 19 | 627 |
| 33 и 20 | 660 |
| 33 и 21 | 231 |
| 33 и 22 | 66 |
| 33 и 23 | 759 |
| 33 и 24 | 264 |
| 33 и 25 | 825 |
| 33 и 26 | 858 |
| 33 и 27 | 297 |
| 33 и 28 | 924 |
| 33 и 29 | 957 |
| 33 и 30 | 330 |
| 33 и 31 | 1 023 |
| 33 и 32 | 1 056 |
| 33 и 33 | 33 |
| 33 и 34 | 1 122 |
| 33 и 35 | 1 155 |
| 33 и 36 | 396 |
| 33 и 37 | 1 221 |
| 33 и 38 | 1 254 |
| 33 и 39 | 429 |
| 33 и 40 | 1 320 |
| 33 и 41 | 1 353 |
| 33 и 42 | 462 |
| 33 и 43 | 1 419 |
| 33 и 44 | 132 |
| 33 и 45 | 495 |
| 33 и 46 | 1 518 |
| 33 и 47 | 1 551 |
| 33 и 48 | 528 |
| 33 и 49 | 1 617 |
| 33 и 50 | 1 650 |
| 33 и 51 | 561 |
| 33 и 52 | 1 716 |
| 33 и 53 | 1 749 |
| 33 и 54 | 594 |
| 33 и 55 | 165 |
| 33 и 56 | 1 848 |
| 33 и 57 | 627 |
| 33 и 58 | 1 914 |
| 33 и 59 | 1 947 |
| 33 и 60 | 660 |
| 33 и 61 | 2 013 |
| 33 и 62 | 2 046 |
| 33 и 63 | 693 |
| 33 и 64 | 2 112 |
| 33 и 65 | 2 145 |
| 33 и 66 | 66 |
| 33 и 67 | 2 211 |
| 33 и 68 | 2 244 |
| 33 и 69 | 759 |
| 33 и 70 | 2 310 |
| 33 и 71 | 2 343 |
| 33 и 72 | 792 |
| 33 и 73 | 2 409 |
| 33 и 74 | 2 442 |
| 33 и 75 | 825 |
| Номера | ЛКМ |
|---|---|
| 33 и 76 | 2 508 |
| 33 и 77 | 231 |
| 33 и 78 | 858 |
| 33 и 79 | 2 607 |
| 33 и 80 | 2 640 |
| 33 и 81 | 891 |
| 33 и 82 | 2 706 |
| 33 и 83 | 2 739 |
| 33 и 84 | 924 |
| 33 и 85 | 2 805 |
| 33 и 86 | 2 838 |
| 33 и 87 | 957 |
| 33 и 88 | 264 |
| 33 и 89 | 2 937 |
| 33 и 90 | 990 |
| 33 и 91 | 3 003 |
| 33 и 92 | 3 036 |
| 33 и 93 | 1 023 |
| 33 и 94 | 3 102 |
| 33 и 95 | 3 135 |
| 33 и 96 | 1 056 |
| 33 и 97 | 3 201 |
| 33 и 98 | 3 234 |
| 33 и 99 | 99 |
| 33 и 100 | 3 300 |
| 33 и 101 | 3 333 |
| 33 и 102 | 1 122 |
| 33 и 103 | 3 399 |
| 33 и 104 | 3 432 |
| 33 и 105 | 1 155 |
| 33 и 106 | 3 498 |
| 33 и 107 | 3 531 |
| 33 и 108 | 1 188 |
| 33 и 109 | 3 597 |
| 33 и 110 | 330 |
| 33 и 111 | 1 221 |
| 33 и 112 | 3 696 |
| 33 и 113 | 3 729 |
| 33 и 114 | 1 254 |
| 33 и 115 | 3 795 |
| 33 и 116 | 3 828 |
| 33 и 117 | 1 287 |
| 33 и 118 | 3 894 |
| 33 и 119 | 3 927 |
| 33 и 120 | 1 320 |
| 33 и 121 | 363 |
| 33 и 122 | 4 026 |
| 33 и 123 | 1 353 |
| 33 и 124 | 4 092 |
| 33 и 125 | 4 125 |
| 33 и 126 | 1 386 |
| 33 и 127 | 4 191 |
| 33 и 128 | 4 224 |
| 33 и 129 | 1 419 |
| 33 и 130 | 4 290 |
| 33 и 131 | 4 323 |
| 33 и 132 | 132 |
| 33 и 133 | 4 389 |
| 33 и 134 | 4 422 |
| 33 и 135 | 1 485 |
| 33 и 136 | 4 488 |
| 33 и 137 | 4 521 |
| 33 и 138 | 1 518 |
| 33 и 139 | 4 587 |
| 33 и 140 | 4 620 |
| 33 и 141 | 1 551 |
| 33 и 142 | 4 686 |
| 33 и 143 | 429 |
| 33 и 144 | 1 584 |
| 33 и 145 | 4 785 |
| 33 и 146 | 4 818 |
| 33 и 147 | 1 617 |
| 33 и 148 | 4 884 |
| 33 и 149 | 4 917 |
| 33 и 150 | 1 650 |
| Номера | ЛКМ |
|---|---|
| 33 и 151 | 4 983 |
| 33 и 152 | 5 016 |
| 33 и 153 | 1 683 |
| 33 и 154 | 462 |
| 33 и 155 | 5 115 |
| 33 и 156 | 1 716 |
| 33 и 157 | 5 181 |
| 33 и 158 | 5 214 |
| 33 и 159 | 1 749 |
| 33 и 160 | 5 280 |
| 33 и 161 | 5 313 |
| 33 и 162 | 1 782 |
| 33 и 163 | 5 379 |
| 33 и 164 | 5 412 |
| 33 и 165 | 165 |
| 33 и 166 | 5 478 |
| 33 и 167 | 5 511 |
| 33 и 168 | 1 848 |
| 33 и 169 | 5 577 |
| 33 и 170 | 5 610 |
| 33 и 171 | 1 881 |
| 33 и 172 | 5 676 |
| 33 и 173 | 5 709 |
| 33 и 174 | 1 914 |
| 33 и 175 | 5 775 |
| 33 и 176 | 528 |
| 33 и 177 | 1 947 |
| 33 и 178 | 5 874 |
| 33 и 179 | 5 907 |
| 33 и 180 | 1 980 |
| 33 и 181 | 5 973 |
| 33 и 182 | 6 006 |
| 33 и 183 | 2 013 |
| 33 и 184 | 6 072 |
| 33 и 185 | 6 105 |
| 33 и 186 | 2 046 |
| 33 и 187 | 561 |
| 33 и 188 | 6 204 |
| 33 и 189 | 2 079 |
| 33 и 190 | 6 270 |
| 33 и 191 | 6 303 |
| 33 и 192 | 2 112 |
| 33 и 193 | 6 369 |
| 33 и 194 | 6 402 |
| 33 и 195 | 2 145 |
| 33 и 196 | 6 468 |
| 33 и 197 | 6 501 |
| 33 и 198 | 198 |
| 33 и 199 | 6 567 |
| 33 и 200 | 6 600 |
| 33 и 201 | 2 211 |
| 33 и 202 | 6 666 |
| 33 и 203 | 6 699 |
| 33 и 204 | 2 244 |
| 33 и 205 | 6 765 |
| 33 и 206 | 6 798 |
| 33 и 207 | 2 277 |
| 33 и 208 | 6 864 |
| 33 и 209 | 627 |
| 33 и 210 | 2 310 |
| 33 и 211 | 6 963 |
| 33 и 212 | 6 996 |
| 33 и 213 | 2 343 |
| 33 и 214 | 7 062 |
| 33 и 215 | 7 095 |
| 33 и 216 | 2 376 |
| 33 и 217 | 7 161 |
| 33 и 218 | 7 194 |
| 33 и 219 | 2 409 |
| 33 и 220 | 660 |
| 33 и 221 | 7 293 |
| 33 и 222 | 2 442 |
| 33 и 223 | 7 359 |
| 33 и 224 | 7 392 |
| 33 и 225 | 2 475 |
| Числа | ЛКМ |
|---|---|
| 33 и 226 | 7 458 |
| 33 и 227 | 7 491 |
| 33 и 228 | 2 508 |
| 33 и 229 | 7 557 |
| 33 и 230 | 7 590 |
| 33 и 231 | 231 |
| 33 и 232 | 7 656 |
| 33 и 233 | 7 689 |
| 33 и 234 | 2 574 |
| 33 и 235 | 7 755 |
| 33 и 236 | 7 788 |
| 33 и 237 | 2 607 |
| 33 и 238 | 7 854 |
| 33 и 239 | 7 887 |
| 33 и 240 | 2 640 |
| 33 и 241 | 7 953 |
| 33 и 242 | 726 |
| 33 и 243 | 2 673 |
| 33 и 244 | 8 052 |
| 33 и 245 | 8 085 |
| 33 и 246 | 2 706 |
| 33 и 247 | 8 151 |
| 33 и 248 | 8 184 |
| 33 и 249 | 2 739 |
| 33 и 250 | 8 250 |
| 33 и 251 | 8 283 |
| 33 и 252 | 2 772 |
| 33 и 253 | 759 |
| 33 и 254 | 8 382 |
| 33 и 255 | 2 805 |
| 33 и 256 | 8 448 |
| 33 и 257 | 8 481 |
| 33 и 258 | 2 838 |
| 33 и 259 | 8 547 |
| 33 и 260 | 8 580 |
| 33 и 261 | 2 871 |
| 33 и 262 | 8 646 |
| 33 и 263 | 8 679 |
| 33 и 264 | 264 |
| 33 и 265 | 8 745 |
| 33 и 266 | 8 778 |
| 33 и 267 | 2 937 |
| 33 и 268 | 8 844 |
| 33 и 269 | 8 877 |
| 33 и 270 | 2 970 |
| 33 и 271 | 8 943 |
| 33 и 272 | 8 976 |
| 33 и 273 | 3 003 |
| 33 и 274 | 9 042 |
| 33 и 275 | 825 |
| 33 и 276 | 3 036 |
| 33 и 277 | 9 141 |
| 33 и 278 | 9 174 |
| 33 и 279 | 3 069 |
| 33 и 280 | 9 240 |
| 33 и 281 | 9 273 |
| 33 и 282 | 3 102 |
| 33 и 283 | 9 339 |
| 33 и 284 | 9 372 |
| 33 и 285 | 3 135 |
| 33 и 286 | 858 |
| 33 и 287 | 9 471 |
| 33 и 288 | 3 168 |
| 33 и 289 | 9 537 |
| 33 и 290 | 9 570 |
| 33 и 291 | 3 201 |
| 33 и 292 | 9 636 |
| 33 и 293 | 9 669 |
| 33 и 294 | 3 234 |
| 33 и 295 | 9 735 |
| 33 и 296 | 9 768 |
| 33 и 297 | 297 |
| 33 и 298 | 9 834 |
| 33 и 299 | 9 867 |
| 33 и 300 | 3 300 |
Наименьший общий кратный — JavaTpoint
следующий → ← предыдущая В арифметике, Наименьшее общее кратное (НОК) из двух или более чисел — это наименьшее положительное число, которое можно разделить на оба числа, не оставляя остатка. Используется, когда мы складываем, вычитаем или сравниваем дроби. Пока мы выполняем сложение или вычитание дробей, мы находим НОК знаменателей, а затем решим дроби. НОК знаменателей известен как Наименьший общий знаменатель (LCD). Свойства LCMКак найти LCMЕсть три способа найти LCM: Использование табличного метода Это простой метод, который работает для любого количества номеров. Давайте разберемся на примерах. Пример 1: найти НОК 8 и 10. Решение: Следовательно, НОК 8 и 10 равен 40. Пример 2: Найдите НОК 60 и 282. Решение: Следовательно, НОК 60 и 282 равно 2820. Пример 3: Что такое LCM 20, 28 и 35. Решение: Следовательно, НОК 20, 28 и 35 равен 140. Пример 4. Найдите НОК 120, 144, 160 и 180. Решение: Следовательно, НОК 120, 144, 160 и 180 равен 1440. Пример 5. Найдите НОК 64, 72, 96 и 108. Решение: Следовательно, НОК 64, 72, 96 и 108 равен 1728. Использование метода наибольшего общего делителя (НОД)Мы также можем рассчитать LCM, используя НОД. Формула НОК с использованием НОД: . Наибольший общий делитель: Это наибольшее число, которое полностью делит два или более чисел. Это сокращенно GCD . Он также известен как Наибольший общий делитель (GCF) или Наибольший общий делитель (HCF). Как найти НОДСледуйте инструкциям ниже, чтобы найти НОД: Давайте разберемся на примерах. Пример 6: Найдите НОК 8 и 10. Решение: Согласно формуле, которую мы узнали выше: Сначала находим НОД чисел 8 и 10. Факторы 8: 1, 2, 4, 8 Факторы 10: 1, 2, 5, 10 Общие множители: 1, 2 Наибольший общий делитель: 2 Следовательно, НОК 8 и 10 равен 40. Пример 7: Найдите НОК 11 и 42. Решение: Согласно формуле, которую мы узнали выше: Сначала находим НОД чисел 11 и 42. Факторы 11: 1, 11 Коэффициенты 42: 1, 2, 3, 6, 7, 14, 21, 42 Общие факторы: 1 Наибольший общий делитель: 1 НОК(11,42)=462 Следовательно, НОК 11 и 42 равно 462. Пример 8: Найдите НОК 64 и 112. Решение: Согласно формуле, которую мы узнали выше: Сначала находим НОД 64 и 112. Коэффициенты 64: 1, 2, 4, 8, 16, 32, 64 Коэффициенты 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, 112 Общие множители: 1, 2, 4, 7, 8, 16 Наибольший общий делитель: 16 Следовательно, НОК 64 и 112 равен 448. Использование метода простой факторизацииВыполните шаги, чтобы найти LCM, используя метод простой факторизации. Примечание. Когда мы записываем множители в форме, это называется экспоненциальной формой, а процесс известен как факторизация с использованием показателей. Давайте разберемся на примерах. Пример 9: найти LCM 17 и 28. Решение: Простые множители 17: 17 В экспоненциальной форме: Простые множители 17: 17 1 Следовательно, НОК 17 и 28 равен 476. Пример 10: Что такое LCM для 35 и 78. Решение: Простые множители 35: 5×7 В экспоненциальной форме: Простые множители 35: 5 1 × 7 1 Следовательно, НОК 35 и 78 равен 2730. Пример 11: Найдите LCM 223 и 432. Решение: Простые множители 223: 223 В экспоненциальной форме: Простые множители 223: 223 1 Следовательно, НОК 223 и 432 равен 96336. Пример 12. Найдите НОК 12, 23 и 29. Решение: Простые множители 12: 2 × 2 × 3 В экспоненциальной форме: Простой множитель 12: 2 2 ×3 1 Следовательно, НОК 12, 23 и 29 равен 8004. Использование нескольких чиселЭто очень длительный метод, поэтому он обычно не используется. Следуйте приведенным ниже инструкциям, чтобы найти LCM, используя кратные числа. Давайте разберемся на примерах. Пример 13: Что такое LCM 12, 9 и 33. Решение: Кратность 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135, 144, 153, 162, 171, 180, 189, 198 , 207, 216, 225, 234, 243, 252, 261, 270, 279, 288, 297, 306, 315, 324, 333, 342, 351, 360, 369, 378, 387, 396 , 405, 414 Кратность 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180, 192, 204, 216, 228, 240, 252, 264 , 276, 288, 300, 312, 324, 336, 348, 360, 372, 384, 396 , 408, 420 Кратность 33: 33, 66, 99, 132, 165, 198, 231, 264, 297, 330, 363, 396 , 429, 462 Следовательно, LCM 9, 12 и 33 равно 396. Пример 14: Что такое LCM 15 и 16. Решение: Кратность 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240 , 255, 270 Кратность 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240 , 256, 272 НКМ (15,16)=240 Следовательно, НОК 15 и 16 равен 240. LCM фракцийМы также можем найти НОК дробей, используя следующую формулу: Пример 15: Что такое LCM для и . Решение: LCM числителей: ХКФ знаменателей: Коэффициенты 2: 1, 2 ХКФ: 2 Подставляя значения в формулу, получаем: Следовательно, LCM и . Пример 16: Что такое LCM для и . Решение: LCM числителей: ХКФ знаменателей: Коэффициенты 2: 1, 2 Факторы 3: 1, 3 Коэффициенты 4: 1, 2, 4 Коэффициенты 5: 1, 5 ХФУ: 1 Подставляя значения в формулу, получаем: Следовательно, НОК и равен 70. Пример 17: Что такое LCM для ,3 и . Решение: LCM числителей: ХКФ знаменателей: Коэффициенты 9: 1, 3, 9 Коэффициент 1:1 Коэффициенты 5: 1, 5 ХФУ: 1 Подставляя значения в формулу, получаем: Следовательно, НОК ,3 и равен 168. Следующая темаPerfect Squares ← предыдущая следующий → |
3.5: Наименьшее общее кратное
Цели обучения
Кратные
Когда целое число умножается на другие целые числа, за исключением нуля, полученные произведения называются кратными данного целого числа. Обратите внимание, что любое целое число кратно самому себе.
Обратите внимание, что любое целое число кратно самому себе.
Набор образцов A
| Кратность 2 | Кратно 3 | Несколько 8 | Кратность 10 |
|---|---|---|---|
| \(2\1 = 2\) | \(3 умножить на 1 = 3\) | \(8 \умножить на 1 = 8\) | \(10 \х1 = 10\) |
| \(2 \умножить на 2 = 4\) | \(3 умножить на 2 = 6\) | \(8 \умножить на 2 = 16\) | \(10 х 2 = 20) |
| \(2\х3 = 6\) | \(3 умножить на 3 = 9\) | \(8 \х3 = 24\) | \(10 \х3 = 30\) |
| \(2\4 = 8\) | \(3\4 = 12\) | \(8 \х4 = 32\) | \(10\4 = 40\) |
| \(2 \х5 = 10\) | \(3 умножить на 5 = 15\) | \(8 \умножить на 5 = 40\) | \(10 \х5 = 50\) |
. .. .. | … | … | … |
Тренировочный набор A
Найдите первые пять кратных следующих чисел.
4
Тренировочный набор A
5
Тренировочный набор A
6
Тренировочный набор A
7
Тренировочный набор A
9
Общие кратные
Бывают случаи, когда нам дают два или более целых числа, и нам нужно будет знать, есть ли какие-либо кратные, общие для каждого из них. Если они есть, нам нужно знать, что они из себя представляют. Например, некоторые из кратных, общих для 2 и 3, это 6, 12 и 18.
Если они есть, нам нужно знать, что они из себя представляют. Например, некоторые из кратных, общих для 2 и 3, это 6, 12 и 18.
Образец набора B
Мы можем визуализировать общие кратные, используя числовую прямую.
Обратите внимание, что общие кратные можно разделить на и целых чисел.
Тренировочный набор B
Найдите первые пять общих кратных следующих чисел.
2 и 4
Тренировочный набор B
3 и 4
Тренировочный набор B
2 и 5
Тренировочный набор B
3 и 6
Тренировочный набор B
4 и 5
Наименьшее общее кратное (НОК)
Обратите внимание, что в нашей визуализации общих кратных в числовой строке (выше) первое общее кратное также является наименьшим, или наименьшее общее кратное , сокращенно LCM .
Определение: наименьшее общее кратное
наименьшее общее кратное ( LCM) двух или более целых чисел — это наименьшее целое число, на которое каждое из заданных чисел делится без остатка.
Наименьшее общее кратное будет чрезвычайно полезно при работе с дробями.
Нахождение наименьшего общего кратного
Нахождение НОК
Чтобы найти НОК двух или более чисел:
Существуют некоторые существенные различия между использованием процессов получения GCF и LCM, на которые следует обратить внимание:
Разница между процессами получения GCF и LCM
Таким образом, 7260 — это наименьшее число, на которое без остатка делятся 33, 110 и 484.
Тренировочный набор C
Найдите LCM следующих чисел.
20 и 54
Тренировочный набор C
14 и 28
Тренировочный набор C
6 и 63
Тренировочный набор C
28, 40 и 98
Тренировочный набор C
16, 27, 125 и 363
Упражнения
Для следующих задач найдите наименьшее общее кратное чисел.
Упражнение \(\PageIndex{1}\)
8 и 12
Упражнение \(\PageIndex{2}\)
6 и 15
Упражнение \(\PageIndex{3}\)
8 и 10
Упражнение \(\PageIndex{4}\)
10 и 14
Упражнение \(\PageIndex{5}\)
4 и 6
Упражнение \(\PageIndex{6}\)
6 и 12
Упражнение \(\PageIndex{7}\)
9 и 18
Упражнение \(\PageIndex{8}\)
6 и 8
Упражнение \(\PageIndex{9}\)
5 и 6
Упражнение \(\PageIndex{10}\)
7 и 8
Упражнение \(\PageIndex{11}\)
3 и 4
Упражнение \(\PageIndex{12}\)
2 и 9
Упражнение \(\PageIndex{13}\)
7 и 9
Упражнение \(\PageIndex{14}\)
28 и 36
Упражнение \(\PageIndex{15}\)
24 и 36
Упражнение \(\PageIndex{16}\)
28 и 42
Упражнение \(\PageIndex{17}\)
240 и 360
Упражнение \(\PageIndex{18}\)
162 и 270
Упражнение \(\PageIndex{19}\)
20 и 24
Упражнение \(\PageIndex{20}\)
25 и 30
Упражнение \(\PageIndex{21}\)
24 и 54
Упражнение \(\PageIndex{22}\)
16 и 24
Упражнение \(\PageIndex{23}\)
36 и 48
Упражнение \(\PageIndex{24}\)
24 и 40
Упражнение \(\PageIndex{25}\)
15 и 21
Упражнение \(\PageIndex{26}\)
50 и 140
Упражнение \(\PageIndex{27}\)
7, 11 и 33
Упражнение \(\PageIndex{28}\)
8, 10 и 15
Упражнение \(\PageIndex{29}\)
18, 21 и 42
Упражнение \(\PageIndex{30}\)
4, 5 и 21
Упражнение \(\PageIndex{31}\)
45, 63 и 98
Упражнение \(\PageIndex{32}\)
15, 25 и 40
Упражнение \(\PageIndex{33}\)
12, 16 и 20
Упражнение \(\PageIndex{34}\)
84 и 96
Упражнение \(\PageIndex{35}\)
48 и 54
Упражнение \(\PageIndex{36}\)
12, 16 и 24
Упражнение \(\PageIndex{37}\)
12, 16, 24 и 36
Упражнение \(\PageIndex{38}\)
6, 9, 12 и 18
Упражнение \(\PageIndex{39}\)
8, 14, 28 и 32
Упражнение \(\PageIndex{40}\)
18, 80, 108 и 490
Упражнение \(\PageIndex{41}\)
22, 27, 130 и 225
Упражнение \(\PageIndex{42}\)
38, 92, 115 и 189
Упражнение \(\PageIndex{43}\)
8 и 8
Упражнение \(\PageIndex{44}\)
12, 12 и 12
Упражнение \(\PageIndex{45}\)
3, 9, 12 и 3
Упражнения для обзора
Упражнение \(\PageIndex{46}\)
Округлите 434 892 до ближайших десяти тысяч.
Упражнение \(\PageIndex{47}\)
Насколько больше 14 061, чем 7 5097\). Не найти значение.
Упражнение \(\PageIndex{50}\)
Найдите наибольший общий делитель чисел 48 и 72.
Эта страница под названием 3.5: Наименее распространенный множитель распространяется по лицензии CC BY, ее автор, ремикс и/или куратор — Денни Бурзински и Уэйд Эллис-младший (OpenStax CNX).
Сержант из Нью-Джерси получил 33 месяца тюрьмы за помощь коррумпированным полицейским воровать у жителей
Бывший сержант полиции Патерсона из группы полицейских, которые преследовали и воровали у жителей, был приговорен к 33 месяцам в федеральной тюрьме в понедельник.
Окружной судья США Кэтрин С. Хейден вынесла приговор Майклу Чеффу в федеральном суде Ньюарка после судебного разбирательства и осуждения в мае по обвинению в сговоре с целью лишения человека гражданских прав и фальсификации полицейского отчета.
«Этот подсудимый охотился на общественность, которую он поклялся защищать, и нарушал права граждан в процессе, чтобы набить свои карманы и карманы офицеров, которых он должен был контролировать», — заявил прокурор США Филип Р. Селлинджер в заявление.
Чефф настаивает на своей невиновности и планирует снова обжаловать приговор после того, как ему отказали в новом судебном процессе в июле.
«Нельзя раскаиваться в том, чего вы не делали», — сказал его адвокат Джон Линч.
Дело правительства против Чеффа основывалось на показаниях подчиненных ему офицеров, которые безнаказанно совершали преступления с 2016 по 2018 год. Группа называла себя «отрядом грабежей», потому что они патрулировали улицы Патерсона в поисках людей, у которых можно украсть.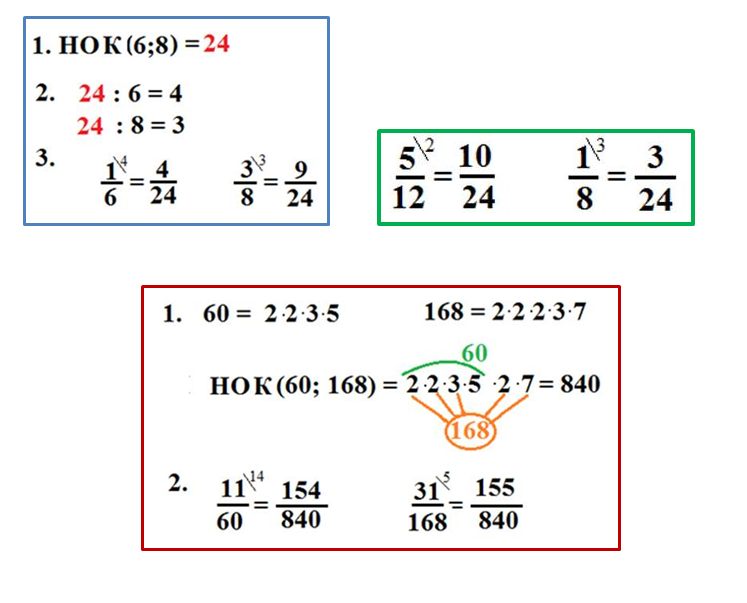
Пятеро бывших офицеров — Мэтью Торрес, Джонатан Бустиос, Даниэль Пент, Фрэнк Толедо и Юди Рамос — все признали себя виновными в своих ролях в отряде и дали показания против своего бывшего начальника в обмен на мягкий приговор. Все они были приговорены на прошлой неделе и получили меньшие сроки, чем Чефф.
Офицеры сказали, что Чефф одобрял их ложные сообщения, помогал регистрировать сфабрикованные доказательства, принимал откаты и следил за тем, чтобы жалобы на них никуда не делись.
Прокуроры обратили внимание на инцидент 2017 года, когда офицеры заявили, что видели, как Чефф воровал из дома мужчины во время незаконного обыска. Несколько офицеров показали, что Чефф помог принудить мужчину разрешить ему обыскать его квартиру с намерением украсть деньги. Оказавшись внутри, офицеры сказали, что Чефф сунул деньги в карман из сейфа.
Потерпевший, Хосе Санчес-Асеведо, показал во время суда, что в сейфе было около 2700 долларов. По его словам, когда офицеры ушли, никого не было.
На протяжении всего дела прокуроры описывали, как роль Чеффа позволяла офицерам совершать преступления и жестоко обращаться с жертвами без особого надзора.
«(Офицеры) попирали гражданские права людей, живущих в Патерсоне, проезжая через Патерсоне», — заявил на суде помощник прокурора США Томас Кирни. «…(Чефф) был их начальником. Он был их командиром.
«Он был общим знаменателем», — добавил он.
В понедельник помощник прокурора США Джихи Джиллиан Су повторила, что влияние «группы грабежей» имело реальные последствия для жертв и отношений правоохранительных органов с обществом, которые еще больше ухудшились из-за неправомерных действий офицеров.
Лиза Чоудхури, исполнительный директор Paterson Healing Collective, программы по борьбе с насилием, сказала, что надеется, что департамент создал систему сдержек и противовесов, чтобы этого больше не происходило.
«Члены сообщества доверяют сотрудникам правоохранительных органов соблюдение морально-этических норм. Они находятся на переднем крае системы уголовного правосудия», — сказала она. «Когда они отражают коррупцию, злоупотребления и сами нарушают закон, как сообщество может продолжать доверять системе, которая позволила этому произойти?»
Они находятся на переднем крае системы уголовного правосудия», — сказала она. «Когда они отражают коррупцию, злоупотребления и сами нарушают закон, как сообщество может продолжать доверять системе, которая позволила этому произойти?»
Джерри Специале-младший, директор по общественной безопасности города, сказал, что у департамента есть «многочисленные меры безопасности, от технологий до наших внутренних расследований и проверок персонала, и он будет продолжать охранять наш департамент».
Вынося приговор Чеффу, Хейден признал, что офицер-ветеран не получил большой прибыли от этой схемы и не совершал самых вопиющих преступлений, но сказал, как их начальник, «он позволил этому случиться. Он помог этому случиться».
Судья сказал, что обвинительный вердикт «возлагает очень сильную и подлинную вину на мистера Чеффа».
«В итоге он был там ради них, и они пошли к нему», — сказал Хейден. «…Вместо того, чтобы сделать их хорошими полицейскими, он сделал их плохими полицейскими».
Линч выступил за меньший срок для своего клиента, заявив, что диапазон сроков от 33 до 41 месяца был чрезмерным по сравнению с наказаниями, которые получили другие. Бустиос, Рамос и Толедо были приговорены к двум годам заключения, Пент — к 18 месяцам, а Торрес — к трем годам условно.
Более 50 человек, в том числе нынешние и бывшие полицейские Патерсона, написали письма в поддержку Чеффа, назвав его преданным семьянином и «человеком, вокруг которого сплачиваются люди». Его семья наблюдала, как он узнал о своей судьбе.
Линч сказал, что он и Чефф не согласны с вердиктом и приговором, но уважают его. Адвокат сказал, что нет графика, когда они подадут апелляцию или когда Чефф начнет отбывать наказание.
Наша журналистика нуждается в вашей поддержке. Пожалуйста, подпишитесь сегодня на NJ.com .
С Джо Атмонавэджем можно связаться по телефону [email protected]
Примечание для читателей: если вы покупаете что-то по одной из наших партнерских ссылок, мы можем заработать комиссию.
Модель вычитания дробей с примерами
Основные понятия
Мы знаем, что дроби считаются частью целого. Мы можем легко сложить две одинаковые дроби так же, как складываем целые числа.
Мы научились складывать одинаковые дроби, используя линейки дробей, числовые ряды и прямое сложение.
Когда мы сложили две одинаковые дроби напрямую, мы выполнили следующие шаги:
Например,
3/5+1/5= 3+1/5= 4/5
Вычитание дробей аналогично сложению дробей.
Различные способы вычитания, такие как фракции, —
, в то время как подразделение, а не подразделяя, а не подразделяя, а не подразделяя, а не подразделяя, а не подразделяя. Научимся вычитать дроби разными способами.
Научимся вычитать дроби разными способами.
Используя полосы дробей, мы можем представить дробь с несколькими единицами дробей
Например,
и т. д. …… дроби, а затем мы можем отнять сумму, чтобы найти разницу .
Рассмотрим пример
Дроби с одинаковыми знаменателями – это дроби с общими знаменателями. Это означает, что их знаменатели совпадают.
7/8−2/8
Чтобы вычесть одинаковые дроби с помощью полос дробей, мы сначала смотрим на общий знаменатель и делим целое на такое количество единичных дробей.
Следовательно, при нахождении разности с помощью дробных полосок мы удаляем количество заштрихованных частей, которые мы вычитали, и подсчитываем, сколько осталось.
7/8−2/8= 5/8
Пример 1:
Мистер Уолтер использует 4/5
цветного листа для изготовления поздравительных открыток. Сколько цветного листа осталось?
Решение:
Известно, что 4/5 цветного листа используется для изготовления поздравительных открыток.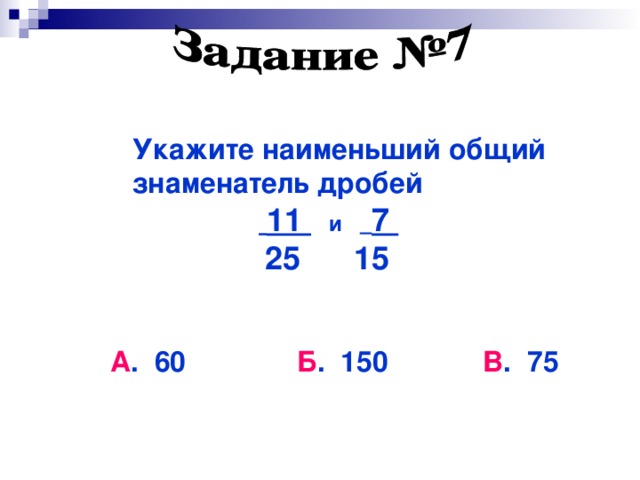
Здесь знаменатель говорит, на сколько частей разделен цветной лист, а числитель говорит, сколько частей используется.
Если представить один цветной лист с
, он был разделен на 5 равных частей.
Из этих 5 равных частей 4 части используются
Теперь из приведенной выше полоски дробей можно сказать, что у него осталась одна часть из 5 частей.
5/5−4/5= 1/5
Пример 2:
Цветник разделен на восьмые части. Если 2/8 сада используется для выращивания желтых роз. Какая доля осталась для выращивания других цветов?
Решение:
Дано, что сад разделен на восьмые части.
Это означает, что если представлен сад Он разделен на восьмые части
Из этих 8 частей 2/8 сада используется для выращивания желтых роз
То есть
Доля сада, оставленная для других цветов, равна
⸫ 8/8− 2/8= 6/8
Использование числовой прямойЧто такое числовая прямая?
Числовая линия представляет собой прямую горизонтальную линию с числами, расположенными с равными интервалами по длине.
Как представить дробь на числовой прямой?
Чтобы представить дроби на числовой прямой, выполните следующие действия:
Итак, используя числовые строки, мы можем складывать или вычитать дроби. Давайте воспользуемся числовой линией, например, 2 выше.
Пример: Цветник разделен на восьмые части. Если [2/8] сада используется для выращивания желтых роз. Какая доля осталась для выращивания других цветов?
Проведем числовую прямую, разделенную на восьмые.
8/8= 1/8+1/8+1/8+1/8+1/8+1/8+1/8+1/8
Теперь, поскольку 2/8 сада используется для выращиваем желтые розы, отделим 2/8 от 8/8
8/8= 1/8+1/8+1/8+1/8+1/8+1/8+1/8+1/ 8
1/8+1/8=2/8
Осталось 1/8+1/8+1/8+1/8+1/8+1/8= 6/8
is 8/8−2/8= 6/8
То есть
8/8−2/8 = 6/8
:Сначала нарисуйте числовую прямую и начертите 5/7
Теперь давайте посмотрим на вычитаемое 2/7, часть, которую нужно отнять от 5/7.
2/7 означает, что 2 из 7 частей, мы можем считать назад или прыгать назад от уменьшаемого 5/7.
Итак, вычитание 2/7 из 5/7 означает, что мы прыгаем назад на 2 шага.
⸫ 5/7−2/7=3/7
Пример 2:
Найти 7/9− 3/9
Решение:
Нарисуйте числовую прямую и постройте
Так как нам нужно вычесть 3/9, прыгните на 3 шага назад от 7/9 тот же знаменатель, просто вычтите числители, затем скопируйте общий знаменатель. Всегда сокращайте свой окончательный ответ до наименьшего термина.
Например,
Найдите 27.10−27.04
Решение:
Две дроби имеют одинаковые знаменатели, что означает, что мы можем легко их вычесть.
Итак, вычтите числители, затем один раз напишите знаменатель.
То есть
10−4/27= 6/27
Ответ можно упростить, используя общий делитель 3.
6/27÷3/3= 29
Рик поделился своим мешком винограда с друзьями. Решение: Учитывая, что у Рика есть мешок винограда, которым он поделился со своими друзьями Разделим мешок на 10 частей. Доля мешка винограда, который Рик дал Мелисе = 2/10 Доля мешка винограда, который Рик дал Райану = 4/10 Суммарная доля мешка винограда, отданного его друзьям = 2/10+4/10 =2+4/10=6/10 Доля мешка с виноградом, оставшаяся у Рика = 10/10−6/10= 4/10 Ответ можно упростить, используя общий делитель 2 4 /10÷2/2=2/5 ⸫ Доля мешка винограда, оставшегося у Рика = 2/5 Концептуальная карта : 13/12-8/13 = ___________ Он отдал 2/10 мешка Мелисе и 4/10 мешка Райану. Какая часть мешка с виноградом осталась у Рика?
Он отдал 2/10 мешка Мелисе и 4/10 мешка Райану. Какая часть мешка с виноградом осталась у Рика?






 2
2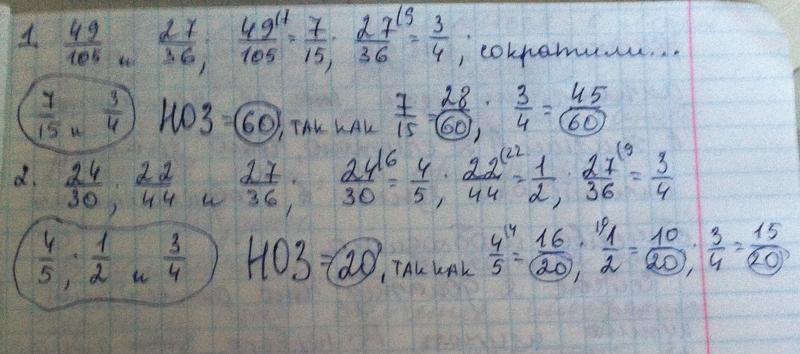 А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
 Метод заключается в следующем:
Метод заключается в следующем:
 Посмотрите на примеры:
Посмотрите на примеры: Они встречаются постоянно, и приведенные выше задачи — не предел!
Они встречаются постоянно, и приведенные выше задачи — не предел! А искомые числа, «выравнивающие» знаменатели, называются.
А искомые числа, «выравнивающие» знаменатели, называются. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
 Затем приводим к этому числу знаменатели обеих дробей.
Затем приводим к этому числу знаменатели обеих дробей. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
 Найдите значения выражений:
Найдите значения выражений: Заодно резко снижается вероятность ошибки.
Заодно резко снижается вероятность ошибки.
 Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Поэтому НОК(15; 20) = 5 · 3 · 4 = 60. Здесь мы не будем этого касаться.
Здесь мы не будем этого касаться. По-другому эту операцию никак не выполнить;
По-другому эту операцию никак не выполнить; Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.

 Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
 Для решения задания предполагаются следующие действия:
Для решения задания предполагаются следующие действия:

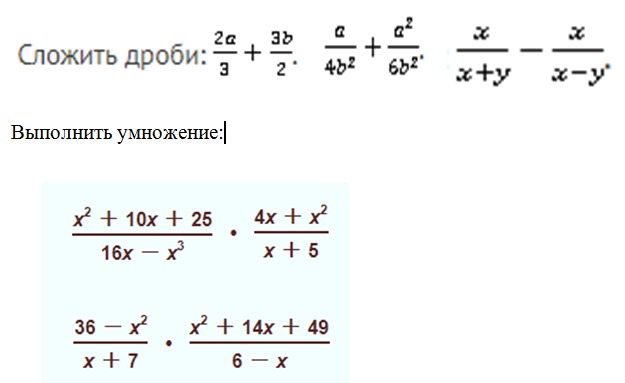 Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.
Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.
 Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.
Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.

 Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3}
.
Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3}
.
 Каждый результат деления запишите под соответствующим частным.
Каждый результат деления запишите под соответствующим частным.

 Он также известен как наименьшее общее кратное (НОК), наименьший общий знаменатель, и наименьшее общее кратное . Он обозначается как LCM (a, b) или lcm (a, b) , где a и b — два целых числа.
Он также известен как наименьшее общее кратное (НОК), наименьший общий знаменатель, и наименьшее общее кратное . Он обозначается как LCM (a, b) или lcm (a, b) , где a и b — два целых числа. Следуйте инструкциям ниже, чтобы найти LCM.
Следуйте инструкциям ниже, чтобы найти LCM.






 Для GCF мы используем только основания, которые являются общими в простых факторизациях, тогда как для LCM мы используем для каждого оснований, которые появляются в простых факторизациях.
Для GCF мы используем только основания, которые являются общими в простых факторизациях, тогда как для LCM мы используем для каждого оснований, которые появляются в простых факторизациях.