Как вычислять логарифмы: Логарифм и его свойства. Как решать логарифмы

§ 4. Приближенное вычисление иррациональных чисел . Том 1. Механика, излучение и теплота

Теперь такой вопрос: как возвести число в иррациональную степень? Например, нам хочется узнать, что такое 10^?2. Ответ в принципе очень прост. Возьмем вместо ?2 его приближение в виде конечной десятичной дроби — это рациональное число. Возводить в рациональную степень мы умеем; дело сводится к возведению в целую степень и извлечению корня. Мы получим приближенное значение числа 10^?2. Можно взять десятичную дробь подлиннее (это снова рациональное число). Тогда придется извлечь корень большей степени; ведь знаменатель рациональной дроби увеличится, но зато мы получим более точное приближение. Конечно, если взять приближенное значение ?2 в виде очень длинной дроби, то возведение в степень будет делом очень трудным. Как справиться с этой задачей?

Вычисление квадратных корней, кубичных корней и других корней невысокой степени — вполне доступный нам арифметический процесс; вычисляя, мы последовательно, один за другим, пишем знаки десятичной дроби.

Но для того, чтобы возвести в иррациональную степень или взять логарифм (решить обратную задачу), нужен такой труд, что применить прежнюю процедуру уже не просто. На помощь приходят таблицы. Их называют таблицами логарифмов или таблицами степеней, смотря по тому, для чего они предназначены. Они экономят время: чтобы возвести число в иррациональную степень, мы не вычисляем, а только перелистываем страницы.

Хотя вычисление собранных в таблицы значений — процедура чисто техническая, а все же дело это интересное и имеет большую историю. Поэтому посмотрим, как это делается. Мы вычислим не только x=10^?2, но решим и другую задачу: 10^x=2, или x=log₁₀2. При решении этих задач мы не откроем новых чисел; это просто вычислительные задачи. Решением будут иррациональные числа, бесконечные десятичные дроби, а их как-то неудобно объявлять новым видом чисел.

Подумаем, как решить наши уравнения. Общая идея очень проста. Если вычислить 10

1 и 10^1/10, и 10^1/100, и 10^1/1000, и т. д., а затем перемножить результаты, то мы получим 10^1,414…, или 10 ^?2. Поступая так, мы решим любую задачу такого рода. Однако вместо 10^1/10 и т. д. мы будем вычислять 10^1/2, 10^1/4 и т. д. Прежде чем начинать вычисления, объясним еще, почему мы обращаемся к числу 10 чаще, чем к другим числам. Мы знаем, что значение таблиц логарифмов выходит далеко за рамки математической задачи вычисления корней, потому что

(22.3)

Это хорошо известно всем, кто пользовался таблицей логарифмов, чтобы перемножить числа. По какому же основанию b брать логарифмы? Это безразлично; ведь в основу таких вычислений положен только принцип, общее свойство логарифмической функции. Вычислив логарифмы один раз по какому-нибудь произвольному основанию, можно перейти к логарифмам по другому основанию при помощи умножения. Если умножить уравнение (22.3) на 61, то оно останется верным, поэтому если перемножить все числа в таблице логарифмов по основанию b на 61, то можно будет пользоваться и такой таблицей.

Предположим, что нам известны логарифмы всех чисел по основанию b. Иначе говоря, можно решить уравнение b^а=с для любого с; для этого существует таблица. Задача состоит в том, как найти логарифм этого же числа с по другому основанию, например х. Нам нужно решить уравнение х^а‘=с. Это легко сделать, потому что х всегда можно представить так: x=b^t. Найти t, зная х и b, просто: t=log_bx . Подставим теперь х=b^t в уравнение x^a‘=с; оно перейдет в такое уравнение: (b^t)^а‘=b^ta’=с. Иными словами, произведение ta‘ есть логарифм с по основанию b. Значит, a‘=a/t. Таким образом, логарифмы по основанию х равны произведениям логарифмов по основанию b на постоянное число 1/t. Следовательно, все таблицы логарифмов эквивалентны с точностью до умножения на число 1/log_bx. Это позволяет нам выбрать для составления таблиц любое основание, но мы решили, что удобнее всего взять за основание число 10. (Может возникнуть вопрос: не существует ли все-таки какого-нибудь естественного основания, при котором все выглядит как-то проще? Мы попытаемся ответить на этот вопрос позднее. Пока все логарифмы будут вычисляться по основанию 10.)

Теперь посмотрим, как составляют таблицу логарифмов. Работа начинается с последовательных извлечений квадратного корня из 10. Результат можно увидеть в табл. 22.1.

Таблица 22.1 последовательные извлечения КВАДРАТНОГО КОРНЯ ИЗ 10

Показатели степеней записаны в ее первом столбце, а числа 10^S— в третьем. Ясно, что 10¹=10. Возвести 10 в половинную степень легко — это квадратный корень из 10, а как извлекать квадратный корень из любого числа, знает каждый[16]. Итак, мы нашли первый квадратный корень; он равен 3,16228. Что это дает? Кое-что дает. Мы уже можем сказать, чему равно 10^0,5, и знаем по крайней мере один логарифм. Логарифм числа 3,16228 очень близок к 0,50000. Однако нужно еще приложить небольшие усилия: нам нужна более подробная таблица. Извлечем еще один квадратный корень и найдем 10

1/4,что равно 1,77828. Теперь мы знаем еще один логарифм: 1,250— это логарифм числа 17,78; кроме того, мы можем сказать, чему равно 10^0,75: ведь это 10^(0,5+0,25), т. е. произведение второго и третьего чисел из третьего столбца табл. 22.1. Если сделать первый столбец таблицы достаточно длинным, то таблица будет содержать почти все числа; перемножая числа из третьего столбца, мы получаем 10 почти в любой степени. Такова основная идея таблиц. В нашей таблице содержится десять последовательных корней из 10; основной труд по составлению таблицы вложен в вычисления этих корней.

Почему же мы не продолжаем повышать точность таблиц дальше? Потому что мы кое-что уже подметили. Возведя 10 в очень малую степень, мы получаем единицу с малой добавкой. Это, конечно, происходит потому, что если возвести, например, 10

1/1000 в 1000-ю степень, то мы снова получим 10; ясно, что 10^1/1000 не может быть большим числом: оно очень близко к единице. Более того, малые добавки к единице ведут себя так, будто их каждый раз делят на 2; поглядите-ка на таблицу повнимательнее: 1815 переходит в 903, потом в 450, 225 и т. д. Таким образом, если вычислить еще один, одиннадцатый, квадратный корень, он с большой точностью будет равен 1,00112, и этот результат мы угадали еще до вычисления. Можно ли сказать, какова будет добавка к единице, если возвести 10 в степень ?/1024, когда ? стремится к нулю? Можно. Добавка будет приблизительно равна 0,0022511?. Конечно, не в точности 0,0022511 ?; чтобы вычислить эту добавку поточнее, делают такой трюк: вычитают из 10^S единицу и делят разность на показатель степени s. Отклонения полученного таким образом частного от его точного значения одинаковы для любой степени s. Видно, что эти отношения (см. четвертый столбец табл. 22.1) примерно равны. Сначала они все-таки сильно отличаются друг от друга, но потом все ближе подходят друг к другу, явно стремясь к какому-то числу. Что это за число? Проследим, как меняются числа четвертого столбца, если опускаться вниз по столбцу. Сначала разность двух соседних чисел равна 0,0211, потом 0,0104, потом 0,0053 и, наконец, 0,0026. Разность каждый раз убывает наполовину. Сделав еще один шаг, мы доведем ее до 0,0013, потом до 0,0007, 0,0003, 0,0002 и, наконец, примерно до 0,0001; надо последовательно делить 26 на 2. Таким образом, мы спустимся еще на 26 единиц и найдем для предела 2.3025. (Позднее мы увидим, что правильнее было бы взять 2.3026, но давайте возьмем то, что у нас получилось.) Пользуясь этой таблицей, можно возвести 10 в любую степень, если ее показатель каким угодно способом выражается через 1/1024.

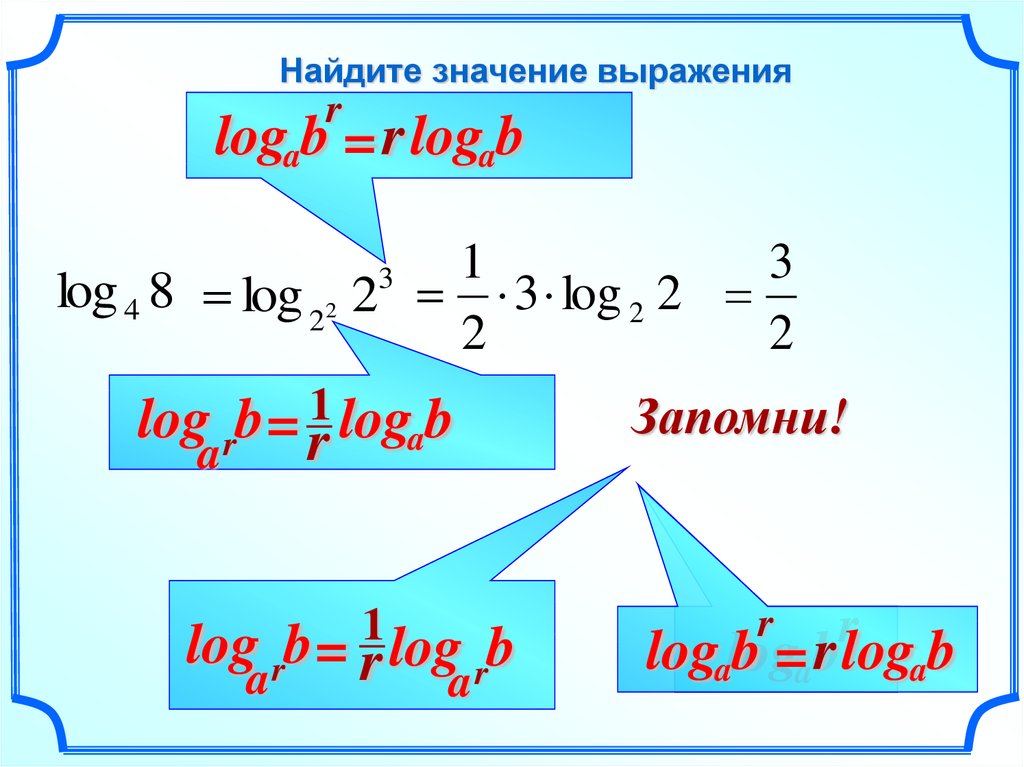
Теперь легко составить таблицу логарифмов, потому что все необходимое для этого мы уже припасли. Процедура этого изображена в табл. 22.2, а нужные числа берутся из второго и третьего столбцов табл. 22.1.

Таблица 22.2 ВЫЧИСЛЕНИЯ log₁₀2

Предположим, что мы хотим знать логарифм 2. Это значит, что мы хотим знать, в какую степень надо возвести 10, чтобы получить 2. Может быть, возвести 10 в степень ¹/₂? Нет, получится слишком большое число. Глядя на табл. 22.1, можно сказать, что нужное нам число лежит между ¹/₄ и ¹/₂. Поиск его начнем с ¹/₄; разделим 2 на 1,788…, получится 1,124…; при делении мы отняли от логарифма двух 0,250000, и теперь нас интересует логарифм 1,124…. Отыскав его, мы прибавим к результату ¹/₄

=256/1024. Найдем в табл. 22.1 число, которое бы при движении по третьему столбцу сверху вниз стояло сразу за 1,124… . Это 1,074607. Отношение 1,124… к 1,074607 равно 1,046598. В конце концов мы представим 2 в виде произведения чисел из табл. 22.1:

Для последнего множителя (1,000573) в нашей таблице места не нашлось; чтобы найти его логарифм, надо представить это число в виде 10^?/¹⁰²⁴?1+2,3025?/1024.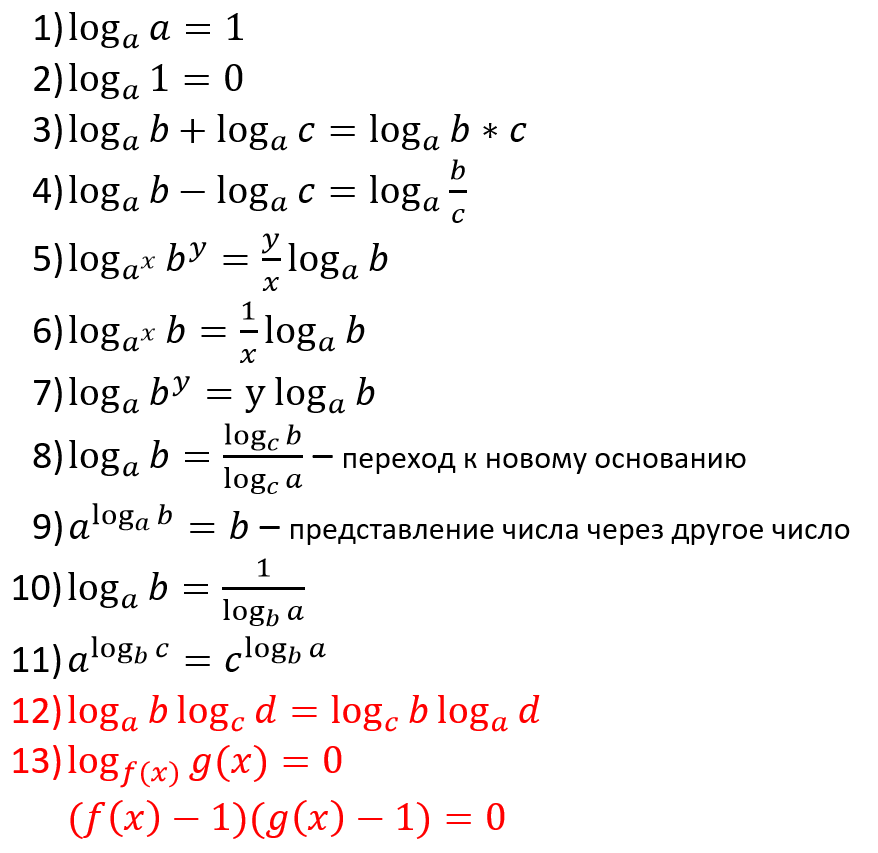 Отсюда легко найти, что ?=0,254. Таким образом, наше произведение можно представить в виде десятки, возведенной в степень 1/1024 (256+32+16+4+0,254). Складывая и деля, мы получаем нужный логарифм: log₁₀2=0,30103; этот результат верен до пятого десятичного знака!

Мы вычисляли логарифмы точно так же, как это делал мистер Бриггс из Галифакса в 1620 г. Закончив работу, он сказал: «Я вычислил последовательно 54 квадратных корня из 10». На самом деле он вычислил только 27 первых корней, а потом сделал фокус с ?. Вычислить 27 раз квадратный корень из 10, вообще-то говоря, немного сложнее, чем 10 раз, как это сделали мы. Однако мистер Бриггс сделал гораздо большее: он вычислял корни с точностью до шестнадцатого десятичного знака, а когда опубликовал свои таблицы, то оставил в них лишь 14 десятичных знаков, чтобы округлить ошибки. Составить таблицы логарифмов с точностью до четырнадцатого десятичного знака таким методом — дело очень трудное. Зато целых 300 лет спустя составители таблиц логарифмов занимались тем, что уменьшали таблицы мистера Бриггса, выкидывая из них каждый раз разное число десятичных знаков.

Только в последнее время при помощи электронных вычислительных машин оказалось возможным составить таблицы логарифмов независимо от мистера Бриггса. При этом использовался более эффективный метод вычислений, основанный на разложении логарифма в ряд.

Составляя таблицы, мы натолкнулись на интересный факт: если показатель степени ? очень мал, то очень легко вычислить 10^?; это просто 1+2,3025?. Это значит, что 10ⁿ/^2,3025=1+n для очень малых n. Кроме того, мы говорили с самого начала, что вычисляем логарифмы по основанию 10 только потому, что у нас на руках 10 пальцев и по десяткам нам считать удобнее. Логарифмы по любому другому основанию получаются из логарифмов по основанию 10 простым умножением. Теперь настало время выяснить, не существует ли математически выделенного основания логарифмов, выделенного по причинам, не имеющим ничего общего с числом пальцев на руке. В этой естественной шкале формулы с логарифмами должны выглядеть проще. Составим новую таблицу логарифмов, умножив все логарифмы по основанию 10 на 2,3025. … Это соответствует переходу к новому основанию — натуральному, или основанию е. Заметим, что log_? (l+n)?n или еⁿ?1+n, когда n?0.

Легко найти само число е; оно равно 10¹/^2,3025 или 10^0,434294… Это 10 в иррациональной степени. Для вычисления е можно воспользоваться таблицей корней из 10. Представим 0,434294… сначала в виде 444,73/1024, а числитель этой дроби в виде суммы 444,73=256+128+32+16+2+0,73. Число е поэтому равно произведению чисел

(Числа 0,73 нет в нашей таблице, но соответствующий ему результат можно представить в виде 1+2,3025?/1024 и вычислить, чему равна ?.) Перемножив все 7 сомножителей, мы получим 2,7184 (на самом деле должно быть 2,7183, но и этот результат хорош). Используя такие таблицы, можно возводить число в иррациональную степень и вычислять логарифмы иррациональных чисел. Вот как надо обращаться с иррациональностями.

Свойства логарифмов.

Логарифм степени 11 класс онлайн-подготовка на Ростелеком Лицей

1. Некоторые напоминания

 

Рассмотрим показательное уравнение:

 

Напомним, здесь

Данное уравнение имеет единственное решение (т. к. показательная функция монотонна), оно названо логарифмом:

напомним основное логарифмическое тождество:

Проиллюстрируем на конкретном примере.

. Рис. 15.1.

Данная функция монотонно убывает, как и любая другая показательная функция, основание которой лежит в пределах от нуля до единицы. Любое положительное значение b функция достигает при единственном значении аргумента – . Например, значение  достигается при . Проверим:

Равенство верно.

Рис. 1. График функции

 

2. Логарифм степени, формула

 

 

Напомним уже известные нам свойства логарифма:

 

Логарифм произведения:

Логарифм частного:

Обратим внимание: здесь

 

3.

Решение некоторых типовых задач

 

 

Пример 1 – вычислить:

 

а)

б)

Теперь наша цель – научиться вычислять логарифм степени.

Дано:

Доказать:

Другими словами, в данном случае показатель степени выносится как сомножитель, сложная операция возведения в степень заменяется более простой операцией умножения.

Доказательство:

Представим число b с помощью основного логарифмического тождества:

Обе части возведем в степень r:

Согласно свойствам степени получаем:

По определению логарифма имеем:

Что и требовалось доказать.

Рассмотрим задачи на применение выведенной формулы.

Пример 2 – прологарифмировать по основанию 3 выражение:

Имеем логарифм произведения трех положительных выражений, распишем по известной формуле:

Преобразуем подлогарифмические выражения:

Согласно свойству логарифма вынесем показатели степеней как сомножители:

Пример 3 – решить уравнение:

Внесем множители под знак логарифма как показатели степени согласно свойству логарифма:

Заменим сумму логарифмов логарифмом произведения:

Заменим разность логарифмов логарифмом частного:

Упростим правую часть:

Из определения логарифма:

Исходя из основного логарифмического тождества, получаем:

Пример 4:

Дано:

, а и b считать известными числами.

Найти:

Таким образом, задача заключается в том, чтобы выразить искомый логарифм через а и b.

Согласно основной теореме арифметики, разложим составное число 300 на простые множители:

Имеем:

Согласно свойству логарифма, логарифм произведения представим как сумму логарифмов:

Вынесем показатели степени как сомножители:

Подставим заданные значения:

Итак, мы рассмотрели новое свойство логарифма, вывели формулу для логарифма степени. Мы рассмотрели применение свойств логарифма в некоторых типовых задачах. Далее мы продолжим изучать свойства логарифмов и решать различные задачи, применяя изученные факты.

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Edu.glavsprav.ru (Источник).
2. Nado5.ru (Источник).
3. Uztest.ru (Источник).

 

Домашнее задание

1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 508;

2. Вычислить:

а) ; б) ;

в) ; г)

3. Выразить через  и :

а) ; б) ; в) ; г)

 

x = 8, x=3$)

А если нет? Например, как найти $x$, когда:

$$\log_{1.03} 2 = x\quad ?$$

$$\log_{8} 33 = x\quad ?$$

• функции
• логарифмы

$\endgroup$

3

$\begingroup$

Логарифм $\log_{b} (x)$ можно вычислить из логарифмов $x$ и $b$ по положительному основанию $k$ по следующей формуле:

$$\log_{b} (x) = \frac{\log_{k} (x)}{\log_{k} (b)}. $$

Итак, ваши примеры можно решить следующим образом с помощью калькулятора:

$$x = \log_{1,03} (2) = \frac{\log_{10} (2)}{\log_{10} (1,03)} = \frac{0,301}{0,013} = 23,450, $$

$$x = \log_{8} (33) = \frac{\log_{10} (33)}{\log_{10} (8)} «=» \frac{1.519}{0.903} = 1.681.$$

Если вы знаете, что $b$ и $x$ являются степенями некоторого $k$, то вы можете вычислить логарифм без калькулятора по степени тождества логарифмов , например, 93}{3}-…$, а если нет, найдите логарифм обратного и вычтите из нуля. Степени $x$ можно вычислить путем свертки в виде степенного ряда в $10$.

$\endgroup$

1

$\begingroup$

Здесь нечего решать. У вас есть точное выражение для $x$ в каждом случае — вы можете не знать точно, какому числу оно соответствует, точно так же, как вы можете не знать, чему равен квадратный корень из трех, когда решаете что-то вроде $x^2=3$, но это все еще просто число — в первом случае это будет степень, в которую я возвожу 1,03, чтобы получить 2, что примерно равно 23,45 9x=2$$ теперь возьмем логарифмы обеих сторон$$x \times \log(1. 03)=\log(2)$$ Теперь , используйте свой калькулятор

$\endgroup$

4

$\begingroup$

$$\log_bn=\frac{\ln n}{\ln b}=\frac{\log_{10}n}{\log_{10}b}=\frac{\log_2n}{\log_2b}= \ldots$$ Редактировать: Теперь добавлено в комментарий:

Я хочу найти значение без калькулятора.

9{-4}$.

$\endgroup$

Обзор логарифмов и антилогарифмов — часто задаваемые вопросы 1447

Примеры логарифмов с основанием 10

Лучший способ понять логарифмы — это рассмотреть пример. Если вы возьмете 10 в третьей степени (10 х 10 х 10), результат будет 1000. Логарифм — это обратная функция этой степени. Логарифм (по основанию 10) числа 1000 — это степень числа 10, которая дает ответ 1000. Таким образом, логарифм 1000 равен 3. Если вы умножите 10 само на себя 3 раза, вы получите 1000.

10 можно возвести в отрицательную степень. Например, возведение 10 в степень -3 равносильно получению обратного числа 10 ³ . Таким образом, 10 ^-3 равно 1/10 ³ или 0,001. Логарифм 0,001 — это степень числа 10, равная 0,001, что равно -3.

Вы можете перевести 10 в дробную степень. Десять в степени 1/2 равняется квадратному корню из 10, что равно 3,163. Таким образом, логарифм 3,163 равен 0,5.

Десять в нулевой степени равняется 1, поэтому логарифм 1,0 равен 0,0.

Вы можете логарифмировать любое положительное число. Логарифм значений между нулем и единицей отрицательный; логарифмы значений больше единицы положительны. Логарифмы нуля и всех отрицательных чисел не определены; нет степени 10, которая дает отрицательное число или ноль.

Логарифмы по другим основаниям

Логарифмы, показанные в предыдущем разделе, называются логарифмами по основанию 10, потому что вычисления занимают 10 в некоторой степени. Их также называют десятичными логарифмами.

Вы можете вычислять логарифмы любой степени. Математики предпочитают натуральные логарифмы, используя основание e (2,7183…). Несмотря на это название, использование логарифмов по основанию е не кажется естественным большинству ученых, которым удобнее работать с логарифмами по основанию 10.

Биологи иногда используют логарифмы по основанию 2, часто не осознавая этого. Логарифм по основанию 2 — это количество удвоений, необходимое для достижения значения. Таким образом, логарифмическая база 2 из 16 равна 4, потому что если вы начнете с 1 и удвоите ее четыре раза (2, 4, 8 и 16), результат будет 16. Иммунологи часто серийно разводят антитела в 2 раза, поэтому часто графически отображают данные шкала log2. Клеточные биологи используют логарифмы по основанию 2 для преобразования числа клеток в число удвоений.

Логарифмы, использующие разные основания, пропорциональны друг другу. Таким образом, преобразование из натуральных журналов в обычные журналы похоже на изменение единиц измерения. Разделите натуральный логарифм на 2,303, чтобы вычислить десятичный логарифм того же значения. Умножьте обычный журнал на 2,303, чтобы получить соответствующий натуральный журнал.

Математические свойства логарифмов

Логарифмы превращают умножение в сложение, деление в вычитание и возведение в степень в умножение:

log(A ^. B) = log(A) + log(B)

log(A/B) = log(A) — log(B)

log(A ⁿ ) = номер ^. log(A)

Что такое Antilog?

Антилогарифм (также называемый антилогарифмом) является обратным логарифмическому преобразованию. Поскольку логарифм (по основанию 10) числа 1000 равен 3, антилогарифм 3 равен 1000. Чтобы вычислить антилогарифм логарифма по основанию 10, возьмите десять в этой степени.

Антилог формула

 y= b ³

Чтобы вычислить антилогарифм натурального логарифма, возведите e в эту степень. Натуральный логарифм 1000 равен 6,980. Таким образом, антилогарифм числа 6,908 равен e ^6,908 , что равно 1000. В электронных таблицах и компьютерных языках используется обозначение exp(6,908).

Термины, похожие на логарифм: логит и логистика

Термин логистика звучит так, как будто он связан с логарифмами. На самом деле термин «логистика» имеет три различных значения, не все из которых связаны с логарифмами.

Логит-функция, используемая в логистической регрессии, представляет собой натуральный логарифм вероятности (P со значением от 0,0 до 1,0), деленный на 1-P:   

Logit(P) = ln[P/(1-P )]

логарифмически нормальное  распределение – это распределение значений, логарифмы которых соответствуют распределению Гаусса. Логнормальное распределение само по себе асимметрично с тяжелым хвостом вправо. Легко ввести в заблуждение из-за асимметрии и ошибочно исключить значения в хвосте распределения как выбросы.