Какие углы называются вертикальными какими свойствами они обладают?
Какие углы называются вертикальными какими свойствами они обладают?
Углы, которые не являются смежными: … Пары этих углов называются вертикальными углами. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Свойство вертикальных углов: вертикальные углы равны.
Какие углы называются соответственными?
Сравнительный словарь-справочник понятий и фактов элементарной математики — Соответственные углы Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей.
Какие углы образуются при пересечении двух прямых третьей?
При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.
Как доказать что углы соответственные?
Если две параллельные прямые пересечены секущей, то соответственные углы равны. Доказательство: Пусть параллельные прямые а и b пересечены секущей c.
Доказательство: Пусть параллельные прямые а и b пересечены секущей c.
Сколько в сумме дают соответственные углы?
сумма соответственных углов, образованных при пересечении параллельных прямых секущей, равна 180 градусов? Соответственные углы равны, а вот одностороннее в сумме составляют 180 градусов. нет, они равны между собой. Сумма соответственных углов равна 180 градусов.
Сколько в сумме дают накрест лежащие углы?
Накрест лежащие углы Сумма пары накрест лежащих углов, образованных при пересечении параллельных прямых секущей, равна 110°.
Чему равна сумма односторонних углов?
Если две параллельные прямые пересечены секущей, то: накрест лежащие углы равны; соответственные углы равны; сумма односторонних углов равна 180°.
Как понять что стороны параллельны?
Если две прямые на плоскости перпендикулярны одной и той же прямой, то они параллельны. Этот признак легко доказать, если вспомнить, что к прямой в плоскости из любой точки можно провести только один перпендикуляр. Допустим, что прямые, перпендикулярные одной и той же прямой, не параллельны, то есть имеют общую точку.
Этот признак легко доказать, если вспомнить, что к прямой в плоскости из любой точки можно провести только один перпендикуляр. Допустим, что прямые, перпендикулярные одной и той же прямой, не параллельны, то есть имеют общую точку.
Какие признаки параллельности прямых вы знаете?
Признаки параллельности двух прямых: 1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны. 2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.
Как доказать параллельность?
Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180 градусам.
Что значит параллельно прямой?
Прямая и плоскость называются параллельными, если они не имеют общих точек. Теорема 5 «Признак параллельности прямой и плоскости». Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Как проверить параллельность прямой и плоскости?
Если прямая, не лежащая в плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна данной плоскости. Теорема. Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Официальный сайт МБОУ СОШ с.Паниковец
| Размер шрифта: | Межстрочный интервал: стандартный средний большой |
| Цвет фона: | Межбуквенный интервал: стандартный средний большой |
Версия для слабовидящих Отключить версию для слабовидящих
Липецкая область, Задонский район, с.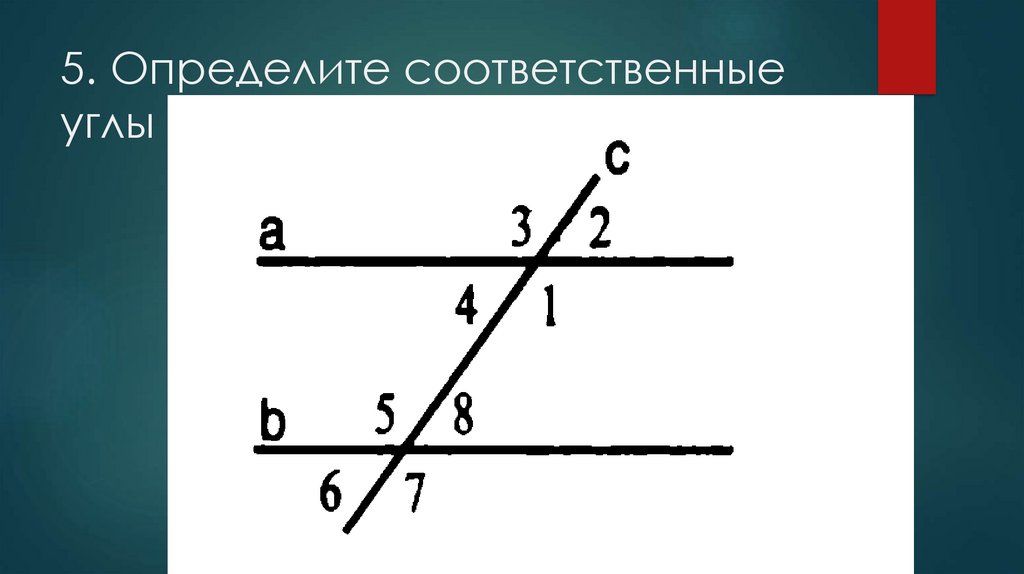 Пани́ковец, ул. Запрудная, д. 18. Телефон: 8 (47471) 4-72-12
Пани́ковец, ул. Запрудная, д. 18. Телефон: 8 (47471) 4-72-12
Электронная почта школы: [email protected]
28.03.2023
Урок ГТО
С 20 по 24 марта в нашей школе проходила акция «Урок ГТО». Ученики 1-го класса узнали, что такое ГТО и как правильно выполнять комплекс. Учащиеся старших классов узнали о возможности получения дополнительных баллов при поступлении в ВУЗ.
Читать далее
27.03.2023
Детское кресло — спасенная жизнь!
Уважаемые родители! Многие из вас являются автомобилистами, осуществляющими перевозку детей на личном автотранспорте. Поэтому чтобы ваша машина была оазисом безопасности для вашего ребёнка, беспрекословно соблюдайте правила перевозки детей в автомобиле!
Читать далее
27.03.2023
Международный день театра
С 20 по 27 марта в нашей школе прошли мероприятия, посвященные театру.
Читать далее
20.03.2023
«Крым – Россия!»
18 марта в России отмечается день воссоединения Крыма с Россией.
Читать далее
15.03.2023
Патриот 2023
15 февраля 2023 года среди образовательных учреждений Задонского муниципального района прошла военно-спортивная игра «Патриот», посвященная 80-летию победы советских войск в Сталинградской битве.
Читать далее
14.03.2023
Посетили выставку картин
Учащиеся 6-8 классов посетили выставку картин «Победа народного духа».
Читать далее
07.03.2023
Праздник весны и цветов
Вместе с весной к нам пришёл замечательный праздник – Международный Женский день, 8 Марта. Этот день согрет лучами солнца, женскими улыбками, украшенными россыпью цветов.
Читать далее
07.03.2023
Юным – наставление, незнающим – вразумление
Год учителя, педагога и наставника набирает обороты. В школе организована выставка-экскурс «Юным – наставление, незнающим – вразумление». В коридорах размещены высказывания великих деятелей истории и культуры с мудрыми наставлениями в учении.
Читать далее
01.03.2023
Памяти павших, памяти вечно молодых ребят…
Война… Какой болью она отзывается в сердцах тех, чьи сыновья снова выполняют свой воинский долг и погибают…
Читать далее
28.02.2023
Учитель учителей
«Если педагогика хочет воспитывать человека во всех отношениях, то она должна прежде узнать его тоже во всех отношениях».
Читать далее
Все новости >>>
Соответствующие углы — определение, теорема и примеры
Соответствующий угол — это угол, который занимает ту же относительную позицию, что и другой угол в другом месте на рисунке.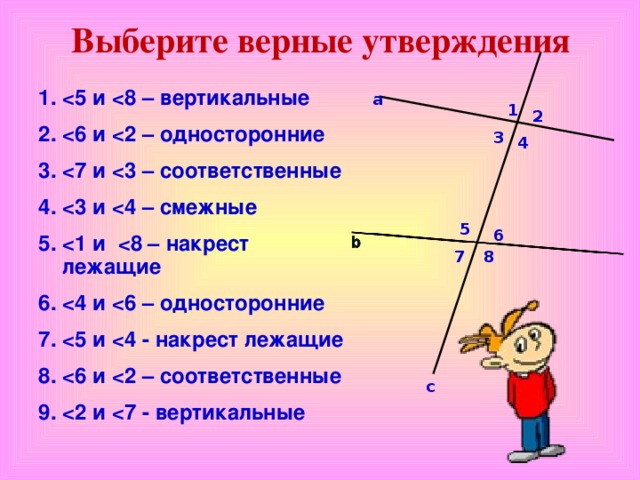 Соответствующие углы в планиметрии образуются при пересечении двух прямых секущими.
Соответствующие углы в планиметрии образуются при пересечении двух прямых секущими.
Два угла соответствуют или относятся друг к другу, поскольку они находятся на одной стороне поперечной. Один — внешний угол (вне параллельных прямых) и один внутренний угол (внутри параллельных прямых).
Соответствующие углы и поперечное объяснениеСоответствующие углы — это всего лишь один тип пары углов. Углы, лежащие по другую сторону от секущей, называются противоположными углами. У вас могут быть альтернативные внутренние углы и альтернативные внешние углы.
Соответствующие углы никогда не являются смежными углами. Они не соприкасаются, поэтому никогда не могут быть последовательными внутренними углами.
Что такое соответствующие углыКакие углы являются соответствующими углами?
Можете ли вы найти соответствующий угол для угла 2 на нашем рисунке?
Пример определения соответствующих углов Вы заметили, что угол 6 соответствует угол 2 ? Это пара соответствующих углов.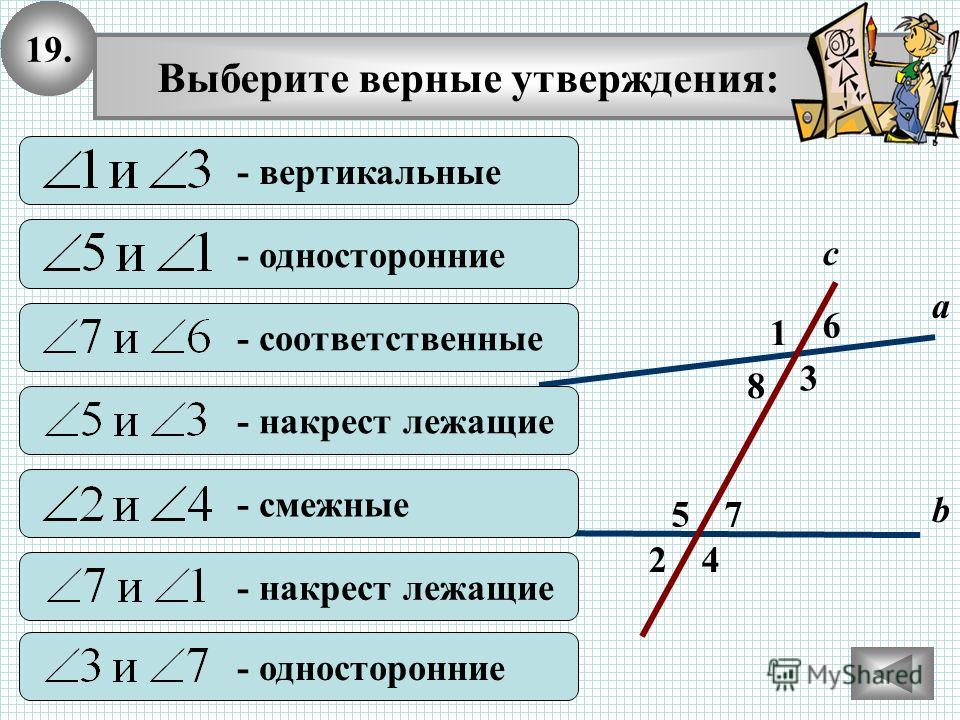 Сможете ли вы найти все четыре соответствующие пары углов?
Сможете ли вы найти все четыре соответствующие пары углов?
Вот четыре пары соответствующих углов:
Углы 1 и 5
Углы 2 и 6
Углы 3 и 7
Углы 4 и 8
Соответствующие углы Теорема
, когда трансверстная линия пересекает две линии. Теорема о соответствующих углах утверждает, что:
Постулат о соответствующих углах прост, но он обладает преимуществом, поскольку с его помощью вы можете установить отношения для всех восьми углов фигуры.
Теорема о соответствующих углахБлагодаря теореме о соответствующих углах вы уже знаете кое-что о восьми углах, образованных тремя прямыми:
Если один угол прямой, то все прямые
Если один острый, четыре острые углы
Если один тупой, то четыре тупых угла
Все восемь углов можно классифицировать как смежные углы, вертикальные углы и соответствующие углы
Если у вас есть две параллельные прямые, пересеченные секущей, и один угол ( угол 2 ) помечен 57° , что делает его острым, наша теорема говорит нам, что есть еще три острых угла.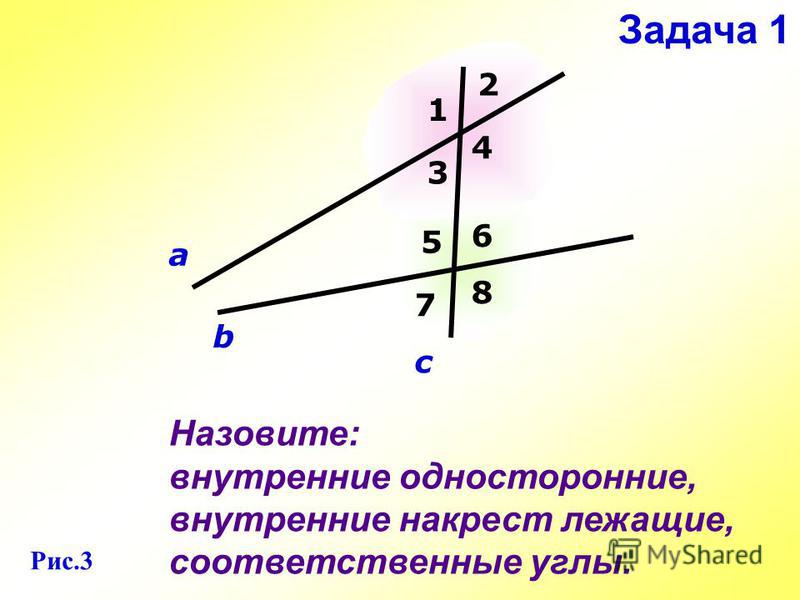
Углы по обе стороны от нашего 57° угла — смежных углов — тупые. Угол 3 – это угол по вертикали к углу 2 . Они имеют общую вершину и находятся друг напротив друга.
Обращение теоремы о соответствующих углах
Интересна также обратная теорема о соответствующих углах:
Обратная теорема позволяет быстро оценить фигуру. Если вам дана фигура, подобная приведенной ниже, но с обозначенными только двумя углами, сможете ли вы по ней что-либо определить?
Обращение теоремы о соответствующих углахТак как соответствующие углы равны, вы знаете, что две линии, пересекаемые секущей, параллельны.
Если линии, пересекаемые секущей, не параллельны, то соответствующие углы не равны. Они просто соответствуют местоположению. 9Примеры соответственных углов мера?
Теорему о соответствующих углах можно использовать даже без чертежа. Если два соответствующих угла секущей, пересекающей параллельные прямые, прямые, что вы знаете о фигуре?
Можете ли вы провести параллельные прямые с секущей, образующей пару соответствующих углов, каждый из которых имеет размеры 181° ?
Представьте себе поперечное сечение двух линий.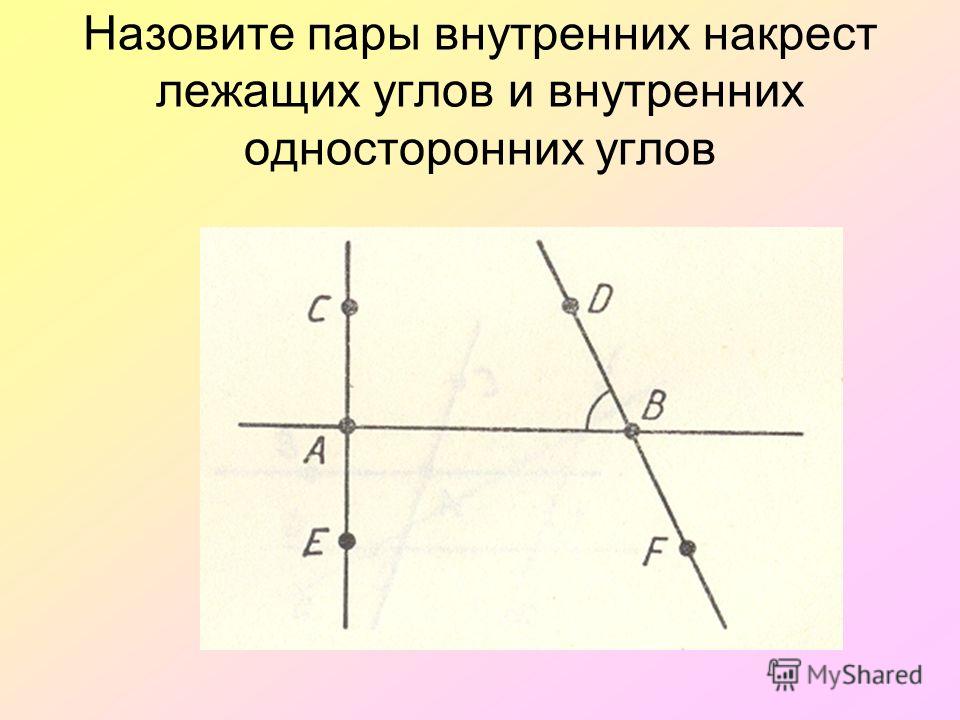 Вы узнали, что соответствующие углы не равны. Что это говорит вам о линиях, пересекаемых секущей?
Вы узнали, что соответствующие углы не равны. Что это говорит вам о линиях, пересекаемых секущей?
А теперь ответы (постарайтесь сначала!):
Угол 5 также измеряет 123° . Из-за теоремы о вертикальных углах составляют угол 4 и 8 , а также измеряют 123° .
Если два соответствующих угла секущей, пересекающей параллельные прямые, прямые, то все углы прямые, а секущая перпендикулярна параллельным прямым.
Вы не можете провести параллельные линии с секущей, которая создает пару соответствующих углов, каждый из которых имеет размеры 181° .
При поперечном разрезании двух прямых, образующих неконгруэнтные соответствующие углы, вы знаете, что эти две прямые не параллельны.
Соответствие углов: определение, теорема и примеры
Слово «соответствие» подразумевает, что углы могут быть сравнимы или эквивалентны (конгруэнтны). Удивительно, но поперечная, пересекающая две параллельные прямые, образует равные конгруэнтные углы. Соответствующие углы не равны, когда секущая соединяет две непараллельные прямые. Когда две линии пересекаются другой линией в плоской геометрии, образуются соответствующие углы. Эквивалентные углы — это углы, образованные совмещением углов в каждом стыке. Другими словами, сопоставимый угол — это угол, который в то же время сохраняет то же корреляционное положение, что и другой угол на рисунке. Соответствующие углы представляют собой форму пары углов, которые очень похожи друг на друга. Вы можете иметь альтернативные внутренние углы и альтернативные внешние углы в качестве совпадающих углов.
Удивительно, но поперечная, пересекающая две параллельные прямые, образует равные конгруэнтные углы. Соответствующие углы не равны, когда секущая соединяет две непараллельные прямые. Когда две линии пересекаются другой линией в плоской геометрии, образуются соответствующие углы. Эквивалентные углы — это углы, образованные совмещением углов в каждом стыке. Другими словами, сопоставимый угол — это угол, который в то же время сохраняет то же корреляционное положение, что и другой угол на рисунке. Соответствующие углы представляют собой форму пары углов, которые очень похожи друг на друга. Вы можете иметь альтернативные внутренние углы и альтернативные внешние углы в качестве совпадающих углов.
Определение соответствующих углов
«В геометрии соответствующие углы образуются, когда пересекающаяся поперечная линия пересекает две прямые линии. Соответствующие углы — это углы, расположенные в одном и том же относительном месте на различных пересечениях».
Первая и вторая линии параллельны.
 В результате у нас есть две прямые, которые параллельны.
В результате у нас есть две прямые, которые параллельны.Линии 1 и 2 пересекаются на пересечении линии 3. В результате пересекаются параллельные линии.
Углы 1 и 2 показаны на схеме в одинаковом взаимном положении – верхние правые боковые углы в области стыка.
Рисунок 1: соответствующие углы
Когда два луча, каждый с одним концом, пересекаются в одной точке, они образуют угол. Вершина – это точка пересечения двух лучей. Угол измеряется расстоянием между двумя лучами. Углы часто упоминаются в геометрии с помощью символа.
Углы, поперечные линии и параллельные линии — это лишь некоторые элементы.
Поперечная линия: Поперечная линия — это линия, которая соединяет две другие линии, пересекая их или проходя через них. Секущая проходит через обе прямые под одним и тем же углом, когда две другие прямые параллельны.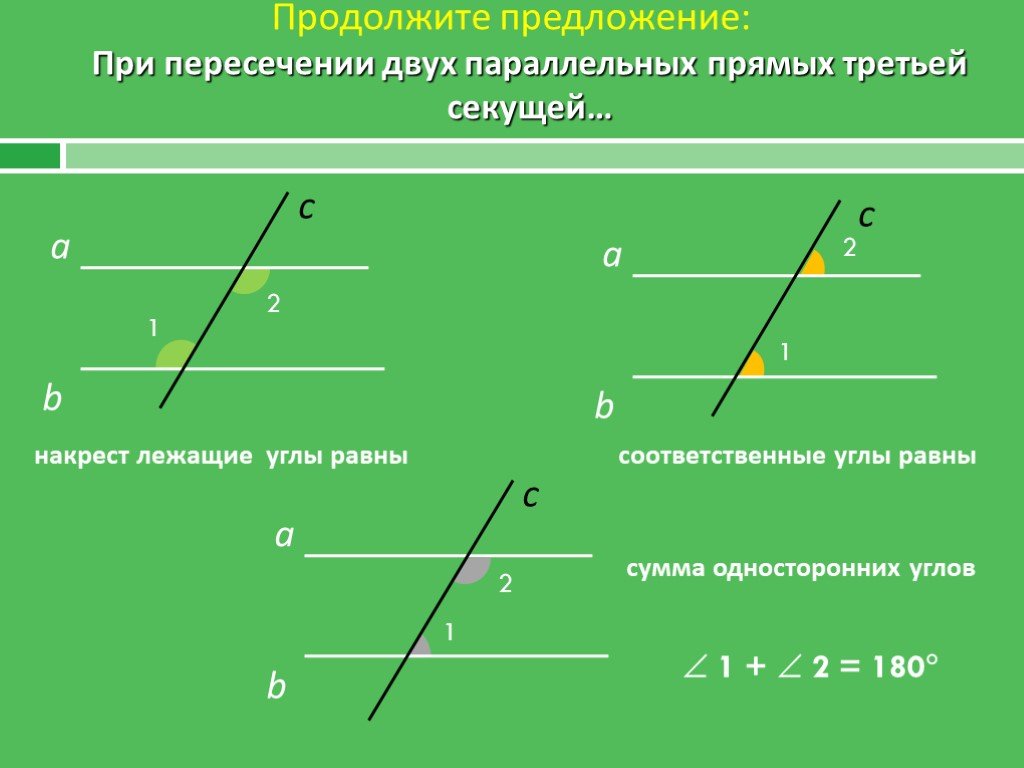 С другой стороны, две другие линии не обязательно должны быть параллельны, чтобы их пересекала поперечная, как показано здесь:
С другой стороны, две другие линии не обязательно должны быть параллельны, чтобы их пересекала поперечная, как показано здесь:
Прямая линия: Прямая линия, также известная как плоский угол, образует прямой угол. Этот угол имеет длину 180 градусов. Два или более угла, сумма которых составляет 180 °, также могут составлять прямой угол.
Параллельные линии: На двумерной плоскости параллельные линии — это две линии, которые никогда не встречаются и не пересекаются. Существуют особые свойства, касающиеся углов, образующихся при пересечении секущих между параллельными прямыми, которые не возникают, когда прямые не параллельны. Линии m и n имеют стрелки, указывающие налево. Прямые m и n параллельны, как показано этими стрелками.
Существуют различные виды соответственных углов
Соответствующие углы образованы параллельными прямыми и поперечными.
Соответствующие углы, созданные непараллельными линиями и попереками
Теорема соответствующих углов
в соответствии с соответствующими теоремы,
, когда трансверсальные линии,
.
 .
.Теорема — это доказанное утверждение или широко распространенное убеждение, правильность которого доказана. Обратное к этой теореме, которое по сути является обратным, также является доказанным утверждением:
Прямые параллельны, если секущей пересекает две прямые и прилежащие углы равны.
Эти теоремы можно использовать для решения геометрических задач и выявления недостающих данных.
Как найти соответствующие углы?
Нанесение буквы F на прилагаемой иллюстрации является одним из методов определения согласующихся углов. Нарисуйте букву так, как вам нравится, и совместите углы.
Пример 1. Найдите недостающие углы на приведенной ниже диаграмме с ∠d=30°
Рисунок 2
Ϫd = 30 °
↑d = ↑b …… .. Вправо противоположные углы
↑B = 30 °
потряно =∠f Соответствующие углы
∠f=30°
∠b+∠a=180° Дополнительные углы
∠a+30°=180°
∠a=∠a=150°
1
∠e=150°
∠d=∠h=30° ………Соответствующие углы
Пример 2.
 Два совпадающих угла фигуры равны 9x + 10 и 55. Вычислите значение x.
Два совпадающих угла фигуры равны 9x + 10 и 55. Вычислите значение x.9x+10 И 55.
Решение:
Два угла, соответствующие друг другу, всегда равны.
9x+10=55
9x=55-10
9x=45
x=5
Соответствующие углы Применение
Существует множество применений соответствующих углов.
Оконные решетки обычно горизонтальные и вертикальные, образующие несколько квадратов. Совпадающие углы образованы каждой вершиной квадрата.
Столбы поддерживают мост. Все столбы соединены таким образом, что углы соответствующих столбов одинаковы.
Железнодорожные пути устроены таким образом, что все соответствующие углы на пути равны.
Заключение
В этой статье мы узнаем, Слово «соответствие» подразумевает, что углы могут быть сравнимы или эквивалентны (конгруэнтны).


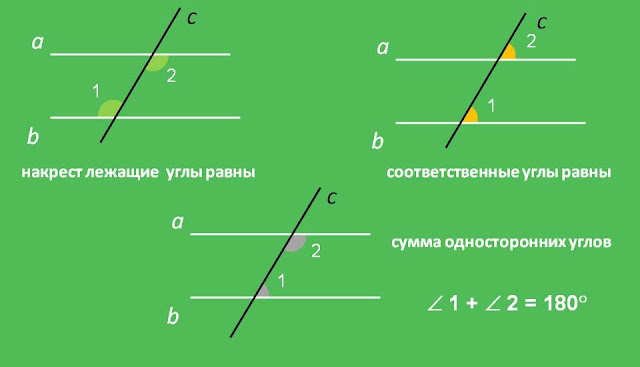 В результате у нас есть две прямые, которые параллельны.
В результате у нас есть две прямые, которые параллельны.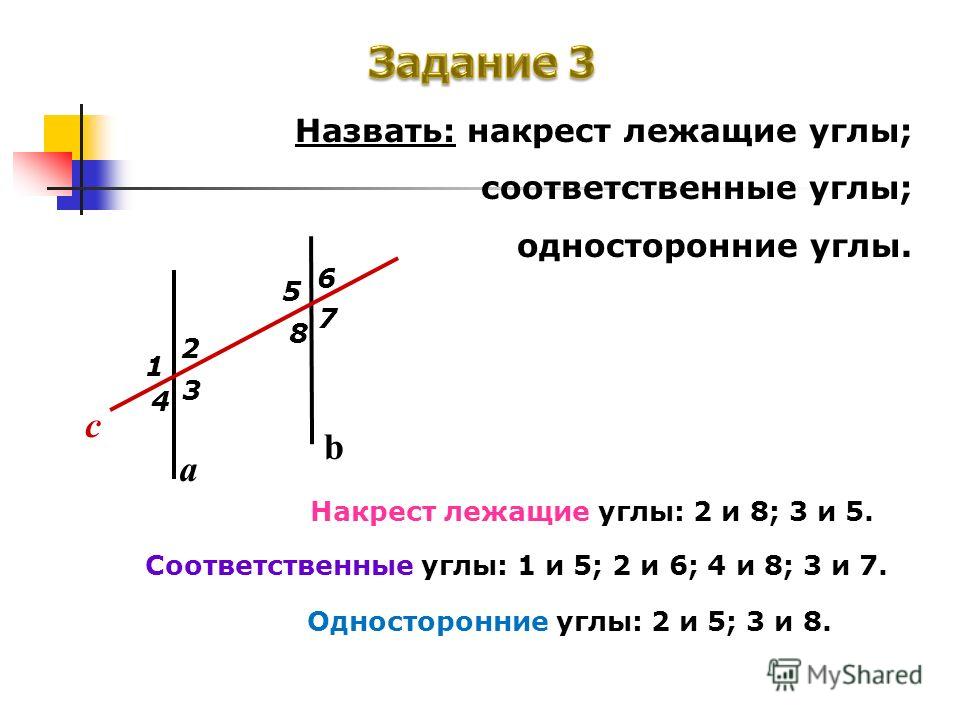 .
. Два совпадающих угла фигуры равны 9x + 10 и 55. Вычислите значение x.
Два совпадающих угла фигуры равны 9x + 10 и 55. Вычислите значение x.