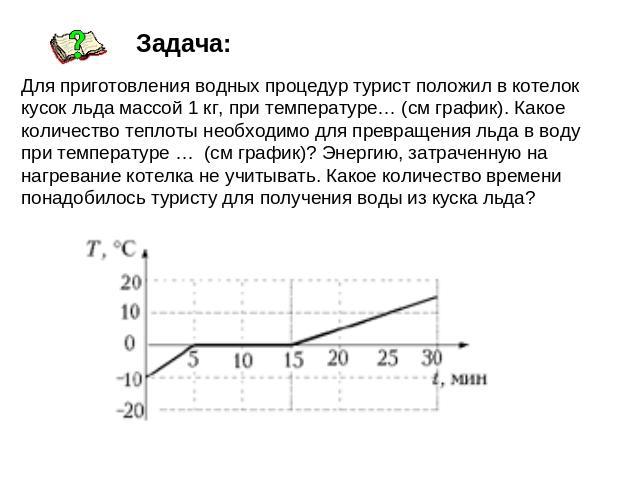
Методические рекомендации и сборник задач по физике для учащихся 8-х классов часть I (стр. 8 из 17)
кДж.
Так как Q2 > Q1, то лед не может таять, и могут осуществиться случаи 2 или 4. Для осуществления случая 2 необходимо, чтобы Q1 + Q4 < Q2
Q1 + Q4 = 702 кДж, Q2 = 420 кДж.
Соответственно реализуется случай 4: температура смеси
и часть воды замерзнет. Обозначим массу замерзшей воды m3, и составим уравнение теплового баланса:
— количество теплоты, которое отдает вода, остывая до 0
.
— количество теплоты, которое отдает замерзающая вода.
— количество теплоты, полученное льдом при нагревании до 0
.
Отсюда
Из этого выражения находим массу замерзшей воды
После установления теплового равновесия, масса воды
, и масса льда будет
. Объем полученной смеси
Вычисления:
кг.
0,75 м3 = 7,5 дм3.
Задачи для самостоятельного решения.
Задача 182. Во сколько раз требуется больше энергии для плавления льда при температуре 0
, чем для изменения температуры той же массы льда на 1
?
Задача 183. Какое количество теплоты потребуется для плавления тел из нафталина, золота, платины массой 10 г, взятых при температуре плавления?
Задача 184. Какое количество теплоты необходимо затратить, чтобы расплавить лед массой 5 кг, если начальная температура льда 0; -1; -10
?
Задача 185.
Какое количество теплоты необходимо для плавления куска свинца массой 1 г, начальная температура которого равна 27
? олова массой 10 г, взятого при температуре 32
?
Задача 186. Сколько энергии требуется для плавления куска свинца массой 0,5 кг, взятого при температуре 27
?
Задача 187. Сколько энергии необходимо для плавления бруска из цинка массой 0,5 кг, взятого при температуре 20
?
Задача 188. Сколько энергии необходимо для плавления железного металлолома массой 4 т, если начальная температура железа равна 39
?
Задача 189. Масса серебра 10 г. Сколько энергии выделится при его кристаллизации и охлаждении до 60
, если серебро взято при температуре плавления?
Задача 190. Сколько энергии выделится при кристаллизации и охлаждении от температуры плавления до 27
свинцовой пластинки размером
см?
Задача 191.
Из копильника вагранки для отливки детали выпустили расплавленное железо массой 50 кг. Какое количество теплоты выделилось при его кристаллизации и охлаждении до температуры 39
?
Задача 192. Для приготовления пищи полярники используют воду, полученную из расплавленного льда. Какое количество теплоты потребуется для того, чтобы расплавить лед массой 20 кг и полученную воду вскипятить, если начальная температура льда -10
?
Задача 193. Объем формы для пищевого льда 750 см3. Сколько энергии отдают вода и лед форме и окружающему ее воздуху в холодильнике, если начальная температура воды 12
, а температура образовавшегося льда -5
?
Задача 194. Какое количество теплоты пошло на приготовление в полярных условиях питьевой воды из льда массой 10 кг, взятого при температуре -20
, если температура воды должна быть равной 15
?
Задача 195.
Сколько энергии выделилось при отвердевании и охлаждении до 25
заготовки маховика массой 80 кг, отлитой из белого чугуна? Удельную теплоемкость чугуна принять равной удельной теплоемкости железа. Температура плавления чугуна 1165
.
Задача 196. Свинцовая деталь массой 100 г охлаждается от 427
до температуры плавления, отвердевает и охлаждается до 27
. Какое количество теплоты отдает деталь окружающим телам? (Удельную теплоемкость расплавленного свинца принять равной 170
.)
Задача 197. В железной коробке массой 300 г мальчик расплавил 100 г олова. Какое количество теплоты пошло на нагревание коробки и плавление олова, если их начальная температура была равна 32
?
Задача 198. Железная заготовка, охлаждаясь от температуры 800 до 0
, растопила лед массой 3 кг, взятый при 0
.
Какова масса заготовки, если вся энергия, выделенная ею, пошла на плавление льда?
Задача 199. Чтобы охладить 4,5 л воды от 30 до 10
, в воду бросают кусочки льда при 0
. Какое количество льда потребуется для охлаждения воды?
Задача 200. Для приготовления дроби расплавленный свинец при температуре плавления влили струями в воду с начальной температурой 17
. Сколько потребовалось воды, чтобы охладить 40 кг свинцовой дроби при конечной температуре воды не выше 47
?
Задача 201. В сосуд, содержащий воду массой 100 кг при температуре 10
, положили кусок льда, охлажденный до –50
. После установления теплового равновесия температура ледяной массы оказалась равной –4
. Какова масса куска льда?
Задача 202.
В калориметр налита вода массой 2 кг при температуре 5
и положен кусок льда массой 5 кг, имеющий температуру –4
. Определите температуру и объем содержимого калориметра после установления теплового равновесия. Теплоемкостью калориметра и теплообменом со средой пренебречь.
Задача 203. В сосуд, содержащий 10 кг воды при температуре 10
, положили кусок льда, охлажденный до –50
, после чего температура образовавшейся ледяной массы оказалась равной –4
. Какое количество льда было положено в сосуд?
Задача 204. Кусок свинца массой 1 кг расплавился наполовину при сообщении ему количества теплоты
Дж. Какова была начальная температура свинца?
Задача 205. Тигель, содержащий некоторое количество олова, нагревается электрическим током.
Выделяемое в единицу времени количество теплоты постоянно. За 10 мин температура олова повышается от 20 до 70
. Спустя еще 83 мин олово полностью расплавилось. Найти удельную теплоемкость олова.
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №39 с углубленным изучением отдельных предметов» города Чебоксары » Лабораторная физика (Осокина Г.Г.)
Лабораторная физика.
Программа и дидактические материалы элективного курса для предпрофильной подготовки учащихся 9-го класса по физике.
Программа курса. Пояснительная записка.
В соответствии с Концепцией профильного обучения наряду с базовыми общеобразовательными предметами вводится принципиально новый тип учебного предмета — элективные курсы — обязательные для посещения учащимися курсов по выбору.
Предлагаемый курс рассчитан на ученика средней школы, который в результате пробы должен выбрать будущее.
Программы предметно-ориентированных курсов по выбору включают углубление отдельных тем базовых общеобразовательных программ по физике, а также изучение некоторых тем, выходящих за рамки. Поэтому считаем целесообразным включение предметно-ориентированного элективного курса «Лабораторная физика» в систему предпрофильной подготовки учащихся по физике. Этот курс дополняет базовую программу, не нарушая ее целостности, дает учащимся сведения практического характера, выводит их на деятельностный подход.
Цель курса: способствовать углублению теоретических и практических знаний.
1) Овладение умениями проводить наблюдения, планировать и выполнять эксперименты, обрабатывать результаты измерений, применять полученные знания по физике для объяснения разнообразных физических явлений и свойств веществ, практического использования физических знаний.
2) Развитие познавательных интересов, интеллектуальных и творческих способностей в процессе выполнения экспериментальных исследований, решения задач, самостоятельного приобретения новых знаний.
3) Воспитание убежденности в возможности познания законов природы; необходимости сотрудничества в процессе совместного выполнения задач.
4) Использование приобретенных знаний для решения практических задач повседневной жизни, обеспечение безопасности жизнедеятельности в процессе использования транспортных средств, бытовых электроприборов, электронной техники.
Место курса в системе предпрофильной подготовки
Курс ориентирован на предпрофильную подготовку учащихся по физике. Он расширяет базовый курс по физике, является предметно ориентированным, знакомит с весьма распространенными методами решения физических задач, позволяет проверить способности к физике.
Содержание программы (17 ч.)
Тема 1. Архимедова сила.(2 ч.)
Действие жидкости и газа на погруженное в них тело. Архимедова сила. Плавание тел. Плавание судов. Воздухоплавание.
Тема 2.Тепловые явления.(2 ч.)
Количество теплоты.
Тема 3. Электрические явления.(3 ч.)
Сила тока. Электрическое напряжение. Электрическое сопротивление. Закон Ома. Последовательное и параллельное соединение проводников. Работа и мощность электрического тока. Закон Джоуля — Ленца.
Тема 4. Криволинейное движение.(3 ч )
Движение тела, брошенного горизонтально. Движение тела, брошенного под углом к горизонту.
Тема 5. Сила трения. Движение тела под действием силы трения.(3 ч.)
Сила внешнего трения. Сила трения покоя. Сила трения скольжения. Сила трения качения. Роль силы внешнего трения в жизни и в технике.
Тема 6. Кинематика периодического движения. (3 ч.)
Колебательное движение. Свободные колебания. Математический маятник. Пружинный маятник. Гармонические колебания. Величины, характеризующие гармоническое колебательное движение. Законы колебаний математического и пружинного маятника.
Тематический план курса.
|
№ п/п |
Тема |
Кол-во часов |
Виды деятельности |
|
1. |
Архимедова сила. Плавание тел. |
2 |
Лекция. Экспериментальная работа «Определение плотности данной жидкости». |
|
|
|
|
Решение задач |
|
2. |
Тепловые явления. |
2 |
Семинары. Лабораторная работа «Определение удельной теплоты парообразования воды». |
|
|
|
|
Решение задач. |
|
3. |
Электрические явления. |
3 |
Семинары. Лабораторная работа « Исследование зависимости общей мощности тока на лампочках от способа их включения при неизменном напряжении источника тока». |
|
|
|
|
Решение задач. |
|
4 |
Криволинейное движение. |
3 |
Лекция. Экспериментальная работа « Измерение модуля начальной скорости тела, брошенного горизонтально». |
|
|
|
|
Решение задач. |
|
5 |
Сила трения. Движение тела под действием силы трения. |
3 |
Лекция. Экспериментальная работа «Измерение модуля начальной скорости и времени торможения тела, движущегося под действием силы трения». |
|
|
|
|
Решение задач. |
|
6 |
Кинематика периодического движения. |
3 |
Семинары. Экспериментальная работа «Измерение массы колеблющегося тела». Решение задач. |
|
7 |
Итоговый зачет. |
1 |
Тестирование. |
|
|
Всего |
17 ч. |
|
|
|
|
|
|
Формы проведения занятий.
1. Лекции, семинары.
2. Экспериментальные, лабораторные работы.
3. Работа с рекомендованной литературой.
4. Самостоятельное решение предложенных задач с последующим разбором вариантов решения.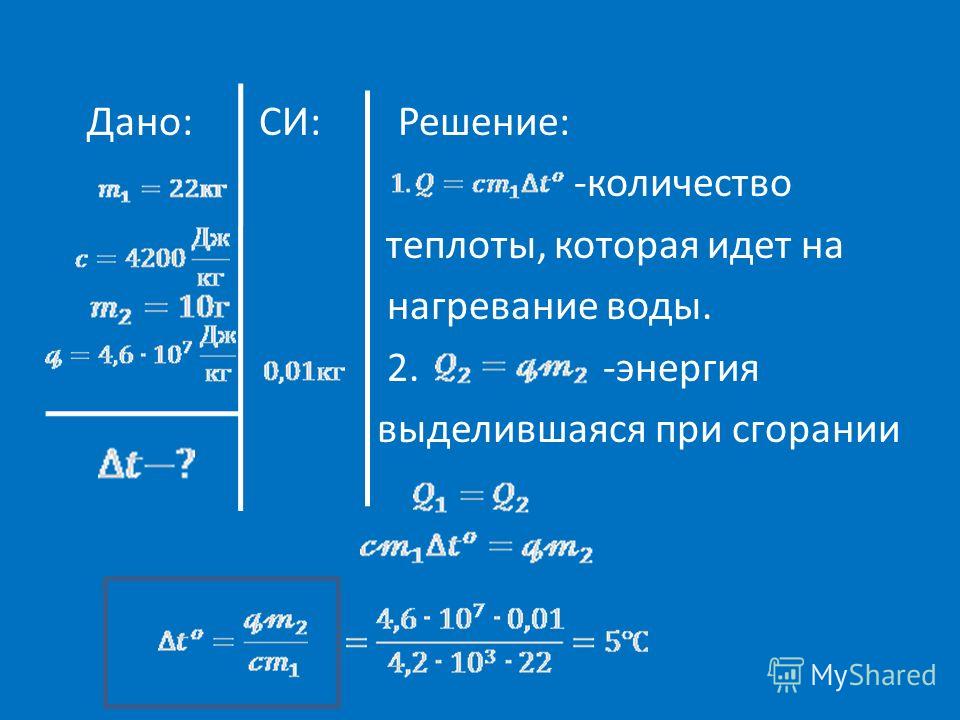
1. Архимедова сила. Плавание тел.
Экспериментальная работа «Определение плотности данной жидкости».
Оборудование: динамометр, латунная гиря массой 200 г, стакан с жидкостью, плотность которой надо определить.
Решение задач. Предлагаемые задачи.
— С какой силой тело объемом 1 дм3 будет выталкиваться из ртути?
— Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?
— Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?
— Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
— Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?
— Кусок мрамора в воздухе весит 5,4 Н, а когда его поместили в жидкость, то динамометр показал 3,8 Н. Объем мрамора 0,2 дм3 . В какую жидкость был помещен кусок мрамора?
— Шар, на который действует сила тяжести 0,2 Н, погружен в воду.
— Чему равна грузоподъемность судна, водоизмещение которого в морской воде без груза 30000 кН, а при полной нагрузке — 50000 кН.
— Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать).
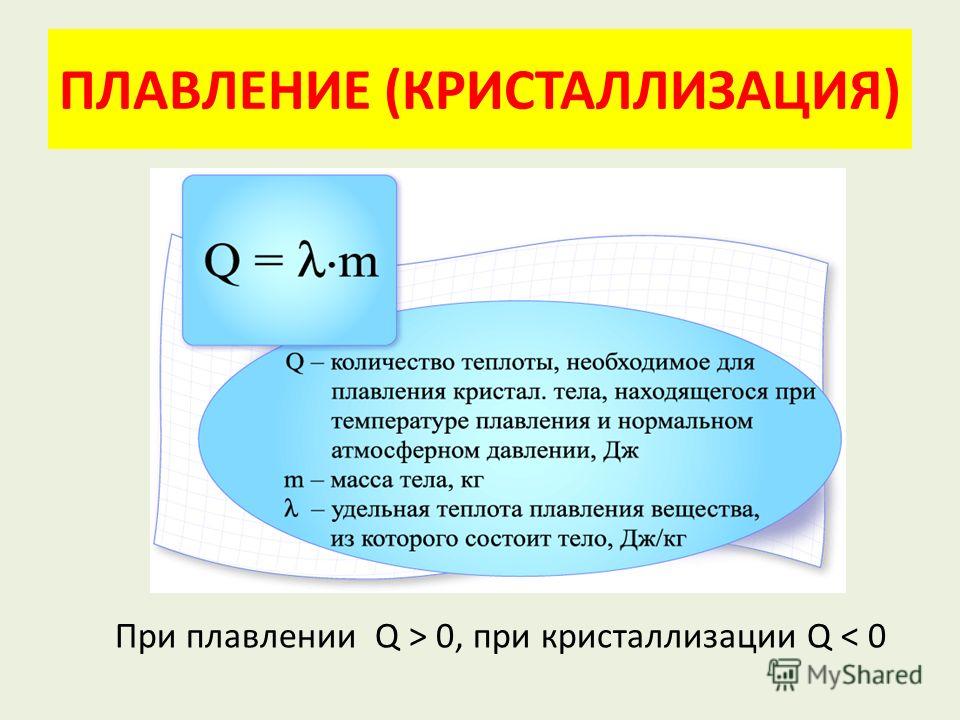
2. Тепловые явления.
Лабораторная работа «Определение удельной теплоты парообразования воды.
Оборудование: электроплитка, сосуд с водой, часы, термометр, калориметр.
Выполнение работы:
Нальем в калориметр 50 г воды и поставим на электроплитку. Будем считать, что калориметр принимает от плитки в единицу времени количество теплоты q. Измерим время τ1, необходимое для того, чтобы вода нагрелась от 80 до 90ºС. Затем измерим время
Поскольку значения температуры 80-90 и 100ºС близки, будем считать, что полезная тепловая отдача плитки ηq в обоих случаях одинакова.Решение задач. Предлагаемые задачи.
— Какое количество теплоты выделилось при охлаждении чугунной болванки массой 32 кг, если ее температура изменилась от 1115 до 15ºС.
— В алюминиевой кастрюле массой 800 г нагревается вода объемом 5 л от 10ºС до кипятка. Какое количество теплоты пойдет на нагревание кастрюли и воды?
— Сколько энергии требуется для плавления куска свинца массой 0,5 кг, взятого при температуре 27 ºС.
— Какое количество теплоты необходимо, чтобы из льда массой 2 кг, взятого при 10 ºС, получить пар при 100 ºС?
— В двигателе мотороллера сгорело 2,5 кг бензина. Вычислите КПД двигателя, если им было произведено 2,3 х 104 кДж полезной работы.
3. Электрические явления.
Лабораторная работа ««Исследование зависимости общей мощности тока на лампочках от способа их включения (последовательное или параллельное) при неизменном напряжении источника тока».
Оборудование: две электрические лампы на подставке, источник тока, амперметр, вольтметр, соединительные провода, ключ.
Решение задач. Предлагаемые задачи.
— Какую работу совершит ток в электродвигателе за 90 с, если при напряжении 220 В сила тока в обмотке двигателя равна 0,2 А?
— Определите мощность тока в электрической лампочке, если при напряжении 5 В сила тока в ней 100 мА.
— Какое количество теплоты выделится в реостате сопротивлением 50 Ом за 2 мин при силе тока в цепи 2 А?
— На сколько градусов за 5 мин можно нагреть на электроплитке 1,5 кг воды, если при напряжении 220 В сила тока в ней 5 А? Потерями энергии пренебречь.
— За какое время можно с помощью электрического кипятильника мощностью 500 Вт нагреть 500 г воды в стакане от 20 ºС до кипения?
4. Криволинейное движение.
Экспериментальная работа «Измерение модуля начальной скорости тела, брошенного горизонтально».
Приборы и материалы: резинка ученическая (ластик), лента измерительная с сантиметровыми делениями.
Порядок выполнения работы.
1. Положите ластик на край стола и сообщите ему щелчком пальца некоторую скорость в горизонтальном направлении. Заметьте место падения ластика на полу.
2. Выполните необходимые измерения и вычислите модуль начальной скорости ластика.
3. Результаты измерений и вычислений запишите в тетрадь.
4. Ответьте на вопросы:
а) По какой траектории двигался ластик?
б) Какая сила действовала на ластик во время его движения?
в) Как направлены векторы скорости, ускорения и силы, действующие на ластик во время движения?
г) Изобразите их направления для какой — либо точки траектории.
5. Это задание представляет собой экспериментальную задачу. Цель задания: расширить навыки учащихся в решении экспериментальных задач. В задании учащиеся сами должны выяснить, какие измерения необходимо выполнить, чтобы решить задачу.
Время выполнения задания 8-10 мин.
Решение задач. Предлагаемые задачи:
— Тело упало с высоты 45м. Каково время падения тела?
— Мальчик бросил горизонтально мяч из окна, находящегося на высоте 20м. Определите, с какой скоростью был брошен мяч, если он упал на расстоянии 6 м от основания дома.
— Мальчик бросил вертикально вверх мяч и поймал его через 2с. На какую максимальную высоту поднялся мяч?
— Камень, брошенный горизонтально с высоты 2м над землей, упал на расстоянии 7м. Найдите начальную и конечную скорости мяча.
— Тело, брошенное с поверхности земли вертикально вверх со скоростью 30 м/с, дважды побывало на высоте 40м. Какой промежуток времени разделяет эти два события?
— Тело брошено под углом 60º к горизонту с начальной скоростью 30 м/с. На какой высоте вектор скорости составит угол 45º с горизонтом?
5. Сила трения. Движение тела под действием силы трения.
Экспериментальная работа «Измерение модуля начальной скорости и времени торможения тела, движущегося под действием силы трения».
Приборы и материалы: брусок от лабораторного трибометра, динамометр учебный, лента измерительная с сантиметровыми делениями.
Порядок выполнения работы:
1. Положите брусок на стол и заметьте его начальное положение на столе.
2. Толкните слегка брусок рукой и заметьте его новое положение на столе.
3. Измерьте тормозной путь бруска относительно стола.
4. Измерьте модуль веса бруска и вычислите его массу.
5. Измерьте модуль силы трения скольжения бруска по столу.
6. Зная массу, тормозной путь и модуль силы трения скольжения, вычислите модуль начальной скорости и время торможения бруска.
7. Результаты измерений и вычислений запишите в тетрадь.
Задание выполняют при изучении движения тела под действием силы трения, после вывода формулы тормозного пути и времени торможения тела. Модуль силы трения и массу тела измеряют динамометром, тормозной путь – измерительной лентой.
Время выполнения задания «12-15 мин.
Решение задач. Предлагаемые задачи:
— Автомобиль, двигаясь равномерно, проходит путь 20м за 4с. после чего начинает тормозить и останавливается через 10 с. Определите ускорение и тормозной путь автомобиля?
— Автомобиль движется со скоростью 10 м/с по гладкой горизонтальной дороге. Пройдя с выключенным мотором расстояние 150 м, автомобиль останавливается. Сколько времени автомобиль двигался с выключенным мотором и каков коэффициент трения при его движении?
— Лыжник массой 60 кг имеющий в конце спуска скорость 10м/с останавливается через 40с после окончания спуска. Определить величину силы сопротивления.
— Тело скользит равномерно по наклонной плоскости с углом наклона 30º. Определите коэффициент трения тела о плоскость.
— С какой наибольшей скоростью может ехать мотоциклист по горизонтальной плоскости, описывая дугу радиусом 80 м, если коэффициент трения резины о почву 0,4? На какой угол от вертикального положения он при этом отклоняется?
6.
Кинематика периодического движения.
Лабораторная работа «Измерение массы колеблющегося груза».
Приборы и материалы: цилиндр металлический из набора тел для калориметра, шнур резиновый сечением 1х1 мм длиной 150 мм с петлей на конце, динамометр учебный, груз массой 100 г с двумя крючками, линейка измерительная длиной 30 см с миллиметровыми делениями, метроном электронный (один на класс).
Порядок выполнения работы:
1. Подвесьте к шнуру металлический цилиндр. Измерьте период его вертикальных колебаний с помощью метронома.
2. Вычислите жесткость шнура.
3. Зная жесткость шнура и период колебаний цилиндра, вычислите его массу.
4.Измерьте массу цилиндра с помощью динамометра.
5.Вычислите абсолютную погрешность для первого и второго измерений массы цилиндра. 6.Результаты измерений и вычислений запишите в тетрадь. Какой из способов измерений массы цилиндра оказался точнее?
Работа представляет собой экспериментальное задание.
Его выполняют при решении задач с использованием формулы периода колебаний пружинного маятника. Цель – ознакомить учащихся с одним из возможных косвенных способов измерения массы тела с помощью пружинного маятника. Наибольшая трудность выполнения задания состоит в измерении периода колебаний маятника, так как время его колебаний небольшое и равно 10 -15 с. Поэтому измерение следует провести несколько раз. Один ученик измеряет время колебаний, а другой считает число полных колебаний. Особое внимание обращают на совпадение моментов запуска колебаний и начала отсчета времени.
Время выполнения задания ≈ 15 мин.
Решение задач. Предлагаемые задачи:
— Математический маятник длиной 2,45 м совершил 100 колебаний за 314 с. Определить ускорение свободного падения для данной местности.
— Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1.
6 .
— Груз массой 0,4 кг, подвешенный к невесомой пружине, совершает 30 колебаний в минуту. Чему равна жесткость пружины?
— Груз массой 400г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
— Два маятника отклонены от своих положений равновесия и одновременно отпущены. Первый маятник с длиной подвеса 2м совершил за некоторый промежуток времени 15 колебаний. Какова длина второго маятника?
Наиболее подходящей формой аттестации учащихся для элективных заданий может быть оценка результатов самостоятельного выполнения экспериментальных заданий. При написании отчетов о выполненных экспериментах учащиеся должны выделять главные признаки наблюдаемых явлений, формулировать обязательные условия осуществления опыта, кратко и логически последовательно излагать свои мысли.
Итоговый зачет проводится по тесту.
Литература.
1. Л.Б. Милковская. Повторим физику. Москва «Высшая школа», 1977.
2. И.Г. Власова. Справочник школьника. Филологическое общество «Слово»,1996.
3. А.Е. Марон, Е.А. Марон. Дидактические материалы. Физика. 7, 8, 9 класс.
4. Ю.Я. Иванов. Творческие экспериментальные задания по физике для 7-8 классов. Чебоксары, 2003.
5. В.А. Буров, А.И. Иванов, В.И. Свиридов. Фронтальные экспериментальные задания по физике. Москва. «Просвещение», 1987.
6. Л.А. Кирик. Физика. Самостоятельные и контрольные работы. «Илекса» Москва, 2005.
Дидактическая игра
Дидактическая играИгры? Не только…С.А. ТРУБАЧЕЕВА,
дер. Алагуй, Иркутская обл.
8-й класс
1. Электрические явления
Класс разбивается на две группы, а каждая
группа – на команду участников и «болельщиков».
В каждом конкурсе участвуют по одному-два
представителя от команды, им выдаются карточки с
номерами 1, 2, 3, 4, 5.
Вопросы составляются так, чтобы
на них можно было ответить, подняв один номер. В
задании с логическими цепочками нужно поднять
две карточки с номерами, которые нужно
переставить, чтобы формула (или выражение) стала
верной. Столы в классе следует расставить так,
чтобы каждая команда сидела за своим столом.
I тур
На доске портреты ученых-физиков: Ш.Кулона, Э.Резерфорда, А.Ампера, А.Вольта, Г.Ома. Назовите ученого, о котором говорится в вопросе, и покажите его портрет:
1) итальянский физик, один из основателей учения об электрическом токе, создавший первый гальванический элемент;
2) немецкий физик, открывший закон, выражающий связь между силой тока в цепи, напряжением и сопротивлением;
3) ученый, изучавший строение атома;
4) известный французский физик, военный инженер; изобрел прибор, с помощью которого установил основные законы электрического и магнитного взаимодействия.
II тур
На столе находятся амперметр, вольтметр,
электрофорная машина, аккумулятор.
Назовите и
покажите прибор:
1) которым измеряют силу тока в цепи;
2) который является источником тока;
3) которым пользуются для измерения напряжения.
III тур
На доске написаны обозначения физических величин: I, U, R, r, q. Как обозначаются:
1) напряжение;
2) электрический заряд;
3) сила тока;
4) удельное сопротивление?
IV тур
На доске написаны условные обозначения, применяемые на схемах:
Как обозначается:
1) соединение приводов;
2) электрическая лампа;
3) плавкий предохранитель;
4) ключ;
5) гальванический элемент или аккумулятор?
V тур
На доске написаны обозначения единиц физических величин: 1 Ом; 1 Кл; 1 А; 1 Ом • мм2/м; 1 В. Покажите:
1) единицу сопротивления;
2) единицу напряжения;
3) единицу силы тока.
VI тур
На гранях десяти кубиков – буквы. Из десяти букв, выпавших при бросании этих кубиков, составьте слова, являющиеся именами существительными в единственном числе, именительном падеже, которые обозначают физические термины. Подберите слова-физические термины, которые начинаются на каждую выпавшую букву.
Кто придумает больше слов?
VII тур
На доске написаны логические цепочки и формулы, в каждой из которых допущена ошибка. Найдите ее и исправьте:
1)
2)
3)
VIII тур
Выберите правильный ответ.
1) Если напряжение на концах проводника 6 В, его сопротивление 3 Ом, то сила тока равна:
А) 12 А; Б) 2 А;
В) 0,5 А.
2) Работа электрического тока на участке цепи за 5 с при напряжении 10 В и силе тока 2 А равна:
А) 20 Дж;
Б) 50 Дж;
В) 100 Дж.
3) Мощность тока, выделяемая на участке цепи за 5 с при напряжении 10 В и силе тока 2 А, равна:
А) 20 Вт;
Б) 10 Вт;
В) 4 Вт.
4) Если длина константанового провода 10 м, площадь поперечного сечения 2 мм2, удельное сопротивление константана 0,5 Ом • мм2/м, то электрическое сопротивление такого провода равно:
А) 0,4 Ом;
Б) 2,5 Ом;
В) 10 Ом.
IX тур
За 2 мин всей командой придумайте как можно больше предложений, в которых используется слово сопротивление.
2. Изменение агрегатных состояний вещества
Играют командами. На доску вывешивается красочно оформленный маршрут путешествия.
Остановка 1. Каждая команда решает две качественные задачи.
1. Почему на Севере для измерения температуры воздуха пользуются не ртутными термометрами, а спиртовыми?
2. Наблюдали бы мы привычные нам изменения в природе весной, если бы удельная теплота плавления льда была так же мала, как у ртути?
1′. В чем проявляется закон сохранения и превращения энергии при плавлении и кристаллизации вещества?
2′.Два одинаковых сосуда из полиэтилена заполнили водой, температура которой 0 °С. Один сосуд поместили в воду, другой – в измельченный лед, имеющий, как и окружающий воздух, температуру 0 °С. Замерзнет ли вода в каком-нибудь из этих сосудов?
Два одинаковых сосуда из полиэтилена
заполнили водой, температура которой 0 °С. Один
сосуд поместили в воду, другой – в измельченный
лед, имеющий, как и окружающий воздух,
температуру 0 °С. Замерзнет ли вода в
каком-нибудь из этих сосудов?Остановка 2. Каждая команда решает свой кроссворд.
Первая команда
1. Одна из частей двигателя внутреннего сгорания. 2. Процесс перехода жидкости в газообразное состояние. 3. Переход вещества из твердого состояния в жидкое. 4. Двигатель, в котором внутренняя энергия топлива превращается в механическую энергию. 5. Переход вещества из жидкого состояния в твердое. 6. Способ образования пара. 7. Явление превращения пара в жидкость.
Вторая команда
1. Тип теплового двигателя, в котором пар
вращает вал двигателя без помощи поршня, шатуна и
коленчатого вала. 2. Обозначение удельной
теплоты плавления. 3. Одна из частей двигателя
внутреннего сгорания.
4. Такт цикла двигателя
внутреннего сгорания. 5. Переход вещества из
жидкого состояния в твердое.
6. Парообразование, происходящее с поверхности
жидкости.
Остановка 3. Командам выдаются модели двигателей внутреннего сгорания.
1. Из каких основных частей состоит двигатель внутреннего сгорания?
2. Изобразите схему работы теплового двигателя.
Остановка 4. Решите задачи.
1. Сколько энергии требуется для плавления куска свинца массой 0,5 кг, взятого при температуре 27 °С?
2. Какое количество теплоты необходимо для превращения в пар воды массой 10 г, имеющей температуру кипения?
3. Сколько энергии необходимо для плавления бруска цинка массой 0,5 кг, взятого при температуре 20 °С?
4. Какое количество теплоты необходимо для превращения в пар спирта массой 2 г, имеющего температуру 78 °С?
Остановка 5. Напишите:
– единицу удельной теплоты плавления;
– формулу для вычисления количества теплоты, необходимого для превращения в пар жидкости массой m;
– формулу для вычисления количества теплоты, необходимого для плавления кристаллического тела массой m;
– единицу удельной теплоты парообразования.
.
Математическая задача: Расплав свинца — вопрос № 49341, основы физики
Найдите теплоту, необходимую для плавления предмета из свинца массой 250 г при начальной температуре 35°С. Свинец плавится при 327°С при нормальном давлении. Массовая теплоемкость свинца c = 129 Дж/кг • K и массовая скрытая теплота свинца lt (t — нижний индекс) = 22,6 кДж/кг.
Правильный ответ:
Q = 15,067 кДжПошаговое объяснение:
м=250 г→ кг=250:1000 кг=0,25 кг t1=35 °C t2=327 °C c= 129Дж/кг/К l=22,6 кДж/кг T=t2−t1=327−35=292KQQ1=m⋅c⋅T=0,25⋅129⋅292=9417JQ2=l⋅m=22,6 ⋅ 0,25=20113=5,65 кДж Q=Q1/1000+Q2=9417/1000+5,65=15,067 кДж
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Благодарю вас!
Советы для связанных онлайн-калькуляторов
Вы хотите перевести единицы массы?
Для решения этой задачи по математике вам необходимо знать следующие знания:
Единицы физических величин:
- MASS
- Конверсия единицы
- Energy
- Температура
Темы, темы:
- Основы физики
Слова Проблема:
- . olds
olds- Скрытая теплота
Сколько теплоты необходимо взять из 100 г воды при 20°C, чтобы охладить до состояния льда при -18°C? Массовая теплоемкость с (лед) = 21 кДж/кг/°С; с (вода) = 4,19КДж/кг/°С, а массовая групповая теплота затвердевания воды l = 334 кДж/кг - Теплопередача
Мы поместили свинцовый предмет массой 0,4 кг и температурой 250°С в 0,4 л воды. Какой была начальная температура воды t2, если температура тела и воды после достижения равновесия была 35°С? Будем считать, что теплообмен происходил только между свинцом o - Получающим тепло
На сколько градусов Цельсия был нагрет на водяной бане железный цилиндр массой 300 г, если он получил тепло 7,2 кДж? (удельная теплоемкость железа c = 0,46 кДж/кг/ºC) - Алюминий
Мы поместили алюминиевый предмет массой 0,80 кг и температурой 250°С в воду массой 1,6 кг и температурой 23°С. Какова будет температура системы после достижения равновесия? Предположим, что теплообмен произошел только между - Льдом и кипящей водой
Рассчитайте количество теплоты, необходимое для превращения 5 кг льда с температурой -5°С в воду с температурой 100°С. с (вода) = 4200 Дж/°С/кг, с (лед) = 2100 Дж/°С/кг. Массовая групповая теплота затвердевания воды l = 334 кДж/кг. Вычислите тепло, которое 1k - Температура 38971
Цинковое тело имеет объем 20 дм³. Какое тепло необходимо, чтобы нагреть его от температуры 25 до 100 градусов Цельсия? Чему равна теплоемкость этого тела С (единица Дж/К)? - Температура 63004
Латунь массой 2,5 кг поглощает тепло 180 кДж. Как изменится температура латуни? Удельная теплоемкость латуни 0,36 кДж/Кл - Ванна
В бане вода объемом 220 л и температурой 65°С. Найдите массу m 2 воды температурой 15°С нужно налить, поэтому в результате температура в бане будет 40°С. Пренебрегаем теплообменом между водой и окружающей средой. Масса - Рассчитайте 71684
Рассчитайте массу воды, которая выделила 520,5 кДж тепла при охлаждении с 69 °C до 27 °C. - Температура 16633
Какое количество теплоты необходимо для подачи медного тела массой 8 кг, чтобы повысить его температуру на 136 градусов Цельсия? - Экстремальные температуры
На США обрушилась экстремальная жара. Рассчитайте процент изменения температуры воздуха от нормальной летней температуры 23 °С до 40 °С. - Температура 7477
Бассейн длиной l = 50 м и шириной s = 15 м имеет глубину h2 = 1,2 м в самой мелкой части стенки. Затем глубина постепенно увеличивается до глубины h3 = 1,5 м в середине бассейна. = 4,5 м стены в самой глубокой части бассейна. - Температура 7595
Бесцветная жидкость массой m = 200 г нагревается при постоянном перемешивании на плите мощностью P0 = 600 Вт. 80% подводимой энергии используется для нагрева жидкости. Выбранные измеренные значения температуры жидкости в зависимости от времени записываются в t - Плита электрическая
За какое время электрическая плита потребляемой мощностью P = 500 Вт и КПД n = 75% нагреет воду массой m = 2 кг и температурой t1 = 10°С до точки кипения (t2 = 100 °С). Удельная теплоемкость воды с = 4 180 Дж. кг-1. К-1 - Термометр
Погрузить термометр теплоемкостью 2,0 Дж. К-1 в воду массой 67,0 грамм. До погружения в воду термометр показывал температуру 17,8 градусов по Цельсию. После достижения равновесия температура составляет 32,4 градуса. Какая была вода те - Температура 61484
Воздушный пузырь на дне озера на глубине h = 21 м имеет радиус r1 = 1 см при температуре t1 = 4 °C. Пузырь медленно поднимается к поверхности, и его объем увеличивается. Рассчитайте его радиус при выходе на поверхность озера, с температурой - индекс ИМТ
Рассчитайте ИМТ (индекс массы тела, индекс, указывающий на ожирение, избыточный вес, нормальный вес, недостаточный вес) человека массой m = 70 кг и ростом h = 156 см. Индекс рассчитывается по уравнению (формуле): ИМТ = (м)/(ч²) При индексе ИМТ возможно t
с (вода) = 4200 Дж/°С/кг, с (лед) = 2100 Дж/°С/кг. Массовая групповая теплота затвердевания воды l = 334 кДж/кг. Вычислите тепло, которое 1k
Рассчитайте процент изменения температуры воздуха от нормальной летней температуры 23 °С до 40 °С.
До погружения в воду термометр показывал температуру 17,8 градусов по Цельсию. После достижения равновесия температура составляет 32,4 градуса. Какая была вода те- all math problems15548
- algebra 4299
- arithmetic 2901
- basic functions 4657
- combinatorics 801
- geometry 2566
- goniometry and trigonometry 472
- numbers 4463
- physical quantity 4786
- planimetrics 2784
- solid геометрия 1951
- статистика 571
- темы, темы 2229
-
- новые математические задачи
- самые просматриваемые математические задачи
- Самые сложные задачи
- Самые простые задачи со словами
ChemTeam: задачи по термохимии — нужно два уравнения
ChemTeam: Проблемы термохимии — нужны два уравненияЗадачи по термохимии:
Необходимо два уравнения
| Перейти к файлу графика время-температура | Проблемы с использованием четырех частей графика Т-Т |
| Проблемы с использованием одной части графика Т-Т | Проблемы с использованием пяти частей графика Т-Т |
| Задачи с использованием трех частей графика Т-Т | Вернуться в меню термохимии |
Пример №1: Сколько кДж требуется, чтобы нагреть 45,0 г H 2 O при 25,0 °C и затем все это выкипятить?
Решение:
Комментарий: Мы должны сделать два вычисления, а затем просуммировать ответы.
1) В первом расчете используется это уравнение:
q = (масса) (Δt) (C p )Это резюмирует необходимую информацию:
Δt = 75,0 °C
Масса = 45,0 г
C p = 4,184 Дж г¯ 1 °C¯ 1
2) Подставляя, имеем:
q = (45,0 г) (75,0 °С) (4,184 Дж г¯ 1 °С¯ 1 )q = 14121 Дж = 14,121 кДж
3) Второй расчет использует это уравнение:
q = (моль воды) (ΔH vap )Это резюмирует необходимую информацию:
ΔH vap = 40,7 кДж/моль
Масса = 45,0 г
Молярная масса H 2 O = 18,0 г/моль
4) Подставляя, получаем:
q = (45,0 г / 18,0 г моль¯ 1 ) (40,7 кДж/моль)q = 101,75 кДж
5) Добавление:
101,75 кДж + 14,121 кДж = 116 кДж (до трех знаков)
Пример #2: Сколько кДж нужно удалить из образца воды массой 120,0 г при начальной температуре 25,0 °C, чтобы заморозить ее при 0 °C? (Область три, затем область два на графике время-температура.
)
Решение:
1) Первый расчет:
q = (масса) (Δt) (C p )q = (120,0 г) (25,0 °С) (4,184 Дж г¯ 1 °С¯ 1 )
q = 12 552 Дж = 12,552 кДж
2) Второй расчет:
q = (моль воды) (ΔH vap )q = (120,0 г / 18,0 г моль¯ 1 ) (6,02 кДж/моль)
q = 40,13 кДж
3) Суммируя значения двух шагов, получаем 52,8 кДж (три знака рис.).
Пример №3: Вам дали 12,0 г льда при температуре -5,00 °C. Сколько энергии нужно, чтобы полностью растопить лед до воды?
Решение:
1) Первый расчет:
q = (масса) (Δt) (C p )q = (12,0 г) (5,0 °C) (2,06 Дж г¯ 1 °C¯ 1 )
q = 123,6 Дж = 0,1236 кДж
2) Второй расчет:
q = (моль воды) (ΔH vap )q = (12,0 г / 18,0 г моль¯ 1 ) (6,02 кДж/моль)
q = 4,0133 кДж
3) Суммируя значения двух шагов, получаем 4,14 кДж с точностью до трех значащих цифр.
Пример №4: Свинец имеет температуру плавления 327,5 °C, удельную теплоемкость 0,128 Дж/г ⋅ °C, молярную энтальпию плавления 4,80 кДж/моль. Какое количество теплоты в килоджоулях потребуется, чтобы нагреть образец свинца массой 500,0 г от 23,0 °С до его температуры плавления и затем расплавить его?
Решение:
1) Требуются два расчета:
1) нагреть утюг с 23,0 до 327,5
2) расплавить железо на 327,5
2) Вот настройки расчета:
q 1 = (500,0 г) (304,5 °C) (0,128 Дж/г ⋅ °C) = 19488 Дж
q 2 = (500,0 г / 55,845 г/моль) (4,80 кДж/моль) = 42,976 кДж
3) Добавить:
19,488 кДж + 42,976 кДж = 62,5 кДж (до трех цифр)Обратите внимание, что перед добавлением я изменил 19488 Дж на кДж.
Пример №5: Удельная теплоемкость серебра составляет 0,235 Дж/г-К. Температура плавления 962,0 °С, энтальпия плавления 11,3 кДж/моль.
Какое количество энергии в джоулях требуется для превращения 9,10 г серебра из твердого состояния при 25,0 °С в жидкое состояние при 962 °С?
Решение:
1) Требуются два расчета:
1) каленое серебро от 25,0 до 962
2) плавить серебро на 962
2) Вот настройки расчета:
q 1 = (9,10 г) (937,0 К) (0,235 Дж/г-К) = 2003,77 Дж
q 2 = (9,10 г / 107,87 г/моль) (11,3 кДж/моль) = 0,953277 кДж = 953,277 Дж
3) Ответ:
2003,77 Дж + 953,277 Дж = 2957,047 ДжИнжир до трех знаков, 2960 Дж
Обратите внимание, как я использую 937,0 К. Это потому, что это разница, а не фактическая температура. Разница между 962,0 ° C и 25,0 ° C составляет 937,0 K. Вы можете увидеть это, преобразовав два значения Цельсия в их значения Кельвина, а затем вычтя. Вы получите 937,0 К за разницу.
Пример #6: Какая масса CCl 2 F 2 (теплота парообразования = 289 Дж/г) должна испариться, чтобы заморозить 210 г воды при начальной температуре 24,0 °C? (теплота плавления воды 334 Дж/г, удельная теплоемкость воды 4,184 Дж/г К)
Решение:
1) Определим, какое количество теплоты необходимо для охлаждения воды и ее замерзания:
холодная вода с 24 до 0:q 1 = (210 г) (24 К) (4,184 Дж/г К)q 1 = 21087,36 Дж
заморозить воду:
q 2 = (210, г) (334 Дж/г)q 2 = 70140 Дж
добавить их:
q 1 + q 2 = 91227,36 Дж
2) Определим массу CCl 2 F 2 необходимо:
91227,36 Дж / 289 Дж/г = 316 г (до трех цифр)
Пример №7: Сколько тепловой энергии требуется для преобразования 98,1 г жидкого диоксида серы SO 2 при 200 К в газообразный SO 2 при 263 К? Молярная теплота парообразования SO 2 равна 24,9 кДж/моль, а удельная теплоемкость жидкого SO 2 равна 1,36 Дж г¯ 1 °С¯ 1 .
Решение:
1) Чтобы ответить на этот вопрос, нам нужно знать температуру кипения SO 2 . Глядя вверх, мы находим 14 ° C, что преобразуется в 263 K.
2) Нагрейте жидкость до точки кипения:
q = (масса) (Δt) (удельная теплоемкость)q = (98,1 г) (63 °C) (1,36 Дж/г °C)
q = 8405,208 Дж
3) Выпарить жидкость:
q = (моль) (молярная теплота плавления)q = (98,1 г / 64,0638 г/моль) (24,9 кДж/моль) = 38,129 кДж
3) Добавьте их:
8,405208 кДж + 38,129 кДж = 46,5 кДж
Пример #8: Рассчитайте количество тепла, необходимое для плавления 77,9 г твердого октана (C 8 H 18 ) и доведения его до температуры 119°С. (Молярная теплота плавления октана составляет 21 кДж/моль. Его молярная масса составляет 114,23 г/моль, а удельная теплоемкость жидкого октана составляет 255,68 Дж К¯ 1 моль¯ 1 .
)
Решение:
1) Первое, что нужно сделать, это предположить, что октан находится в твердом состоянии и находится при температуре плавления. Рассчитайте энергию, необходимую для плавления 77,9 г твердого октана при его температуре плавления:
q = (моль) (молярная теплота плавления)q = (77,9 г / 114,23 г/моль) (21 кДж/моль)
q = 14,3211 кДж
2) Следующий шаг требует от нас знания температуры плавления и точки кипения октана. Итак, мы смотрим на эти значения и находим, что они составляют -57,0 ° C и 126 ° C. Это означает, что наш образец с октановым числом не закипит. Все, что нам нужно сделать сейчас, это рассчитать энергию, необходимую для нагревания октана с -57,0 °C до 119 °C:
q = (моль) (Δt) (удельная теплоемкость)q = (77,9 г / 114,23 г/моль) (176 К) (255,68 Дж К¯ 1 моль¯ 1 )
q = 30687,867 Дж
3) Добавьте их:
14,3211 кДж + 30,6879 кДж = 45,009 кДжДва знака инжира кажутся разумными, поэтому 45 кДж — это окончательный ответ.
4) Комментарии:
(a) Обратите внимание на единицу удельной теплоемкости на шаге 2, что заставило меня вычислить моли, а не использовать массу.(b) Я также выполнил плавное преобразование из градусов Цельсия в кельвины на шаге 2. Поскольку 176 — это разность , я могу опустить °C и заменить K. Это основано на том факте, что «размер 1 ° C равен «размеру» 1 К.
(c) Если вы посмотрите на температуру кипения и точку плавления октана, вы обнаружите, что они даны в виде диапазона, а не в виде одного значения. Это связано с тем, что октан представляет собой смесь множества изомеров C 8 H 18 . Получить их все слишком дорого, поэтому, в зависимости от небольших различий в составе тестируемого вами образца C 8 H 18 , вы получите небольшие различия в температурах плавления и кипения от образца к образцу. Я использовал одно значение для целей этого вопроса.
Пример #9: Блок железа массой 3,60 кг при температуре 807,0°C был помещен в изолированный от окружающей среды контейнер, содержащий 1,00 л воды при температуре 30,0°C.
Процесс охлаждения железа происходит в два этапа: на первом этапе вода нагревается до точки кипения, а на втором этапе вода испаряется. Эта фаза продолжается до тех пор, пока температура утюга не сравняется с температурой воды. Конечная температура воды и железа составляет 100,0 °С. Сколько литров жидкой воды останется в конце процесса? (Удельная теплоемкость твердого железа 0,450 Дж·г¯ 1 K¯ 1 , а теплота парообразования для воды равна 2259,23 Дж/г.)
Решение:
1) Мы знаем, что произойдет с железом: оно останется твердым и упадет в общей сложности на 707 °C. Сколько тепловой энергии выделяется?
q = (3600 г) (707,0 К) (0,450 Дж г¯ 1 К¯ 1 ) = 1145340 ДжОбратите внимание, что я использовал 707 K, а не 707 °C. Это допускается, так как это разница температур и 1 К равен 1 °С по «размеру».
2) Определим, какое количество теплоты необходимо для нагрева 1,00 л воды с 30,0 до 100,0 °С.
q = (1000 г) (70,0 °C) (4,184 Дж g¯ 1 °C¯ 1 ) = 292880 ДжОбратите внимание на бесшумное изменение 1,00 л на 1000 г.
3) Сколько энергии осталось?
1145340 − 292880 = 852460 Дж
4) Определить количество воды, которое испарилось бы при 852460 Дж.
852460 Дж / 2259,23 Дж/г = 377,3 г
5) Какой объем жидкой воды останется?
1000 — 377,3 = 622,7 гИспользуя плотность воды, это 622,7 мл.
до трех знаков инжира, 0,623 л — окончательный ответ.
Пример #10: Было использовано несколько пакетов со льдом, содержащих 1300 г замороженной воды при температуре 0°C, и в конце концов температура воды составила 32,0°C. Сколько килоджоулей тепловой энергии поглотила вода?
Решение:
1) Растопим лед:
q 1 = (1300 г / 18,015 г/моль) (6,02 кДж/моль)q 1 = 434,416 кДж
2) Подогреем уже жидкую воду:
q 2 = (1300, г) (32,0 °С) (4,184 Дж/г¯ 1 °С¯ 1 )q 2 = 174054,4 Дж = 174,0544 кДж
3) Добавьте их:
434,416 + 174,0544 = 608 кДж (до трех цифр)
| Перейти к файлу графика время-температура | Проблемы с использованием четырех частей графика Т-Т |
| Проблемы с использованием одной части графика Т-Т | Проблемы с использованием пяти частей графика Т-Т |
| Задачи с использованием трех частей графика Т-Т | Вернуться в меню термохимии |
Как рассчитать поглощение тепла
Обновлено 23 апреля 2018 г.
Ли Джонсон
В повседневном языке люди используют термины «тепло» и «температура» как синонимы. Однако в области термодинамики и физики в более широком смысле эти два термина имеют очень разные значения. Если вы пытаетесь рассчитать, сколько тепла поглощается чем-то при повышении его температуры, вам нужно понимать разницу между ними и как рассчитать одно из другого. Вы можете сделать это легко: просто умножьте теплоемкость вещества, которое вы нагреваете, на массу вещества и изменение температуры, чтобы найти поглощенное тепло.
TL;DR (Too Long; Didn’t Read)
Calculate heat absorption using the formula:
Q = mc ∆ T
Q means the heat поглощается, m — масса вещества, поглощающего тепло, c — удельная теплоемкость и ∆ T — изменение температуры.
Первый закон термодинамики и теплота
Первый закон термодинамики гласит, что изменение внутренней энергии вещества равно сумме переданного ему тепла и совершенной над ним работы (или переданного ему тепла минус работы, выполненной на ее).
«Работа» — это просто слово, которое физики используют для передачи физической энергии. Например, помешивание кофе в чашке работает с жидкостью внутри нее, и вы работаете с предметом, когда поднимаете его или бросаете.
Тепло — это еще одна форма передачи энергии, но она происходит, когда два объекта имеют разные температуры по отношению друг к другу. Если вы нальете холодную воду в кастрюлю и включите плиту, пламя нагреет кастрюлю, а горячая кастрюля нагреет воду. Это повышает температуру воды и дает ей энергию. Второй закон термодинамики гласит, что тепло передается только от более горячих объектов к более холодным, а не наоборот.
Объяснение удельной теплоемкости
Ключом к решению задачи расчета поглощения тепла является понятие удельной теплоемкости. Разным веществам требуется передать разное количество энергии для повышения температуры, а удельная теплоемкость вещества говорит вам, насколько она велика. Это количество, обозначенное символом c и измеренное в джоулях/кг градусах Цельсия.
Короче говоря, теплоемкость говорит вам, сколько тепловой энергии (в джоулях) необходимо, чтобы поднять температуру 1 кг материала на 1 градус Цельсия. Удельная теплоемкость воды составляет 4181 Дж/кг градуса Цельсия, а удельная теплоемкость свинца составляет 128 Дж/кг °C. Это сразу говорит о том, что для повышения температуры свинца требуется меньше энергии, чем воды.
Расчет поглощения тепла
Вы можете использовать информацию из двух последних разделов вместе с одной простой формулой для расчета поглощения тепла в конкретной ситуации. Все, что вам нужно знать, это нагреваемое вещество, изменение температуры и массу вещества. Уравнение:
Q = mc ∆ T
Здесь Q означает теплоту (то, что вы хотите знать, м означает массу),
655 c
означает удельную теплоемкость, а ∆ T — изменение температуры. Вы можете найти изменение температуры, вычитая начальную температуру из конечной температуры.
В качестве примера представьте себе повышение температуры 2 кг воды с 10°C до 50°C. Изменение температуры равно ∆ T = (50 – 10)°C = 40°C. В последнем разделе удельная теплоемкость воды равна 4,181 Дж/кг град С, поэтому уравнение дает:
Q = 2 кг × 4181 Дж/кг °С × 40 °С воды на 40 градусов C.
Советы по альтернативным единицам измерения
Иногда удельная теплоемкость указывается в других единицах измерения. Например, она может выражаться в джоулях/грамм-градусах Цельсия, калориях/грамм-градусах Цельсия или джоулях/моль-градусах Цельсия. Калория — это альтернативная единица энергии (1 калория = 4,184 джоуля), граммы — это 1/1000 килограмма. , а моль (сокращенно моль) — это единица измерения, используемая в химии. Пока вы используете постоянные единицы измерения, приведенная выше формула будет работать.
Например, если удельная теплоемкость указана в джоулях на грамм °C, укажите массу вещества также в граммах или, в качестве альтернативы, переведите удельную теплоемкость в килограммы, умножив ее на 1000.