Объем в геометрии: Формулы объема геометрических фигур

alexxlab / / Геометрии

Содержание

Формулы вычисления объема всех геометрических фигур » Kupuk.net

Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба: 

V = a 3

где:

V — объем куба, 
a — длина грани куба.

Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

где:

V- объем призмы, 
So — площадь основания призмы, 
h — высота призмы.

Объем параллелепипеда

Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

где:

V- объем параллелепипеда, 
So — площадь основания, 
h — длина высоты.

Объем пирамиды

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).

Формула объема пирамиды:

где:

V — объем пирамиды, 
So — площадь основания пирамиды, 
h — длина высоты пирамиды.

Объем усеченной пирамиды

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.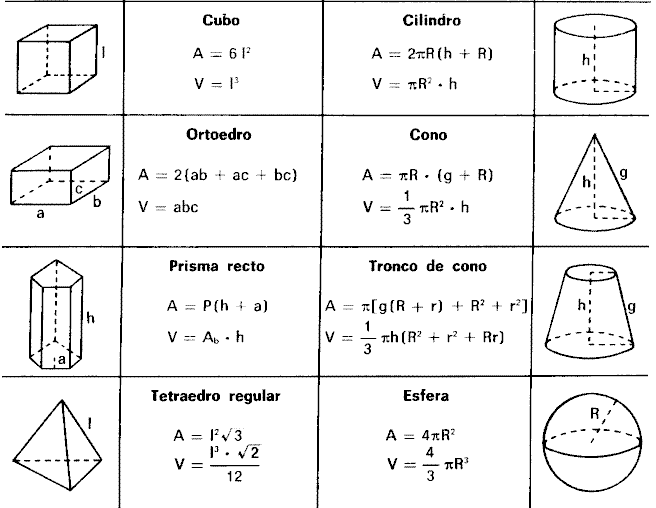

Формула объема усеченной пирамиды:

Где:

S1 — площадь верхнего основания усеченной пирамиды,
S2 — площадь нижнего основания усеченной пирамиды,
h — высота усеченной пирамиды.

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формула объема цилиндра:

V= π R2 h

V= Sоh

Где:

V — объем цилиндра, 
So — площадь основания цилиндра, 
R — радиус цилиндра, 
h — высота цилиндра, 
π = 3.141592

Объем правильной треугольной пирамиды

Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS).

Формула объема правильной треугольной пирамиды:

Где:

V — объем пирамиды;
h — высота пирамиды;
a — сторона основания пирамиды.

Объем конуса

Объем круглого конуса равен трети произведения площади основания S на высоту H.

Формула объема конуса:

Где:

V — объем конуса;
R — радиус основания;
H — высота конуса;
I — длина образующей;
S — площадь боковой поверхности конуса.

Объем усеченного конуса

Объем усеченного конуса равен разности объемов двух полных конусов.

Формула объема усеченного конуса:

Где:

V — объем усеченного конуса;
H — высота усеченного конуса;
R и R2 — радиусы нижнего и верхнего оснований.

Объем тетраэдра

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

Формула тетраэдра:

Где:

V — объем тетраэдра;
a — ребро тетраэдра.

Объем шара

Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.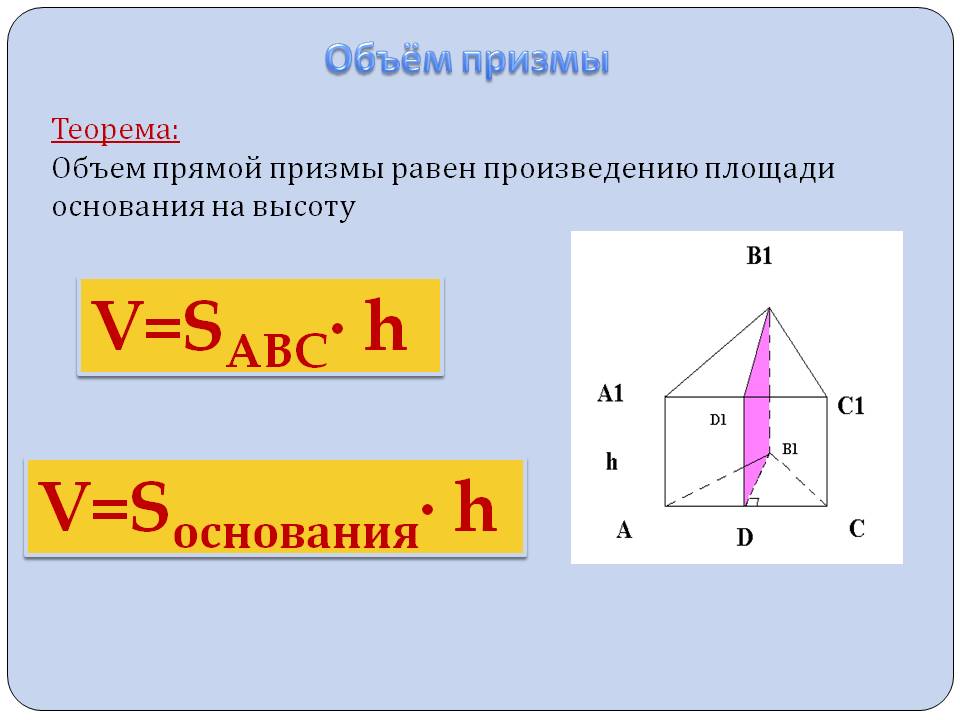

Формула объема шара:

Где:

V  — объем шара;
R — радиус шара;
S — площадь сферы.

Объем шарового сегмента и сектора

      

Шаровый сегмент — это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

Формула объема шарового сегмента:

Где:

R — радиус шара
H — высота сегмента
π ≈ 3,14

Формула объема шарового сектора:

Где:

h — высота сегмента
R — радиус шара
π ≈ 3,14

Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

Где:

V — объем прямоугольного параллелепипеда, 
a — длина, 
b — ширина, 
h — высота.

Объемы геометрических фигур. Объем геометрических фигур таблица.

    3\)

     

     

     

    Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

    Запишитесь на бесплатное тестирование знаний!

    Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

    Наши преподаватели

    Анастасия Сергеевна Роствинская

    Репетитор по математике

    Стаж (лет)

    Образование:

    Нижегородский Государственный Технический университет имени Р. Е. Алексеева

    Проведенных занятий:

    Форма обучения:

    Дистанционно (Скайп)

    Репетитор по химии для 7-9 классов. Подготовка к ОГЭ. Я занимаюсь репетиторством уже 3 года, являюсь именным стипендиатом от крупной компании Теплоэнерго, так же победитель конкурса Профстажировки 2.0 2019 и 2021 года, уже со второго курса написала 2 статьи по химическим технологиям, университет закончила с аттестатом отличия. Мои ученики с достоинством сдали ОГЭ и уже закончили школу. Так же я оказывала помощь студентам младших курсов.

    Ирина Владимировна Никитина

    Репетитор по математике

    Стаж (лет)

    Образование:

    Проведенных занятий:

    Форма обучения:

    Дистанционно (Скайп)

    Репетитор 1-6 классов. Я люблю математику за то, что математика- царица точных наук. Она не только интересна и «красива», она еще и полезна, как для других наук, так и в быту. Стараюсь прививать и поддерживать интерес детей к предмету.

    Виктория Анатольевна Шилова

    Репетитор по математике

    Стаж (лет)

    Образование:

    Северо-Казахстанский государственный университет имени Козыбаева

    Проведенных занятий:

    Форма обучения:

    Дистанционно (Скайп)

    Репетитор по русскому языку 5-11 классов, подготовка к ОГЭ и ЕГЭ. Также репетитор по истории и обществознанию 5-11 классы, готовлю к ВПР/ОГЭ/ЕГЭ. Скорочтение для 5-11 классов. Я преподаю по авторской методике. Она включает в себя разные подходы и методы преподавания. Все мои ученики сдают выпускные экзамены .Всегда настраиваю на позитивное мышление, мотивирую на успех. Индивидуальный подход к каждому ученику.

    Похожие статьи

    • Приведение к общему знаменателю
    • Как легко разделить на 0,1; 0,01; 0,001
    • Как построить график гиперболы?
    • ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 6)
    • ЕГЭ по математике, базовый уровень. Планиметрия. Равнобедренный треугольник (вариант 1)
    • ЕГЭ по математике, базовый уровень. Задачи на движение по прямой (вариант 3)
    • Задачи на исследование функций
    • Что делать, если ребенок выбрал «не ту» профессию?

    Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

    Объем геометрических тел

    Объёмы геометрических тел.

    Урок геометрии в 11 классе.

    Аннотация.

    Представленный урок является первым уроком-лекцией по теме «Объёмы». Компьютерные технологии позволяют сделать этот урок красочным и ярким по форме , продуктивным и наполненным по содержанию. Во время урока продемонстрированы модели геометрических фигур: призмы, наклонной призмы, пирамиды, цилиндра, конуса. Модели выполнены с элементами анимации. Рядом с каждой фигурой сначала появляются известные формулы площади, а затем в другом , более ярком цвете появляется формула объёма. Для пояснения некоторых свойств объёмов. Фигуры накладываются друг на друга. В ходе урока проводится дифференцированная проверочная работа с использованием тестов. При решении ряда задач также используются готовые рисунки ,что позволяет экономить время урока. Все рисунки из меловых на доске превращаются в яркие и действительно стереометрические.

    • Представленный урок является первым уроком-лекцией по теме «Объёмы». Компьютерные технологии позволяют сделать этот урок красочным и ярким по форме , продуктивным и наполненным по содержанию. Во время урока продемонстрированы модели геометрических фигур: призмы, наклонной призмы, пирамиды, цилиндра, конуса. Модели выполнены с элементами анимации. Рядом с каждой фигурой сначала появляются известные формулы площади, а затем в другом , более ярком цвете появляется формула объёма. Для пояснения некоторых свойств объёмов. Фигуры накладываются друг на друга. В ходе урока проводится дифференцированная проверочная работа с использованием тестов. При решении ряда задач также используются готовые рисунки ,что позволяет экономить время урока. Все рисунки из меловых на доске превращаются в яркие и действительно стереометрические.

      План урока

      • 1.Повторение ранее изученного.
      • 2.Объяснение нового материала:
      • а) понятие объёма; б) свойства объёма; в) объём куба; г) объём прямоугольного параллелепипеда.
      • а) понятие объёма;
      • б) свойства объёма;
      • в) объём куба;
      • г) объём прямоугольного параллелепипеда.
      • 3.Закрепление.
      • а) контрольные вопросы. б) устная работа; в) решение задач по готовым чертежам.
      • а) контрольные вопросы.
      • б) устная работа;
      • в) решение задач по готовым чертежам.
      • 4.Объём прямой призмы.
      • 5.Решение задач.
      • 6.Домашнее задание : теория п. 63, 64. №647, 649.

      О с н о в н а я ц е л ь у р о к а .

      • Ввести понятие объёма тела.
      • Ввести формулы объёма куба, прямоугольного параллелепипеда и прямой призмы.
      • Сформировать навык решения задач на нахождение объёма куба, прямоугольного параллелепипеда, прямой призмы.

      S = S осн.+ S бок

      Повторим формулы площади поверхностей геометрических тел.

      S =2 S осн+ S бок

      S =2 S осн.+ S бок.

      S = S осн.+ S бок

      Объёмы геометрических тел.

      За единицу объёма принимают объём куба со стороной, равной единице измерения отрезков.

      Равные тела имеют равные объёмы.

      Если тело состоит из нескольких тел, то его объём равен сумме объёмов его частей .

      Понятие объёма тела вводится по аналогии с понятием площади плоской фигуры. Заполним вторую половину таблицы.

      S -это положительная величина,

      численное значение которой обладает следующими свойствами.

      V- это положительная величина, численное значение которой обладает следующими свойствами.

      1.Равные фигуры имеют равные площади.

      1.Равные тела имеют равные объёмы.

      2. Если фигура,составлена

      Из нескольких фигур,то её площадь равна сумме площадей этих фигур.

      2.Если тело состоит из нескольких тел, то его объём равен сумме объёмов этих тел.

      3. В качестве единицы измерения площади обычно берут квадрат со стороной равной единицы измерения отрезка.

      3.В качестве единицы измерения объёма обычно берут куб со стороной,равной единице измерения отрезков.

      Объём куба с ребром a

      равен кубу его ребра. V= a 3

      Куб-частный случай прямоугольного параллелепипеда. Чему равен объём прямоугольного параллелепипеда? Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

      V=abc . Или объём прямоугольного параллелепипеда равен произведению площади основания на высоту. V=S осн * H

      Контрольные вопросы.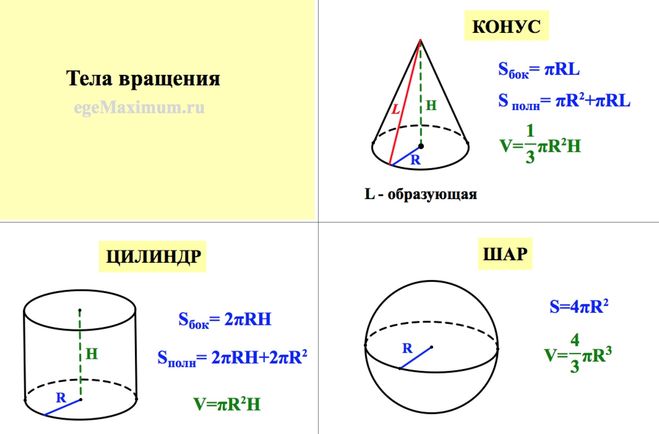

      • 1.Что называется объёмом тела?
      • 2.Что значит измерить объём тела?
      • 3.Что значит:»Объём комнаты 60 м 3 ?»
      • 4.Что значит :»Объём бочки для воды 200м 3 ?»
      • 5.Как получить 1 /8 ; 1 /125 ; 1 /1000 единичного куба?
      • 6.Чему равен объём куба с ребром а?

      Устная работа ( по готовым чертежам.)

      Найти объём прямоугольного параллелепипеда.

      6

      5

      3

      3

      4

      5

      6

      10

      45 0

      45 0

      8

      2

      Решение задач .

      1 .Площадь полной поверхности куба равна 6 м 2 . Найти его объём.

      2. Объём куба равен 8 м 3 . Найти площадь полной поверхности.

      3 .Если каждое ребро куба увеличить на 2 см , то его объём увеличится на 98 см 3 . Чему равно ребро куба?

      4 .Три куба, сделанные из свинца, имеют рёбра 3, 4 и 5 см. Они переплавлены в один куб. Найти его ребро.

      Объём призмы и цилиндра.

      Объём призмы равен произведению

      площади основания на высоту.

      Объём цилиндра равен произведению

      площади основания на высоту.

      Решение задач .

      F

      Дано: ABCDFS -прямая призма, AB = BC =5см AC =6см, AD=10c м ________________________________ Найти: V -объём призмы.

      D

      S

      Решение. V = S осн * H S осн = 1 /2 AB * BK , где BK -высота ∆ ABC .

      Из ∆ ABK- прямоугольного, BK =4(см)

      S осн.=1 /2 *6 * 4 =12 ( см 2 ) V=12 *10 = 120 ( см 3 ) Ответ V=120 см 3 .

      B

      A

      C

      К

      Самостоятельная работа.

      • Вариант-1.
      • 1.Объём прямоугольного параллелепипеда равен 96 см3, боковое ребро 8 см.Чему равна площадь основания?
      • Вариант-2.
      • 1.Объём прямоугольного параллелепипеда равен 100 см3, площадь основания 23 см2. Найти высоту параллелепипеда.

      Л и т е р а т у р а .

      • 1.Учебник «Геометрия 10-11 класс « автор Л.С. Атанасян.
      • 2.Геометрия 11 класс.(Поурочные планы.) автор Г. И. Ковалёва.
      • 3.Дидактические материалы по геометрии 10-11 класс.
      • 4. Разрезные карточки по стереометрии 10-11 класс.

      9.10: Решение геометрических задач — объем и площадь поверхности (часть 2)

      1. Последнее обновление
      2. Сохранить как PDF
    • Идентификатор страницы
      7134
      • OpenStax
      • OpenStax

      Найдите объем и площадь поверхности сфер

      Сфера имеет форму баскетбольного мяча, похожую на трехмерный круг. Как и в случае с кругом, размер сферы определяется ее радиусом, то есть расстоянием от центра сферы до любой точки на ее поверхности. Ниже приведены формулы объема и площади поверхности шара.

      Показать, откуда берутся эти формулы, как мы это делали для прямоугольного тела, выходит за рамки этого курса. Мы аппроксимируем \(\pi\) с помощью 3,14.

      Определение: объем и площадь поверхности сферы

      Для сферы радиусом r:

      Пример \(\PageIndex{5}\):

      Радиус сферы составляет 6 дюймов. Найдите его объем (а) и площадь поверхности (б).

      Решение

      Шаг 1 одинаков для (а) и (б), поэтому мы покажем его только один раз.

      9{3} \\ В &\ок 904,32\; кубический\; дюймы \end{split}$$
      Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
      Шаг 6. Проверить . Дважды проверьте свою математику на калькуляторе.
      Шаг 7. Ответьте на вопрос. Объем составляет приблизительно 904,32 кубических дюйма.

      (b)

      9{2} \\ S &\ок 452,16\; кв.\; дюймы \end{split}$$
      Шаг 2. Определите , что вы ищете.
      Шаг 6. Проверить . Дважды проверьте свою математику на калькуляторе.
      Шаг 7. Ответьте на вопрос. Площадь поверхности составляет примерно 452,16 квадратных дюймов.
      Упражнение \(\PageIndex{9}\):

      Найдите (а) объем и (б) площадь поверхности сферы радиусом 3 сантиметра.

      Ответить на

      113,04 куб. см

      Ответ б

      113,04 кв. см

      Упражнение \(\PageIndex{10}\):

      Найдите (a) объем и (b) площадь поверхности каждой сферы радиусом 1 фут

      Ответьте на

      4,19 куб.

      футов
      Ответ б

      12,56 кв. футов

      Пример \(\PageIndex{6}\):

      Земной шар имеет форму сферы с радиусом 14 сантиметров. Найдите его объем (а) и площадь поверхности (б). Округлите ответ до сотых.

      Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.

      (a)

      Шаг 2. Определите , что вы ищете. 9{3} \end{split}$$
      Шаг 5. Решить . $$V \ приблизительно 11 488,21 \tag{9.6.14}$$
      Шаг 6. Проверить . Мы оставляем вам возможность проверить свои расчеты.
      Шаг 7. Ответьте на вопрос. Объем составляет приблизительно 11 488,21 кубических дюйма.

      (б)

      9{2} \end{split}$$
      Шаг 5. Решить . $$S \ приблизительно 2461,76 \tag{9.6.15}$$
      Шаг 6. Проверить . Мы оставляем вам возможность проверить свои расчеты.
      Шаг 7. Ответьте на вопрос. Площадь поверхности составляет примерно 2461,76 квадратных дюймов.
      Упражнение \(\PageIndex{11}\):

      Пляжный мяч имеет форму сферы с радиусом 9 дюймов. Найдите его объем (а) и площадь поверхности (б).

      Ответить на

      3052,08 куб. в

      Ответ б

      1017,36 кв. дюйма

      Упражнение \(\PageIndex{12}\):

      Римская статуя изображает Атласа, держащего земной шар радиусом 1,5 фута. Найдите объем (а) и площадь поверхности (б) земного шара.

      Ответить на

      14,13 куб.

      футов
      Ответ б

      28,26 кв. футов

      Найдите объем и площадь поверхности цилиндра

      Если вы когда-нибудь видели банку газировки, то знаете, как выглядит цилиндр. Цилиндр представляет собой объемную фигуру с двумя параллельными кругами одинакового размера вверху и внизу. Верх и низ цилиндра называются основаниями. Высота h цилиндра — это расстояние между двумя основаниями. Для всех цилиндров, с которыми мы будем здесь работать, стороны и высота h будут перпендикулярны основаниям.

      Рисунок \(\PageIndex{5}\) — Цилиндр имеет два круглых основания одинакового размера. Высота — это расстояние между основаниями.

      Прямоугольные тела и цилиндры в чем-то похожи, потому что они оба имеют два основания и высоту. Формула объема прямоугольного тела V = Bh также может быть использована для нахождения объема цилиндра.

      Для прямоугольного твердого тела площадь основания B равна площади прямоугольного основания, длина × ширина. Для цилиндра площадь основания B равна площади его круглого основания \(\pi\)r 2 . На рисунке \(\PageIndex{6}\) сравнивается использование формулы V = Bh для прямоугольных тел и цилиндров.

      Рисунок \(\PageIndex{6}\) — Наблюдение сходства цилиндра с прямоугольным телом может облегчить понимание формулы объема цилиндра.

      Чтобы понять формулу площади поверхности цилиндра, представьте себе банку с овощами. У него три поверхности: верхняя, нижняя и часть, образующая стенки банки. Если вы аккуратно отрежете этикетку сбоку от банки и развернете ее, то увидите, что это прямоугольник. См. рисунок \(\PageIndex{7}\).

      Рисунок \(\PageIndex{7}\) — Разрезав и развернув этикетку банки с овощами, мы видим, что поверхность цилиндра представляет собой прямоугольник. Длина прямоугольника — это окружность основания цилиндра, а ширина — высота цилиндра.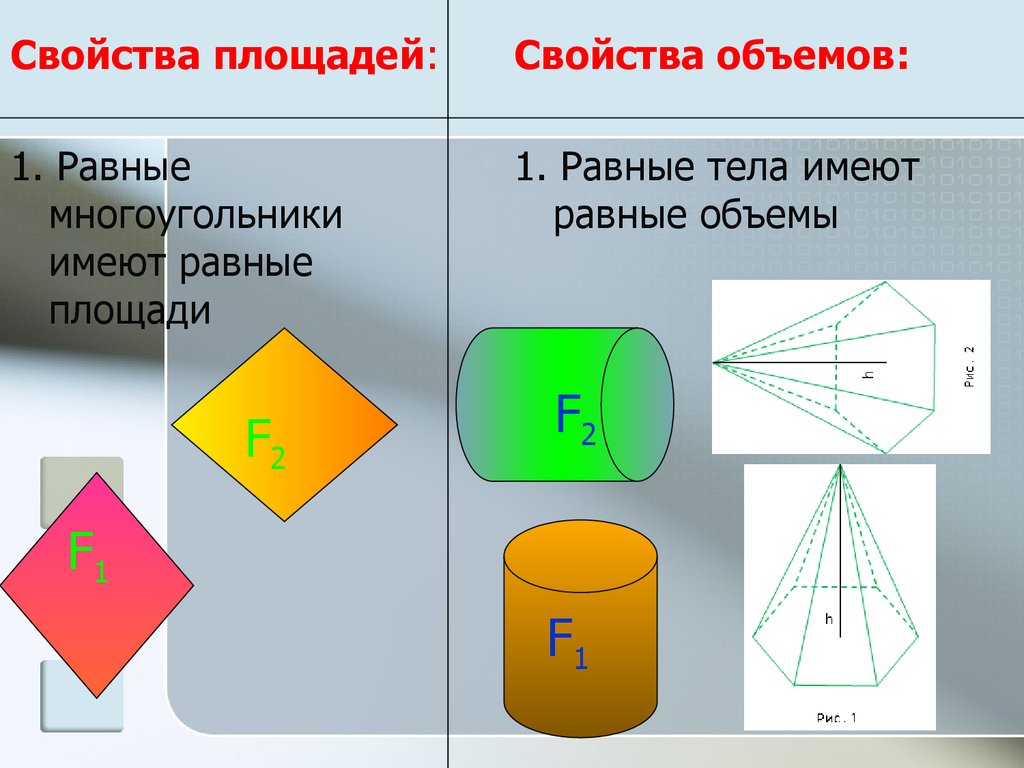

      Расстояние вокруг края банки равно окружности основания цилиндра, а также длине L прямоугольной этикетки. Высота цилиндра равна ширине W прямоугольной этикетки. Таким образом, площадь этикетки можно представить как 9{2} + 2 \pi rh \tag{9.6.16}\]

      Определение: объем и площадь поверхности цилиндра

      Для цилиндра с радиусом r и высотой h:

      Пример \(\PageIndex{ 7}\):

      Цилиндр имеет высоту 5 сантиметров и радиус 3 сантиметра. Найдите объем (а) и площадь поверхности (б).

      Решение

      Шаг 1. Прочтите задачу. Нарисуйте рисунок и подпишите его с помощью данной информации.

      (a)

      Шаг 2. Определите , что вы ищете. объем цилиндра
      Шаг 3. Имя . Выберите переменную для ее представления. {2} \cdot 5 \end{split}$$
      Шаг 5. Решить . $$V \ приблизительно 141,3 \tag{9.6.17}$$
      Шаг 6. Проверить . Мы оставляем вам возможность проверить свои расчеты.
      Шаг 7. Ответьте на вопрос. Объем примерно 141,3 кубических дюйма.

      (б)

      Шаг 2. 9{2} + 2(3,14)(3)5 \end{split}$$
      Шаг 5. Решить . $$S \ приблизительно 150,72 \tag{9.6.18}$$
      Шаг 6. Проверить . Мы оставляем вам возможность проверить свои расчеты.
      Шаг 7. Ответьте на вопрос. Площадь поверхности составляет приблизительно 150,72 квадратных дюйма.
      Упражнение \(\PageIndex{13}\):

      Найдите объем (а) и площадь поверхности (б) цилиндра радиусом 4 см и высотой 7 см.

      Ответить на

      351,68 куб. см

      Ответ б

      276,32 кв. футов

      Упражнение \(\PageIndex{14}\):

      Найдите (a) объем и (b) площадь поверхности цилиндра с данным радиусом 2 фута и высотой 8 футов.

      Ответ на

      100,48 куб. футов

      Ответ б

      125,6 кв. футов

      Пример \(\PageIndex{8}\):

      Найдите (а) объем и (б) площадь поверхности банки газировки. Радиус основания 4 сантиметра, а высота 13 сантиметров. Предположим, что банка имеет форму цилиндра.

      Решение

      Шаг 1. Прочтите задачу. Нарисуйте рисунок и подпишите его с помощью данной информации.

      (a)

      9{2} \cdot 13 \end{split}$$
      Шаг 2. Определите , что вы ищете. объем цилиндра
      Шаг 3. Имя . Выберите переменную для ее представления. пусть V = объем
      Шаг 4. Перевести . Напишите соответствующую формулу. Заменять. (Используйте 3.14 для \(\pi\))
      Шаг 5. Решить . $$V \ приблизительно 653,12 \tag{9.6.19}$$
      Шаг 6. Проверить . Мы предоставляем вам проверить.
      Шаг 7. Ответьте на вопрос. Объем примерно 653,12 кубических сантиметра.

      (б)

      9{2} + 2(3,14)(4)13 \end{split}$$
      Шаг 5. Решить . $$S \ приблизительно 427,04 \tag{9.6.20}$$
      Шаг 6. Проверить . Мы оставляем вам возможность проверить свои расчеты.
      Шаг 7. Ответьте на вопрос. Площадь поверхности составляет приблизительно 427,04 квадратных сантиметра.
      Упражнение \(\PageIndex{15}\):

      Найдите (a) объем и (b) площадь поверхности банки с краской радиусом 8 сантиметров и высотой 19 сантиметров. Предположим, что банка имеет форму цилиндра.

      Ответить на

      3818,24 куб. см

      Ответ б

      1 356,48 кв. см

      Упражнение \(\PageIndex{16}\):

      Найдите (a) объем и (b) площадь поверхности цилиндрического барабана радиусом 2,7 фута и высотой 4 фута. Предположим, что барабан имеет форму цилиндра.

      Ответить на

      91,5624 куб.

      футов
      Ответ б

      113,6052 кв. футов

      Найдите объем рожков

      Первое, что возникает у многих из нас, когда мы слышим слово «рожок», — это рожок мороженого. Есть много других применений рожков (но большинство из них не такие вкусные, как рожки для мороженого). В этом разделе мы увидим, как найти объем конуса.

      В геометрии конус представляет собой объемную фигуру с одним круглым основанием и вершиной. Высота конуса — это расстояние между его основанием и вершиной. Конусы, которые мы рассмотрим в этом разделе, всегда будут иметь высоту, перпендикулярную основанию. См. рисунок \(\PageIndex{8}\).

      Рисунок \(\PageIndex{8}\) — Высота конуса — это расстояние между его основанием и вершиной.

      Ранее в этом разделе мы видели, что объем цилиндра равен V = \(\pi\)r 2 ч. Мы можем думать о конусе как о части цилиндра. Рисунок \(\PageIndex{9}\) показывает конус, помещенный внутрь цилиндра той же высоты и с тем же основанием. Если мы сравним объем конуса и цилиндра, то увидим, что объем конуса меньше объема цилиндра.

      Рисунок \(\PageIndex{9}\) — Объем конуса меньше объема цилиндра с тем же основанием и высотой.

      На самом деле объем конуса составляет ровно одну треть объема цилиндра с таким же основанием и высотой. Объем конуса

      9{2}} h \tag{9.6.22}\]

      В этой книге мы найдем только объем конуса, а не площадь его поверхности.

      Определение: Объем конуса

      Для конуса с радиусом r и высотой h .

      Пример \(\PageIndex{9}\):

      Найдите объем конуса высотой 6 дюймов и радиусом основания 2 дюйма.

      Решение

      Шаг 1. Прочтите задачу. Нарисуйте рисунок и подпишите его с помощью данной информации.
      Шаг 2. Определите , что вы ищете. {2 } (6) \end{split}$$
      Шаг 5. Решить . $$V \ приблизительно 25,12 \tag{9.6.23}$$
      Шаг 6. Проверить . Мы оставляем вам возможность проверить свои расчеты.
      Шаг 7. Ответьте на вопрос. Объем примерно 25,12 кубических дюймов.
      Упражнение \(\PageIndex{17}\):

      Найдите объем конуса высотой 7 дюймов и радиусом 3 дюйма

      Ответить

      65,94 куб. в.

      Упражнение \(\PageIndex{18}\):

      Найдите объем конуса высотой 9 см и радиусом 5 см

      Ответ

      235,5 куб. см

      Пример \(\PageIndex{10}\):

      В любимом гастропабе Марти подают картофель фри в бумажной обертке в форме конуса. Каков объем конической обертки высотой 8 дюймов и диаметром 5 дюймов? Округлите ответ до сотых.

      Решение

      9{2} (8) \end{split}$$
      Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
      Шаг 2. Определите , что вы ищете. объем конуса
      Шаг 3. Имя . Выберите переменную для ее представления. пусть V = объем
      Шаг 5. Решить . $$V \ приблизительно 52,33 \tag{9.6.24}$$
      Шаг 6. Проверить . Мы оставляем вам возможность проверить свои расчеты.
      Шаг 7. Ответьте на вопрос. Объем упаковки составляет приблизительно 52,33 кубических дюйма.
      Упражнение \(\PageIndex{19}\):

      Сколько кубических дюймов конфет поместится в конической пиньяте длиной 18 дюймов и шириной основания 12 дюймов? Округлите ответ до сотых.

      Ответить

      678,24 куб. в.

      Упражнение \(\PageIndex{20}\):

      Каков объем конусообразной праздничной шляпы высотой 10 дюймов и шириной у основания 7 дюймов? Округлите ответ до сотых.

      Ответить

      128,2 куб. в.

      Сводка геометрических формул

      В следующих таблицах приведены все формулы, описанные в этой главе.

      ДОСТУП К ДОПОЛНИТЕЛЬНЫМ ОНЛАЙН-РЕСУРСАМ

      Объем конуса

      Практика делает совершенным

      Найдите объем и площадь поверхности прямоугольных тел

      В следующих упражнениях найдите (a) объем и (b) площадь поверхности прямоугольное тело с заданными размерами.

      1. длина 2 метра, ширина 1,5 метра, высота 3 метра
      2. длина 5 футов, ширина 8 футов, высота 2,5 фута
      3. длина 3,5 ярда, ширина 2,1 ярда, высота 2,4 ярда
      4. длина 8,8 см, ширина 6,5 см, высота 4,2 см

      В следующих упражнениях решите.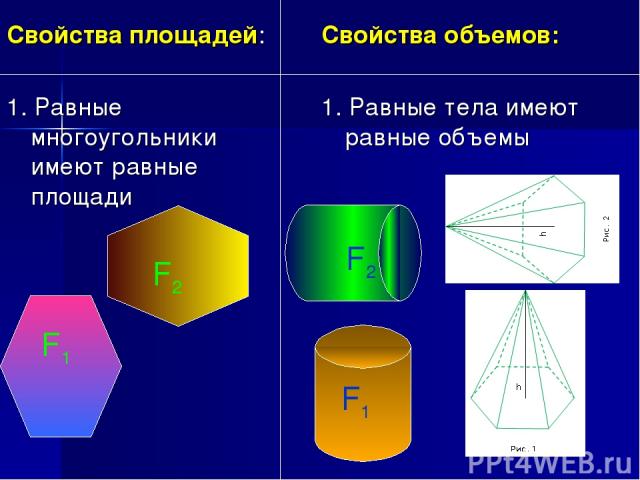

      1. Автофургон Прямоугольный автофургон имеет длину 16 футов, ширину 8 футов и высоту 8 футов. Найдите его объем (а) и площадь поверхности (б).
      2. Подарочная коробка Прямоугольная подарочная коробка имеет длину 26 дюймов, ширину 16 дюймов и высоту 4 дюйма. Найдите его объем (а) и площадь поверхности (б).
      3. Коробка Прямоугольная коробка имеет длину 21,3 см, ширину 24,2 см и высоту 6,5 см. Найдите его объем (а) и площадь поверхности (б).
      4. Транспортный контейнер Прямоугольный транспортный контейнер имеет длину 22,8 фута, ширину 8,5 фута и высоту 8,2 фута. Найдите его объем (а) и площадь поверхности (б).

      В следующих упражнениях найдите (а) объем и (б) площадь поверхности куба с заданной длиной стороны.

      1. 5 сантиметров
      2. 6 дюймов
      3. 10,4 фута
      4. 12,5 м

      В следующих упражнениях решите.

      1. Научный центр Длина каждой стороны куба в Научном центре Дискавери в Санта-Ане составляет 64 фута. Найдите его объем (а) и площадь поверхности (б).
      2. Музей Музей в форме куба со стороной 45 метров. Найдите его объем (а) и площадь поверхности (б).
      3. Основание статуи Основание статуи представляет собой куб со стороной 2,8 метра. Найдите его объем (а) и площадь поверхности (б).
      4. Коробка для салфеток Коробка для салфеток представляет собой куб со стороной 4,5 дюйма в длину. Найдите его объем (а) и площадь поверхности (б).

      Найдите объем и площадь поверхности сфер

      В следующих упражнениях найдите (а) объем и (б) площадь поверхности сферы с заданным радиусом. Ответы округлить до сотых.

      1. 3 сантиметра
      2. 9 дюймов
      3. 7,5 футов
      4. 2,1 ярда

      В следующих упражнениях решите. Ответы округлить до сотых.

      1. Мяч для упражнений Мяч для упражнений имеет радиус 15 дюймов. Найдите его объем (а) и площадь поверхности (б).
      2. Полет на воздушном шаре Воздушный шар в Большом парке представляет собой большую оранжевую сферу радиусом 36 футов. Найдите его объем (а) и площадь поверхности (б).
      3. Мяч для гольфа Мяч для гольфа имеет радиус 4,5 сантиметра. Найдите его объем (а) и площадь поверхности (б).
      4. Бейсбольный мяч Бейсбольный мяч имеет радиус 2,9 дюйма. Найдите его объем (а) и площадь поверхности (б).

      Найдите объем и площадь поверхности цилиндра

      В следующих упражнениях найдите (а) объем и (б) площадь поверхности цилиндра с заданными радиусом и высотой. Ответы округлить до сотых.

      1. радиус 3 фута, высота 9 футов
      2. радиус 5 сантиметров, высота 15 сантиметров
      3. радиус 1,5 метра, высота 4,2 метра
      4. радиус 1,3 ярда, высота 2,8 ярда

      В следующих упражнениях решите. Ответы округлить до сотых.

      1. Банка из-под кофе Банка из-под кофе имеет радиус 5 см и высоту 13 см. Найдите его объем (а) и площадь поверхности (б).
      2. Закусочная упаковка Закусочная упаковка печенья имеет форму цилиндра радиусом 4 см и высотой 3 см. Найдите его объем (а) и площадь поверхности (б).
      3. Стойка для парикмахерской Цилиндрическая стойка для парикмахерской имеет диаметр 6 дюймов и высоту 24 дюйма. Найдите его объем (а) и площадь поверхности (б).
      4. Архитектура Цилиндрическая колонна имеет диаметр 8 футов и высоту 28 футов. Найдите его объем (а) и площадь поверхности (б).

      Найдите объем конусов

      В следующих упражнениях найдите объем конуса с заданными размерами. Ответы округлить до сотых.

      1. высота 9 футов и радиус 2 фута
      2. высота 8 дюймов и радиус 6 дюймов
      3. высота 12,4 см и радиус 5 см
      4. высота 15,2 метра и радиус 4 метра

      В следующих упражнениях решите. Ответы округлить до сотых.

      1. Типи Каков объем конусообразной палатки вигвама высотой 10 футов и шириной у основания 10 футов?
      2. Чашка для попкорна Каков объем конусообразной чашки для попкорна, имеющей высоту 8 дюймов и ширину у основания 6 дюймов?
      3. Бункер Каков объем конусообразного бункера высотой 50 футов и шириной у основания 70 футов?
      4. Песчаная куча Каков объем конусообразной кучи песка высотой 12 м и шириной у основания 30 м?

      Повседневная математика

      1. Столб уличного фонаря Столб уличного фонаря имеет форму усеченного конуса, как показано на рисунке ниже. Это большой конус минус меньший верхний конус. Большой конус имеет высоту 30 футов и радиус основания 1 фут. Меньший конус имеет высоту 10 футов и радиус основания 0,5 фута. С точностью до десятых: а) найти объем большого конуса. б) найти объем маленького конуса. в) найдите объем столба, вычитая объем малого конуса из объема большого конуса.

      1. Вафельные рожки для мороженого Обычный рожок для мороженого имеет высоту 4 дюйма и диаметр 2,5 дюйма. Вафельный рожок имеет высоту 7 дюймов и диаметр 3,25 дюйма. С точностью до сотой: а) найдите объем обычного рожка мороженого. б) найдите объем вафельного рожка. в) насколько больше мороженого помещается в вафельный рожок по сравнению с обычным рожком?

      Письменные упражнения

      1. Формулы для объема цилиндра и конуса аналогичны. Объясните, как вы можете запомнить, какая формула подходит к какой фигуре.
      2. Что имеет больший объем, куб со стороной 8 футов или сфера диаметром 8 футов? Объясните свои рассуждения.

      Самопроверка

      (a) После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.

      (b) Изучив этот контрольный список, что вы сделаете, чтобы стать уверенным в достижении всех целей?

      Авторы и авторство

      1. Наверх
        • Была ли эта статья полезной?
        1. Тип изделия
          Раздел или Страница
          Автор
          ОпенСтакс
          Версия лицензии
          4,0
          Показать страницу TOC
          нет
        2. Теги
            На этой странице нет тегов.

        Расчет объема и поверхности в трехмерной геометрии

        Ключевые термины

        o Полиэдрон

        O лицо

        O Edge

        O Prism

        o Правый Prism

        o Prism

        o Правый Prism

        O

        O0036

        Цели

        o распознавать многогранники и призмы и иметь возможность анализировать простые примеры этих рисунков

        o Знайте, как использовать формы для объема и площади поверхности для сферов и цилиндров

        6 3

        464646464646464646464646464646446446446446446464646464646464646446446446446446446446464644646464646464646464644646

         

        Сначала рассмотрим объем и площадь поверхности некоторых простых трехмерных фигур, затем перейдем к составным фигурам в трех измерениях.

         

        Объем и площадь поверхности

         

        Мы рассмотрим два основных типа геометрических тел: многогранники и сферы. Многогранник по сути является n -гранной сплошной фигурой — это трехмерный аналог многоугольника. Некоторые примеры многогранников показаны ниже.

           

                           

         

        Многогранники определяются своими гранями , которые являются областями многоугольника, ребрами, которые являются отрезками линий, очерчивающими грани, и поэтому они определяются таким же образом, как и вершины, и определяются таким же образом, как и вершины предназначены для полигонов. Особый тип многогранника — это призма , представляющая собой многогранник с одинаковыми (и параллельными) вершиной и низом. Если стороны призмы встречаются с верхом и низом под прямым углом, то она называется прямой призмой . Два многогранника в левой части приведенного выше ряда примеров являются призмами — мы можем увидеть это более точно, используя пунктирные линии, чтобы показать части, которые находятся вне поля зрения.

         

                                                     

         

        Опять же, обратите внимание, что верхняя и нижняя грани (основания) идентичны; кроме того, это на самом деле прямые призмы (при условии, что углы, образованные между сторонами и основаниями, прямые, как они выглядят на диаграммах). Очевидно, том V 91 296 прямой призмы — это просто площадь 91 295 A 91 296 основания, умноженная на высоту 91 295 h 91 296 сторон, как показано ниже для куба (шестигранной призмы).

         

         

        Но что, если призма не правильная? Применяется та же формула. Давайте посмотрим, почему это так, снова используя шестигранную призму. Мы будем смотреть на эту фигуру «с торца» так, чтобы ее глубина была перпендикулярна поверхности страницы (другими словами, два основания не видны). Из определения призмы мы знаем, что противоположные отрезки (ребра) конгруэнтны.

         

                                                                     

         

        Обратите внимание, что пунктирная линия также является высотой призмы.

         

                                                                     

         

        Из следующих свойств прямоугольников мы знаем:

         

                                                                 

         

        Таким образом, по условию SSS мы знаем, что два треугольника конгруэнтны. Обозначим фигуру следующим образом, отметив, что основание b 91 296 фигуры равно 91 295 b 91 296 91 369 1 91 370 + 91 295 b 91 296 91 369 2 91 370 .

         

        Хотите узнать больше? Почему бы не пройти онлайн-курс по геометрии?

                                                                

         

        Теперь мы можем вычислить площадь этой грани фигуры.

         

         

        Но площадь оснований не меняется между правым и неправильным вариантами призмы. Другими словами, глубина в этом случае и в случае правильной призмы (при одинаковой ориентации) одинакова. Соответственно и объем одинаковый. Хотя мы продемонстрировали этот факт только для шестигранных призм, то же самое относится ко всем призмам: объем равен площади основания, умноженной на высоту.

         

         

        Практическая задача : Вычислите объем призмы, показанной ниже.

         

         

        Решение : Многогранник на диаграмме идентифицирован как призма. На основании прямых углов в основании (и, следовательно, обоих оснований) мы можем идентифицировать основания как прямоугольники с длиной 4 единицы и шириной 9 единиц. Таким образом, площадь основания призмы равна 36 квадратных единиц. Высота призмы показана на схеме как 4 единицы. Таким образом, мы можем вычислить объем В призмы следующим образом.

        V = BH = (36 единиц 2 ) (4 единицы) = 144 единицы 3

        3

        3

        3

        3

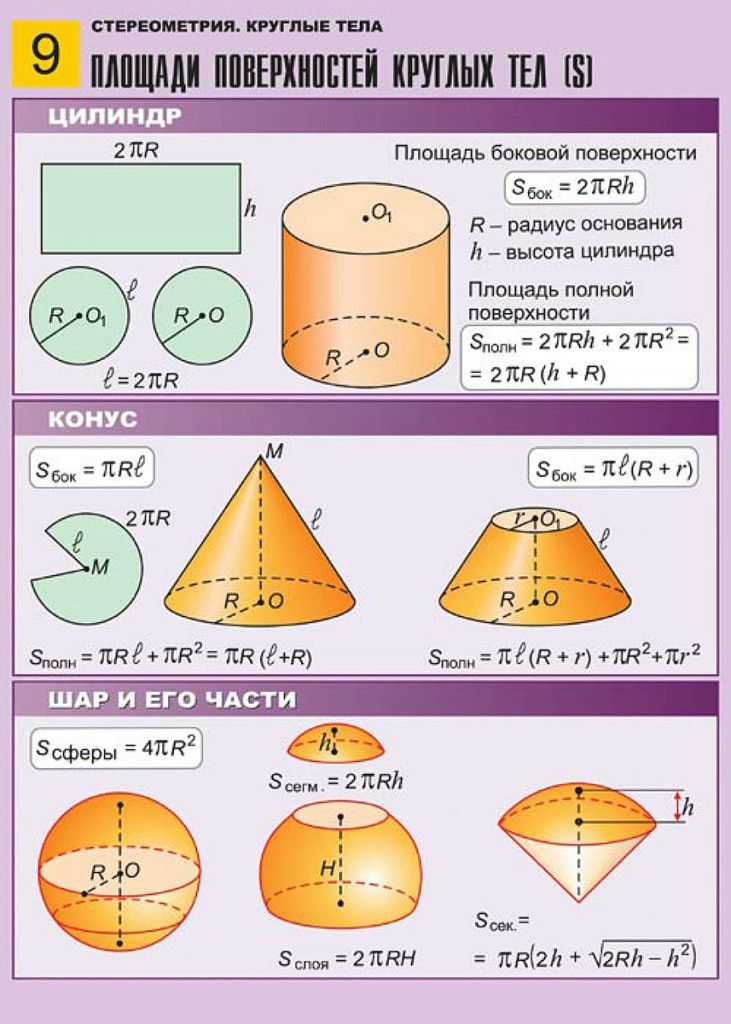        . рассмотреть их в любой большей глубины. Формулы есть в книгах и в интернете, правда, для некоторых многогранников.

         

        Еще один параметр, который мы можем рассчитать, — это площадь поверхности фигуры. Независимо от многогранника, площадь поверхности — это просто сумма площадей всех граней фигуры. Например, в случае куба (шестигранной призмы) площадь поверхности просто в шесть раз больше площади любой грани (все грани имеют одинаковую площадь, поскольку все ребра конгруэнтны). (Или, если каждое ребро имеет длину s , площадь поверхности 6 s 2 .)

         

         

        Задача : Вычислить площадь поверхности фигуры Направо.

         

        Решение : Посмотрите еще раз на призменную диаграмму в первой практической задаче. Мы можем найти площадь поверхности, вычислив площадь каждой грани. Мы уже знаем, что каждое основание имеет площадь 36 квадратных единиц. Остаются четыре неизвестные стороны. Задача говорит нам, что фигура наклонена только вправо (показана на диаграмме ниже дугой) — таким образом, единственные непрямые углы находятся на передней и задней гранях. Эти две грани являются параллелограммами. Левая и правая грани — прямоугольники.

         

         

        Площадь левой и правой граней равна произведению 4 и 5 единиц, или 20 квадратных единиц. Передняя и задняя грани представляют собой параллелограммы с основанием в 9 единиц и высотой в 4 единицы, поэтому каждая имеет площадь 36 квадратных единиц. Давайте теперь найдем общую площадь поверхности, S .

         

        S = (36 + 36) + (20 + 20) + (36 + 36) = 184 единицы 3

         

         

        Сферы — это еще один тип трехмерных фигур, объем и площадь поверхности которых можно вычислить относительно легко. Сфера является трехмерным аналогом окружности и определяется точкой центра O и радиусом r . Сфера — это множество всех точек, находящихся на расстоянии r от O . Пример сферы показан ниже.

         

         

        Как и в случае с кругами, сложно вывести формулы геометрически, но формулы хорошо известны. Том V и площадь поверхности S приведены ниже для сферы радиусом r .

         

         

         

        Подобной фигурой является (круглый) цилиндр, который имеет два конгруэнтных круглых основания и трубчатое тело, как показано ниже. Цилиндр определяется радиусом 91 295 r 91 296 его оснований и высотой 91 295 h 91 296 .

         

         

        Аналогично призме объем V цилиндра есть произведение площади его основания на высоту.

         

        V = πr 2 h

         

        Площадь поверхности немного сложнее, но ее можно рассчитать, просто расширив наши текущие знания. Мы знаем, что длина окружности основания равна 2 πr ; таким образом, если мы просто умножим эту формулу на ч , мы получим площадь поверхности «бочки» цилиндра. Теперь нам нужно только добавить площадь оснований, которая в два раза больше площади любого круглого основания. Общая площадь S тогда следующее.

         

        S = 2 πrh + πr 2 + πr 2 = 2( πrh + πr 2 )

         

         

        Практическая задача : Цилиндр высотой 16 футов и радиусом 5 футов закрыт с каждого конца полусферой (половиной сферы), как показано ниже. Какова площадь поверхности и объем фигуры?

        Решение : Мы уже знаем, как рассчитать площадь поверхности стороны цилиндра: 2 πrh . Мы также должны рассчитать площадь поверхности двух полусферических крышек. Обратите внимание, что «основание» полушарий представляет собой поперечное сечение полной сферы. Поскольку это поперечное сечение имеет радиус 5 футов, оба полушария имеют одинаковый радиус.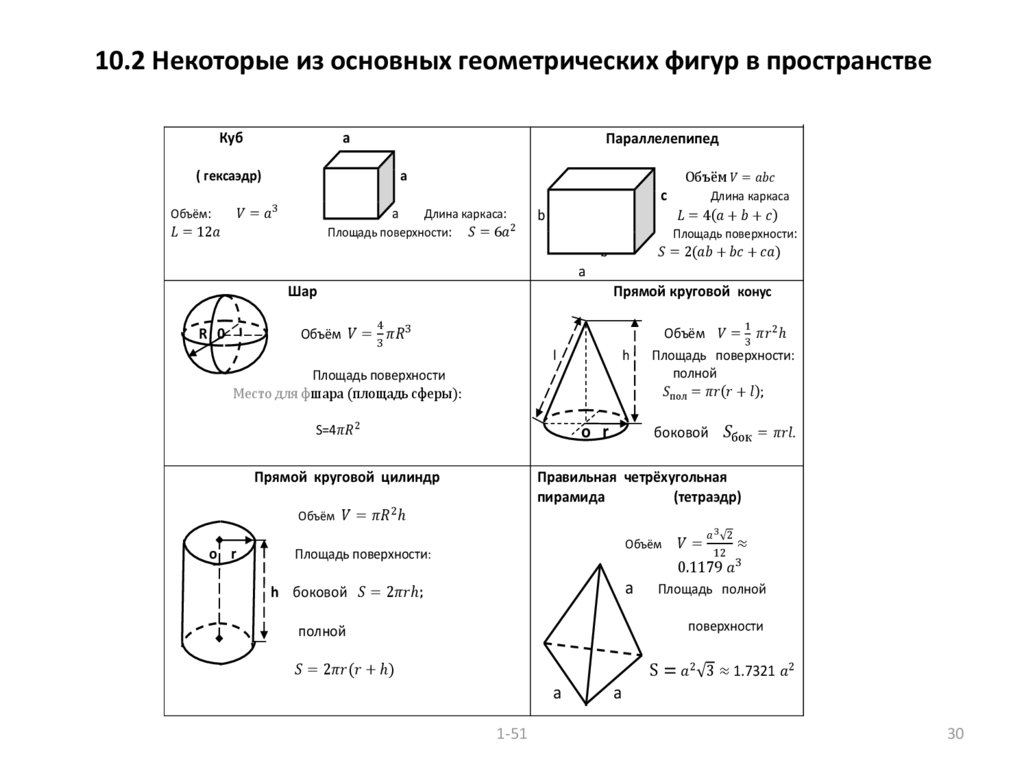 Площадь поверхности обоих полушарий вместе равна тогда просто площади поверхности полной сферы радиусом 5 футов. Площадь этой поверхности равна 4 πr 2 . Теперь мы можем вычислить площадь поверхности фигуры.

         

        S = 2 π (5)(16) + 4 π (5) 2 = 160 π + 100 π = 260 π ≈ 816.8 feet 2

         

        Чтобы рассчитать объем, просто найдите объем цилиндра плюс объем сферы радиусом 5 футов.

         

         

         

        Составные фигуры в трех измерениях

         

        Работа с составными фигурами в трех измерениях требует почти тех же принципов, что и для работы с составными фигурами в двух измерениях. Например, вычисление объема прямоугольного твердого тела со сферическим пустым пространством просто включает вычитание объема сферы из общего объема внутри прямоугольной области. Кроме того, наш подход к разделению сложных фигур на более простые и легкие в управлении фигуры применим и к трехмерным фигурам.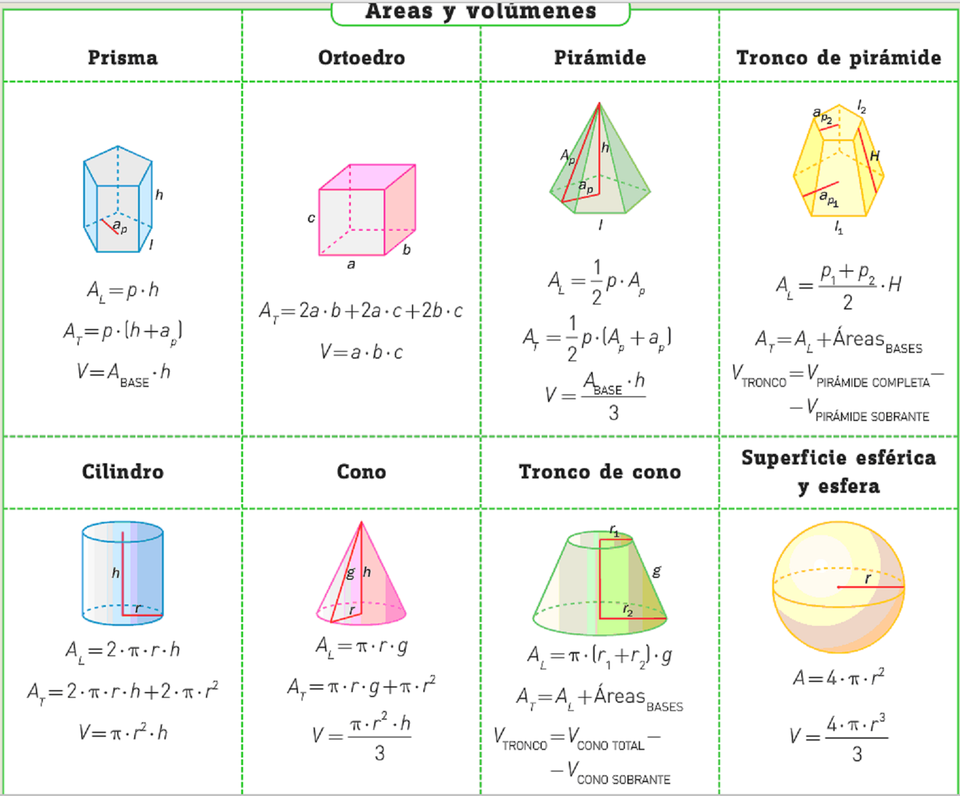 Следующая практическая задача иллюстрирует подход к трехмерной фигуре.

         

         

        Практическая задача : Прямоугольная призма содержит две одинаковые сферические полости радиусом 2 единицы, как показано ниже. Вычислите объем фигуры.

         

                                                        

         

        Первый прямоугольный объем в пределах м. , : Основание 32 квадратных единицы, а высота 4 единицы. Таким образом, объем составляет 128 кубических единиц. Каждая сфера имеет радиус 2 единицы; таким образом, каждый имеет следующий объем В .

         

         

        Сетки, объем и площадь поверхности призм — Криста Кинг Математика

        Определение сетей, объема и площади поверхности для различных призм

        В этом уроке мы рассмотрим введение в трехмерные геометрические фигуры, в частности сети, объем и площадь поверхности призм.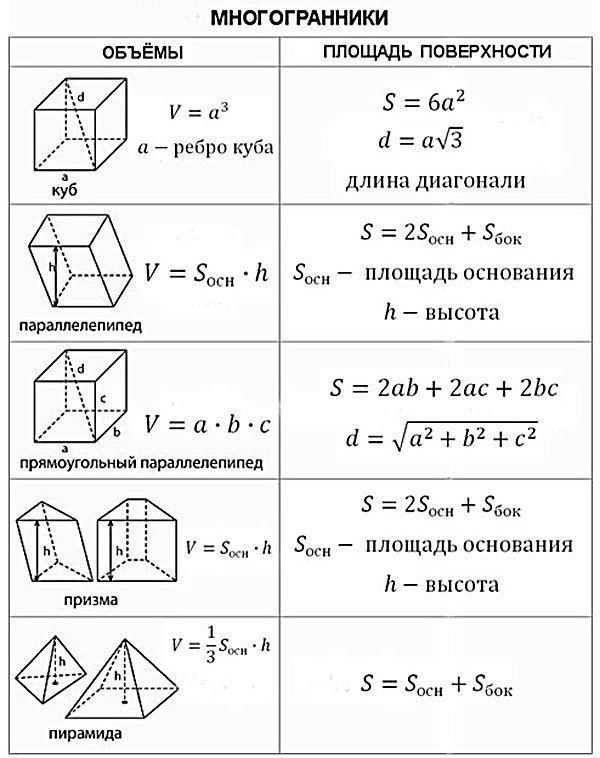

        Привет! Я Криста.

        Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

        Призма

        Призма  – это фигура, имеющая два конгруэнтных основания любой формы и стороны, составленные из прямоугольников. Вот несколько примеров призм:

        Основания призмы — это пары конгруэнтных фигур, а высота — это длина, соединяющая два основания. В прямоугольной призме в качестве оснований можно использовать любые две пары конгруэнтных прямоугольников, соединенных высотой.

        Сеть

        Сеть многогранника представляет собой его двумерную сплющенную версию. Мы делаем сеть, разрезая многогранник вдоль одного или нескольких ребер, пока мы не сможем разложить все это на плоскости.

        Когда у нас есть сеть многогранника, мы должны быть в состоянии реконструировать ее, складывая части сети, используя многоугольники в сети в качестве граней и используя каждый сегмент линии в сети как границу между некоторой парой грани многогранника. Вот треугольная призма (слева) и ее сетка (справа).

        Площадь поверхности прямоугольной призмы

        Вы также можете представить каждую сторону прямоугольной призмы как прямоугольник с определенной площадью, а площадь поверхности призмы равна сумме площадей всех шести сторон.

        Площадь каждой стороны прямоугольной призмы указана в таблице:

        Формула площади поверхности прямоугольной призмы равна

        ???A=2lw+2wh+2lh???

        Площадь поверхности призмы

        Чтобы найти площадь поверхности призмы, может быть полезно начертить сеть, найти площадь каждой фигуры в сети, а затем сложить площади. Чтобы найти площадь поверхности этой треугольной призмы, найдите площади трех прямоугольников и двух треугольников в ее сети и сложите все площади вместе.

        Объем прямоугольной призмы

        Объем прямоугольной призмы равен произведению длины на ширину и на высоту.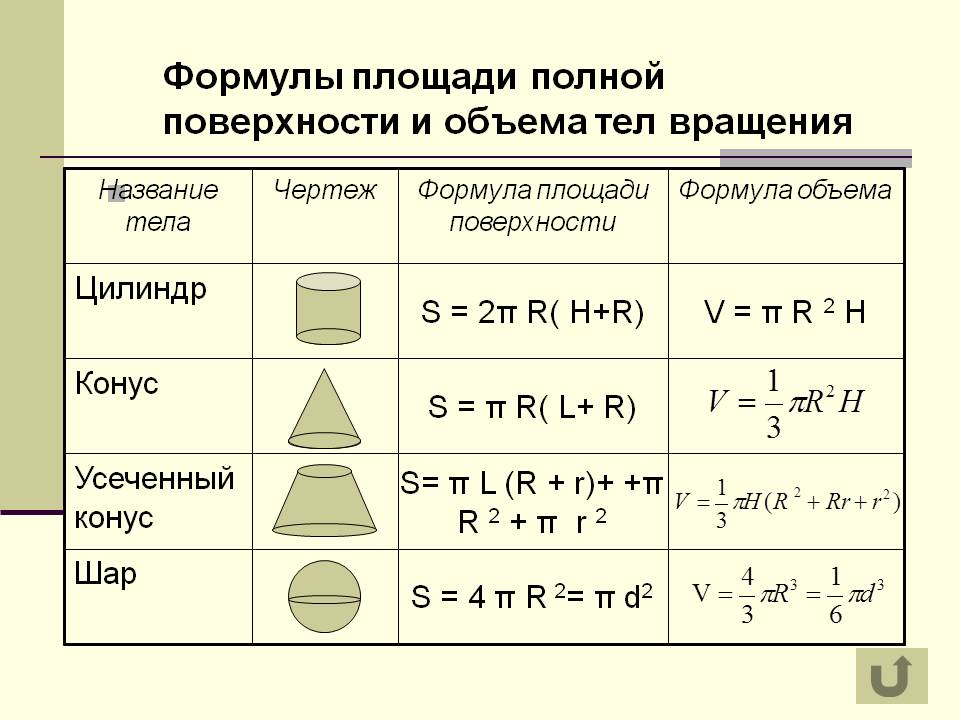

        ???V=lwh???

        Объем призмы

        Объем любой призмы равен произведению площади основания на высоту.

        ???V=\text{(площадь основания)(высота)}???

        Объем этой треугольной призмы равен площади одного из треугольников, умноженной на длину стороны, соединяющей два треугольных основания.

        Расчет площади поверхности призмы

        Пройти курс

        Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂

        Учить больше

        Заголовок

        Пример

        Какая сеть не принадлежит прямоугольной призме?

        Сеть С представляет собой сеть треугольной пирамиды. Все остальные сети являются примерами призм, потому что у них два конгруэнтных основания, а остальные грани — прямоугольники.

        No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *