Корень из 3 sin2x cos2x: Корень из 3 sin2x-cos2x =2 — Таловская средняя школа

36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x 13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град.

2+n-72)=1/(n+9)

Содержание

Квадратный корень из 3*sin2x=cos2x… -reshimne.ru

Новые вопросы

Ответы

Помогите пожалуйста решить неравенства; 4sin 2x cos 2x= Корень из 3






Лучший ответ по мнению автора

17.

12.17

Лучший ответ по мнению автора

Евгений

Читать ответы

Алиса

Читать ответы

Андрей Андреевич

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Решено

Помогите пожалуйста решить задачу 4-го класса. Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько

Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно

Алла на 6 лет моложе Веры. Сейчас папа в 11 раз старше Аллы и на 24 года старше Веры. Через сколько лет папа будет в 3 раза старше Веры?

Сколько существует 2016-значных чисел таких, что при вычёркивании его любой одной цифры получается 2015-значное число, и это 2015-значное число является делителем исходного числа (Напомним, что

Решено

В треугольнике ABC известно что AB=3 BC=8 AC=7. Найдите косинус (COS) угла ABC. Помогите пожалуйста с решением-очень очень нужно. Спасибо.

Пользуйтесь нашим приложением

3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт.

92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

Как найти x в 3sin 2x cos 2x для интервального класса 11 по математике CBSE

Подсказка: В этом вопросе мы должны решить тригонометрическое уравнение, чтобы получить значения для \[x\], сначала мы преобразует уравнение в терминах \[\tan x\], используя тригонометрическое тождество \[\dfrac{{\sin x}}{{\cos x}} = \tan x\], а теперь используя общее решение для функции \[\tan x\], которая задается \[n\pi + x\], где \[n \in Z\], теперь заменяя \[n\] другими значениями, чтобы получить требуемые значения в интервале \[0 \leqslant x < 2\pi \].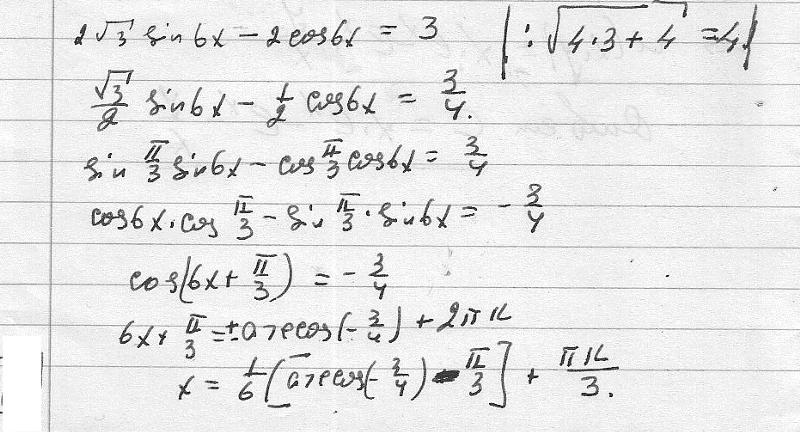

Полный пошаговый ответ:
Данное уравнение имеет вид \[3\sin 2x = \cos 2x\].
Теперь разделим обе части на 3, получим
\[ \Rightarrow \dfrac{{3\sin 2x}}{3} = \dfrac{{\cos 2x}}{3}\],
Теперь, упростив, получим ,
\[ \Rightarrow \sin 2x = \dfrac{{\cos 2x}}{3}\],
Теперь снова делим обе части на \[\cos 2x\], получаем,
\[ \Rightarrow \dfrac {{\sin 2x}}{{\cos 2x}} = \dfrac{{\cos 2x}}{{3\cos 2x}}\],
Теперь, упрощая, получаем,
\[ \Rightarrow \dfrac{{ \sin 2x}}{{\cos 2x}} = \dfrac{1}{3}\], 9{ — 1}}\left( {\dfrac{1}{3}} \right) = 0,3217\] в приведенном выше уравнении мы получаем,
\[ \Rightarrow 2x = n\pi + 0,3217\],
Теперь разделив с обеих сторон с 2 получаем,
\[ \Rightarrow \dfrac{{2x}}{2} = \dfrac{{n\pi + 0.3217}}{2}\],
Теперь, упрощая, получаем,
\[ \ Rightarrow x = \dfrac{{n\pi }}{2} + \dfrac{{0,3217}}{2}\],
Снова упрощая, получаем,
\[ \Rightarrow x = \dfrac{{n\pi }}{2} + 0,1608\],
Итак, теперь заданный интервал равен \[0 \leqslant x < 2\pi \], теперь принимая разные значения для \[n\] и подставляя значения в выше уравнение мы получаем,
Сначала возьмем \[n = 0\], так как данный интервал начинается с 0,
\[ \Rightarrow x = \dfrac{{\left( 0 \right)\pi}}{2} + 0,1608\],
Теперь, упрощая, получаем,
\[ \Rightarrow x = 0,1608\], и оно лежит между заданным интервалом,
Сначала возьмем \[n = 1\], так как заданный интервал от 0,
\[ \Rightarrow x = \dfrac{{\left( 1 \right)\pi }}{2} + 0,1608\],
Упрощая, получаем,
\[ \Rightarrow x = \dfrac{{3,14}}{2} + 0,1608\]
Снова упрощая, получаем
\[ \Стрелка вправо x = 1,57 + 0,1608\]
Теперь упрощая сложением получаем,
\[ \Rightarrow x = 1. 7308\], и лежит между заданным интервалом,
Теперь возьмем \[n = 2\], так как заданный интервал от 0,
\[ \ Rightarrow x = \dfrac{{\left( 2 \right)\pi }}{2} + 0,1608\],
Упрощая, получаем,
\[ \Rightarrow x = 3,14 + 0,1608\]
Теперь упрощая, добавляя получить,
\[ \Rightarrow x = 3,302\], и он лежит между заданным интервалом,
Теперь возьмем \[n = 3\], так как данный интервал от 0,
\[ \Rightarrow x = \dfrac{ {\ влево ( 3 \ вправо) \ пи} {2} + 0,1608 \],
Теперь, упрощая, получаем,
\[ \Rightarrow x = \dfrac{{3\left( {3.14} \right)}}{2} + 0,1608\],
Теперь, упрощая, получаем,
\[ \Rightarrow x = \dfrac{{9.42}}{2} + 0.1608\],
Теперь разделив и упростив, получим,
\[ \Rightarrow x = 4.71 + 0.1608\],
Теперь упростив сложением, получим,
\[ \Rightarrow x = 4,8708\], и он лежит между заданным интервалом,
Теперь возьмем \[n = 4\], так как данный интервал начинается с 0,
\[ \Rightarrow x = \dfrac{{\left( 4 \right) \pi}}{2} + 0,1608\],
Теперь, упрощая, получаем,
\[ \Rightarrow x = \dfrac{{4\left( {3. 14} \right)}}{2} + 0,1608\],
Теперь, упрощая, получаем,
\[ \Rightarrow x = \dfrac{{12.56}}{2} + 0.1608\],
Теперь разделив и упростив, получим,
\[ \Rightarrow x = 6.28 + 0.1608\],
Теперь упростив сложением, получим,
\[ \Rightarrow x = 6,4408\], и оно не лежит между заданным интервалом,
Таким образом, возможные значения \[x\] для данного уравнения: 0,1608, 1,7308, 3,302 и 4,8708.

Возможные значения \[x\] в \[3\sin 2x = \cos 2x\] для интервала \[0 \leqslant x < 2\pi \] равны 0,1608, 1,7308, 3,302 и 4,8708.

Примечание:
Уравнение, включающее одно или несколько тригонометрических соотношений неизвестного угла, называется тригонометрическим уравнением. Тригонометрическое уравнение отличается от тригонометрического тождества. Тождество выполняется для каждого значения неизвестного угла, а тригонометрическое уравнение выполняется для некоторых частных значений неизвестного угла. Значение неизвестного угла, удовлетворяющее тригонометрическому уравнению, называется его решением. Вот некоторые общие решения для некоторых тригонометрических уравнений, 9n}\alpha \] \[\cos x = \cos \alpha \] \[x = 2n\pi \pm \alpha \] \[\tan x = \tan \ alpha \] \[x = n\pi \pm \alpha \]

Найдите sin2x, cos2x и tan2x по данной информации: cosec(x) = 6, а tan (x)

Тригонометрия – это отношение между углами и сторонами прямоугольного треугольника. В прямоугольном треугольнике 3 угла, один из которых прямой (90°), а два других угла острые и имеют 3 стороны. Сторона, противоположная прямому углу, называется гипотенузой. Между этими сторонами существует 6 отношений, основанных на угле между ними, и они называются тригонометрическими отношениями.

. Прямоугольный треугольник ACB

Синус (sin):

Синус угла определяется отношением длин сторон, противолежащих углу, и гипотенузы. Для приведенного выше треугольника sin A = BC/AB

Косинус (cos):

Косинус угла определяется отношением длин сторон, примыкающих к углу, и гипотенузы. Для приведенного выше треугольника cos A = AC/AB

Тангенс (тангенс):

Тангенс угла определяется отношением длин сторон, противоположных углу, и стороны, примыкающей к углу. угол. Для приведенного выше треугольника tan A = BC/AC

Косеканс (косек):

Косеканс угла определяется отношением длины гипотенузы и стороны, противоположной углу. Для приведенного выше треугольника cosec A = AB/BC

Секанс (сек):

Секанс угла определяется отношением длины гипотенузы и стороны, и стороны, прилегающей к углу. треугольник, сек A = AB/AC

Котангенс (кот):

Котангенс угла определяется отношением длины стороны, примыкающей к углу, и стороны, противолежащей углу. Для приведенного выше треугольника кроватка A = AC/BC

Найдите sin2x, cos2x и tan2x по предоставленной информации. csc (x) = 6, tan (x) < 0.
Решение:
Прямоугольный треугольник XYZ
Дано, что cosecX = 6
Мы знаем, что sinX = 1/cosec9X 9090
⇒ sinx = 1/6 ……………… . . (1)
⇒ sinx положительный
. Дается, что Tanx <0
⇒ Tanx отрицательный
Так как sinX положителен, а tanX отрицателен,
⇒ X лежит во 2-м квадранте.
Мы знаем, что, cos ² x = 1 — sin ² x
⇒ cos ² x = 1 — (1/6) ²
⇒ Cos ² X = 35 /36 /360909
⇒ COS ² X = 35 /36 /36 /36 /36 /36 /36 /36 /36 /36 /36 /36 /36 /360909
лять
⇒ cosx = ± √35 / 6
, но, поскольку x лежит во 2 -м квадранте, а Cosecant отрицателен во 2 -м квадранте,
⇒ Cosx = — √35 / 6 …………. (2)
sin(2X) = 2.sinX.cosX
Из (1) и (2),
⇒ sin(2X) = 2.(1/6).(– √35 / 6)
⇒ sin (2x) = — √35/18 …………………… (3)
cos (2x) = cos ² x — sin ² x
из (1) и (2),
⇒ cos(2X) = ( – √35/6) ² – (1/6) ²
⇒ cos(2X) = 35/36 – 1/36
⇒ cos(2X) = 34/ 36
⇒ cos(2X) = 17/180909
tan(2X) = sin(2X) / cos(2X)
Из (3) и (4),
⇒ tan(2X) = (– √35/18)/(17/18)
⇒ tan(2X) = – √35/17
Следовательно, значения sin(2X), cos(2X) и tan(2X) равны – √35/18, 17/18 и – √35/17 соответственно.
Аналогичные вопросы
Вопрос 1. Найдите sin(2X),cos(2X) и tan(2X) по данным: secX = 8, X лежит в квадранте IV
дано, что secX = 8
Мы знаем, что, cosx = 1 / secx
⇒ cosx = 1/8 ……………… .. (1)
Мы знаем, что SIN ² x = 1 — cos ² x
⇒ sin ² x = 1 — (1 /8) ²
⇒ SIN ² x = 1 — 1/64
⇒ SIN ² x = 63 /64
⇒ sinx = ± ± ± ± ± ± ± 63 /64
⇒ = ± ± ± ± ± 63 /64
⇒ sin. √63 / √64
⇒ sinX = ± 3√7 / 8
Поскольку синус(sin) отрицателен в квадранте IV,
⇒ sinx = — 3√7 / 8 ………………. (2)
sin (2x) = 2.sinx.cosx
из (1) и (2),
⇒ sin (2x (1) и (2),
⇒ sin (2x 2x (1) и (2),
⇒ sin (2x 2x (1) и (2),
⇒ sin (2x ) = 2.( – 3√7 / 8).(1 / 8)
⇒ sin( 2X ) = – 3√7 / 32 cos ² X – sin ² X
Из (1) и (2),
⇒ cos(2X) = (1/8) ² – (– 3√7/8) ^{2 ^{2 ³}}
⇒ cos (2x) = (1/64) — (63/64)
⇒ cos (2x) = — 62/64
⇒ cos (2x) = — 31/32 ……………… . . (4)
tan(2X) = sin(2X) / cos(2X)
Из (3) и (4),
⇒ tan(2X) = (– 3√7/32) / (– 31 / 32)
⇒ tan( 2X ) = 3√7 / 31
Следовательно, значения sin( 2X ), cos( 2X ) и tan( 2X ) равны – 3√7 / 32, – 31 / 32 и 3√7/31 соответственно.
Вопрос 2: Найдите sin(2X), cos(2X) и tan(2X) по данной информации: sinX = 3/5, X лежит в квадранте I
Решение:
Дано, что sinX = 3/5 ………………. (1)
Мы знаем, что, COS ² x = 1 — SIN ² x
⇒ COS ² x = 1 — (3/5) ²
⇒ cos ² X = 16 / 25
⇒ cosX = ± 4 / 5
Поскольку X лежит в 1-м квадранте, а косеканс положителен в 1-м квадранте,
⇒ cosx = 4/5 …………………. (2)
sin (2x) = 2.sinx.cosx
из (1) и (2),
⇒ sin (2x) = 2 . (3/5). (4/5)
⇒ sin (2x) = 24/25 ………………… .. (3)
cos (2x) = cos ² x — sin ² X
Из (1) и (2),
⇒ cos(2X) = (4/5) ² – (3/5) ²
⇒ cos(2X 2) – 16/5 9/25
⇒ cos( 2X ) = 7/25 …………………. .( 4 )
tan( 2X ) = sin( 3 ( 909 ) / 909 ) / cos(2X) Из ),
⇒ tan( 2X ) = ( 24/25 ) / (7/25)
⇒ tan( 2X ) = 24/7
Следовательно, значения sin(2X), cos(2X) и tan (2X) 24/25, 7/25 и 24/7 соответственно.
Вопрос 3: Найдите sin(2X),cos(2X) и tan(2X) по полученным данным: cosX = 15/17, X лежит в квадранте IV
Решение:
Удажается, что, COSX = 15/17 ………………. (1)
Мы знаем, что SIN ² X = 1 — COS ² X
⇒ SIN ² X = 1 — (15/17) ²
⇒ SIN ² x = 1 — 225 /289
⇒ SIN ² x = 64 /289
⇒ SINX 2 x = 64 /289
⇒ sinx = ± ± 649 /289
. 8 / 17
Поскольку X лежит в 1-м квадранте, а синус (sin) положителен в 4-м квадранте,
⇒ sinx = — 8/17 ………………. (2)
sin (2x) = 2.sinx.cosx
из (1) и (2),
⇒ sin (2x) = 2.
No related posts.