вычисление матрицы онлайн методом гаусса онлайн
Вы искали вычисление матрицы онлайн методом гаусса онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить систему уравнений онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление матрицы онлайн методом гаусса онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.

Где можно решить любую задачу по математике, а так же вычисление матрицы онлайн методом гаусса онлайн Онлайн?
Решить задачу вычисление матрицы онлайн методом гаусса онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Ранг матрицы методом Гаусса | Мозган калькулятор онлайн
Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.
Рассмотрим метод Гаусса или метод элементарных преобразований.
Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.
Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.
Метод Гаусса использует элементарные преобразования, которые не изменяют ее ранг:
- Транспонирование.
- Перестановка местами строк или столбцов.
- Прибавление одной строки/столбца к другой строке/столбцу умноженного на ненулевое число.
- Умножение строки или столбца на ненулевое число.
С помощью данного метода нужно привести матрицу к ступенчатому виду и посчитать количество строк, в которых есть хоть один не нулевой элемент.
Пример
Рассмотрим данный метод на примере. Дана матрицы:
Для облегчения дальнейших расчетов поменяем местами строку №1 со строкой №2.
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 3/2.
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычитаем строку №1, умноженную на 2.
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычтем строку №2, умноженную на -1/4. Мы его получили разделив элимент a3,2 = -0.5 на элимент a2,2 = 2.
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычтем строку №2, умноженную на -1/2.
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычитаем строку №3, умноженную на 2.
В получившейся матрице одна строка содержит нулевые элементы, а три строки имеют не нулевые элементы. Ответ: Ранг=3.
Решение уравнений методом сложения. Калькулятор онлайн
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 — некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Алгоритм решения способом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.
1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
5. Сделать проверку решения.
Пример решения способом сложения
Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:
{3*x + 2*y = 10;
{5*x + 3*y = 12;
Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.
{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2
Получим следующую систему уравнений:
{9*x+6*y = 30;
{10*x+6*y=24;
Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.
10*x+6*y — (9*x+6*y) = 24-30; x=-6;
Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.
{3*(-6) + 2*y =10;
{2*y=28; y =14;
Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.
{3*x + 2*y = 10;
{5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, получились два верных равенства, следовательно, мы нашли верное решение.
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы — это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода — избавиться от 1-ой из переменных.
-4 — y + 5 = 0 → y = 1,
В виде системы решение выглядит где-то так:
Ответ: x = -4 , y = 1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.
Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.
Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.

- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, а b n — свободные члены.
Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.
В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:
Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .
Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.

- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице).
 Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы. - Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2).
 Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения. - Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}).
 В последнем столбце новой матрицы получаем корни уравнения.
В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Система комплексных линейных уравнений
| Вы ввели следующую систему уравнений |
| Решение системы следующее |
Решение системы линейных уравнений
Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:
— иметь только одно верное решение;
— иметь бесконечное множество корней;
— иметь несовместный тип (когда решений быть не может).
Метод Гаусса, используемый нашим АБАК-ботом — самое мощное и безотказное средство для поиска решения любой системы уравнений линейного типа.
Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т.н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами — ровно то же самое, что и элементарные преобразования матриц в переложении для строк.
Наш бот умеет молниеносно выдавать решения системы линейных уравнений с неограниченным количеством переменных!
Практическое применение решение таких систем находит в электротехнике и геометрии: расчетах токов в сложных контурах и выведение уравнения прямой при пересечении трех плоскостей а также в множестве специализированных задач.
Данный сервис позволяет решать неограниченную по размерам систему линейных уравнений с комплексными коэффициентами.
Практическое применение:
Ну, раз бот умеет считать решения комплексных систем, то для него не составит труда считать частный случай, когда элементы системы являются вещественные числа.
Второе, в школе Вам это наверняка не понадобится, но вот в институте, особенно институтах связи, при расчетах токов в сложных контурах в электротехнике, наверняка пригодится.
Синтаксис
Для пользователей XMPP клиентов: linur_i <список элементов системы>
список элементов системы — является список значений перечисленных в одну или несколько строк разделенными пробелами между собой
linur_i 5:2 3 10 2 -11:3 0:-30
Примеры
linur_i 5:2 3 10 2 -11:3 0:-30
Корни системы линейных уравнений равны следующим значениям.
Переменные считаются слева направо
1.4389598942265:-1.941383869546
-0.3591890700749:2.2763331864257
то есть x1=1.4389598942265 — 1.941383869546 i
x2=-0.3591890700749+2.2763331864257 i
Рассчитаем комплексную систему линейных уравнений
такого вида
Записываем все элементы в поле ввода. Как видите, данные могут быть не только числовые но и быть произвольным выражением, включающее в себя комплексные числа.
И получаем следующий результат.
| Вы ввели следующую систему уравнений |
| Решение системы следующее |
Успехов в расчетах !
- Скалярное произведение двух матриц >>
Карта сайта
Карта сайта- Екзамены, тесты
- Экзамены, тесты по математике. Числа
- Экзамены, тесты по математике. Числа 1
- Экзамены, тесты по математике. Числа 2
- Экзамены, тесты по математике. Числа 3
- Экзамены, тесты по математике. Логарифм
- Экзамены по математике. Дроби и корни
- Экзамены, тесты по математике. Раскритие иррациональности
- Экзамены, тесты по математике. Уравнения на проценты
- Экзамены, тесты по математике. Арифметическая прогрессия
- Экзамены, тесты по математике. Выражения с синусом и косинусом
- Экзамены, тесты по математике. Упрощение логарифма
- Экзамены, тесты по математике. Примеры на синус и косинус
- Экзамены, тесты по математике. Свойства логарифма
- Экзамены, тесты по математике. Решения уравнений
- Экзамены, тесты по математике. Решение уравнений и неравенств
- Экзамены, тесты по математике. Решение уравнений
- Экзамены, тесты по математике. Решение неравенств
- Экзамены, тесты по математике. Решение системы уравнений
- Экзамены, тесты по математике. Тригонометрические уравнения и их решения
- Экзамены, тесты по математике. Решение уравнений на синус и косинус
- Экзамены, тесты по математике. Показательные уравнения и неравенства
- Экзамены, тесты по математике. Логарифмические уравнения и неравенста
- Экзамены, тесты по математике. Решение задач на уравнения
- Экзамены, тесты по математике. Уравнения с корнями
- Экзамены, тесты по математике. Решение уравнений с корнями
- Экзамены, тесты по математике. Решение иррациональных уравнений
- ВНО по математике 2013. № 1-10
- ВНО по математике 2013. № 11-16
- ВНО по матиматике 2013. № 17-22
- ВНО по матиматике 2013. № 23-28
- ВНО по математике 2013. № 29-33
- ВНО математика. № 1-9
- ВНО математика. № 10-15
- ВНО математика. № 16-21
- ВНО математика. № 22-27
- ВНО математика. № 28-33
Численные методы: решение систем линейных уравнений
В прикладных задачах часто возникает необходимость решать системы линейных уравнений.
Система линейных алгебраических уравнений с n неизвестными — это система уравнений вида
(1)
Слово система означает, что все уравнения рассматриваются как одно целое.
В общем случае у нас имеется m — уравнений, n — количество неизвестных. x1, x2,…, xn — неизвестные, которые следует определить.
В системе (1) – фиксированные коэффициенты, b1, b2, …, bm — свободные члены — предполагаются известными.
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Задача состоит в том, чтобы найти такие которые удовлетворяют всем уравнениям (1).
В частном случае мы имеем одно линейное уравнение:
Конечно, такое уравнение легко решить, если предположить, что коэффициент не равен 0, имеем: = .
Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения.
Система линейных уравнений может быть представлена в матричной форме как:
или:
Ax = b
Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов.
Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.
Рассмотрим, например, систему вида и поймем, как найти ее решение:
(2)
Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.
Вопрос: как исходную систему привести к такому виду и можно ли это сделать.
Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.
От этих операций тождество не меняется.
В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:
(3)
Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).
Система (3) точно такая же, как система (2).
Из второго уравнения системы (3) сразу получим:
Никто не мешает нам подставить это значение в первое уравнение:
Отсюда сразу находим, что
Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:
Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.
Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:
Опишем этот метод в общем случае.
Вначале исходная система приводится к верхнетреугольному виду.
Это достигается следующей последовательностью преобразований (прямой ход).
Будем считать для удобства, что элемент aij исходной матрицы и компоненты вектора bi есть, соответственно, элементы aij (1) первого шага преобразованной матрицы A1 и преобразованного вектора b1:A = A1, b=b1.
Далее, на втором шаге прибавим к второй строке первую, умноженную на
Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент
При этом соответственно изменится и вектор b1.
Таким образом, 2 шаг.
Имеем систему уравнений A2x = b2:
где
3 шаг.
Прибавим к новой третьей строке новую вторую, умноженную на
То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к i-ой строке вторую, умноженную на
При этом получим систему A3x = b3:
(k+1)-ый шаг:
Здесь
Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:
При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:
Решение полученной треугольной системы как легко видеть, имеет вид (обратный ход метода Гаусса):
Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.
Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).
Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.
Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.
Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).
Введем матрицы Mk по правилу:
На каждом шаге метода Гаусса получается некоторая промежуточная матрица:
и вектор
Нетрудно видеть, что
Вопрос. Почему
Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:
При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения
Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.
Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.
При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.
Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.
Идея состоит в том, чтобы найти неподвижную точку матричного уравнения
(5)
эквивалентного начальной системе линейных алгебраических уравнений.
При итерации в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
.
Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.
Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.
Обусловленность линейных систем, погрешность
При решении абстрактной задачи Ax = b, где A — оператор произвольной природы, важным моментом является корректность ее постановки.
Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при также стремится к нулю).
Однако и непрерывная зависимость от входных данных может иметь свои нюансы.
Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.
Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.
Кроме того, существуют ошибки округления, возникающие при вычислениях.
Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.
Чем можно охарактеризовать количественно обусловленность для линейных систем?
Пусть A — квадратная NxN — матрица.
Рассмотрим задачу Ax = b.
Пусть также некоторая норма в пространстве RN
Норма оператора A определяется стандартно:
Обозначим y = Ax и введем число m по правилу:
Величина называется числом обусловленности.
Очевидно:
- если A — диагональная, то (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть вариация правой части, а соответствующее изменение решения.
Тогда справедливо следующее неравенство:
Доказательство. Имеем:
Так как
то
Аналогично, поскольку
Объединяя два неравенства, окончательно получаем для оценки погрешности:
В начало
Содержание портала
Решающих систем с исключением Гаусса — College Algebra
Цели обучения
В этом разделе вы:
- Запишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполняет операции со строками в матрице.
- Решите систему линейных уравнений с помощью матриц.
Немецкий математик Карл Фридрих Гаусс (1777–1855).
Карл Фридрих Гаусс жил в конце 18 — начале 19 века, но до сих пор считается одним из самых плодовитых математиков в истории.Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Мы впервые столкнулись с методом исключения Гаусса в системах линейных уравнений: две переменные. В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством представления и решения системы уравнений.Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей.
Например, рассмотрим следующую систему уравнений.
Мы можем записать эту систему в виде расширенной матрицы:
Мы также можем написать матрицу, содержащую только коэффициенты.Это называется матрицей коэффициентов.
Система уравнений три на три, например
имеет матрицу коэффициентов
и представлена расширенной матрицей
Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: члены x идут в первый столбец, y -термы во втором столбце и z -термы в третьем столбце. Очень важно, чтобы каждое уравнение было написано в стандартной форме, чтобы переменные совпадали.Если в уравнении отсутствует член переменной, коэффициент равен 0.
Для данной системы уравнений напишите расширенную матрицу.
- Запишите коэффициенты членов x как числа в первом столбце.
- Запишите коэффициенты членов y в виде чисел во втором столбце.
- Если есть z -термин, запишите коэффициенты в виде чисел в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
Запишите расширенную матрицу данной системы уравнений.
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Напишите систему уравнений из расширенной матрицы.
Выполнение операций со строками в матрице
Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение строковых операций над матрицей — это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме.Вот рекомендации по получению формы рядного эшелона.
- В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
- Любые нулевые строки помещаются внизу матрицы.
- Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
- Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.
- Поменяйте местами ряды. (Обозначение 🙂
- Умножить строку на константу. (Обозначение 🙂
- Добавить произведение одной строки на константу к другой строке. (Замечание:
Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными. С помощью этих операций есть несколько ключевых шагов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строку 1 можно было использовать для преобразования оставшихся строк.
Исключение по Гауссу
Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы записать матрицу с номером 1 в качестве записи по главной диагонали и иметь все нули внизу.
Первый шаг стратегии Гаусса включает получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».
- Первое уравнение должно иметь старший коэффициент 1. Поменяйте местами строки или умножьте на константу, если необходимо.
- Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбец 2.
- Используйте операции со строками, чтобы получить нули в нижнем столбце 2, под записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбец 3.
- Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу будут только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Решите данную систему методом исключения Гаусса.
Решите данную систему методом исключения Гаусса.
Использование исключения Гаусса для решения системы уравнений
Используйте метод исключения Гаусса для решения данной системы уравнений.
Решение зависимой системы
Решите систему уравнений.
Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon
Выполняет строковые операции с заданной матрицей для получения формы «строка-эшелон».
Запишите систему уравнений в виде ряда.
Решение системы линейных уравнений с использованием матриц
Мы увидели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения строчно-эшелонированной формы.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
Решите систему, используя матрицы.
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Дана система уравнений, решите с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную
- Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.
Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 фунтов стерлингов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 фунтов стерлингов. Сколько было вложено по каждой ставке?
Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 фунтов стерлингов в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 фунтов стерлингов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
У нас есть система трех уравнений с тремя переменными. Пусть будет сумма, вложенная под 5%, пусть будет сумма, вложенная под 8%, пусть будет сумма, вложенная под 9%. Таким образом,
В качестве матрицы имеем
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
Третья строка сообщает usthus
Вторая строка говорит нам, что подставляя мы получаем
Первая строка говорит нам о замене и получаем
Ответ: 3000 евро вложено под 5%, 1000 евро вложено под 8% и 6000 евро вложено под 9%.
Небольшая обувная компания взяла ссуду в размере 1 500 000 фунтов стерлингов для расширения своих запасов. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 фунтов стерлингов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
? 150 000 при 7%, 750 000 фунтов стерлингов при 8%, 600 000 фунтов стерлингов при 10%
Ключевые концепции
- Расширенная матрица — это матрица, которая содержит коэффициенты и константы системы уравнений.См. (Рисунок).
- Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. (Рисунок).
- Операции со строками включают в себя умножение строки на константу, добавление одной строки к другой строке и замену строк местами.
- Мы можем использовать метод исключения Гаусса для решения системы уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
- Операции со строками выполняются над матрицами для получения формы «строка-эшелон». См. (Рисунок).
- Чтобы решить систему уравнений, запишите ее в форме расширенной матрицы.Выполните операции со строками, чтобы получить форму эшелона строк. Обратно-заменитель, чтобы найти решения. См. (Рисунок) и (Рисунок).
- Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
- Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).
Упражнения по разделам
Словесный
Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как написать эту расширенную матрицу.
Да. Для каждой строки коэффициенты переменных записываются поперек соответствующей строки и помещается вертикальная черта; затем константы помещаются справа от вертикальной полосы.
Можно ли записать любую матрицу в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.
Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно выполнить для расширенной матрицы
.Нет, существует множество правильных методов использования строковых операций над матрицей.Есть два возможных способа: (1) Поменять местами строки 1 и 2. Затем (2) Разделить строку 1 на 9.
Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.
Нет. Матрица с 0 элементами для всей строки будет иметь либо ноль, либо бесконечно много решений.
Алгебраические
Для следующих упражнений напишите расширенную матрицу линейной системы.
Для следующих упражнений запишите линейную систему из расширенной матрицы.
Для следующих упражнений решите систему методом исключения Гаусса.
Расширения
Для следующих упражнений используйте метод исключения Гаусса для решения системы.
Реальные приложения
Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?
В конкурирующем магазине кексов ежедневно продаются кексы на сумму 4520 фунтов стерлингов.Шоколадные кексы стоят 2,25 евро, а кексы из красного бархата — 1,75 евро. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
860 красный бархат, 1340 шоколад
Вы вложили 10 000 евро в два счета: один с простой процентной ставкой 3%, а другой — с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283,50 фунтов стерлингов, какая сумма была на каждом счете по истечении года?
Вы вложили 2300 евро на счет 1 и 2700 евро на счет 2.Если общая сумма процентов по истечении одного года составляет 254 евро, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
4% на счет 1, 6% на счет 2
Bikes’R’Us производит велосипеды по 250 фунтов стерлингов. Это стоит производителю 180 фунтов стерлингов за велосипед, плюс стартовый взнос в размере 3500 фунтов стерлингов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
Крупный магазин бытовой техники рассматривает возможность приобретения пылесосов у небольшого производителя.Магазин сможет приобрести пылесосы по цене 86 фунтов стерлингов каждый, с оплатой доставки в размере 9 200 фунтов стерлингов, независимо от того, сколько пылесосов будет продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?
Три самых популярных вкуса мороженого — это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?
В магазине мороженого растет спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге выросли вдвое, продажи бананов увеличились на 50%, а продажи тыквы — на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено каждым отдельным мороженым в прошлом году.
Банан — 3%, тыква — 7%, а каменистая дорога — 2%
Пакет с ореховой смесью содержит кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки — 4 г, миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.
100 миндальных орехов, 200 кешью, 600 фисташек
Глоссарий
- дополненная матрица
- матрица коэффициентов, примыкающая к столбцу констант, разделенному вертикальной линией в скобках матрицы
- матрица коэффициентов
- матрица, содержащая только коэффициенты из системы уравнений
- Гауссово исключение
- с использованием элементарных операций со строками для получения матрицы в виде строки-эшелона
- главная диагональ
- записей из левого верхнего угла по диагонали в правый нижний угол квадратной матрицы
- рядная форма
- после выполнения операций со строками матричная форма, которая содержит единицы по главной диагонали и нули в каждом пробеле ниже диагонали
- эквивалент ряда
- две матрицы и эквивалентны строкам, если одна может быть получена из другой путем выполнения основных операций со строками
- строковые операции
- : добавление одной строки к другой строке, умножение строки на константу, перестановка строк и т. Д. С целью получения формы «строка-эшелон»
М.7 Исключение Гаусса-Джордана | STAT ONLINE
Исключение Гаусса-Жордана — это алгоритм, который может использоваться для решения систем линейных уравнений и нахождения обратной матрицы любой обратимой матрицы. Он основан на трех элементарных операциях со строками , которые можно использовать с матрицей:
- Поменять местами две строки
- Умножьте одну из строк на ненулевой скаляр.
- Сложить или вычесть скалярное кратное одной строки из другой строки.
В качестве примера операции с первой элементарной строкой поменяйте местами 1-ю и 3-ю строки.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 7 & 5 & 0 \\ 2 & -2 & 3 \\ 4 & 0 & -1 \ end {pmatrix} \]
Для примера операции второй элементарной строки умножьте вторую строку на 3.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 6 & -6 & 9 \\ 7 & 5 & 0 \ end {pmatrix} \]
В качестве примера операции с третьей элементарной строкой добавьте дважды первую строку ко второй строке.
\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 10 & -2 & 1 \\ 7 & 5 & 0 \ end {pmatrix} \]
Редукторный эшелон
Цель метода исключения Гаусса-Жордана состоит в том, чтобы использовать три операции элементарных строк для преобразования матрицы в форму с сокращенными строками. Матрица находится в форме сокращенного ряда строк , также известной как каноническая форма строки , если выполняются следующие условия:
- Все строки с нулевыми записями находятся внизу матрицы
- Первая ненулевая запись в строке, называемая ведущей записью или поворотной точкой , каждой ненулевой строки находится справа от ведущей записи строки над ней.
- Начальная запись, также известная как опорная точка, в любой ненулевой строке — 1.
- Все остальные записи в столбце, содержащие в начале 1, являются нулями.
Например,
\ [A = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \ end {pmatrix}, B = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix}, C = \ begin {pmatrix} 0 & 7 & 3 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \ end {pmatrix}, D = \ begin {pmatrix} 1 & 7 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix} \]
Матрицы A, и B имеют вид уменьшенного ряда, а матрицы C и D — нет. C не находится в форме пониженного ряда, поскольку нарушает условия два и три. D не находится в форме пониженного ряда, так как нарушает четвертое условие. Кроме того, операции с элементарными строками могут использоваться для уменьшения матрицы D в матрицу B .
Шаги для исключения Гаусса-Джордана
Для выполнения исключения Гаусса-Джордана:
- Поменяйте местами строки так, чтобы все строки со всеми нулевыми записями находились внизу
- Поменяйте местами строки так, чтобы строка с самой большой левой ненулевой записью была наверху.
- Умножьте верхнюю строку на скаляр так, чтобы ведущая запись верхней строки стала 1.
- Сложить / вычесть кратные числа верхней строки из других строк, чтобы все остальные записи в столбце, содержащем ведущую запись верхней строки, были равны нулю.
- Повторите шаги 2–4 для следующей самой левой ненулевой записи, пока все ведущие записи не станут 1.
- Поменять местами строки так, чтобы первая запись каждой ненулевой строки была справа от первой записи строки над ней.
Выбранные примеры видео показаны ниже:
Чтобы получить инверсию матрицы n × n A :
- Создайте разделенную матрицу \ ((A | I) \), где I — единичная матрица.{-1} = I \).
Решение системы с исключением Гаусса
Результаты обучения
- Используйте метод исключения Гаусса для решения системы уравнений, представленной в виде расширенной матрицы.
- Интерпретировать решение системы уравнений, представленной в виде расширенной матрицы.
Мы видели, как написать систему уравнений с расширенной матрицей , а затем как использовать строковые операции и обратную подстановку для получения строковой формы .Теперь мы будем использовать метод исключения Гаусса как инструмент для решения системы, записанной в виде расширенной матрицы. В нашем первом примере мы покажем вам процесс использования исключения Гаусса в системе двух уравнений с двумя переменными.
Пример: решение системы 2 X 2 методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {array} {l} 2x + 3y = 6 \ hfill \\ \ text {} x-y = \ frac {1} {2} \ hfill \ end {array} [/ latex]
Показать решениеВо-первых, мы запишем это как расширенную матрицу.
[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 3 \\ \ hfill 1 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 6 \\ \ hfill \ frac {1} {2} \ end {array} \ right] [/ latex]
Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.
[латекс] {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 2 & \ hfill 3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 6 \ end {array} \ right] [/ latex]
Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Это можно сделать, умножив строку 1 на [latex] -2 [/ latex], а затем прибавив результат к строке 2.
[латекс] -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill 5 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 5 \ end {массив } \ right] [/ latex]
У нас есть только один шаг, чтобы умножить строку 2 на [latex] \ frac {1} {5} [/ latex].
[латекс] \ frac {1} {5} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \ \ \ hfill 0 & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {cc} & \ frac {1} {2} \\ & 1 \ end {array} \ right] [/ latex]
Использовать обратную замену.Вторая строка матрицы представляет [латекс] y = 1 [/ латекс]. Подставьте обратно [latex] y = 1 [/ latex] в первое уравнение.
[латекс] \ begin {array} {l} x- \ left (1 \ right) = \ frac {1} {2} \ hfill \\ \ text {} x = \ frac {3} {2} \ hfill \ end {array} [/ latex]
Решение — точка [латекс] \ left (\ frac {3} {2}, 1 \ right) [/ latex].
Попробуй
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {массив} {l} 4x + 3y = 11 \ hfill \\ \ text {} \ text {} \ text {} x — 3y = -1 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ влево (2,1 \ вправо) [/ латекс]
В нашем следующем примере мы решим систему двух уравнений с двумя зависимыми переменными.Напомним, что зависимая система имеет бесконечное количество решений, и результатом операций со строками в ее расширенной матрице будет уравнение, такое как [latex] 0 = 0 [/ latex]. Мы также рассмотрим написание общего решения для зависимой системы.
Пример: решение зависимой системы
Решите систему уравнений.
[латекс] \ begin {array} {l} 3x + 4y = 12 \\ 6x + 8y = 24 \ end {array} [/ latex]
Показать решение Выполните строковых операций на расширенной матрице, чтобы попытаться получить строково-эшелонированную форму .[латекс] A = \ left [\ begin {array} {llll} 3 \ hfill & \ hfill & 4 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 12 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] [/ latex]
[латекс] \ begin {array} {l} \ hfill \\ \ begin {array} {l} — \ frac {1} {2} {R} _ {2} + {R} _ {1} = { R} _ {1} \ to \ left [\ begin {array} {llll} 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end { array} | \ begin {array} {ll} \ hfill & 0 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] \ hfill \\ {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {llll} 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \\ 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 24 \ hfill \\ \ hfill & 0 \ hfill \ end {array} \ right] \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Матрица заканчивается всеми нулями в последней строке: [latex] 0y = 0 [/ latex].Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите для [latex] y [/ latex].
[латекс] \ begin {array} {l} 3x + 4y = 12 \ hfill \\ \ text {} 4y = 12 — 3x \ hfill \\ \ text {} y = 3- \ frac {3} {4} x \ hfill \ end {array} [/ latex]
Итак, решение этой системы — [латекс] \ left (x, 3- \ frac {3} {4} x \ right) [/ latex].
Теперь мы перейдем к строковой форме на шаг дальше, чтобы решить систему линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Пример: решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
[латекс] \ begin {массив} {c} \ begin {array} {l} \ hfill \\ \ hfill \\ x-y + z = 8 \ hfill \ end {array} \\ 2x + 3y-z = -2 \\ 3x — 2y — 9z = 9 \ end {array} [/ latex]
Показать решениеСначала мы пишем расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill -1 \\ \ hfill 3 & \ hfill -2 & \ hfill -9 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 8 \\ \ hfill -2 \\ \ hfill 9 \ end {array} \ right] [/ latex]
Затем мы выполняем строковые операции, чтобы получить форму «строка-эшелон».
[латекс] \ begin {array} {rrrrr} \ hfill -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} { rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 3 & \ hfill & \ hfill -2 & \ hfill & \ hfill -9 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill 9 \ end {массив} \ right] & \ hfill & \ hfill & \ hfill & \ hfill -3 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill -15 \ end {array} \ right] \ end {array} [/ latex]
Самый простой способ получить 1 в строке 2 столбца 1 — это поменять местами [латекс] {R} _ {2} [/ latex] и [latex] {R} _ {3} [/ latex].
[латекс] \ text {Interchange} {R} _ {2} \ text {и} {R} _ {3} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill — 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 8 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill & \ hfill -15 \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill & \ hfill -18 \ end {array} \ right] [/ latex]
Затем
[латекс] \ begin {array} {l} \\ \ begin {array} {rrrrr} \ hfill -5 {R} _ {2} + {R} _ {3} = {R} _ {3} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 57 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \\ \ hfill & \ hfill 57 \ end {array} \ right] & \ hfill & \ hfill & \ hfill & \ hfill — \ frac {1} {57} {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \ \ \ hfill & \ hfill 1 \ end {array} \ right] \ end {array} \ end {array} [/ latex]
Последняя матрица представляет собой эквивалентную систему.
[латекс] \ begin {массив} {l} \ text {} x-y + z = 8 \ hfill \\ \ text {} y — 12z = -15 \ hfill \\ \ text {} z = 1 \ hfill \ end {array} [/ latex]
Используя обратную подстановку, мы получаем решение как [latex] \ left (4, -3,1 \ right) [/ latex].
Напомним, что есть три возможных результата для решений линейных систем. В предыдущем примере решение [латекс] \ left (4, -3,1 \ right) [/ latex] представляет точку в трехмерном пространстве. Эта точка представляет собой пересечение трех плоскостей.В следующем примере мы решаем систему, используя операции со строками, и обнаруживаем, что она представляет зависимую систему. Зависимая система в 3-х измерениях может быть представлена двумя идентичными плоскостями, как в 2-х измерениях, где зависимая система представляет две идентичные линии.
Пример: решение 3 x 3 зависимой системы
Решите следующую систему линейных уравнений, используя метод исключения Гаусса.
[латекс] \ begin {array} {r} \ hfill -x — 2y + z = -1 \\ \ hfill 2x + 3y = 2 \\ \ hfill y — 2z = 0 \ end {array} [/ latex]
Показать решениеЗапишите расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill -2 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill 2 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Сначала умножьте строку 1 на [latex] -1 [/ latex], чтобы получить 1 в строке 1, столбце 1. Затем выполните операций со строками , чтобы получить форму эшелона строк.
[латекс] — {R} _ {1} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 & \ hfill & \ hfill 2 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill & \ hfill 0 \ end {array} \ справа] [/ латекс]
[латекс] {R} _ {2} \ leftrightarrow {R} _ {3} \ to \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 \ \ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 \ end {array} \ text {} | \ begin {array} { rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]
[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -1 & \ hfill & \ hfill 2 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
[латекс] {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 & \ hfill \ end { array} | \ begin {array} {rr} \ hfill & \ hfill 2 \\ \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
Последняя матрица представляет следующую систему.
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y — 2z = 0 \ hfill \\ \ text {} 0 = 0 \ hfill \ конец {array} [/ latex]
По тождеству [latex] 0 = 0 [/ latex] мы видим, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение. Решив второе уравнение для [latex] y [/ latex] и подставив его в первое уравнение, мы можем решить для [latex] z [/ latex] через [latex] x [/ latex].
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y = 2z \ hfill \\ \ hfill \\ x + 2 \ left (2z \ справа) -z = 1 \ hfill \\ \ text {} x + 3z = 1 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \ end {array} [/ latex]
Теперь мы подставляем выражение для [latex] z [/ latex] во второе уравнение, чтобы решить для [latex] y [/ latex] через [latex] x [/ latex].
[латекс] \ begin {массив} {l} \ text {} y — 2z = 0 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \\ \ hfill \\ y — 2 \ left (\ frac {1-x} {3} \ right) = 0 \ hfill \\ \ text {} y = \ frac {2 — 2x} {3} \ hfill \ end {array} [/ latex ]
Общее решение — [latex] \ left (x, \ frac {2 — 2x} {3}, \ frac {1-x} {3} \ right) [/ latex].
Общее решение для зависимой системы 3 X 3
Напомним, что когда вы решаете зависимую систему линейных уравнений с двумя переменными с использованием исключения или подстановки, вы можете записать решение [latex] (x, y) [/ latex] через x, потому что существует бесконечно много (x, y) пары, которые будут удовлетворять зависимой системе уравнений, и все они попадают на линию [латекс] (x, mx + b) [/ latex].Теперь, когда вы работаете в трех измерениях, решение будет представлять собой плоскость, поэтому вы должны записать его в общей форме [латекс] (x, m_ {1} x + b_ {1}, m_ {2} x + b_ { 2}) [/ латекс].
Попробуй
Решите систему методом исключения Гаусса.
[латекс] \ begin {array} {c} x + 4y-z = 4 \\ 2x + 5y + 8z = 15 \ x + 3y — 3z = 1 \ end {array} [/ latex]
Показать решение[латекс] \ левый (1,1,1 \ правый) [/ латекс]
Вопросы и ответы
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Как: решить систему уравнений с помощью матриц с помощью калькулятора
- Сохраните расширенную матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right] \ text {,} \ dots [/ latex].
- Используйте в калькуляторе функцию ref (, вызывая каждую матричную переменную по мере необходимости.
Пример: решение систем уравнений с помощью калькулятора
Решите систему уравнений.
[латекс] \ begin {array} {r} \ hfill 5x + 3y + 9z = -1 \\ \ hfill -2x + 3y-z = -2 \\ \ hfill -x — 4y + 5z = 1 \ end { array} [/ latex]
Показать решениеНапишите расширенную матрицу для системы уравнений.
[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 3 & \ hfill 9 \\ \ hfill -2 & \ hfill 3 & \ hfill -1 \\ \ hfill -1 & \ hfill -4 & \ hfill 5 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill -2 \\ \ hfill 1 \ end {array} \ right] [/ latex]
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ left [A \ right] = \ left [\ begin {array} {rrrrrrr} \ hfill 5 & \ hfill & \ hfill 3 & \ hfill & \ hfill 9 & \ hfill & \ hfill -1 \\ \ hfill — 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill -1 & \ hfill & \ hfill -2 \\ \ hfill -1 & \ hfill & \ hfill -4 & \ hfill & \ hfill 5 & \ hfill & \ hfill 1 \ end {массив } \ right] [/ latex]
Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ text {ref} \ left (\ left [A \ right] \ right) [/ латекс]
Оценить.
[латекс] \ begin {array} {l} \ hfill \\ \ left [\ begin {array} {rrrr} \ hfill 1 & \ hfill \ frac {3} {5} & \ hfill \ frac {9} {5 } & \ hfill \ frac {1} {5} \\ \ hfill 0 & \ hfill 1 & \ hfill \ frac {13} {21} & \ hfill — \ frac {4} {7} \\ \ hfill 0 & \ hfill 0 & \ hfill 1 & \ hfill — \ frac {24} {187} \ end {array} \ right] \ to \ begin {array} {l} x + \ frac {3} {5} y + \ frac {9} {5} z = — \ frac {1} {5} \ hfill \\ \ text {} y + \ frac {13} {21} z = — \ frac {4} {7} \ hfill \\ \ text {} z = — \ frac {24} {187} \ hfill \ end {array} \ hfill \ end {array} [/ latex]
При использовании обратной подстановки решение: [latex] \ left (\ frac {61} {187}, — \ frac {92} {187}, — \ frac {24} {187} \ right) [/ latex] .
Приложения систем уравнений
Теперь обратимся к приложениям, для которых используются системы уравнений. В следующем примере мы определяем, сколько денег было инвестировано по двум разным ставкам, учитывая сумму процентов, полученных на обоих счетах.
Пример: применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов.Сколько было вложено по каждой ставке?
Показать решениеУ нас есть система двух уравнений с двумя переменными. Пусть [latex] x = [/ latex] сумма, инвестированная под 10,5% годовых, и [latex] y = [/ latex] сумма, инвестированная под 12% годовых.
[латекс] \ begin {массив} {l} \ text {} x + y = 12 000 \ hfill \\ 0,105x + 0,12y = 1,335 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0.105 & \ hfill 0.12 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 12,000 \\ \ hfill 1,335 \ end {array} \ right] [/ latex]
Умножить строку 1 на [латекс] -0.105 [/ latex] и добавьте результат в строку 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill 0.015 \ end {array} \ text {} | \ text {} \ begin {array} {r } \ hfill 12,000 \\ \ hfill 75 \ end {array} \ right] [/ latex]
Затем,
[латекс] \ begin {array} {l} 0,015y = 75 \ hfill \\ \ text {} y = 5,000 \ hfill \ end {array} [/ latex]
Итак [латекс] 12 000 — 5 000 = 7 000 [/ латекс].
Таким образом, 5000 долларов были инвестированы под 12% годовых, а 7000 долларов — под 10,5%.
Пример: применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Показать решениеУ нас есть система трех уравнений с тремя переменными. Пусть [latex] x [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] y [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] z [/ latex] будет инвестированной суммой. под 9% годовых. Таким образом,
[латекс] \ begin {array} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0.05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 1 & \ hfill 1 \\ \ hfill 0,05 & \ hfill 0,08 & \ hfill 0,09 \\ \ hfill 2 & \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 10,000 \\ \ hfill 770 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \ frac {1} {0.03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill — \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Третья строка сообщает нам [латекс] — \ frac {1} {3} z = -2,000 [/ latex]; таким образом [латекс] z = 6,000 [/ латекс].
Вторая строка сообщает нам [латекс] y + \ frac {4} {3} z = 9000 [/ latex].
Подставляя [латекс] z = 6,000 [/ латекс], получаем
[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]
Первая строка сообщает нам [латекс] x + y + z = 10,000 [/ latex]. Подставив [latex] y = 1,000 [/ latex] и [latex] z = 6,000 [/ latex], мы получим
[latex] \ begin {array} {l} x + 1,000 + 6,000 = 10,000 \ hfill \\ \ text {} x = 3,000 \ text {} \ hfill \ end {array} [/ latex]
Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.
Попробуй
Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
Показать решение150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Матрица
МатрицаПростой матричный калькулятор
Это примет матрицу размером до 5×6 в уменьшенную форму эшелона строк на Исключение Гаусса. Каждая операция элементарной строки будут напечатаны. Учитывая матрицу размером меньше 5×6, поместите ее в верхнем левом углу и оставьте лишнее строки и столбцы пустые. Были включены некоторые примерные значения. Нажмите «Очистить», чтобы от них избавиться.A — это матрица 2×2, а B — матрица 2×1.Этот калькулятор попытается найти AB и решить AX = B путем вычисления A -1 B, когда это возможно. В противном случае он сообщит, согласован ли он. Он также дает det, rank и собственные значения.
Несколько комментариев о том, что происходит за кулисами: Исключение Гаусса использует то же алгоритм, который вы использовали бы вручную: работа оставлена вправо, и выполните элементарные операции со строками, чтобы каждый столбец иметь правильную форму. Это помещает матрицу в эшелон форма. Затем вернитесь и удалите лишние записи, чтобы получить это в сокращенной форме.
Для второй части обратное вычисляется стандартная формула с использованием определителей A -1 = (1 / det (A)) присоединенный (A) Это отлично работает в нашем случае (2×2), хотя это невозможно. для матриц большего размера. Тест на согласованность основан на идее, что для разрешимости AX = B нам нужно, чтобы B находилась в пространство столбцов A. Итак, достаточно проверить, что размерность Col (A) = Col (A | B). Это то, что ранги A и (A | B) совпадают. Разряды вычисляется с использованием несовершеннолетних. Собственные значения получаются путем решения характеристическое уравнение det (tI-A) = t 2 -trace (A) t + det (A) = 0 Поскольку он квадратичный, это легко сделать явно.
По сути, это «демонстрация», которую я собрал для учебные цели. Это должно быть хорошо для простых примеров но иногда он может давать неправильные ответы из-за до ошибки округления . Обычно он пытается предупредить вас, когда такие ошибки вероятны. Существует множество серьезных программ для обработки матриц. там. Некоторые из них бесплатны (октава или scilab), а некоторые нет (матлаб).
— Дону Арапура
Обращение матрицы с использованием исключения Гаусса-Джордана
М.Борн
В этом разделе мы увидим, как работает метод исключения Гаусса-Жордана, на примерах.
Вы можете повторно загружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел. Вы также можете выбрать матрицу другого размера (внизу страницы).
(Если вам сначала нужна дополнительная информация, вернитесь к «Введение в матрицы»).
Выберите размер матрицы, который вас интересует, и нажмите кнопку.
Матрица A:
Пример, сгенерированный случайным образом, показан ниже.
Пользователи телефона
ПРИМЕЧАНИЕ: Если вы разговариваете по телефону, вы можете прокрутить любые матрицы шириной на этой странице вправо или влево, чтобы увидеть все выражение.
Пример (3 × 3)
Найдите матрицу, обратную матрице A , используя метод исключения Гаусса-Жордана.
| A = | 13 | 3 | 5 | ||
| 6 | 2 | 7 | |||
| 11 | 8 | 9 |
Наша процедура
Запишем матрицу A слева и матрицу идентичности I справа, разделенные пунктирной линией, как показано ниже.Результат называется расширенной матрицей .
Мы включили номера строк, чтобы было понятнее.
| 1 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Затем мы выполняем несколько операций со строками для двух матриц, и наша цель — получить единичную матрицу на слева , например:
| ? | ? | ? | Ряд [1] | |
| ? | ? | ? | Ряд [2] | |
| ? | ? | ? | Ряд [3] |
(Технически мы сокращаем матрицу A до сокращенной формы эшелона строк , также называемой канонической формой строки ).
Результирующая матрица справа будет обратной матрицей для A .
Наша процедура операций со строками выглядит следующим образом:
- Получим «1» в верхнем левом углу, разделив первую строку
- Тогда мы получим «0» в оставшейся части первого столбца
- Тогда нам нужно получить «1» во второй строке, втором столбце
- Затем мы делаем все остальные записи во втором столбце «0».
Продолжаем так до тех пор, пока слева не останется единичная матрица.
Давайте теперь продолжим и найдем обратное.
Решение
Начнем с:
| 1 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [1]
Разделите строку [1] на 13 (чтобы получить «1» в нужной позиции):
Это дает нам:
| 1 | 0.2308 | 0,3846 | |
| 6 | 2 | 7 | |
| 11 | 8 | 9 |
| 0,0769 | 0 | 0 | Ряд [1] | |
| 0 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [2]
Ряд [2] — 6 × Ряд [1] (чтобы получить 0 в желаемой позиции):
6 — 6 × 1 = 0
2 — 6 × 0.2308 = 0,6154
7 — 6 × 0,3846 = 4,6923
0 — 6 × 0,0769 = -0,4615
1 — 6 × 0 = 1
0 — 6 × 0 = 0
Это дает нам новую строку [2]:
| 1 | 0,2308 | 0,3846 | |
| 0 | 0,6154 | 4.6923 | |
| 11 | 8 | 9 |
| 0,0769 | 0 | 0 | Ряд [1] | |
| -0.4615 | 1 | 0 | Ряд [2] | |
| 0 | 0 | 1 | Ряд [3] |
Новый ряд [3]
Ряд [3] — 11 × Ряд [1] (чтобы получить 0 в желаемой позиции):
11 — 11 × 1 = 0
8 — 11 × 0,2308 = 5,4615
9 — 11 × 0,3846 = 4,7692
0 — 11 × 0,0769 = -0,8462
0 — 11 × 0 = 0
1 — 11 × 0 = 1
Это дает нам новую строку [3]:
| 1 | 0.2308 | 0,3846 | |
| 0 | 0,6154 | 4.6923 | |
| 0 | 5,4615 | 4,7692 |
| 0,0769 | 0 | 0 | Ряд [1] | |
| -0,4615 | 1 | 0 | Ряд [2] | |
| -0,8462 | 0 | 1 | Ряд [3] |
Новый ряд [2]
Разделить строку [2] на 0.6154 (чтобы получить «1» в желаемой позиции):
Это дает нам:
| 1 | 0,2308 | 0,3846 | |
| 0 | 1 | 7,625 | |
| 0 | 5,4615 | 4,7692 |
| 0,0769 | 0 | 0 | Ряд [1] | |
| -0,75 | 1.625 | 0 | Ряд [2] | |
| -0,8462 | 0 | 1 | Ряд [3] |
Новый ряд [1]
Ряд [1] — 0,2308 × Ряд [2] (чтобы получить 0 в желаемой позиции):
1 — 0,2308 × 0 = 1
0,2308 — 0,2308 × 1 = 0
0,3846 — 0,2308 × 7,625 = -1,375
0,0769 — 0,2308 × -0,75 = 0,25
0 — 0,2308 × 1,625 = -0,375
0 — 0,2308 × 0 = 0
Это дает нам новую строку [1]:
| 1 | 0 | -1.375 | |
| 0 | 1 | 7,625 | |
| 0 | 5,4615 | 4,7692 |
| 0,25 | -0,375 | 0 | Ряд [1] | |
| -0,75 | 1,625 | 0 | Ряд [2] | |
| -0,8462 | 0 | 1 | Ряд [3] |
Новый ряд [3]
Ряд [3] — 5.4615 × Ряд [2] (чтобы дать нам 0 в желаемой позиции):
0 — 5,4615 × 0 = 0
5,4615 — 5,4615 × 1 = 0
4,7692 — 5,4615 × 7,625 = -36,875
-0,8462 — 5,4615 × -0,75 = 3,25
0 — 5,4615 × 1,625 = -8,875
1 — 5,4615 × 0 = 1
Это дает нам новую строку [3]:
| 1 | 0 | -1,375 | |
| 0 | 1 | 7,625 | |
| 0 | 0 | -36.875 |
| 0,25 | -0,375 | 0 | Ряд [1] | |
| -0,75 | 1,625 | 0 | Ряд [2] | |
| 3,25 | -8,875 | 1 | Ряд [3] |
Новый ряд [3]
Разделите строку [3] на -36,875 (чтобы получить «1» в желаемой позиции):
Это дает нам:
| 1 | 0 | -1.375 | |
| 0 | 1 | 7,625 | |
| 0 | 0 | 1 |
| 0,25 | -0,375 | 0 | Ряд [1] | |
| -0,75 | 1,625 | 0 | Ряд [2] | |
| -0,0881 | 0,2407 | -0,0271 | Ряд [3] |
Новый ряд [1]
Ряд [1] — -1.375 × Ряд [3] (чтобы дать нам 0 в желаемой позиции):
1 — -1,375 × 0 = 1
0 — -1,375 × 0 = 0
-1,375 — -1,375 × 1 = 0
0,25 — -1,375 × -0,0881 = 0,128
-0,375 — -1,375 × 0,2407 = -0,0441
0 — -1,375 × -0,0271 = -0,0373
Это дает нам новую строку [1]:
| 0.1288 | -0,0441 | -0,0373 | Ряд [1] | |
| -0,75 | 1,625 | 0 | Ряд [2] | |
| -0.0881 | 0,2407 | -0,0271 | Ряд [3] |
Новый ряд [2]
Ряд [2] — 7,625 × Ряд [3] (чтобы получить 0 в желаемой позиции):
0 — 7,625 × 0 = 0
1 — 7,625 × 0 = 1
7,625 — 7,625 × 1 = 0
-0,75 — 7,625 × -0,0881 = -0,078
1,625 — 7,625 × 0,2407 = -0,2102
0 — 7,625 × — 0,0271 = 0,2068
Это дает нам новую строку [2]:
| 0.1288 | -0.0441 | -0,0373 | Ряд [1] | |
| -0,078 | -0,2102 | 0,2068 | Ряд [2] | |
| -0,0881 | 0,2407 | -0,0271 | Ряд [3] |
Мы достигли нашей цели по созданию матрицы идентичности слева. Таким образом, мы можем заключить, что инверсия матрицы A является правой частью расширенной матрицы:
| A -1 = | 0.1288 | -0,0441 | -0,0373 | ||
| -0,078 | -0,2102 | 0,2068 | |||
| -0,0881 | 0,2407 | -0,0271 |
Примечания
- Приведенное выше объяснение показывает все шаги. Человек обычно может пойти несколькими путями. Кроме того, иногда в правильной позиции уже есть «1» или «0», и в этих случаях нам не нужно ничего делать для этого шага.
- Всегда записывайте, что вы делаете на каждом этапе — очень легко заблудиться!
- Я показал результаты с точностью до 4 знаков после запятой, но с максимальной точностью использовалась повсюду. Имейте в виду, что небольшие ошибки округления будут накапливаться во всей задаче. Всегда используйте полную точность калькулятора! (Используйте всю память вашего калькулятора.)
- Очень иногда возникают странные результаты из-за внутреннего представления чисел компьютером.То есть он может хранить «1» как 0,999999999872.
Смотрите еще?
Вы можете вернуться к началу страницы и выбрать другой пример.
Исключение Гаусса
Тип 2. Умножьте строку на ненулевую константу.
Тип 3. Добавьте одну строку, кратную одной, в другую.
Цель этих операций — преобразовать — или уменьшить — исходную расширенную матрицу в одну из форм, где A ′ — верхний треугольник ( a ij ′ = 0 для i> j ), любые нулевые строки появляются внизу матрицы, и первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке; такая матрица, как говорят, имеет форму эшелон .Решения системы представлены более простой расширенной матрицей [ A ′ | b ′], можно найти путем осмотра нижних рядов и обратной подстановки в более высокие ряды. Поскольку элементарные операции со строками не меняют решений системы, векторы x , которые удовлетворяют более простой системе A ′ x = b ′, как раз те, которые удовлетворяют исходной системе, A x = b .
Пример 3 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица, которая представляет эту систему:
Первая цель — получить нули под первой записью в первом столбце , что означает исключение первой переменной x из второго и третьего уравнений.Для этого выполняются следующие операции со строками:
Вторая цель — получить ноль под второй записью во втором столбце, что означает исключение второй переменной y из третьего уравнения. Один из способов добиться этого — добавить -1/5 второй строки к третьей строке. Однако, чтобы избежать дробей, есть еще один вариант: сначала поменять местами второй и третий ряды. Замена двух строк просто меняет местами уравнения, что явно не изменит решения системы:
Теперь прибавьте −5 раз вторую строку к третьей строке:
Поскольку матрица коэффициентов преобразована в эшелонированную форму, «прямая» часть исключения Гаусса завершена.Теперь остается использовать третью строку для оценки третьего неизвестного, затем выполнить обратную подстановку во вторую строку для оценки второго неизвестного и, наконец, выполнить обратную замену в первой строке для оценки первого неизвестного.
Третья строка окончательной матрицы переводится в 10 z = 10, что дает z = 1. Обратная подстановка этого значения во вторую строку, которая представляет уравнение y — 3 z = — 1, дает y = 2.Обратная подстановка обоих этих значений в первую строку, которая представляет уравнение x — 2 y + z = 0, дает x = 3. Таким образом, решение этой системы: ( x, y, z ) = (3, 2, 1).
Пример 4 : Решите следующую систему с помощью исключения Гаусса:
Для этой системы расширенная матрица (вертикальная линия опущена) —
Сначала умножьте строку 1 на 1/2:
Теперь добавление -1 первой строки ко второй строке дает нули под первой записью в первом столбце:
Перестановка второй и третьей строк дает желаемую матрицу коэффициентов верхней треугольной формы:
В третьей строке теперь указано z = 4.Обратная подстановка этого значения во вторую строку дает y = 1, а обратная подстановка обоих этих значений в первую строку дает x = −2. Следовательно, решение этой системы: ( x, y, z ) = (−2, 1, 4).
Исключение Гаусса-Джордана . Исключение Гаусса осуществляется путем выполнения элементарных операций со строками для получения нулей ниже диагонали матрицы коэффициентов, чтобы привести ее к эшелонированной форме. (Напомним, что матрица A ′ = [ a ij ′] имеет эшелонированную форму, когда a ij ′ = 0 для i> j , любые нулевые строки появляются в нижней части матрицы , и первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке.) Как только это будет сделано, проверка нижней строки (строк) и обратная подстановка в верхние строки определяют значения неизвестных.
Однако можно сократить (или полностью исключить) вычисления, связанные с обратной подстановкой, выполнив дополнительные операции со строками для преобразования матрицы из эшелонированной формы в сокращенную форму эшелона. Матрица находится в форме сокращенного эшелона, когда, помимо того, что она находится в форме эшелона, каждый столбец, содержащий ненулевую запись (обычно равную 1), имеет нули не только под этой записью, но и над этой записью.Грубо говоря, исключение Гаусса работает сверху вниз, чтобы создать матрицу в форме эшелона, тогда как исключение Гаусса-Жордана продолжается с того места, где остановилось Гаусса, а затем работает снизу вверх для создания матрицы в форме уменьшенного эшелона. Техника будет проиллюстрирована на следующем примере.
Пример 5 : Известно, что высота, y , подброшенного в воздух объекта задается квадратичной функцией от t (время) в форме y = at 2 + BT + c .Если объект находится на высоте y = 23/4 в момент времени t = 1/2, при y = 7 в момент времени t = 1 и при y = 2 при t = 2 , определите коэффициенты a, b и c .
Так как т = 1/2 дает y = 23/4
, а два других условия, y ( t = 1) = 7 и y ( t = 2) = 2, дают следующие уравнения для a, b и c :
Следовательно, цель — решить систему
Расширенная матрица для этой системы сокращается следующим образом:
На этом прямая часть исключения Гаусса завершена, поскольку матрица коэффициентов приведена к эшелонированной форме.Однако, чтобы проиллюстрировать исключение Гаусса-Жордана, выполняются следующие дополнительные элементарные операции со строками:
Эта окончательная матрица сразу дает решение: a = −5, b = 10 и c = 2.
Пример 6 : Решите следующую систему с помощью исключения Гаусса:
Расширенная матрица для этой системы —
Кратные значения первой строки добавляются к другим строкам, чтобы получить нули под первой записью в первом столбце:
Затем −1 раз вторая строка добавляется к третьей строке:
В третьей строке теперь указано 0 x + 0 y + 0 z = 1, уравнение, которому не могут соответствовать никакие значения x, y и z .Процесс останавливается: у этой системы нет решений.
Предыдущий пример показывает, как метод исключения по Гауссу обнаруживает противоречивую систему. Небольшое изменение этой системы (например, изменение постоянного члена «7» в третьем уравнении на «6») проиллюстрирует систему с бесконечным числом решений.
Пример 7 : Решите следующую систему с помощью исключения Гаусса:
Те же операции, которые применяются к расширенной матрице системы в примере 6, применяются к расширенной матрице для данной системы:
Здесь третья строка переводится в 0 x + 0 y + 0 z = 0, уравнение, которому удовлетворяют любые x, y и z .Поскольку здесь нет ограничений на неизвестные, на неизвестные не три условия, а только два (представленные двумя ненулевыми строками в окончательной расширенной матрице). Поскольку имеется 3 неизвестных, но только 2 константы, 3–2 = 1 неизвестных, скажем, z , произвольно; это называется свободной переменной . Пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = −6) дает
Обратная подстановка z = t и y = 6 + 5 t в первую строку ( x + y — 3 z = 4) определяет x :
Следовательно, каждое решение системы имеет вид
, где т — любое действительное число.Существует бесконечно много решений, поскольку каждое действительное значение т дает свое конкретное решение. Например, выбор t = 1 дает ( x, y, z ) = (−4, 11, 1), а t = 3 дает ( x, y, z ) = (4, — 9, −3) и т. Д. Геометрически эта система представляет три плоскости в R 3 , которые пересекаются по линии, и (*) является параметрическим уравнением для этой линии.
Пример 7 дает иллюстрацию системы с бесконечным множеством решений, как возникает этот случай и как записывается решение.Каждая линейная система, имеющая бесконечно много решений, должна содержать хотя бы один произвольный параметр (свободная переменная). После того как расширенная матрица была приведена к эшелонированной форме, количество свободных переменных равно общему количеству неизвестных минус количество ненулевых строк:
Это согласуется с теоремой B выше, которая утверждает, что линейная система с меньшим количеством уравнений, чем неизвестных, если она согласована, имеет бесконечно много решений. Условие «меньше уравнений, чем неизвестных» означает, что количество строк в матрице коэффициентов меньше количества неизвестных.Следовательно, приведенное выше уравнение в рамке подразумевает, что должна быть хотя бы одна свободная переменная. Поскольку такая переменная по определению может принимать бесконечно много значений, система будет иметь бесконечно много решений.
Пример 8 : Найдите все решения для системы
Во-первых, обратите внимание, что есть четыре неизвестных, но только три уравнения. Следовательно, если система непротиворечива, гарантировано, что у нее будет бесконечно много решений, а это состояние характеризуется по крайней мере одним параметром в общем решении.После того, как соответствующая расширенная матрица построена, исключение Гаусса дает
Тот факт, что в эшелонированной форме расширенной матрицы остаются только две ненулевые строки, означает, что 4-2 = 2 переменных свободны:
Следовательно, выбрав y и z в качестве свободных переменных, пусть y = t 1 и z = t 2 . Во второй строке сокращенной расширенной матрицы следует
, а первая строка дает
Таким образом, решения системы имеют вид
, где т 1 т 2 могут принимать любые реальные значения.
Пример 9 : Пусть b = ( b 1 , b 2 , b 3 ) T и пусть A будет матрицей
Для каких значений b 1 , b 2 и b 3 будет ли система A x = b согласованной?
Расширенная матрица для системы A x = b читает
, который гауссовский элиминатин сокращает следующим образом:
Нижняя строка теперь означает, что b 1 + 3 b 2 + b 3 должен быть равен нулю, чтобы эта система была согласованной.Следовательно, в данной системе есть растворины (фактически бесконечно много) только для тех векторов-столбцов b = ( b 1 , b 2 , b 3 ) T , для которых b 1 + 3 b 2 + b 3 = 0,
Пример 10 : Решите следующую систему (сравните с Примером 12):
Такая система, как эта, где постоянный член в правой части каждого уравнения равен 0, называется гомогенной системой .В матричной форме он читается как A x = 0 . Поскольку каждая гомогенная система согласована — поскольку x = 0 всегда является решением — однородная система имеет либо ровно одно решение ( тривиальное решение , x = 0 ), либо бесконечно много. Сокращение строки матрицы коэффициентов для этой системы уже было выполнено в примере 12. Нет необходимости явно дополнять матрицу коэффициентов столбцом b = 0 , поскольку никакая элементарная операция со строкой не может повлиять на эти нули.То есть, если A ‘является эшелонированной формой A , то операции элементарной строки преобразуют [ A | 0 ] в [ A ′ | 0 ]. По результатам Примера 12,
Поскольку последняя строка снова подразумевает, что z можно принять как свободную переменную, пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = 0) дает
и обратная подстановка z = t и y = 5 t в первую строку ( x + y — 3 z = 0) определяет x :
Следовательно, каждое решение этой системы имеет вид ( x, y, z ) = (−2 t , 5 t, t ), где t — любое действительное число.Растворителей бесконечно много, так как каждое действительное значение т дает уникальное частное решение.
Обратите внимание на разницу между набором решений для системы в Примере 12 и здесь. Хотя у обоих была одна и та же матрица коэффициентов A , система в примере 12 была неоднородной ( A x = b , где b ≠ 0 ), а здесь — соответствующая однородная система, A x = 0 .Помещая свои решения рядом,
общее решение для Ax = 0 : ( x, y, z ) = (−2 t , 5 t , t )
общее решение для Ax = b : ( x, y, z ) = (−2 t , 5 t , t ) + (−2, 6, 0)
иллюстрирует важный факт:Теорема C . Общие решения для согласованной неоднородной лиенарной системы, A x = b , равны общему решению соответствующей однородной системы, A x = 0 , плюс частному решению неоднородная система.То есть, если x = x h представляет собой общее решение A x = 0 , то x = x h + x представляет общее решение A x + b , где x — любое конкретное решение (согласованной) неоднородной системы A x = b .
[Техническое примечание: теорема C, которая касается линейной системы , имеет аналог в теории линейных дифференциальных уравнений .Пусть L — линейный дифференциальный оператор; то общее решение разрешимого неоднородного линейного дифференциального уравнения, L (y) = d (где d ≢ 0), равно общему решению соответствующего однородного уравнения, L (y) = 0 плюс частное решение неоднородного уравнения. То есть, если y = y h повторно отображает общее решение L (y) = 0, то y = y h + y представляет собой общее решение L (y ) = d , где y — любое частное решение (решаемого) неоднородного линейного уравнения L (y) = d .]
Пример 11 : Определить все решения системы
Запишите расширенную матрицу и выполните следующую последовательность операций:
Поскольку в этой конечной (эшелонированной) матрице остаются только 2 ненулевые строки, есть только 2 ограничения, и, следовательно, 4-2 = 2 из неизвестных — скажем, y и z — являются свободными переменными. Пусть y = t 1 и z = t 2 .Обратная подстановка y = t 1 и z = t 2 во второй строке ( x — 3 y + 4 z = 1) дает
Наконец, обратная замена x = 1 + 3 t 1 — 4 2 , y = t 1 и z = t 2 в первую строка (2 w — 2 x + y = −1) определяет w :
Следовательно, каждое решение этой системы имеет вид
, где т 1 и т 2 — любые действительные числа.Другой способ написать решение:
, где т 1 , т 2 ∈ R .
Пример 12 : Определите общее решение
, которая является однородной системой, соответствующей неоднородной в примере 11 выше.
Поскольку решение неоднородной системы в примере 11 равно
Теорема C означает, что решение соответствующей однородной системы (где t 1 , t 2 ∈ R ) получается из (*), просто отбрасывая конкретное решение, x = (1 / 2,1,0,0) неоднородной системы.
Пример 13 : Докажите теорему A: независимо от ее размера или количества неизвестных, содержащихся в ее уравнениях, линейная система не будет иметь решений, ровно одно решение или бесконечно много решений.
Проба . Пусть данная линейная система записана в матричной форме A x = b . Теорема действительно сводится к следующему: если A x = b имеет более одного решения, то на самом деле их бесконечно много.Чтобы установить это, пусть x 1 и x 2 будут двумя разными решениями A x = b . Теперь будет показано, что для любого реального значения t вектор x 1 + t ( x 1 — x 2 ) также является решением A x = b ; Поскольку t может принимать бесконечно много различных значений, из этого следует желаемый вывод.Поскольку A x 1 = b и A x 2 ,
Следовательно, x 1 + t ( x 1 — x 2 ) действительно является решением A x = b , и теорема доказана.
3.3: Решение систем с исключением Гаусса-Джордана
Цели обучения
- Запишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Решите систему линейных уравнений с помощью матриц и графического калькулятора.
- Решайте финансовые приложения с помощью матриц и графического калькулятора.
Необходимые навыки
Перед тем, как начать, пройдите предварительный тест.
Введите в калькулятор следующие матрицы и затем выполните указанные операции. Если операция не может быть проведена, укажите причину.
\ (A = \ begin {bmatrix} 5 & 1 & -2 \\ 2 & 6 & 7 \\ 4 & 1 & −5 \ end {bmatrix} \), \ (B = \ begin {bmatrix} 3 & -7 \\ 0 & 1 \\ 2 & −8 \ end {bmatrix} \), \ (C = \ begin {bmatrix} 9 & 4 \\ 6 & -5 \\ 7 & −1 \ end {bmatrix} \)
а. \ (А \ cdot B \)
г. \ (B \ cdot A \)
г. \ (4B-2C \)
г. \ (А + С \)
- Нажмите здесь, чтобы проверить свой ответ
а. {th} \) века, но он по-прежнему считается одним из самых плодовитых математиков в истории.Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Рисунок \ (\ PageIndex {1} \): немецкий математик Карл Фридрих Гаусс (1777–1855).Ранее в этой главе мы исследовали методы решения систем уравнений. В этом разделе мы изучим другую технику решения систем, на этот раз с использованием матриц.
Расширенные матрицы
Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей .
Например, рассмотрим следующую систему уравнений \ (2 × 2 \).
\ [\ begin {align *} 3x + 4y & = 7 \\ 4x-2y & = 5 \ end {align *} \]
Мы можем записать эту систему в виде расширенной матрицы:
\ (\ left [\ begin {array} {cc | c} 3 & 4 & 7 \\ 4 & -2 & 5 \ end {array} \ right] \)
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .
\ (\ begin {bmatrix} 3 & 4 \\ 4 & −2 \ end {bmatrix} \)
Система уравнений три на три , например
\ [\ begin {align *} 3x-y-z & = 0 \\ x + y & = 5 \\ 2x-3z & = 2 \ end {align *} \]
имеет матрицу коэффициентов
\ (\ begin {bmatrix} 3 & −1 & −1 \\ 1 & 1 & 0 \\ 2 & 0 & −3 \ end {bmatrix} \)
и представлена расширенной матрицей
\ (\ left [\ begin {array} {ccc | c} 3 & −1 & −1 & 0 \\ 1 & 1 & 0 & 5 \\ 2 & 0 & −3 & 2 \ end {array} \ right] \)
Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: \ (x \) — члены идут в первый столбец, \ (y \) — термины во втором столбце, и \ (z \) — термины в третьем столбце.Очень важно, чтобы каждое уравнение было записано в стандартной форме \ (ax + by + cz = d \), чтобы переменные совпадали. Когда в уравнении отсутствует член переменной, коэффициент равен \ (0 \).
Как: для данной системы уравнений написать расширенную матрицу
- Запишите коэффициенты членов \ (x \) как числа в первом столбце.
- Запишите коэффициенты членов \ (y \) в виде чисел во втором столбце.
- Если есть \ (z \) — члены, запишите коэффициенты как числа в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Пример \ (\ PageIndex {1} \): написание расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
\ [\ begin {align *} x + 2y-z & = 3 \\ 2x-y + 2z & = 6 \\ x-3y + 3z & = 4 \ end {align *} \]
Решение
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
\ (\ left [\ begin {array} {ccc | c} 1 & 2 & −1 & 3 \\ 2 & −1 & 2 & 6 \\ 1 & −3 & 3 & 4 \ end {array} \ right] \)
Упражнение \ (\ PageIndex {1} \)
Запишите расширенную матрицу данной системы уравнений.
\ [\ begin {align *} 4x-3y & = 11 \\ 3x + 2y & = 4 \ end {align *} \]
- Ответ
\ (\ left [\ begin {array} {cc | c} 4 & −3 & 11 \\ 3 & 2 & 4 \ end {array} \ right] \)
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Пример \ (\ PageIndex {2} \): Написание системы уравнений из расширенной матричной формы
Найдите систему уравнений из расширенной матрицы.
\ (\ left [\ begin {array} {ccc | c} 1 & −3 & −5 & -2 \\ 2 & −5 & −4 & 5 \\ — 3 & 5 & 4 & 6 \ end {array} \ right] \)
Решение
Когда столбцы представляют переменные \ (x \), \ (y \) и \ (z \),
\ [\ left [\ begin {array} {ccc | c} 1 & -3 & -5 & -2 \\ 2 & -5 & -4 & 5 \\ — 3 & 5 & 4 & 6 \ end {array} \ right] \ rightarrow \ begin {align *} x-3y-5z & = -2 \\ 2x-5y-4z & = 5 \\ -3x + 5y + 4z & = 6 \ end {align *} \]
Упражнение \ (\ PageIndex {2} \)
Напишите систему уравнений из расширенной матрицы.
\ (\ left [\ begin {array} {ccc | c} 1 & -1 & 1 & 5 \\ 2 & -1 & 3 & 1 \\ 0 & 1 & 1 & -9 \ end {array} \ right] \)
- Ответ
\ (\ begin {align *} x-y + z & = 5 \\ 2x-y + 3z & = 1 \\ y + z & = -9 \ end {align *} \)
Уменьшенная форма рядка-эшелон
Чтобы решить систему уравнений, мы хотим преобразовать ее матрицу в сокращенную форму строки , в которой единицы по главной диагонали от верхнего левого угла до нижнего правого угла, а нули в каждое положение выше и ниже главной диагонали, как показано.
Уменьшенная форма строки-эшелона \ (\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)
Следующие расширенные матрицы представлены в сокращенной форме строки-эшелона.
\ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)
Следующие расширенные матрицы не являются сокращенными строками.
\ (\ left [\ begin {array} {cc | c} 2 & 4 & -6 \\ 4 & 0 & 7 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 0 & 2 & 3 & 3 \\ 1 & 5 & 0 & 2 \\ 0 & 0 & 1 & 0 \ end {array} \ right] \)
Пример \ (\ PageIndex {3} \): матрицы в сокращенной форме строки-эшелон
Запишите систему уравнений из каждой из матриц в приведенной строчно-эшелонированной форме сверху. В чем преимущество этой формы?
а. \ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \)
г.\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)
Решение
а. \ (\ begin {align *} x = -2 \\ y = 5 \ end {align *} \)
г. \ (\ begin {align *} x = 4 \\ y = 3 \\ z = 2 \ end {align *} \)
Преимущество сокращенной формы строки-эшелон состоит в том, что решение системы уравнений приводится в правом столбце.
УСТРАНЕНИЕ ПО ГАУСС-ИОРДАНИИ
Метод исключения Гаусса-Жордана относится к стратегии, используемой для получения уменьшенной строковой формы матрицы.Цель состоит в том, чтобы записать матрицу \ (A \) с числом \ (1 \) в качестве записи вниз по главной диагонали и иметь все нули сверху и снизу.
\ (A = \ begin {bmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33} \ end {bmatrix} \ xrightarrow {После \ space Gauss-Jordan \ space elimination} A = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)
Мы можем выполнить операций со строками над матрицей, например сложение, умножение на константу и перестановку строк, чтобы создать сокращенную форму строки-эшелон.Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ.
Решение систем уравнений с исключением Гаусса-Жордана
В рамках этого курса мы продемонстрируем, как найти сокращенную форму строки-эшелон в графическом калькуляторе.
Как: решить систему уравнений с помощью матриц с помощью калькулятора
- Сохранить расширенную матрицу как матричную переменную \ ([A], [B], [C] ,… \)
Нажмите 2 и MATRIX. На экране отобразится меню матрицы. Дважды нажмите кнопку со стрелкой вправо, чтобы выбрать меню ПРАВКА. В меню EDIT используйте стрелку вниз для перемещения курсора, чтобы выбрать желаемое имя матрицы из меню, и нажмите ENTER. Появится экран ввода матрицы.
Введите размеры общего размера матрицы в виде строк \ (\ times \) столбцов. Введите количество строк, нажмите ENTER, введите количество столбцов и снова нажмите ENTER.Форма матрицы настраивается на экране, чтобы отобразить требуемое количество строк и столбцов. Убедитесь, что форма соответствует желаемой матрице; в противном случае вернитесь в верхний ряд и отрегулируйте размеры. Если матрица слишком велика для экрана, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы увидеть оставшиеся строки и столбцы.
Введите элементы матрицы, нажимайте ENTER после каждого. Курсор прокручивает матрицу, перемещаясь по каждой строке слева направо, а затем вниз к следующей строке.Использование клавиш со стрелками для перемещения курсора вместо нажатия ENTER может привести к тому, что значение не будет сохранено в памяти калькулятора.
Нажмите 2 и QUIT, чтобы завершить процесс сохранения и вернуться на главный экран.
- Используйте функцию rref (в калькуляторе, чтобы найти сокращенную форму строки-эшелона матрицы.
На главном экране нажмите 2 nd MATRIX.Используйте стрелку вправо один раз, чтобы перейти в меню МАТЕМАТИКА.
Прокрутите вниз (или вверх) до rref (, стараясь не выбрать ref (, и нажмите ENTER.
Снова нажмите 2 и MATRIX и используйте стрелку вниз (при необходимости), чтобы выбрать имя матрицы, и нажмите ENTER.
Нажмите ENTER, чтобы завершить операцию.
- Если существует сокращенная форма строки-эшелона матрицы, калькулятор отобразит ее на главном экране. ×
Пример \ (\ PageIndex {4} \): решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
\ [\ begin {align *} 6x + 4y + 3z & = -6 \\ x + 2y + z & = \ dfrac {1} {3} \\ -12x-10y-7z & = 11 \ end {align *} \ ]
Решение
Напишите расширенную матрицу для системы уравнений.
\ (\ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ — 12 & -10 & -7 & 11 \ end {array} \ right] \)
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).
\ ([A] = \ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ — 12 & -10 & -7 & 11 \ end {array} \ right] \)
Используйте функцию rref ( в калькуляторе, вызывая матричную переменную \ ([A] \).
rref ([A])
Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.
Оценить
\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & — \ dfrac {2} {3} \\ 0 & 1 & 0 & \ dfrac {5} {2} \\ 0 & 0 & 1 & — 4 \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = — \ dfrac {2} {3} \\ y + 0z & = \ dfrac {5} {2 } \\ z & = -4 \ end {align *}} \ end {array} \]
Таким образом, решение, которое легко найти в правом столбце приведенной строковой формы матрицы, будет \ (\ left (- \ dfrac {2} {3}, \ dfrac {5} {2}, −4 \ справа) \).
Упражнение \ (\ PageIndex {3} \)
Решите систему уравнений.
\ [\ begin {align *} 4x-7y + 2z & = -5 \\ -x + 3y-8z & = -10 \\ -5x-4y + 6z & = 19 \ end {align *} \]
- Ответ
Напишите расширенную матрицу для системы уравнений.
\ (\ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).
\ ([A] = \ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)
Используйте функцию rref ( в калькуляторе, вызывая матричную переменную \ ([A] \).
rref ([A])
Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.
Оценить
\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \ dfrac {3} {2} \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = -2 \\ y + 0z & = 0 \\ z & = \ dfrac {3} {2} \ end {align *}} \ end {array} \]
Таким образом, решение, которое можно легко прочитать из правого столбца приведенной строковой формы матрицы, будет \ (\ left (-2, 0, \ dfrac {3} {2} \ right) \).
Пример \ (\ PageIndex {5} \): применение матриц \ (2 × 2 \) к финансам
Кэролайн инвестирует в общей сложности \ (12 000 долларов) в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил \ (1335 долларов). Сколько было вложено по каждой ставке?
Решение
У нас есть система двух уравнений с двумя переменными. Пусть \ (x = \) сумма, инвестированная под 10,5% годовых, а \ (y = \) сумма, инвестированная под 12%.
\ [\ begin {align *} x + y & = 12,000 \\ 0,105x + 0,12y & = 1,335 \ end {align *} \]
В качестве матрицы имеем
\ (\ left [\ begin {array} {cc | c} 1 & 1 & 12,000 \\ 0.105 & 0.12 & 1335 \ end {array} \ right] \)
Введите эту матрицу как матричную переменную \ ([A] \). Используйте rref (функция , вызывающая матричную переменную \ ([A] \).
rref ([A])
\ (\ left [\ begin {array} {cc | c} 1 & 0 & 7000 \\ 0 & 1 & 5000 \ end {array} \ right] \)
Таким образом, \ ($ 7000 \) было инвестировано по ставке 10.5% годовых и \ (5000 долларов \) под 12% годовых.
Пример \ (\ PageIndex {6} \): применение матриц \ (3 × 3 \) к финансам
Ava инвестирует в общей сложности \ (10 000 долларов США) в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%. Годовой процент, полученный по трем инвестициям в прошлом году, составил \ (770 долларов). Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Решение
У нас есть система трех уравнений с тремя переменными.Пусть \ (x \) будет суммой, инвестированной под 5% годовых, пусть \ (y \) будет суммой, инвестированной под 8%, и пусть \ (z \) будет суммой, инвестированной под 9%. Таким образом,
\ [\ begin {align *} x + y + z & = 10,000 \\ 0,05x + 0,08y + 0,09z & = 770 \\ 2x-z & = 0 \ end {align *} \]
В качестве матрицы имеем
\ (\ left [\ begin {array} {ccc | c} 1 & 1 & 1 & 10,000 \\ 0,05 & 0,08 & 0,09 & 770 \\ 2 & 0 & -1 & 0 \ end {array} \ right] \)
Введите эту матрицу как матричную переменную \ ([A] \).Используйте rref (функция , вызывающая матричную переменную \ ([A] \).
rref ([A])
\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 3000 \\ 0 & 1 & 0 & 1000 \\ 0 & 0 & 1 & 6000 \ end {array} \ right] \)
Ответ: \ (3000 долларов \) вложены под 5%, \ (1000 долларов \) вложены под 8%, и \ (6000 долларов \) инвестированы под 9%.
Упражнение \ (\ PageIndex {4} \)
Небольшая обувная компания взяла ссуду в размере \ (1 500 000 долларов) на расширение своих запасов.Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла \ (130 500 долларов США). Используйте матрицы, чтобы найти сумму займа по каждой ставке.
- Ответ
\ (150 000 долларов \) под 7%, \ (750 000 долларов \) под 8%, \ (600 000 долларов \) под 10%
СМИ
Получите доступ к этим онлайн-ресурсам, чтобы получить дополнительные инструкции и попрактиковаться в решении систем линейных уравнений с использованием исключения Гаусса.
Ключевые понятия
- Расширенная матрица — это матрица, которая содержит коэффициенты и константы системы уравнений. См. Пример \ (\ PageIndex {1} \).
- Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. Пример \ (\ PageIndex {2} \).
- Мы можем использовать метод исключения Гаусса-Жордана для решения системы уравнений. См. Пример \ (\ PageIndex {4} \).
- Многие реальные проблемы можно решить с помощью расширенных матриц.См. Пример \ (\ PageIndex {5} \) и Пример \ (\ PageIndex {6} \).
Авторы и авторство
.




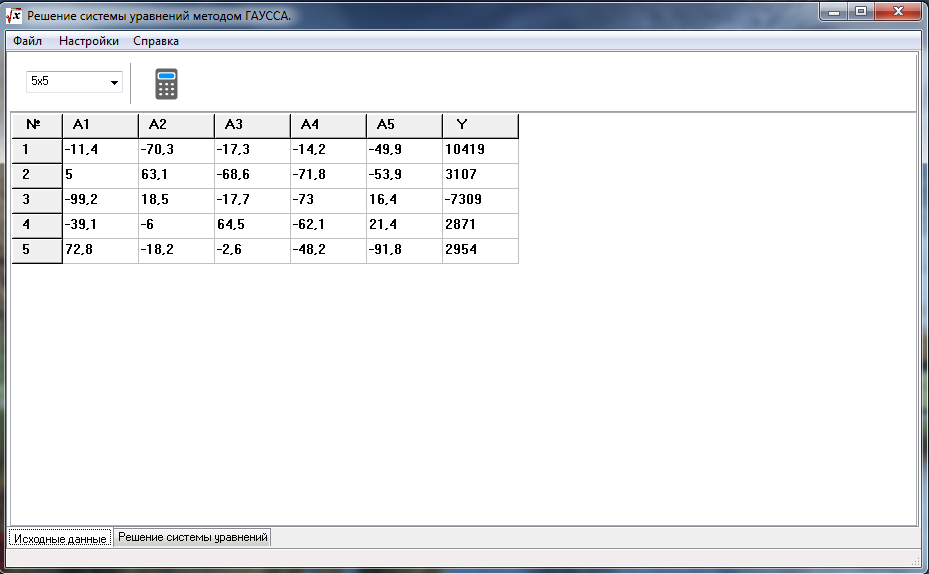 Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.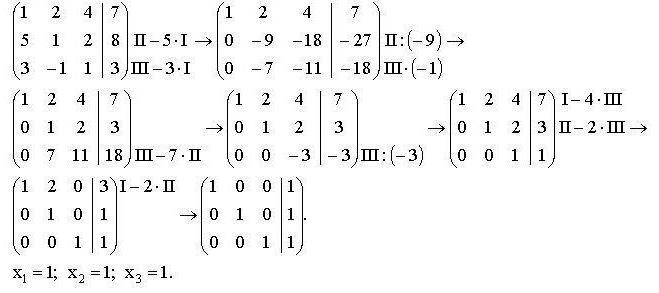 Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения..png) В последнем столбце новой матрицы получаем корни уравнения.
В последнем столбце новой матрицы получаем корни уравнения.