Калькулятор Смешанных Чисел — Mathcracker.Com
Решатели Алгебра
Инструкции: Используйте этот калькулятор для вычисления смешанных дробей. Укажите смешанную дробь в поле ниже.
Смешанная дробь, которую вы хотите преобразовать (Например: 2 3/2)
Как использовать этот калькулятор смешанных чисел
Калькулятор смешанных дробей поможет вам вычислить любое алгебраическое выражение со смешанными числами и дробями, которые вы предоставите. Например, вы можете ввести смешанное число ‘2 3/4’, и калькулятор преобразует его в обычную дробь и уменьшит ее.
Например, вы можете ввести смешанное число ‘2 3/4’, и калькулятор преобразует его в обычную дробь и уменьшит ее.
После того, как вы ввели смешанное число/ дробное выражение, вам нужно нажать «Вычислить», и все шаги будут показаны для вас.
Что такое смешанная дробь
A смешанная фракция
это просто целое число, которое идет вместе с дробью. Формат такой: сначала идет целое число, затем пробел, а затем дробь. Например, следующая дробь является смешанной:\[2\,\,\frac{2}{3}\]
В данном случае целое число — «2», а дробь — «2/3». Наличие этих двух элементов вместе в данном случае означает, что мы их складываем. Таким образом, когда мы пишем смешанная дробь, мы имеем в виду следующее:
Наличие этих двух элементов вместе в данном случае означает, что мы их складываем. Таким образом, когда мы пишем смешанная дробь, мы имеем в виду следующее:
\[2\,\,\frac{2}{3} = 2 + \frac{2}{3}\]
Как вычислить смешанные числа
Основная идея заключается в простом сокращении смешанного числа до суммы дробей. То есть необходимо разделить целую и дробную части смешанного числа и оперировать ими как обычными дробями.
Каковы этапы вычисления смешанных чисел
- Шаг 1: Четко определите, какое смешанное число мы хотим проанализировать
- Шаг 2: Извлечение целой части и дробной части смешанного числа
- Шаг 3: Преобразуйте целую часть в дробь, а затем просто оперируйте ими как дробями
Зачем иметь дело со смешанными дробями?
Использование смешанных дробей (также известных как смешанные числа) — это своего рода унаследованная нотация. На самом деле она не имеет заметного значения и не играет никакой важной роли. Но знать, как ими оперировать, полезно, поскольку они время от времени появляются в формулах.
На самом деле она не имеет заметного значения и не играет никакой важной роли. Но знать, как ими оперировать, полезно, поскольку они время от времени появляются в формулах.
Пример: вычисление смешанного числа
Запишите в виде дроби: \(1\,\,\frac{1}{3}\).
Решение:
Нам нужно упростить следующую заданную смешанную дробь: \(\displaystyle 1 \,\, \frac{ 1}{ 3}\).
Получается следующий расчет:
\( \displaystyle 1 \,\, \frac{ 1}{ 3}\)
This is the given mixed fraction
\( = \,\,\)
\(\displaystyle 1\,\,\frac{ 1}{ 3}\)
By definition, the mixed fraction can be written this way
\( = \,\,\)
\(\displaystyle 1+\frac1{ 3}\)
Using \(3\) as the common denominator
\( = \,\,\)
\(\displaystyle \frac{ 1 \times 3 + 1}{ 3}\)
This is a regular fraction obtained after expanding the denominator
\( = \,\,\)
\(\displaystyle \frac{ 4}{ 3}\)
чем завершается расчет.
Пример: еще одно вычисление смешанных дробей
Вычислите следующее смешанное число \(3 + 2\,\,\frac{2}{3}\).
Решение:
Сначала нужно упростить следующую заданную смешанную дробь: \(\displaystyle 2 \,\, \frac{ 2}{ 3}\).
Получается следующий расчет:
\( \displaystyle 2 \,\, \frac{ 2}{ 3}\)
This is the given mixed fraction
\( = \,\,\)
\(\displaystyle 2\,\,\frac{ 2}{ 3}\)
By definition, the mixed fraction can be written this way
\( = \,\,\)
\(\displaystyle 2+\frac2{ 3}\)
Using \(3\) as the common denominator
\( = \,\,\)
\(\displaystyle \frac{ 2 \times 3 + 2}{ 3}\)
This is a regular fraction obtained after expanding the denominator
\( = \,\,\)
\(\displaystyle \frac{ 8}{ 3}\)
Теперь нам нужно вычислить и упростить следующее выражение: \(\displaystyle 3+\frac{8}{3}\).
Получается следующий расчет:
\( \displaystyle 3+\frac{8}{3}\)
Amplifying in order to get the common denominator 3
\( = \,\,\)
\(\displaystyle 3\cdot\frac{3}{3}+\frac{8}{3}\)
Finding a common denominator: 3
\( = \,\,\)
\(\displaystyle \frac{3\cdot 3+8}{3}\)
Expanding each term: \(3 \times 3+8 = 9+8\)
\( = \,\,\)
\(\displaystyle \frac{9+8}{3}\)
Adding up the terms in the numerator
\( = \,\,\)
\(\displaystyle \frac{17}{3}\)
чем завершается расчет.
Другие дробные вычисления
Смешанные числа реже используются в математических обозначениях, поскольку более практичным является их выражение в виде обычных дробей. В определенной степени преобразование дробей в смешанные числа почти аналогично перевод из дробной в десятичную систему , поскольку вы определяете целую часть и десятичную часть.
Смешанные дроби по сути соответствуют дробному исчислению, в котором «пустое место» между целым числом и дробью можно заменить знаком «+», так что получается простое сложение дробей.
Преобразование смешанной дроби в неправильную дробь: онлайн калькулятор
Преобразовать
{$ main. types[data.type] $}
types[data.type] $}
{$ error $}!
Результат расчёта
Неправильная дробь = {$ result[0] $}/{$ result[1] $}
Смешанная дробь = {$ result[0] $} {$ result[1] $}/{$ result[2] $}
Смешанная дробь = целому числу {$ result[0] $}
Дробь — это рациональное число, которое представляет собой одну или несколько частей единицы. Наряду с натуральными числами дроби широко используются в бытовых расчетах и реальной жизни.
История возникновения
Нужда в дробных числах возникла у людей еще до начала цивилизации. Разделение мяса и шкур убитых животных между участниками охоты иногда приводило к серьезным проблемам, если количество добычи не совпадало с количеством охотников или не было кратным ему. Проблемы с разделением ресурсов привели первобытного человека к понятию дробного числа.
С зарождением цивилизации людям потребовалось вычислять все больше и больше параметров при строительстве жилья и организации сельского хозяйства. Необходимость измерять длины, объемы и площади, которые далеко не всегда можно выразить целым числом, привела к активному использованию дробей в жизни древних людей. Впервые дроби начали использоваться в Древнем Вавилоне и Древнем Египте, причем египтяне применяли дроби исключительно с единицей в числителе. Позднее знание о дробях распространилось по всему миру и появилось на Руси только в VIII веке.
Необходимость измерять длины, объемы и площади, которые далеко не всегда можно выразить целым числом, привела к активному использованию дробей в жизни древних людей. Впервые дроби начали использоваться в Древнем Вавилоне и Древнем Египте, причем египтяне применяли дроби исключительно с единицей в числителе. Позднее знание о дробях распространилось по всему миру и появилось на Руси только в VIII веке.
Проблема измерений всегда остро стояла перед человечеством. Если для счета предметов хватает однозначных натуральных чисел, то для измерения параметров их недостаточно. Небольшие ошибки в инженерных расчетах, оперирующих натуральными числами, нередко приводили к разрушению возведенных конструкций. Именно тогда в зодчестве начали активно использовать десятичные дроби для более точного выражения величин. Однако проблема точности вычислений до сих пор актуальна, так как точность можно повышать до бесконечности.
Определение термина
Дробь — это число, состоящее из нескольких долей единицы. Записываются такие числа в виде обыкновенной или десятичной дроби. Обыкновенная дробь имеет общий вид m/n, где n ≠ 0. Рациональные числа имеют две формы записи: через горизонтальную черту, которая называется «винкулум» или через наклонную — «солидус». В нашей статье мы будем использовать солидус для удобства записи.
Записываются такие числа в виде обыкновенной или десятичной дроби. Обыкновенная дробь имеет общий вид m/n, где n ≠ 0. Рациональные числа имеют две формы записи: через горизонтальную черту, которая называется «винкулум» или через наклонную — «солидус». В нашей статье мы будем использовать солидус для удобства записи.
Если m < n, то такое число является правильной дробью (например, 3/5, 8/10 или 35/100). Если m > n, то такая дробь носит название неправильной (к примеру, 3/2, 8/3 или 54/21). Любое целое число легко записать в форме дроби, и в общем виде это выглядит как m/1. Если же величина записывается в виде комбинации целого числа и правильной дроби, то она носит названия смешанного дробного числа. Такие числа можно преобразовывать из одного вида в другой.
Перевод дробей из одного типа в другой
При решении примеров по арифметике иногда возникает потребность преобразовать неправильную дробь в смешанную или наоборот. Это легко сделать, если использовать следующие алгоритмы.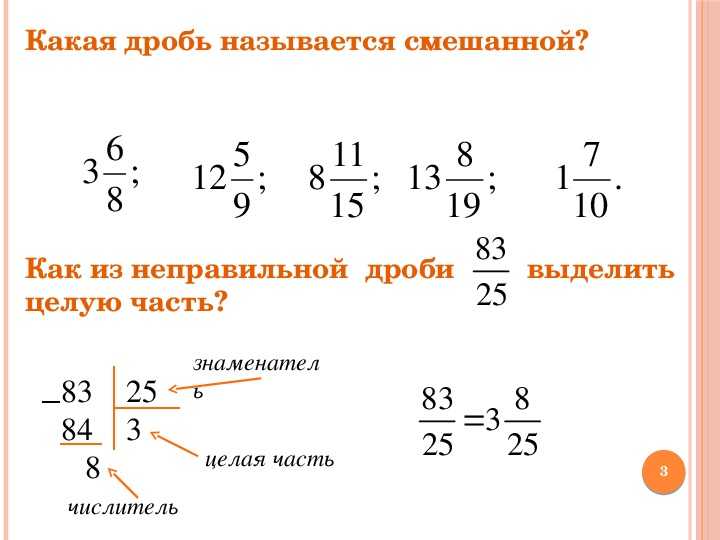 Для преобразования «смешанная — неправильная» нужно:
Для преобразования «смешанная — неправильная» нужно:
- целую часть смешанного числа умножить на знаменатель дроби, после чего сложить результат с числителем;
- знаменатель оставить без изменения.
Преобразуем смешанную дробь 4 и 2/3 в неправильную. Умножим целое 4 на знаменатель 3 и результат 12 добавим к числителю. В итоге получаем 14. Знаменатель оставляем без изменений и записываем неправильную дробь 14/3.
Для трансформации «неправильная — смешанная» используется следующий алгоритм:
- числитель делим на знаменатель и полученное число принимаем за целую часть смешанной дроби;
- остаток от деления записываем в числитель обыкновенной дроби, а знаменатель оставляем тем же.
На примере это выглядит так. Для дроби 22/7 разделим 22 на 7, получим 3 и 1 в остатке. После это занесем остаток в числитель правильной дроби и запишем 3 и 1/7.
Если для решения заданий по арифметике требуется перевести целое число в дробь, то в знаменатель просто пишут единицу, а затем приводят дроби к общему знаменателю.
Небольшие дроби легко вручную переводить из одного вида в другой. Однако если требуется выразить в виде неправильной дроби выражение вида 135 и 784/623, то проще воспользоваться нашим онлайн-калькулятором. Инструмент мгновенно переводит смешанные дроби в неправильные и наоборот. Для этого в меню программы следует выбрать направление преобразования и ввести нужное число. Достаточно одного клика мышкой для получения мгновенного результата. Например, при помощи калькулятора легко подсчитать, что 135 и 784/623 тождественно равно неправильной дроби 84889/623.
Заключение
Дробные числа — неотъемлемая часть жизни. Люди пользуются дробями даже в таких простых ситуациях, как разрезание пиццы или подбор пропорций для приготовления коктейля. Умение преобразовывать числа из одной формы в другую несомненно пригодится даже в простых бытовых расчетах, не говоря уже о школьных задачах и профессиональных вычислениях.
Калькулятор дроби смешанных чисел — Онлайн-калькулятор дроби смешанных чисел
Калькулятор дроби смешанных чисел – бесплатный онлайн-инструмент, который преобразует смешанную дробь в неправильную дробь.
Что такое калькулятор дроби смешанного числа?
Калькулятор смешанных дробей — это бесплатный онлайн-инструмент, который преобразует смешанную дробь в неправильную дробь. Этот калькулятор поможет вам преобразовать смешанные дроби в неправильные дроби за несколько секунд.
Калькулятор дроби смешанного числа
Как пользоваться калькулятором дроби смешанного числа?
Выполните следующие шаги и попробуйте использовать калькулятор.
- Шаг 1: Введите смешанную дробь в три соответствующих поля ввода.
- Шаг 2: Нажмите «Вычислить» , чтобы получить форму неправильной дроби введенной смешанной дроби.
- Шаг 3: Нажмите «Сброс» , чтобы ввести новый набор дробей.
Как преобразовать смешанную дробь в неправильную дробь?
Смешанная фракция представляет собой смесь целой и правильной фракции.
Чтобы преобразовать смешанную дробь в неправильную, нужно умножить знаменатель на целую часть числа, а затем прибавить к произведению числитель.
Результат будет новым числителем, тогда как знаменатель останется прежним.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запишитесь на бесплатный пробный урок
Решенные примеры на Калькуляторе смешанных дробейПример 1:
Преобразование \(4\dfrac{3}{5}\) в неправильную дробь.
Решение:
Новый числитель = (Знаменатель × Целое число) + Числитель
Числитель = (5 × 4) + 3 = 20 + 3 = 23
Знаменатель = 5
Следовательно, неправильная дробь = 23/5
Пример 2:
Преобразуйте \(8\dfrac{7}{9}\) в неправильную дробь.
Решение:
Новый числитель = (Знаменатель × целое число) + Числитель
Числитель = (9 × 8) + 7 = 72 + 7 = 79
Знаменатель = 9
Следовательно, неправильная дробь 79/9
Пример 3:
Преобразование \(6\dfrac{7}{11}\) в неправильную дробь.
Решение:
Новый числитель = (Знаменатель × целое число) + Числитель
Числитель = (11 × 6) + 7 = 66 + 7 = 73
Знаменатель = 11
73/11
Аналогично,
Теперь воспользуйтесь калькулятором и преобразуйте следующие смешанные дроби в неправильные дроби:
\(4\dfrac{2}{5}\)
\(2\dfrac{3}{7}\)
\(5\dfrac{1}{6}\)
- Типы фракций
- Неправильные дроби
- Числитель
- Знаменатель
Калькулятор / конвертер неправильных дробей в смешанные числа
Онлайн-калькулятор неправильных дробей в смешанные числа специально разработан для быстрого преобразования неправильных дробей в смешанные числа. Не только это, вы также можете решить правильные дроби, используя калькулятор дроби для смешанного числа.
Давайте прочитаем статью ниже, чтобы понять, как преобразовать дробь в смешанное число.
Сосредоточьтесь!
Что такое неправильная дробь?
В контексте математики:
«Особая дробь, у которой числитель больше знаменателя, называется неправильной дробью»
Например: неправильные дроби:
$$ \frac{3}{2} \hspace{0,25in} \frac{9}{7} \hspace{0.25in} \frac{65}{34} $$
Все вышеперечисленные дроби считаются неправильными и могут быть преобразованы в форму смешанных чисел с помощью нашего лучшего калькулятора неправильных дробей в калькуляторе смешанных чисел.
Шаги, необходимые для преобразования неправильных дробей в смешанные числа:
Давайте вспомним шаги, которые необходимо выполнить, чтобы выполнить преобразование неправильных дробей в смешанные числа:
- Во-первых, разделите числитель на знаменатель
- После этого запишите целое число отдельно, то есть частное
- Наконец, запишите остаток как новый числитель и возьмите тот же знаменатель, что и в исходной дроби
Правила для упрощения дробей:
Всякий раз, когда вы хотите упростить дроби, вам нужно запомнить несколько правил, которые перечислены ниже: дробь

Как преобразовать неправильные дроби в смешанные числа?
Здесь мы будем решать пару примеров для выполнения преобразований между неправильными дробями и смешанными числами. Давайте двигаться вперед!
Пример № 01:
Как преобразовать неправильные дроби в смешанные числа, приведенные ниже:
$$ \frac{8}{3} \hspace{0,25in} и \frac{9}{2} $$
Решение:
Заменим неправильные дроби на смешанные числа следующим образом:
$$ \frac{8}{3} $$
Шаг № 01:
Когда мы разделим эту дробь, мы получим остаток от 2 .
Шаг № 02:
Частное представляет целое число, которое в нашем случае также равно 2 .
Шаг № 03:
Теперь следующим шагом будет запись остатка в числителе. Кроме того, выберите первый в истории знаменатель, равный 3 , и считайте его таким, какой он есть здесь. Наконец, умножьте дробь на целое число, которое является частным. Весь процесс показан ниже:
Наконец, умножьте дробь на целое число, которое является частным. Весь процесс показан ниже:
$$ Частное \frac{Остаток}{Знаменатель} $$
$$ 2\frac{2}{3} $$
Требуемая смешанная числовая форма данной дроби.
Теперь имеем:
$$ \frac{9}{2} $$
Шаг № 01:
Разделив полученную дробь, получим остаток 1
Шаг № 02:
Второй шаг — найти целое число, которое есть не что иное, как частное 4 .
Шаг № 03:
Наконец, возьмите остаток в числитель, знаменатель останется без изменений и снова будет 2 . После этого умножьте целое число на дробь, как показано ниже:
$$ Частное \frac{Остаток}{Знаменатель} $$
$$ 2\frac{1}{4} $$
Вы также можете проверить результаты с помощью неправильной дроби к калькулятору смешанных чисел.
Как работает калькулятор преобразования неправильных дробей в смешанные числа?
Получите мгновенные и наилучшие упрощенные результаты, используя наш бесплатный калькулятор в один клик. Позвольте нам помочь вам правильно о его использовании!
Позвольте нам помочь вам правильно о его использовании!
Ввод:
- Запишите числитель в верхнем специальном поле
- Также напишите знаменатель в нижнем обозначенном поле
- Теперь нажмите кнопку расчета
Вывод:
Калькулятор бесплатного преобразования неправильных дробей в смешанные числа определяет:
- Смешанная числовая форма заданной неправильной дроби
- Все этапы вычислений
Часто задаваемые вопросы:
Является ли \(1\frac{0}{2}\) неправильной дробью?
Упрощенная форма данного уравнения: \(\frac{2}{2}\), что равно 1. Таким образом, это не неправильная дробь.
Какова форма неправильной дроби смешанного числа \(2\frac{1}{2}\)?
Эквивалентная неправильная дробь данного смешанного числа задается как:
$$ \frac{5}{2} $$
Как преобразовать смешанные дроби в неправильные дроби?
Вы можете определить соответствующую неправильную дробь смешанного числа с помощью бесплатного онлайн калькулятора смешанных чисел для неправильных дробей.
