Калькулятор решить матричное уравнение: Умножение матриц онлайн

Решить {l}{-6y+11x=-36}{-4y+7x=-24} | Microsoft Math Solver

x=0

y=6

Викторина

Simultaneous Equation

5 задач, подобных этой:

\left. \begin{array} { l } { — 6 y + 11 x = — 36 } \\ { — 4 y + 7 x = — 24 } \end{array} \right.

Подобные задачи из результатов поиска в Интернете

Поделиться

Скопировано в буфер обмена

-6y+11x=-36,-4y+7x=-24

Чтобы решить два уравнения методом подстановки, сначала решите одно из уравнений для одной из переменных. Затем подставьте результат для этой переменной в другое уравнение.

-6y+11x=-36

Выберите один из уравнений и решите его для y, изолируя y в левой части знака равенства.

-6y=-11x-36

Вычтите 11x из обеих частей уравнения.

y=-\frac{1}{6}\left(-11x-36\right)

Разделите обе части на -6.

y=\frac{11}{6}x+6

Умножьте -\frac{1}{6} на -11x-36.

-4\left(\frac{11}{6}x+6\right)+7x=-24

Подставьте \frac{11x}{6}+6 вместо y в другом уравнении -4y+7x=-24.

-\frac{22}{3}x-24+7x=-24

Умножьте -4 на \frac{11x}{6}+6.

-\frac{1}{3}x-24=-24

Прибавьте -\frac{22x}{3} к 7x.

-\frac{1}{3}x=0

Прибавьте 24 к обеим частям уравнения.

x=0

Умножьте обе части на -3.

y=6

Подставьте 0 вместо x в y=\frac{11}{6}x+6. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для y.

y=6,x=0

Система решена.

-6y+11x=-36,-4y+7x=-24

Приведите уравнения к стандартному виду, а затем решите систему уравнений с помощью матриц.

\left(\begin{matrix}-6&11\\-4&7\end{matrix}\right)\left(\begin{matrix}y\\x\end{matrix}\right)=\left(\begin{matrix}-36\\-24\end{matrix}\right)

Запишите уравнения в матричном виде.

inverse(\left(\begin{matrix}-6&11\\-4&7\end{matrix}\right))\left(\begin{matrix}-6&11\\-4&7\end{matrix}\right)\left(\begin{matrix}y\\x\end{matrix}\right)=inverse(\left(\begin{matrix}-6&11\\-4&7\end{matrix}\right))\left(\begin{matrix}-36\\-24\end{matrix}\right)

Левое произведение с матрицей, обратной \left(\begin{matrix}-6&11\\-4&7\end{matrix}\right).

\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}y\\x\end{matrix}\right)=inverse(\left(\begin{matrix}-6&11\\-4&7\end{matrix}\right))\left(\begin{matrix}-36\\-24\end{matrix}\right)

Произведение матрицы на обратную ей является единичной матрицей.

\left(\begin{matrix}y\\x\end{matrix}\right)=inverse(\left(\begin{matrix}-6&11\\-4&7\end{matrix}\right))\left(\begin{matrix}-36\\-24\end{matrix}\right)

Перемножение матриц слева от знака равенства.

\left(\begin{matrix}y\\x\end{matrix}\right)=\left(\begin{matrix}\frac{7}{-6\times 7-11\left(-4\right)}&-\frac{11}{-6\times 7-11\left(-4\right)}\\-\frac{-4}{-6\times 7-11\left(-4\right)}&\frac{-6}{-6\times 7-11\left(-4\right)}\end{matrix}\right)\left(\begin{matrix}-36\\-24\end{matrix}\right)

Для матрицы \left(\begin{matrix}a&b\\c&d\end{matrix}\right) с размерностью 2\times 2 обратная матрица имеет вид \left(\begin{matrix}\frac{d}{ad-bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc}\end{matrix}\right), поэтому матричное уравнение можно переписать в виде задачи умножения матриц.

\left(\begin{matrix}y\\x\end{matrix}\right)=\left(\begin{matrix}\frac{7}{2}&-\frac{11}{2}\\2&-3\end{matrix}\right)\left(\begin{matrix}-36\\-24\end{matrix}\right)

Выполните арифметические операции.

\left(\begin{matrix}y\\x\end{matrix}\right)=\left(\begin{matrix}\frac{7}{2}\left(-36\right)-\frac{11}{2}\left(-24\right)\\2\left(-36\right)-3\left(-24\right)\end{matrix}\right)

Перемножьте матрицы.

\left(\begin{matrix}y\\x\end{matrix}\right)=\left(\begin{matrix}6\\0\end{matrix}\right)

Выполните арифметические операции.

y=6,x=0

Извлеките элементы матрицы y и x.

-6y+11x=-36,-4y+7x=-24

Для решения методом исключения коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сократилась при вычитании одного уравнения из другого.

-4\left(-6\right)y-4\times 11x=-4\left(-36\right),-6\left(-4\right)y-6\times 7x=-6\left(-24\right)

Чтобы сделать -6y и -4y равными, умножьте все члены в обеих частях первого уравнения на -4 и все члены в обеих частях второго уравнения на -6. {2}+2 x-3}

Онлайн калькулятор с неизвестным числом. Решение матричных уравнений

Инструкция

Примечание: π записывается как pi; корень квадратный как sqrt().

Шаг 1. Введите заданный пример, состоящий из дробей.

Шаг 2. Нажмите кнопку “Решить”.

Шаг 3. Получите подробный результат.

Чтобы калькулятор посчитал дроби правильно, вводите дробь через знак: “/”. Например: . Калькулятор посчитает уравнение и даже покажет на графике, почему получился такой результат.

Что такое уравнение с дробями

Уравнение с дробями – это уравнение, в котором коэффициенты являются дробными числами. Линейные уравнения с дробями решается по стандартной схеме: неизвестные переносятся в одну сторону, а известные – в другую.

Рассмотрим на примере:

Дроби с неизвестными переносятся влево, а остальные дроби – вправо. Когда переносятся числа за знак равенства, тогда у чисел знак меняется на противоположный:

Теперь нужно выполнить только действия обеих частей равенства:

Получилось обыкновенное линейное уравнение.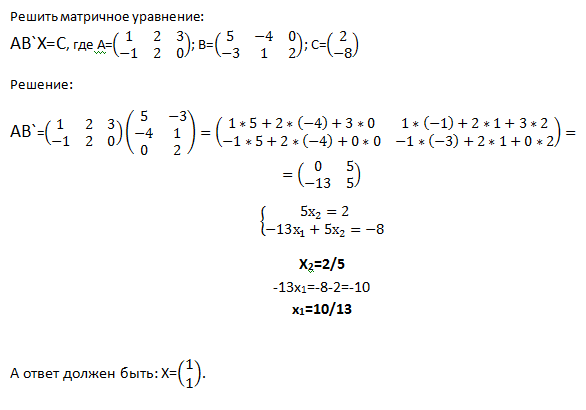

Теперь нужно поделить левую и правую части на коэффициент при переменной.

Решить уравнение с дробями онлайн обновлено: 7 октября, 2018 автором: Научные Статьи.Ру

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант

.

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:

a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0.

Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).

Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц. где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B . Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат .

Рекомендуется также ознакомиться с основными действиями над матрицами .

Пример №1 . Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1

Обратная матрица A -1:
Найдем обратную матрицу B -1 .

Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1

Ответ:

Пример №2 . Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.

Пример №3 . Задание. Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:

Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1

Ответ: >

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Степенные или показательные уравнения называют уравнения, в которых переменные находятся в степенях, а основанием является число. Например:

Решение показательного уравнения сводится к 2 довольно простым действиям:

1. Нужно проверить одинаковые ли основания у уравнения справа и слева. {nm}:\]

Прибавляем к исходному уравнению:

Вынесем за скобки \

Выразим \

Поскольку степени одинаковые, отбрасываем их:

Ответ: \

Где можно решить показательное уравнение онлайн решателем?

Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы.